the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Water vapour retrieval using the Precision Solar Spectroradiometer
Panagiotis-Ioannis Raptis
Stelios Kazadzis
Julian Gröbner
Natalia Kouremeti
Lionel Doppler
Ralf Becker
Constantinos Helmis
The Precision Solar Spectroradiometer (PSR) is a new spectroradiometer developed at Physikalisch-Meteorologisches Observatorium Davos – World Radiation Center (PMOD–WRC), Davos, measuring direct solar irradiance at the surface, in the 300–1020 nm spectral range and at high temporal resolution. The purpose of this work is to investigate the instrument's potential to retrieve integrated water vapour (IWV) using its spectral measurements. Two different approaches were developed in order to retrieve IWV: the first one uses single-channel and wavelength measurements, following a theoretical water vapour high absorption wavelength, and the second one uses direct sun irradiance integrated at a certain spectral region. IWV results have been validated using a 2-year data set, consisting of an AERONET sun-photometer Cimel CE318, a Global Positioning System (GPS), a microwave radiometer profiler (MWP) and radiosonde retrievals recorded at Meteorological Observatorium Lindenberg, Germany. For the monochromatic approach, better agreement with retrievals from other methods and instruments was achieved using the 946 nm channel, while for the spectral approach the 934–948 nm window was used. Compared to other instruments' retrievals, the monochromatic approach leads to mean relative differences up to 3.3 % with the coefficient of determination (R2) being in the region of 0.87–0.95, while for the spectral approach mean relative differences up to 0.7 % were recorded with R2 in the region of 0.96–0.98. Uncertainties related to IWV retrieval methods were investigated and found to be less than 0.28 cm for both methods. Absolute IWV deviations of differences between PSR and other instruments were determined the range of 0.08–0.30 cm and only in extreme cases would reach up to 15 %.
- Article
(2886 KB) - Full-text XML
- BibTeX
- EndNote
Water vapour is a very important component of the thermodynamic state of the atmosphere (Hartman et al., 2013), being a greenhouse gas with relatively high concentrations. The quantity of water in the vapour state depends on temperature. So, from a climate change perspective, it is considered to be a feedback agent (Soden and Held, 2006). Also, it is an important component of the hydrological cycle and estimations of it are used in meteorological forecast models (e.g. Hong et al., 2015; Bock et al., 2016). Finally, a robust estimation is needed to study microphysical processes that lead to the formation of clouds and determine their composition (water droplets or ice crystals) as well as the statistical shape and size of these components (Reichard et al., 1996; Yu et al., 2014).
IWV in the vertical atmospheric column is a very common variable in meteorological and climatological studies. It is defined as the height that water would stand at if completely condensed and collected in a vessel of the same unit cross section (American Meteorological Society, 2015). Water vapour in the atmosphere has been monitored through radiosondes and provided through measurements of vertical profiles of humidity. These measurements are limited to relatively infrequent (radiosonde) launches; thus, during the last decades methods have been developed to retrieve IWV from other devices:
-
Continuous monitoring of IWV is established through Global Positioning System (GPS) satellite observations (Bevis et al., 1992), which can be used to retrieve IWV anywhere in the globe at relatively high temporal frequencies. The theoretical basis for these measurement is that delays in the signals emitted by GPS satellites are caused by the amount of water in the atmosphere, and through proper calibration, such delays could be expressed as a function of the IWV. Thus, as long as there are ground-based GPS receivers, after the appropriate post-processing of the received signals, IWV can be retrieved.
-
Microwave radiometer profilers (MWPs) measure the emitted microwave radiation of the atmosphere and retrieve water vapour vertical profiles and then IWV, providing continuous data at very high frequencies under all weather conditions (e.g. Güldner and Spänkuch, 2001; Güldner, 2013). These instruments provide very high accuracy but are not very common.
-
Measurements from sun photometers (e.g. CIMEL, PREDE-POM, MFR) have also been used to calculate water vapour transmittance and thus estimate IWV. Filter radiometer recordings in the spectral region around water vapour absorption bands in the near-infrared region are used to calculate this quantity (Halthore et al., 1997; Campanelli et al., 2018; Nyeki et al., 2005). The World Meteorological Organization (WMO) recommends the use of spectral windows centred around 719, 817 and 946 nm, though the most frequently used is the 946 nm bandpass, which Ingold et al. (2000) showed provides the most robust results.
Global networks of deployed sun-photometric devices are capable of providing IWV time series. The AErosol RObotic NETwork (AERONET) retrieves IWV at more than 500 stations around the globe since the 1990s (Holben et al., 1998, https://aeronet.gsfc.nasa.gov/) using the Cimel instrument. Other sun photometers such as precision filter radiometers (PFRs) (Nyeki et al., 2005) have also been used by the Global Atmosphere Watch (GAW) WMO programme to monitor IWV. Furthermore, the SKYNET radiometer network (details at http://atmos2.cr.chiba-u.jp/skynet/) also retrieves IWV using Prede-POM sun photometers at many stations (Campanelli et al., 2012, 2014). Finally, national networks of sun photometers that are installed and operating in some countries also provide integrated water vapour (IWV) retrievals; e.g. China Aerosol Remote Sensing NETwork (CARSNET) uses the 936 nm channel to provide IWV (Che et al., 2016).
Schneider et al. (2010) provided a very detailed comparison of different instrument retrievals over a 4-year data set recorded at Izaña Atmospheric Observatory, Tenerife, Spain. They found that MWP is the most precise technique and is independent of weather conditions, while sun-photometric retrievals were limited by clouds and biased by dry/humid atmospheres, and GPS-retrieved IWV showed deviations at lower IWV values. Deviations were also recorded when compared to radiosondes, which was explained by the difference in air masses and timescales among radiosondes and other IWV retrievals.
Technological advances in recent years have made feasible the manufacturing of operational spectral sun photometers for environmental monitoring. The Precision Solar Spectroradiometer (PSR), designed and manufactured at PMOD–WRC, Davos, Switzerland, is one of the most accurate instruments of this class (Gröbner et al., 2012). In this study we developed tools to retrieve IWV using PSR recordings, adopting two different approaches, one using single wavelength channels and another retrieving from a wider spectral region, the latter being impossible with filter radiometers. Retrievals in different channels and spectral windows in the water vapour absorbing region of the near-infrared spectrum were evaluated and selected. Both methods were applied to a 2-year-long PSR data set at the German Meteorological Service (Deutscher Wetterdienst, DWD) site in Lindenberg, Germany and results have been compared with sun-photometric (CIMEL), GPS, radiosonde and MWP IWV data sets from the same station. This study presents the technical details of all instrumentation used, describes all the details of the development of these two methodological approaches, estimates the uncertainties linked to them, and finally all the comparisons for the 2-year data set are reported.
Methodologies for retrieving IWV were applied to PSR measurements at Meteorologisches Observatorium Lindenberg – Richard Assmann Observatorium (MOL–RAO) from the German Meteorological Service (DWD) in Lindenberg (Tauche), in the north-east of Germany (52∘12′ N, 14∘7′ E), where a 2-year-long PSR data set is available (May 2014–April 2016). MOL–RAO is a supersite for measurements of aerology and radiation; thus it provides a variety of collocated measurements that could be used for validation. MOL–RAO is exclusively devoted to instrumental measurements of the atmosphere and a sizeable technical staff guarantees daily maintenance of the instruments. All instruments and corresponding techniques are described below. Sunshine at the area ranges from 55 h month−1 in December to 256 h month−1 during summer months on average; also, rain is recorded almost for a third of days over all 12 months (Beyrich and Adam, 2005). Minimum solar zenith angle (SZA) reaches 30∘ during summer months while during winter it is over 70∘. Aerosol optical depth (AOD) is generally very low in the area, with maximum mean monthly values of 0.25 and 0.27 during June and July.
2.1 PSR
A new generation of solar spectroradiometer, the Precision Solar Spectroradiometer (PSR) (Fig. 1), is being developed at PMOD–WRC in order to eventually replace current filter sun photometers. It is based on a grating monochromator of stabilised temperature with a 1024 pixel Hamamatsu diode-array detector, operating in a hermetically sealed nitrogen-flushed enclosure. The spectroradiometer is designed to measure the solar spectrum within the 300–1020 nm wavelength range with an average step of ∼ 0.7 nm and spectral resolution from 1.5 to 6 nm (full width at half maximum, depending on the measured wavelength) (Kouremeti and Gröbner, 2012). The design benefits from the experience gained from successive generations of the successful precision filter radiometers (PFRs), including an in-built solar pointing sensor, an ambient pressure sensor and temperature sensors to provide routine quality control information, which allows autonomous operation at remote sites with state-of-the-art data exchange via Ethernet interfaces. The PSR used in this study is the PSR#006, which is installed on the MOL–RAO site. This instrument has been calibrated at PMOD–WRC using a 1000 W transfer standard lamp source, in May 2014 and October 2015. A comparison between the two calibrations showed relative differences less than 1 % for most spectral channels and more than 2 % only in the region above 980 nm (Kouremeti et al., 2015). Moreover, stray light corrections have been applied and absolute direct and global (horizontal) irradiance time series are available for all 1024 available channels (Gröbner et al., 2014). The cycle of routine measurements during this period was in a set of five direct solar irradiance and five dark current measurements, and average values for each pixel were saved at 1 min resolution. An evaluation of AOD retrievals from PSR has been performed during the 4th Filter Radiometer Comparison (WMO, 2016; Kazadzis et al., 2017).
2.2 CIMEL sun photometer
The CIMEL sun photometer is a filter radiometer developed by Cimel Electronique (Paris, France), which performs direct sun and sky radiance measurements. These measurements are processed centrally and are widely available through the AErosol RObotic NEtwork (AERONET) (Holben et al., 1998). Measurements are performed at nine bandpass filters between 340 and 1640 nm (eight of them are dedicated to AOD retrieving and one used for IWV). Direct measurements are performed usually every 10–15 min. Direct sun measurements at 940 nm are used to retrieve IWV. At this channel the full width at half maximum is 10 nm (Schmid et al., 2001), which means that the solar signal recorded represents a relatively wide spectral region. The method used to retrieve IWV is described in detail in Smirnov et al. (2004). The principle of this method is to calculate the fit of two constant using radiative transfer model calculations in order to retrieve IWV from the transmittance recorded at 940 nm. The precision of this retrieval was investigated by Alexandrov et al. (2009), who showed an error in the region of 0.05–0.18 cm depending on the amount of IWV.
The CIMEL level 2 AOD data for MOL–RAO has been directly downloaded from AERONET website (https://aeronet.gsfc.nasa.gov/). During the 2 years of this study, the station has been equipped with three different instruments:
-
Cimel CE318N, #787;
-
Cimel CE318N, #873 supplying #787 during its AERONET calibration;
-
Cimel CE318T (Triple) since October 2015, instrument of higher temporal resolution (∼ 1 min).
2.3 Global Positioning System
GPS is a space-based system that uses the signal transmitted from specific satellite instrumentation in order to define the geolocation of ground-based receivers. The signal delays could be separated into dry (dependent on dry air gases) and wet (water vapour) components. The biggest fraction of the delay is caused by the dry component, estimated by hydrostatic equations using the surface pressure and subtracted from the total delay. This is considered a very accurate retrieval of the wet component, to which IWV is directly proportional (Bevis et al., 1992). Wang et al. (2007) showed that the random error of GPS IWV retrievals is of the order of 0.7 mm. GPS IWV retrievals are very valuable, since this method could be applied to any receiver and a very reliable and dense data set of frequent observations could be obtained both for daytime and night-time, without being affected by cloud conditions. Differences among GPS and sun-photometric retrievals are expected, as different optical paths are used in each case and different air masses are detected: the GPS path is a quasi-random path depending on the position of the satellites while the sun-photometer path is defined by the sun-instrument's relative positions.
2.4 Microwave radiometer profiler
At MOL–RAO, a 22-channel MWP, MP-3000A Radiometrics (Ware et al., 2003) provides vertical temperature and humidity profiles. In principle, observations from these instruments are based on recording the downwelling thermal emission of the atmosphere in the region between 22 and 30 GHz, using a zenith-sky sensor. A full description of the water vapour retrieval methodology of MWP can be found at Westwater et al. (2005). Cadeddu et al. (2013) have estimated the uncertainty of this technique to the order of 5 % for IWV less than 10 mm.
2.5 Meteorological radiosonde
Meteorological radiosondes (RS) are launched in many places around the world, recording vertical profiles of various meteorological variables (temperature, wind speed, humidity, etc). Water vapour profiles provided by the soundings can be used to calculate IWV. This is the most objective approach for validating ground-based remote sensing techniques, since water vapour is measured in situ during the ascending procedure. Uncertainty for IWV retrieval in this approach is introduced by the nature of the method, as the total ascendant of a radiosonde to the stratosphere takes approximately an hour and the path of the radiosonde in the atmosphere is determined by winds; thus, it is not directly comparable to sun-photometric estimations, which retrieve water vapour on the sun-point of the observation optical path. High uncertainties – up to 20 % – for relative humidity, caused by warming due to sunlight and thermal lag, have been reported (Pratt, 1985). Also, studies have reported differences due to the use of different sensors (e.g. Soden and Lanzante, 1996). Vaisalla RS92 radiosondes are used in this study with a reported uncertainty of the order of 5 % for the RH (relative humidity) measurements during daytime in the troposphere (Miloshevich et al., 2009). Radiosondes from MOL–RAO are launched 4 times per day (00:00, 06:00, 12:00, 18:00 h UTC). So, for this study 1–3 daytime soundings per day can be used, depending on the season. Corrections, as suggested by Vömel et al. (2007) for the dependence of the humidity sensor on temperature and radiation, were applied.
In the near-infrared measuring spectral region of PSR the most important water absorption has been found in the 700–1000 nm wavelength region. Figure 2 shows the transmittance from Rayleigh scattering, aerosols and IWV, as calculated by the MODerate resolution atmospheric TRANsmisson radiative transfer model (MODTRAN RTM) (Berk et al., 1987, 1999). Aerosols direct effect on irradiance is measured through AOD, which is the integrated extinction coefficient on vertical column due to aerosols. Spectral variation of AOD at different wavelengths is measured through Ångström exponent. For the example in Fig. 2, Ångström exponent equal to 1.5 was considered and aerosol of AOD 0.1 and 0.2. Inclination of aerosol transmittance lines is proportional to Ångström exponent and higher AOD will lead to lower absolute values. WMO (2005) recommends 719, 817 and 946 nm central wavelengths to retrieve IWV, which appears as significant drops in the solar transmittance spectra in Fig. 2. Ingold et al. (2000) investigated the quality of the retrievals at these wavelengths and found that the one at 946 nm is the most robust, which could be translated as the wavelength range with the strongest absorption of IWV. Considering that absorption of water vapour is higher in the 910–950 nm region, all calculations were performed for PSR channels in the spectral range.
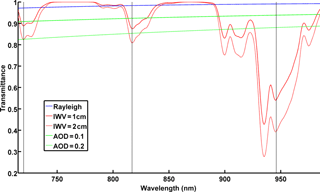
Figure 2Transmittance of water vapour, aerosols and Rayleigh scattering in the spectral region 700–1000 nm, calculated using MODTRAN set at 0.1 nm resolution, at SZA = 0∘ IWV = 1 cm, IWV = 2 cm and AOD = 0.1 and AOD = 0.2 at 700 nm using an Ångström exponent of 1.5. Black vertical dotted lines represent WMO recommendations for IWV retrieval.
3.1 Monochromatic approach
The methodology in use is described in detail by Ingold et al. (2000) and it is the most common procedure to calculate IWV for sun-photometric devices using individual wavelength (filter) measurements. It is labelled as monochromatic in contrast to the second approach presented in Sect. 3.2, although it is calculated for a spectral region defined by the instrument's slit function or the limits of its bandpass filter.
The first step of the procedure is to calculate the water vapour transmittance Tw in the spectral window of use and afterwards to develop empirical formulas using RTM calculations to determine the IWV from the calculated transmittance.
For specific spectral regions in the near infrared, where absorption of dominant trace gases can be considered negligible, we can express the transmittance of the Atmosphere (Tatmo) as follows:
where Iλ is the recorded spectral irradiance at wavelength λ (in W m−2 nm−1) and I0,λ is the value of the solar irradiance at the top of the atmosphere at the same wavelength.
We can express the Beer–Lambert law (Swinehart, 1962) ith respect to water vapour transmittance as follows:
where Tw is the transmittance of water vapour, τray is the Rayleigh scattering optical depth, τa is the aerosol optical depth (AOD), and m is the relative optical air mass of aerosol and Rayleigh scattering accordingly. For the Rayleigh scattering cross section we used the formula found in Bodhaine et al. (1999).
Also, for I0λ we used extraterrestrial values calculated for each of the PSR wavelengths measured as presented by Gröbner et al. (2017a, b). Spectral AODs were calculated using the Beer–Lambert law and the above extraterrestrial solar spectrum (Kouremeti and Gröbner, 2012). To calculate AOD at the wavelengths in the 920–950 nm region, where direct sun measurements are affected by water vapour, we applied a least square quadratic spectral extrapolation, using ln(AOD) as a function of ln(wavelength) and the PSR AODs at 500–865 nm following Eck et al. (1999) suggestion for AERONET retrievals.
In order to convert Tw into IWV we used the three-parameter expression found in Ingold et al. (2000):
where
with u0=10 kg m−2, u representing IWV, mw as the H2O air mass and a, b, c the three-wavelength-dependent coefficients. At this step the coefficients of Eq. (4) can be estimated. For that purpose, we used MODTRAN multiple runs for solar zenith angle (SZA) in the region of 0 to 85∘ with steps of 2.5∘. We used the midlatitude built-in model atmosphere in the spectral region 0.7 to 1.0 µm and IWV from 0 to 40 mm with steps of 2 mm for site elevation set at 110 m (MOL–RAO). The modelled spectra were convolved by the spectrally dependent instrument slit function in order to derive comparable (model-PSR) results. Then Tw retrieved from the output spectra was calculated as a function of slant water vapour path (mw∗u), and a fit of these values is used to estimate the coefficients ( of Eq. (4). This procedure was repeated for all PSR channels in the whole spectral region of 900–950 nm. In Fig. 3, we present these fits for wavelengths 935.5 and 946 nm. Fits for wavelengths lower than 926 nm were unsatisfactory (R2<0.7), suggesting that a different parameterisation should be used in this area instead of Eq. (4).
After determining the coefficients a, b, c, equations could be solved in order to calculate the IWV:
Thus, IWV now depends only on Tw and air mass, although the coefficients depend on the altitude of the measurement site; so, different RTM runs are needed for each installation.
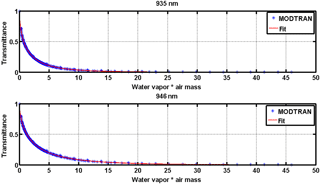
Figure 3Transmittance of IWV versus slant water vapour path (mw∗u) calculated by MODTRAN and three-parameter expression fit for 935 and 946 nm bandpasses.
In order to test the above methodology, we retrieved IWV on 30 September 2015 for each PSR channel in the 920–950 nm region separately, after calculating wavelength-dependent a, b, and c coefficients. Also, aerosol and Rayleigh transmissions were calculated separately for each wavelength. The standard deviation of the residuals retrieved from different wavelengths is 0.11. The IWV retrievals at 946 and 935.5 nm have the smallest deviations compared to the GPS and CIMEL retrievals, because at these wavelengths the absorption due to water vapour absorption is higher. At these two wavelengths, the agreement with CIMEL measurements is very good, with correlations (expressed as the R2 coefficient) of 0.94 and 0.93. The lowest R2 is found for wavelengths shorter than 928 nm which is of the order of 0.6. At Fig. 4 the mean IWV from all wavelengths for 1 day (30 September 2015) is presented as an example, alongside with the standard deviation of all monochromatic retrievals and retrievals at 946 nm are presented as reference. The standard deviation of the residuals retrieved from different wavelengths is 0.11. Following WMO guidelines, we decided to use retrievals at 946 nm for this study and the monochromatic approach.
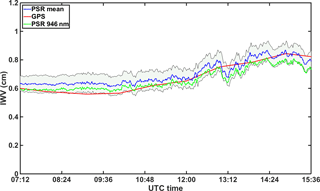
Figure 4Retrievals of monochromatic approach on 30 September 2015 at various wavelengths. Average IWV retrieved using the monochromatic approach at different wavelengths represented by blue line; the shaded area represents the standard deviation (1σ) of retrievals at different wavelengths, the green line represent retrievals at suggested 946 nm and the red curve represents the IWV retrieved from GPS.
3.2 IWV retrieval using integrated spectral windows
In order to benefit from the high resolution spectral measurements available from the PSR we developed a method that uses direct sun integrated irradiances for a spectral window in contrast to individual/single wavelengths as previously described. This methodology is expected to improve the IWV retrieval, since the large variability found in the IWV retrievals at different wavelengths suggests that an approach that combines different wavelengths could possibly be more accurate. Figure 5 shows two theoretical spectra in the region of 700–1000 nm (calculated using MODTRAN), at SZA = 0∘ with no aerosol load and with 0 and 2 cm of IWV respectively. In this approach we used the transmittance of the whole spectral window, and then Eq. (3) can be written as follows:
where λ1 and λ2 are the area wavelength limits, and .
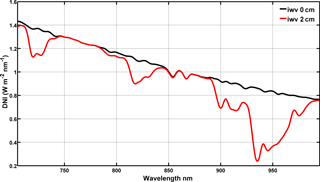
Figure 5Spectra of direct solar irradiance at SZA = 0∘ with AOD = 0 and IWV = 0 cm (black) and 2 cm (red), as calculated from MODTRAN 5.2.1 RTM.
A similar methodology for converting transmittance to IWV, as in the monochromatic approach described above is applied again in order to calculate a third-order polynomial function, valid for the wide spectral region. The same MODTRAN outputs were used as in the monochromatic approach but integrated over each spectral window, and the coefficients for Eq. (4) were calculated accordingly. Calculations have been performed for spectral windows with variable wavelength limits. An investigation on the selection of spectral window has been performed because, as monochromatic retrievals suggested (Fig. 4), the IWV calculation depends on the wavelength region in use. This investigation was made by changing the window, keeping the upper limit fixed at 948 nm and having the lower one varying between 930 to 946 nm with a step of 1 nm. This selection was made based on the water vapour absorption features as shown in Fig. 5, so that the spectral window always includes the high absorption region of 943–947 nm. Longer than 947 nm wavelengths were avoided as there were higher uncertainties in the PSR calibration (Kouremeti et al., 2015; Gröbner et al., 2017a). As demonstrated in Fig. 6 (for the 934–948 nm window), fitting of the 3-parameter equation had results of similar statistics with the monochromatic approach in that region. Residuals from fitting at this window are at average at 0.007 but there are also some up to 0.04. So, for each spectral window a new 3-parameter function is calculated.
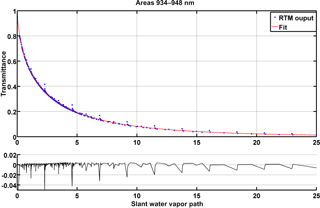
Figure 6Integrated transmittance of IWV in the 934–948 nm window versus the slant water vapour path (mw∗u) calculated by MODTRAN with a third-order polynomial fit (upper plot) and the residuals of this fit (lower plot).
In Fig. 7 results from different spectral windows have been compared to other instruments' retrievals for the whole MOL–RAO data set. The coefficient of determination R2 has been used to evaluate the performance of the spectral approach at different spectral windows, and was calculated as below:
where yi are the IWV values from the other instruments (CIMEL, MW, GPS, RS), is the average of those values and fi are the IWV values from PSR.
Horizontal axis of Fig. 7 represents the lower limit of the spectral window, the higher always being fixed at 948 nm. The aim of this step is to find out which spectral window produces the more robust IWV retrieval results. These comparisons suggest that selection of different spectral windows leads to different coefficients of determination for IWV retrieval compared with different instruments. However, results converge to define a lower wavelength limit between 932 and 936 nm that will provide the best agreement for all the comparisons. The window 934–948 nm was selected to be used for further analysis, as a median of the above-mentioned area.
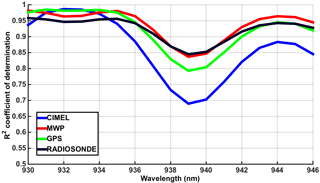
Figure 7IWV retrievals from PSR using a spectral approach with different spectral windows, a fixed upper boundary at 946 nm and a moving lower boundary on the x axis, compared to synchronous ones of CIMEL, GPS, MWP and radiosonde for the full 2-year measuring period.
It is interesting to observe different R2 of the PSR IWV retrievals compared to using different instruments. Especially the fact that by minimising the spectral window the R2 decrease, showing a minimum window of 939–946 nm. For this particular range all R2 are below 0.85 with the one for CIMEL-PSR showing a minimum. The differences observed when comparing the PSR using different instruments can be partly explained based on the results of Sect. 5.
Uncertainty estimation of the IWV retrieval is crucial for evaluating our comparison results. Beginning from Eqs. (3) and (7) and the calculations of Tw, errors introduced from each variable are estimated and their propagation to the total uncertainty of IWV retrieval is calculated.
From Eq. (3), the term that introduces the higher uncertainty in the retrieval of the IWV through the use of Beer–Lambert law is the AOD. A benefit of the methodology applied in this case is that the same set of I0 are used for calculating Tw and AOD, and so errors related to the determination of I0 do not propagate in the calculations. PSR AOD retrievals at 865 nm have been found in accordance with prototype PFR triad when compared during FRC IV, 2015 (Filter Radiometer Comparison, WMO, 2016) with average AOD differences at 865 nm less than 0.02. Also, a calibration stability study of the PSR was performed (Kouremeti et al., 2015) and showed that the instrument was stable in the 2-year data set of MOL–RAO, demonstrating a mean difference of 0.3 % with a maximum of 4 % in some channels. In addition, comparison with different CIMEL instruments for longer periods in all cases showed differences smaller than 0.03 at AOD at visible and near-infrared wavelengths (Kouremeti and Gröbner, 2014). So, the AOD-related uncertainty calculated in all studies for the PSR has a maximum of 0.03.
Rayleigh optical depths in this spectral region are very low (∼ 0.01 for 1000 mb pressure) and the uncertainty is 1 % (Teillet, 1990) and, thus, we may consider it negligible for the IWV retrieval. Air masses were calculated using the formula found in Kasten (1965), which assumes a standard vertical profile of humidity in the troposphere and introduces an error of 10 % at SZA higher than 85∘, due to variations in real atmospheric conditions but is negligible for SZA lower than 75∘ (Tomasi et al., 1998).
Coefficients a, b, c derived from fitting MODTRAN outputs introduce an uncertainty that is related to the goodness of the calculated fit. For the monochromatic approach at 946 nm, root mean square error (RMSE) is 0.0021 and for the spectral approach at window 934–948 nm it is 0.0029. So, the uncertainties introduced using the empirical equation to estimate IWV from Tw is 0.2 and 0.3 % for each approach accordingly, due to the fitting.
Uncertainty is also introduced by the extrapolation of AOD from the 865 nm and lower wavelength region to water absorbing wavelengths in the range of 934–948 nm. A sensitivity analysis of the IWV retrieval with respect to fluctuations in AOD caused by the uncertainty of AOD was performed. The uncertainty of this extrapolation was calculated to be 0.03.
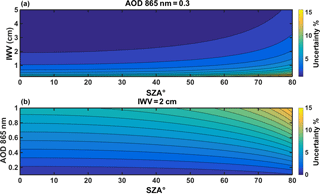
Figure 8 shows the total expected uncertainty of IWV retrieval with respect to SZA, for the case of AOD = 0.3 at 865 nm and the case of IWV equal to 2 cm. The highest uncertainties are expected for higher than 75∘ SZA, when IWV is very low or AOD very high. Very low IWV values can be found only at very dry atmospheres and even then, those are rarely below 0.2 cm. In the range of values found in the data set of MOL–RAO (0.3–4.5 cm), the maximum uncertainty is 0.28 cm. For the 0.3–0.5 cm values in our data set, absolute uncertainty is calculated as 0.08–0.12 cm. Thus, the maximum expected uncertainty of the method using PSR instruments is found at the range of 15 %, when the solar zenith angle is very high (SZA > 75∘) and AOD is higher than 0.9.
In order to validate the results retrieved from both methodologies, we used the various IWV data sets recorded at MOL–RAO. Calculations have been performed for all PSR measurements, but we used only the ones synchronous to CIMEL level data in order to avoid cloud contamination. So indirectly the AERONET cloud-screening procedure (Smirnov et al., 2000) has been used. For each CIMEL data point we calculated the synchronous PSR value by averaging all values in a ±5 min interval. This approach produced a data set of 3501 synchronous data points between PSR and CIMEL, 2507 between PSR and GPS and 2964 between PSR and MWP. For radiosondes, in order to have a robust coincidence criterion, we followed the approach of Schneider et al. (2010), averaging PSR measurements for ±20 min from the time that the radiosonde reaches a 4 km height, in order to minimise spatial and temporal PSR and radiosonde measurement differences.
For all the comparisons statistics are calculated for the differences
where x is the corresponding instrument/method, μX is the average value for DX and
where N is the number of available, quality controlled observations.
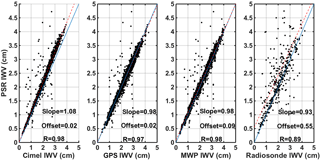
Figure 9IWV retrievals from PSR using the monochromatic approach at 946 nm compared to synchronous ones of CIMEL, GPS, MWP and radiosonde for the full 2-year measuring period.
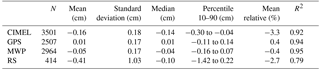
For the monochromatic approach at 946 nm, the comparison is presented in Fig. 9 and corresponding statistics are in Table 1. Better agreement was found when PSR retrievals were compared to MWP retrievals, but at a similar level to the comparisons with CIMEL and GPS retrievals. Mean absolute difference is slightly lower when compared to GPS (0.01 cm), but the spread of the differences is almost the same for CIMEL, GPS and MWP (standard deviation between 0.17 and 0.18 cm). Differences with the CIMEL retrieval are within the CIMEL uncertainty range. It appears that PSR overestimates the IWV compared to CIMEL for IWV larger than 3 cm, which causes a different slope in the graphs. This feature is not shown in the comparison with GPS and MWP at these IWV values. Schneider et al. (2010) also observed different behaviour in CIMEL retrievals compared to other methods, regarding dry or wet conditions in the atmosphere and linked to filter characterisation errors. Radiosonde retrievals had the largest deviations and more scattered differences, which is expected because of the different temporal and spatial scales of the RS retrieval. Percentiles 10–90 of the differences are also presented in Table 1 and GPS, MWP and CIMEL retrievals have a spread of differences in the range of the uncertainties described for these instruments. In general RS retrievals demonstrate the most spread differences from the PSR retrievals, though the average and median are in the uncertainty range of the instruments. The high spread of the differences is explained by the random error introduced by the temporal variability of IWV in the time range averaged (±20 min) and by the different paths of the sounding.
Table 1Statistics of differences among retrievals from PSR using monochromatic approach at 946 nm and retrievals from other instruments for the whole data set.
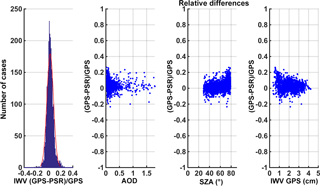
A histogram of relative difference of this retrieval compared to the GPS is demonstrated in Fig. 10. Also, relative differences of IWV retrievals are shown against other parameters (AOD, SZA and IWV from GPS). A normal distribution with a mean of 0.024 cm and standard deviation of 0.084 is fitted to the differences and passed the one-sample Kolmogorov–Smirnov test (Marsaglia et al., 2003). Thus 95 % of the absolute differences are lower than 0.16 cm. IWV differences against AOD at 865 nm show that almost all absolute relative differences higher than 0.2 cm (20 %) are linked to AOD values higher than 0.5. This pattern could be connected to the larger uncertainty of AOD calculated by extrapolation at 946 nm, when AOD values are higher. Furthermore, it appears that most of the large differences appear at high SZA, but there are also some individual points showing large differences at lower SZA that could be linked to AOD uncertainty. Compared to IWV retrieved from the GPS it appears that extreme differences are linked to overestimations from PSR when the absolute value is above 2 cm, and to underestimations when below, though GPS retrievals are not optimal at more dry conditions (Schneider et al., 2010).
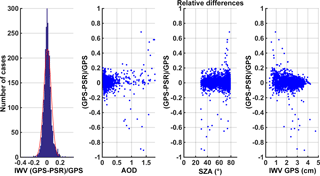
Figure 10Histogram of relative difference among synchronous GPS and PSR retrievals – using monochromatic approach at 946 nm – and plotted against AOD (retrieved from PSR at 865 nm), solar zenith angle and IWV (retrieved from GPS).
Comparison of the PSR spectral method with other instruments is presented in Fig. 11 and corresponding statistics in Table 2. It is clear that the spread of differences with all methods is significantly lower than for the monochromatic approach. All comparisons are found with R2 between 0.96 and 0.98. CIMEL seems to underestimate, compared to this method, but also compared with the other instruments at higher IWV values. Although the slope caused by the overestimation is still presented in this approach, the spread of the differences among CIMEL and PSR retrievals is significantly lower than any other comparison, with σ=0.07 and 10–90 percentiles of differences in a range of −0.23–0.02. Differences with GPS and MWP retrievals have the same spread and statistical behaviour. Radiosonde data are in significantly better agreement with the spectral approach retrieval than with the monochromatic approach. Standard deviation of the differences is at least halved compared to the monochromatic approach and all mean relative differences when compared to any other instrument are lower than 0.7 %. Comparison with RS data set still has a significantly larger standard deviation than other comparisons but it is less than a quarter of the monochromatic approaches. Extreme values observed with the monochromatic approach are significantly reduced and the standard deviation is reduced to values of 0.07 for CIMEL to 0.18 for RS retrievals. A wider spread is observed at higher SZA, which is explained by the increase of the instrument-related uncertainty at these angles.
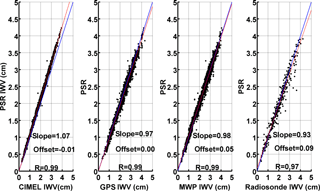
Figure 11IWV retrievals from PSR using the spectral approach in the 934–948 nm region, compared to synchronous ones of CIMEL, GPS, MWP and radiosonde, for the full 2-year measuring period.
Table 2Statistics of differences among retrievals from PSR using the spectral approach in a 934–948 nm window and retrievals from other instruments for the whole data set.
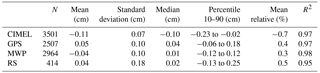
Figure 12 displays a histogram of relative differences of the spectral approach for the spectral window 934–948 nm, the GPS data set and a relative IWV comparison between AOD at 865 nm, SZA and GPS. A normal distribution with a mean of 0.021 cm and σ at 0.042 is fitted to the data, passes the one-sample Kolmogorov–Smirnov test (Marsaglia et al., 2003), and 95 % of differences are lower than 0.08 cm. The quality of spectral retrieval shows no dependence on absolute IWV values, as the distribution of differences in Fig. 12 is independent of IWV. When the IWV relative difference is shown against AOD, higher relative differences than 0.1 are more frequent for AOD lower than 0.2.
The aim of this study was to develop methodologies and tools in order to retrieve IWV from PSR spectral measurements. The methods which were developed can be applied to provide long-term time series of IWV using any direct sun spectroradiometer able to measure in the 930–950 spectral range.
Two approaches to retrieve IWV from PSR spectral direct solar irradiance measurements have been developed. The first one is the monochromatic approach using an individual wavelength, and the second uses a spectral window. For both methods the corresponding water vapour transmittance has been retrieved from the PSR measurements, from which IWV can be calculated using a three-parameter formula following the principles of Ingold et al. (2000).
The dependence of the retrievals on other parameters has been investigated for both approaches and found to be affected in cases of low (< 0.2) AOD coincidences. Larger deviations were observed at high solar zenith angles, which are linked to higher uncertainties in those retrievals.
Comparisons to other instruments (CIMEL, MWP) and methods (GPS, radiosondes) have been performed to select the optimum wavelength and spectral window for the IWV retrieval of the PSR. All the channels in the infrared region of 900–950 nm were tested for a monochromatic approach and a 946 nm bandpass was selected to give significantly better results than other channels. For the spectral approach all possible spectral windows limits combinations were tested and the spectral window of 934–948 nm was finally chosen.
Uncertainties of the methodologies have been investigated and in more frequent atmospheric conditions have been found to be less than 5 %, but might reach up to 15 % in cases of very high AOD, very low IWV and SZA higher than 75∘ combined. In general, absolute uncertainty is found to be in the range of 0.08–0.3 cm.
Retrievals from a 2-year-long time series at MOL–RAO in Lindenberg, Germany showed that the monochromatic approach had differences of the order of 0.4 % compared to GPS and MWP, 2.7 % compared to RS and 3.3 % compared to CIMEL; 95 % of differences with GPS retrievals are less than 0.15 cm.
Spectral approach retrievals showed better agreement with other data sets, having differences of 0.7 % compared to CIMEL, 0.4 % compared to GPS, 0.3 % compared to MWP and 0.5 % when compared to RS. Also, the differences to other retrievals were always at least half spread compared to the monochromatic approach. Differences with GPS retrievals were less than 0.08 cm in 95 % of the data set. Differences among the other instruments found independent of other variables, suggesting robust appliance of the method.
Overall, the accuracy of IWV retrieval is of the same order as the other well-established methods and devices. The spectral approach, benefiting from the characteristics of PSR, provided statistically better results. Also, when the method was applied to a 2-year data set, it indicated a stable long-term performance of the instrument, which shows that it can be used for IWV calculations. The IWV method development and assessment presented in this work provided an added value to the PSR instrument, being able to measure simultaneously spectral solar irradiance components (direct and horizontal), aerosol spectral optical properties (AOD, Ångström exponents) and IWV, constituting the PSR as a unique sun-photometric instrument.
All data sets used in the current study are freely available. AERONET IWV data are downloadable from the AERONET webpage: https://aeronet.gsfc.nasa.gov. PSR data can be accessed through personal communication with Lionel Doppler or Stelios Kazadzis. MWP and radiosonde data can be accessed though personal communication with Lionel Doppler. Codes developed for spectral IWV retrievals can be used after consultation with corresponding author.
| AERONET | AErosol RObotic NETwork |
| AOD | Aerosol optical depth |
| CIMEL | Sun photometer Cimel CE318 used in AERONET network |
| DWD | Deutscher Wetterdienst (German Meteorological Service) |
| GPS | Global Positioning System |
| IWV | Integrated water vapour (water vapour column) |
| MODTRAN RTM | MODerate resolution atmospheric TRANsmisson radiative transfer model |
| MOL–RAO | Meteorologisches Observatorium Lindenberg – Richard Assmann Observatorium |
| MWP | Microwave radiometer profiler |
| PMOD–WRC | Physikalisch-Meteorologisches Observatorium Davos – World Radiation Center |
| PFR | Precision filter radiometer |
| PSR | Precision Solar Spectroradiometer |
| RH | Relative humidity |
| RS | Meteorological radiosondes |
| WMO | World Meteorological Organisation |
The authors declare that they have no conflict of interest.
This article is part of the special issue “SKYNET – the international network for aerosol, clouds, and solar radiation studies and their applications”. It is not associated with a conference.
This research was partly funded by theH2020 GEO-CRADLE project under grant agreement
no. 690133.
Edited by: Monica Campanelli
Reviewed by: three anonymous referees
Alexandrov, M. D., Schmid, B., Turner, D. D., Cairns, B., Oinas, V., Lacis, A. A., Gutman, S. I., Westwater, E. R., Smirnov, A., and Eilers, J.: Columnar water vapor retrievals from multifilter rotating shadowband radiometer data, J. Geophys. Res.-Atmos., 114, D02306, https://doi.org/10.1029/2008JD010543, 2009.
American Meteorological Society: Precipitable Water Vapor, Glossary of Meteorology, available at: http://glossary.ametsoc.org/wiki/Precipitable_water, last access date: 24 February 2018.
Berk, A., Bernstein, L. S., and Robertson, D. C.: MODTRAN: A moderate resolution model for LOWTRAN (No. SSI-TR-124), Spectral Sciences Inc. Burlington, MA, USA, 1987.
Berk, A., Anderson, G. P., Bernstein, L. S., Acharya, P. K., Dothe, H., Matthew, M. W., Adler-Golden, S. M., Chetwynd Jr., J. H., Richtsmeier, S. C., Pukall, B., and Allred, C. L.: MODTRAN 4 radiative transfer modeling for atmospheric correction, in: Proceedings of SPIE – The International Society for Optical Engineering, 3756, 348–353, 1999.
Bevis, M., Businger, S., Herring, T. A., Rocken, C., Anthes, R. A., and Ware, R. H.: GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System, J. Geophys. Res., 97, 15787–15801, 1992.
Beyrich, F., and Adam, W. K.: Site and Data Report for the Lindenberg Reference Site in CEOP – Phase I: Berichte des Deutschen Wetterdienstes, no. 230, Offenbach am Main, Germany, 55 pp., 2007.
Bock, O., Bosser, P., Pacione, R., Nuret, M., Fourrié, N., and Parracho, A.: A high-quality reprocessed ground-based GPS dataset for atmospheric process studies, radiosonde and model evaluation, and reanalysis of HyMeX Special Observing 30 Period, Q. J. Roy. Meteor. Soc., 142, 56–71, https://doi.org/10.1002/qj.2701, 2016.
Bodhaine, B. A., Wood, N. B., Dutton, E. G., and Slusser, J. R.: On Rayleigh optical depth calculations, J. Atmos. Ocean. Tech., 16, 1854–1861, 1999.
Cadeddu, M. P., Liljegren, J. C., and Turner, D. D.: The Atmospheric radiation measurement (ARM) program network of microwave radiometers: instrumentation, data, and retrievals, Atmos. Meas. Tech., 6, 2359–2372, https://doi.org/10.5194/amt-6-2359-2013, 2013.
Campanelli, M., Estellés, V., Smyth, T., Tomasi, C., Martínez- Lozano, M. P., Claxton, B., Muller, P., Pappalardo, G., Pietruczuk, A., Shanklin, J., Colwell, S., Wrench, C., Lupi, A., Mazzola, M., Lanconelli, C., Vitale, V., Congeduti, F., Dionisi, D., and Cacciani, M.: Monitoring of Eyjafjallajoekull volcanic aerosol by the new European SkyRad users(ESR) sun-sky radiometer network, Atmos. Environ., 48, 33–45, 2012.
Campanelli, M., Nakajima, T., Khatri, P., Takamura, T., Uchiyama, A., Estelles, V., Liberti, G. L., and Malvestuto, V.: Retrieval of characteristic parameters for water vapour transmittance in the development of ground-based sun–sky radiometric measurements of columnar water vapour, Atmos. Meas. Tech., 7, 1075–1087, https://doi.org/10.5194/amt-7-1075-2014, 2014.
Campanelli, M., Mascitelli, A., Sanò, P., Diémoz, H., Estellés, V., Federico, S., Iannarelli, A. M., Fratarcangeli, F., Mazzoni, A., Realini, E., Crespi, M., Bock, O., Martínez-Lozano, J. A., and Dietrich, S.: Precipitable water vapour content from ESR/SKYNET sun–sky radiometers: validation against GNSS/GPS and AERONET over three different sites in Europe, Atmos. Meas. Tech., 11, 81–94, https://doi.org/10.5194/amt-11-81-2018, 2018.
Che, H., Gui, K., Chen, Q., Zheng, Y., Yu, J., Sun, T., Zhang, X., and Shi, G.: Calibration of the 936 nm water-vapor channel for the China aerosol remote sensing NETwork (CARSNET) and the effect of the retrieval water-vapor on aerosol optical property over Beijing, China, Atmos. Pollut. Res., 7, 743–753, 2016.
Eck, T. F., Holben, B. N., Reid, J. S., Dubovik, O., Smirnov, A., O'neill, N. T., Slutsker, I., and Kinne, S., Wavelength dependence of the optical depth of biomass burning, urban, and desert dust aerosols, J. Geophys. Res.-Atmos., 104, 31333–31349, https://doi.org/10.1029/1999JD900923, 1999.
Gröbner, J., Kouremeti, N., Coulon, E., Durig, F., Gyo, M., Soder, R., and Wasser, D.: Spectroradiometer for Spectral Aerosol Optical Depth and Solar Irradiance Measurements, annual report PMOD/WRC, p. 13, available at: http://pmodwrc.ch/annual_report/2012_PMODWRC_Annual_Report.pdf, 2012.
Gröbner, J., Kouremeti, N., Nevas, S., and Blattner, P.: Characterisation Studies of Precision Solar Spectroradiometer, PMOD-WRC Annual Report 2014, p. 26, available at: http://pmodwrc.ch/annual_report/2014_PMODWRC_Annual_Report.pdf, 2014.
Gröbner, J., Kazadzis, S., Kouremeti, N., Doppler, L., Tagirov, R., and Shapiro, A. I.: Spectral solar variations during the eclipse of 20 March 2015 at two European sites, in: AIP Conference Proceedings, 1810, 080008, AIP Publishing, 2017a.
Gröbner, J., Kröger, I., Egli, L., Hülsen, G., Riechelmann, S., and Sperfeld, P.: The high-resolution extraterrestrial solar spectrum (QASUMEFTS) determined from ground-based solar irradiance measurements, Atmos. Meas. Tech., 10, 3375–3383, https://doi.org/10.5194/amt-10-3375-2017, 2017b.
Güldner, J.: A model-based approach to adjust microwave observations for operational applications: results of a campaign at Munich Airport in winter 2011/2012, Atmos. Meas. Tech., 6, 2879–2891, https://doi.org/10.5194/amt-6-2879-2013, 2013.
Güldner, J. and Spänkuch, D.: Remote sensing of the thermodynamic state of the atmospheric boundary layer by ground-based microwave radiometry, J. Atmos. Ocean. Tech., 18, 925–933, 2001.
Halthore, R. N., Eck, T. F., Holben, B. N., and Markham, B. L.: Sun photometric measurements of atmospheric water vapor column abundance in the 940-nm band, J. Geophys. Res.-Atmos., 102, 4343–4352, 1997.
Hartmann, D., Klein Tank, A., Rusticucci, M., Alexander, L., Brönnimann, S., Charabi, Y., Dentener, F., Dlugokencky, E., Easterling, D., Kaplan, A., Soden, B., Thorne, P.,Wild, M., and Zhai, P.: Observations: Atmosphere and Surface, in: Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK, New York, NY, USA, 2013.
Holben, B. N., Eck, T. F., Slutsker, I., Tanre, D., Buis, J. P., Setzer, A., Vermote, E., Reagan, J. A., Kaufman, Y. J., Nakajima, T., and Lavenu, F.: AERONET – A federated instrument network and data archive for aerosol characterization, Remote Sens. Environ., 66, 1–16, 1998.
Hong, L., Yunchang, C., Xiaomin, W., Zhifang, X., Haishen, W., and Heng, H.: Meteorological applications of precipitable water vapor measurements retrieved by the national GNSS network of China, Geodesy Geodynam., 6, 135–142, https://doi.org/10.1016/j.geog.2015.03.001, 2015.
Ingold, T., Schmid, B., Matzler, C., Demoulin, P., and Kampfer, N.: Modeled and empirical approaches for retrieving columnar water vapor from solar transmittance measurements in the 0.72, 0.82, and 0.94 µm absorption bands, J. Geophys. Res., 105, 24327–24343, https://doi.org/10.1029/2000JD900392, 2000.
Kasten, F.: A new table and approximation formula for the relative optial air mass, Arch. Meteor. Geophy. B, 14, 206–223, 1965.
Kazadzis, S., Kouremeti, N., Diémoz, H., Gröbner, J., Forgan, B. W., Campanelli, M., Estellés, V., Lantz, K., Michalsky, J., Carlund, T., Cuevas, E., Toledano, C., Becker, R., Nyeki, S., Kosmopoulos, P. G., Tatsiankou, V., Vuilleumier, L., Denn, F. M., Ohkawara, N., Ijima, O., Goloub, P., Raptis, P. I., Milner, M., Behrens, K., Barreto, A., Martucci, G., Hall, E., Wendell, J., Fabbri, B. E., and Wehrli, C.: Results from the 4th WMO Filter Radiometer Comparison for aerosol optical depth measurements, Atmos. Chem. Phys. Discuss., https://doi.org/10.5194/acp-2017-1105, in review, 2017.
Kouremeti, N. and Gröbner, J.: Spectral Aerosol Optical Depth from a Precision Spectroradiometer, PMOD-WRC Annual Report 2012, p. 33, available at: http://pmodwrc.ch/annual_report/2012_PMODWRC_Annual_Report.pdf, 2012.
Kouremeti, N. and Gröbner, J.: Spectral Aerosol Optical Depth From a Precision Solar Spectroradiometer During Three Field Campaigns, PMOD-WRC Annual Report 2014, p. 30, available at: http://pmodwrc.ch/annual_report/2014_PMODWRC_Annual_Report.pdf, 2014.
Kouremeti, N., Gröbner, J., and Doppler, L.: Stability of the Precision Solar Spectroradiometer, PMOD-WRC Annual Report 2015, p. 40, available at: http://pmodwrc.ch/annual_report/2015_ PMODWRC_Annual_Report.pdf, 2015.
Marsaglia, G., Tsang, W., and Wang, J.: Evaluating Kolmogorov's Distribution, J. Stat. Softw., 8, 1–4, https://doi.org/10.18637/jss.v008.i18, 2003.
Miloshevich, L. M., Vömel, H., Whiteman, D. N., and Leblanc, T.: Accuracy assessment and correction of Vaisala RS92 radiosonde water vapor measurements, J. Geophys. Res.-Atmos., 114, D11305, https://doi.org/10.1029/2008JD011565, 2009.
Nyeki, S., Vuilleumier, L., Morland, J., Bokoye, A., Viatte, P., Mätzler, C., and Kämpfer, N.: A 10-year integrated atmospheric water vapor record using precision filter radiometers at two high-alpine sites, Geophys. Res. Lett., 32, 1–4, L23803, https://doi.org/10.1029/2005GL024079, 2005.
Pratt, R. W.: Review of radiosonde humidity and temperature errors, J. Atmos. Ocean. Tech., 2, 404–407, 1985.
Reichard, J., Wandinger, U., Serwazi, M., and Weitkamp, C.: Combined Raman lidar for aerosol, ozone and moisture measurements, Opt. Eng., 35, 1457–1465, 1996.
Schneider, M., Romero, P. M., Hase, F., Blumenstock, T., Cuevas, E., and Ramos, R.: Continuous quality assessment of atmospheric water vapour measurement techniques: FTIR, Cimel, MFRSR, GPS, and Vaisala RS92, Atmos. Meas. Tech., 3, 323–338, https://doi.org/10.5194/amt-3-323-2010, 2010.
Schmid, B., Michalsky, J. J., Slater, D. W., Barnard, J. C., Halthore, R. N., Liljegren, J. C., Holben, B. N., Eck, T. F., Livingston, J. M., Russell, P. B. and Ingold, T.: Comparison of columnar water-vapor measurements from solar transmittance methods, Appl. Opt., 40, 1886–1896, 2001.
Smirnov, A., Holben, B. N., Eck, T. F., Dubovik, O., and Slutsker, I.: Cloud-screening and quality control algorithms for the AERONET database, Remote Sens. Environ., 73, 337–349, 2000.
Smirnov, A, Holben, B. N., Lyapustin, A., Slutsker, I., and Eck, T. F.: AERONET processing algorithms refinement, AERONET Workshop, El Arenosillo, Spain, 10–14 May 2004.
Soden, B. J. and Held, I. M.: An assessment of climate feedbacks in coupled ocean–atmosphere models, J. Climate, 19, 3354–3360, https://doi.org/10.1175/JCLI3799.1, 2006.
Soden, B. J. and Lanzante, J. R.: An assessment of satelliteand radiosonde climatologies of upper-tropospheric water vapor, J. Climate, 9, 1235–1250, 1996.
Swinehart, D. F.: The Beer–Lambert law, J. Chem. Educ., 39, 333, https://doi.org/10.1021/ed039p333, 1962.
Teillet, P. M.: Rayleigh optical depth comparisons from various sources, Appl. Opt., 29, 1897–1900, https://doi.org/10.1364/AO.29.001897, 1990.
Tomasi, C., Vitake, V., and De Santis, L. V.: Relative optical mass functions for air, water vapour, ozone and nitrogen dioxide in atmospheric models presenting different latitudinal and seasonal conditions, Meteorol. Atmos. Phys., 65, 11–30, 1998.
Vömel, H., Selkirk, H., Miloshevich, L., Valverde-Canossa, J., Valdés, J., Kyrö, E., Kivi, R., Stolz, W., Peng, G., and Diaz, J. A.: Radiation dry bias of the Vaisala RS92 humidity sensor, J. Atmos. Ocean. Tech., 24, 953–963, 2007.
Wang, J., Zhang, L., Dai, A., Van Hove, T., and Van Baelen, J.: A near-global, 2-hourly dataset of atmospheric precipitable water from ground-based GPS measurements, J. Geophys. Res., 112, D11107, https://doi.org/10.1029/2006JD007529, 2007.
Ware, R., Carpenter, R., Güldner, J., Liljegren, J., Nehrkorn, T., Solheim, F., and Vandenberghe, F.: Amulti-channel radiometric pro- filer of temperature, humidity and cloud liquid, Radio Sci., 38, 8079, https://doi.org/10.1029/2002RS002856, 2003.
Westwater, E. R., Crewell, S., Mätzler, C., and Cimini, D.: Principles of surface-based microwave and millimeter wave radio- metric remote sensing of the troposphere, Quaderni della Societa Italiana di Elettromagnetismo, 1, 50–90, 2005.
WMO: GAW Report-No 231, Fourth WMO Filter Radiometer Comparison (FRC-IV), Davos, Switzerland, 28 September–16 October 2015, WMO, available at: https://library.wmo.int/opac/doc_num.php?explnum_id=3369, 2016.
WMO/GAW: Experts workshop on Global Surface-based Networkm for long term observations of column aerosol optical properties, in: World Meteorological Organization Global Atmosphere Watch, Davos, Switzerland, 8–10 March 2004, edited by: Baltensperger, U., Barrie, L., and Wehrli, C., GAW report No. 162, WMO TD No. 1287, 153 pp., available at: https://library.wmo.int/pmb_ged/wmo-td_1287.pdf (last access: 21 October 2016), 2005.
Yu, S., Alapaty, K., Mathur, R., Pleim, J., Zhang, Y., Nolte, C., Eder, B., Foley, K., and Nagashima, T.: Attribution of the United States “warming hole”: Aerosol indirect effect and precipitable water vapor, Scientific reports, 4, 6929, https://doi.org/10.1038/srep06929, 2014.