the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
The WeIzmann Supercooled Droplets Observation on a Microarray (WISDOM) and application for ambient dust
Naama Reicher
Lior Segev
The WeIzmann Supercooled Droplets Observation on Microarray (WISDOM) is a new setup for studying ice nucleation in an array of monodisperse droplets for atmospheric implications. WISDOM combines microfluidics techniques for droplets production and a cryo-optic stage for observation and characterization of freezing events of individual droplets. This setup is designed to explore heterogeneous ice nucleation in the immersion freezing mode, down to the homogeneous freezing of water (235 K) in various cooling rates (typically 0.1–10 K min−1). It can also be used for studying homogeneous freezing of aqueous solutions in colder temperatures. Frozen fraction, ice nucleation active surface site densities and freezing kinetics can be obtained from WISDOM measurements for hundreds of individual droplets in a single freezing experiment. Calibration experiments using eutectic solutions and previously studied materials are described. WISDOM also allows repeatable cycles of cooling and heating for the same array of droplets. This paper describes the WISDOM setup, its temperature calibration, validation experiments and measurement uncertainties. Finally, application of WISDOM to study the ice nucleating particle (INP) properties of size-selected ambient Saharan dust particles is presented.
In mixed phase clouds, water droplets remain stable in a supercooled state below 273 K and ice nucleates spontaneously as droplets reach the homogeneous freezing temperature, below 236 K (Pruppacher et al., 1998). At warmer temperatures, ice particles may coexist with supercooled droplets, due to heterogeneous nucleation facilitated by the presence of ice nucleating particles (INPs) (Cantrell and Heymsfield, 2005). In cases where INPs are immersed in the droplet before supercooling, referred to as immersion freezing mechanism, the droplets first grow to supercritical size before freezing occurs (de Boer et al., 2011). Observations and modeling studies suggest that immersion freezing is the prominent mechanism for heterogeneous ice formation in mixed phase clouds (Rosenfeld and Woodley, 2000; Ansmann et al., 2008; Field et al., 2012; Nagare et al., 2016; Possner et al., 2017).
Ice particles affect the radiative and microphysical properties of mixed phase clouds and Earth's hydrological cycle. Therefore, they can influence present and possibly future climate (Hoose and Möhler, 2012; IPCC, 2013). Studying ice formation in clouds is hence important, and yet, due to its complexity, this process is still not fully understood and presents a great challenge to laboratory and field researchers as well as for clouds and climate modelers (DeMott et al., 2010; Schnaiter et al., 2016; Ullrich et al., 2017).
Offline studies of immersion freezing often use cold stage techniques (Budke and Koop, 2015). The basic idea is to place an array of droplets over a cold stage and cool continuously until all are frozen, to obtain a quantitative measurement of their corresponding freezing temperatures (Vali, 1971). The droplets may be microliter sized and observed with a simple camera. Smaller droplets, down to the picoliter range, are usually observed under a microscope. In both cases, freezing events are identified by optical changes in the droplets when they crystalize (Knopf and Lopez, 2009; Murray et al., 2011; Atkinson et al., 2013; Hiranuma et al., 2015).
Cold stage techniques may suffer from technical issues such as droplets evaporation and vapor transfer due to the Wegener–Bergeron–Findeisen process, where ice grows on the expense of supercooled droplets or from seeding of neighboring droplets by formation and surface growth of frost halos (Budke and Koop, 2015). Some cold stages instruments place oil over the droplets or use droplets in oil emulsions to prevent these effects (Murray et al., 2012). Still, results from cold stage experiments may be biased by effects of inhomogeneous temperature of the substrate and the surroundings or by various contaminations caused during droplets' preparation and measurement (Hiranuma et al., 2015). Furthermore, supercooling is limited due to the presence of impurities, which increases with the volume of the droplet. Hence, to allow comprehensive studies down to the homogeneous region, low volumes (<1 µL) are used, and generation of these volumes is not trivial and may cause further complications.
Microfluidics is a technology of fluids manipulation in microchannel arrays on a small device. Microfluidics is widely used in a range of fields, such as physics, chemistry, biology, life sciences and the food industry (Whitesides, 2006; Neethirajan et al., 2011; Sackmann et al., 2014). Recent studies used a microfluidic apparatus to study ice nucleation processes. Riechers et al. (2013) used a microfluidics device to produce and collect monodisperse droplets of water in various sizes, which were subsequently observed under a microscope to study their homogeneous freezing. Stan et al. (2009) recorded nucleation in water droplets and silver-iodide-seeded droplets, while droplets were flowing during cooling. Schmitz et al. (2009) established “Dropspots”, a static microfluidic array of droplets, later used by Edd et al. (2009) to measure nucleation kinetics. However, in the atmospheric heterogeneous ice nucleation field, microfluidics techniques are not widely adopted, despite many potential advantages.
The WeIzmann Supercooled Droplets Observation on Microarray (WISDOM) is a new instrument combining the cold stage technique with microfluidics technology and is designed to study immersion freezing of micrometer-sized droplets, while addressing most of the technical issues listed above. The WISDOM setup introduces several advantages of microfluidics to the atmospheric ice nucleation field. WISDOM is based on the “Dropspots” static array (Schmitz et al., 2009), which enables the separation and the fixation of the droplets, so that each individual droplet is recorded and studied, and also can be used for repetition of freezing cycles and further exploration of the nucleation process of a specific sample.
In this paper, we present the WISDOM setup, its calibration and validation procedures. For validation experiments, homogeneous and heterogeneous freezing were examined by following homogeneous freezing rates of pure aqueous or solutions or deriving the efficiencies of three types of mineral dust surrogates and collected ambient Saharan dust to validate heterogeneous freezing experiments.
Homogeneous nucleation rates are described stochastically using the volume-dependent ice nucleation rate (Jv (T)) in supercooled droplets, given by the frozen fraction (fice) of droplets with volume V at a certain temperature (T) and time intervals (Δt) (Murray et al., 2010; Alpert et al., 2011; Riechers et al., 2013),
Heterogeneous freezing is described by a singular approach that assumes that nucleation occurs at a certain temperature due to a special nucleation site. Hence, a cumulative number of nucleation sites per unit surface area, ns, is used to describe the heterogeneous nucleation efficiency at a certain temperature,
where fice is the fraction of frozen droplets at temperature T and A is the specific surface area of the immersed particles in each droplet (Vali, 1971; Vali et al., 2015; Whale et al., 2015).
Validation of WISDOM was further extended below the homogeneous nucleation temperature of pure water, using aqueous solutions as the freezing temperatures of solutions decrease as a function of the solution water activity.
2.1 Droplets production and trapping
The WISDOM setup, shown in Fig. 1, is made of a microfluidic setup which include a pressure-controlled pump with four independent flow channels (OB1 MK3 by Elveflow), a stereoscope (SMZ-171 by Motic) that permits a full view of all channels and inlets, and a charge-coupled device (CCD) camera (GS3 by Point Grey) that enable real-time monitoring of the droplets production. The flows in the channels are continuous and controlled by the pressure pump. One channel is connected to the continuous (oil) phase, and a second channel contains the sample (aqueous solution that can contain INPs). The two phases meet in a narrow junction where monodisperse droplets are generated due to the pressure exerted by one phase over the other. The ratio between the flows determines the size of the emerging droplets; the volume increases with increasing flow rate of the sample. In this setup, droplets are suspended in an oil mixture, consisting of mineral oil (Sigma Aldrich) and a 2 weight percent (wt %) nonionic surfactant (span80®, Sigma Aldrich), added for droplets stabilization (Riechers et al., 2013). Hence, an array of picoliter (micrometer-size) droplets is generated directly on a device.
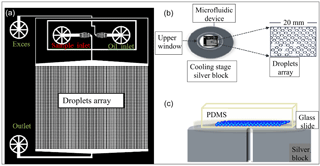
Figure 1The WISDOM setup. (a) The design of the microfluidic device is based on Schmitz et al. (2009). Aqueous solutions (including the sample) and oil are connected through the inlets and merge in a junction to generate monodisperse droplets. Subsequently, droplets flow into a trap array and settle in them as the flow is stopped. The device is transferred into a cooling stage for subsequent freezing experiments. (b) Upper and (c) side views of the device, which is made of PDMS (polydimethylsiloxane), plasma glued to a microscope glass slide, placed over the cooling silver block.
The principle of the Schmitz et al. (2009) design is that the droplets flow into round chambers that are connected by the constriction channel. At a certain flow, the droplets are squeezed through the constriction channel and the array fills up with droplets. When the flow is too weak or stopped, the constriction channel stops the droplets' movement and they are trapped in the chambers. The droplets are isolated and stable in the chambers and it is safe to move the device from the generation stage to the cold stage for the freezing experiments.
Devices are fabricated following the Schmitz et al. (2009) protocol. Briefly, the device pattern is imprinted on a polydimethylsiloxane (PDMS) polymer, later glued to a 1 mm thick microscope glass slide using air plasma treatment. After the plasma treatment the PDMS surfaces are hydrophilic (Eddings et al., 2008). Therefore, the devices were used only in the following day, after their surfaces became hydrophobic, following their exposure to the atmosphere, or after their annealing at 60 ∘C for 30 min.
2.2 Freezing experiments and detection
The droplets array is placed in a commercial cryostage (Linkam, THMS600) coupled to an optical microscope (Olympus, BX-51 with 10x magnification, transmission mode). Experiments are monitored by a microscope-mounted CCD camera (Allied Vision Technologies, Oscar F-510C) for automatic identification of droplets and their freezing events. Both the device and the cooling stage are cleaned with 2-propanol. Then the device is placed over the stage together with a thin layer of oil on its bottom to provide good thermal conductivity. Each freezing experiment starts with dry N2 purging to replace the moist atmosphere inside the cryostage to prevent condensation. During the experiment, N2 flow prevents water condensation on the cryostage window. Freezing experiments are conducted with a cooling rate of 1 K min−1, which is relevant for atmospheric conditions and also allows good thermalization of the droplets, as will be shown in the calibration section (Sect. 3.1). Each cooling cycle is followed by a heating cycle, where melting is observed. Analysis of the melting onset is then used to verify that the thermal conductivity is good and thus validate the measurement.
In-house LabVIEW software is used to record a freezing experiment movie file and analyze it offline. The temperature readings by the Linkam cryostage temperature sensor (0.25 K for the operated temperature range) and the movie frames are synchronized and integrated. In most cases, 1 s (or 0.017 K at 1 K min−1) per frame is used. Currently, the WISDOM setup operates with two types of devices that differ in their droplets' trap diameter: 40 and 100 µm. Approximately 550 and 120 droplets can be monitored per experiment in the smaller and larger diameter devices, respectively. Statistically, for the same sample, larger droplets encompass more INP surface area within each droplet, which can be more sensitive for detecting rare active sites. The device can be reused for the same sample, if it is not clogged or destroyed during the experiment. However, because the channels of the 40 µm device are smaller they tend to clog faster (for instance by large particles).
2.3 Automatic detection of phase transitions
The optical brightness of a droplet changes during a phase transition (freezing or melting) due to the different interaction of light with the liquid and the solids. For phase transition detection, an in-house image processing LabVIEW program monitors automatically the optical brightness change. The program detects the droplets using a spherical shape criterion and sets a square surrounding the droplet that defines an array of pixels that are attributed to that specific droplet. A change in the optical brightness is represented by the gray level value of the image's pixels, ranging from 0 to 255. Freezing is calculated per movie frame and is defined as the subtraction of the brightness mean value for each droplet in two consecutive frames (ΔGL), thus allowing derivation of freezing rates. At the beginning of the analysis, the first 15 frames are used to identify the noise level of the signal by calculating its standard deviation SD (ΔGL). The program then searches for the maximal freezing signal that is also greater than 5 times the noise level. The temperature associated with this freezing signal is assigned as the freezing temperature for that droplet.
In this algorithm, the program can distinguish successfully between a phase transition event and noise that arises from the camera signal, droplet movement or any other interruption. Figure 2 presents a spectral analysis for different types of phase transitions observed in WISDOM. Since WISDOM operates in transmission microscopy mode, the light is scattered more efficiently by ice crystals in comparison with a liquid droplet and a freezing event involves droplet darkening and a negative signal. The negative signal of a freezing event of a single droplet is shown in Fig. 2a. In comparison, during melting, the droplet becomes brighter until all the crystals melt and the signal is positive. In Fig. 2b and c the analysis of a melting signal and a eutectic melting signal are presented for the entire frame.
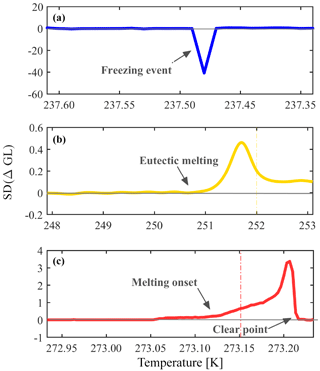
Figure 2Spectra of different phase transition events as observed in WISDOM. (a) Freezing, (b) eutectic melting, and (c) melting onset and clear point (liquefaction) are the mean of all sampled droplets in a single experiment. The phase transition is defined optically by the brightness information obtained by the gray level of the image pixels. SD (ΔGL) describes the standard deviation of the difference in mean GL for two consecutive frames. At the beginning of the experiment the noise level is studied and freezing or melting are detected only if SD (ΔGL) is as least 5 times greater than the noise standard deviation level. Freezing and melting examples are for pure water droplets and the eutectic melting example is for aqueous solution droplets of NaCl. The eutectic melting point of NaCl and pure water melting point are marked by the yellow and red lines in (b) and (c), respectively. In all cases the droplet diameter was 100 µm.
3.1 Temperature calibration
Temperature accuracy is a most important parameter in ice nucleation experiments. An error propagation analysis by Riechers et al. (2013) demonstrated how the temperature uncertainty may lead to a distribution of temperatures between different instruments. Therefore, we performed a thorough temperature calibration using the known eutectic melting points and the melting points of several aqueous solutions as calibration reference points. Although ice nucleation experiments are performed while cooling, the calibration experiments were done while heating to improve the calibration precision and to avoid biases associated with supercooling of the liquids (Budke and Koop, 2015).
3.1.1 Droplets thermalization
The temperature of the Linkam stage was measured at the upper center part of the cooling stage and hence may differ from the actual temperature of the droplets in the device due to thermal effects such as temperature gradients and temperature lag. During cooling or heating, a vertical temperature gradient may develop between the top of the device, in contact with the inner ambient of the cryostage, and the bottom of the device, which is in contact with the cooling silver block. This gradient is expected to increase in magnitude, as the temperature of the stage decreases or increases below or above ambient temperature. Edd et al. (2009) used a similar setup and found a difference between the top temperature and the bottom temperature of about 2 K around 237 K and 3 K around 227 K. Stan et al. (2009) also reported a vertical gradient of 1–2 K, which was reduced to 0.5 K with a flow of cooled N2 over their device. In addition, a thermal lag may arise during cooling or heating as the rate of temperature change is high and precludes proper temperature equilibration. Hence, a more accurate measurement of the droplet temperature is taken as a sum of the stage temperature with the contributions of both thermal gradient and lag.
Figure 3 demonstrates the combined effects of the temperature change rate and device properties on the thermalization of pure water droplets (double deionized water, DDW; 18.2 MΩ⋅cm). Specifically, freezing and melting experiments at different rates were performed. The temperature difference (ΔT) is the difference between the measured values and the extrapolated temperature at equilibrium conditions (0 K min−1). As expected, at slower temperature cooling (heating) rates, the droplets are more equilibrated with the stage temperature and ΔT is negligible. However, ΔT increases at higher temperature cooling (heating) rates (e.g., 10 K min−1). We observed that during cooling (heating) the droplet is warmer (colder) than the stage and will freeze (melt) at colder (warmer) temperature at higher cooling (heating) rates. We also found that because ΔT is higher, in absolute value, for devices of thicker PDMS and/or in devices which hold larger droplets, it should be considered in the final temperature calibration for these scenarios. Furthermore, ΔT was found to be almost symmetric for higher temperature cooling (heating) rates. However, for 1 K min−1, ΔT during cooling is higher than that for heating. Our conjecture is that this can be an effect of the higher thermal gradient that develops as the temperature decreases well below ambient (236 K).
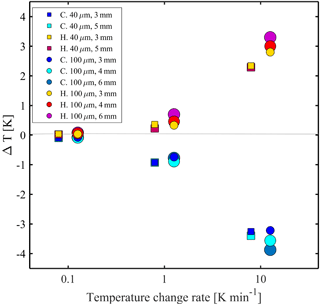
Figure 3The temperature difference (ΔT), defined as the temperature difference between the stage temperature and the droplet extrapolated temperature at equilibrium conditions at different cooling (heating) rates. Freezing and melting points of pure water are represented by circles and squares (40 and 100 µm droplet diameter, respectively) for different PDMS thicknesses and are represented by different colors. C denotes cooling and H denotes heating. Droplets are close to equilibrium with the stage temperature at rates <0.1 K min−1 and ΔT increases with increasing temperature change rate and with the PDMS height.
3.1.2 Melting of aqueous solutions
Figure 4 presents the measured melting points of NaCl solutions with different water activities. Reported melting points represent the temperature in which all ice crystals in the droplets completely melted, in contrast with melting temperatures reported for pure liquids such as water, where the onset of melting is defined as the melting point. Melting temperature results were consistent with theoretical melting temperatures reported in Koop and Zobrist (2009). This provides support to our conclusion that droplets thermalize with the cooling stage when using a heating rate of 0.1–1 K min−1. For faster heating rates (i.e., 10 K min−1), the thermal lag was more pronounced, leading to a melting point shift of about 2–3 K. For more concentrated solutions, faster heating rates shifted the melting points more.
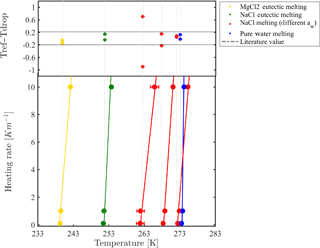
Figure 4Temperature calibration by melting points of eutectic solutions and pure water droplets for different heating rates. Calibration is presented for 100 µm droplets with 4 mm PDMS thickness. The onsets of pure water droplets are also considered. Eutectic melting is used for the colder temperature range (<253 K) while clear point (liquefaction) at various water activities is taken for the warmer temperature range. The upper panel presents the temperature difference between the reference value and the cooling stage temperature after calibration. Most of the differences are within the range ±0.2 K.
3.1.3 Melting of eutectic solutions
Some aqueous solutions, such as NaCl and MgCl2, arrange in a superlattice at a certain weight percent to form a solid with a well-defined melting point (eutectic) (252.05 K for NaCl and at 239.95 K for MgCl2) (Borgognoni et al., 2009; Farnam et al., 2016). Interestingly, this type of melting has a smaller optical signature compared to that of melting points of pure substances, as can be seen in Fig. 2b. We have set a specific water activity for a solution by determining its quantitative composition using the extended aerosol inorganic model (E-AIM) (Clegg et al., 1998) at room temperature (298 K). For calibration purposes, because eutectic melting had a negligible variation for different water activities used in the range of 0.99 to 0.95, we decided to take their average to achieve a single melting value. These eutectic melting temperatures are colder than the melting point of pure water and, therefore, are used for expanding the WISDOM calibration range.
The final calibration is obtained for a device with a specific PDMS thickness and at a specific cooling (heating) rate. For example, devices with 100 µm diameter sized droplet and of 4 mm PDMS thickness have a linear calibration curve of at 0.1 K min−1.
3.2 Measurement reproducibility and device variability
The device's inter-variability was determined from 20 devices by comparing their corresponding homogeneous freezing temperatures of pure water. Specifically, each device was recycled three times with freshly prepared droplets. Our results showed high reproducibility in the median freezing temperature, where 50 % of the probed droplets froze (T50), and high reproducibility in the melting point temperature. Variation within devices was always smaller than ±0.2 K at 1 and 0.1 K min−1 (variation within the devices over the whole freezing range is presented in Appendix A).
3.3 Homogeneous freezing rates of pure water
Homogeneous nucleation in supercooled water occurs in WISDOM between 238 and 237 K for a cooling rate of 1 K min−1 and droplet diameter of 100 µm. Figure 5 shows WISDOM nucleation rates in comparison with other similar instruments. It is seen that the slopes of the rate and temperatures are similar to the slopes reported for other instruments. The temperature where 50 % of droplets froze (T50) is also in the expected range according to model results of Hoffer (1961). WISDOM rates are slightly slower, but within the uncertainty of the instruments used by Stan et al. (2009) and Riechers et al. (2013). Stöckel et al. (2005) show a higher nucleation rate. This discrepancy can be explained by a decrease in the number of surface nucleation events due to the oil phase surrounding our droplets, whereas in Stöckel et al. (2005) droplets are suspended in air which allows surface nucleation to occur.
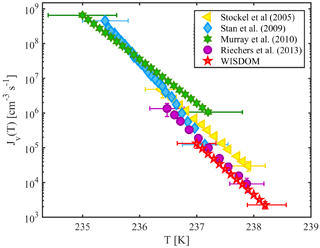
Figure 5The volume-dependent homogeneous freezing of pure water, derived for 100 µm droplets with 4 mm PDMS height. WISDOM rates are compared to relevant literature data. The obtained fit from WISDOM is . Temperature uncertainty for WISDOM is ±0.3 K.
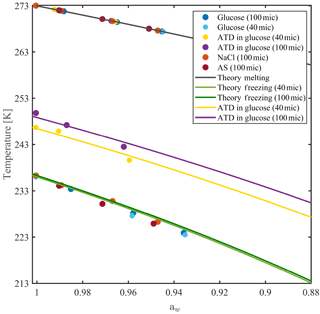
Figure 6Homogeneous and heterogeneous ice nucleation temperatures for 40 and 100 µm aqueous solution droplets as a function of solution water activity. Freezing and melting curves are derived from Koop et al. (2000). Heterogeneous ice nucleation is performed with 0.1 wt % of Arizona test dust (ATD) particles immersed in the droplets.
3.4 Homogeneous and heterogeneous freezing of aqueous solutions
The water-activity-based ice nucleation theory by Koop et al. (2000) describes the dependence of the freezing temperature depression on the water activity (aw) of the solution, regardless of the solute nature. Figure 6 presents the theoretical freezing and melting temperature curves from Koop et al. (2000) with homogeneous ice nucleation results measured in WISDOM, for four solutions with atmospheric relevance. Water activities for NaCl, ammonium sulfate (AS), glucose and levoglucosan mixtures were derived from the AIM model and were corrected for glucose and levoglucosan, for which water activity is temperature dependent (Zobrist et al., 2008; Knopf and Lopez, 2009). The experiments were conducted at 1 K min−1 for 40 and 100 µm droplet diameters. The results follow the theoretical curves of the water-activity-based ice nucleation, and the dependence of the homogeneous freezing on the droplet volume is as expected (Hoffer, 1961; Kuan-Ting and Wood, 2016) as the curve of the smaller diameter droplets (green curve) is slightly colder compared with the larger volume droplets (dark green curve).
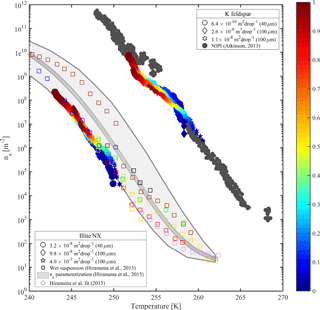
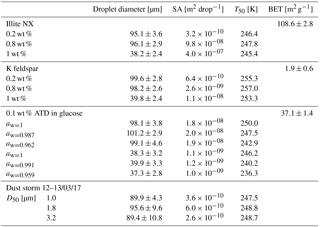
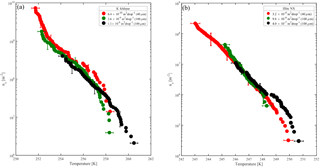
Figure 7Accumulated active site density spectra (ns) of K-feldspar and illite-NX particles as a function of temperature from validation experiments of immersion freezing in WISDOM. Frozen fraction values are represented by a color bar for a few surface area values that are exposed in 40 and 100 µm droplets. The dependence of the nucleation site density on the surface area is illustrated here. WISDOM uncertainties, propagated from surface area estimation and measured frozen fraction errors, are included within the size of the markers. For validation, previous immersion freezing measurements are also presented (Hiranuma et al., 2015 and Atkinson et al., 2013). T-binned data (1 ∘C) normalized by the Brunauer–Emmett–Teller (BET) surface area from Hiranuma et al. (2015) are presented in the color squares only for wet suspension analysis Bielefeld Ice Nucleation ARraY (BINARY), red; Colorado State University Ice Spectrometer (CSU-IS), orange; Leeds Nucleation by Immersed Particles Instrument (Leeds-NIPI), purple; Mainz acoustic levitator (M-AL), green; Mainz vertical wind tunnel (M-WT), black; North Carolina State cold stage (NC State-CS), brown; and University of Colorado Raman microscope cold stage (CU-RMCS), blue. The Hiranuma et al. (2015) log fit and ns (BET) parameterization are also presented.
Similar experiments were conducted for 0.1 wt % of Arizona test dust particles (ATD, Powder Technology Inc.) immersed in glucose solution droplets. The ATD particles facilitate the ice nucleation at warmer temperatures, in agreement with similar studies (Niedermeier et al., 2010; Hartmann et al., 2011), and the freezing depression follows the water-activity-based ice nucleation curves. Here, the dependence of the freezing point on the droplet volume is more pronounced, as the surface area of the immersed particles is higher; hence, they contain higher number of nucleation sites (Marcolli et al., 2007) as will be shown in the next section for two more types of dust.
Below 223 K, ice nucleation occurs at slightly lower temperatures than expected by the theoretical freezing curve. As the WISDOM temperature calibration is not valid in this temperature range, we cannot conclude if this is due to a change in the thermal conductivity of the device or an effect of the high concentration of the solute in the water.
3.5 Heterogeneous nucleation and ns spectra of INP in pure water
3.5.1 Standard dust powder
Heterogeneous freezing efficiencies of suspended mineral dusts K feldspar and illite NX in supercooled water droplets are presented in Fig. 7 and summarized in Table 1 and are compared to recent published data. The particles are suspended at different wt % and the frozen fraction of each suspension is derived as a function of temperature as represented by the color bar. To examine the freezing efficiency and compare the different mineral dust types, the results are normalized to the surface area within each droplet. Experiments were performed at 1 K min−1 for 40 and 100 µm droplet diameters. Suspension preparation and evaluation of the surface area are described in Appendix B.
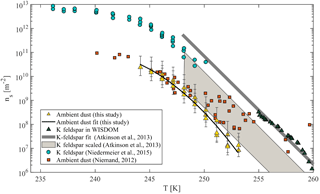
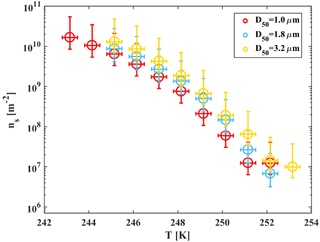
Figure 9Accumulated active site density spectra (ns) of ambient super-micron mineral dust particles collected in Israel during the dust event in 2017 for three MOUDI stages that were analyzed with D50 of 1, 1.8 and 3.2 µm. The fit (R2=0.98) is also presented. References of K-feldspar standard particles activated in WISDOM, Leeds-NIPI (Atkinson et al., 2013) and Leipzig Aerosol Cloud Interaction Simulator (LACIS; Niedermeier et al., 2015) instruments are presented, as well as ambient dust particles that were analyzed in AIDA and included Israeli dust (Niemand et al., 2012).
The results demonstrate the effect of dust surface area immersed in the droplets on the freezing parameters. The freezing temperatures increase with increasing surface area and are also reflected in the warming of the median frozen fraction (T50) colored in yellow. The spectra of the number of nucleation sites per unit surface area (ns) also support surface area dependence because all spectra converge to a single line. The ns results show the increase of nucleation sites at colder temperatures. Results from WISDOM are in good agreement with similar analyses from other instruments. In particular, ns is in best agreement with the Leeds-NIPI (Murray et al., 2011; Broadley et al., 2012) results both for K-feldspar and for illite-NX particles. Results of illite-NX particles are also in good agreement with the BINARY instrument (Budke and Koop, 2015) and reside within the uncertainty of both instruments. The linear trend of a few weight percent values supports the assumption that particles in suspension are uniformly distributed and the droplets contain approximately the same surface area.
3.5.2 Ambient mineral dust
WISDOM can also be used for analyzing collected ambient particles. Mineral dust particles were collected in Rehovot, Israel (31.9∘ N, 34.8∘ E; about 80 ), during dust storm events on 12–13 March 2017). The dust was transported from the Sahara and North Africa. Size-segregated ambient dust particles were collected on cyclopore polycarbonate filters using a micro-orifice uniform deposit impactor (MOUDI; MSP Corporation model 110-R, Marple et al., 1991), which operated at 30 L min−1 and for 24 h, similarly to Huffman et al. (2013) and Mason et al. (2015). The MOUDI has eleven stages with cut points (D50) of 0.056, 0.10, 0.18, 0.32, 0.56, 1.0, 1.8, 3.2, 5.6, 10 and 18 µm. The size distribution of the particles was obtained using an optical particle counter (OPC; GRIMM Technologies model 1.109) in the range of 0.25–32 µm and used for estimations of surface area immersed in the droplets (further details in Appendix C).
For heterogeneous freezing experiments, a quarter of each filter is placed with 300 µL DDW in a 1.5 mL Eppendorf vial and particles were extracted by intensive dry sonication (Hielcher; model UP200St VialTweeter). In Fig. 8, the spectra of the nucleation sites per unit surface area (ns) of three super-micron stages (D50 of 1.0, 1.8, 3.2 µm) are presented and summarized in Table 1. It is also seen that there are slightly more active sites for the larger particles (3.2 µm), as their surface area is higher and there is a higher probability to contain an active site. In Fig. 9, ns curves of the collected dust are compared to references of K-feldspar standard particles, analyzed in different instruments (the Leeds-NIPI, Atkinson et al., 2013; LACIS, Niedermeier et al., 2015), and to measurements of ambient dust samples, from different locations around the world, including Israeli settled dust, which was analyzed in the Aerosol Interaction and Dynamics in the Atmosphere (AIDA) chamber. Moreover, the freezing of the size-resolved mineral dust analyzed in this study by WISDOM (slope in the temperature range) is consistent with the (gray) polygon that represents the estimated freezing efficiency for natural concentrations of K feldspar in internally mixed mineral types (Atkinson et al., 2013). The results are also in agreement with Niemand et al. (2012), especially between 243 and 249 K. At warmer temperatures, the ns of ambient dust in this study showed lower efficiency than in Niemand et al. (2012). This difference can extend to 1 order of magnitude in ns and is more pronounced at smaller particles that were analyzed (around 1–1.8 µm diameter). For the larger particles, more nucleating sites are observed. Both the current study and Niemand et al. (2012) suggest that K feldspar is involved with the warmer part of their data (>248 K) as the results are consistent with the Atkinson et al. (2013) scale for ambient samples. The slope of the ns derived in this study is similar to the slope from Atkinson et al. (2013) at warmer temperatures. For the colder regime, the slope is similar to the slope presented by standard K-feldspar particles in Niedermeier et al. (2015).
3.6 WISDOM in comparison to other cold stage instruments
The microfluidics technology used in WISDOM solves some substantial issues inherent in other currently used instruments. (1) It allows for good control of the size and number of monodisperse droplets. (2) Additionally, it also allows for the fast production of hundreds of nearly monodisperse droplets, which minimizes sample sedimentation or agglomeration that may occur in a suspension, leading to a good estimation of the surface area of the suspended material. Moreover, several droplet diameters can be employed in the same device without its modification, which allows for (3) good statistics achieved by the individual analysis of hundreds of droplets; (4) the individual analysis of monodisperse droplets, in contrast to some emulsion techniques (such as a differential scanning calorimeter, DSC), which allows for obtaining the frozen fraction at each temperature and acquiring detailed information about active sites and freezing rates. (5) The use of oil minimizes possible artifacts from the droplets' evaporation, neighbor seeding or vapor transfer due to the Wegener–Bergeron–Findeisen processes. (6) The small volumes decrease freezing artifacts by impurities, thus allowing us to reach the homogeneous freezing threshold (−37 ∘C). (7) The static droplet array allows the recycling of the droplets for multiple freeze–thaw cycles. (8) The microfluidics method and the small droplet volumes enable working with small sample volumes which can be an advantage when working with atmospheric samples.
WISDOM has a very accurate temperature calibration that spans a wide temperature range, using the eutectic freezing method. WISDOM most resembles the instrument used by in Edd et al. (2009). However, it seems that issues with temperature calibration in Edd et al. (2009) led to a temperature offset and hence different freezing rates. Stan et al. (2009) achieved better temperature accuracy and high statistics. However, the freezing experiment was conducted in a flow mode, which is more complicated than in the WISDOM setup and requires complicated modeling. In addition, the cooling rates that were used were very fast, which induces additional errors. Riechers et al. (2013) had high temperature accuracy as they also used a DSC. However, they had to collect the droplets from the device as there was no static array option and this may add further complication and contamination.
The microfluidics technology also has disadvantages. These may include the following: (1) oil may interact with some of the analyzed particles, possibly leading to biased data; (2) the microchannels are susceptible to clogging; (3) it is not possible to perform any post analysis to the droplets' content after the experiment; (4) the small droplets' volumes reduce the sensitivity to rare active sites. This may be solved by performing many experiments or by using larger droplets with more surface area within the droplets.
The new setup WISDOM is based on microfluidics technology and its detailed validation is presented. Based on a set of validation measurements and a good agreement with other instruments, we conclude that WISDOM is a suitable tool for studying atmospheric ice nucleation, both in homogeneous and heterogeneous immersion freezing modes. Results of homogeneous freezing correspond to water-activity-based nucleation theory in supercooled droplets and represent volume nucleation rates well. Heterogeneous freezing in supercooled droplets also agrees well with literature data. Furthermore, freezing efficiency dependence on the particles' surface area within the droplets is clearly observed. Using microfluidics allows a mass production of picoliter monodisperse droplets using low volumes of suspensions, which can be beneficial for immersion freezing studies over a wide range of supercooling down to the homogenous temperature region. The good reproducibility of the devices, proved using pure water freezing cycles, enables the recycling of the same device for a few freezing cycles. It is also shown that the temperature uncertainty can be reduced if the temperature calibration includes the microfluidic devices' properties in the working temperature change rates, especially for melting experiments. In this work we have also demonstrated how WISDOM can be applied for studying the ice nucleation properties of ambient samples that contain a very small quantity of sample. The particles were collected using the MOUDI during Saharan dust storm event. Results are in correspondence with literature data of ambient dust and further support Atkinson et al. (2013) and the possible importance of K feldspar for ice nucleation in clouds, but further analysis of the mineralogy is still needed in order to verify that.
Data presented in this article are available from the first author upon request (naama.reicher@weizmann.ac.il).
Figure A1 presents the reproducibility of the microfluidic devices. For each device, the temperature variation between different freezing cycles of pure water is presented for the entire range of the freezing at various frozen fractions (0.1 to 1). These experiments were conducted for three cooling rates, 0.1, 1 and 10 K min−1. For 1 K min−1 the device's variability was the smallest, and the deviation in the results between different cycles was <0.2 K for most cases. While in some cycles the temperature was reproducible in <0.05 K, in other cycles the temperature varied in <0.2 K. This is not valid for frozen fractions <0.2, where the variability was the highest, as was the case for the other two cooling rates. This may be due to contaminants that exist in the water or in the devices themselves. The preparation of the devices is mostly inside a hood, but ambient particles may be trapped during the process. For a cooling rate of 0.1 K min−1, the variability between the different cycles was also <0.2 K, but the variability was higher in comparison to the variability seen at 1 K min−1. This can be explained stochastically and also may be attributed to better resolution of temperature reading during slower cooling rates. For 10 K min−1 the variability was between 0.2 and 0.3 K. The faster cooling rate may slow the equilibration of droplets' temperature with respect to the stage (as demonstrated in this work), and also low resolution of temperature reading due to the fast cooling rate. The variability presented here is also probably affected by the uncertainty of the temperature sensor of the Linkam stage (< 0.25 K).
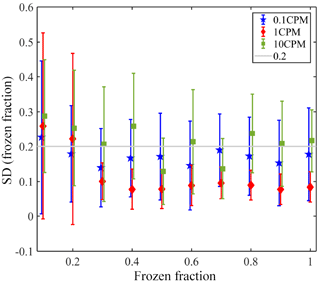
Figure A1Variability in the WISDOM devices for three cooling rates. The markers present the average temperature variability for all the devices and the error bars represent 1 standard deviation. A line is placed at Δ=0.2 K, the upper value of which explains the variability in the results of different freezing cycles at 0.1 and 1 K min−1.
Illite-NX, ATD and K-feldspar powders were suspended in DDW and sonicated twice for 30 s with a 20 s pause, using a Hielcher UP200St VialTweeter, adjusted especially for Eppendorf vials. K-feldspar suspensions were additionally stirred overnight as sonication alone was not enough to achieve a good suspension and intensive sedimentation was observed. For validation experiments, suspensions of 0.1 to 1 wt % were used. Figure B1 presents nucleation site densities for illite-NX and K-feldspar particles and the freezing efficiencies as function of the surface area in the droplets. Characterization of the powders can be found in Marcolli et al. (2007), in Atkinson et al. (2013) and in Hiranuma et al. (2015), and quantification the powders' specific surface area was based on N2 adsorption analysis of Brunauer–Emmett–Teller (BET) (Brunauer et al., 1938) using a Quantachrome Instruments Nova 2200e and resulted in 1.9±0.6 m2 g−1 for the K-feldspar powder, 108.6±2.8 m2 g−1 for the illite-NX powder and 37.1±1.4 m2 g−1 for the ATD powder. In order to ensure a proper analysis of the surface area, and avoid possible surface contaminants such as water, surface cleaning was done by degassing the powders at 60 ∘C for 3 h ahead of the BET analysis. Evaluation of the surface area in each droplet was then calculated by the wt % which was used, knowing the approximate surface area per mass and assuming that the mass is distributed uniformly inside the droplet with the same volume.
The GRIMM measurement was synchronized to the MOUDI stages for the estimation of the total surface area that was collected on the filter for droplet surface area estimation. For that, two base assumptions were made: (1) all the particles that were collected are extracted to the water later used for the freezing experiments; (2) sphericity of the particles is assumed. The GRIMM bins are synchronized to the MOUDI stages based on collection efficiency of the MOUDI, obtained from Marple et al. (1991). For example, on certain MOUDI stages, all the particles whose own diameter is larger than the D50 have a high chance of being impacted on that stage. All the rest of the sizes, which are smaller in their diameter, will continue to the next stage and will have a high chance of depositing there. Hence, the GRIMM's bins were synchronized to the MOUDI D50 stages. For the ns calculations, the surface area was based on the number of particles that were measured in a certain bin and their total surface area. To calculate the surface area of a particle (assuming sphericity) in a certain bin, the midpoint of that bin was used as a radius. To calculate the total mass of the particles in each filter, dust density of quartz was used (2.65 g cm−3), as this is usually the dominant mineral (Mahowald et al., 2014). The error of the ns data is propagated from the error in the frozen fraction, the error of the droplet's volume and the error of the MOUDI's collection efficiency in the different stages – the latter was the dominant one.
For control, analysis of blank filters was done. The blanks were sonicated before analyzing them and freezing was mostly colder than the freezing temperatures that are presented here and hence no special reduction of the final active sites was done.
The authors declare that they have no conflict of interest.
We gratefully acknowledge support from the Ice Nuclei Research Unit
(INUIT) of the German DFG, to The Helen Kimmel Center for Planetary
Sciences, The de Botton Center for Marine Sciences and the
Weizmann–UK Making Connections program for funding this work. We
also thank Daniel Knopf, Carsten Budke, Thomas
Koop, Ido Braslavski, and Nir Freidman for their advices
as well as Ben Murray and Heinz Bingemer for sharing
the K-feldspar and illite-NX powder standards.
Edited by: Joachim Curtius
Reviewed by: two anonymous referees
Alpert, P. A., Aller, J. Y., and Knopf, D. A.: Ice nucleation from aqueous NaCl droplets with and without marine diatoms, Atmos. Chem. Phys., 11, 5539–5555, https://doi.org/10.5194/acp-11-5539-2011, 2011.
Ansmann, A., Tesche, M., Althausen, D., Müller, D., Seifert, P., Freudenthaler, V., Heese, B., Wiegner, M., Pisani, G., Knippertz, P., and Dubovik, O.: Influence of Saharan dust on cloud glaciation in southern Morocco during the Saharan Mineral Dust Experiment, J. Geophys. Res.-Atmos., 113, D04210, https://doi.org/10.1029/2007JD008785, 2008.
Atkinson, J. D., Murray, B. J., Woodhouse, M. T., Whale, T. F., Baustian, K. J., Carslaw, K. S., Dobbie, S., O'Sullivan, D., and Malkin, T. L.: The importance of feldspar for ice nucleation by mineral dust in mixed-phase clouds, Nature, 498, 355–358, 2013.
Borgognoni, C. F., Tattini Junior, V., Ayrosa, A. M. I. B., Polakiewicz, B., Leirner, A. A., Maizato, M. J. S., Higa, O. Z., Beppu, M. M., and Pitombo, R. N. d. M.: The influence of freezing rates on bovine pericardium tissue Freeze-drying, Braz. Arch. Biol. Techn., 52, 1493–1504, 2009.
Broadley, S. L., Murray, B. J., Herbert, R. J., Atkinson, J. D., Dobbie, S., Malkin, T. L., Condliffe, E., and Neve, L.: Immersion mode heterogeneous ice nucleation by an illite rich powder representative of atmospheric mineral dust, Atmos. Chem. Phys., 12, 287–307, https://doi.org/10.5194/acp-12-287-2012, 2012.
Brunauer, S., Emmett, P. H., and Teller, E.: Adsorption of gases in multimolecular layers, J. Am. Chem. Soc., 60, 309–319, 1938.
Budke, C. and Koop, T.: BINARY: an optical freezing array for assessing temperature and time dependence of heterogeneous ice nucleation, Atmos. Meas. Tech., 8, 689–703, https://doi.org/10.5194/amt-8-689-2015, 2015.
Cantrell, W. and Heymsfield, A.: Production of Ice in Tropospheric clouds: a review, B. Am. Meteorol. Soc., 86, 795–807, 2005.
Clegg, S. L., Brimblecombe, P., and Wexler, A. S.: Thermodynamic Model of the System H+––––H2O at Tropospheric Temperatures, J. Phys. Chem. A, 102, 2137–2154, available at: http://www.aim.env.uea.ac.uk/aim/model3/model3a.php, 1998.
de Boer, G., Morrison, H., Shupe, M. D., and Hildner, R.: Evidence of liquid dependent ice nucleation in high-latitude stratiform clouds from surface remote sensors, Geophys. Res. Lett., 38, L01803, https://doi.org/10.1029/2010GL046016, 2011.
DeMott, P. J., Prenni, A. J., Liu, X., Kreidenweis, S. M., Petters, M. D., Twohy, C. H., Richardson, M. S., Eidhammer, T., and Rogers, D. C.: Predicting global atmospheric ice nuclei distributions and their impacts on climate, P. Natl. Acad. Sci. USA, 107, 11217–11222, 2010.
Edd, J. F., Humphry, K. J., Irimia, D., Weitz, D. A., and Toner, M.: Nucleation and solidification in static arrays of monodisperse drops, Lab Chip, 9, 1859–1865, 2009.
Eddings, M. A., Johnson, M. A., and Gale, B. K.: Determining the optimal PDMS–PDMS bonding technique for microfluidic devices, J. Micromech. Microeng., 18, 067001, https://doi.org/10.1088/0960-1317/18/6/067001, 2008.
Farnam, Y., Villani, C., Washington, T., Spence, M., Jain, J., and Jason Weiss, W.: Performance of carbonated calcium silicate based cement pastes and mortars exposed to NaCl and MgCl2 deicing salt, Constr. Build. Mater., 111, 63–71, 2016.
Field, P. R., Heymsfield, A. J., Shipway, B. J., DeMott, P. J., Pratt, K. A., Rogers, D. C., Stith, J., and Prather, K. A.: Ice in clouds experiment–layer clouds, Part II: Testing characteristics of heterogeneous ice formation in lee wave clouds, J. Atmos. Sci., 69, 1066–1079, 2012.
Hartmann, S., Niedermeier, D., Voigtländer, J., Clauss, T., Shaw, R. A., Wex, H., Kiselev, A., and Stratmann, F.: Homogeneous and heterogeneous ice nucleation at LACIS: operating principle and theoretical studies, Atmos. Chem. Phys., 11, 1753–1767, https://doi.org/10.5194/acp-11-1753-2011, 2011.
Hiranuma, N., Augustin-Bauditz, S., Bingemer, H., Budke, C., Curtius, J., Danielczok, A., Diehl, K., Dreischmeier, K., Ebert, M., Frank, F., Hoffmann, N., Kandler, K., Kiselev, A., Koop, T., Leisner, T., Möhler, O., Nillius, B., Peckhaus, A., Rose, D., Weinbruch, S., Wex, H., Boose, Y., DeMott, P. J., Hader, J. D., Hill, T. C. J., Kanji, Z. A., Kulkarni, G., Levin, E. J. T., McCluskey, C. S., Murakami, M., Murray, B. J., Niedermeier, D., Petters, M. D., O'Sullivan, D., Saito, A., Schill, G. P., Tajiri, T., Tolbert, M. A., Welti, A., Whale, T. F., Wright, T. P., and Yamashita, K.: A comprehensive laboratory study on the immersion freezing behavior of illite NX particles: a comparison of 17 ice nucleation measurement techniques, Atmos. Chem. Phys., 15, 2489–2518, https://doi.org/10.5194/acp-15-2489-2015, 2015.
Hoffer, T. E.: A laboratory investigation of droplet freezing, J. Meteorol., 18, 766–778, 1961.
Hoose, C. and Möhler, O.: Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments, Atmos. Chem. Phys., 12, 9817–9854, https://doi.org/10.5194/acp-12-9817-2012, 2012.
Huffman, J. A., Prenni, A. J., DeMott, P. J., Pöhlker, C., Mason, R. H., Robinson, N. H., Fröhlich-Nowoisky, J., Tobo, Y., Després, V. R., Garcia, E., Gochis, D. J., Harris, E., Müller-Germann, I., Ruzene, C., Schmer, B., Sinha, B., Day, D. A., Andreae, M. O., Jimenez, J. L., Gallagher, M., Kreidenweis, S. M., Bertram, A. K., and Pöschl, U.: High concentrations of biological aerosol particles and ice nuclei during and after rain, Atmos. Chem. Phys., 13, 6151–6164, https://doi.org/10.5194/acp-13-6151-2013, 2013.
IPCC: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013.
Knopf, D. A. and Lopez, M. D.: Homogeneous ice freezing temperatures and ice nucleation rates of aqueous ammonium sulfate and aqueous levoglucosan particles for relevant atmospheric conditions, Phys. Chem. Chem. Phys., 11, 8056–8068, 2009.
Koop, T. and Zobrist, B.: Parameterizations for ice nucleation in biological and atmospheric systems, Phys. Chem. Chem. Phys., 11, 10839–10850, 2009.
Koop, T., Luo, B., Tsias, A., and Peter, T.: Water activity as the determinant for homogeneous ice nucleation in aqueous solutions, Nature, 406, 611–614, 2000.
Mahowald, N., Albani, S., Kok, J. F., Engelstaeder, S., Scanza, R., Ward, D. S., and Flanner, M. G.: The size distribution of desert dust aerosols and its impact on the Earth system, Aeolian Res., 15, 53–71, 2014.
Marcolli, C., Gedamke, S., Peter, T., and Zobrist, B.: Efficiency of immersion mode ice nucleation on surrogates of mineral dust, Atmos. Chem. Phys., 7, 5081–5091, https://doi.org/10.5194/acp-7-5081-2007, 2007.
Marple, V. A., Rubow, K. L., and Behm, S. M.: A Microorifice Uniform Deposit Impactor (MOUDI): description, calibration, and use, Aerosol Sci. Tech., 14, 434–446, 1991.
Mason, R. H., Chou, C., McCluskey, C. S., Levin, E. J. T., Schiller, C. L., Hill, T. C. J., Huffman, J. A., DeMott, P. J., and Bertram, A. K.: The micro-orifice uniform deposit impactor–droplet freezing technique (MOUDI-DFT) for measuring concentrations of ice nucleating particles as a function of size: improvements and initial validation, Atmos. Meas. Tech., 8, 2449–2462, https://doi.org/10.5194/amt-8-2449-2015, 2015.
Murray, B. J., Broadley, S. L., Wilson, T. W., Bull, S. J., Wills, R. H., Christenson, H. K., and Murray, E. J.: Kinetics of the homogeneous freezing of water, Phys. Chem. Chem. Phys., 12, 10380–10387, 2010.
Murray, B. J., Broadley, S. L., Wilson, T. W., Atkinson, J. D., and Wills, R. H.: Heterogeneous freezing of water droplets containing kaolinite particles, Atmos. Chem. Phys., 11, 4191–4207, https://doi.org/10.5194/acp-11-4191-2011, 2011.
Murray, B. J., O'Sullivan, D., Atkinson, J. D., and Webb, M. E.: Ice nucleation by particles immersed in supercooled cloud droplets, Chem. Soc. Rev., 41, 6519–6554, 2012.
Nagare, B., Marcolli, C., Welti, A., Stetzer, O., and Lohmann, U.: Comparing contact and immersion freezing from continuous flow diffusion chambers, Atmos. Chem. Phys., 16, 8899–8914, https://doi.org/10.5194/acp-16-8899-2016, 2016.
Neethirajan, S., Kobayashi, I., Nakajima, M., Wu, D., Nandagopal, S., and Lin, F.: Microfluidics for food, agriculture and biosystems industries, Lab Chip, 11, 1574–1586, 2011.
Niedermeier, D., Hartmann, S., Shaw, R. A., Covert, D., Mentel, T. F., Schneider, J., Poulain, L., Reitz, P., Spindler, C., Clauss, T., Kiselev, A., Hallbauer, E., Wex, H., Mildenberger, K., and Stratmann, F.: Heterogeneous freezing of droplets with immersed mineral dust particles – measurements and parameterization, Atmos. Chem. Phys., 10, 3601–3614, https://doi.org/10.5194/acp-10-3601-2010, 2010.
Niedermeier, D., Augustin-Bauditz, S., Hartmann, S., Wex, H., Ignatius, K., and Stratmann, F.: Can we define an asymptotic value for the ice active surface site density for heterogeneous ice nucleation?, J. Geophys. Res.-Atmos., 120, 5036–5046, 2015.
Niemand, M., Möhler, O., Vogel, B., Vogel, H., Hoose, C., Connolly, P., Klein, H., Bingemer, H., DeMott, P., Skrotzki, J., and Leisner, T.: A particle-surface-area-based parameterization of immersion freezing on desert dust particles, J. Atmos. Sci., 69, 3077–3092, 2012.
O, K.-T. and Wood, R.: Exploring an approximation for the homogeneous freezing temperature of water droplets, Atmos. Chem. Phys., 16, 7239–7249, https://doi.org/10.5194/acp-16-7239-2016, 2016.
Possner, A., Ekman, A. M. L., and Lohmann, U.: Cloud response and feedback processes in stratiform mixed-phase clouds perturbed by ship exhaust, Geophys. Res. Lett., 44, 1964–1972, 2017.
Pruppacher, H. R., Klett, J. D., and Wang, P. K.: Microphysics of clouds and precipitation, Aerosol Sci. Tech., 28, 381–382, 1998.
Riechers, B., Wittbracht, F., Hutten, A., and Koop, T.: The homogeneous ice nucleation rate of water droplets produced in a microfluidic device and the role of temperature uncertainty, Phys. Chem. Chem. Phys., 15, 5873–5887, 2013.
Rosenfeld, D. and Woodley, W. L.: Deep convective clouds with sustained supercooled liquid water down to −37.5 ∘C, Nature, 405, 440–442, 2000.
Sackmann, E. K., Fulton, A. L., and Beebe, D. J.: The present and future role of microfluidics in biomedical research, Nature, 507, 181–189, 2014.
Schmitz, C. H. J., Rowat, A. C., Koster, S., and Weitz, D. A.: Dropspots: a picoliter array in a microfluidic device, Lab Chip, 9, 44–49, 2009.
Schnaiter, M., Järvinen, E., Vochezer, P., Abdelmonem, A., Wagner, R., Jourdan, O., Mioche, G., Shcherbakov, V. N., Schmitt, C. G., Tricoli, U., Ulanowski, Z., and Heymsfield, A. J.: Cloud chamber experiments on the origin of ice crystal complexity in cirrus clouds, Atmos. Chem. Phys., 16, 5091–5110, https://doi.org/10.5194/acp-16-5091-2016, 2016.
Stan, C. A., Schneider, G. F., Shevkoplyas, S. S., Hashimoto, M., Ibanescu, M., Wiley, B. J., and Whitesides, G. M.: A microfluidic apparatus for the study of ice nucleation in supercooled water drops, Lab Chip, 9, 2293–2305, 2009.
Stöckel, P., Weidinger, I. M., Baumgärtel, H., and Leisner, T.: Rates of homogeneous ice nucleation in levitated H2O and D2O droplets, J. Phys. Chem. A, 109, 2540–2546, 2005.
Ullrich, R., Hoose, C., Möhler, O., Niemand, M., Wagner, R., Höhler, K., Hiranuma, N., Saathoff, H., and Leisner, T.: A new ice nucleation active site parameterization for desert dust and soot, J. Atmos. Sci., 74, 699–717, 2017.
Vali, G.: Quantitative evaluation of experimental results an the heterogeneous freezing nucleation of supercooled liquids, J. Atmos. Sci., 28, 402–409, 1971.
Vali, G., DeMott, P. J., Möhler, O., and Whale, T. F.: Technical Note: A proposal for ice nucleation terminology, Atmos. Chem. Phys., 15, 10263–10270, https://doi.org/10.5194/acp-15-10263-2015, 2015.
Whale, T. F., Murray, B. J., O'Sullivan, D., Wilson, T. W., Umo, N. S., Baustian, K. J., Atkinson, J. D., Workneh, D. A., and Morris, G. J.: A technique for quantifying heterogeneous ice nucleation in microlitre supercooled water droplets, Atmos. Meas. Tech., 8, 2437–2447, https://doi.org/10.5194/amt-8-2437-2015, 2015.
Whitesides, G. M.: The origins and the future of microfluidics, Nature, 442, 368–373, 2006.
Zobrist, B., Marcolli, C., Peter, T., and Koop, T.: Heterogeneous ice nucleation in aqueous solutions: the role of water activity, J. Phys. Chem. A, 112, 3965–3975, 2008.
- Abstract
- Introduction
- Experimental setup
- Results and WISDOM validation
- Summary and conclusions
- Data availability
- Appendix A: Device inter-variability over the whole freezing range
- Appendix B: Suspension preparation and characterization
- Appendix C: Collection of ambient particles during dust storm events in Rehovot
- Competing interests
- Acknowledgements
- References
- Abstract
- Introduction
- Experimental setup
- Results and WISDOM validation
- Summary and conclusions
- Data availability
- Appendix A: Device inter-variability over the whole freezing range
- Appendix B: Suspension preparation and characterization
- Appendix C: Collection of ambient particles during dust storm events in Rehovot
- Competing interests
- Acknowledgements
- References