the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The influence of instrumental line shape degradation on NDACC gas retrievals: total column and profile
Youwen Sun
Mathias Palm
Frank Hase
David Griffith
Christine Weinzierl
Christof Petri
Wei Wang
Justus Notholt
We simulated instrumental line shape (ILS) degradations with respect to typical types of misalignment, and compared their influence on each NDACC (Network for Detection of Atmospheric Composition Change) gas. The sensitivities of the total column, the root mean square (rms) of the fitting residual, the total random uncertainty, the total systematic uncertainty, the total uncertainty, degrees of freedom for signal (DOFs), and the profile with respect to different levels of ILS degradation for all current standard NDACC gases, i.e. O3, HNO3, HCl, HF, ClONO2, CH4, CO, N2O, C2H6, and HCN, were investigated. The influence of an imperfect ILS on NDACC gases' retrieval was assessed, and the consistency under different meteorological conditions and solar zenith angles (SZAs) were examined. The study concluded that the influence of ILS degradation can be approximated by the linear sum of individual modulation efficiency (ME) amplitude influence and phase error (PE) influence. The PE influence is of secondary importance compared with the ME amplitude. Generally, the stratospheric gases are more sensitive to ILS degradation than the tropospheric gases, and the positive ME influence is larger than the negative ME. For a typical ILS degradation (10 %), the total columns of stratospheric gases O3, HNO3, HCl, HF, and ClONO2 changed by 1.9, 0.7, 4, 3, and 23 %, respectively, while the columns of tropospheric gases CH4, CO, N2O, C2H6, and HCN changed by 0.04, 2.1, 0.2, 1.1, and 0.75 %, respectively. In order to suppress the fractional difference in the total column for ClONO2 and other NDACC gases within 10 and 1 %, respectively, the maximum positive ME degradations for O3, HNO3, HCl, HF, ClONO2, CO, C2H6, and HCN should be less than 6, 15, 5, 5, 5, 5, 9, and 13 %, respectively; the maximum negative ME degradations for O3, HCl, and HF should be less than 6, 12, and 12 %, respectively; the influence of ILS degradation on CH4 and N2O can be regarded as being negligible.
- Article
(15934 KB) - Companion paper
- BibTeX
- EndNote
In order to achieve consistent results between different FTIR (Fourier transform infrared) sites, the TCCON (Total Carbon Column Observing Network; http://www.tccon.caltech.edu/, last access: 11 May 2018) and NDACC (Network for Detection of Atmospheric Composition Change; http://www.ndacc.org/, last access: 11 May 2018) have developed strict data acquisition and retrieval methods to minimize site to site differences (Hase et al., 2012; Wunch et al., 2010, 2011; Washenfelder, 2006; Messerschmidt et al., 2010; Kurylo, 1991; Davis et al., 2001; Schneider et al., 2008; Kohlhepp et al., 2011; Hannigan and Coffey, 2009; Vigouroux et al., 2008, 2015). Interferograms are acquired with similar instruments operated with common detectors, acquisition electronics, and/or optical filters. These interferograms are first converted to spectra and then these spectra are analysed using dedicated processing algorithms, i.e. GFIT, PROFFIT, or SFIT (Wunch et al., 2010, 2015; Hase et al., 2006; Hannigan and Coffey, 2009). Typically, the TCCON only uses Bruker 125HR instruments (http://www.tccon.caltech.edu/; https://www.bruker.com/, last access: 11 May 2018) with specified settings (entrance aperture, amplification of the detected signal). In the NDACC, other instruments are used as well, e.g. the Bruker M series, a BOMEM DA8 in Toronto, Canada, and a self-built spectrometer in Pasadena, USA (http://www.ndacc.org/; https://www.bruker.com/). FTIR spectrometers are highly precise and stable devices, and if carefully aligned, the instrumental line shape (ILS) might not be far from the theoretical limit. However, their alignment can change abruptly as a consequence of operator intervention or drift slowly due to mechanical degradation over time (Olsen and Randerson, 2004; Duchatelet et al., 2010; Hase et al., 2012; Feist et al., 2016). Moreover, the NDACC observation may change the entrance field stop size if incident radiation changes. This practice may introduce a dependency of the instrument alignment status on the optical settings because the mechanical errors between different field stops may be non-negligible and inconsistent (Sun et al., 2017). Biases between sites would arise if all these misalignments were not properly characterized.
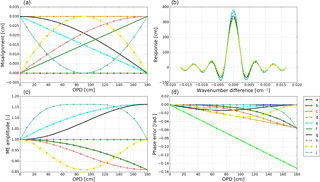
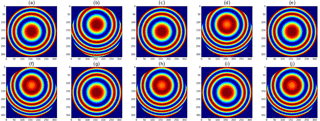
Figure 1Simulated ILS degradation with respect to different types of misalignment. The results are derived from ALIGN60. Panel (a) demonstrates different types of misalignment (a to j) used in the simulation, panel (b) shows the resulting ILS, panel (c) shows the resulting ME amplitude, and panel (d) shows the resulting PE. Descriptions of the misalignments a to j are listed in Table 1.
The TCCON only operates in the near-infrared region (NIR) and focuses on columns of fewer gases, while the NDACC operates in both the NIR and the mid-infrared region (MIR) and focuses on both columns and profiles of many gases. The TCCON assumes an ideal ILS in spectra retrieval, and the maximum ILS degradation is prescribed as 5 % for the modulation efficiency (ME) amplitude (Wunch et al., 2011, 2015). This assumption still holds within the required accuracy of the results. In the NDACC gases' retrieval, the ILS can be assumed to be ideal if the spectrometer is well aligned, or if misalignment exists, described by LINEFIT results derived from dedicated cell measurements or retrieved together with the gas profile from an atmospheric spectrum using a polynomial (Vigouroux et al., 2008, 2015). The answers to how these ILS treatments influence the NDACC gases' retrieval and how much ILS deviation from unity is acceptable for each NDACC gas if an ideal line shape is assumed are still not fully quantified, and it may be better to assume an ideal ILS. The practice of co-retrieving ILS parameters from atmospheric spectra without dedicated cell measurements is not to be recommended because the observed shapes of spectral lines are exploited primarily for inferring the vertical distribution of the trace gases; the ILS and the trace gas profiles have similar effects on the line shape, i.e. changing the shape and width of the line. Overlapping lines, i.e. due to interfering gases, may introduce asymmetry in the absorption lines which may be undistinguishable from an ILS phase deviation.
This paper investigates the influence of ILS degradation on the total column and the profile of current standard NDACC gas retrievals and deduces the maximum ILS deviations allowable for suppressing the influence within a specified acceptable range.
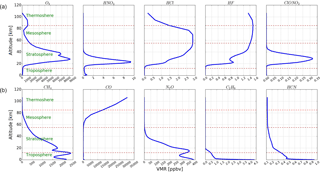
Figure 3Typical profiles of 10 NDACC gases. The panels in (b) show the five tropospheric gases, i.e. CH4, CO, N2O, C2H6, and HCN. The panels in (a) show the five stratospheric gases, i.e. O3, HNO3, HCl, HF, and ClONO2. Although the CO concentration above 60 km is much higher than that in the troposphere, it is regarded as tropospheric gas because it is an anthropologic pollution gas and shows large variation in the troposphere.
The ILS is the Fourier transform of the weighting applied to the interferogram. This weighting consists of two parts: an artificially applied part to change the calculated spectrum and an unavoidable part which is due to the fact that the interferogram is finite in length (box car function), the divergence of the beam is non-zero (due to the non-zero entrance aperture), and several other effects which are due to misalignment (Davis et al., 2001, chap. 9). The ILS consisting of only the unavoidable parts of the line shape is called the ideal line shape.
The theoretical ideal ILS, as defined in Eq. (3), when the instrument is well aligned, is a convolution of sinc and rectangular functions (defined in Eqs. 1 and 2), representing the finite length of the interferogram and the finite circular field of view (FOV) of the spectrometer (Davis et al., 2001).
where σ is the wavenumber, σ0 is the central wavenumber, L is the optical path difference (OPD), and θ is the angular radius of the circular internal FOV of the spectrometer. For standard NDACC measuring conditions, L≥180 cm and θ defined by the entrance field stop size in the light path.
The LINEFIT software calculates the deviation of the measured ILS from the ideal ILS (Hase et al., 2001, 2012). It retrieves a complex ME as a function of the OPD, which is represented by a ME amplitude and a phase error (PE) (Hase et al., 1999). The ME amplitude is connected to the width of the ILS, while the PE quantifies the degree of ILS asymmetry. For a perfectly aligned spectrometer, it would meet the ideal nominal ILS characteristics if smear and vignetting effects were neglected, and thus have an ME amplitude of unity and a PE of zero along the whole interferogram. However, if a FTIR spectrometer were subject to misalignment, the ME amplitude would deviate from unity and the PE would deviate from zero (Hase et al., 2012). This results in an imperfect ILS.
We use the program ALIGN60 to simulate ILS degradation in a high-resolution FTIR spectrometer typically used in the NDACC. As an auxiliary tool of LINEFIT, ALIGN60 is a ray-tracing model for FTIR spectrometers following the classical Michelson design, assuming one fixed and one movable arm, and using cube corners instead of plane mirrors. It calculates the resulting phase distortions in the recombined beam and from these deduces the variable intensity observed by the detector. ALIGN60 takes into account the lateral shear error of the movable retro-reflector as a function of the OPD, a decentring of the field stop with respect to the optical axis, an unsharp boundary line or deformation of the field stop image (as possibly caused by a defocused collimator), and vignetting effects with increasing OPD. It can generate trustworthy results with respect to all types of misalignment (Hase et al., 1999). In this simulation, the entrance beam section was assumed to be circular with a diameter of 8.0 cm. The ILS was only calculated from the positive side of the interferogram. The smear and vignetting effects were not taken into account. The misalignment of a FTIR spectrometer can be expressed via two perpendicular axes perpendicular to the beam direction. For a circular entrance beam, the same misalignment in either direction results in a similar ILS. Thus, this work only considers misalignment in one axis.
The misalignments as inputs of ALIGN60 are listed in Table 1, the resulting ILSs are shown in Fig. 1, and the corresponding Haidinger fringes at the maximum OPD are shown in Fig. 2. The ME deviation, the decentring of Haidinger fringes, and the ILS deterioration varying over misalignment are evident. All types of misalignment cause non-linear ME deviations except the decentring of measuring laser (c) and the constant shear (d), which mainly affect PE and result in linear PE deviation. Two types of ILS degradation are evident; one is referred to as a positive ME and has a ME amplitude of larger than unity. The other one is referred to as a negative ME and has a ME amplitude of less than unity. Typically, the increasing misalignment with increasing OPD (b, f, h, or i) causes negative ME amplitude and the decreasing misalignment with increasing OPD (e, g, or j) causes positive ME amplitude. For the same misalignment amplitude, the decreasing misalignment causes more ME deviation than the increasing misalignment. Regardless of positive or negative ME, the ME deviation shape depends on misalignment type and the same misalignment amplitude causes the same deviation in ME amplitude. The decentring of the entrance filed stop is equivalent to the linear increasing misalignment.
4.1 Retrieval strategy
The influence of ILS degradation on all current standard NDACC gases, i.e. O3, HNO3, HCl, HF, ClONO2, CH4, CO, N2O, C2H6, and HCN, is investigated. Typical atmospheric vertical profiles of these gases are shown in Fig. 3. There are five stratospheric gases and five tropospheric gases. The retrieval settings for all these gases as recommended by the NDACC are listed in Table 2 (https://www2.acom.ucar.edu/irwg/links, last access: 11 May 2018). The latest version of the profile retrieval algorithm SFIT4 v 0.9.4.4 is used (http://www.ndacc.org/, last access: 11 May 2018). The basic principle of SFIT4 is the use of an optimal estimation technique for fitting calculated to observed spectra (Rodgers, 2000; Hannigan and Coffey, 2009). All spectroscopic line parameters are adopted from HITRAN 2008 (Rothman et al., 2009). This might not be ideal, but we maintain this to achieve consistent results. A priori profiles of pressure, temperature, and water vapour for the measurement days are interpolated from the National Centers for Environmental Protection and National Center for Atmospheric Research (NCEP/NCAR) reanalysis (Kalnay et al., 1996). A priori profiles of the target gases and the interfering gases except H2O use the WACCM4 (Whole Atmosphere Community Climate Model) model data. We follow the NDACC standard convention with respect to microwindows' (MWs) selection and the interfering gases consideration (https://www2.acom.ucar.edu/irwg/links). For the interfering molecules that affect the target gas retrieval, H2O should be treated with care as it is almost always present in all MWs, to varying degrees. It has been dealt with differently for different gases. For HNO3 and ClONO2, H2O is treated as the other interfering species: only scaling of a single a priori profile is done. For other gases, the H2O profile is retrieved simultaneously with the target gas profile. No de-weighting signal-to-noise ratios (SNRs) are used, except for CO and HCl which utilize a de-weighting SNR of 500 and 300, respectively.
The selection of the regularization (a priori covariance matrix Sa and SNR) cannot be easily standardized because it depends on the real variability for each gas. In optimal estimation, the selection of Sa is very important in the inversion process and, together with the measurement noise error covariance matrix Sε, will lead to the following averaging kernel matrix A (Rodgers, 2000):
where Gy is the sensitivity of the retrieval to the measurement. Kx is the weighting function matrix or Jacobian matrix that links the measurement vector y to the state vector x: Δy=KxΔx. A characterizes the vertical information contained in the FTIR retrievals. In this study, we assume Sε to be diagonal and its diagonal elements are the inverse square of the SNR. The vertical information content of the retrieved target gas profile can be quantified by the number of degrees of freedom for signal (DOFs), which is the trace of A, defined in Rodgers (2000) by
The diagonal elements of Sa represent the assumed variability of the target gas volume mixing ratio (VMR) at a given altitude, and the off-diagonal elements represent the correlation between the VMR at different altitudes. We can see in Table 3 that, except CO and HCN, the target gases are using an a priori covariance matrix with diagonal elements constant, with altitudes corresponding to 10, 20, 50, or 100 % variability; the largest variabilities are for HNO3, HCl, and ClONO2. For CO, the diagonal elements of Sa correspond to 27 % from the ground up to 34 km and decrease down to 11 % at the top of the atmosphere. For HCN, the diagonal elements of Sa correspond to 79 % from the ground up to 5 km and decrease down to 21 % at the top of atmosphere. No correlation of off-diagonal matrix elements is assumed in all retrievals except for ClONO2, which assumes exponential correlation with a HWHM (half-width at half-maximum) of 8 km. The SNR values for all retrievals are the real values taken from each individual spectrum. The ILSs for all retrievals are obtained using the simulations in Sect. 3.
4.2 Averaging kernels
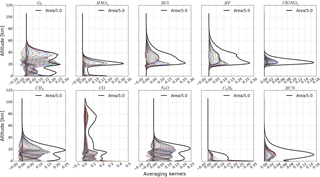
The rows of A are the so-called averaging kernels and they represent the sensitivity of the retrieved profile to the real profile. Their full-width at half-maximum (FWHM) is a measure of the vertical resolution of the retrieval at a given altitude. The area of averaging kernels represents sensitivity of the retrievals to the measurement. This sensitivity at altitude k is calculated as the sum of the elements of the corresponding averaging kernels, ∑iAki. It indicates the fraction of the retrieval at each altitude that comes from the measurement rather than from the a priori information (Rodgers, 2000). A value close to zero at a certain altitude indicates that the retrieved profile at that altitude is nearly independent of the measurement and is therefore approaching the a priori profile.
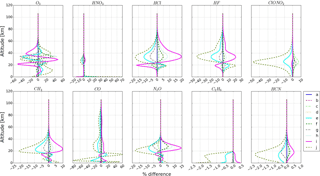
The averaging kernels and their areas for these 10 NDACC gases are shown in Fig. 4. The altitude ranges with sensitivity larger than 0.5 and the corresponding total DOFs are summarized in Table 3. These sensitivity ranges indicate that the retrieved profile information comes, by more than 50 %, from the measurement, or, in other words, that the a priori information influences the retrieval by less than 50 %. Each gas has a different sensitivity range. The sensitivity range for HCN, CO, and C2H6 is mainly tropospheric, and for ClONO2, HCl, and HF, it is mainly stratospheric. O3, CH4, and N2O have high retrieval sensitivity in both the troposphere and the stratosphere. The HNO3 has high retrieval sensitivity in the stratosphere and in the atmospheric boundary layer below 1.5 km.
4.3 Error analysis
As listed in Table 2, we classified errors as systematic or random according to whether they are constant between consecutive measurements or whether they vary randomly. For comparison, the error items considered in error analysis are the same for the retrieval of all gases. The smoothing error Es is calculated via Eq. (6), the measurement error Em is calculated via Eq. (7), and all other error items Evar are calculated via Eq. (8) (Rodgers, 2000).
where Svar is the error covariance matrix of var. Kvar is the weighting function matrix of var. Here var refers to any one of the error items in Table 2, except smoothing error and measurement error. In this study, the a priori error covariance for all non-retrieval parameters is set the same for all gases' retrieval.
This section presents the ILS influence study, whereby the degraded ILSs that are simulated by ALIGN60 are used in the SFIT forward model, and the fractional differences (D %) in various quantities for each gas relative to the retrieval with an ideal ILS are computed. For each gas, in Sect. 5.1 and 5.2 only one typical spectrum is selected for study. In order to retrieve these 10 gases, 5 spectra with different wavenumber coverage are used. All of them are randomly selected from the routine measurements on a clear day at Hefei on 16 February 2016. The consistency of the resulting deduction is evaluated in Sect. 5.3, for which 1 year of measurements from August 2015 to August 2016 was used. The Hefei site has run NDACC observations with the Bruker 125HR for more than 3 years. We regularly use a low-pressure HBr cell to diagnose the misalignment of the spectrometer and to realign the instrument when indicated. As shown in Fig. 5, all actual ILS degradations of the FTIR spectrometer within this selected period are less than 2 % and can be regarded as being ideal. For all spectra used in this study, the retrievals with all levels of ILS degradation fulfil the following filter criteria.
-
The root mean square (rms) of the residual (difference between measured and calculated spectra after the fit) in all fitting windows has to be less than 3 %.
-
The retrievals should converge for all levels of ILS degradation.
-
The concentrations of the target and interfering gases at each sublayer should be positive.
-
The solar intensity variation (SIV) should be less than 10 %. The SIV within the duration of a spectrum is the ratio of the standard deviation to the average of the measured solar intensities.
These criteria are used to remove those spectra that have sampling errors or are contaminated by aerosols, clouds, hazes, or other unpredictable objects which cause a low SNR or a large detecting intensity variation. In the following calculations, we have taken the retrievals with an ideal ILS as the reference. The fractional difference is defined here as
where X is a vector which can include multiple elements such as the gas profile or only one element such as DOFs, the rms, the total column, the total random uncertainty, the total systematic uncertainty, or the total uncertainty. The total random uncertainty and the systematic uncertainty are the sum in quadrature of each individual uncertainty listed in Table 2, and the total uncertainty is the sum in quadrature of the total random uncertainty and the total systematic uncertainty. Xref is the same as X but for the nominal ideal ILS.
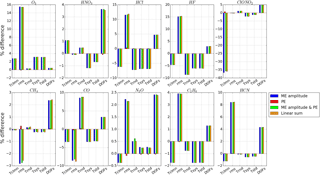
Figure 6Fractional difference in the total column, the rms, the total random uncertainty, the total systematic uncertainty, the total uncertainty, and DOFs for misalignment j. “ME amplitude” represents the ILS which only took ME amplitude deviation into account. “PE” represents the ILS which only took PE deviation into account. “ME amplitude & PE” represents the ILS which took both the ME amplitude and PE deviations into account. The fractional difference of each item is the “linear sum” of the ME amplitude and PE. The ME amplitude and PE are obtained from ALIGN60 with misalignment j in Fig. 1. The results are deduced from the spectra recorded at Hefei on 16 February 2016.
5.1 ME amplitude and PE influence
In order to determine how the ILS degradation affects the NDACC gas retrievals, the results deduced from ILS considering both ME amplitude and PE are compared to those only considering ME amplitude or PE. All types of ILS degradation in Sect. 3 are used in this study. Figure 6 exemplifies the case of ILS j, where the differences in the total column, the rms, the random uncertainty, the systematic uncertainty, the total uncertainty, and DOFs for each gas relative to the retrieval are compared with an ideal ILS. Figure 7 shows the fractional difference in profile of each gas for ILS j. The results show that the influence of ILS degradation on the total column, the rms, the random uncertainty, the systematic uncertainty, the total uncertainty, DOFs, and the profile can be approximated by the linear sum of individual ME amplitude influence and PE influence. The PE influence is of secondary importance compared with the ME amplitude influence. The comparisons for the results retrieved with ILS a to i come to the same conclusions.
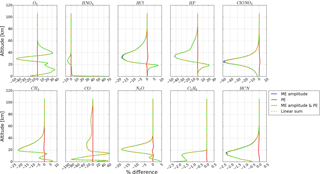
Figure 7Fractional difference in the profile for misalignment j. The nomenclature in the plot legend is the same as Fig. 6. The results are deduced from the spectra recorded at Hefei on 16 February 2016.
Figures 8 and 9 show the influence of ILS a to j on the total column and the profile of all NDACC gases. The resulting influence amounts depend on the deviation amount and the deviation shape of ME. For positive MEs, in most cases, the ILS j causes the maximum influence, and for negative MEs, the ILS i causes the maximum influence. In a real instrument, the misalignment is a combination of misalignment a to j. In principle, for the same misalignment amplitude, it should not cause influence exceeding misalignment i or j. In the following, misalignment i and j are selected on behalf of negative and positive ME, respectively, to investigate how the ILS degradation influences the NDACC gas retrievals.
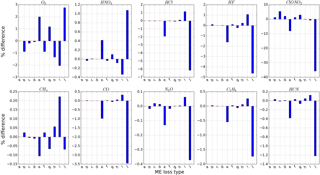
Figure 8Sensitivity of the total column to different types of ILS degradation. The ILSs a to j correspond to misalignment a to j in Table 1. The results are deduced from the spectra recorded at Hefei on 16 February 2016.
5.2 Sensitivity study
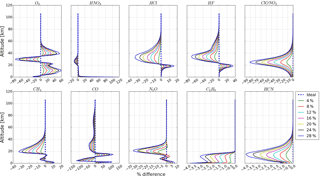
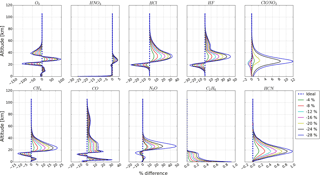
We simulated seven levels of negative ME i and positive ME j with ALIGN60, incorporated them in the SFIT forward model, and then calculated the fractional difference in various quantities for each gas relative to the retrieval with an ideal ILS. The misalignments as inputs of ALIGN60 and the resulting ILSs are shown in Figs. 10 and 12. The corresponding Haidinger fringes at the maximum misalignment position are shown in Figs. 11 and 13. The ME deviation, the decentring of Haidinger fringes, and the ILS deterioration varying over misalignment are evident. Figure 14 is the sensitivity of the total column with respect to different levels of ILS degradation. Figures 15–18 are the same as Fig. 14 but for DOFs, the rms, the uncertainty, and the profile. The results show that the ILS degradation affected the total column, the rms, DOFs, the retrieval uncertainty, and the profile. Generally, the larger the ME deviation, the larger the influence. The positive and negative ME have opposite influence on total column, DOFs, the total uncertainty and profile.
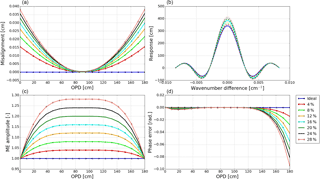
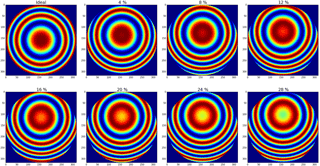
Figure 10Simulated positive ME deviations along with the OPD. Panel (a) demonstrates the misalignment, panel (b) shows the resulting ILS, panel (c) shows the resulting ME amplitude, and panel (d) shows the resulting PE.
With respect to the total column, the influence of ILS degradation on the stratospheric gases is generally larger than the tropospheric gases. For a typical ILS degradation (10 %), the total columns of stratospheric gases O3, HNO3, HCl, HF, and ClONO2 changed by 1.9, 0.7, 4, 3, and 23 %, respectively, while the total columns of tropospheric gases CH4, CO, N2O, C2H6, and HCN changed by 0.04, 2.1, 0.2, 1.1, and 0.75 %, respectively. For O3 and HNO3, positive ME causes an overestimated total column and negative ME causes an underestimated total column. For other gases, negative ME causes an overestimated total column and positive ME causes an underestimated total column. For all gases except O3 and CH4, the positive ME influence is larger than the negative ME influence. For CH4, the negative ME influence is larger than the positive ME influence. For O3, the level of the positive ME influence and the negative ME influence is very close.
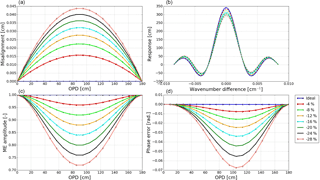
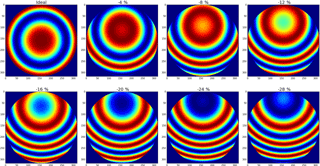
Figure 12Simulated negative ME deviations along with the OPD. Panel (a) demonstrates the misalignment, panel (b) shows the resulting ILS, panel (c) shows the resulting ME amplitude, and panel (d) shows the resulting PE.
For all gases, positive ME increases the DOFs and negative ME decreases DOFs. For all gases except HF and CH4, both positive ME and negative ME increase rms. For HF, positive ME increases rms, while negative ME decreases rms. For CH4, positive ME decreases rms and negative ME increases rms.
The influence on the systematic uncertainty and the random uncertainty depends on the ME deviation type and the gas type. The influence on the total uncertainty is the combination of the influence on the total systematic uncertainty and the total random uncertainty. For all gases except O3, positive ME decreases the total uncertainty and negative ME increases the total uncertainty. For O3, positive ME increases the total uncertainty and negative ME decreases the total uncertainty.
The ILS degradation causes an evident difference in the profile within the altitude ranges that show high retrieval sensitivity in Fig. 4, or in other words, the sensitive ranges listed in Table 3. Generally, the profile is more sensitive to positive ME than negative PE, and the influence of ILS degradation on the stratospheric gases is larger than on the tropospheric gases.
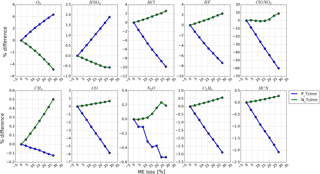
Figure 14Sensitivity of the total column with respect to ME deviation. “P_Tclmn” represents the sensitivity of the total column with respect to positive ME deviation and “N_Tclmn” represents the sensitivity of the total column with respect to negative ME deviation. The results are deduced from the spectra recorded at Hefei on 16 February 2016.
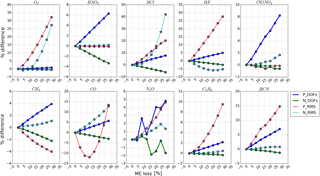
Figure 15The same as Fig. 14 but for DOFs and rms of the fitting residual. The acronyms in the legend are similar to those in Fig. 14.
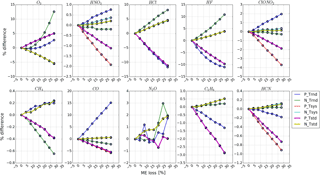
Figure 16The same as Fig.14 but for the total random uncertainty, the total systematic uncertainty, and the total uncertainty. The acronyms in the legend are similar to those in Fig. 14. “Trnd”, “Tsys”, and “Tstd” represent the total random uncertainty, the total systematic uncertainty, and the total uncertainty, respectively.
5.3 Consistency evaluation
This section uses the spectra recorded at Hefei from August 2015 to August 2016 to evaluate the consistency of the above study. These spectra span a large range of atmospheric water vapour, solar zenith angles (SZAs), surface pressures, surface temperatures, wind speeds, and wind directions (Fig. 19). All retrievals that fulfil the above filter criteria are included in this study. A simulated ILS j with a maximum ME amplitude deviation of 5 % is used in the retrieval. The results are compared to the retrievals deduced from an ideal ILS.
Figure 20 exemplifies the fractional differences in the total column, the rms, the total uncertainty, and DOFs for each gas as a function of the SZA. The results show that the fractional differences in the total column, the total uncertainty, and DOFs for all gases are consistent under different SZAs. For most gases, the fractional difference in rms exhibits more scatter than the total column, the total uncertainty, and DOFs. However, they are independent of the SZA, and most of them are less than 10 %. In general, the influence of ILS degradation on NDACC gases' retrieval shows good consistency under different SZAs. The fractional differences as a function of the humidity, the pressure, the SZA, the temperature, the wind direction, and the wind speed show the same conclusions.
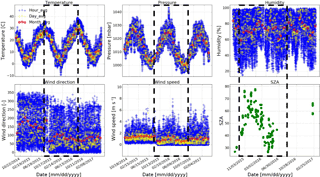
Figure 19The meteorological data and SZA record at Hefei. Large span of all these parameters is shown for the period from August 2015 to August 2016 (black dotted squares).
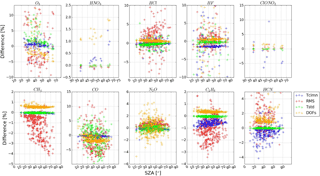
Figure 20Fractional difference in the total column, the rms, the total uncertainty, and DOFs as a function of the SZA from August 2015 to August 2016, for which the ILS j with a maximum ME deviation of 5 % is used.
Table 4Recommendations for suppressing the fractional difference in the total column for ClONO2 and other NDACC gases within 10 and 1 %, respectively.

* The influence on ClONO2 is less than 10 % and the influences on all other NDACC gases are less than 1 %. Even an excessively large ILS degradation of 28 % can normally be regarded as being negligible.
For each gas, the a priori covariance matrices of Sa, Sε, and Svar are the same in the aforementioned study. According to Eqs. (6–8), we conclude that the ILS degradation altered the weighting function matrix Kx and eventually altered the quantities such as the total column, the rms, the random uncertainty, the systematic uncertainty, the total uncertainty, DOFs, and the profile. The change of Kx is attributed to the fact that the ILS degradation alters the gas absorption line shape, and hence alters the structure of calculated spectra and aggravates the mismatch between the calculated spectra and the measured spectra.
The stratospheric gases are more sensitive to ILS degradation than the tropospheric gases, and ClONO2 exhibits the largest sensitivity. This is because the absorption structure in the stratosphere is narrower than that in the troposphere and is therefore more easily affected by ILS degradation. We set the acceptable fractional difference in the total column for ClONO2 and other NDACC gases as 10 and 1 %, respectively. Considering that an excessively large ME degradation (e.g. > 20 %) seldom occurred within NDACC because of the regular alignment at each site, the maximum permitted ILS degradation for each gas is given in Table 4 and is deduced by the following points.
-
The influence of ILS degradation on CH4 and N2O can be regarded as being negligible.
-
If a misalignment causes positive ME degradation, the maximum degradations for O3, HNO3, HCl, HF, ClONO2, CO, C2H6, and HCN should be less than 6, 15, 5, 5, 5, 5, 9, and 13 %, respectively.
-
If a misalignment causes negative ME degradation, the maximum degradations for O3, HCl, and HF should be less than 6, 12, and 12 %, respectively.
Note that the retrievals of certain gases, e.g. O3, CH4, CO, and N2O, can be divided into multiple independent sublayers depending on total DOFs. The above deductions do not apply to the partial column integrated over each sublayer because, as Figs. 17 and 18 show, the sensitivity of the profile to ILS degradation is altitude-dependent. The answers to how ILS degradation influences the partial column of each NDACC gas and how much ILS deviation from unity is acceptable if an ideal line shape is assumed are beyond the scope of this paper and will be published elsewhere.
We assessed the influence of instrumental line shape degradation on all current NDACC gases' retrieval via investigation of sensitivities of the total column, the root mean square of the fitting residual, the total random uncertainty, the total systematic uncertainty, the total uncertainty, degrees of freedom, and the profile with respect to modulation efficiency degradations. The study concluded that the influence of instrumental line shape degradation can be approximated by the linear sum of the individual modulation efficiency amplitude influence and the phase error influence. The phase error influence is of secondary importance compared with the modulation efficiency amplitude influence. The influence amounts depend on the deviation amount and the deviation shape of the modulation efficiency.
The stratospheric gases are more sensitive to instrumental line shape degradation than the tropospheric gases, and the positive modulation efficiency has more influence on the total column or the profile than the negative modulation efficiency. For a typical ILS degradation (10 %), the columns of stratospheric gases O3, HNO3, HCl, HF, and ClONO2 changed by 1.9, 0.7, 4, 3, and 23 %, respectively, while the columns of tropospheric gases CH4, CO, N2O, C2H6, and HCN changed by 0.04, 2.1, 0.2, 1.1, and 0.75 %, respectively. The influence of instrumental line shape degradation on NDACC gas retrievals shows good consistency under different meteorological conditions and solar zenith angle. In order to suppress the fractional difference in the total column for ClONO2 and other NDACC gases within 10 and 1 %, respectively, the maximum positive modulation efficiency degradations for O3, HNO3, HCl, HF, ClONO2, CO, C2H6, and HCN should be less than 6, 15, 5, 5, 5, 5, 9, and 13 %, respectively. The maximum negative modulation efficiency degradations for O3, HCl, and HF should be less than 6, 12, and 12 %, respectively; the influence of ILS degradation on CH4 and N2O can be regarded as being negligible.
The ALIGN60 software is obtained on request from KIT Karlsruhe (http://www.imk-asf.kit.edu/english/897.php) (Hase et al., 1999). The SFIT4 software can be found via https://www2.acom.ucar.edu/irwg/links (last access: 11 May 2018). The input files used for ALIGN60 and SFIT4 are attached in the Supplement.
The authors declare that they have no conflict of interest.
This work is jointly supported by the National High Technology Research and
Development Program of China (no. 2016YFC0200800, 2016YFC0203302,
2016YFC0200404, and 2017YFC0210002), the National Science Foundation of
China (no. 41605018, 41775025, 41405134, 41575021, 51778596, 91544212, and 41722501), the Anhui Province Natural Science Foundation of
China (no. 1608085MD79), and the German Federal Ministry of Education and
Research (BMBF) (grant no. 01LG1214A). The processing environment of SFIT4
and some plot programs are provided by the National Center for Atmospheric
Research (NCAR), Boulder, Colorado, USA. The NDACC is acknowledged
for supplying the SFIT software and giving advice.
Edited by: Gabriele Stiller
Reviewed by: two anonymous referees
Davis, S. P., Abrams, M. C., and Brault, J. W.: Fourier transform spectrometry, Academic Press, ISBN: 0-12-042510-6, 2001.
Duchatelet P., Demoulin P., Hase F., Ruhnke R., Feng W., Chipperfield M. P., Bernath P. F., Boone C. D., Walker K. A., and Mahieu E.: Hydrogen fluoride total and partial column time series above the Jungfraujoch from long term FTIR measurements: Impact of the line shape model, characterization of the error budget and seasonal cycle, and comparison with satellite and model data, J. Geophys. Res., 115, D22306, https://doi.org/10.1029/2010JD014677, 2010.
Feist, D. G., Arnold, S. G., Hase, F., and Ponge, D.: Rugged optical mirrors for Fourier transform spectrometers operated in harsh environments, Atmos. Meas. Tech., 9, 2381–2391, https://doi.org/10.5194/amt-9-2381-2016, 2016.
Hannigan, J. and Coffey, M.: semiautonomous FTS observation system for remote sensing of stratospheric and tropospheric gases, J. Atmos. Ocean. Tech., 26, https://doi.org/10.1175/2009JTECHA1230.1, 2009.
Hase, F.: Improved instrumental line shape monitoring for the ground-based, high-resolution FTIR spectrometers of the Network for the Detection of Atmospheric Composition Change, Atmos. Meas. Tech., 5, 603–610, https://doi.org/10.5194/amt-5-603-2012, 2012.
Hase, F., Blumenstock, T., and Paton-Walsh, C.: Analysis of the instrumental line shape of high-resolution Fourier transform IR spectrometers with gas cell measurements and new retrieval software, Appl. Opt., 38, 3417–3422, https://doi.org/10.1364/AO.38.003417, 1999 (data available at: http://www.imk-asf.kit.edu/english/897.php, last access: 11 May 2018).
Hase, F., Demoulin, P., Sauval, A., Toon, G. C., Bernath, P., Goldman, A., Hannigan, J., and Rinsland C.: An empirical line-by-line model for the infrared solar transmittance spectrum from 700 to 5000 cm−1, J. Quant. Spectrosc. Ra., 102, 450–463, 2006.
Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., Iredell, M., Saha, S., White, G., Woollen, J., Zhu Y., Chelliah, M., Ebisuzaki, W., Higgins, W., Janowiak, J., Mo, K. C., Ropelewski, C., Wang, J., Leetmaa, A., Reynolds, R., Jenne, R., and Joseph, D. : The NCEP/NCAR 40-year reanalysis project, B. Am. Meteorol. Soc., 77, 437–472, 1996.
Kohlhepp, R., Barthlott, S., Blumenstock, T., Hase, F., Kaiser, I., Raffalski, U., and Ruhnke, R.: Trends of HCl, ClONO2, and HF column abundances from ground-based FTIR measurements in Kiruna (Sweden) in comparison with KASIMA model calculations, Atmos. Chem. Phys., 11, 4669–4677, https://doi.org/10.5194/acp-11-4669-2011, 2011.
Kurylo, M. J.: Network for the detection of stratospheric change (NDSC), SPIE Proceedings 1991, P. Soc. Photo-Opt. Ins., 1491, 168–174, 1991.
Messerschmidt, J., Macatangay, R., Notholt, J., Petri, C., Warneke, T., and Weinzierl, C.: Side by side measurements of CO2 by ground-based Fourier transform spectrometry (FTS), Tellus B, 62, 749–758, https://doi.org/10.1111/j.1600-0889.2010.00491.x, 2010.
Olsen, S. C. and Randerson, J. T.: Differences between surface and column atmospheric CO2 and implications for carbon cycle research, J. Geophys. Res.-Atmos., 109, D02301, https://doi.org/10.1029/2003JD003968, 2004.
Rodgers, C. D.: Inverse methods for atmospheric sounding: Theory and Practice, Series on Atmospheric, Oceanic and Planetary Physics, vol. 2, World Scientific Publishing Co., Singapore, 2000.
Rothman, L. S., Gordon, I. E., Barbe, A., Benner, D. C., Bernath, P. F., Birk, M., Boudon, V., Brown, L. R., Campargue, A., Champion, J.-P., Chance, K., Coudert, L. H., Danaj, V., Devi, V. M., Fally, S., Flaud, J.-M., Gamache, R. R., Goldmanm, A., Jacquemart, D., Kleiner, I., Lacome, N., Lafferty, W. J., Mandin, J.-Y., Massie, S. T., Mikhailenko, S. N., Miller, C. E., Moazzen-Ahmadi, N., Naumenko, O. V., Nikitin, A. V., Orphal, J., Perevalov, V. I., Perrin, A., Predoi-Cross, A., Rinsland, C. P., Rotger, M., Šime. cková, M., Smith, M. A. H., Sung, K., Tashkun, S. A., Tennyson, J., Toth, R. A., Vandaele, A. C., and Vander Auwera, J.: The Hitran 2008 molecular spectroscopic database, J. Quant. Spectrosc. Ra., 110, 533–572, 2009.
Schneider, M., Redondas, A., Hase, F., Guirado, C., Blumenstock, T., and Cuevas, E.: Comparison of ground-based Brewer and FTIR total column O3 monitoring techniques, Atmos. Chem. Phys., 8, 5535–5550, https://doi.org/10.5194/acp-8-5535-2008, 2008.
Sun, Y., Palm, M., Weinzierl, C., Petri, C., Notholt, J., Wang, Y., and Liu, C.: Technical note: Sensitivity of instrumental line shape monitoring for the ground-based high-resolution FTIR spectrometer with respect to different optical attenuators, Atmos. Meas. Tech., 10, 989–997, https://doi.org/10.5194/amt-10-989-2017, 2017.
Vigouroux, C., De Mazière, M., Demoulin, P., Servais, C., Hase, F., Blumenstock, T., Kramer, I., Schneider, M., Mellqvist, J., Strandberg, A., Velazco, V., Notholt, J., Sussmann, R., Stremme, W., Rockmann, A., Gardiner, T., Coleman, M., and Woods, P.: Evaluation of tropospheric and stratospheric ozone trends over Western Europe from ground-based FTIR network observations, Atmos. Chem. Phys., 8, 6865–6886, https://doi.org/10.5194/acp-8-6865-2008, 2008.
Vigouroux, C., Blumenstock, T., Coffey, M., Errera, Q., García, O., Jones, N. B., Hannigan, J. W., Hase, F., Liley, B., Mahieu, E., Mellqvist, J., Notholt, J., Palm, M., Persson, G., Schneider, M., Servais, C., Smale, D., Thölix, L., and De Mazière, M.: Trends of ozone total columns and vertical distribution from FTIR observations at eight NDACC stations around the globe, Atmos. Chem. Phys., 15, 2915–2933, https://doi.org/10.5194/acp-15-2915-2015, 2015.
Washenfelder, R. A.: Column abundances of carbon dioxide and methane retrieved from ground-based near-infrared solar spectra, PhD thesis, California Institute of Technology, Pasadena, California, available at: http://thesis.library.caltech.edu (last access: 11 May 2018), 2006.
Wunch, D., Toon, G. C., Wennberg, P. O., Wofsy, S. C., Stephens, B. B., Fischer, M. L., Uchino, O., Abshire, J. B., Bernath, P., Biraud, S. C., Blavier, J.-F. L., Boone, C., Bowman, K. P., Browell, E. V., Campos, T., Connor, B. J., Daube, B. C., Deutscher, N. M., Diao, M., Elkins, J. W., Gerbig, C., Gottlieb, E., Griffith, D. W. T., Hurst, D. F., Jiménez, R., Keppel-Aleks, G., Kort, E. A., Macatangay, R., Machida, T., Matsueda, H., Moore, F., Morino, I., Park, S., Robinson, J., Roehl, C. M., Sawa, Y., Sherlock, V., Sweeney, C., Tanaka, T., and Zondlo, M. A.: Calibration of the Total Carbon Column Observing Network using aircraft profile data, Atmos. Meas. Tech., 3, 1351–1362, https://doi.org/10.5194/amt-3-1351-2010, 2010.
Wunch, D., Toon, G. C., Blavier, J.-F. L.,Washenfelder, R., Notholt, J., Connor, B. J., Griffith, D. W. T., Sherlock, V., and Wennberg, P. O.: The Total Carbon Column Observing Network, Philos. T. Roy. Soc. A, 369, 2087–2112, https://doi.org/10.1098/rsta.2010.0240, 2011.
Wunch, D., Toon G. C., Sherlock V., Deutscher N. M., Liu C., Feist D. G., and Wennberg P. O.: The Total Carbon Column Observing Network's GGG2014 Data Version, https://doi.org/10.14291/tccon.ggg2014.documentation.R0, 2015.