the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A highly miniaturized satellite payload based on a spatial heterodyne spectrometer for atmospheric temperature measurements in the mesosphere and lower thermosphere
Friedhelm Olschewski
Klaus Mantel
Brian Solheim
Gordon Shepherd
Michael Deiml
Jilin Liu
Rui Song
Qiuyu Chen
Oliver Wroblowski
Daikang Wei
Yajun Zhu
Friedrich Wagner
Florian Loosen
Denis Froehlich
Tom Neubert
Heinz Rongen
Peter Knieling
Panos Toumpas
Jinjun Shan
Geshi Tang
Ralf Koppmann
Martin Riese
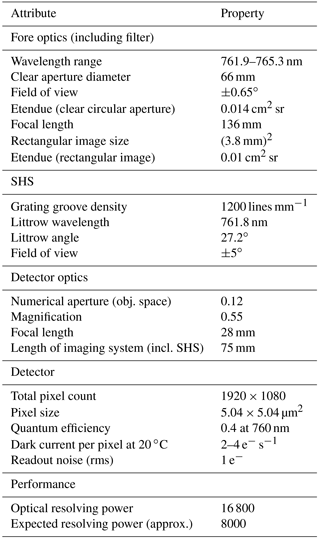
A highly miniaturized limb sounder for the observation of the O2 A-band to derive temperatures in the mesosphere and lower thermosphere is presented. The instrument consists of a monolithic spatial heterodyne spectrometer (SHS), which is able to resolve the rotational structure of the R-branch of that band. The relative intensities of the emission lines follow a Boltzmann distribution and the ratio of the lines can be used to derive the kinetic temperature. The SHS operates at a Littrow wavelength of 761.8 nm and heterodynes a wavelength regime between 761.9 and 765.3 nm with a resolving power of about 8000 considering apodization effects. The size of the SHS is 38 × 38 × 27 mm3 and its acceptance angle is ±5∘. It has an etendue of 0.01 cm2 sr. Complemented by front optics with an acceptance angle of ±0.65∘ and detector optics, the entire optical system fits into a volume of about 1.5 L. This allows us to fly this instrument on a 3- or 6-unit CubeSat. The vertical field of view of the instrument is about 60 km at the Earth's limb when operated in a typical low Earth orbit. Integration times to obtain an entire altitude profile of nighttime temperatures are on the order of 1 min for a vertical resolution of 1.5 km and a random noise level of about 1.5 K. Daytime integration times are 1 order of magnitude shorter. This work presents the design parameters of the optics and a radiometric assessment of the instrument. Furthermore, it gives an overview of the required characterization and calibration steps. This includes the characterization of image distortions in the different parts of the optics, visibility, and phase determination as well as flat fielding.
Atmospheric waves drive important atmospheric circulation patterns such as the Brewer–Dobson circulation in the stratosphere and mesosphere. Wave structures are detectable in atmospheric wind and temperature fields. Small-scale gravity waves are particularly important in the mesosphere and even lower thermosphere.
To demonstrate new ways to measure atmospheric waves at high spatial resolution, Song et al. (2017) presented a new satellite observation strategy for the detection of gravity waves in the mesosphere and lower thermosphere (MLT). This measurement mode requires an agile satellite platform to make multi-angle observations of a particular atmospheric volume and a spectrometer particularly suited for the detection of faint emission lines.
The concept and optical layout for such an instrument is presented, which fits onto a nano-satellite platform, such as a CubeSat (Poghosyan and Golkar, 2017). To customize an instrument to the constraints of a CubeSat gives access to a variety of standardized satellite-bus components and flight opportunities, because CubeSat deployers are nowadays an integral part of many launch vehicles. In return for these advantages, the payload has to cope with very restricted mass, volume, and power resources.
The most common technique to obtain temperatures in the upper mesosphere and lower thermosphere is to measure the emission of CO2 in the mid-infrared or to measure the absorption of sunlight by CO2. Although the modelling of CO2 emissions has its own problems regarding the determination of the non-local thermodynamic equilibrium state of CO2, this method is well accepted and gives temperatures over a broad altitude range at a good signal-to-noise ratio. The most prominent instruments using infrared emissions to derive MLT temperature are ISAMS (Nightingale and Crawford, 1991), CRISTA (Grossmann et al., 2002; Offermann et al., 1999), MIPAS (Fischer et al., 2008) and SABER (Russell et al., 1999) for emission measurements and HALOE (Russell et al., 1994) and ACE-FTS (Bernath, 2017) for occultation measurements.
Instruments measuring at infrared or longer wavelengths are quite large or high energy consuming, so that measurements in the ultraviolet–visible–near-infrared spectral regime are most appropriate for a CubeSat platform. In this wavelength regime, mesospheric temperature measurements can be performed by the evaluation of the rotational distribution of a molecular emission band. The emitting states should be sufficiently long-lived, and the rotational distribution should be thermalized, such that it can be described by the kinetic temperature. It is best if this emission is visible during day- and nighttime, such that temperatures can be obtained at all local times. The O2 atmospheric band system fulfills all of these requirements. The strongest band within this system is the O2 (0,0) atmospheric A-band at 762 nm, which was investigated in several studies (McDade and Llewellyn, 1986; Meriwether, 1989; Rodrigo et al., 1985; Slanger and Copeland, 2003; Torr et al., 1985). The O2 A-band has been used to derive global MLT temperatures in recent years using UARS HRDI Fabry–Pérot interferometer data (Ortland et al., 1998) and Odin OSIRIS grating spectrometer data (Sheese et al., 2010).
This temperature measurement technique builds upon relative intensity measurements. The requirements to monitor the radiometric performance of such instruments are much more relaxed than for measurement strategies which rely on absolute intensities. Another advantage is that the A-band emits at wavelengths below 1 µm, so that silicon-based detectors operating at ambient or moderately cooled conditions can be used for detection. This reduces the power consumption, mass, and costs of such an instrument significantly.
In this work we give an overview of the design of a highly miniaturized instrument to measure O2 A-band limb radiances. We summarize various topics on the radiometric and optical design as well as the calibration and processing of the data. Further and more detailed studies on these subjects are currently in preparation for publication. We are preparing such an instrument for a detailed laboratory characterization and an in-orbit verification in the near future.
Light emitted in the O2 atmospheric band system stems from the transition of O2() to O2(). There are three absorption bands in this system (A, B, and γ bands). All of these bands end up in a vibrational ground state. The upper states are at v=0, 1, and 2 for the A, B, and γ bands, respectively. None of these bands can be observed from the ground because of the high abundance of ground state molecular oxygen in the atmosphere. The radiative lifetime of the O2() state is about 12 s (Burch and Gryvnak, 1969). This long lifetime assures that the molecule is in rotational equilibrium with the ambient atmosphere, such that rotational and ambient temperature are identical. An overview of the chemistry and molecular dynamics of excited O2 is given by, for example, Slanger and Copeland (2003) and references cited therein. It can be briefly summarized as follows: O2() is excited by collisions of ground state O2 with O(1D), which is produced in the photolysis of O2 in the Schumann–Runge continuum and in the photolysis of O3 in the Hartley band. Due to the long radiative lifetime of O(1D) (about 2 min), most of the energy of O(1D) is lost by quenching with N2 and O2, producing a multitude of excited N2 and O2 states, including the ones emitting the atmospheric band system. Another excitation mechanism of O2() is resonance scattering or absorption of photons in the atmospheric bands itself. The third process is the collision of ground state O2 with a metastable, highly excited state of O2 produced in the recombination of two atomic oxygen atoms. This two-step process was first proposed by Barth and Hildebrandt (1961) and Barth (1964). It is the only excitation process which is active during day- and nighttime. Figure 1 shows simulated volume emission rates of O2() separated by excitation processes, as simulated with the model described by Song et al. (2017). According to these simulations, the day- to nighttime ratio of the O2() number densities is about a factor of 50 in the vicinity of the mesopause.
The spectral shape of the A-band for two different temperatures is illustrated in Fig. 2. Higher temperatures give a flatter spectrum. A 10 K change in temperature affects the rotational distribution of strong emission lines at 760–765 nm between ±6 %. This means that the band structure must be measured better than 1 % to derive temperatures with a precision of 2 K.
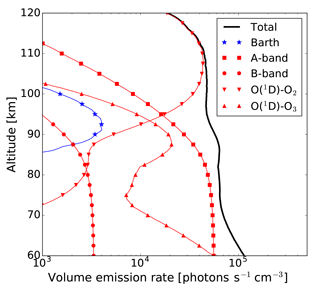
Figure 1Volume emission rate of O2() separated by excitation processes. “Barth” indicates the emission rates created by the recombination of atomic oxygen. This is the only excitation process being active during day and night. “A-band” and “B-band” label the fraction of emissions excited by resonance absorption in those bands. “O2” and “O3” mark the excitation by collisions with O(1D), which is created by photolysis of O2 and O3, respectively.
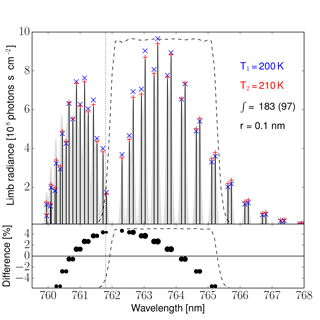
Figure 2O2 A-band limb emission line calculations assuming a global temperature of 200 and 210 K (upper panel). The spectra in the upper panel have been normalized to show identical band intensities. The vertical bars and the blue signs mark the emission line intensities for 200 K; the light gray area shows their intensities (multiplied by a factor of 10) as seen from an instrument with a spectral resolution of 0.1 nm. The red + signs show line intensities for 210 K. The dashed line is the filter transmission curve of the instrument presented later. The dotted vertical line is drawn at the Littrow wavelength. Within the filter, more than 50 % of the total band intensity (at 200 K) are emitted (97 out of 183 photons s−1 cm−2 sr−1). The percentage difference of the line intensities at 200 and 210 K is shown in the lower panel; the symbol size scales with the absolute intensity of the lines. The atmospheric background data are taken from the HAMMONIA model, and the spectroscopic data stem from the HITRAN database (Gordon et al., 2017).
At the beginning of this project, different instrument concepts were considered to detect the mesospheric A-band limb emissions from a CubeSat (Deiml et al., 2014). For a variety of reasons, we decided to develop the instrument with a spectrometer. Performance considerations lead to the selection of a Fourier transform spectrometer (FTS). With its compact and monolithic design (Shepherd et al., 2016), a spatial heterodyne spectrometer (SHS) deemed the most appropriate candidate, in accordance with the findings of Watchorn et al. (2014) in the framework of another study.
In principle, a SHS is a FTS, where the mirrors in each arm are replaced by diffraction gratings (Fig. 3). The incoming wavefront is diffracted at the gratings, with a wavelength-dependent angle. The superposition of the two wavefronts then produces straight, parallel, and equidistant fringes with a spatial frequency depending on the wavelength of the light. The zero frequency of the fringe pattern is at the Littrow wavelength and small wave number changes result in fringes with a discernable spatial frequency, which can be observed with available imaging detectors. The concept was originally proposed by Pierre Connes in a configuration called Spectromètre interférential à selection par l'amplitude de modulation (SISAM) (Connes, 1958). With the advent of imaging detectors, this idea was taken up by Harlander and Roesler (1990), Douglas (1997), Smith and Harlander (1999), Watchorn et al. (2001), Harris et al. (2004), Roesler (2007), Englert et al. (2010), Watchorn et al. (2010), Bourassa et al. (2016), and Lenzner and Diels (2016), among others. The design of a SHS for a particular wavelength and spectral resolution follows a few simple relations, which are shortly summarized to illustrate the main characteristics of this device. For a derivation of the mathematical expressions see, e.g. Harlander (1991), Cooke et al. (1999), Smith and Harlander (1999), and references cited therein.
The tilt angle of the gratings with respect to the optical axis is called Littrow angle ΘL. Light at the Littrow wave number σL is returned in the same direction as the incoming path, as described by the grating equation (for diffraction order 1 and grating groove density 1∕d):
Combining the intensity equation of a conventional FTS and the grating equation for small incident angles at the grating gives the SHS equation for ideal conditions, relating the incoming radiation S at wave number σ to the spectral density I at position x, parallel to the dispersion plane:
κ is the heterodyned fringe frequency:
The maximum resolving power R of a SHS is nearly proportional to the number of grating grooves illuminated by the incoming beam or in other words the illuminated spot size W on the grating multiplied by the grating groove density g times 2:
The bandpass of a SHS is limited by the detector resolution due to the Nyquist theorem. This means that the spectral range , which can be detected for given spectral resolution Δλ, has to be lower than half the pixel number N:
As for conventional FTS or Fabry–Pérot instruments, the acceptance angle of light for a conventional SHS is inversely proportional to its resolving power R (Harlander, 1991), which is a few orders of magnitude larger than for conventional grating spectrometers of the same size. The acceptance angle of a SHS can be increased significantly when prisms are inserted into the two interferometer arms. This configuration was first implemented for upper-atmospheric temperature measurements by Hilliard and Shepherd (1966) with a Michelson interferometer and first introduced for a SHS by Roesler and Harlander (1990). The prisms incline the image of the gratings so that they appear to be located in a common virtual plane which is oriented perpendicular to the optical axis for a wide range of incident angles. At the end, the acceptance angle of the SHS, including field widening prisms, is only limited by spherical aberration for systems with small Littrow angles and astigmatism for large Littrow angles (Harlander et al., 1992). Depending on the actual design, the prisms increase the etendue or throughput of a SHS by 1–2 orders of magnitude. The calculation of the prism apex angle is given by, for example, Harlander et al. (1992).
A general advantage of SHS is the relaxed alignment tolerances, because in most optical setups the gratings are imaged onto a focal plane array. As a result, each detector pixel sees only a small area of the optical elements, so that moderate misalignments or inaccuracies in the surface quality affect limited spatial regions on the detector only. This means that the interferogram is distorted locally rather than reduced in contrast. The main benefit of the SHS is that they can be built monolithically, making them very robust for harsh environments, e.g. during rocket launches.
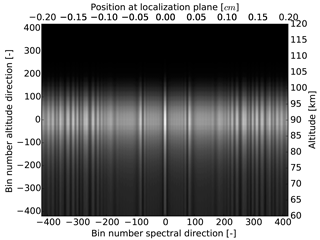
The basic design parameters of the SHS were calculated analytically using the SHS equations mentioned above. The materials of the optical glass components, the apex angle of the prisms, and the distances between the various components were optimized and iterated by means of optical ray tracing software (ZEMAX). The resulting basic design parameters are summarized in Table 1. A simulated interferogram of the O2 A-band as seen from this instrument is illustrated in Fig. 4.
An integral part of a SHS design is the optical filter located between the SHS and the scene to be observed. For this instrument, a six-cavity design bandpass filter with a centre wavelength of 763.6 nm and a bandwidth of 3.3 nm was chosen. The filter is illuminated at an angle of incidence of ±0.65∘, resulting in a blue shift of 0.8 nm. The temperature coefficient of this filter is 5 pm K−1, resulting in a spectral shift of the bandpass of 0.3 nm between −10 and +50∘.
Since a SHS instrument maps the spectrum on both sides of the Littrow wavelength symmetrically into Fourier space, the filter must be adapted in such a way that there is no overlap of lines from different sides of the Littrow wavelength in the interferogram. In our design, the Littrow wavelength is at 761.8 nm; i.e. the filter blocks most of the radiance from the shorter wavelength side of the Littrow wavelength (Fig. 2).
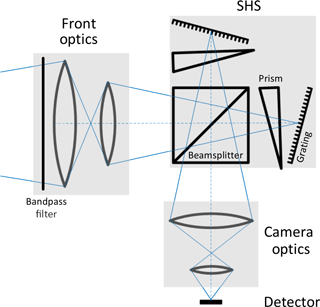
The purpose of the front optics is to image a scene at the Earth's limb onto the gratings. The detector optics images the gratings onto the focal plane of the 2-D detector. The image at the detector contains spatial information about the scene in both dimensions. An interferogram is superimposed on this scene in the direction perpendicular to the grating grooves. For the instrument presented in this work, the gratings are oriented in such a way that the interferogram spans over the horizontal direction, assuming that intensity fluctuations in the horizontal direction are small or smeared out during the exposure of the image compared to the modulation depth of the interferogram, which is valid in atmospheric limb sounding. The front optics (Fig. 5) consists of four lenses, which image an object at infinity onto a square with an edge length of 7 mm on the virtual image of the gratings. This corresponds to a theoretical spectral resolution of about 16 800 (Eq. 4). The maximum chief ray angle extent is about 1.9∘, such that a rectangular object with an angular extent of 1.3∘ can be captured without vignetting. The clear aperture diameter of the front lens is 66 mm and the distance between the first lens and the SHS is 104 mm. The etendue of this configuration is 0.014 cm2 sr for the clear circular aperture and 0.01 cm2 sr for the rectangle mentioned above.
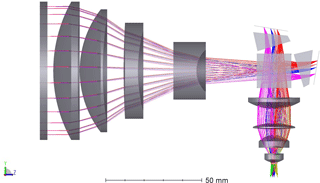
Figure 5Optical components of the instrument, including the interference filter, the front optics, the SHS, the detector optics, and the detector.
The detector optics images the active area of the gratings onto the detector and consists of lenses as well. The magnification is 0.55; i.e. the illuminated area at the detector has a diameter of about 3.8 mm. This value was chosen as a trade-off between the form factor required and the desired spectral and spatial resolution (see below). The distance between the beam splitter and the detector focal plane is 46 mm.
The aperture stop of the optical system, which limits the amount of light passing through the instrument, is the mounting of the first lens of the front optics. In the current version of the instrument, there is a Lyot stop after the last lens of the detector optics.
The detector chosen for this instrument is a low noise silicon-based CMOS image sensor from Fairchild Imaging (HWK1910A). The optical format is 2∕3 (9.7 mm × 5.4 mm) and the pixel size is 5 µm × 5 µm, resulting in 1920 × 1080 pixels in total; from those 760 × 760 pixels are needed to capture a rectangular image of 3.8 mm2. The quantum efficiency of the detector at 762 nm is about 0.4.
Like the SHS, the entire optical system was optimized using optical ray tracing software as well. The wavefront peak-to-valley extension of the optical system is less than a half wavelength for centre rays and one wavelength at maximum for the edge region of the field. The extension of the point spread function is 5 µm for inner and 10 µm for outer pixels, which does not deteriorate the determination of the different waves in the interferogram, because the highest spatial frequency to be observed has a wavelength of about 45 µm. Optical distortions introduced in the common optical path are not part of the optimization procedure, because they can be removed in the post-processing or calibration of the instrument.
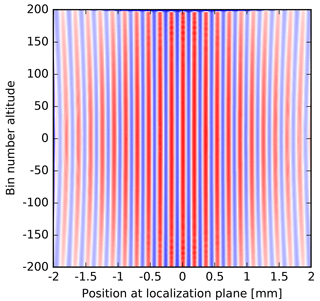
To evaluate the spectrometric performance of the system, the differences in the phase distortion of the two arms are most relevant, because this would result in an irreversible loss of contrast. This quantity is not directly accessible by the figures of merit mentioned above. This effect was investigated by calculating the wave aberrations in the exit pupil of the system for object and reference arm, respectively. The corresponding complex amplitudes are then superposed and propagated into the detector plane by a Fourier transformation. Taking the absolute square of the resulting amplitude gives the intensity distribution for the corresponding light source point (Fig. 6). The detection plane was placed between the focal planes for the on-axis and the 0.65∘ off-axis light source points as a compromise and closer to the latter to enhance the visibility on the edges of the interferogram. Nevertheless, the visibility reduction is about one-third towards the edges. Interestingly, the highest visibility is achieved by placing the detector plane outside both focal planes in a plane which is near the on-axis focal point. The suspected reason is that the shape of the focal spots, which are blurred by aberrations resulting in a reduction of visibility, becomes more compact if the detector plane is positioned slightly out of the on-axis focus, yielding to higher contrast (Fig. 7). The SHS has a fairly athermal design, but the foci and the modulation transfer function (MTF) of the entire optical system depend more on temperature. For low spatial frequencies this effect is small, but for the highest spatial frequencies seen by the instrument the MTF reduces from about 85 % at 20 ∘C to about 70 % at 0 ∘C. Further simulations and comparison with measurements are in preparation.
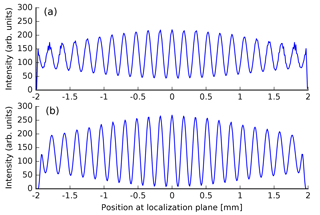
Figure 7Simulated interferograms for the centre row of the 2-D interferogram (Fig. 6). The upper plot shows the interferogram at the Gaussian focal point and the lower one at a slightly shifted position, where the foci across the image considering wave aberrations are more compact than at the Gaussian focus.
To determine the expected signal-to-noise ratio of the instrument for a given integration time, we estimate the amount of incoming light that is available in the modulated part of the interferogram and the noise of the detector. In a SHS, 50 % of the incoming radiation are lost at the beam splitter. The holographic gratings used have an efficiency of about two-third at 765 nm, so that another one-third of the radiation is not available in the modulated part of the radiance. Misalignments and aberrations of optical components are estimated to reduce the contrast of the interferogram, so that we expect to detect about 20 % in the modulated part of the interferogram.
The limb radiances of a strong line in the O2 A-band nightglow maximum recorded over an altitude range of 1.5 km are about 1×109 photons s−1 cm−2 sr−1 (cf. Fig. 2). Considering the etendue of the system and the fraction of the detector illuminated by this emission layer (about 2 %), and assuming that 20 % of the photons end up in the modulated part of the signal, this yields to about 50 photons s−1 at every pixel recording the interferogram. Since the intensities from a vertical layer of 1.5 km thickness illuminate 20 detector rows, the average signal introduced by one emission line on an individual detector pixel is 3 photons s−1. Considering that the detector records light from all spectral elements within the bandpass of the instrument, and some radiance will end up in the unmodulated part of the interferogram, each detector pixel will record about 40 photons s−1.
The noise of the signal is, by far, limited by shot noise, which scales with the square root of the (electrical) signal. The latter consists of the electrons excited by the signal of interest and the dark current caused by thermal processes. According to our own measurements, the dark current of the detector is 2–4 e− s−1 pixel−1 (corresponding to a photon flux of 5–10 photons/s/pixel) at 20 ∘C, which is a factor of 7–10 lower than the threshold given by the manufacturer. The dark current decreases a factor of 2 every 7 K (Liu et al., 2018).
At 20 ∘C, the dark current is at least a factor of 5 lower than the atmospheric signal in the emission layer maximum and therefore not a dominant source of random noise at these altitudes. This becomes more critical at other altitudes and for higher detector temperatures. Therefore the detector should be operated below 20 ∘C. The readout noise of the detector was measured to 1 e−, which is in agreement with the specification given by the manufacturer. Taking into account that 20 detector rows are summed up for each altitude bin, this noise component is negligible for integration times larger than 1 s compared to the shot noise.
The required signal-to-noise ratio to achieve a given temperature precision was determined by Monte Carlo simulations: first, a simulated spectrum with the optical resolving power of 16 800 was calculated. This spectrum was inverse Fourier-transformed and white noise was added. In the next step, the spectral power in the various frequencies was estimated by applying a Fourier transformation using a windowing function. The resulting spectra were then used to retrieve an atmospheric temperature profile and some other instrumental parameters, such as the spectral resolution of the data. Considering the intensity of the A-band signal of the nightglow layer maximum and the detector performance, the expected signal-to-noise ratio for a vertical resolution of 1.5 km and an integration time of 60 s will be 10–20 in the nightglow maximum, resulting in a retrieved temperature precision of 1–2 K.
The conversion of the detector signal into calibrated spectra involves a number of calibration steps. As pointed out in the previous section, the modulated to unmodulated signal ratio is one of the key points here. To quantify this ratio, the SHS equation for idealized conditions (Eq. 2) has to be extended (Englert and Harlander, 2006):
For better clarity, the integration variable in these expression is the heterodyned fringe frequency κ instead of wave number σ, which is a normal linear dependency. One of the extensions compared to Eq. (2) is the introduction of different intensity transmission functions tA and tB for the two SHS arms. In addition, a term ϵ(x,κ) was added, which considers that the modulation efficiency can depend on the location within the interferogram and its frequency. Finally, a phase distortion term Δ(x,κ) quantifying any phase and frequency distortions within the interferogram was introduced.
Before the interferograms of the instrument are analysed, barrel or pincushion distortions of the image are corrected because they affect the distribution of spatial information and modify the frequency of the interferogram at the same time. Due to the highly compact design of the optics and the use of spherical lenses only, significant image distortions are expected. To characterize image distortions of the entire optical system, a line grid target will be positioned in front of the instrument. Then, the SHS arms are blocked one by one to record two images of the test target. The division model (Fitzgibbon, 2001) will be used to correct for the spherical symmetric distortions. Within this model, radial distortion coefficients are fitted to straighten lines in the image. These measurements will also verify the geometrical point spread functions, which are expected to be much smaller than the required spatial resolution of the instrument.
According to computer simulations, about 90 % of the image distortions are introduced by the detector optics. Therefore it is also possible to verify and to monitor the image distortions using interferograms. Here, the reference image is generated from an interferogram by an adaptive edge detection algorithm. The edges correspond in a sense to the reference lines of a test image. It is expected that image distortions affect interferograms with different spatial frequencies in the same way.
To characterize and quantify the modulated part of the intensity, an optical setup with a tunable laser is used. First, the laser light is homogenized using microlens arrays and imaged onto a rotating diffusor. The laser spot on the diffusor is set to infinity by a large lens, such that the full aperture of the instrument is uniformly illuminated by plane waves with a divergence of at least ±0.65∘. The laser frequency and power are continuously monitored during the measurement. The laser power and the flux are calibrated before the measurements are taken.
The first step in the analysis of these measurements is to fit a frequency-dependent polynomial correction of the phase depending on the position in the localization plane. Depending on the real instrument performance, the usage of a lookup table is another option to homogenize the phase across the interferograms.
Next, the modulated part of the signal is quantified by looking at a quantity called visibility ν, which is defined as the amplitude of the modulation normalized to the average signal (times 2):
The visibility depends on several factors, such as internal stray light, the grating performance, surface or material properties or imperfections, misalignments, and contamination. Visibility depends on the MTF and can be frequency dependent. It can also vary across the field as a consequence of strong aberrations or misalignments of the system. Since the total power for each spectral element is needed for temperature retrieval, the visibility calibration is as important as a radiometric calibration, and it can even cover the radiometric calibration if the power of the laser scene is known well enough. To get the modulation or envelope function of the monochromatic interferogram as needed for the visibility calibration, we calculate its Hilbert transform, which is fundamentally the same idea as the methods described in Englert et al. (2004) and Englert and Harlander (2006), where the corresponding complex or imaginary interferogram is generated from the real interferogram. The sum of the signal and its Hilbert transform as imaginary part gives an analytic or holomorphic representation of the interferogram (Feldman, 2011). The absolute value of this complex-valued signal gives the instantaneous amplitude or envelope of the signal.
In theory and for ideal conditions, the visibility characterization covers an additional calibration step called “flat fielding” that corrects for non-uniformities caused by different sensitivities of detector elements, inhomogeneities within optical components, or any kind of misalignment of the optical components including the SHS. Englert and Harlander (2006) give an overview about different flat-fielding approaches. To verify the uniformity of the calibrated signal, we plan to perform the “balanced arm flat-fielding approach”, where the entire instrument is illuminated by our laser-driven optical setup or any other uniform radiation source and one by one SHS arm is blocked. In this case, the measured radiation corresponds to the “non-modulated” intensity term.
We presented a design for a CubeSat-sized instrument to obtain mesospheric temperatures. A spatial heterodyne spectrometer is used to measure the rotational structure of the O2 A-band, which is complemented by fore and detector optics. The size of the entire instrument including a stray light baffle is around 3.5 L. A three-dimensional design image of the instrument is shown in Fig. 8. The utilization of an extendable baffle and some minor design modifications allow us to fly the instrument on a 3-unit CubeSat. The power consumption is about 6 W and the data rate is 50 kB/image. The instrument can deliver temperatures at a 1–2 K precision for an integration time of about 1 min for nightglow and a few seconds for day glow. A prototype version of this instrument was tested in March 2017 on a sounding rocket by a student team (Deiml et al., 2017). The instrument survived the rocket launch and worked nominally. Unfortunately, it was not possible to record limb spectra with a stable attitude due to a failure of the detumbling mechanism of the rocket. The next step in this project is the advancement of this instrument for an in-orbit verification on a satellite. The main requirements on a satellite platform are a stable line-of-sight attitude, which should be a few arc minutes for the time of one measurement (a few seconds) (Kaufmann et al., 2017). The control of that angle could be an order of magnitude less precise, since it can be compensated to some degree by an extended vertical field of view of the instrument.
Design data can be found directly throughout the text and in Table 1.
The authors declare that they have no conflict of interest.
We acknowledge the consultancy of the optics section at European Space
Agency. Part of this work was supported by the Chinese Scholarship
Council.
The article processing charges for
this open-access
publication were covered by a Research
Centre of the Helmholtz Association.
Edited by: Markus Rapp
Reviewed by: two
anonymous referees
Barth, C.: Upper atmosphere three-body reactions study leading to light emission with laboratory results applied to night airglow, NASA Technical Report, USA, 1964. a
Barth, C. A. and Hildebrandt, A. F.: The 5577 A airglow emission mechanism, J. Geophys. Res., 66, 985–986, https://doi.org/10.1029/JZ066i003p00985, 1961. a
Bernath, P.: The Atmospheric Chemistry Experiment (ACE), J. Quant. Spectrosc. Ra., 186, 3–16, https://doi.org/10.1016/j.jqsrt.2016.04.006, 2017. a
Bourassa, A. E., Langille, J., Solheim, B., Degenstein, D., and Dupont, F.: The Spatial Heterodyne Observations of Water (SHOW) Instrument for High Resolution Profiling in the Upper Troposphere and Lower Stratosphere, in: Light, Energy and the Environment, Opt. Soc. Am., FM3E.1, https://doi.org/10.1364/FTS.2016.FM3E.1, 2016. a
Burch, D. E. and Gryvnak, D. A.: Strengths, Widths, and Shapes of the Oxygen Lines near 13,100 cm−1 (7620 Å), Appl. Optics, 8, 1493–1499, https://doi.org/10.1364/AO.8.001493, 1969. a
Connes, P.: Spectromètre interférentiel à sélection par l'amplitude de modulation, J. Phys. Radium, 19, 215–222, https://doi.org/10.1051/jphysrad:01958001903021500, 1958. a
Cooke, B. J., Smith, B. W., Laubscher, B. E., Villeneuve, P. V., and Briles, S. D.: Analysis and system design framework for infrared spatial heterodyne spectrometers, Proc. SPIE, 3701, https://doi.org/10.1117/12.352971, 1999. a
Deiml, M., Kaufmann, M., Knieling, P., Olschewski, F., Toumpas, P., Langer, M., Ern, M., Koppmann, R., and Riese, M.: DiSSECT – Development of a small satellite for climate research, Proceedings of the 65th International Astronautical Congress, Toronto, Canada, 2014. a
Deiml, M., Song, R., Fröhlich, D., Rottland, B., Wagner, F., Liu, J., Wroblowski, O., Chen, Q., Loosen, F., Kaufmann, M., Rongen, H., Neubert, T., Schneider, H., Olschweski, F., Knieling, P., Mantel, K., Solheim, B., Shepherd, G., Koppmann, R., and Riese, M.: Test of a remote sensing Fourier transform interferometer for temperature measurements in the mesosphere on a REXUS rocket, Proceedings of the 23rd ESA Symposium on European Rocket and Balloon Programmes and Related Research, Visby, Sweden, 2017. a
Douglas, N. G.: Heterodyned Holographic Spectroscopy, Publ. Astron. Soc. Pac., 109, 151–165, 1997. a
Englert, C. R. and Harlander, J. M.: Flatfielding in spatial heterodyne spectroscopy, Appl. Optics, 45, 4583–4590, https://doi.org/10.1364/AO.45.004583, 2006. a, b, c
Englert, C. R., Harlander, J. M., Cardon, J. G., and Roesler, F. L.: Correction of phase distortion in spatial heterodyne spectroscopy, Appl. Optics, 43, 6680–6687, https://doi.org/10.1364/AO.43.006680, 2004. a
Englert, C. R., Stevens, M. H., Siskind, D. E., Harlander, J. M., and Roesler, F. L.: Spatial Heterodyne Imager for Mesospheric Radicals on STPSat-1, J. Geophys. Res.-Atmos., 115, D20306, https://doi.org/10.1029/2010JD014398, 2010. a
Feldman, M.: Analytic Signal Representation, 7–21, https://doi.org/10.1002/9781119991656.ch2, John Wiley & Sons, Ltd, Hoboken, N.J., 2011. a
Fischer, H., Birk, M., Blom, C., Carli, B., Carlotti, M., von Clarmann, T., Delbouille, L., Dudhia, A., Ehhalt, D., Endemann, M., Flaud, J. M., Gessner, R., Kleinert, A., Koopman, R., Langen, J., López-Puertas, M., Mosner, P., Nett, H., Oelhaf, H., Perron, G., Remedios, J., Ridolfi, M., Stiller, G., and Zander, R.: MIPAS: an instrument for atmospheric and climate research, Atmos. Chem. Phys., 8, 2151–2188, https://doi.org/10.5194/acp-8-2151-2008, 2008. a
Fitzgibbon, A. W.: Simultaneous linear estimation of multiple view geometry and lens distortion, in: Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2001, Vol. 1, https://doi.org/10.1109/CVPR.2001.990465, 2001. a
Gordon, I., Rothman, L., Hill, C., Kochanov, R., Tan, Y., Bernath, P., Birk, M., Boudon, V., Campargue, A., Chance, K., Drouin, B., Flaud, J.-M., Gamache, R., Hodges, J., Jacquemart, D., Perevalov, V., Perrin, A., Shine, K., Smith, M.-A., Tennyson, J., Toon, G., Tran, H., Tyuterev, V., Barbe, A., Császár, A., Devi, V., Furtenbacher, T., Harrison, J., Hartmann, J.-M., Jolly, A., Johnson, T., Karman, T., Kleiner, I., Kyuberis, A., Loos, J., Lyulin, O., Massie, S., Mikhailenko, S., Moazzen-Ahmadi, N., Müller, H., Naumenko, O., Nikitin, A., Polyansky, O., Rey, M., Rotger, M., Sharpe, S., Sung, K., Starikova, E., Tashkun, S., Auwera, J. V., Wagner, G., Wilzewski, J., Wcisło, P., Yu, S., and Zak, E.: The HITRAN2016 molecular spectroscopic database, J. Quant. Spectrosc. Ra., 203, 3–69, https://doi.org/10.1016/j.jqsrt.2017.06.038, 2017. a
Grossmann, K. U., Offermann, D., Gusev, O., Oberheide, J., Riese, M., and Spang, R.: The CRISTA-2 mission, J. Geophys. Res.-Atmos., 107, 8173, https://doi.org/10.1029/2001JD000667, 2002. a
Harlander, J. M.: Spatial Heterodyne Spectroscopy: Interferometric Performance at any Wavelength Without Scanning, PhD thesis, The University of Wisconsin – Madison, 1991. a, b
Harlander, J. M. and Roesler, F. L.: Spatial heterodyne spectroscopy: a novel interferometric technique for ground-based and space astronomy, Proc. SPIE, 1235, 1235-12, https://doi.org/10.1117/12.19125, 1990. a
Harlander, J. M., Reynolds, R. J., and Roesler, F. L.: Spatial heterodyne spectroscopy for the exploration of diffuse interstellar emission lines at far-ultraviolet wavelengths, Astrophys. J., 396, 730–740, https://doi.org/10.1086/171756, 1992. a, b
Harris, W. M., Roesler, F. L., Harlander, J., Ben-Jaffel, L., Mierkiewicz, E., Corliss, J., and Oliversen, R. J.: Applications of reflective spatial heterodyne spectroscopy to UV exploration in the solar system, Proc. SPIE, 5488, 5488-12, https://doi.org/10.1117/12.553107, 2004. a
Hilliard, R. and Shepherd, G.: Wide-Angle Michelson Interferometer for Measuring Doppler Line Widths, J. Opt. Soc. Am., 56, 362, 1966. a
Kaufmann, M., Deiml, M., Olschewski, F., Mantel, K., Wagner, F., Loosen, F., Fröhlich, D., Rongen, H., Neubert, T., Rottland, B., Schneider, H., Riese, M., Knieling, P., Liu, J., Song, R., Wroblowski, O., Chen, Q., Koppmann, R., Solheim, B., Shan, J., and Shepherd, G.: A miniaturized satellite payload hosting a spatial heterodyne spectrometer for remote sensing of atmospheric temperature, Proceedings of the 11th IAA Symposium on Small Satellites for Earth Observation, Berlin, Germany, 2017. a
Lenzner, M. and Diels, J.-C.: Concerning the Spatial Heterodyne Spectrometer, Opt. Express, 24, 1829–1839, https://doi.org/10.1364/OE.24.001829, 2016. a
Liu, J., Kaufmann, M., Zhu, Y., Who, E., Olschewski, F., Koppmann, R., and Riese, M.: Level-0 data processing of a spatial heterodyne spectrometer, Atmos. Meas. Tech. Discuss., in preparation, 2018. a
McDade, I. C. and Llewellyn, E. J.: The excitation of O(1S) and O2 bands in the nightglow: a brief review and preview, Can. J. Phys., 64, 1626–1630, https://doi.org/10.1139/p86-287, 1986. a
Meriwether, J. W.: A review of the photochemistry of selected nightglow emissions from the mesopause, J. Geophys. Res.-Atmos., 94, 14629–14646, https://doi.org/10.1029/JD094iD12p14629, 1989. a
Nightingale, T. J. and Crawford, J.: A Radiometric Calibration System for the ISAMS Remote Sounding Instrument, Metrologia, 28, 233–237, 1991. a
Offermann, D., Grossmann, K.-U., Barthol, P., Knieling, P., Riese, M., and Trant, R.: Cryogenic Infrared Spectrometers and Telescopes for the Atmosphere (CRISTA) experiment and middle atmosphere variability, J. Geophys. Res.-Atmos., 104, 16311–16325, https://doi.org/10.1029/1998JD100047, 1999. a
Ortland, D. A., Hays, P. B., Skinner, W. R., and Yee, J.-H.: Remote sensing of mesospheric temperature and O2(1Σ) band volume emission rates with the high-resolution Doppler imager, J. Geophys. Res.-Atmos., 103, 1821–1835, https://doi.org/10.1029/97JD02794, 1998. a
Poghosyan, A. and Golkar, A.: CubeSat evolution: Analyzing CubeSat capabilities for conducting science missions, Prog. Aerosp. Sci., 88, 59–83, https://doi.org/10.1016/j.paerosci.2016.11.002, 2017. a
Rodrigo, R., Lopez-Moreno, J., Lopez-Puertas, M., and Molina, A.: Analysis of OI-557.7 nm, NAD, OH(6-2) and O2() (0–1) nightglow emission from ground-based observations, J. Atmos. Terr. Phys., 47, 1099–1110, https://doi.org/10.1016/0021-9169(85)90028-5, 1985. a
Roesler, F. L.: An Overview of the SHS Technique and Applications, in: Fourier Transform Spectroscopy/Hyperspectral Imaging and Sounding of the Environment, Opt. Soc. Am., https://doi.org/10.1364/FTS.2007.FTuC1, 2007. a
Roesler, F. L. and Harlander, M.: Spatial heterodyne spectroscopy: interferometric performance at any wavelength without scanning, Proc. SPIE, 1318, 1318-10, https://doi.org/10.1117/12.22119, 1990. a
Russell, J., Gordley, L., Deaver, L., Thompson, R., and Park, J.: An overview of the halogen occultation experiment (HALOE) and preliminary results, Adv. Space Res., 14, 13–20, https://doi.org/10.1016/0273-1177(94)90110-4, 1994. a
Russell, J. M., Mlynczak, M. G., Gordley, L. L., Tansock, J. J., and Esplin, R. W.: Overview of the SABER experiment and preliminary calibration results, Proc. SPIE, 3756, 3756-12, https://doi.org/10.1117/12.366382, 1999. a
Sheese, P., Llewellyn, E., Gattinger, R., Bourassa, A., Degenstein, D., Lloyd, N., and McDade, I.: Temperatures in the upper mesosphere and lower thermosphere from OSIRIS observations of O2 A-band emission spectra, Can. J. Phys., 88, 919–925, https://doi.org/10.1139/p10-093, 2010. a
Shepherd, G., Desaulniers, D.-L., Gault, W., Hersom, C., Smith, K., Scott, A., Solheim, B., and Wimperis, J.: Optical Payloads for Space Missions, in: Wind Imaging Interferometer on NASA's Upper Atmosphere Research Satellite, edited by: Qian, S.-E., chap. 18, John Wiley & Sons, Ltd, UK, 2016. a
Slanger, T. G. and Copeland, R. A.: Energetic Oxygen in the Upper Atmosphere and the Laboratory, Chem. Rev., 103, 4731–4766, https://doi.org/10.1021/cr0205311, 2003. a, b
Smith, B. W. and Harlander, J. M.: Imaging spatial heterodyne spectroscopy: theory and practice, Proc. SPIE, 3698, 3698-7, https://doi.org/10.1117/12.354497, 1999. a, b
Song, R., Kaufmann, M., Ungermann, J., Ern, M., Liu, G., and Riese, M.: Tomographic reconstruction of atmospheric gravity wave parameters from airglow observations, Atmos. Meas. Tech., 10, 4601–4612, https://doi.org/10.5194/amt-10-4601-2017, 2017. a, b
Torr, M. R., Torr, D. G., and Laher, R. R.: The O2 atmospheric 0-0 band and related emissions at night from Spacelab 1, J. Geophys. Res.-Space, 90, 8525–8538, https://doi.org/10.1029/JA090iA09p08525, 1985. a
Watchorn, S., Roesler, F. L., Harlander, J. M., Jaehnig, K. P., Reynolds, R. J., and Sanders, W. T.: Development of the spatial heterodyne spectrometer for VUV remote sensing of the interstellar medium, Proc. SPIE, 4498, 284–295, https://doi.org/10.1117/12.450063, 2001. a
Watchorn, S., Roesler, F. L., Harlander, J., Jaehnig, K. P., Reynolds, R. J., and Sanders, W. T.: Evaluation of payload performance for a sounding rocket vacuum ultraviolet spatial heterodyne spectrometer to observe C IV λλ1550 emissions from the Cygnus Loop, Appl. Optics, 49, 3265–3273, https://doi.org/10.1364/AO.49.003265, 2010. a
Watchorn, S. R., Noto, J., Doe, R. A., and Fish, C. S.: Development of the Nanosat Oxygen A-Band Spatial Heterodyne Interferometer (NOASHIN), AGU Fall Meeting Abstracts, A23I-3357, 2014. a