the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
An in situ flow tube system for direct measurement of N2O5 heterogeneous uptake coefficients in polluted environments
Weihao Wang
Chuan Yu
Xiang Peng
Yan Zhou
Dingli Yue
Yubo Ou
The heterogeneous reactivity of dinitrogen pentoxide (N2O5) on ambient aerosols plays a key role in the atmospheric fate of NOx and formation of secondary pollutants. To better understand the reactive uptake of N2O5 on complex ambient aerosols, an in situ experimental approach to direct measurement of N2O5 uptake coefficient (γN2O5) was developed for application in environments with high, variable ambient precursors. The method utilizes an aerosol flow tube reactor coupled with an iterative chemical box model to derive γN2O5 from the depletion of synthetically generated N2O5 when mixed with ambient aerosols. Laboratory tests and model simulations were performed to characterize the system and the factors affecting γN2O5, including mean residence time, wall loss variability with relative humidity (RH), and N2O5 formation and titration with high levels of NO, NOx, and O3. The overall uncertainty was estimated to be 37 %–40 % at γN2O5 of 0.03 for RH varying from 20 % to 70 %. The results indicate that this flow tube coupled with the iterative model method could be buffered to NO concentrations below 8 ppbv and against air mass fluctuations switching between aerosol and non-aerosol modes. The system was then deployed in the field to test its applicability under conditions of high ambient NO2 and O3 and fresh NO emission. The results demonstrate that the iterative model improved the accuracy of γN2O5 calculations in polluted environments and thus support the further field deployment of the system to study the impacts of heterogeneous N2O5 reactivity on photochemistry and aerosol formation.
- Article
(9776 KB) -
Supplement
(471 KB) - BibTeX
- EndNote
Dinitrogen pentoxide (N2O5) is a nocturnal reactive intermediate in the atmospheric oxidation of nitrogen oxides (NOx), which plays an important role in atmospheric photochemistry and the production of secondary pollutants (e.g., Chang et al., 2011). N2O5 is formed from the reaction of nitrogen dioxide (NO2) and nitrate radical (NO3). Because NO3 is photolytically unstable, it (and therefore N2O5) only accumulates under dark conditions (i.e., at night). The heterogeneous reactions of N2O5 on aerosols have been recognized as a major sink for NOx, affecting the atmospheric lifetime of NOx and the formation of ozone and other secondary pollutants (e.g., Brown et al., 2007; Wang et al., 2016). The heterogeneous N2O5 loss rate on aerosols (kaerosols) depends on the uptake coefficient of N2O5 (γN2O5) and the available aerosol surface area, and can be expressed using Eq. (1) when the gas-phase diffusion effect is negligible (Fuchs and Sutugin, 1971; Tang et al., 2014).
where c (m s−1) is the mean molecular speed of N2O5 and Sa (m2 m−3) is the aerosol surface area concentration. γN2O5 is the reaction probability of a N2O5 molecule colliding with the aerosol surface, resulting in net removal via reactions on aerosols. Because γN2O5 is a critical parameter for determining N2O5 uptake on aerosols, it is necessary to develop reliable methods to measure it.
γN2O5 has typically been determined in the laboratory using different types of flow tubes and reactors to measure the decay rate of N2O5 in the presence of pure inorganic and organic aerosols or mixed aerosols under different conditions (e.g., Thornton et al., 2003; Tang et al., 2017, and references cited therein). The γN2O5 has been shown to be highly dependent on aerosol composition, temperature, and relative humidity; different parameterizations of varying degrees of complexity have thus been proposed to relate γN2O5 to aerosol composition (Anttila et al., 2006; Bertram and Thornton, 2009; Davis et al., 2008; Evans and Jacob, 2005; Riemer et al., 2009). In ambient conditions, several methods have been developed to derive γN2O5 directly from atmospheric concentrations of N2O5. Brown et al. (2007) utilized steady-state approximation of NO3 and N2O5 to derive γN2O5 based on the correlation of inverse N2O5 steady-state lifetime with NO2 concentration and aerosol surface area; Phillips et al. (2016) assumed a conserved air mass and used the production rates of and ClNO2 to derive γN2O5; and Wagner et al. (2013) applied an iterative chemical box model to derive the appropriate γN2O5 to match the predicted N2O5 concentration to the measured values with the assumption of the reaction time starting at sunset and with no interception of other NOx emissions.
Bertram et al. (2009a) introduced an approach to directly measure γN2O5 on ambient aerosols by utilizing an entrained aerosol flow reactor coupled with a chemical ionization mass spectrometer (CIMS). By switching sampling between filtered and unfiltered ambient air, the reactivity of N2O5 was determined based on a comparison of the pseudo-first-order loss rate of N2O5 in ambient air with and without aerosols. The loss rate of N2O5 to aerosols (kaerosols) could be derived from the concentration ratio at the exit of the flow reactor, with the assumption that the wall loss of N2O5 is constant in the successive two measurements and that all losses are first order (Bertram et al., 2009a):
where Δt is the mean residence time in the flow tube reactor and [N2O5]Δt is the N2O5 concentration measured at the exit of the flow reactor in the two modes (i.e., the presence and absence of aerosols). This flow tube apparatus was deployed at two urban sites in Boulder and one coastal site in La Jolla to measure γN2O5 on ambient aerosols (Bertram et al., 2009b; Riedel et al., 2012). They found that the fluctuation of relative humidity (RH) and NO3 reactivity (mainly dominated by NO) could lead to great uncertainty in measured γN2O5, and they therefore applied some screening criteria, including only data with a RH fluctuation of less than 2 % and NO concentration lower than 750 pptv. This constraint resulted in about 20 % of the data being used for further analysis. It was necessary to adopt these criteria because only first-order loss is considered in the flow tube reactor and other reactions involving ambient NO, NO2, and O3 are not. The latter treatment is suitable when ambient concentrations are low and the air mass is relatively stable, but it may be problematic in polluted environments with high fresh NOx emissions, high O3 concentrations, and rapidly changing air mass.
Several recent studies have revealed active N2O5 heterogeneous processes on aerosols at polluted sites and its significant impacts on photochemistry and secondary aerosol formation due to abundant NOx, O3, and aerosols (e.g., Li et al., 2016; Tham et al., 2016; Wang et al., 2016; X. Wang et al., 2017; Z. Wang et al., 2017; Yun et al., 2018). The γN2O5 derived from ambient concentration measurements showed different characteristics and dependence compared to previous measurements in relatively clean environments (Morgan et al., 2015; Z. Wang et al., 2017). To better understand the reactive uptake of N2O5 on complex ambient aerosols, a flow tube reactor approach was developed for direct N2O5 reactivity measurement under highly polluted conditions. In the following sections, we describe in detail the method used for determining the N2O5 uptake coefficient with an iterative box model and discuss the factors affecting the system's performance and uncertainty. Laboratory tests and field deployment of the method are presented to demonstrate its application under conditions with high ambient concentrations of NO2 and O3 and fresh NO emission.
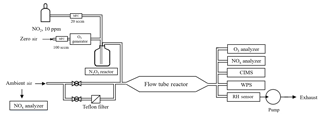
2.1 Flow tube reactor
The flow tube system consists of an N2O5 generation part, a sample inlet with aerosol filter manifold, a flow tube reactor, and detection instruments. A schematic diagram of the experimental apparatus is given in Fig. 1. The sample inlet with an aerosol filter manifold is made of 1∕4 in. outer diameter (OD) stainless-steel tubing. By switching two stainless-steel ball valves, ambient air can be introduced directly into the flow tube or through a PTFE membrane (Pall Life Sciences) to remove aerosols. The flow tube is a Teflon-coated stainless-steel tube, 120 cm in length with an internal diameter of 12.5 cm. The ambient or filtered air enters and exits the flow tube via 10 cm deep 60∘ tapered end caps. The total flow rate through the flow tube is 4.6 standard liter per minute (SLPM) and includes 120 standard cubic centimeter per minute (SCCM) of N2O5 flow, which is introduced through an orthogonal entry to minimize the entrance length of the injected flow. The air pressure in the flow tube reactor is around 730 torr. The adopted flow rate and pressure give a Reynolds number of 55 (i.e., laminar flow) in the flow tube reactor. At the exit of the flow tube reactor, several detection instruments are used to measure the concentrations of N2O5, O3, NOx, and aerosol surface area.
2.2 Generation of N2O5
N2O5 is generated in situ from the reaction of O3 with excess NO2 at room temperature via Reactions (R1) and (R2), which has been used in many previous lab and field measurements (e.g., Bertram et al., 2009a).
In this study, ozone was generated from O2 photolysis with a mercury lamp in a commercial calibrator (model 4010, Sabio Instrument Inc.). One hundred SCCM of produced O3 flow was mixed with 20 SCCM of NO2 (10 ppmv balanced in N2; Arkonic, USA) in a Teflon reaction chamber (volume = 68 cm3) for about 28 s prior to injection into the flow tube reactor. Under conditions of excessive NO2, the system was expected to shift the R2 equilibrium towards N2O5. Concentrations of synthesized N2O5 were calculated from observed changes in NO2 (before and after addition of O3), and the N2O5 content had also been inter-validated with a cavity ring-down spectrometer (CRDS) in our previous studies (Wang et al., 2016). Prior to the N2O5 generation, the system was purged with dry zero air and NO2 for at least 2 h, to minimize the water content level and stabilize the NO2 source. This system was shown to be able to produce N2O5 concentrations from 1 to 10 ppbv (after dilution in the flow tube). In a typical experiment used in the present study, the input of the N2O5 source to the top of the flow tube contained 4.3 ppbv of N2O5, together with 106 ppbv of O3 and 57 ppbv of NO2. The stability of the synthetic-N2O5 source was tested continuously for 8 h, and the variation of the signal was within ±2 % in each hour. More detailed description of the N2O5 generation can be found in Wang et al. (2016).
2.3 Detection instruments
At the exit of the flow tube reactor, O3 was measured by a UV photometric analyzer (Thermo, Model 49i) and NO2 was measured by a chemiluminescence NOx analyzer (Thermo, Model 42i) equipped with a blue-light photolytic converter (BLC). The aerosol number concentration and size distribution (10 nm to 10 µm) were measured by a wide-range particle spectrometer (WPS, model 1000XP, MSP Corporation, USA) to determine the aerosol surface area. The uncertainty of the aerosol surface area measurement was 20 %–30 % (Z. Wang et al., 2017; Tham et al., 2018). The transmission of aerosols in the flow tube was evaluated using laboratory-generated (NH4)2SO4 particles. The passing efficiency was around 50 % for particles with a size of 20 nm and more than 90 % for particles larger than 100 nm. The total surface area loss in the flow tube was around 10 %–25 %. The N2O5 and ClNO2 concentrations were quantified by an iodide-adduct chemical ionization mass spectrometer (CIMS; THS Instrument, Atlanta). The CIMS has been deployed in several field campaigns, and the setup and operation have been previously described (Tham et al., 2016; Wang et al., 2016; X. Wang et al., 2017; Z. Wang et al., 2017). Briefly, the primary ion I− was generated from ionization of CH3I diluted in N2 flow through a 210Po source. The N2O5 and ClNO2 were detected as ion clusters of I(N2O5)− and I(ClNO2)− at 235 and 208 m∕z by the quadrupole mass spectrometer. Because of the higher pipeline resistance in the flow tube reactor compared to ambient measurement, a smaller orifice with a 0.0135 in diameter was utilized in the CIMS inlet to reduce the sample flow, and another orifice was added before the scroll pump to keep the pressure in the ionization reaction chamber at 50 torr. The corresponding sample flow was 0.4 SLPM. The detection limit of the instrument was estimated to be 2 pptv (1 min averaged data), and the uncertainty of the CIMS measurement was estimated as ±25 % (Tham et al., 2016). The ambient volatile organic compounds (VOCs) were determined using an online gas chromatograph (GC) coupled with a flame ionization detector (FID) and a mass spectrometer (MS). The VOC concentrations were used to determine the in the aerosol flow tube system, which was treated as constant during the short time period of flow tube measurement. The ambient NO level was measured by another chemiluminescence NOx analyzer (Thermo, Model 42i) equipped with a molybdenum converter.
The mean residence time that represents the average reaction time of the gases in the flow tube reactor is an essential parameter in calculation of the reactive uptake coefficient. In a previous flow reactor studies (e.g., Thornton et al., 2003), the average residence time has usually been calculated from the flow rate and flow tube volume assuming an ideal laminar flow. To determine the mean residence time for non-ideal flow more accurately, the residence time distribution (RTD) method introduced by Danckwerts (1953) was used in the present study. The RTD method involves introduction of an inert tracer species into the reactor and detection of its transient concentration leaving the reactor outlet, and it has been widely used in previous lab studies to characterize the mixing and flow behavior of non-ideal aerosol flow reactors (e.g., Lambe et al., 2011).
Pulse injection of highly concentrated ClNO2 was used in the present study to measure the RTD and hence determine the mean residence time. ClNO2 is an inert gas within the dark Teflon-coated flow tube reactor and can be measured by CIMS with high time resolution (>1 Hz). ClNO2 was synthesized in situ via passing the N2O5 through a NaCl slurry in the Teflon tubing reactor (Wang et al., 2016). The pulse injection was controlled by a solenoid valve. At t=0 s, 120 SCCM (the same flow as N2O5 injection during the uptake measurement) of ClNO2 was directly injected into the flow tube reactor; at t=2 s, the solenoid valve switched and the ClNO2 flow was passed through a charcoal filter to provide zero gas into the flow tube reactor. The RTD function E(t) is defined by the following equation:
where C(t) represents the ClNO2 concentration measured at time t. Then the mean residence time can be calculated as follows:
The measurement result of the residence time test is shown in Fig. 2. With a flow rate of 4.6 SLPM in the flow tube reactor, the mean residence time determined from the RTD method was 149±2 s. In comparison, the residence time calculated using the flow rate and reactor volume gives a value of 159±5 s, which is 6.7 % higher than that given by the RTD method, and could lead to underestimation of the rate constant. The RTD function in Fig. 2 is clearly different from the ideal laminar flow reactor. Bertram et al. (2009a) have suggested that the determined rate constant would be underestimated by up to 25 % due to non-ideal plug flow conditions. More discussion of the uncertainty in γN2O5 calculation associated with residence time distribution is presented in Sect. 5.
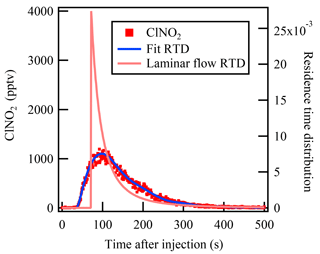
Figure 2The measured residence time distribution of the injected ClNO2 in the flow tube reactor. The blue line represents the fitted residence time distribution of the ClNO2 pulse injection experiment. The pink line represents the expected residence time distribution of an ideal laminar flow reactor without diffusion.
As described previously, the reactivity of N2O5 can be investigated using the aerosol modulation by comparing the loss rate of generated N2O5 in the flow tube reactor with and without ambient aerosols. Previous studies (e.g., Bertram et al., 2009a) utilized the exit-concentration ratio of N2O5 to obtain the N2O5 loss rate on aerosols. However, air mass changes lead to different NO3 loss rates and production rates over a short time period (i.e., a typical sampling cycle for about 1 h), and high background NO2 and O3 in the ambient air would affect the exit N2O5 concentration and hence bias the measurement of loss rate and uptake coefficient from the flow tube experiments. To minimize the potential influences of high levels of ambient pollutants and rapidly changing air mass, a time-dependent box model constrained by the real measurement data was used in the present study to directly calculate the N2O5 loss rate in both aerosol and non-aerosol mode, considering multiple reactions describing the production and loss of NO3 and N2O5 (Reactions R1–R6) under ambient conditions.
The rate constants for Reactions (R1) to (R4) recommended by the National Aeronautics and Space Administration–Jet Propulsion Laboratory (Sander et al., 2009) were used. The loss rate coefficient from NO3 reactions with VOCs (Reaction R5) was determined by ambient measured VOC concentrations and rate coefficients from Atkinson and Arey (2003). The N2O5 heterogeneous loss rate coefficient khet (Reaction R6) including heterogeneous loss on both aerosol and reactor surfaces was the only adjustable parameter, while other parameters such as N2O5, NO, NO2, and O3 concentration were constrained by concurrent measurements. The model simulated the reactions starting from the entrance of the reactor after mixing the ambient air sample and synthetic-N2O5 source. The initial concentrations of [NO2]t=0 and [O3]t=0 were calculated from the ambient measured levels of NO2 and O3 and those from the N2O5 source. Given the constraint of measured parameters at the entrance of the flow tube reactor – including [NO]t=0, [NO2]t=0, [O3]t=0, [N2O5]t=0, [VOCs]t=0, temperature, and pressure – these reactions could be integrated in time (performed in Matlab with the Kinetic PreProcessor using a Radau5.integrator) (Damian et al., 2002) to obtain the exit concentrations of NO2, O3, and N2O5. The calculated concentrations were then compared with the measured concentrations at the exit of the flow tube reactor, and the N2O5 loss rate coefficient was tuned until the N2O5 concentration predicted by the box model agreed with the measured N2O5 concentration, [N2O5]Δt. Assuming that kwall are constant between successive flow tube experiments with and without aerosols, the loss rate coefficient on aerosols surfaces can be determined from the differences between two modes: . Then the uptake coefficient of N2O5 on aerosol surfaces (γN2O5) can be calculated by the following equation:
In circumstances without concurrent ambient measurement of NO2 and O3 and when accurate measurements are only available at the flow tube outlet, as in the present study, an iterative box model including both backward and forward simulation is needed. Following the method suggested by Wagner et al. (2013), the relevant reactions can be integrated backward starting with the measured concentrations at the exit of the reactor (t=Δt) to obtain the initial concentrations. As the cycle between NO3 and N2O5 is fast and quickly established in high-NOx conditions, the NO3 and N2O5 are considered as one singular N2O5∗ species by assuming NO3 and N2O5 are in equilibrium (Brown et al., 2003). Doing this also makes backward reaction simulation possible by avoiding unstable equilibrium in the box model. The NO at the entrance of the flow tube could react quickly with O3 and NO3, with a short lifetime of a few seconds, resulting in near-zero concentration at the exit of the flow tube. To initialize the simulation, a time-dependent NO concentration in the flow tube must be derived. An approximate [NO] profile can be estimated from a forward simulation with inputs of measured initial NO, N2O5, guessed khet, and estimated initial NO2 and O3 concentrations from the following equations. The measured initial NO data used 3 min earlier data as input data considering the mean residence time of 150 s.
The estimated [NO] profile was then constrained in the backward model simulation – together with inputs of measured concentrations of N2O5, NO2, and O3 at the exit of the flow tube reactor and the initially guessed khet – to derive the initial mixing ratios. The box model was run forward and backward iteratively with updated values and adjusted khet until simulated N2O5 concentration matched the measurement at the exit of the flow tube reactor. The agreement of simulated NO2 and O3 concentrations with measurements was also used as a check to validate the model calculation. Thus, the uptake coefficient of N2O5 was determined from Eq. (5). An example of the iterative box model calculation is shown in Fig. 3.
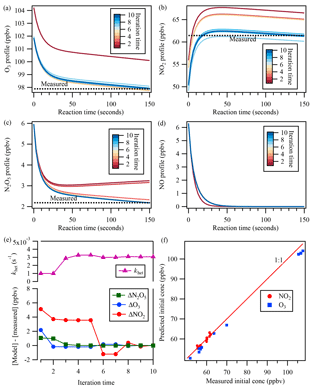
Figure 3An example of the iterative box model simulation to derive khet from the measured concentrations of NO2, O3, and N2O5 at the exit of the flow tube reactor. The concentration profiles obtained from the simulation in 10 iterations are shown for (a) O3, (b) NO2, (c) N2O5, and (d) NO. In the upper part of (e), the adjusted N2O5 loss rate is shown for each iteration. The lower part of (e) shows the concentration differences between the model simulation and measurements of N2O5, O3, and NO2 at the exit of the reactor for each iteration. (f) shows the comparison between measured initial concentrations from laboratory test and predicted initial concentrations from the iterative model.
For some conditions, the iterative box model returns a negative N2O5 loss rate coefficient. This non-physical result might result from much larger fluctuations of or kwall in the system during each measurement cycle. When kaerosol is small due to the low Sa or insignificant uptake, the or kwall may dominate the N2O5 loss in flow tube reactor, and the fluctuations of or kwall due to the air mass or temperature/RH changes would bias the kaerosol determination and lead to large uncertainty or negative values. This situation often occurred under conditions of fresh NO emission; more discussion of the influence of NO is presented in Sect. 6.
Laboratory tests of N2O5 uptake on (NH4)2SO4 aerosols were also performed with different NO, NO2, and O3 conditions, and the uptake coefficients were determined from the iterative box model analysis described above with input of measured concentrations. The determined uptake coefficient ranged from 0.018 to 0.026 (Table S1 in the Supplement), which are similar to previous laboratory study results with (NH4)2SO4 aerosols (Davis et al., 2008). The consistency also can serve as a validation of the applicability of the introduced system and method. In addition, we also compared the measured initial concentration of NO2 and O3 during the lab tests with that predicted from the iterative model (Fig. 3f). The NO2 concentration matched well between model prediction and measurement, while O3 was a little lower from the model simulation, which might be due to the wall loss or other loss ways of O3 in the flow tube reactor.
In the present work, the determination of kaerosols is independent of the magnitude of kwall, but the stability of kwall is critical for the accurate retrieval of kaerosols. kwall depends on RH, and the variability in RH on the timescale of the measurement can introduce additional uncertainty (Bertram et al., 2009a). Laboratory experimental tests have been conducted to investigate the variability of kwall with RH in the current flow tube system. kwall can be determined from the previously described iterative model with the measurement of N2O5 loss through the flow tube in a zero air flow in the absence of aerosols. As shown in Fig. 4, kwall has a strong positive relationship with RH and increases with RH, especially when RH is higher than 50 %. The consistent kwall at each RH condition with different initial N2O5 concentrations suggests that kwall in the current system is relatively stable under different chemical conditions but varies as a function of RH.
The sample air exiting the flow reactor was continuously measured by a RH probe, and the results showed that the RH variation between the aerosol presence and absence modes was within 1 % more than 80 % of the time during the ambient measurement cases. This result would translate into an uncertainty of () to () in γN2O5 with RH of 20 % to 70 %, respectively, and a Sa of 1000 µm2 cm−3. To minimize the magnitude of the variability in kwall, the wall of the reactor was coated with Teflon PFA, and the flow tube reactor was cleaned daily with distilled water. Ultrasonic baths were also utilized after a 1-week period of ambient measurement to remove aerosol buildup from the wall of the flow tube reactor.
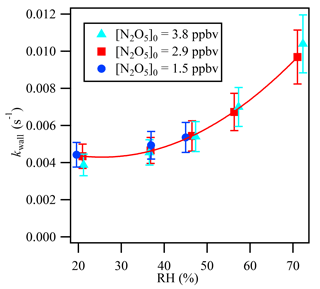
Figure 4Relative humidity dependence of the wall loss rate coefficient (kwall) of N2O5 in the flow reactor.
Table 1Parameters varied in the Monte Carlo simulations.

a 1σ standard deviation for the varied parameters. b The kwall is calculated from RH, using the relation fitting equation in Fig. 4. c The variation of kwall is calculated as RH varied 1 %.
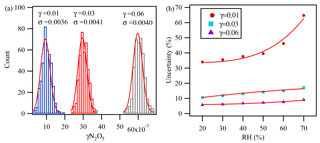
Figure 5The partial uncertainty in γN2O5 determination associated with kwall changes, VOC variation, and the variation of different parameters during the measurement cycles derived from Monte Carlo simulations for three individual sets with 400 simulations at (a) RH =40 % and (b) different RH values. In these three data sets, the condition was set as follows: surface area =1000 µm2 cm−3, reaction time =150 s, initial O3=80 ppbv, initial NO2=50 ppbv, initial NO =2 ppbv, initial N2O5=5 ppbv, temp =25 ∘C, and s−1.
In addition to kwall being affected by RH, uncertainty in kaerosols determination can also result from N2O5 source variability, NO3 reactivity with VOCs, and precision as well as accuracy associated with the measurement of all parameters. The long measurement cycle may also bring about uncertainty due to variation in concentrations in two operation modes. As described in Sect. 2.2, the stability of the N2O5 generation source was within ±2 % over an hour. In the present study, online VOCs were measured with a time resolution of 1 h. A ±0.01 s−1 variation of would lead to a single-point uncertainty in γN2O5 of for Sa = 1000 µm2 cm−3. NO reacts at a faster rate with NO3, having a larger impact on the γN2O5 calculation compared to VOCs. With a constrained real-time NO concentration, the iterative model can buffer against small NO changes. Stability of NO, NO2, O3, and N2O5 for a period of at least 5 min for each mode is required to ensure that the flow tube reactor measurement and iterative model yield reasonable results. The measurement precision and variation of these species during each cycle might also introduce uncertainty in the iterative model calculation.
The uncertainty in the γN2O5 determination associated with kwall changes, VOC variation, and the variation of the different parameters during the measurement cycles was estimated with a Monte Carlo approach, as described in Groß et al. (2014), by assessing the uncertainty from individual key parameters (shown in Table 1) in the calculation model. γN2O5 was found to be most sensitive to RH, which was closely related to kwall as discussed before. Figure 5a shows the partial uncertainty of γN2O5 derived from Monte Carlo simulations with RH at 40 %. The single-point uncertainty in γN2O5 was estimated to be for γN2O5 around 0.03 and for γN2O5 around 0.01, with RH of 40 %. The uncertainty increased with RH and would be 9 % to 17 % at γN2O5 around 0.03 for RH ranging from 20 % to 70 % (Fig. 5b).
Sensitivity tests with the iterative model calculation were performed to evaluate the uncertainty associated with measurement accuracy of N2O5 and VOCs, by varying the input N2O5 concentrations and in both modes. It is found that the N2O5 measurement uncertainty of 25 % (Tham et al., 2016; Z. Wang et al., 2017) would translate into an uncertainty of 12 % in the γN2O5 (shown in the Supplement). The VOC measurement uncertainty, however, has negligible influence on γN2O5 calculation. In a previous flow tube method introduced by Bertram et al. (2009a), the homogeneous reaction was expected to be independent of the aerosol and non-aerosol modes and was thus able to be canceled out in the calculation. Only strong atmospheric variation in VOC in a short time period would influence the N2O5 uptake measurement. The uncertainty introduced by the aerosol surface area measurement including aerosol loss influence would be propagated to an uncertainty in the γN2O5 calculation of 30 %.
As mentioned in Sect. 3, the use of mean residence time rather than RTD function by assuming an ideal reactor and ignoring diffusion and dispersion processes would also introduce uncertainties. In order to evaluate the magnitude of this bias, we performed a simplified test by comparing a first-order loss rate from mean residence time with a residence time distribution range. Briefly, the mean concentration of N2O5 at the exit of the reactor could be expressed by
where [N2O5]t is the average concentration exit from the reactor between t and t+dt, E(t) is the residence time distribution function, and k is the first-order loss rate coefficient of N2O5. The results showed that the first-order loss rate calculated from the distribution function was higher than that with a mean residence time and was about 5 % or 16 % higher when the ratio of was 0.6 or 0.2 in the flow tube system, respectively. When all of these factors are incorporated, the estimated total uncertainty is propagated to be 37 % to 40 % at γN2O5 around 0.03 with 1000 µm2 cm−3 Sa for RH ranging from 20 % to 70 %.
In polluted environments, high concentrations of NO2, O3, or NO in ambient air would affect the determination of the N2O5 loss rate and uptake coefficient in the flow tube experiments. To investigate the effect of multiple reactions of these species in polluted conditions, a series of tests with different conditions were simulated to compare the derived loss rate and uptake coefficient with and without consideration of N2O5 regeneration and NO titration in the flow tube system. Using the forward box model described in Sect. 4, the process in the flow tube reactor was simulated with an assumed fixed Sa of 1000 µm2 cm−3, γN2O5 of 0.03, kwall of 0.004 s−1, and of 0.01 s−1. Various conditions were simulated with different O3, NO2, and NO levels introduced into the flow tube, and the resulting concentrations of N2O5, NO2, and O3 at the exit of the reactors with and without aerosols modes were obtained. The loss rate and uptake coefficients of N2O5 were then calculated using the simple exit-concentration ratio approach (Eq. 2) and time-dependent iterative box model, respectively. The difference in γN2O5 obtained from these two methods reflects the effect of N2O5 regeneration and NO titration on uptake coefficient determination.
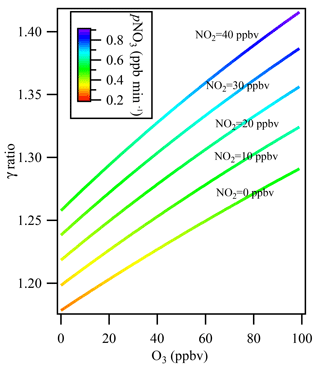
Figure 6The influence of multiple reactions resulting from high ambient NO2 and O3 levels under different ambient NO2 levels from 0 to 40 ppbv. The colors indicate the NO3 production rate (pNO3) at the entrance of the flow tube reactor after mixing with 106 ppbv of O3 and 57 ppbv of NO2 from the N2O5 source.
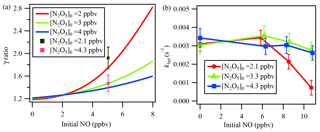
Figure 7(a) Simulation results of NO titration effect on γN2O5. The γN2O5 ratio represents (γN2O5 from the iterative model) ∕ (γN2O5 from the method of ignoring multiple reactions). Initial NO and initial N2O5 represent the respective initial concentrations of NO and N2O5 in the flow tube reactor. The lines represent the simulation result, and the cubes represent the lab test result. (b) khet calculated via the iterative model in laboratory experiments with constant RH of 21 %, different initial N2O5, and varied NO additions.
Figure 6 shows the simulation results for the derived uptake coefficients regarding the effect of N2O5 formation in the flow tube reactor, with O3 varying in the range of 0–100 ppbv and NO2 in the range of 0–40 ppbv without NO presence in the ambient air. The N2O5 source input was fixed at 4.3 ppbv, as measured in the laboratory, together with 106 ppbv of O3 and 57 ppbv of NO2 from the N2O5 source. The N2O5 regeneration effect on γN2O5 calculation was significant when O3 and NOx levels in the ambient air were high. For example, at NO2=40 ppbv and O3=100 ppbv, which may frequently be encountered in city cluster regions in China, neglecting N2O5 formation in the flow tube would result in underestimating γN2O5 by 42 %.
To demonstrate the influence of NO titration, simulation tests were performed with NO varying from 0 to 8 ppbv. Because the reaction rate of NO with NO3 is 2 orders of magnitude faster than that of NO with O3, the initial N2O5 level would affect the NO titration process. We performed the simulation with different initial N2O5 concentrations injected into the flow tube reactor. As the green line in Fig. 7a indicates, the calculated γN2O5 will be greatly underestimated when NO concentration increases, up to 55 % at a NO level of 8 ppbv with an initial N2O5 level of 3 ppbv compared to a NO level of 0. During the laboratory experiments, two initial N2O5 conditions with the input of an additional 5 ppbv of NO were also tested. The determined γN2O5 from the iterative model simulation and exit-concentration method was compared and is shown as cubes in Fig. 7a. The model results lie within the uncertainty range of the measurements, further cross-validating the NO influences and the model simulation. Figure 7a also shows that a lower initial N2O5 leads to a larger underestimation of γN2O5 in the presence of NO. It is not desirable to use N2O5 concentrations above 5 ppbv to minimize the NO effect, because of other potential artifacts associated with working at high concentration (Thornton et al., 2003).
To explore which NO level would leave an extremely low N2O5 concentration in the exit of the reactor and make N2O5 loss rate measurement impossible, a series of experiments in clean air with additional NO was conducted in the laboratory to investigate NO titration effects and the performance of the iterative model in buffering against high NO. As shown in Fig. 7b, the derived khet showed consistent results for zero NO and NO <6 ppbv conditions when RH and other parameters were unchanged. With higher NO addition and a lower initial N2O5 level, the calculated khet, however, could be underestimated due to greater uncertainty when NO3 and N2O5 were insufficient to titrate with NO. Figure 7b also shows that the introduced box model method could buffer against NO below 8 ppbv with an initial N2O5 level of 4.3 ppbv. For future development, an activated-carbon scrubber in the inlet to reduce the gas-phase interferers (NO, NO2, O3, VOCs) but transmit aerosols could be a complementary approach to apply the flow tube system coupled with iterative box model analysis to even more polluted conditions.
In summary, the simulation and laboratory results demonstrate that neglecting the formation and titration reactions in a flow tube reactor will result in underestimating γN2O5. To reduce the NO titration effect, a relatively high level of N2O5 (but less than 5 ppbv) should be introduced to the flow tube reactor. Consideration of the multiple reactions in the iterative model is sufficiently robust to encourage further development to improve the accuracy of γN2O5 calculations.
During winter 2017, the flow tube system was deployed to measure the N2O5 uptake coefficient at a sub-urban site in Heshan, Guangdong, in southern China. The sampling time for each mode with and without ambient aerosols lasted for at least 15 min to ensure 5 min stable data at the exit for subsequent modeling analysis. The measured 5 min average concentrations of initial NO and exit N2O5, NO2, and O3 were used as the inputs in the iterative box model to derive khet and γN2O5. Most measurements were conducted during the daytime to avoid interruption of nighttime ambient N2O5, and daytime N2O5 levels could be neglected. The average ambient temperature, RH, NO, NO2, and O3 during the field campaign were 23 ∘C, 51 %, 3.2 ppbv, 23 ppbv, and 32 ppbv, respectively. As discussed previously, changes in RH and temperature can influence the stability of kwall and N2O5–NO3 equilibrium, and thus upset γN2O5 measurement. In the cases where γN2O5 measurement was affected by extreme fluctuations in NO (above 8 ppbv), temperature and RH (fluctuation >2 %) were discarded from the analysis.
In addition to the iterative box model approach, we also used the exit-concentration ratio approach (cf. Eq. 2) to calculate the γN2O5. Figure 8 exhibits the comparison of γN2O5 obtained using these two methods. Fifteen out of 51 measurements occurred under relatively “clean and stable” conditions (defined as ambient NO <1 ppbv, fluctuation of NO <0.3 ppbv, NO3 production rate <0.8 ppbv min−1, and fluctuation of NO2 and O3 <4 ppbv), and the corresponding values of γN2O5 from the two methods show good correlation, with an average ratio of 1.34, which is consistent with our previous simulation results that the exit-concentration ratio approach could underestimate γN2O5 mainly due to N2O5 regeneration reaction. For conditions with higher precursor concentrations and fluctuations, a larger discrepancy between γN2O5 from two methods was found (see Fig. 8). As described previously, greater uncertainty in the exit-concentration ratio approach could result from multiple reactions and air mass changes. The fluctuations of NO, NO2, and O3 could greatly affect the exit N2O5 concentration ratio. For example, a lower NO level and higher NO2 and O3 levels in the aerosol mode relative to the non-aerosol mode would result in a higher exit N2O5 concentration ratio, which would lead to underestimation of γN2O5 and even negative values (see Fig. 8 and Supplement). As even a 1 ppbv fluctuation of NO concentration could largely affect the exit N2O5 concentration, it would result in significant uncertainty for the exit-concentration ratio approach. When NO concentration is much higher, for example in the aerosol-existing mode, the measured N2O5 concentration is lower due to NO titration; thus the uptake coefficient is overestimated when only the end concentration ratio of N2O5 in two modes is compared.
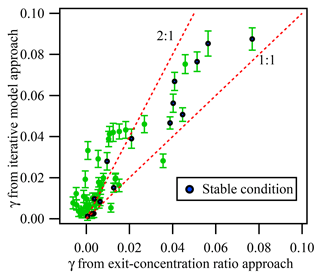
Figure 8Comparison of γN2O5 determined from the exit-concentration ratio approach and the iterative model approach for all available data measured in the Heshan campaign. The blue points represent the data obtained under “clean and stable condition”, while green points are data obtained from other condition. The “clean and stable condition” is defined as follows: ambient NO <1 ppbv, the change of NO <0.3 ppbv, the NO3 production rate <0.8 ppbv min−1, and the change of NO2 and O3 <4 ppbv. The error bar represents the uncertainty calculated by the Monte Carlo approach under the measurement condition.
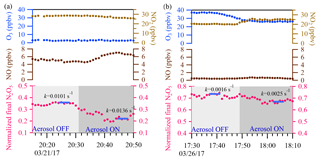
Figure 9Two sample cases are shown. In the upper panel, the blue and light brown dots represent 1 min ambient O3 and NO2 data, respectively. In the middle panel, the brown dots represent 1 min ambient NO data. In the lower panel, the pink dots represent 1 min average of N2O5 concentration normalized to the initial N2O5 concentration in the flow tube reactor. The calculated total N2O5 loss rate derived from the iterative model with 5 min average input data (the blue bar) is also shown for each cycle.
Two example cases with large air mass changes are shown in Fig. 9. In Fig. 9a, a case with high and fluctuating NO emission was observed on the night of 21 March 2017, with average ambient concentrations of NO of 6 ppbv, NO2 of 27 ppbv, O3 of 2 ppbv, and Sa of 1880 µm2 cm−3. γN2O5 was determined to be 0.028 from the iterative model approach, and a higher γN2O5 value of 0.036 was obtained from the exit-concentration ratio approach. The overestimated γN2O5 from the exit-concentration ratio approach could be explained by the increased NO level (∼1.5 ppbv) in the aerosol mode. For comparison, another two periods of data points in the 21 March case (Fig. 9a) with different NO levels were also selected to derive the khet, and the results showed good consistency (0.0136–0.0140 s−1) (Fig. S2 in the Supplement), also demonstrating the applicability of the iterative model in buffering against fluctuating NO. In Fig. 9b, another case with fluctuating NO2 and O3 levels was observed on 26 March 2017, and the NO2 level was about 5 ppbv higher, but the O3 level was about 11 ppbv lower in aerosol mode. With Sa of 681 µm2 cm−3, γN2O5 was determined to be 0.020 from the iterative model approach and a much lower value of 0.008 from the exit-concentration ratio approach. The consideration of multiple reactions in the iterative model approach was able to buffer against small fluctuations of precursors in switching between aerosol and non-aerosol modes. The results demonstrated the applicability of the iterative model approach to directly measuring the N2O5 heterogeneous uptake coefficient under conditions of high NO2 and O3 and fresh NO emission.
An in situ experimental approach for direct measurement of N2O5 heterogeneous reactivity in a polluted environment was developed and introduced in the present study. The method uses an aerosol flow tube reactor combined with an iterative box model, to determine the heterogeneous loss rate of synthesized N2O5 on ambient aerosols with consideration of multiple reactions affecting N2O5 in the flow tube. A series of laboratory and model simulations were conducted to test the applicability of the system under different conditions. The overall γN2O5 uncertainty from the variations of parameters during two operation modes and uncertainties associated with measurements of gaseous and aerosol species was propagated to be 37 %–40 % at γN2O5 around 0.03 with Sa of 1000 µm2 cm−3 and RH ranging from 20 % to 70 %. Field deployment of this system at a polluted suburban site in southern China demonstrated the applicability of the introduced method in measuring N2O5 uptake coefficients in polluted environments with high ambient levels of O3, NO, and NO2 and rapid air mass changes. Both field results and simulation tests demonstrate that neglecting multiple reactions within the flow tube reactor leads to underestimating γN2O5 values. The introduced approach could also be used to investigate the heterogeneous reactivity of other trace gases on ambient aerosols in polluted environments.
The data used in this study are available upon request from the corresponding author (z.wang@polyu.edu.hk or cetwang@polyu.edu.hk).
The supplement related to this article is available online at: https://doi.org/10.5194/amt-11-5643-2018-supplement.
TW and ZW designed the research in this study; WW and ZW developed the method; WW and XP carried out the lab testing; WW, CY, and MX conducted the filed measurement and analyzed the data; YZ, DY, and YO contributed to the field measurement and data analysis; and WW, ZW, and TW wrote the manuscript. All authors contributed to discussion and commented on the manuscript.
The authors declare that they have no conflict of interest.
This work was funded by the National Natural Science Foundation of China
(grant nos. 91544213 and 41505103); the Research Grants Council of Hong Kong Special
Administrative Region, China (grant nos. C5022-14G and 15265516); and the National Key
R&D Program of China (grant no. 2016YFC0200500). The authors also acknowledge
the support of the Research Institute for Sustainable Urban Development
(RISUD).
Edited by: Lisa Whalley
Reviewed by: two anonymous referees
Anttila, T., Kiendler-Scharr, A., Tillmann, R., and Mentel, T. F.: On the reactive uptake of gaseous compounds by organic-coated aqueous aerosols: Theoretical analysis and application to the heterogeneous hydrolysis of N2O5, J. Phys. Chem. A, 110, 10435–10443, 2006.
Atkinson, R. and Arey, J.: Gas-phase tropospheric chemistry of biogenic volatile organic compounds: a review, Atmos. Environ., 37, 197–219, 2003.
Bertram, T. H. and Thornton, J. A.: Toward a general parameterization of N2O5 reactivity on aqueous particles: the competing effects of particle liquid water, nitrate and chloride, Atmos. Chem. Phys., 9, 8351–8363, https://doi.org/10.5194/acp-9-8351-2009, 2009.
Bertram, T. H., Thornton, J. A., and Riedel, T. P.: An experimental technique for the direct measurement of N2O5 reactivity on ambient particles, Atmos. Meas. Tech., 2, 231–242, https://doi.org/10.5194/amt-2-231-2009, 2009a.
Bertram, T. H., Thornton, J. A., Riedel, T. P., Middlebrook, A. M., Bahreini, R., Bates, T. S., Quinn, P. K., and Coffman, D. J.: Direct observations of N2O5 reactivity on ambient aerosol particles, Geophys. Res. Lett., 36, L19803, https://doi.org/10.1029/2009GL040248, 2009b.
Brown, S. S., Stark, H., and Ravishankara, A.: Applicability of the steady state approximation to the interpretation of atmospheric observations of NO3 and N2O5, J. Geophys. Res.-Atmos., 108, 4539, https://doi.org/10.1029/2003JD003407, 2003.
Brown, S. S., Dubé, W. P., Osthoff, H. D., Wolfe, D. E., Angevine, W. M., and Ravishankara, A. R.: High resolution vertical distributions of NO3 and N2O5 through the nocturnal boundary layer, Atmos. Chem. Phys., 7, 139–149, https://doi.org/10.5194/acp-7-139-2007, 2007.
Chang, W. L., Bhave, P. V., Brown, S. S., Riemer, N., Stutz, J., and Dabdub, D.: Heterogeneous Atmospheric Chemistry, Ambient Measurements, and Model Calculations of N2O5: A Review, Aerosol Sci Tech., 45, 665–695, 2011.
Damian, V., Sandu, A., Damian, M., Potra, F., and Carmichael, G. R.: The kinetic preprocessor KPP-a software environment for solving chemical kinetics, Comput. Chem. Eng., 26, 1567–1579, 2002.
Danckwerts, P. V.: Continuous flow systems: distribution of residence times, Chem. Eng. Sci., 2, 1–13, 1953.
Davis, J. M., Bhave, P. V., and Foley, K. M.: Parameterization of N2O5 reaction probabilities on the surface of particles containing ammonium, sulfate, and nitrate, Atmos. Chem. Phys., 8, 5295–5311, https://doi.org/10.5194/acp-8-5295-2008, 2008.
Evans, M. and Jacob, D. J.: Impact of new laboratory studies of N2O5 hydrolysis on global model budgets of tropospheric nitrogen oxides, ozone, and OH, Geophys. Res. Lett., 32, L09813, https://doi.org/10.1029/2005GL022469, 2005.
Fuchs, N. and Sutugin, A. G.: High-dispersed aerosols, in: Topics in current aerosol research, vol. 2, edited by: Hidy, G. M. and Brock, J. R., Pergamon, New York, USA, 1971.
Groß, C., Dillon, T., Schuster, G., Lelieveld, J., and Crowley, J.: Direct kinetic study of OH and O3 formation in the reaction of CH3C(O)O2 with HO2, J. Phys. Chem. A, 118, 974–985, 2014.
Lambe, A. T., Ahern, A. T., Williams, L. R., Slowik, J. G., Wong, J. P. S., Abbatt, J. P. D., Brune, W. H., Ng, N. L., Wright, J. P., Croasdale, D. R., Worsnop, D. R., Davidovits, P., and Onasch, T. B.: Characterization of aerosol photooxidation flow reactors: heterogeneous oxidation, secondary organic aerosol formation and cloud condensation nuclei activity measurements, Atmos. Meas. Tech., 4, 445–461, https://doi.org/10.5194/amt-4-445-2011, 2011.
Li, Q., Zhang, L., Wang, T., Tham, Y. J., Ahmadov, R., Xue, L., Zhang, Q., and Zheng, J.: Impacts of heterogeneous uptake of dinitrogen pentoxide and chlorine activation on ozone and reactive nitrogen partitioning: improvement and application of the WRF-Chem model in southern China, Atmos. Chem. Phys., 16, 14875–14890, https://doi.org/10.5194/acp-16-14875-2016, 2016.
Morgan, W. T., Ouyang, B., Allan, J. D., Aruffo, E., Di Carlo, P., Kennedy, O. J., Lowe, D., Flynn, M. J., Rosenberg, P. D., Williams, P. I., Jones, R., McFiggans, G. B., and Coe, H.: Influence of aerosol chemical composition on N2O5 uptake: airborne regional measurements in northwestern Europe, Atmos. Chem. Phys., 15, 973–990, https://doi.org/10.5194/acp-15-973-2015, 2015.
Phillips, G. J., Thieser, J., Tang, M., Sobanski, N., Schuster, G., Fachinger, J., Drewnick, F., Borrmann, S., Bingemer, H., Lelieveld, J., and Crowley, J. N.: Estimating N2O5 uptake coefficients using ambient measurements of NO3, N2O5, ClNO2 and particle-phase nitrate, Atmos. Chem. Phys., 16, 13231–13249, https://doi.org/10.5194/acp-16-13231-2016, 2016.
Riedel, T. P., Bertram, T. H., Ryder, O. S., Liu, S., Day, D. A., Russell, L. M., Gaston, C. J., Prather, K. A., and Thornton, J. A.: Direct N2O5 reactivity measurements at a polluted coastal site, Atmos. Chem. Phys., 12, 2959–2968, https://doi.org/10.5194/acp-12-2959-2012, 2012.
Riemer, N., Vogel, H., Vogel, B., Anttila, T., Kiendler-Scharr, A., and Mentel, T.: Relative importance of organic coatings for the heterogeneous hydrolysis of N2O5 during summer in Europe, J. Geophys. Res.-Atmos., 114, D17307, https://doi.org/10.1029/2008JD011369, 2009.
Sander, S. P., Friedl, R., Barker, J., Golden, D., Kurylo, M., Wine, P., Abbatt, J., Burkholder, J., Kolb, C., and Moortgat, G.: Chemical kinetics and photochemical data for use in Atmospheric Studies Evaluation Number 16: supplement to Evaluation 15: update of key reactions, Jet Propulsion Laboratory, National Aeronautics and Space Administration, Pasadena, CA, USA, 2009.
Tang, M. J., Cox, R. A., and Kalberer, M.: Compilation and evaluation of gas phase diffusion coefficients of reactive trace gases in the atmosphere: volume 1. Inorganic compounds, Atmos. Chem. Phys., 14, 9233–9247, https://doi.org/10.5194/acp-14-9233-2014, 2014.
Tang, M., Huang, X., Lu, K., Ge, M., Li, Y., Cheng, P., Zhu, T., Ding, A., Zhang, Y., Gligorovski, S., Song, W., Ding, X., Bi, X., and Wang, X.: Heterogeneous reactions of mineral dust aerosol: implications for tropospheric oxidation capacity, Atmos. Chem. Phys., 17, 11727–11777, https://doi.org/10.5194/acp-17-11727-2017, 2017.
Tham, Y. J., Wang, Z., Li, Q., Yun, H., Wang, W., Wang, X., Xue, L., Lu, K., Ma, N., Bohn, B., Li, X., Kecorius, S., Größ, J., Shao, M., Wiedensohler, A., Zhang, Y., and Wang, T.: Significant concentrations of nitryl chloride sustained in the morning: investigations of the causes and impacts on ozone production in a polluted region of northern China, Atmos. Chem. Phys., 16, 14959–14977, https://doi.org/10.5194/acp-16-14959-2016, 2016.
Tham, Y. J., Wang, Z., Li, Q., Wang, W., Wang, X., Lu, K., Ma, N., Yan, C., Kecorius, S., Wiedensohler, A., Zhang, Y., and Wang, T.: Heterogeneous N2O5 uptake coefficient and production yield of ClNO2 in polluted northern China: roles of aerosol water content and chemical composition, Atmos. Chem. Phys., 18, 13155–13171, https://doi.org/10.5194/acp-18-13155-2018, 2018.
Thornton, J. A., Braban, C. F., and Abbatt, J. P.: N2O5 hydrolysis on sub-micron organic aerosols: The effect of relative humidity, particle phase, and particle size, Phys. Chem. Chem. Phys., 5, 4593–4603, 2003.
Wagner, N., Riedel, T., Young, C., Bahreini, R., Brock, C., Dubé, W., Kim, S., Middlebrook, A., Öztürk, F., and Roberts, J.: N2O5 uptake coefficients and nocturnal NO2 removal rates determined from ambient wintertime measurements, J. Geophys. Res.-Atmos., 118, 9331–9350, 2013.
Wang, T., Tham, Y. J., Xue, L., Li, Q., Zha, Q., Wang, Z., Poon, S. C., Dubé, W. P., Blake, D. R., and Louie, P. K.: Observations of nitryl chloride and modeling its source and effect on ozone in the planetary boundary layer of southern China, J. Geophys. Res.-Atmos., 121, 2476–2489, 2016.
Wang, X., Wang, H., Xue, L., Wang, T., Wang, L., Gu, R., Wang, W., Tham, Y. J., Wang, Z., and Yang, L.: Observations of N2O5 and ClNO2 at a polluted urban surface site in North China: High N2O5 uptake coefficients and low ClNO2 product yields, Atmos. Environ., 156, 125–134, 2017.
Wang, Z., Wang, W., Tham, Y. J., Li, Q., Wang, H., Wen, L., Wang, X., and Wang, T.: Fast heterogeneous N2O5 uptake and ClNO2 production in power plant and industrial plumes observed in the nocturnal residual layer over the North China Plain, Atmos. Chem. Phys., 17, 12361–12378, https://doi.org/10.5194/acp-17-12361-2017, 2017.
Yun, H., Wang, T., Wang, W., Tham, Y. J., Li, Q., Wang, Z., and Poon, S. C.: Nighttime NOx loss and ClNO2 formation in the residual layer of a polluted region: Insights from field measurements and an iterative box model, Sci. Total Environ., 622, 727–734, 2018.
- Abstract
- Introduction
- Methodology
- Determination of residence time
- Iterative box model for determination of loss rate and uptake coefficient
- Laboratory test and overall uncertainty
- Demonstration of γN2O5 measurements under polluted conditions
- Ambient measurement
- Summary and conclusion
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement
- Abstract
- Introduction
- Methodology
- Determination of residence time
- Iterative box model for determination of loss rate and uptake coefficient
- Laboratory test and overall uncertainty
- Demonstration of γN2O5 measurements under polluted conditions
- Ambient measurement
- Summary and conclusion
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement