the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Analysis of the performance of a ship-borne scanning wind lidar in the Arctic and Antarctic
Svenja H. E. Kohnemann
Günther Heinemann
In the present study a non-motion-stabilized scanning Doppler lidar was operated on board of RV Polarstern in the Arctic (June 2014) and Antarctic (December 2015–January 2016). This is the first time that such a system measured on an icebreaker in the Antarctic. A method for a motion correction of the data in the post-processing is presented. The wind calculation is based on vertical azimuth display (VAD) scans with eight directions that pass a quality control. Additionally a method for an empirical signal-to-noise ratio (SNR) threshold is presented, which can be calculated for individual measurement set-ups. Lidar wind profiles are compared to total of about 120 radiosonde profiles and also to wind measurements of the ship.
The performance of the lidar measurements in comparison with radio soundings generally shows small root mean square deviation (bias) for wind speed of around 1 m s−1 (0.1 m s−1) and for wind direction of around 10∘ (1∘). The post-processing of the non-motion-stabilized data shows a comparably high quality to studies with motion-stabilized systems.
Two case studies show that a flexible change in SNR threshold can be beneficial for special situations. Further the studies reveal that short-lived low-level jets in the atmospheric boundary layer can be captured by lidar measurements with a high temporal resolution in contrast to routine radio soundings. The present study shows that a non-motion-stabilized Doppler lidar can be operated successfully on an icebreaker. It presents a processing chain including quality control tests and error quantification, which is useful for further measurement campaigns.
Changes in the Arctic and Antarctic climate system are strongly related to atmosphere–ocean–ice interactions and feedbacks between the atmospheric boundary layer and the free atmosphere. Hence, the knowledge about the state of the atmospheric boundary layer (ABL) is crucial for the understanding of atmosphere–ocean–ice processes, atmospheric transport, air pollution processes and the verification and improvement of numerical weather forecast and climate models for polar regions. Profiles of wind speed and direction at high spatial and temporal resolutions are fundamental meteorological quantities for ABL studies. While at midlatitudes the ABL is studied using tall towers and ground-based remote-sensing instruments such as lidar, radar or sodar at several observatories, these measurements are rare or absent in the Arctic and Antarctic. Thus radiosondes are generally the main source for measuring quantities of the ABL in the polar regions. Since the radiosonde stations are primarily located over land, there are huge data gaps over the ocean. Furthermore, the temporal resolution of radio soundings is generally of the order of a couple of hours. Over the polar oceans, only a few research vessels provide radio soundings, which are very valuable for improving the initial conditions for numerical weather forecasts and for reanalyses (Dee et al., 2011), but are insufficient for detailed studies of boundary layer processes.
Ship-based Doppler lidar measurements are able to fill the gap in radio soundings over oceans, since they provide wind profiles with high spatial and temporal resolutions (Achtert et al., 2015; Tucker et al., 2009). In addition, Doppler wind lidar measurements allow for the determination of the turbulence structure of the ABL (Banta et al., 2006; Kumer et al., 2016; Pichugina et al., 2012). If two Doppler lidars are available, techniques like the “virtual tower” can be applied (Calhoun et al., 2006; Damian et al., 2014). In synergy with additional remote-sensing instruments measuring the temperature profile, the turbulent mixing conditions in the ABL can be described at high temporal and vertical resolutions of 10 min and 10 m (Brooks et al., 2017). Note that our literature research was focused on lidars similar to our own; thus it is likely biased towards lidars from the same manufacturer.
In this study we analyse data from a scanning Doppler lidar on board of RV Polarstern in the Arctic (June 2014) and Antarctic (December 2015–January 2016). There are two important aspects of measuring with a Doppler lidar on board of a moving ship in polar regions: (a) the ship's movement requiring data corrections regarding its orientation and (b) the adaptation of lidar measurement settings and analysis configuration for conditions with low backscatter due to the low aerosol concentration. Some studies present measurement campaigns dealing with challenge (a) (Achtert et al., 2015; Pichugina et al., 2012; Tucker et al., 2009). All of them use a motion-stabilization platform to remove the effects of the ship's motion. We present a different option to deal with the varying orientation of the ship. The adaptation of measurement settings for the polar environment (challenge b) is less documented. The goal of these adaptions is the improvement of the signal-to-noise ratio (SNR). Hirsikko et al. (2014) recommend the use of an optimized telescope focal length of the lidar and an increase in the integration time for measurements in Finland. The main goal of the present paper is the assessment of the wind lidar performance in comparison with radiosondes on the German icebreaker Polarstern. A similar study was made by Achtert et al. (2015), who used a motion-stabilized scanning wind lidar during a cruise of the Swedish icebreaker ODEN in the Arctic in 2014 (Tjernström et al., 2014). Their 3-month campaign started immediately after our Arctic campaign in 2014. No ship-based measurement campaign of a Doppler wind lidar is known for the Antarctic. The combination of the measurement framework and the presented comprehensive analysis of the settings serve as a basis for improvements in further data collections. The outline of the paper is as follows: in Sect. 2 an overview of the measurement campaigns and the data processing is given. Section 3 presents the results for intercomparisons of lidar data with radiosondes and the ship's wind measurements. Two case studies are shown in Sect. 4. A summary and conclusions are given in Sect. 5.
The measurements were performed during the two Polarstern cruises PS85 and PS96 of the Alfred Wegener Institute Bremerhaven (Germany). The cruises are shown in Fig. 1 with approximate sea ice conditions during the measuring periods. PS85 took place in the Arctic from the 6 June to 3 July 2014 and PS96 in the Antarctic from the 6 December 2015 to 14 February 2016. Lidar measurements were taken for a period of 18 days (12 to 29 July) during PS85 and for 38 days (24 December to 30 January) during PS96. Polarstern is the German research icebreaker and has a length of 118 m and a weight of 17 300 tons (Fig. 2). The typical cruise speed is 12 knots.
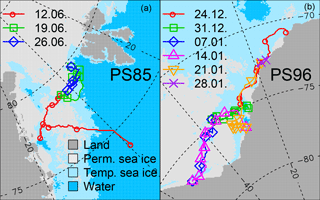
Figure 1Cruise track of Polarstern during PS85 (a) and PS96 (b) with different colours for every week (symbol mark every day 00:00 UTC). Beside land (dark grey) and water (dark blue), sea ice concentration (> 15 %) during the measuring period is shown to be present every day (light grey) and present at least 1 day (light blue). Sea ice concentration is taken from AMSR2 (Spreen et al., 2008).
2.1 Doppler wind lidar
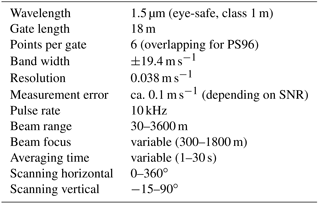
The instrument is a Halo Photonics Stream Line Doppler wind lidar, which is a scanner and can operate with a maximum range of 10 km, but was used only for a range up to 3600 m due to the low aerosol concentration (Table 1). The lidar was installed on the port (starboard) side of the ship during PS85 (PS96) approximately 20 m above the waterline (see Fig. 2). Besides the lidar, an external attitude and heading reference system (AHRS; XSENS MTi-G-700-GPS/INS) was installed for higher-frequency (sampled with up to 400 Hz) recordings of the ship's pitch and roll, in addition to lower-frequency (1 Hz) navigation data from the ship's internal systems.
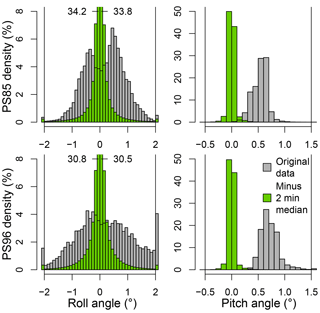
Figure 3Frequency distribution of the ship angle (grey) and ship angle minus a 2 min running median (green) during the measurement time.
A variety of different scanning programs were used: vertical azimuth display (VAD), horizontal stare in two or three directions, range-height indicator (RHI) and vertical stare. In the present paper we will focus on the VAD measurements that allow the computation of vertical profiles of horizontal wind speed. One VAD scan is composed of eight rays with fixed elevation and different azimuth (0, 45, 90, 135, 180, 225, 270, 315∘). During PS96 we changed the elevation from 85 to 75∘ after 3 days. The averaging time for each ray was usually 12–15 s. During PS85 the averaging time for each ray was only 1.5 s but azimuth circles were done at 25, 50 and 75∘ elevation. For the analysis we will either use only the 75∘ or all 25, 50 and 75∘ elevations. To make them comparable when using all three elevations, we will count the 3 × 8 = 24 rays as one VAD. One ray is divided into sections of 3 m length and one measured Doppler velocity is representative for gate length of six sections (18 m). During PS85 those six sections were non-overlapping; thus measurements were available every 18 m. During PS96 the six sections were overlapping; thus measurements were available every 3 m. But the measurements with overlapping sections are not independent as they are computed based partially on same data. VAD wind profiles are typically available every 15 min and a whole VAD scan required about 2 min for PS96. Photos of the weather condition were taken manually for special situations during PS85 and automatically with a GoPro (with constant power connection) every minute during PS96.
2.2 Radiosondes
Radiosondes at Polarstern (König-Langlo, 2014a, 2016a) were usually launched twice a day at 05:00 and 11:00 UTC during PS85 (39 radiosondes over the 18 days) and 07:00 and 11:00 UTC during PS96 (70 radiosondes over the 38 days). Radiosondes of the type Vaisala RS92 (Vaisala, 2013) were used. The measurement uncertainty for wind is specified as 0.15 m s−1 for speed and 2∘ for direction. For the intercomparison of lidar wind profiles with the radiosonde profiles additional aspects to instrumental errors have to be considered. As shown below, the vertical range of the lidar is generally limited to the height of the ABL of a few hundred metres. When the ship is cruising, the radiosondes are launched close to the ship's superstructure and are affected by the turbulent wake of the ship. The radiosonde also needs time to accelerate to the ambient wind speed after launch, and exhibits strong pendulum motions during this phase. This results in a strong noise in the raw wind data, and a low-pass filter is applied, resulting in a reduced vertical resolution (estimated as about 200 m by Päschke et al., 2015). As documented by Achert et al. (2015) for the RV Oden, the ship's superstructure modifies the mean flow depending on flow direction. The largest effect occurs for relative wind along the ship's axis. For these conditions, the disturbance decreases with height and is estimated as smaller than 2 % for horizontal wind speeds at altitudes above 75 m. For a flow that is perpendicular to the ship, this effect also reduces to 2 % below 75 m. A study of Berry et al. (2001) for RV Polarstern shows that the largest flow distortion for the ship orientated into the wind occurs as wind decreases up to 30 % in the lee of the main superstructure in the lowest 50 m (where the radiosonde is launched).
2.3 Analysis of the lidar data
The wind analysis consists of different steps. First we look at the influence and correction of the ship's motions. In the second part we describe our data processing method and computation of horizontal winds. In the third part we discuss our choice of the SNR threshold.
2.3.1 Ship's motion correction
The main difficulty in receiving reliable wind data results from the movements of the ship. The ship's velocity and orientation and their changes influence the directions of the lidar's outgoing and incoming rays. Therefore the ship's velocity and orientation angles are the two main factors for the correction of the measured data. During both cruises PS86 and PS96, the ship was moving with more than 1 m s−1 about 50 % of the time. The lidar was aligned with the ship by eye as best as possible (deviations of the yaw angle between lidar and the ship are discussed later in the results section). Measured ship data from the scientific navigational platform are taken to correct each single lidar measurement by the ship's speed and roll–pitch–yaw angles. The resolution of these data is 1 Hz. The correction for the ship's roll and pitch movements can be avoided by using a motion-stabilizing platform (Achtert et al., 2015). We had no such platform, but additionally to the ship's 1 Hz navigation data, we also recorded roll and pitch movements at high-frequency (up to 400 Hz) by the AHRS that was attached to the lidar. The AHRS data were used to determine the roll and pitch offset between the AHRS (or lidar) reference system and the ships reference system. During PS96 the averaging time of a single ray was typically 12–15 s, so that we corrected each single measurement with the mean value over the averaging time. This introduces an error whenever the ship angle, and thus the lidar angle, changes during this averaging time. In order to reduce the error, all measurements that have a standard deviation of roll or pitch angle larger than 0.5∘ or yaw angle larger than 2∘ over this averaging time were excluded from the analysis. Correcting the direction of the lidar measurement by the mean roll and pitch angle during the averaging time should already cause most of the error to average out, as it measures partly too much and partly too little wind speed. But even if this is not the case, for a data point at 1 km distance from the lidar a change in elevation from 75 to 75.5∘ (25 to 25.5∘) causes a difference in height of 2 m (8 m) and the resulting horizontal wind speed error is less than 3.3 % (0.4 %). This is acceptable as we will later interpolate over height intervals of 50 m and only evaluate the horizontal wind in our paper. It should be noted that the correction and filtering process causes almost no loss of data. Only 6 % of the time is the standard deviation of the yaw angle over 15 s larger than 2∘ and the ship's movement even during ice breaking conditions generally does not result in high-frequency changes of roll and pitch (except some cases of ramming). The important part is in fact the low-frequency change in roll and pitch (e.g. pumping water from one tank to another, changing cargo) that gets corrected. This can be seen by subtracting a 2 min running median from the roll and pitch data (Fig. 3). The remaining angles are within −0.1 and 0.1∘ 60–70 % of the time. Without roll and pitch correction, values amount from −2 to 2∘ for roll (for 95 % of the cases) and 0 to 1.5∘ for pitch. Therefore a set-up without any roll or pitch correction at all would still provide usable data if a high data quality is not of importance. For example, for a data point at a 1 km distance from the lidar a change in elevation from 75 to 77∘ (25 to 27∘) causes a difference in height of 8 m (31 m) and horizontal wind speed error of less than 13 % (17 %). We also corrected for the influence of the angular velocity of roll pitch and yaw, but it was found to be negligible. For PS96 (PS85) the correction due to angular velocity was less than 0.2 m s−1 99.7 % (99.9 %) of the time and never greater than 0.5 m s−1.
2.3.2 Data processing
First, an SNR threshold was chosen and all data points within one ray with a worse SNR were removed. The SNR is a value given in the lidar output for each scanned Doppler velocity value. It is separate from the empirical noise defined in Sect. 2.3.3 as well as from the “noisy influence” due to other error sources like uncertainties related to the ships movement. The background noise is usually measured at least once a day and at most every hour. For this, the scanning head is turned away from the sky towards the lidar casing and measures the signal while sending no pulses out. Thus the background noise can vary with time and operating conditions and can be different for different HALO instruments. To compute the SNR, the signal strength of the background noise is subtracted from the signal strength of the measurement and afterwards divided by the signal strength of the background noise. If the signal during a measurement is lower than during the background noise scan, it can therefore cause a negative SNR. In general, more background noise scans were performed during PS85, but we did not investigate the background noise further.
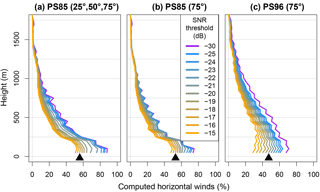
Figure 4Percentage of wind calculations (speed and direction) from VAD scans as a function of SNR threshold at different heights during PS85 using all elevations (a), only an elevation of 75∘ (b) and PS96 (c). The total number of VADs for PS85/PS96 was 3552/4250. The black triangle indicates the chosen SNR threshold based on Fig. 5. For the height between 0 and 1750 m this chosen threshold results in 15 % (PS85, all elevations), 14 % (PS85, only 75∘) or 21 % (PS96) of computed horizontal winds.
Furthermore the first data points near the lidar were removed (approx. the first 30 m) as these measurements are often affected by the outgoing pulse. Then each single ray was segmented into bins of 100 m. For each bin, outliers (radial velocity > 3× standard deviation) were removed. If less than 50 % of the data remained or if the standard deviation of the radial velocity of remaining data in the bin was greater than 3 m s−1, the whole bin was removed.
To compute a vertical profile of horizontal wind speed from a complete VAD, we first divided all data points into layers of different heights. A thickness of 50 m was chosen for each layer for the radiosonde comparison, but thicknesses down to 10 m were tested as well. We used the standard assumption for VAD processing that the wind field is horizontally homogenous in each layer. The general approach for the processing of VAD scans is the calculation of the 3-D wind by finding the solution to a system of equations. There are two common perspectives on their definition. The first perspective operates in the (local) Cartesian coordinate system (east, north, up), in which wind is described by the components (u, v, w) and the direction of the lidar beam (normalized radius vector (xL, yL, zL)). Each measured Doppler velocity d (negative if wind is blowing towards the lidar) satisfies the following linear equation:
The second perspective describes wind with horizontal wind speed and direction and the vertical component ( horizontal wind speed, ϕh wind direction, w). The Doppler velocity is then a function of the scanning directions in polar coordinates (ϕ = azimuth, θ = elevation).
As Eq. (1) can be transformed into Eq. (2), they are equivalent (see Appendix). Assuming that the lidar remains stationary and has a fixed elevation angle θ (which is not the case in our set-up), the equation further simplifies to
with the constants c1=cos(θ) and c2=tan(θ). Wind speed and direction can then be determined by a cosine fit for all available scan directions. Although the Eqs. (2) and (3) are more intuitive, and our lidar software already uses the parameters elevation and azimuth, we found it is easier to work in a Cartesian coordinate system to apply corrections and thus choose Eq. (1). Since we have eight rays per VAD (and more than one measurement per ray in each layer), we get a system of linear equations. Given a measured set of Doppler velocities di () in directions (xi, yi, zi) (east, north, up), the wind speed (u, v, w) can be calculated by solving the overdetermined system:
using the least squares method. To ensure the quality of the data we added the condition that at least six out of eight azimuth angles had data (that was not removed); thus at least measurements in a sector of 270∘ were available.
As the system of equations is only solved approximately for a given a solution , we can define a measure for the goodness of the fit. Päschke et al. (2015) define the coefficient of determination. We define the fit deviation in our paper as follows:
For the purpose of comparing the fit deviation, only scans with the same elevation should be used. It should also be noted that measuring a non-homogenous or non-stationary wind field would result in a larger fit deviation value.
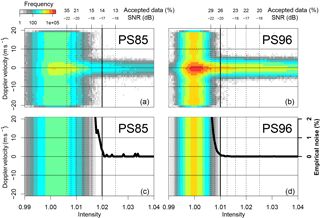
Figure 5(a, b) Frequency of Doppler velocities of VAD scans with 75∘ elevation depending on the intensity/SNR and for PS85 (a, c) and PS96 (b, d). Bottom row: empirical noise computed as the mean for points above 10 m s−1 or below −10 m s−1. The solid black line shows the ratio of empirical noise and all measured data (a, b) at each intensity/SNR. On the top axis it is also noted how much data would be accepted if the respective (minimal) SNR was chosen.
In Fig. 4 we show the amount of computed wind speed and direction data from VAD scans for different SNR thresholds. The increase in computed data stagnates around −30 dB. A further decrease in the SNR threshold only adds data that are thrown out again by the 100 m bin method or for other reasons. One can also see the zig-zag artefact that is produced by this 100 m bin combined with computing winds every 50 m. It is more dominant for PS96 as the measurement was taken every 3 m, while the measurements for PS85 were taken every 18 m. The benefit of using additional scans with 25 and 50∘ elevation for PS85 can be seen for the lowest 750 m if a higher SNR threshold is chosen. The choice of the SNR threshold for this paper is explained in the next section.
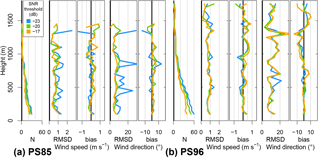
Figure 6RMSD, bias and number of used radio soundings (N) by height of wind speed and direction for PS85 (a) and PS96 (b). Different colours show different SNR thresholds (−23 blue, −20 dB green, −17 dB orange). Only scans with an elevation of 75∘ were used.
Table 2Statistics for all available lidar data compared to radio soundings. M indicates the number of used radio soundings. N indicates the number of compared measurements (N is lower for the wind direction because up to six cases with wind speed < 0.5 m s−1 are removed). PS85 computed for a −17 dB SNR threshold with only 75∘ elevation scans (first column, as shown in Fig. 6) and with all 25, 50 and 75∘ (second column). PS96 was computed for −20 dB SNR threshold with the default case (standard deviation of yaw angle below 2∘ for each ray; third column, as shown in Fig. 6) and a stricter case (standard deviation of yaw angle below 0.5∘ for each ray; fourth column). aR is the correlation coefficient for angular variables.

2.3.3 Choice of signal-to-noise ratio thresholds
SNR-based thresholds for the separation between reliable and unreliable data points are a common technique for lidar data processing (Barlow et al., 2011; Frehlich and Yadlowsky, 1994; Pearson et al., 2009; Päschke et al., 2015). This value can vary depending on the instrument-specific performance (detector noise) and the variability of atmospheric conditions within the measured volume. The recommendation of the manufacturer for the lidar is −18.2 dB. However, Päschke et al. (2015) showed that this value is rather conservative and reduces the amount of data by up to 40 % (between −20 and −18.2 dB). Hirsikko et al. (2014) use a threshold of −21 dB and state that −25 dB could still suitable for horizontal wind measurements. Pearson et al. (2009) experimentally find an SNR threshold for reliable data of −23 dB. The potential SNR threshold was already considered during our measurements by adjusting the telescope focal length of the lidar and the integration time (following the recommendations Hirsikko et al., 2014). This is necessary during the measurements, since raw data on single pulses were not stored and thus no post-processing is possible. Figure 4 shows the sensitivity of available data for PS85 and PS96 on the SNR threshold. We find a similar reduction to Päschke et al. (2015). A rule of thumb for our measurements seems to be that increasing the SNR threshold by 1 dB results in a (relative) loss of 5–10 % of the data. Additionally, due to the different averaging times for each ray during PS85 and PS96 (1.5 vs. 12–15 s), the PS96 data allow for a lower SNR threshold compared to the PS85 data, because averaging over a longer period given the same SNR results in better data. Thus, it makes sense to choose a less strict SNR threshold for the PS96 data set to make both data sets more comparable. Päschke et al. (2015) checked the measured wind speed of vertical stares. Knowing that vertical velocities are close to zero, Päschke et al. (2015) could evaluate the influence of noise from vertical stares for quiescent atmospheric conditions. As we did not have a stabilizing platform, the evaluation of the vertical stares is not possible because of the influence of horizontal wind on the signal. To circumnavigate this problem, we followed a similar approach and evaluated the Doppler velocity from all individual rays for VAD scans with an elevation of 75∘ (only the first data points near the lidar were removed; see subsection data processing). Since the Doppler velocity is less than 26 % at this elevation due to horizontal wind speed, the range of realistic Doppler velocities should be ±10 m s−1. Data points outside this range can be regarded as wrong (or empirical noise). This condition is used to find an SNR threshold in a three-step procedure. First, we look at the overall frequency distribution of measured Doppler velocities (Fig. 5, top). We assume that the data mainly consist of two parts: the empirical noise (homogenous along all wind speeds; top to bottom) and the wind signal (relatively homogenous along the signal intensity or SNR; left to right). Signal intensity is defined as SNR+1. All points above 10 m s−1 or below −10 m s−1 are taken to construct an empirical noise distribution as a function of intensity using the mean value (Fig. 5, bottom). In the second step, we take the ratio of the empirical noise and the mean of the measured Doppler velocities for each intensity, which results in an empirical noise fraction (plotted as solid line in Fig. 5, bottom). The empirical noise fraction is close to zero for high intensities and starts to increase rapidly at different SNR values for both data sets. We choose an SNR threshold (step three) of −17 dB for PS85 and −20 dB for PS96. This empirical SNR threshold results in about 14 %∕26 % of usable raw data for PS85/96. Comparing this to the resulting VAD percentages 14 %∕21 % (Fig. 4), it should be noted that the decrease for PS96 comes mostly from the restriction sd(yaw) < 2∘ and sd(roll/pitch) < 0.5∘. Without this condition, the computed VAD percentage is 25 %.
Table 3Statistics as in Table 2 but showing the range of the statistic variables for different computations. These include all possible combinations of the following two (default marked with *): (1) the thickness of layers and thus the interpolation in height of lidar data [10, 20, 30, 40, 50* m] and (2) the time range of used lidar measurements around the radio sounding measurement (100 s after start) [±5, 10*, 15, 30 min].
A verification of the lidar wind data is presented in the following by comparisons with radiosondes and the ship measurements. For the statistics of wind direction, the absolute values of the differences are adjusted to be smaller than 180∘ to avoid the discontinuity in northerly directions (e.g. a difference of 270∘ becomes −90∘). For the correlation of wind direction we used the correlation coefficient for angular variables (Jammalamadaka and Sarma, 1988). Radiosonde data were interpolated linearly with height to match the lidar data. Lidar wind speed and direction were first computed for every VAD and then averaged over a 20 min interval centred around the launch time (plus 100 s) of the radiosonde (100 s after the start the radiosonde is at a height of around 500 m). We excluded all data points with wind speed < 0.5 m s−1 for the statistics of wind direction, but this condition was only met during PS96 and only for up to six data points at different heights and times. Figure 6 shows the calculated root mean square deviation (RMSD) and bias by height for different SNR thresholds. While −23 dB leads to some larger differences, particularly for PS85, our empirical thresholds of −20 and −17 dB are found to be reasonable. Furthermore, a systematic dependence on height is not present. We also check for a height dependence of the correlation (not shown), but there was none present. At heights above 1000 m the sample size is relatively small and differences between different SNR thresholds are not robust.
The overall statistics of the radiosonde comparisons are shown in Table 2. Although our data set is smaller than that of Achtert et al. (2015), we find similar results (RMSD for wind speed around 1 m s−1 and wind direction around 10∘). The biases for the wind speed and direction are very small. When applying a stricter condition for the allowed standard deviation of yaw angle during the measuring and averaging time (last row in Table 2), a clear improvement in the data quality is not seen.
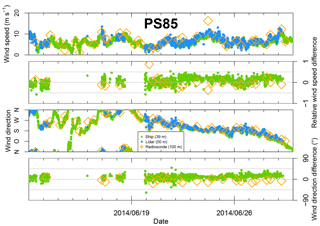
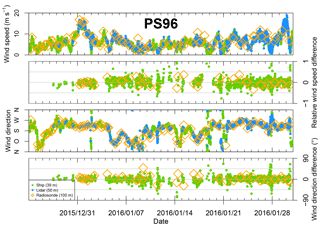
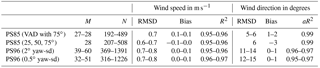
Figure 7Comparison of wind speed and wind direction between lidar at 50 m height (blue) and ship anemometer (green) for PS85. Radiosonde winds at 100 m are marked (orange diamond) for reference. The (relative) difference is computed as lidar minus anemometer (divided by anemometer) or radiosonde (divided by radiosonde). Only scans with an elevation of 75∘ were used.
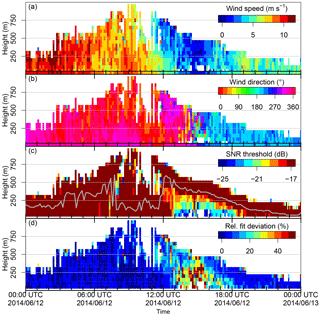
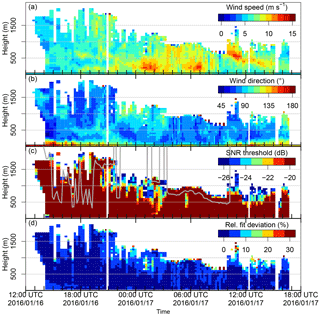
Figure 9Lidar wind speed (a) and direction (b) for the −25 dB SNR threshold for the 12 June 2014 (location see PS85 in Fig. 1). Colours below the black line (40 m) show the wind measurements of RV Polarstern (anemometer). The plot (c) presents the SNR thresholds that would allow for a wind calculation. The grey line is the cloud base from ceilometer measurements of RV Polarstern. The relative fit deviation (fit deviation divided by wind speed) is shown in (d). Values exceeding the upper limit in (a) and (d) are included in the highest colour bar bin. Only scans with a 75∘ elevation were used.
In order to quantify the impact of changes in our standard data processing, the effects of changing the layer thickness and changing the averaging time around the radiosonde launch were investigated. Table 3 summarizes the ranges of the effects RMSD, bias and R2. None of these changes had any relevant influence. We also computed the 95 % confidence interval bounds for the biases and found them to be 0.1 m s−1 and 1∘ higher or lower than the biases given in Tables 2 and 3.
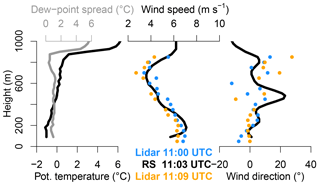
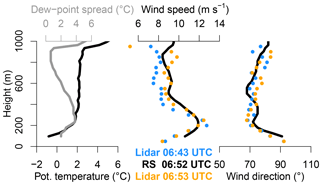
Figure 10Vertical profiles of potential temperature, dew-point spread, wind speed and direction of radiosondes vs. lidar wind speed and direction for around 11:00 UTC on 12 June 2016. A SNR threshold of −23 dB and elevations of 25, 50 and 75∘ were used.
As mentioned above, our results are similar to Achert et al. (2015), who used a motion-stabilized platform and found mean bias for wind speed and direction of 0.3 m s−1 and 2∘, and a mean standard deviation of 1.1 m s−1 and 12∘ for wind speed and direction respectively. Since the lidar was aligned with the ship's axis only by eye (see Sect. 2), this might cause a yaw offset. We tried to estimate this yaw offset by checking the correlation of the roll and pitch 1 Hz data from the AHRS (or lidar) and the ship's navigation system. By assuming a yaw offset and correcting the roll and pitch angles, we determined the peak of the correlation. As a result, we found lidar yaw offsets of around −0.5∘ for PS85 and +1∘ for PS96 which are in the range of the observed bias. It should be mentioned that the first evaluations yielded a bias of 5 to 7∘ in wind direction compared to the radio soundings. During maintenance of the lidar after the cruises a misalignment of the lidar scanning direction by the manufacturer was discovered (offset of 5.32∘ in azimuth). This correction was applied to the present evaluations.
In a second analysis we compared the winds measured on the crow's nest of the ship (König-Langlo, 2014b, 2016b). There are two anemometers (2-D-sonic anemometers, one at each side, König-Langlo et al., 2006) mounted at a height of around 39 m above sea level. The first usable data points of the lidar measurements are at approximately 50 m height. Comparing the wind direction measured by the lidar in 50 m with wind direction in 60 to 200 m, we found an overall linear increase (decrease) of wind direction with height during PS85 (PS96). Assuming this change in wind direction is also present between the 39 m anemometer and the lidar data (approx. 50–75 m), this could lead to a slight positive (negative) bias during PS85 (PS96) of about 1∘. An overview is shown in Figs. 7 and 8 and the statistics computed for this comparison are shown in Table 4.
Overall, lidar and ship (anemometer) measurements agree well. However, the anemometers are also disturbed by the ship's superstructure depending on the wind direction (see Sect. 2).
In the following, we present two case studies. The first one focuses on the choice of the SNR threshold and the second one underlines the added value of lidar measurements compared to the standard ship anemometer and radio sounding data.
4.1 PS85 – Arctic (12 June 2014)
The beginning of 12 June 2014 starts with wind speeds around 8.5 m s−1 and a N–NW wind (Fig. 9). By midday, the wind decreases to approx. 2 m s−1 and the direction changes almost by 180∘ to S–SW. Weather charts for this day show that Polarstern was navigating through a synoptic high-pressure ridge, which causes the measured wind changes.
The radiosonde wind profile at 11:03 UTC agrees well with the lidar wind profiles at 11:00 and 11:09 UTC (Fig. 10), and the lidar data also agree with the ship's wind measurements (Fig. 9). The potential temperature profile shows an almost neutral stratification with high humidity topped by a strong inversion at 900 m. The plot for the SNR (Fig. 9c) shows that with the conservative SNR threshold determined by the method presented in this study (−17 dB for PS85) the wind speed decreases in the afternoon would only be partially detected. However, the decrease below 250 m seems to be highly realistic in comparison with the ship measurements. Extending the SNR threshold to −20 or −23 dB yields reasonable results overall, but also adds some outliers particularly at the top height of the measurements. The presented method for determining a conservative SNR threshold seems to distinguish between reliable and unreliable data well. However, for specific cases it does make sense to manually check whether the limit can be extended to gain reliable data. The fit deviation (Fig. 9d) can help with this decision, but note that the high relative fit deviation in the afternoon stems mostly from the low wind speeds. Note that the height difference between the lidar and ceilometer from 08:00 to 12:00 UTC is likely due to a thin layer of low clouds that the lidar could partially penetrate.
4.2 PS96 – Antarctic 16–17 January 2016
The second case study is located in the Antarctic during PS96 (Fig. 11). It is chosen because it presents a stable boundary layer (SBL) with low-level jets (LLJs). The first LLJ was measured just after midnight on the 17 January 2016 between 00:30 and 02:30 UTC, and a second LLJ a few hours later between 05:30 and 07:30 UTC, and the third LLJ between 10:00 and 11:30 UTC (Fig. 11a). The LLJ wind speeds reached a maximum of up to 14 m s−1 at a height of 200 m (Fig. 11a). Three radio soundings are available for 16 January 17:00 UTC, and 17 January at 07:00 and 12:00 UTC. Only the profile at 06:52 UTC on 17 January captured one of the LLJs (Fig. 12). The radiosonde profile agrees well with the lidar winds. The LLJ is located at the top of a surface inversion and is associated with a strong directional shear in the lowest 200 m. It has to be noted that the ship was orientated perpendicular to the wind for this radiosonde launch, so that the ship's influence on the radiosonde winds was minimized for this LLJ situation. The short duration and fast developments of the LLJs illustrate the benefit of vertical wind profiles with high temporal resolution. The dynamics of the LLJs were not studied in detail. They occurred during the passage of a synoptic front, when the ship operated in a polynya in the lee of a huge iceberg (A23A, size about 60 km × 80 km). Baroclinicity is therefore a likely reason for the LLJs. While LLJs caused by inertial oscillations are frequent in the Weddell Sea during winter (Andreas et al., 2000), the observed jets during PS96 are comparable to the situation of the summertime Arctic Ocean, where Jakobson et al. (2013) mostly find baroclinic jets associated with transient cyclones.
We presented a verification of wind speed profiles measured by a wind lidar without a stabilizing platform during two cruises of the research vessel Polarstern in the Arctic and Antarctic. The ship's motions and orientation were measured by the ship's navigation system and by a high-frequency attitude heading reference system. This is the first time that a wind lidar was operated on an icebreaker in the Antarctic. A processing chain including quality control tests with a new empirical SNR threshold method and an error quantification is presented. The wind calculation is generally based on VAD scans with eight directions (rays) at an elevation angle of 75∘ (an elevation of 85∘ was discarded after a short test period), thus there is a high oversampling which allows for additional quality tests. Wind retrievals from scans at multiple elevation angles elevation angles (25, 50 and 75∘) slightly improve the quality of the wind profile but take more time. The low aerosol concentrations in polar regions result in a low backscatter. As a strategy for optimizing the backscatter signal for these conditions, the adjustment of the telescope focal length of the lidar and the averaging time is useful. We present a processing chain for the data, which includes a quality control for each ray and a method for deriving an empirical SNR threshold. This threshold can be calculated for individual measurement set-ups (e.g. different number of rays, averaging time), and robust thresholds of −17 and −20 dB are found for the Arctic and Antarctic cruises respectively. Due to the oversampling, an error estimation of the lidar winds can be made, which can be used as additional quality criteria. The lidar wind profiles were compared with the routine meteorological measurements of the ship and radiosonde data. Overall, the radiosonde comparisons yield similar results to those found in Achtert et al. (2015) using as motion-stabilized lidar. The wind speed bias is very small (0.1 m s−1) for our standard data processing and the RMSD is about 1 m s−1. For wind direction, the RMSD is about 10∘ and the bias is about 1∘, which is comparable to other studies. Overall the results of the post-processing of non-motion-stabilized lidar data achieve comparably high quality to the motion-stabilized lidar study of Achtert et al. (2015). As our study focuses only on horizontal winds it should be noted that the influence on vertical wind and turbulence measurements is higher and was not evaluated. The need for a motion-stabilized lidar for those measurements could be very important. The comparison with the routine wind measurements of the ship at 40 m height yields a larger data set and a similar bias and RMSD. The choice of a longer averaging time is preferred as it allows the SNR threshold to be reduced and thus increases the amount of data. For longer averaging times the influence of the ship's movement can be higher, but this effect is small in our case because the ship operated mainly in sea ice where wave heights are relatively small. It has also to be considered that the wind field around the ship is influenced by the ship's superstructure, particularly if the ship is orientated into the wind. As this often occurs for radiosonde launches during the ship cruise, the lowest 50 m of the radiosonde wind profile should not be used for these situations. Turning the ship perpendicular to the wind is desirable. The two case studies show that for special situations a flexible change in the SNR threshold can be beneficial, and that ABL phenomena like short-lived LLJs are generally not captured by the routine radio soundings. The lidar with a high temporal resolution of 10–15 min can detect these phenomena and would be ideally combined with a temperature profiler with a similar resolution. Alternatively, the lidar measurements can guide dedicated radiosonde launches during future campaigns, since, for example, LLJs can be detected in real-time with the lidar. For conditions with low backscatter due to the low aerosol concentration as it is typical for the polar regions, the possibility of optimizing the averaging time of the lidar would be the storage of the raw data (spectra) for post-processing.
Data are available upon request to the corre- sponding author (zentek@uni-trier.de).
Given measured Doppler velocities d (negative if wind is blowing towards the lidar) in normalized directions (x, y, z) (east, north, up) and the wind speed (u, v, w), we have the following equation:
By transforming the wind to ( horizontal wind speed, ϕh wind direction, w) with if we get
By transforming the direction (x, y, z) to (θ = elevation angle, ϕ = azimuth angle starting north and turning clockwise) with ϕ=0 if we get
By simplifying this, we get
Using the trigonometric formula we get
By simplifying this, we get
RZ carried out the investigation (measurements on PS96), data curation, methodology, formal analysis, verification, software, visualization and writing of the original draft. SK carried out the investigation (measurements on PS85), verification, a review of the writing and editing. GH carried out the investigation (measurements on PS96), conceptualization, methodology, a review of the writing, editing, supervision, project administration and funding acquisition.
The authors declare that they have no conflict of interest.
The measurements were performed during the two Polarstern cruises PS85 and PS96 funded by the Alfred Wegener Institute under Polarstern grants AWI_PS85_01 and AWI_PS96_03. The research was funded by the Federal Ministry of Education and Research (Bundesministerium für Bildung und Forschung–BMBF) as part of the project “Laptev-Sea Transdrift” under grant 03G0833D and by the SPP 1158 “Antarctic research” of the DFG (Deutsche Forschungsgemeinschaft) under grant HE 2740/19.
From all the software that was used we would like to highlight R, RStudio and the R packages doParallel and data.table. We thank our colleague Clemens Drüe for many useful discussions and our colleague Uwe Baltes for help with the cruise preparations.
The publication
was funded by the Open Access Fund of Universität Trier and the German
Research Foundation (DFG) within the Open Access Publishing funding
programme. Edited by: Ulla Wandinger
Reviewed by: two anonymous referees
Achtert, P., Brooks, I. M., Brooks, B. J., Moat, B. I., Prytherch, J., Persson, P. O. G., and Tjernström, M.: Measurement of wind profiles by motion-stabilised ship-borne Doppler lidar, Atmos. Meas. Tech., 8, 4993–5007, https://doi.org/10.5194/amt-8-4993-2015, 2015. a, b, c, d, e, f, g
Andreas, E. L., Claffy, K. J., and Makshtas, A. P.: Low-Level Atmospheric Jets And Inversions Over The Western Weddell Sea, Bound.-Layer Meteorol., 97, 459–486, https://doi.org/10.1023/a:1002793831076, 2000. a
Banta, R. M., Pichugina, Y. L., and Brewer, W. A.: Turbulent Velocity-Variance Profiles in the Stable Boundary Layer Generated by a Nocturnal Low-Level Jet, J. Atmos. Sci., 63, 2700–2719, https://doi.org/10.1175/jas3776.1, 2006. a
Barlow, J. F., Dunbar, T. M., Nemitz, E. G., Wood, C. R., Gallagher, M. W., Davies, F., O'Connor, E., and Harrison, R. M.: Boundary layer dynamics over London, UK, as observed using Doppler lidar during REPARTEE-II, Atmos. Chem. Phys., 11, 2111–2125, https://doi.org/10.5194/acp-11-2111-2011, 2011. a
Berry, D. I., Moat, B. I., and Yelland, M. J.: Airflow distortion at instrument sites on the FS Polarstern, techreport, Southampton, Southampton Oceanography Centre, 36 pp. (Southampton Oceanography Centre Internal Document, 69), available at: http://nora.nerc.ac.uk/id/eprint/502825/ (last access: 18 October 2018), 2001. a
Brooks, I. M., Tjernström, M., Persson, P. O. G., Shupe, M. D., Atkinson, R. A., Canut, G., Birch, C. E., Mauritsen, T., Sedlar, J., and Brooks, B. J.: The Turbulent Structure of the Arctic Summer Boundary Layer During The Arctic Summer Cloud-Ocean Study, J. Geophys. Res.-Atmos., 122, 9685–9704, https://doi.org/10.1002/2017jd027234, 2017. a
Calhoun, R., Heap, R., Princevac, M., Newsom, R., Fernando, H., and Ligon, D.: Virtual Towers Using Coherent Doppler Lidar during the Joint Urban 2003 Dispersion Experiment, J. Appl. Meteorol. Climatol., 45, 1116–1126, https://doi.org/10.1175/jam2391.1, 2006. a
Damian, T., Wieser, A., Träumner, K., Corsmeier, U., and Kottmeier, C.: Nocturnal Low-level Jet Evolution in a Broad Valley Observed by Dual Doppler Lidar, Meteorol. Z., 23, 305–313, https://doi.org/10.1127/0941-2948/2014/0543, 2014. a
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteorol. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
Frehlich, R. G. and Yadlowsky, M. J.: Performance of Mean-Frequency Estimators for Doppler Radar and Lidar, J. Atmos. Ocean. Technol., 11, 1217–1230, https://doi.org/10.1175/1520-0426(1994)011<1217:pomfef>2.0.CO;2, 1994. a
Hirsikko, A., O'Connor, E. J., Komppula, M., Korhonen, K., Pfüller, A., Giannakaki, E., Wood, C. R., Bauer-Pfundstein, M., Poikonen, A., Karppinen, T., Lonka, H., Kurri, M., Heinonen, J., Moisseev, D., Asmi, E., Aaltonen, V., Nordbo, A., Rodriguez, E., Lihavainen, H., Laaksonen, A., Lehtinen, K. E. J., Laurila, T., Petäjä, T., Kulmala, M., and Viisanen, Y.: Observing wind, aerosol particles, cloud and precipitation: Finland's new ground-based remote-sensing network, Atmos. Meas. Tech., 7, 1351–1375, https://doi.org/10.5194/amt-7-1351-2014, 2014. a, b, c
Jakobson, L., Vihma, T., Jakobson, E., Palo, T., Männik, A., and Jaagus, J.: Low-level jet characteristics over the Arctic Ocean in spring and summer, Atmos. Chem. Phys., 13, 11089–11099, https://doi.org/10.5194/acp-13-11089-2013, 2013. a
Jammalamadaka, S. and Sarma, Y.: A correlation coefficient for angular variables, Statistical Theory and Data Analysis, 2, 349 pp., North Holland, 1988. a
König-Langlo, G.: Upper air soundings during POLARSTERN cruise PS85 (ARK-XXVIII/2), https://doi.org/10.1594/PANGAEA.844803, 2014a. a
König-Langlo, G.: Continuous meteorological surface measurement during POLARSTERN cruise PS85 (ARK-XXVIII/2), https://doi.org/10.1594/PANGAEA.839962, 2014b. a
König-Langlo, G.: Upper air soundings during POLARSTERN cruise PS96 (ANT-XXXI/2 FROSN), https://doi.org/10.1594/PANGAEA.861658, 2016a. a
König-Langlo, G.: Continuous meteorological surface measurement during POLARSTERN cruise PS96 (ANT-XXXI/2 FROSN), https://doi.org/10.1594/PANGAEA.861441, 2016b. a
König-Langlo, G., Loose, B., and Bräuer, B.: 25 Years of Polarstern Meteorology, WDC-MARE Reports, 4, 1–137, https://doi.org/10.2312/wdc-mare.2006.4, 2006. a
Kumer, V.-M., Reuder, J., Dorninger, M., Zauner, R., and Grubišić, V.: Turbulent kinetic energy estimates from profiling wind LiDAR measurements and their potential for wind energy applications, Renew. Energy, 99, 898–910, https://doi.org/10.1016/j.renene.2016.07.014, 2016. a
Päschke, E., Leinweber, R., and Lehmann, V.: An assessment of the performance of a 1.5 µm Doppler lidar for operational vertical wind profiling based on a 1-year trial, Atmos. Meas. Tech., 8, 2251–2266, https://doi.org/10.5194/amt-8-2251-2015, 2015. a, b, c, d, e, f, g
Pearson, G., Davies, F., and Collier, C.: An Analysis of the Performance of the UFAM Pulsed Doppler Lidar for Observing the Boundary Layer, J. Atmos. Ocean. Technol., 26, 240–250, https://doi.org/10.1175/2008jtecha1128.1, 2009. a, b
Pichugina, Y. L., Banta, R. M., Brewer, W. A., Sandberg, S. P., and Hardesty, R. M.: Doppler Lidar-Based Wind-Profile Measurement System for Offshore Wind-Energy and Other Marine Boundary Layer Applications, J. Appl. Meteorol. Climatol., 51, 327–349, https://doi.org/10.1175/jamc-d-11-040.1, 2012. a, b
Spreen, G., Kaleschke L., and Heygster, G.: Sea ice remote sensing using AMSR-E 89-GHz channels, J. Geophys. Res-Oceans, https://doi.org/10.1029/2005JC003384, 2008. a
Tjernström, M., Leck, C., Birch, C. E., Bottenheim, J. W., Brooks, B. J., Brooks, I. M., Bäcklin, L., Chang, R. Y.-W., de Leeuw, G., Liberto, L. D., de la Rosa, S., Granath, E., Graus, M., Hansel, A., Heintzenberg, J., Held, A., Hind, A., Johnston, P., Knulst, J., Martin, M., Matrai, P. A., Mauritsen, T., Müller, M., Norris, S. J., Orellana, M. V., Orsini, D. A., Paatero, J., Persson, P. O. G., Gao, Q., Rauschenberg, C., Ristovski, Z., Sedlar, J., Shupe, M. D., Sierau, B., Sirevaag, A., Sjogren, S., Stetzer, O., Swietlicki, E., Szczodrak, M., Vaattovaara, P., Wahlberg, N., Westberg, M., and Wheeler, C. R.: The Arctic Summer Cloud Ocean Study (ASCOS): overview and experimental design, Atmos. Chem. Phys., 14, 2823–2869, https://doi.org/10.5194/acp-14-2823-2014, 2014. a
Tucker, S. C., Senff, C. J., Weickmann, A. M., Brewer, W. A., Banta, R. M., Sandberg, S. P., Law, D. C., and Hardesty, R. M.: Doppler Lidar Estimation of Mixing Height Using Turbulence, Shear, and Aerosol Profiles, J. Atmos. Ocean. Technol., 26, 673–688, https://doi.org/10.1175/2008jtecha1157.1, 2009. a, b
Vaisala: Radiosonde RS92-SGP, data sheet, available at: https://www.vaisala.com/sites/default/files/documents/RS92SGP-Datasheet-B210358EN-F-LOW.pdf (last access: 2 January 2018), 2013. a