the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Recovery of the three-dimensional wind and sonic temperature data from a physically deformed sonic anemometer
Xinhua Zhou
Xiaojie Zhen
Yubin Li
Guanghua Hao
Hui Shen
Yirong Sun
Ning Zheng
A sonic anemometer reports three-dimensional (3-D) wind and sonic temperature (Ts) by measuring the time of ultrasonic signals transmitting along each of its three sonic paths, whose geometry of lengths and angles in the anemometer coordinate system was precisely determined through production calibrations and the geometry data were embedded into the sonic anemometer operating system (OS) for internal computations. If this geometry is deformed, although correctly measuring the time, the sonic anemometer continues to use its embedded geometry data for internal computations, resulting in incorrect output of 3-D wind and Ts data. However, if the geometry is remeasured (i.e., recalibrated) and to update the OS, the sonic anemometer can resume outputting correct data. In some cases, where immediate recalibration is not possible, a deformed sonic anemometer can be used because the ultrasonic signal-transmitting time is still correctly measured and the correct time can be used to recover the data through post processing. For example, in 2015, a sonic anemometer was geometrically deformed during transportation to Antarctica. Immediate deployment was critical, so the deformed sonic anemometer was used until a replacement arrived in 2016. Equations and algorithms were developed and implemented into the post-processing software to recover wind data with and without transducer-shadow correction and Ts data with crosswind correction. Post-processing used two geometric datasets, production calibration and recalibration, to recover the wind and Ts data from May 2015 to January 2016. The recovery reduced the difference of 9.60 to 8.93 ∘C between measured and calculated Ts to 0.81 to −0.45 ∘C, which is within the expected range, due to normal measurement errors. The recovered data were further processed to derive fluxes. As data reacquisition is time-consuming and expensive, this data-recovery approach is a cost-effective and time-saving option for similar cases. The equation development can be a reference for related topics.
- Article
(1941 KB) -
Supplement
(2652 KB) - BibTeX
- EndNote
The three-dimensional (3-D) sonic anemometer is commonly used for both micrometeorological research and applied meteorology (Horst et al., 2015). It directly measures boundary-layer flows at high measurement rates (10 to 50 Hz) and outputs wind speeds expressed in the 3-D right-handed orthogonal anemometer coordinate system relative to its structure frame (see Appendix A, hereafter, referred as 3-D anemometer coordinate system) and sonic temperature calculated from the speed of sound (Hanafusa et al., 1982). Its outputs are commonly used to estimate the fluxes of momentum and sonic temperature and, when combined with fast-response scalar sensors, the fluxes of CO2, H2O, and other atmospheric constituents.
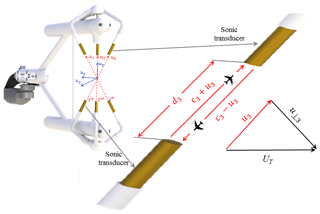
Figure 1Diagram of the IRGASON for the three sonic measurement paths (red dash lines) along which ultrasonic signals transmit, and the three dimensional (3-D) right-handed orthogonal anemometer coordinate system (blue lines) in which 3-D wind is expressed (i.e., u1, u2, and u3 are the flow speeds along the first, second, and third sonic paths, respectively. These three flow speeds are expressed as ux, uy, and uz in this 3-D anemometer coordinate system). d3 is the third sonic path length, c3 is the measured speed of sound along the third sonic path, and UT is the total flow vector whose magnitude is equal to or .
It has three pairs of sonic transducers forming three sonic paths (Fig. 1), each of which is between paired sonic transducers. The three paths are situated as optimized angles for wind measurements in the 3-D anemometer coordinate system, structuring the geometry of sonic anemometer. This geometry is quantitatively defined by the path lengths and path angles that are precisely measured during production calibration. A sonic anemometer measures the time of ultrasonic signals transmitting along each path (hereafter, referred as transmitting time). In reference to the sonic path length, the transmitting time is used to calculate the speeds of flow and sound along the path, which will be detailed in Sect. 4 as follows. According to the angles of three sonic paths, the speeds from the three paths are expressed in the 3-D anemometer coordinate system for wind and as sonic temperature for air heat property.
A sonic anemometer has geometry information embedded into its operating system (OS) for internal data processing (see Appendix A), allowing output of 3-D wind and sonic temperature. However, if it is geometrically deformed from the manufacturer's setting at millimeter scales, or even smaller, due to an unexpected physical impact in transportation, installation, or other handling, the geometry embedded in the OS is not representative of the current geometry of this sonic anemometer. As a result, the anemometer no longer outputs correct wind speeds and sonic temperatures because the deformation in geometry changes the relative spatial relationship among its six sonic transducers. If, an impact displaces a transducer relative to the others, the displacement must change at least one of the sonic path lengths and one of the sonic path angles. Fortunately, if geometrical deformation is the only problem, rather than physical damage to the transducers, the sonic anemometer can, according to its working physics (Schotland, 1955), correctly perform its transmitting-time measurements. Due to the change in a sonic path length, the speeds of air flow and sound along the path are incorrectly computed because the sonic path length embedded in the OS does not match the true length when the transmitting time was measured. As a result, the incorrect speeds along with the change in any sonic path angle might cause all 3-D wind speeds as well as sonic temperature outputs to be incorrect. These incorrect outputs are recoverable because the transmitting time was correctly measured and the deformed geometry can be remeasured (i.e., recalibrated) by the manufacturer to whom the anemometer can be shipped back with care. However, the equations and algorithms for the recovery are needed if a sonic anemometer is found to be geometrically deformed in a remote site where its use has to be continued. From such a site, it could take months, seasons, or even longer for a deformed anemometer to be transported back to the manufacturer for geometry remeasurements, recalibration, and shipped back to the site. In this case, if the measurements were not continued, a measurement season or year could be easily missed.
This study demonstrates data recovery from such a case when a sonic anemometer as a component of the IRGASON (integrated CO2/H2O open-path gas analyzer and 3-D sonic anemometer, Campbell Scientific Inc., 2018) was geometrically deformed during transportation to the Antarctic Zhongshan Station from China in early 2015 and had to be used until its replacement arrived at the site early the next year. If the deformed sonic anemometer was not used, one measurement-year would have been missed because the only transportation of R/V Xue Long (i.e., Snow Dragon in English) from China to the Zhongshan Station served a round-trip to the site on an annual basis. More importantly, the 2015 data were also needed by related projects for collaborations. Therefore, the geometrically deformed sonic anemometer was used to acquire the 2015 data. In early 2016, the deformed anemometer was shipped, with a pair of buffer bumpers for protection, to the manufacturer of Campbell Scientific Inc. in the US for remeasurements of its geometry to update its OS (i.e., recalibration).
Using the measurements of sonic path lengths and sonic path angles for this sonic anemometer from production calibration in April 2014 before its transportation and from recalibration in March 2016 after the field use in the Zhongshan Station, this study aims to develop and verify the equations and algorithms to recover the 2015 data measured using this geometrically deformed sonic anemometer to data as if measured with the this anemometer after recalibration although actually measured before the recalibration, providing a reference to similar cases and/or related topics.
The observation site was in the coastal landfast sea ice area of the Zhongshan Station (69∘22′ S and 76∘22′ E), East Antarctica (Yang et al., 2016; Yu et al., 2017; Zhao et al., 2017). In this area, as influenced by the unique solar cycles, the climate is characterized by the polar night from late March to mid-July and the polar day from mid-November to January. The polar day and the polar night are inhabitable to human life, but drive atmospheric dynamics in a way that is of interest to human beings (Valkonen et al., 2008); therefore, this region has attracted scientists to measure its surface heat balance; However, these measurements are not an easy task in terms of financial support, technical infrastructure, and administrative management. As such, only a few studies on such measurements have been conducted in this region (e.g., Vihma et al., 2009; Liu et al., 2017).
The fluxes of CO2/H2O, heat, radiation, momentum, and atmospheric variables were measured so that the sea ice and snow surface energy budget during both melting and frozen periods can be quantified. For these measurements, the project established two open-path eddy-covariance (OPEC) flux stations in May 2015. One station (see Fig. 2) was configured with the IRGASON (SN: 1131) for the fluxes, four-component net radiometer (model: CNR4, Kipp & Zonen, Delft, the Netherlands) for net radiation and radiation fluxes; one temperature and relative humidity probe (model: HMP155A, SN: H5140031, Vaisala, Helsinki, Finland) inside a 14-plate naturally aspirated radiation shield of model 41005 for air temperature and air relative humidity; and one infrared radiometer (model: SI-111, SN: 2962, Apogee, UT, USA) for surface temperature. In early 2016, a CSAT3B (Campbell Scientific Inc., UT, USA) was added for additional data of 3-D wind and sonic temperature. This OPEC station was also equipped with a built-in barometer (model: MPXAZ6115A, Freescale Semiconductor, TX, USA) for atmospheric pressure and a built-in 107 temperature probe (model: 100K6A1A, BetaTherm, Finland) inside a 6-plate naturally aspirated radiation shield of model 41303-5A for air temperature, the IRGASON was connected to and controlled by an EC100 electronic module (SN: 1542, OS: EC100.04.10) that, in turn, was connected to and instructed by a central CR3000 Measurement and Control Datalogger (SN: 7720, OS 25) for these sensor measurements, data processing, and data output. While receiving the data output from EC100 at 10 Hz, the CR3000 also controlled and measured slow response sensors at 0.1 Hz such as the CNR4, HMP155A, and others in support to this study. EasyFlux_CR3OP (version 1.00, Campbell Scientific Inc., 2016) was used inside CR3000. The data of 3-D wind, sonic temperature, CO2 and H2O amounts, atmospheric pressure, diagnosis codes for the 3-D sonic anemometer and open-path infrared gas analyzer, air temperature, and relative humidity were stored 10 records per second (i.e., 10 Hz). The data from all sensors were computed and stored by the CR3000 at every half-hour interval.

Figure 2The eddy-covariance station located in the coastal landfast sea ice area of Antarctica Zhongshan Station (69∘22′ S, 76∘22′ E). It was configured with the IRGASON integrated CO2/H2O open-path gas analyzer and three-dimensional sonic anemometer, CNR4 four-component net radiometer, HMP155A air temperature and relative humidity probe, and SI-111 infrared radiometer.
Immediately after the station started to run, all measured values were checked. Unfortunately, the sonic temperature from the 3-D sonic anemometer was incorrect because it was around 10 ∘C higher than the air temperature from HMP155A or 100K6A1A. Given a H2O density of about 1.00 g m−3 and air temperature about −20 ∘C, sonic temperature should be around 0.13 ∘C higher than air temperature (see Eq. 5 in Schotanus et al., 1983) if the sonic temperature was measured, although impossible, without an error. Further diagnosis for sonic anemometer measurements found that the sonic temperature values from the three sonic paths unexpectedly deviated around −12, 5, and −7 ∘C, respectively, as shown by device configuration (Campbell Scientific Inc., UT, USA) connected to EC100 through a notebook computer while the station was running. Apparently, the largest absolute difference in sonic temperature among the three paths reached 17 ∘C, although the difference from an IRGASON sonic anemometer was expected to be < 1 ∘C. Such a large unexpected absolute difference (e.g., 17 ∘C) among the three values from the three sonic paths might be caused by the geometrical deformation of sonic anemometer. To confirm the diagnosis, the body of the IRGASON was visually examined and painting on the knuckle of side one (i.e., first sonic path) among the top three claws was found removed as it was apparently impacted (Fig. 3). Therefore, with confidence, it was concluded that the incorrect outputs of sonic temperature were caused by the geometrical deformation of sonic anemometer while being transported to Antarctica from China. The deformation also might cause the incorrect outputs of 3-D wind. Therefore, this IRGASON should have been shipped back to the manufacturer for remeasurements of its geometry to update its OS (recalibration). However, as addressed in the introduction, the 2015 data would have been missed if it was shipped back to the manufacturer at that point. To make measurements as planned, this IRGASON continued its field duty until the next round-trip of R/V Xue Long to Antarctica from China until the end of 2015 when its replacement from the manufacturer arrived at the site.

Figure 3Painting removed where it was apparently impacted on the knuckle of side claw (first sonic path) among the top three sonic transducer claws of the IRGASON sonic anemometer (serial no.: 1131).
In early 2016, it was replaced in the field and was shipped back to the manufacturer, where it was remeasured for sonic geometry in the recalibration process in March. The remeasurements verified our diagnosis conclusion that the IRGASON sonic anemometer was geometrically deformed (see Table A1 in Appendix A). Therefore, the 2015 data from this sonic anemometer needed to be recovered as if measured by the same anemometer after recalibration, although the data were acquired from the measurements before the recalibration.
An IRGASON sonic anemometer measures wind flows along its three non-orthogonal sonic paths (i.e., the three sonic paths non-orthogonally situated in relation to each other, see Fig. 1), each of which is between a pair of sonic transducers. Sensing each other in each sonic path, the pair separately pulse two ultrasonic signals in opposite directions at the same time. The signal pulsed by the transducer facing the air flow direction along the sonic path takes less time to be sensed by its paired one than the one pulsed by the transducer against the air flow direction. In a path, the transmitting time of the ultrasonic signal upward [tui where subscript i can be 1, 2, or 3, denoting the sequential order of sonic path (Fig. 1). This subscript denotes the same variable throughout] and downward (tdi) are measured by the sonic anemometer (Hanafusa, 1982; Foken, 2017). In the case shown in Fig. 1 for the third sonic path, or i=3, the transmitting time of ultrasonic signal upward in the path is given by the following equation:
where, along the third sonic path, d3 is its length precisely measured during production or recalibration process using a coordinate measurement machine (CMM), c3 is the speed of sound, and u3 is the speed of air flow (Fig. 1); and the transmitting time of ultrasonic signal downward is given by the following equation:
4.1 Recovery of 3-D wind data
4.1.1 Algorithm of sonic anemometer to output the 3-D wind data
Equations (1) and (2) lead to
Using the same procedure, u1 and u2 (see Fig. 1) can be derived as the same form. In reference to Eq. (3), the equation for ui; where , or 3; can be expressed as follows:
Similar to d3, d1 and d2 are also precisely measured using CMM. The three flow speeds of ui (i=1, 2, or 3) from the three non-orthogonal paths are expressed in the 3-D anemometer coordinate system of x, y, and z; where x and y are the horizontal coordinate axes and z is the vertical axis; and through a transform matrix A as the 3-D wind speeds (ux, uy, and uz) commonly used in practical applications:
where the 3-D anemometer coordinate system (see Figs. 1 and A1) is defined by its origin at the center of sonic measurement volume, the ux−uy plane, parallel to the imagery plane, leveled by a built-in bubble in the anemometer structure, and the uy−uz plane through the first sonic path and A is a 3×3 matrix constructed using precisely measured geometry of the sonic paths in angles relative to the 3-D anemometer coordinate system (see its derivations in Appendix A). Matrix A is unique for each sonic anemometer and is embedded in its OS; therefore, the 3-D wind data outputted from the anemometer are the three components of ux, uy and uz in the 3-D anemometer coordinate system.
Due to shadowing from the sonic transducer itself (transducer shadowing), the measured ui is assumed to be lower than its true value in magnitude (Wyngaard and Zhang, 1985; Kaimal and Finnigan, 1994). As denoted by uTi_n where subscript T indicates “True” and subscript n indicates that uTi_n was estimated from n counts of iterations of transducer-shadow correction as shown in Appendix B, this true value is assumed to be approached through the transducer-shadow correction from ui. Now, the shadow correction was implemented as an option if the OS of EC100 for the IRGASON sonic anemometer is version 5 or newer. Therefore, depending on the option, Eq. (5) alternatively can be expressed as follows:
Following Host et al. (2015), based on Wyngaard and Zhang (1985), the correction equation for the sonic transducer size and sonic path geometry of the IRGASON sonic anemometer is given by
where αi is the angle of the total wind vector to the wind vector along sonic path i and is unknown before the two vectors are estimated, but, referencing Figs. 1 and 4, the sinαi in Eq. (7) can be alternatively expressed as a function of flow speed values to lead Eq. (7) as follows:
where UT is the magnitude of total true wind vector, given by
In Eq. (8), all independent variables are actually related to the variables in Eq. (5). As such, using this equation, uTi can be computed; however, there are two inconvenient issues in this equation application to transducer-shadow corrections: (1) an analytical solution for uTi is not easily available because uTi is in a second order term under a square root in the right side of Eq. (8), although uTi is analytically expressed in its left side and (2) UT is not available either because ux, uy, and uz are derived from u1, u2, and u3 before the transducer-shadow corrections. Fortunately, the corrections are small in magnitude, as shown in Eq. (8); therefore, ui is closed to uTi. As a result, ux, uy, and uz from Eq. (5) are close to those from Eq. (6). Accordingly, an iteration algorithm may be the right approach to the corrections using Eq. (8), or for the estimation of uTi.
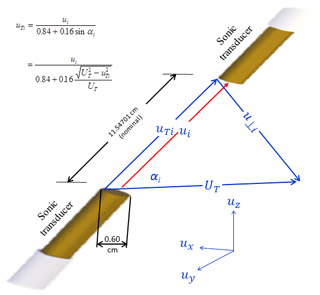
Figure 4Sonic transducer shadowing along the ith (i=1, 2, or 3) sonic path between the two sonic transducers, ui is the measured magnitude of flow vector whose true magnitude is uTi; u⊥i is the flow speed normal to the ith sonic path; ux, uy, and uz are the wind speeds expressed in the three-dimensional orthogonal anemometer coordinate system; and αi is the angle between sonic path i and the total flow vector (UT) equal to or . See Wyngaard and Zhang (1985) and Kaimal and Finnigan (1994) for the equation to calculate uTi.
For the first iteration, uTi in the right side of Eq. (8) could be replaced with ui as its estimation. Given that UT should be calculated using ux, uy, and uz from Eq. (6), before the transducer-shadow corrections, UT can be estimated using ux, uy, and uz from Eq. (5); see Appendix B: Iteration algorithm for sonic transducer-shadow corrections. The iterations ensure that the difference in ux, uy, or uz between the last and previous iterations are <1 mm s < 1, where σ is the maximum precision (i.e., standard deviation at constant wind) among ux, uy, and uz (Campbell Scientific Inc., 2018). The uT1_n, uT2_n, and uT3_n from the last interaction are finally used for Eq. (6) to compute the 3-D wind of ux, uy, and uz as sonic anemometer output.
4.1.2 Procedure to recover 3-D wind data
As addressed in Eqs. (4) to (6), a sonic anemometer measures tui and tdi to calculate the 3-D wind of ux, uy, and uz; therefore, sonic path lengths (di) in Eq. (4) and transform matrix A in Eqs. (5) and (6) are embedded into the OS of sonic anemometer in the manufacture processes (see the embedded data for our study sonic anemometer in Appendix A). If the anemometer was physically deformed in transportation, installation, or other handling; the sonic path lengths and sonic path angles must be changed from what they were at the time when di and A were embedded into its OS; therefore, di in Eq. (4) and sonic path angles reflected by A in Eqs. (5) and (6) are no longer valid for this anemometer. Consequently; the output of ux, uy, and uz still based on embedded di and A from production calibration or recalibration process are erroneous. To correct the erroneous output ux, uy, and uz need to be transformed back into tui and tdi and be recalculated using tui and tdi based on the true sonic path lengths and true sonic path angles at the time when tui and tdi were measured in the field by the sonic anemometer physically deformed away from the manufacturer's geometrical settings before its field deployment.
For the true sonic path lengths and true sonic path angles, the IRGASON (SN: 1131) was returned to the manufacturer in the way described in Sect. 3. In the same way as in the manufacture process, the lengths and angles were remeasured using CMM. The remeasured lengths are denoted by dTi (i=1, 2, or 3) and the remeasured angles were used to reconstruct the transform matrix A as AT (see Appendix A). Both dTi and AT are used to update the OS of this IRGASON for future field uses and to correct ux, uy, uz and Ts (sonic temperature, see Sect. 4.2) that were outputted in the field before the remeasurements. The correction procedures are different for the output of ux, uy, uz with or without transducer-shadow corrections.
With transducer-shadow corrections
Transfer ux, uy, and uz in the 3-D anemometer coordinate system to the flow speeds along the sonic paths after transducer-shadow corrections.
Using Eq. (B5), flow speed along the ith sonic path before transducer-shadow correction (ui) can be expressed as follows:
where UT can be calculated using Eq. (9) and uTi_m can be reasonably approximated using uTi_n because uTi_m and uTi_n are close enough to ensure ux, uy, and uz to converge at their measurement precision (see Appendix B). Using ui and di, the time term inside the square bracket in Eq. (4) can be recovered as follows:
Additionally, according to Eq. (4) and using dTi, the speed of air flow along the ith sonic path can be recalculated as uci:
Further replacing ui with uci in the iteration algorithm for sonic transducer-shadow corrections in Appendix B, uci is corrected for transducer-shadowing as ucTi_n. Using Eq. (6), the recovered vector of 3-D wind in the 3-D anemometer coordinate system [ucx ucy ucz]′ can be expressed as follows:
Without transducer-shadow corrections
Transfer ux, uy, and uz in the 3-D anemometer coordinate system to the flow speeds along individual sonic paths.
Using Eqs. (12) and (13), the speed of flow along the ith sonic path (uci) is recalculated (i.e., recovered). Based on Eq. (5), the recovered speeds of flow along the three sonic paths can be expressed in the 3-D anemometer coordinate system as follows:
4.2 Recover sonic temperature data
4.2.1 Algorithm of sonic anemometer to output sonic temperature
Equations (1) and (2) also lead to
Using the same procedure, c1 and c2 (see Figs. 1 and 5) can be derived as the same form. In reference to Eq. (17), the equation for ci, where subscript i=1, 2, or 3; can be expressed as follows:
Here, ci is the measured speed of sound along the sonic path i (see Fig. 5). When the crosswind (u⊥i), or wind normal to the sonic path i, is zero; ci is the true speed of sound (c0i where subscript 0 indicates the speed of sound at crosswind speed equal to zero). Unfortunately, crosswind is rarely zero and ci needs to be corrected to c0i. According to Figs. 1 and 5, the true speed of sound is given by
Referencing the diagram for wind vectors in the left side of Fig. 5, this equation can be expressed as follows:
According to the definition of sonic temperature (Kaimal and Finnigan, 1994), the sonic temperature (K) along the ith sonic path (Tsi) should be expressed as follows:
where γd (1.4003) is the ratio of dry-air-specific heat at constant pressure (1004 J K−1 kg−1) to dry-air-specific heat at constant volume (717 J K−1 kg−1) and Rd is gas constant for dry air (287.04 J K−1 kg−1). The sonic temperature outputted from the sonic anemometer (Ts in ∘C) is the average from the three sonic paths (van Dijk, 2002), given by
Substituting c0i with Eq. (20) and then substituting ci with Eq. (18), Ts can be expressed as follows:
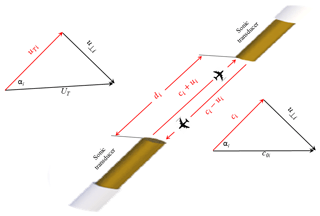
Figure 5Crosswind on the speed of sound. Along the ith (i=1, 2, or 3) sonic path between the two sonic transducers, ui is the measured magnitude of flow vector whose true magnitude is uTi, and ci is measured speed of sound; u⊥i is the crosswind vector normal to sonic path i; UT is the magnitude of total flow vector whose magnitude is equal to or , where ux, uy, and uz are the wind speeds in the three-dimensional right-handed orthogonal anemometer coordinate systems; c0i is the speed of sound at crosswind equal to zero; and αi is the angle between sonic path i and the total flow vector.
4.2.2 Procedure to recover sonic temperature data
Equation (23) indicates that, given di, a sonic anemometer estimates sonic temperature using its measured transmitting time of tui and tdi, the flow speeds along the sonic paths (ui or uTi if corrected for transducer shadowing) that are also calculated from tui and tdi (see Eq. 4), and the resultant wind speed (UT, i.e., the total wind) computed using Eq. (9), inside which the three wind components in the 3-D anemometer coordinate system are transformed from ui using A, as explained by Eq. (5), without transducer-shadow corrections or from uTi also using A as explained by Eq. (6), with transducer-shadow corrections. As discussed in Sect. 4.1.2, when a sonic anemometer is geometrically deformed in an incident, the sonic path lengths and sonic path angles may be changed from what they were at the time when di and A were embedded into its OS; therefore, di in Eq. (23) and A in Eqs. (5) and (6) for ui∕uTi and UT in Eq. (23) are no longer valid for this sonic anemometer. As a result, its output of ux, uy, uz, and Ts still based on embedded di and A must not be representative to the field wind and sonic temperature to be measured. In Sect. 4.1, the procedure to recover 3-D wind data was developed using remeasured sonic path lengths (dTi) and redetermined sonic path angles for AT. The procedure to recover sonic temperature data also needs to be developed using dTi and recovered 3-D wind data in this section.
Based on Eq. (20), the recovered speed of sound from the sonic path i after crosswind corrections (cc0i) can be expressed as follows:
where cci is the recovered speed of sound along sonic path i and . After replacement of with in Eq. (22), the recovered sonic temperature (Tcs in ∘C) can be written as follows:
Now, the term of needs to be derived. Subtracting Eq. (20) from (24) leads to
Using this equation to substitute in Eq. (25), denoting with and denoting with leads to
In this equation, the term of is still unknown. Based on Eq. (18), is given by
Accordingly, the unknown term is given by
In this equation, the only unknown variable is . Based on Eq. (20), this equation can be expressed as follows:
In the right side of this equation, is the only unknown. However, the whole term in the right side of Eq. (30) mathematically is a differential term in which can be reasonably approximated using its neighbor value, as close as possible to . The average of , and can be calculated from Eq. (22) because Ts is an output variable of the sonic anemometer. Without a measurement error and random error, the three c0i should be the same, independent of flow speed, because they are the true speed of sound instead of measured speed of sound along an individual sonic path (Schotanus et al., 1983; Liu et al., 2001); Therefore, can be reasonably approximated using the average of three as , given by
where can be computed from Eq. (22) as follows:
Due to the replacement of with , the relative error of the whole term in the right side of Eq. (31) would be < 4 %, even if the variability in sonic temperature due to the difference among values reaches 10 ∘C at an air temperature of −30 ∘C without wind (i.e., UT=0 and uTi=0), which would be the worst case. Substituting the term of in Eq. (27) with Eq. (31) leads to
In the right side of this equation, the whole term after Ts is the sonic temperature recovery term.
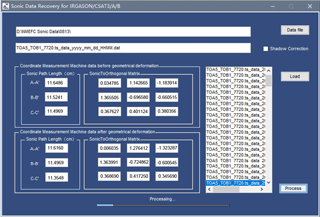
For our case without a transducer-shadow correction, Eqs. (15), (12), (13), and (16) were sequentially used to recover the 3-D wind data. In a case of transducer-shadow correction in option, Eqs. (10) to (16) are used. Based on the data of 3-D wind from the recovery process, Eqs. (9), (32), and (33) were used to recover the sonic temperature data. The whole recovery processes large data files (10 records per second), not only using these equations, but also operating the matrixes (A3) to (A5) (see Appendix A) for Eqs. (15) and (16) along with the data of sonic paths lengths in Table A1 for Eqs. (12) and (13). Apparently, the recovery process is a huge work load in computation. As such, these equations, matrixes, and data were implemented into a software package: “Sonic Data Recovery for IRGASON/CSAT3/A/B Used in Geometrical Deformation after Production/Calibration” (Appendix C and Fig. 6). As long as the path lengths and matrixes from production/calibration and from recalibration are input into the software as instructed by the interface (Appendix C), the software automatically recover the data in batches.
In our station, an additional anemometer for wind was not under deployment when this study IRGASON was used in its deformed state; therefore, no data were available to verify the recovered 3-D wind data. However, the algorithms as addressed using Eqs. (10) to (16) to recover the 3-D wind data are solid without any estimation and the recovered 3-D wind data are not necessary for verification.
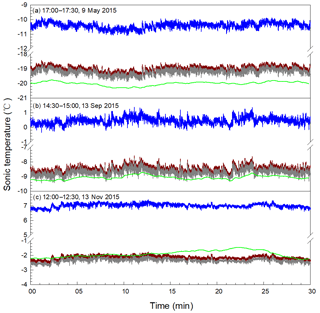
Figure 7Verification of sonic temperature (Ts) recovered against calculated (see Appendix D) from the air temperature (T), relative humidity (RH), and atmospheric pressure (P) that were measured using a HMP155A air temperature and relative humidity probe as well as the IRGASON built-in barometer. Blue curves: Ts measured by the IRGASON sonic anemometer in geometrical deformation (raw Ts); red curves: Ts recovered from raw Ts using Eq. (33); grey curves: Ts recovered also from raw Ts using Eq. (40) (i.e., adjusted Eq. 33); and green curves: Ts calculated from T, RH and P.
Fortunately, the data to verify sonic temperature are available in this station. Air temperature, relative humidity, and atmospheric pressure were measured using research grade sensors of the HMP155A and IRGASON built-in barometer and the data of these variables also stored at 10 Hz (10 records per second). These data can be used to estimate the sonic temperature (see Appendix D: Sonic temperature from air temperature, relative humidity, and atmospheric pressure). The recovered data of sonic temperature using Eq. (33) were compared to the calculated sonic temperature over the range of sonic temperature for three representative values: ∘C in Fig. 7a, ∘C in Fig. 7b, and ∘C in Fig. 7c. The difference between measured (i.e., unrecovered) and calculated sonic temperature values of 9.60±0.14 K in Fig. 7a, 9.53±0.17 K in Fig. 7b, and 8.93±0.24 K in Fig. 7c was narrowed to 0.99±0.14 K, 0.57±0.17 K, and K, respectively, as the difference between recovered and calculated sonic temperature values. Given the accuracy of ±0.5 K in sonic temperature from the IRGASON sonic anemometer (Personal communication with Larry Jacobsen, the designer of the sonic anemometer, 2017) and the accuracy of ±0.2 ∼0.3 K in air temperature below 0 ∘C and 1.2 % in relative humidity from HMP155A (Vaisala Corp., 2017), from which the calculated sonic temperature was derived (see Appendix D), recovered sonic temperature data can be reasonably judged as satisfactory if the difference in mean sonic temperature between recovered and calculated ranges within ±0.80 K or even wider, which could be considered a likelihood range of possible difference between correctly measured and calculated sonic temperature. As shown in Fig. 7, Eq. (33) apparently did an excellent job in recovering the sonic temperature data measured using sonic anemometer in its deformed state, but was less satisfactory in the case of Fig. 7a (i.e., 0.99±0.14 K, the difference in sonic temperature between recovered and calculated) although the range of 0.99±0.14 K was not significantly different from ±0.80 K. The less satisfactory recovery might be caused by the approximation of c0i from c0 that is fully valid if all c0i are not measured by a sonic anemometer in its deformed state, but this is not the case in this study.
According to Eq. (22), it is impossible to have an individual c0i from Ts, which is the sole output for sonic temperature from any sonic anemometer. Now, the average of , and is known and the changes in sonic path lengths are known. It is possible to estimate the difference among the three speeds of sound and to adjust their average ( to , and in approximation, although the exact values are impossible to determine. The adjusted values can reflect the variability among to some degree and are reasonably expected to improve the data recovery.
The measured speed of sound after crosswind correction (c0i) is independent of wind speed (Schotanus et al., 1983; Liu et al., 2001) while depending on moist air density and atmospheric pressure (Barrett and Suomi, 1949). Without wind, c0i is equal to the measured speed of sound (ci) from sonic path i (see Eq. 19). In this case, again without wind, tui and tdi in Eq. (18) are the same and can be denoted by ti. Accordingly, Eq. (18) in this case is equivalent to
In Eq. (33), is the average of three squared c0i (see Eqs. 22 and 32), but an individual c0i is unknown; therefore, for recovery improvement, it has to be estimated from through a reasonable adjustment. The difference in magnitude between and must be related to the error due to the geometrical deformation of sonic anemometer. Squaring both sides of Eq. (34) leads to
The total differentiation of is given by
Given the transmitting time is correctly measured by a sonic anemometer (i.e., Δti=0) even in its geometrical deformation, this equation becomes
Mathematically in differentiation, can be reasonably approximated by c0, given by
This is the error of away from . This error can be reasonably used to represent the deviation of away from . The deviations of three values away from are the measures of variability among three away from .
Although an individual is unknown, the average of three is known as . This average should be unchanged after adjustments because of the adjustment within the variability among away from . If the average of adjusted is not equal to , all adjusted should be added or subtracted with the same constant to make the average of three adjusted values as , but the variability among values is kept the same. This constant must be the mean of three values. Based on these analyses, the adjustment of to can be constructed as follows:
Using this equation to replace in Eq. (30) and the resultant equation with this replacement then is used for in Eq. (27) as follows:
In the right side of this equation, the whole term after Ts is the adjusted sonic temperature recovery term.
The data recovered using Eq. (33) were recovered again using Eq. (40). Apparently, this equation did a better job than Eq. (33). The difference in sonic temperature between the recovered and calculated values was reduced to 0.81±0.14, 0.38±0.17, and K, respectively, as shown from panels a to c in Fig. 7. These values for the difference fell into the range of ±0.80 K in a statistical sense. Eventually, Eq. (40) was used for data recovery and was incorporated into the software (Appendix C).
8.1 Verification of 3-D wind recovery
Although not explicitly verified, the recovered 3-D wind data were implicitly verified through the verification of recovered sonic temperature data because (1) sonic temperature is more sensitive than wind speeds in ultrasonic sonic measurements (Thomas Foken, 2018, review comment for this publication) and (2) the recovery of sonic temperature data must rely on recovered 3-D wind data (Eqs. 33 and 40). According to Eqs. (3), (17), and (21), it is apparent that sonic temperature is sensitive to one order higher than wind speed to the errors in measurements of sonic path lengths and ultrasonic signal transmitting time values. If the recovered sonic temperature is within the accuracy limits of sensors, this should be realized for the wind data recovery as well (Thomas Foken 2018, review comment for this publication). Additionally, the cross wind correction for sonic temperature needs 3-D wind data (Liu et al., 2001). If 3-D wind had not been well recovered, sonic temperature data could not have been recovered satisfactorily. Therefore, the satisfactory recovery of sonic temperature data in this study implicitly verified the satisfactory recovery of 3-D wind data.
8.2 Comparability of recovered temperature to calculated sonic temperature
The recovered sonic temperature was sourced from the measurements of a fast response sonic anemometer, and the calculated sonic temperature was sourced from the measurements of a slow response air temperature and relative humidity probe as well as a barometer built into the IRGASON (see Appendix D). Therefore, the former reflected the fluctuations in the sonic temperature at high frequency, and the latter reflects the same fluctuations at lower frequency. As such, a pair of recovered and calculated sonic temperature values from simultaneous measurements (i.e., the same records in a time series data file) were not comparable. The difference between the pair is meaningless; therefore, the mean difference between recovered and calculated sonic temperature values over a half-hour period was used for their data comparison.
8.3 Recovered temperatures higher than calculated sonic temperature at lower temperatures
See Fig. 7. Compared to calculated sonic temperature, the recovered sonic temperature from Eq. (40) is 0.81±0.14 K higher at −20.01 ∘C (Fig. 7a) and 0.38±0.17 K higher at −9.06 ∘C (Fig. 7b); however, at −1.90 ∘C, even K lower (Fig. 7c). This trend of difference with temperature may be related to the performance of sonic anemometer at different temperature and the lower accuracy of temperature and humidity probe in a lower temperature range (Vaisala Corp., 2017).
The sonic path lengths and geometry of the sonic anemometer were measured in the manufacture environment of an air temperature around 20 ∘C (i.e., manufacture temperature) and embedded into its OS for field applications. However, above or below the manufacture temperature, the sonic path lengths must become, due to thermo-expansion or -contraction of sonic anemometer structure, longer or shorter than those at the manufacture temperature while the length values of sonic paths inside the OS are unchanged. As a result, the sonic anemometer could under- or overestimate the speed of sound, thus sonic temperature. The under- or overestimation may be insignificant when temperature is not much above or below the manufacture temperature while the anemometer must work best around the manufacturer temperature. In this study, the working air temperature for the sonic anemometer was as low as −20 ∘C, within which the sonic paths become shorter to some degree so that its measurement performance was possibly impacted. Although an assessment on the measurement performance of sonic anemometer at low or high air temperature could not be found in literature, overestimation of the speed of sound from a sonic anemometer at temperatures dozens of degrees below the manufacture temperature and thus sonic temperature is anticipated as shown in Fig. 7a to c.
However, at different air temperature the performance of the temperature and relative humidity probe and barometer built into the IRGASON, whose measurements are used to calculate the sonic temperature (see Appendix D), more stable than a sonic anemometer while their accuracies are the best at 20 ∘C and become lower with temperature away from 20 ∘C (Vaisala Corp., 2017). For example, HMP155A has an accuracy in air temperature to be ±0.1 ∘C at 20 ∘C and ±0.25 ∘C at −20 ∘C, as well as an accuracy in relative humidity (RH) of RH) % at 20 ∘C and to be RH) % at −20 ∘C. The greater disagreement between recovered and calculated sonic temperature values at lower temperature in Fig. 7a may also be due to the fact that the lower the air temperature, the lower the accuracies of HMP155A and the barometer.
8.4 Radiation on calculated sonic temperature
Compared to the recovered sonic temperature using Eq. (40), the calculated sonic temperature was 0.45±0.24 ∘C higher over a whole period of 12:00 to 12:30 and even 0.65±0.19 ∘C higher over a partial period of 12:15 to 12:27, which may be contributed to in part by higher incoming solar radiation of 750 W m−2 in short-wave on the radiation shield of HMP155A (Fig. 7c). As addressed in Appendix D, the calculated sonic temperature was sourced from the measurements of air temperature and relative humidity from HMP155A, as well as atmospheric pressure from the barometer built into the IRGASON. The HMP155A housed inside a radiation shield (Fig. 2) was subject to contamination from solar radiation. A radiation shield was used to shade HMP155A from sunlight, when such a shield was used, any heat generated from the shield under sunlight and the sensor under electronic power was dissipated inefficiently (Lin et al., 2001). As a result, the air and HMP155A sensing elements inside the shield were warmer than ambient air of interest. How warm the air is inside the radiation shield depended on shield structure, ambient wind speed, and other environmental conditions (Blonquist et al., 2009). In the case of Fig. 7c at 750 W m−2 of incoming short-wave radiation, air being a degree warmer inside the radiation shield was not unusual (Lin et al., 2001). In our study, this higher air temperature could directly cause the overestimation of calculated sonic temperature (Eq. D1 in Appendix D).
8.5 Possibility and necessity of recovering the data from a geometrically deformed sonic anemometer for fluxes
A geometrically deformed sonic anemometer outputs erroneous data. These data may be recoverable or unrecoverable, depending on the degree of deformation. If the degree is too large, the sonic anemometer cannot perform its normal measurements for the transmitting time. In this case, a Campbell sonic anemometer sets high for one to six of its first six measurement warning flags (low amplitude, high amplitude, poor signal lock, large sonic temperature difference, ultrasonic signal loss, and calibration signature error; see Table 10-2 in Campbell Scientific Inc., 2018). The geometrical deformation in sonic paths could trigger one or two flags high that indicate poor signal lock and/or ultrasonic signal loss. Regardless, in the case that any of the six warning flags from a deformed sonic anemometer were frequently, regularly, or continuously high, the erroneous data must not be recoverable (i.e., data recovery is not possible). While all six warning flags are low under normal measurement conditions, the transmitting time of ultrasonic signals along each sonic path is correctly measured and the data should be recoverable. The 3-D wind data can be recovered without uncertainty although there is little uncertainty in sonic temperature (see Eqs. 33 and 40). The subsequent question is the necessity to recover the recoverable data.
A sonic anemometer is used primarily for the fluxes of momentum and heat from the fluctuations in 3-D wind speeds and sonic temperature. If the fluctuations are not significantly influenced by the geometric deformation of the sonic anemometer, the data from this anemometer may not need recovering although the data are recoverable. The fluctuations in a wind speed component or sonic temperature are measured by variance. Therefore, this influence of sonic anemometer deformation on fluctuations in wind speed and sonic temperature can be tested through analyzing the homogeneity in variance of each wind component and sonic temperature between unrecovered and recovered data.
For this study case, the 2-day data, without a missing record or any high warning flag from 10 and 11 May 2015, were used for the analyses. After data recovery processing (Fig. 6), two datasets, unrecovered and recovered, were acquired. In the unrecovered dataset, for each wind speed component or sonic temperature, the data of 18 000 values from each half-hour were used to compute its variance (, given by
where x represents ux, uy, uz, or Ts; subscript j denotes the jth values in kth half-hour interval, and the upper bar indicates the average over the interval. In the recovered dataset, this variance was similarly computed and denoted by , where subscript R indicates that this variance was computed from recovered dataset. For each wind component or sonic temperature, 96 variance values were available in each datasets and 192 variance values were available in both dataset. The 192 variance values for each wind component or sonic temperature can be used to construct an F-statistic (Snedecor and Cochran, 1989) to analyze the homogeneity in variance of each wind component or sonic temperature between unrecovered and recovered data, given by
From this statistic, four F values were acquired for three wind components and sonic temperature. The four F values were either > 1.00 or < 1.00, showing the inhomogeneity in variance between unrecovered and recovered data (P < 0.001), which indicates that the geometrical deformation of the sonic anemometer did significantly influence the fluctuations in each of its measured variables.
Further, using EddyPro (LI-COR Biosciences, 2016), the same datasets were used to compute two sets of sensible heat flux, latent heat flux, and CO2 flux for each half-hour interval. One set was computed using unrecovered data and the other set from recovered data. The two sets of flux data were shown in Fig. 8. Compared to the flux from unrecovered data, the flux from recovered data was 1.5 W m−2 lower for sensible heat (P=0.031), 0.14 W m−2 higher for latent heat (P=0.001), and 0.08 µmol m−2 s−1 higher for CO2 (P=0.000). These values were small in magnitude, but significant in comparison to these flux values over the ice surface in Antarctica.
Analyses of the F tests and Fig. 8 show that the data measured from a geometrically deformed sonic anemometer need to be recovered; otherwise, there were significant uncertainties in the wind speed and sonic temperature fluctuations for flux estimations.
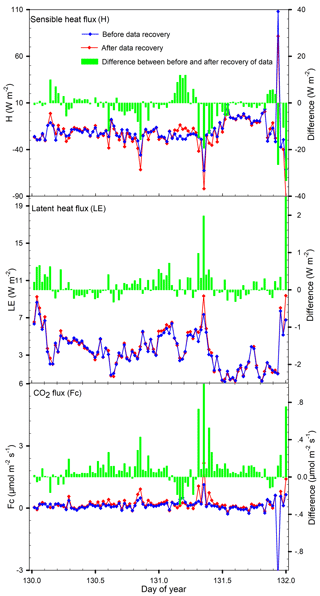
Figure 8Comparison of sensible heat flux, latent heat flux, and CO2 flux from recovered data (red curves) to those from unrecovered data (blue curves). The mean difference (the green bar represents the red curve minus blue curve value) is −1.5 W m−2 < 0 (P=0.031) for sensible heat flux, 0.14 W m−2 > 0 (P=0.001) for latent heat flux, and 0.08 µmol m−2 s−1 > 0 (P=0.000) for CO2 flux.
8.6 Applicability of equations and algorithms in this study
Any sonic anemometer is slender (e.g., < 1.00 cm in each diameter of six claws to hold individual sonic transducers) and as light as possible to minimize its aerodynamic resistance to air flows and to maximize its stability on supporting infrastructure (e.g., tripod) to wind momentum load, which sacrifices its durability in keeping its geometrical shape. Therefore, a sonic anemometer is easily deformed if not well cared for during transportation (e.g., the case in this study), installation, or other handling. As shown in this study, a slight geometrical deformation of sonic path length as small as millimeters or less (see Table A1 in Appendix A) could cause significant errors in 3-D wind and especially in sonic temperature. According to our recalibration experience with 3-D sonic anemometers at Campbell Scientific Inc., these cases as addressed in this study have been not unusual, but the equations and algorithms to recover the data measured by a deformed 3-D sonic anemometer were not available. As requisitions of these datasets are expensive, their recovery would be a cost-effective and time-saving option.
The equations and algorithms in this study were developed based on the measurement working physics and sonic path geometry of the IRGASON sonic anemometer. The physics is the same as those for other models of Campbell Scientific 3-D sonic anemometers in use, such as CSAT3, CSAT3A, and CSAT3B (Campbell Scientific Inc., UT, USA; Horst et al., 2015). However, the sonic path geometry of the IRGASON sonic anemometer is different from other models in the assigned azimuth angle of the first sonic path in the 3-D anemometer coordinate system. This angle was assigned as 90∘ in the IRGASON sonic anemometer, but as 0∘ in other models (e.g., CSAT3, CSAT3A, and CSAT3B). Even so, given the sonic path lengths and transfer matrixes of sonic anemometer that were measured and determined in the manufacture or calibration process (di in Eq. 12 and A in Eq. 15) and in the recalibration process after use in the geometrical deformation state (dTi in Eqs. 13, 33, and 40 and AT in Eqs. 14 and 16), the equations and algorithms from this study are applicable to all models of Campbell Scientific 3-D sonic anemometers (Fig. 6) except for CSAT3 if its bugged OS version 4 is used (Burns et al., 2012). The derivation procedures and even equations based on the measurement working physics are applicable as a reference to the development of the equations and algorithms to recover the data measured using other brands of 3-D sonic anemometers that incurred deformations or to studies on similar topics.
An IRGASON 3-D sonic anemometer (SN: 1131) was geometrically deformed by an impact during transportation to Antarctica from China in early 2015. To fulfill the field measurement plans for the year, it had to be deployed there in the Zhongshan Station until early 2016 when it was replaced in the field with another IRGASON provided by the manufacturer and was returned to the manufacturer, Campbell Scientific Inc., for recalibration through the remeasurement of its sonic path geometry (lengths and angles), redetermination of its transfer matrix, and an update of its operating system (OS). To recover the 3-D wind and sonic temperature data measured by this sonic anemometer in its deformed state before the recalibration, equations and algorithms were developed and implemented into a software package: “Sonic Data Recovery for IRGASON/CSAT3/A/B Used in Geometrical Deformation after Production/Calibration” (Fig. 6 and Appendix C). Given two sets of sonic path lengths and two transfer matrixes of sonic anemometer that were measured and determined in the manufacture and calibration process and also in recalibration process after the use in its deformed state, the data measured by the IRGASON 3-D sonic anemometer, even in its deformed state, were recovered as if measured by the same anemometer recalibrated immediately after its deformation.
Inside a Campbell Scientific sonic anemometer, the transducer-shadow correction for 3-D wind (Wyngaard and Zhang, 1985) is an available, programmable option for a user. However, the crosswind correction for sonic temperature (Liu et al., 2001) is internally applied as default by its OS. In a case of transducer-shadow correction in option, the 3-D wind data are recovered using Eqs. (10) to (16). If not, Eqs. (15), (12), (13), and (16) are sequentially used. Based on the data from the recovery process of 3-D wind, the sonic temperature data are recovered using Eqs. (9), (32), (38), and (40); therefore, the satisfactory recovery for both 3-D wind data and sonic temperature can be eventually reflected by the satisfactory of sonic temperature data recovery.
The software based on the equations and algorithms from this study can recover the 3-D wind data with or without the transducer-shadow correction inside the sonic anemometer and sonic temperature data with crosswind correction also inside the sonic anemometer. It was verified by comparing the recovered to calculated sonic temperature data (Appendix D). As shown in Fig. 7, the recovered data of sonic temperature using Eqs. (33) and (40) were compared to the calculated sonic temperature of three representative values over the range of measured sonic temperature from −20.01 to −1.90 ∘C. The difference of 9.60 to 8.93 K between unrecovered and calculated sonic temperature (i.e., unrecovered minus calculated) was narrowed by Eq. (40) to 0.81 to −0.45 K (i.e., recovered minus calculated), which was satisfactory for measurements of sonic anemometer below 0 to −20 ∘C. After verification, the software was used to recover the data measured by the IRGSON (SN: 1131) 3-D sonic anemometer in its deformed state from May 2015 to January 2016. The 8-month data were recovered using 3 days of one engineer's time. Further, using EddyPro 6.2.0 (LI-COR Inc., 2016), the recovered data were processed for the fluxes of CO2/H2O, sensible heat, and momentum. The data quality (Foken et al., 2012) mostly ranged in 1 to 3 and the energy closure without considering surface heat flux into ice were > 83 % when friction velocity was > 0.2 m s−1. Although energy balance closure is not a good indicator for data quality (Foken et al., 2012), this closure rate is fair.
The use of a deformed 3-D sonic anemometer is a practical case. The analyses of our study case indicated that the measured fluctuations in wind speeds and sonic temperature as well as fluxes were significantly influenced by the deformation. If the data from such a use cannot be recovered, the requisition of these data is expensive and their recovery would be a cost-effective and time-saving option. The equations, algorithms, and software are applicable to all models of Campbell Scientific 3-D sonic anemometers such as CSAT3, CSAT3A, and CSAT3B that are used around the world. The derivation procedures and even equations based on the measurement working physics of sonic anemometers are applicable as a reference to the development of the equations and algorithms to manage the data measured using other brands of 3-D sonic anemometers or recover the data measured by an anemometer in its deformed state.
The data in this paper can be accessed via connecting the Supplement.
In micrometeorological applications, the wind speeds are expressed in a three-dimensional (3-D) orthogonal coordinate system of anemometer or natural wind, but a sonic anemometer measures flow velocities along its three non-orthogonal sonic paths (i.e., situated non-orthogonally from each other, see Figs. 1 and A1); therefore, for applications, the flow velocities along the three sonic paths need to be transformed into a 3-D right-handed orthogonal coordinate system in reference to the geometry of sonic anemometer, as shown in Fig. A1 (i.e., the 3-D orthogonal anemometer coordinate system). Given ux and uy are two horizontal velocities in the x and y direction, respectively, and uz is vertical velocity in the z direction (Fig. A1); x, y, and z are the three coordinate axes in the 3-D orthogonal anemometer coordinate system. This system is defined with the x–y plane, parallel to the anemometer bubble-leveled plane, with the first sonic path on the y–z plane, and with origin in the center of measurement volume. A flow speed along the ith (, or 3) sonic path is a combination of component velocities of ux, uy, and uz; given by
where θi and ϕi are the zenith and azimuth angles of the ith sonic path in the 3-D orthogonal anemometer coordinate system. In this system (see Fig. A1), given the first sonic path has an azimuth angle of ϕ1 equal to 90∘ as fixed on the x−y plane, Eq. (A1) can be expressed in a matrix form of
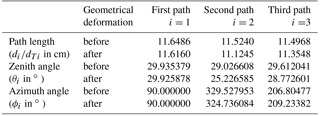
where A is a matrix expressing the flow speeds along the three non-orthogonal sonic paths in the 3-D orthogonal anemometer coordinate system. Nominally for the sonic paths of the IRGASON, θ1, θ2, and θ3 are all 30∘ and ϕ2 and ϕ3 are 330 and 210∘, respectively (see Fig. A1). Given ϕ1=90∘, these angles are calculated using measured data from a coordinate measurement machine and, along with the sonic path lengths, are listed in Table A1 for the IRGASON serial no. of 1131 before and after its geometrical deformation.
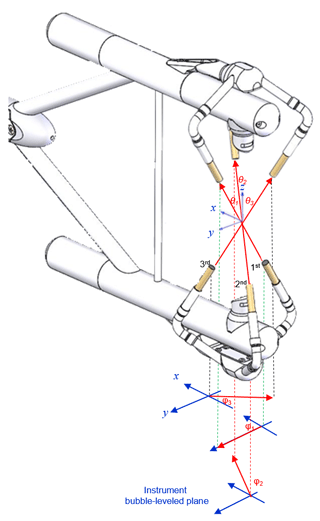
Figure A1IRGASON sonic path angle geometry in the three-dimensional right-handed anemometer coordinate system of x, y, and z. Blue arrows are coordinates; a red arrow between a pair of sonic transducers is the sonic path vector whose direction is defined for air flow direction, the red arrow below the IRGASON is the projection of the corresponding sonic path vector on the x–y plane, i.e., anemometer (instrument) bubble-leveled plane. As indicated by their subscript of 1, 2, or 3 for the first, second, or third sonic path, θ1, θ2, and θ3 are their zenith angles and φ1, φ2, and φ3 are their azimuth angles.
Table A1The lengths, zenith angles, and azimuth angles of sonic paths in the IRGASON (serial no.: 1131) anemometer coordinate system before and after its geometrical deformation (measured using a coordinate measurement machine on 9 September 2014 before the deformation and on 6 March 2016 after deformation).
Using the data in this table, matrix A in Eq. (A2) and its inversion A−1 for this IRGASON before its geometric deformation (i.e., as used in the IRGASON OS but not valid in the field after deformation) are given as follows:
and
After the IRGASON geometrical deformation, matrix A became
where subscript T indicates “True” because, after the IRGASON deformation, it should be used in the field although it was not used. The inversion of this matrix is given as follows:
Matrixes A−1, AT, and were used for our data recovery and A was also used in the sonic anemometer OS.
Given transform matrix A, using Eq. (5), the measured wind vector [u1 u2 u3]′ along the sonic paths is transformed to the wind vector in the 3-dimensional orthogonal anemometer coordinate system [ux uy uz]′. Subsequently, UT is calculated using Eq. (9). Replace uTi with ui under the square root in the right side of Eq. (8), an approximate equation for the first iteration is given as follows:
where i is 1, 2, or 3 and subscript 1 of uTi indicates that it is calculated from the first iteration.
First iteration
Equation (B1) is used for sonic transducer-shadow corrections in the first iteration.
Second iteration
Using Eq. (9), UT is recalculated. Replace ui with uTi_1 under the square root in the right side of Eq. (B1), an approximate equation for the second iteration is given as follows:
Third iteration
…
nth iteration
where subscript . Using Eq. (9), UT is also recalculated. Similar to the calculation for uTi_2, uTi_n is calculated using the following equation:
to ensure that the difference in ux, uy, or uz between the last and previous iterations is <1 mm s, where σ is the maximum precision (i.e., standard deviation at constant wind) among ux, uy, and uz (Campbell Scientific Inc., 2018). Our numerical tests within the measurement ranges in ux, uy, and uz concluded that the iterations mostly converged at n=2 and entirely at n≤3.
Sonic data recovery for the IRGASON/CSAT3/A/B used in geometrical deformation after production/calibration (Code lines were formatted for readability and the electronic version of this code is available from the corresponding authors).
Note: This code can be compiled in MATLAB as an executable file: Data_recovery.exe.
% sonicdatarecovery Sonic Data Recovery for IRGASON/CSAT3/A/B Used in Geometrical Deformation after Production/Calibration
%Syntax:
function [Ux,Uy,Uz,Ts,Ts1,Ts2,Raw] =
sonicdatarecovery(RAW)
% Inputs:
% um Measured 3-D wind speeds in the orthogonal anemometer coordinate system (OCS)
% Ts Measured sonic temperature
% A Matrix of sonic to OCS before geometrical deformation
% AT Matrix of sonic to OCS after geometrical deformation
% di Sonic path length before geometrical deformation (i=1, 2, or 3)
% dTi Sonic path length after geometrical deformation (i=1, 2, or 3)
% Constants
shadow_correction_flag =1; % %Shadow correction has been done (=1) or not (=0) inside OS
gama_d=1.4003; %% the ratio of dry air specific heat at constant pressure to that at constant volume
Rd =287.04; %% gas constant for dry air
RV ; %% gas constant for water vapor
Av =60.064621; Bv =60.973392; Cv =60.387959;
Ah =0.000000; Bh =59.527953; Ch =63.195226;
Avt =60.074122; Bvt =64.773415; Cvt =61.227399;
Aht =0.000000; Bht =54.736084; Cht =60.766176;
% Browse to the raw data file directory to load files in a batch
hwait = waitbar(0,“Please select the file to be processed”);
pause(0.5)
[name,path] = uigetfile(“*.*”,“stabilitylect a folder”);
fname = [path name];
close(hwait);
RAW = dlmread(fname,',', 4, 1);
% Extract sonic anemometer and other meteorological data
UX = RAW(:,2); UY = RAW(:,3); UZ = RAW(:,4);
TRAW = RAW(:,5); H2O = RAW(:,8);
Temp = RAW(:,10); P = RAW(:,11);
amb_e = RV.*H2O.*(Temp +273.15);
TS_emp = (Temp +273.15).*(1+0.32*amb_e./P)−273.15;
% Load transform matrix of Eq. (A2) and data of Table A1 before geometrical deformation
The1 = ((90-Av)/180)*pi; The2 = ((90-Bv)/180)*pi;
The3 = ((90-Cv)/180)*pi;
Phi1 = ((90-Ah)/180)*pi; Phi2 = ((270+Bh)/180)*pi;
Phi3 = ((270-Ch)/180)*pi;
A_inversion = [0 sin(The1) cos(The1);
sin(The2)*cos(Phi2)
sin(The2)*sin(Phi2) cos(The2);
sin(The3)*cos(Phi3) sin(The3)*sin(Phi3) cos(The3)];
A=A_inversion(−1); ;
% Load transform matrix of Eq. (A5) and data of Table A1 after geometrical deformation
The1 = ((90-Avt)/180)*pi; The2 = ((90-Bvt)/180)*pi;
The3 = ((90-Cvt)/180)*pi;
Phi1 = ((90-Aht)/180)*pi; Phi2 = ((270+Bht)/180)*pi;
Phi3 = ((270-Cht)/180)*pi;
AT_inversion = [0 sin(The1) cos(The1);
sin(The2)*cos(Phi2)
sin(The2)*sin(Phi2) cos(The2);
sin(The3)*cos(Phi3) sin(The3)*sin(Phi3)
cos(The3)];
AT = AT_inversion∧(-1);
dT =[11.6159;11.1245;11.3548];
% Prompt data processing is in progress
hwait = waitbar(0,“Processing> > > > > > ”)
%Recover 3-D wind data
%Get measured flow speeds along each of 3 sonic paths
[mRaw,nRaw] = size(RAW);
for i=1:mRaw;
um = [UX(i);UY(i);UZ(i)];
%With transducer-shadow corrections (TSC):
UT = (um(1)2+um(2)∧2+um(3)∧2); %% Calculate the total wind magnitude
if isequal(shadow_correction_flag, 1) %% TSC has been done (=1) inside firmware
u= A_inversion*um; %% Calculate the vector of the three flow speeds using Eq. (10)
ut1(1) =u (1)/(0.84+0.16.*((UT∧2-u
(1)∧2))./UT);
%% Eq. (11), recover flow speed along
sonic path 1 before TSC
ut2(1) =u (2)/(0.84+0.16.*((UT∧2-u
(2)∧2))./UT);
%% Eq. (11), recover flow speed along
sonic path 2 before TSC
ut3(1) =u (3)/(0.84+0.16.*((UT∧2-u
(3)∧2))./UT);
%% Eq. (11), recover flow speed along
sonic path 3 before TSC
uc = [ut1.*(dT (1)./d(1));ut2.*(dT(2)./d(2));ut3.
*(dT(3)./d(3))]; %%
Eq. (13)
uts1 = ut1; uts2 = ut2; uts3 = ut3;
%%Corrected 3-D wind speed
um_c=AT*uc; %% Eq. (16)
%Iteration algorithm of sonic TSC (Appendix B) for recovered data
UT_C=(um_c (1)∧ 2+um_c ()∧2+um_c (3)∧2)∧(1/2); %% Total wind magnitude
% 1st iteration
uct1 = uc (1)/(0.84+0.16.*((UT∧2-uc (1)∧
2)∧(1/2))./UT); % %flow speed 1
uct2 = uc (2)/(0.84+0.16.*((UT∧2-uc (2)∧
2)∧(1/2))./UT); % %flow speed 2
uct3 = uc (3)/(0.84+0.16.*((UT∧2-uc (3)∧
2)∧(1/2))./UT); % %flow speed 3
% 2nd iteration
for q = 2:5; %% 5 steps of iterations after 1st iteration are adequate
%TSC for flow speed 3
uct_m = [uct1(q-1);uct2(q-1);uct3(q-1)]; %% Vector of three path flow speeds
um_C = AT*uct_m; %%Vector in 3-D orthogonal system
UT_C = (um_C (1)∧
2+um_C (2)∧2+um_C
(3)∧2)∧(1/2);
%% Total wind magnitude,
again
uct3(q) = uc (3)/(0.84+0.16.*((UT_C∧2-uct3
(q-1)∧2)∧(1/2))./UT_C);
%% TSC for flow speed 3
% TSC for flow speed 2
uct_mm = [uct1(q-1);uct2(q-1);uct3(q)];
%%Vector of
three flow speeds, again
um_C = AT*uct_mm; %% Vector in 3-D orthogonal system, again
UT_C = (um_C (1)∧
2+um_C (2)∧2+um_C
(3)∧2)∧(1/2); %% Recalculated the
total wind magnitude
uct2(q) = uc (2)/(0.84+0.16.*((UT_C∧2-uct2
(q-1)∧2)∧(1/2))./UT_C);
%%% TSC for flow speed 2
%TSC for flow speed 1
uct_mm = [uct1(q-1);uct2(q);uct3(q)]; %%Vector of three flow speeds, again
um_C = AT*uct_mm; %% Vector in 3-D orthogonal system
UT_C = (um_C (1)∧
2+um_C (2)∧2+um_C
(3)∧2)∧(1/2); %% Total wind magnitude,
again
uct1(q) = u (1)/(0.84+0.16.*((UT_C∧2-uct1
(q-1)∧2)∧(1/2))./UT_C);
%%%TSC for flow speed 1
% Judge the steps of iterations
uct_n = [uct1(q);uct2(q);uct3(q)]; %%Vector from current iteration
ABS_C = uct_n-uct_m; %%Difference between two iterations
% Exit condition
if(abs(ABS_C(1))<
= 0.001&&abs(ABS_C(2))<
= 0.001&&abs(ABS_C(3))< = 0.001);
%Finalize recovered 3-D wind speed
ucm = AT*uct_n; %% Eq. (14)
ucts1 = uct1(q); ucts2 = uct2(q); ucts3 = uct3(q);
break; %% %Exit iterations
end
end
else
%Recover 3-D wind data without TSC
u = A_inversion*um; %% Acquire the flow speeds along 3 sonic paths, Eq. (10)
uc = [dT(1)./d(1).*u(1); dT(2)./d(2).*u(2);
dT(3)./d(3).*u(3)];
%%Correction
ucm = AT*uc; %%3-D orthogonal data after recovery
uts1 = uc(1); uts2 = uc(2); uts3 = uc(3);
ucts1 = ucm(1); ucts2 = ucm(2); ucts3 = ucm(3);
end
%Recover sonic temperature data
Ts = TRAW(i);
UcT = (ucm (1)∧2 + ucm (2)∧2 + ucm (3)∧2)∧(1/2); %% Total wind
C02 = gama_d*Rd*(Ts + 273.15); %% Eq. (32)
DELTUcT2 = UcT∧2 – UT∧2;
DELTucT21 = ucts1∧2 – uts1∧2; DELTucT22 = ucts2∧2 – uts2∧2; DELTucT23 = ucts3∧2 – uts3∧2;
DELTC21 = (C02 - UT∧2 + uts1∧
2)*((dT(1)∧2 –
d(1)∧2)/d(1)∧
2); %% Eq. (30)
DELTC22 = (C02 - UT∧2 + uts2∧
2)*((dT(2)∧2 –
d(2)∧2)/d(2)∧
2); %% Eq. (30)
DELTC23 = (C02 – UT∧2 + uts3∧
2)*((dT(3)∧2 –
d(3)∧2)/d(3)∧
2); %% Eq. (30)
AAA = (DELTC21 + DELTUcT2 – DELTucT21);
BBB = (DELTC22 + DELTUcT2 – DELTucT22);
CCC = (DELTC23 + DELTUcT2 – DELTucT23);
DDD = (AAA + BBB + CCC);
EEE = 3*gama_d*Rd;
Tcs = Ts+(DDD/EEE); %% Eq. (33)
DELTC021_ad = C02*2*(1-dT(1)/d(1)); %% Eq. (38)
DELTC022_ad = C02*2*(1-dT(2)/d(2)); %% Eq. (38)
DELTC023_ad = C02*2*(1-dT(3)/d(3)); %% Eq. (38)
AAA_ad = ((dT(1)∧2-d(1)∧
2)/d(1)∧2)*(C02-
(DELTC021_
ad+((DELTC021_ad+DELTC022_
ad+
DELTC023_ad)/3))-UT∧
2+uts1∧2)
+DELTUcT2-DELTucT21;
BBB_ad = ((dT(2)∧2-d(2)∧
2)/d(2)∧2)
*(C02-(DELTC022_ad+((DELTC021_ad+DELTC022_ad
+DELTC023_ad)/3))-UT∧
2+uts2∧2)
+DELTUcT2-DELTucT22;
CCC_ad = ((dT(3)∧2-d(3)∧
2)/d(3)∧2)
*(C02-(DELTC023_ad+((DELTC021_ad+DELTC022_ad
+DELTC023_ad)/3))-UT∧
2+uts3∧2)
+DELTUcT2-DELTucT23;
DDD_ad = (AAA_ad + BBB_ad + CCC_ad);
Tcs_ad = Ts+(DDD_ad/EEE); %% Eq. (40)
Data_recovery(i,1) = ucm(1); %%Recovered 3-D wind speed in x-direction
Data_recovery(i,2) = ucm(2); %% Recovered 3-D wind speed in y-direction
Data_recovery(i,3) = ucm(3); %% Recovered 3-D wind speed in z-direction
Data_recovery(i,4) = Tcs; %% Recovered Ts from raw Ts, Eq. (33)
Data_recovery (i,5) = Tcs_ad; %% Recovered Ts from raw Ts, Eq. (40)
Data_recovery (i,6) = TS_emp(i); %% Recovered T, Eq. (D1)
Data_recovery (i,7) = TRAW(i); %% Raw Ts
End
% Output the final processing result in excel format
title = {“Recovered ux”,“Recovered uy”,“Recovered uz”,“Recovered Tcs”,“Recovered Tcs_ad”,“Recovered T”,“RAW TS”};
fname = [path “\ Data_recovery”];
xlswrite(fname,title,“sheet1”);
xlswrite(fname,Data_recovery,“sheet1”,“A2”);
waitbar(0,hwait,`Done”);
pause(2);
close(hwait);
In case that air temperature (T in ∘C), relative humidity (RH in percentage), and atmospheric pressure (P in kPa) are measured in the field, sonic temperature (Ts in ∘C) can be calculated using the well-known equation (Kaimal and Gaynor, 1991):
where e is air water vapor pressure (kPa) and can be computed from T, RH, and P.
Given T and P, saturated water vapor pressure (es in kPa) can be calculated using Buck (1981):
where fw(T, P) is the enhancement factor:
Using the definition of air relative humidity, air water vapor pressure is given by
Submit the measured T and P as well as the calculated e into Eq. (D1) and the sonic temperature can be calculated.
The supplement related to this article is available online at: https://doi.org/10.5194/amt-11-5981-2018-supplement.
QY, NZ, and XiaZ proposed this study and coordinated and led the teamwork. They also developed equations and algorithms, analyzed data and results, and finalized the manuscript. YL and TG reviewed the manuscript, provided constructive comments, and helped finalize the manuscript. GH, HS, and YS collected and analyzed data. XinZ integrated research results for publication.
The authors declare that they have no conflict of interest.
This study was supported by the National Key R&D Program of China (grant no.: 2016YFA0600704), and the National Natural Science Foundation of China
(grant nos.: 41376005, 41406218, 41505004, and 31200432). We thank the
Chinese Arctic and Antarctic Administration and the Polar Research Institute
of China for their field logistical support; Campbell Scientific and Beijing
Techno Solutions Limited for their customer support; Steve Harston and
Antoine Rousseau for technical graphic work; Carolyn Ivans, Bo Zhou, Mark Blonquist, and Hayden Mahan for their English polishing; and
Linda Worlton-Jones for her professional English checks and revisions. We greatly
thank Thomas Foken and the anonymous reviewer for their comments and
input that improved our presentation and interpretations in this
paper.
Edited by: Laura Bianco
Reviewed by: Thomas Foken and one anonymous referee
Barrett, E. W. and Suomi V. E.: Preliminary report on temperature measurement by sonic means, J. Atmos. Sci., 6, 273–276, https://doi.org/10.1175/1520-0469(1949)006<0273:PROTMB>2.0.CO;2, 1949.
Blonquist, J. M. J., Norman, J. M., and Bugbee, B.: Automated measurement of canopy stomatal conductance based on infrared temperature, Agr. Forest Meteorol., 149, 2183–2197, https://doi.org/10.1016/j.agrformet.2009.06.021, 2009.
Buck, A. L.: New equations for computing vapor pressure and enhancement factor, J. Appl. Meteorol., 20, 1527–1532, https://doi.org/10.1175/1520-0450(1981)020<1527:NEFCVP>2.0.CO;2, 1981.
Burns, S. P., Horst, T. W., Jacobsen, L., Blanken, P. D., and Monson, R. K.: Using sonic anemometer temperature to measure sensible heat flux in strong winds, Atmos. Meas. Tech., 5, 2095–2111, https://doi.org/10.5194/amt-5-2095-2012, 2012.
Campbell Scientific Inc.: EasyFlux DL CR3000OP for CR3000 and Open-Path eddy-Covariance System, Instruction Manual, 140 pp., Logan, UT, 2016.
Campbell Scientific Inc.: IRGASON Integrated CO2/H2O Open-Path Gas Analyzer and 3-D Sonic Anemometer, Instruction Manual, 63 pp., Logan, UT, 2018.
Foken, T.: Micrometeorology, 2nd ed., Springer, Berlin, Heidelberg, 362 pp., 2017.
Foken, T., Leuning, R., Onley, S.R., Mauder, M., and Aubinet, M.: Corrections and data quality control, in: Eddy Covariance: A Practice Guide to Measurement and Data Analysis, edited by: Aubient, M., Vesala, T., and Papale, D., 85–131, Springer, New York, NY., https://doi.org/10.1007/978-94-007-2351-1_4, 2012.
Hanafusa, T., Fujitana, T., Kobori, Y., and Mitsuta, Y.: A new type sonic anemometer-thermometer for eld operation, Meteorol. Geophys., 33, 1–19, https://doi.org/10.2467/mripapers.33.1, 1982.
Horst, T. W., Semmer, S. R., and Maclean, G.: Correction of a Non-orthogonal, Three-Component Sonic Anemometer for Flow Distortion by Transducer Shadowing, Bound.-Lay. Meteorol., 155, 371–395, https://doi.org/10.1007/s10546-015-0010-3, 2015.
Kaimal, J. C. and Finnigan, J. J.: Atmospheric Boundary Layer Flows: Their Structure and Measurements, 289 pp., Oxford University Press, New York, NY, 1994.
Kaimal, J. C. and Gaynor, J. E.: Another look at sonic thermometry, Bound.-Lay. Meteorol., 56, 401–410, https://doi.org/10.1007/BF00119215, 1991.
LI-COR Biosciences: EddyPro: Eddy Covariance Software, Instruction Manual, V6.2.0., 263–265, Lincoln, NE, 2016.
Lin, X., Hubbard, K. G., Walter-Shea, E. A., Brandle, J. R., and Meyer, G. E.: Some perspectives on recent in-situ air temperature observations: Modeling the microclimate inside the radiation shields, J. Atmos. Ocean. Tech., 18, 1470–1484, https://doi.org/10.1175/1520-0426(2001)018<1470:SPORIS>2.0.CO;2, 2001
Liu, C., Li, Y., Yang, Q., Wang, L., Wang, X., Li, S., and Gao, Z.: On the surface fluxes characteristics and roughness lengths at Zhongshan station, Antarctica, Int. J. Digit. Earth., 10, 1–15, https://doi.org/10.1080/17538947.2017.1335804, 2017.
Liu, H., Peter, G., and Foken, T.: New equations for sonic temperature variance and buoyancy heat flux with an omnidirectional sonic anemometer, Bound.-Lay. Meteorol., 100, 459–468, https://doi.org/10.1023/A:1019207031397, 2001.
Schotanus, P., Nieuwstadt, F. T. M., and de Bruin H. A. R.: Temperature measurement with a sonic anemometer and its application to heat and moisture fluxes, Bound.-Lay. Meteorol., 26, 81–93, https://doi.org/10.1007/BF00164332, 1983.
Schotland, R. M.: The measurement of wind velocity by sonic means, J. Atmos. Sci., 12, 386–390, https://doi.org/10.1175/1520-0469(1955)012<0386:TMOWVB>2.0.CO;2, 1955.
Snedecor, G. W. and Cochran, W. G.: Statistical Methods, 8th ed., Iowa State University Press, Ames, 502 pp., 1989.
Valkonen, E., Venäläinen, E., Rossow, L., and Valaja, J.: Effects of Dietary Energy Content on the Performance of Laying Hens in Furnished and Conventional Cages, Poultry Sci., 87, 844–852, https://doi.org/10.3382/ps.2007-00237, 2008.
Vaisala Corp.: HUMICAP® Humidity and Temperature Probe HMP155, Helsinki, Finland, 2 pp., 2017.
Vihma, T., Johansson, M. M., and Launiainen, J.: Radiative and turbulent surface heat fluxes over sea ice in the western Weddell Sea in early summer, J. Geophys. Res.-Oceans, 114, C04019, https://doi.org/10.1029/2008JC004995, 2009.
van Dijk, A.: Extension to 3-D of “The effect of line averaging on scalar flux measurements with a sonic anemometer near the surface” by Kristensen and Fizjarrald, J. Atmos. Ocean. Tech., 19, 80–82, https://doi.org/10.1175/1520-0426(2002)019<0080:ETOTEO>2.0.CO;2, 2002.
Wyngaard, J. C. and Zhang S.-F.: Transducer-shadow effects on turbulence spectra measured by sonic anemometers, J. Atmos. Ocean. Tech., 2, 548–558, https://doi.org/10.1175/1520-0426(1985)002<0548:TSEOTS>2.0.CO;2, 1985.
Yang, Q., Liu, J., Lepparanta, M., Sun, Q., Li, R., Zhang, L., Jung, T., Lei, R., Zhanhai, Z., Li, M., Zhao, J., and Cheng, J.: Albedo of coastal landfast sea ice in the Prydz Bay, Antarctica: Observations and parameterization, Adv. Atmos. Sci., 33, 535–543, https://doi.org/10.1007/s00376-015-5114-7, 2016.
Yu, L., Yang, Q., Zhou, M., Lenschow, D. H., Wang, X., Zhao, J., Sun, S., Tian, Z., Shen, H., and Zhang, L.: The variability of surface radiation fluxes over landfast sea ice near Zhongshan station, East Antarctica during austral spring, Int. J. Digit. Earth., 11, 1–18, https://doi.org/10.1080/17538947.2017.1304458, 2017.
Zhao, J., Cheng, B., Yang, Q., Vihma, T., and Zhang, L.: Observations and modelling of first-year ice growth and simultaneous second-year ice ablations in the Prydy Bay, East Antarctica, Ann. Glaciol., 58, 59–67, https://doi.org/10.1017/aog.2017.33, 2017.
- Abstract
- Introduction
- Site, instrumentation, and data
- Data check and instrument diagnosis
- Algorithm to recover the data of 3-D wind and sonic temperature
- Application
- Verification
- Adjustment
- Discussion
- Conclusion remarks
- Data availability
- Appendix A: Transform matrixes
- Appendix B: Iteration algorithm for sonic transducer-shadow corrections
- Appendix C: MATLAB code
- Appendix D: Sonic temperature from air temperature, relative humidity, and atmospheric pressure
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement
- Abstract
- Introduction
- Site, instrumentation, and data
- Data check and instrument diagnosis
- Algorithm to recover the data of 3-D wind and sonic temperature
- Application
- Verification
- Adjustment
- Discussion
- Conclusion remarks
- Data availability
- Appendix A: Transform matrixes
- Appendix B: Iteration algorithm for sonic transducer-shadow corrections
- Appendix C: MATLAB code
- Appendix D: Sonic temperature from air temperature, relative humidity, and atmospheric pressure
- Author contributions
- Competing interests
- Acknowledgements
- References
- Supplement