the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Observation of turbulent dispersion of artificially released SO2 puffs with UV cameras
Anna Solvejg Dinger
Kerstin Stebel
Massimo Cassiani
Hamidreza Ardeshiri
Cirilo Bernardo
Arve Kylling
Soon-Young Park
Ignacio Pisso
Norbert Schmidbauer
Jan Wasseng
Andreas Stohl
In atmospheric tracer experiments, a substance is released into the turbulent atmospheric flow to study the dispersion parameters of the atmosphere. That can be done by observing the substance's concentration distribution downwind of the source. Past experiments have suffered from the fact that observations were only made at a few discrete locations and/or at low time resolution. The Comtessa project (Camera Observation and Modelling of 4-D Tracer Dispersion in the Atmosphere) is the first attempt at using ultraviolet (UV) camera observations to sample the three-dimensional (3-D) concentration distribution in the atmospheric boundary layer at high spatial and temporal resolution. For this, during a three-week campaign in Norway in July 2017, sulfur dioxide (SO2), a nearly passive tracer, was artificially released in continuous plumes and nearly instantaneous puffs from a 9 m high tower. Column-integrated SO2 concentrations were observed with six UV SO2 cameras with sampling rates of several hertz and a spatial resolution of a few centimetres. The atmospheric flow was characterised by eddy covariance measurements of heat and momentum fluxes at the release mast and two additional towers. By measuring simultaneously with six UV cameras positioned in a half circle around the release point, we could collect a data set of spatially and temporally resolved tracer column densities from six different directions, allowing a tomographic reconstruction of the 3-D concentration field. However, due to unfavourable cloudy conditions on all measurement days and their restrictive effect on the SO2 camera technique, the presented data set is limited to case studies. In this paper, we present a feasibility study demonstrating that the turbulent dispersion parameters can be retrieved from images of artificially released puffs, although the presented data set does not allow for an in-depth analysis of the obtained parameters. The 3-D trajectories of the centre of mass of the puffs were reconstructed enabling both a direct determination of the centre of mass meandering and a scaling of the image pixel dimension to the position of the puff. The latter made it possible to retrieve the temporal evolution of the puff spread projected to the image plane. The puff spread is a direct measure of the relative dispersion process. Combining meandering and relative dispersion, the absolute dispersion could be retrieved. The turbulent dispersion in the vertical is then used to estimate the effective source size, source timescale and the Lagrangian integral time. In principle, the Richardson–Obukhov constant of relative dispersion in the inertial subrange could be also obtained, but the observation time was not sufficiently long in comparison to the source timescale to allow an observation of this dispersion range. While the feasibility of the methodology to measure turbulent dispersion could be demonstrated, a larger data set with a larger number of cloud-free puff releases and longer observation times of each puff will be recorded in future studies to give a solid estimate for the turbulent dispersion under a variety of stability conditions.
A substance (a “passive scalar”) injected into a turbulent atmospheric flow exhibits complex dynamical behaviour. Its distribution is stochastic, and the probability density function (PDF) of the scalar concentration field exhibits the signature of large fluctuations, which can depart substantially from Gaussian behaviour (Shraiman and Siggia, 2000). This behaviour can be difficult to capture with models. The direct numerical simulation of turbulence (Orszag and Patterson, 1972) is not feasible at Reynolds numbers typical for the atmospheric boundary layer (ABL). Although some Eulerian turbulence properties seem to converge also at relatively low Reynolds number (Dimotakis, 2000; van Heerwaarden and Mellado, 2016), the Lagrangian dispersion statistics in general, and the relative dispersion in particular, require a high Reynolds number to converge and this poses challenges to both DNS and laboratory observations (Ouellette et al., 2006; Yeung, 2002; Yeung et al., 2006). Other models used for tracer dispersion (e.g. Large Eddy Simulation or Lagrangian particle models) require parameterizations and/or validation based on atmospheric observations (Arya, 1999; Hanna, 1984).
Atmospheric tracer experiments are needed for constraining dispersion parameters. The first plume characterization experiments in the early 20th century were based on photographs of smoke clouds (Nappo, 1981; Roberts, 1923). More recent experiments released gaseous tracers such as sulfur dioxide (SO2), sulfur hexafluoride or perfluorocarbons at one point and sampled concentrations in a network of ground stations (and sometimes by aircraft) downwind. The experiments carried out from the late 1950s to the early 1970s were the basis for many tools used in dispersion modelling (Gifford, 1961; Pasquill, 1961). As described in Hanna (2010), the Prairie Grass experiment (Barad, 1958), where near source (<1 km) dispersion of SO2 was measured under many stability conditions was perhaps the one most useful for dispersion model validation. However, none of these experiments could capture the three-dimensional (3-D) evolution of the dispersing plume in detail.
While the mean concentration is often highly accessible to atmospheric measurements, fewer atmospheric observations are available for the higher PDF moments (variance, skewness, kurtosis). Yet, the higher moments are crucial if the relationship between the concentration fluctuations and their consequences is non-linear (Mylne and Mason, 1991). For instance, toxicity, flammability and odour detection depend on exceedances of concentration thresholds (Gant and Kelsey, 2012; Hilderman et al., 1999; Schauberger et al., 2012), and non-linear chemical reactions are influenced by tracer fluctuations if the reaction and turbulence timescales are similar (Brown and Bilger, 1996; Cassiani, 2013; de Arellano et al., 2004).
Atmospheric measurements of the concentration fluctuations in a dispersing plume have been performed by different groups and with different techniques (Mylne, 1992; Mylne and Mason, 1991; Yee et al., 1993, 1994). The most comprehensive observations were made with lidars measuring the backscattered signal from smoke particles (Jørgensen and Mikkelsen, 1993; Jørgensen et al., 2010; Mikkelsen et al., 2002). Other studies have used lidars to measure SO2 concentrations (Schröter et al., 2003). A particular advantage of lidars is that they can measure concentrations throughout the ABL and not only near the Earth's surface, where most in situ measurements have been made. Nevertheless, even lidars provide only 1-D measurements and, when scanning, cannot provide high time resolution in 2-D or 3-D. Thus, the 3-D concentration distribution has never been measured at high time resolution.
The 3-D concentration field is needed to evaluate the meandering and relative dispersion process in the three physical directions. An important point to recognize is that the production and dissipation of concentration fluctuation for a dispersion scalar are intimately linked to the process of relative dispersion of puffs and the related process of centre of mass meandering (Csanady, 1973; Gifford, 1959). Therefore, parameterized expressions of relative dispersion are used in defining simplified models of concentration fluctuations (Cassiani and Giostra, 2002; Cassiani et al., 2005; Luhar et al., 2000; Marro et al., 2015, 2018; Sawford, 2004; Yee and Wilson, 2000).
One possibility to indirectly measure 3-D tracer concentrations at high time and space resolution (thus able to capturing concentration fluctuations) are ultraviolet (UV) cameras. These cameras can measure sulfur dioxide (SO2) column concentrations with a sampling frequency of several hertz (Kern et al., 2010; Lübcke et al., 2013). Non-uniform cloud cover in the image background can cause inhomogeneous illumination of the sky, which complicates the SO2 column concentration retrieval of SO2 camera images. While efforts have been made to correct cloud effects (Osorio et al., 2017), it is generally recommended to measure during clear-sky conditions (Kantzas et al., 2010; Kern et al., 2010). To date, SO2 cameras have been used mostly to monitor SO2 emissions from volcanoes (Burton et al., 2015), power plants (McElhoe and Conner, 1986; Smekens et al., 2015) and ships (Prata, 2014). While each individual camera measures only 2-D distributions of SO2 column concentrations, a combination of several such cameras should allow a tomographic reconstruction of the 3-D SO2 distribution.
However, to our knowledge such a tomographic setup has never been used successfully. The Comtessa project (Camera Observation and Modelling of 4-D Tracer Dispersion in the Atmosphere) is the first attempt at using camera observations to study tracer dispersion in the ABL. For this, we artificially release SO2 into the atmosphere and observe its dispersion with UV cameras.
In this paper, we present results from the first Comtessa field campaign, which was conducted to test our new instrumentation. Not all equipment was fully operational yet, but we were nevertheless able to collect a valuable data set using six UV cameras and meteorological instrumentation. Here, we first describe the release experiments (Sect. 2) and how a tomographic setup of UV cameras can be used to quantify the dispersion of artificially released SO2 puffs in the ABL (Sects. 3 and 4). However, note that a fully resolved tomographic reconstruction is not necessary for this retrieval and is not presented in this paper. As an example, the 3-D trajectories and spreads of six puffs within a short time interval of 60 s are reconstructed (Sect. 5). Then, the time evolution of puff meandering, relative and absolute dispersion are retrieved enabling estimations of turbulent timescales (Sect. 6). The data set does not contain a sufficiently large number of puffs for a reliable statistical analysis; however, the feasibility of the method is demonstrated.
The first Comtessa campaign was performed at a military training ground (11.5∘ E, 61.4∘ N) about 28 km northeast of the small city of Rena, Norway, from 3 to 21 July 2017. The experimental site is located in a remote forested mountain area at an altitude of 850 m above sea level. It is a fenced-in flat gravel field with dimensions of about 900 m × 400 m, which is normally used for ammunition testing by the Norwegian military. Three 9 m high masts equipped with eddy covariance measurement systems were set up to measure the turbulent fluxes of heat and momentum. From the top of one of the masts, pure SO2 gas was released, piped from SO2 bottles at the ground using a commercial blower. The blower speed was set such that the release was nearly isokinetic. That was achieved by adjusting the flow in the pipe to the wind speed monitored online with a sonic anemometer at source elevation. The pipe had a diameter of 12.5 cm at the release point. Figure 1 shows a picture of the top of the release mast.
The weather conditions were generally not favourable for our experiment, with several cyclones passing over Fennoscandia during the campaign period. Daily average temperatures at a meteorological station located in the immediate vicinity (Rena øvingsfelt) ranged between 6.8 and 11.7 ∘C, except for the last 2 days when they rose above 13 ∘C. On 13 of the 19 campaign days, precipitation was recorded, and winds were often strong (up to 9 m s−1). Conditions were suitable for instrument testing on several days, but clear-sky conditions were rare. The best conditions were encountered on 20 July when a ridge of high pressure built over southern Fennoscandia. While even on that day there was no period when the sky was entirely free of clouds, there were periods with relatively little cloud cover, enabling clear-sky camera observations for some viewing directions and yielding clouded scenes for the other cameras. In this paper, we will therefore present results only for this day.
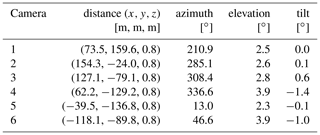
On 20 July, SO2 was released during several experiments, including both several continuous plumes (between 07:19 and 09:53 UTC) and nearly-instantaneous puffs (between 10:24 and 10:47 UTC). In this paper, however, only analyses of the puff experiments will be presented. Six identical UV SO2 cameras observed the SO2 releases, resulting in column-integrated SO2 concentration images from six directions. The six SO2 cameras observed an overlapping volume of roughly 40 m × 40 m × 20 m, centred circa 18 m downwind of the release point. The cameras were arranged on the ground in a half circle with a radius of 160 m around this volume. The release point is visible in the field of view of every camera. Additionally, a meteorological tower, located a few hundred metres northwest of the release tower, is visible in the field of view of some cameras. A map of the setup is shown in Fig. 2 and detailed quantitative information can be found in Appendix A1.
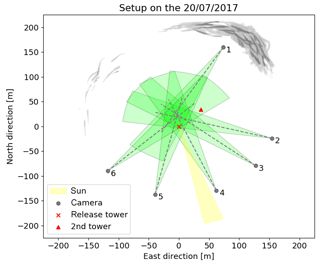
Figure 2Map of the experimental setup. The cameras' FOVs are indicated in green. The sun position (yellow) and the cloud cover (gray) as observed at 10:30 UTC are sketched on the map. Coordinates are given relative to the release location.
The SO2 cameras were custom-built for the Comtessa project (Fig. 3). At the core of each SO2 camera are two UV cameras from PCO (pco.ultraviolet), which record images at two different wavelengths. The wavelengths are selected by mounting two Asahi Spectra band-pass filters (10 nm bandwidth) at 310 and 330 nm, respectively, in front of the cameras. The filters are mounted between the CCD sensor and a 25 mm quartz lens from Universe Kogaku. This setup attenuates radial sensitivity changes due to different light paths through the filter for off-axis rays compared to mounting the filters in front of the lens (Kern et al., 2010). The cameras' CCD sensors have Ni=1392 pixel columns and Nj=1040 pixel rows, resulting in a image resolution of a few centimetres at object distances of a few hundred metres. The camera properties are summarised in Table 1. During the experiment, the exposure times were chosen manually such that the 14-bit-sensor was roughly 80 % saturated. On 20 July, the exposure times for the 310 nm camera were between 160 and 200 ms at apertures of f∕2.8. Further, each camera contains an AvaSpec-ULS2048x64 spectrometer from Avantes for robust SO2-calibration. The spectrometer is coupled via a 3×200 µm cross section converter fibre from loptek to a telescope, pointing in the same direction as the UV cameras. The telescope consists of a quartz lens from Thorlabs with 100 mm focal length and a Hoya U-330 filter which prevents stray light to enter the detector. This setup results in a telescope field of view of 0.572∘ which corresponds to a disk with a 52-pixel diameter within the UV camera image. In the future, a built-in GPS will be used to obtain accurate space and time information. However, during the experiment in summer of 2017, the GPS data were not yet recorded and, therefore, the individual SO2 cameras were synchronised in time by tracking of distinct SO2 features after the experiment (see Appendix A2 for details).
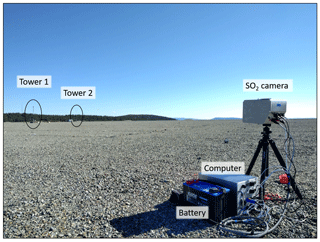
Figure 3SO2 camera and PC (camera 5). In the background, the release and measurement towers are visible.
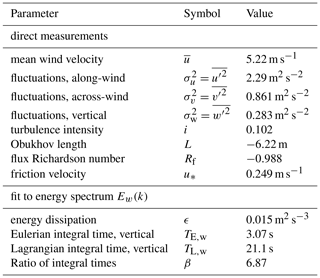
Meteorological measurements were collected on the release tower at three vertical positions (2, 5.4 and 8.7 m) using a state-of-the-art measuring system from Campbell Scientific. It included sonic anemometers at all three levels (model CSAT3A and CSAT3B, respectively) measuring three wind components and sonic temperature with 50 Hz sampling frequency. Additionally, an EC150 gas analyser was coupled to the lowest level. It simultaneously measured water vapour and carbon dioxide densities at 50 Hz, as well as the atmospheric pressure and temperature at lower frequency. During the puff release experiment on 20 July, the mean wind velocity at the source was 5.22 m s−1 and the fluctuations of the vertical velocity component were m2 s−2. The derived value of the Obukhov length indicates an unstable atmosphere with convective conditions. Further measured and derived parameters are summarised in Table 2 and the applied post-processing of the wind data is detailed in Appendix A3.
3.1 Description of turbulent dispersion
The absolute dispersion describes the spread of a scalar relative to a fixed origin along the coordinate axis i. Mathematically, is the variance of the 1-D mean concentration distribution along the considered axis. Taylor (1921) demonstrated that the absolute dispersion is directly linked to the Lagrangian autocorrelation function of the motion of one particle. According to Taylor's theory and assuming homogeneity and an exponential autocorrelation function (Arya, 1999) the evolution of the absolute dispersion with time t in the vertical coordinate z is modelled as
with the vertical velocity w(t) and the vertical Lagrangian timescale TL. Assuming homogeneity, the variance of the vertical velocity can be obtained from the velocity monitored by a sonic anemometer placed at the source location. Given the very short range of our current measurements this is an acceptable approximation. The Lagrangian timescale TL cannot be measured directly by a fixed point measurement, instead the Eulerian timescale TE can be obtained from such measurements. Hay and Pasquill (1959) assumed that the Lagrangian and Eulerian time scales have a fixed ratio . The proportionality constant β can be found using the relationship proposed by Hanna (1981),
where is the turbulence intensity in the along wind direction with mean velocity .
The absolute dispersion of an ensemble of puffs (or clusters of particles) can be assumed to be partitioned between two statistically independent components: the meandering of the puffs as a whole with respect to the source location, and the spread of the puffs around their centre of mass, called relative dispersion. This is sketched in Fig. 4. In mathematical terms, the variance of the mean concentration distribution is decomposed as a sum of the variance of the centre of mass distribution and the variance of the concentration of the puff relative to its centre of mass ,
Experimentally, the variances are obtained by averaging over multiple realisations of single puffs.
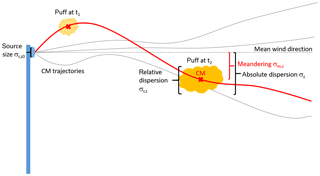
Figure 4Sketch of a puff release. The centre of mass trajectory of a single puff (red) meanders around the mean trajectory of a puff ensemble, while the puff additionally spreads around its centre of mass. Consequently, the absolute dispersion can be separated into the meandering of the centre of mass trajectories and the variance of the puffs' concentration relative to their centre of mass. Both are obtained using data from a large number of realizations of single puff releases.
A cluster of particles released at the same time from a finite source will follow slightly different paths and form a distribution around its centre of mass. The relative dispersion is therefore influenced by the source size r0, i.e. the initial separation of the particles. For an initial particle separation (puff size) in the inertial subrange of turbulence, i.e. larger than the Kolmogorov length scale and smaller than the length scale of (local) energy containing eddies, the particle separation will be first influenced by the source size and then become independent of the initial separation (Franzese and Cassiani, 2007; Monin and Yaglom, 1975). Based on inertial range scaling arguments (Monin and Yaglom, 1975), the characteristic timescale of the source is given by , where ϵ is the mean dissipation of turbulent kinetic energy. The following Eqs. (4)–(6) are valid for puff sizes in the inertial subrange of turbulence, which was observed in our experiment (see Appendix A3 for details).
Batchelor (1952) showed that for t≪ts the spread of a puff, or cluster of particles, is dominated by the initial velocity differences between the particles (“ballistic regime”)
where Ck is the Kolmogorov's constant for the longitudinal structure function in the inertial subrange. Here, r is the 3-D separation between two particles of the cluster and 〈r2〉 is the ensemble mean square separation between all particles of the cluster. In homogeneous isotropic turbulence, 〈r2〉 is related to the 1-D relative dispersion as (Franzese and Cassiani, 2007). Equation (4) reduced to the vertical component reads then
with the 1-D initial vertical separation .
For larger times t≫ts, the rate of change of particle separation becomes independent of the initial separation, and the spread of the puff is proportional to the Richardson–Obukhov constant Cr according to the Richardson–Obukhov scaling (Monin and Yaglom, 1975).
The value of the Richardson–Obukhov constant is uncertain, as it is difficult to estimate from experiments and numerical simulations (Franzese and Cassiani, 2007). However, Cr and the directly related relative dispersion are important for models as the relative dispersion defines the effective rate of mixing of a puff and therefore the decay rate of concentration fluctuations (Cassiani et al., 2005; Marro et al., 2018; Pinsky et al., 2016; Sawford, 2004).
3.2 Turbulent dispersion from image data
Videos of column-integrated concentrations (CIC) of an instantaneous release of a passive tracer can be used to measure different aspects of turbulent dispersion, especially when simultaneous images from different directions are available. The CIC images contain direct information about the puffs' position and spread projected to the image plane (see Fig. 5 for a sketch and Fig. 6 for an example image). The image plane is spanned by two discrete coordinate axes and , describing the image columns and rows. We define a rectangular extension of the projected puff, the so-called region of interest (ROI), to distinguish different puffs that may be present in the image, and to reduce the impact of noise. Then, the total signal Stot of the puff (or, in statistical terms, the zeroth moment of the column-integrated concentration PDF) is given by
where S(i,j) is the CIC at pixel (i,j). The centre of mass (CM) of the puff in the image plane (first moment of the column-integrated concentration PDF) is given by
The spread of mass around its centre as given by the variance (2nd moment of the column-integrated concentration PDF) is described by the weighted covariance matrix C. The diagonal elements of C are the spreads of the SO2 puff in the image plane along the image columns and rows, respectively. Accordingly, the horizontal spread along pixel columns is given by
The spread along pixel rows C2,2 is calculated equivalently.
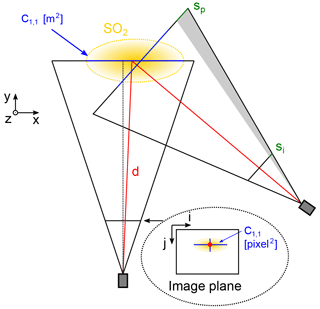
Figure 5Sketch of the field of view of two cameras from above. The three-dimensional SO2 puff (yellow) in the world coordinate system () is projected to the two-dimensional image plane (i,j). The centre of mass in the image plane corresponds to a solid angle in the world coordinate system (red). The apparent size of a pixel scales with the distance to the object plane (grey area).
However, retrieving quantitative dispersion parameters such as the total mass from the camera images requires that the pixel dimensions in the virtual object plane, containing the puff, are known. A pixel is, strictly speaking, a solid angle defined by the focal length of the camera lens f. Thus, for knowing the apparent width of the pixel at the position of the puff, the distance d of the SO2 puff to the camera needs to be known. Then, the apparent width of a pixel sp(d) is given by
where si is the physical width of the pixel on the CCD sensor. The height of the pixel in the virtual object plane is calculated analogously and it is equal in case of a sensor with square pixels. In the following, square pixel are assumed for simplicity.

Figure 6Example of a SO2 CIC image from a SO2 camera (camera 4). The image contains two SO2 puffs marked by the detected ROI (white rectangle). Artefacts produced by a cloud are visible in the upper right corner.
When the puff's 3-D extension is small in comparison to the distance from the puff's CM to the camera, differences in distance over the puff's extension can be neglected and a constant scaling can be assumed for the whole ROI. Scaling the CIC images with the pixels' apparent area , relates the image to a global reference system. It follows for the total mass M of a puff
and the horizontal puff spread in square metres
The spread describes the mass distribution relative to the centre of mass and projected to the image plane. It is hence connected to the relative dispersion. Depending on the relative orientation of the mean wind direction and the camera's optical axis, it can equal the vertical, along- or across-wind direction in some cases. In other cases, assumptions of the plume shape have to be made (e.g. Gaussian plume) or a 3-D reconstruction of the distribution is necessary. When detecting the puff's CM with more than one camera, the CM position in a global coordinate system can be reconstructed. For analysing the statistical nature of the turbulent dispersion, an ensemble of puff releases is required. Then, the meandering is calculated from the variance of the 3-D CM positions and the relative dispersion is connected to the measured puff spread.
In this study, SO2 CIC images recorded simultaneously with six UV SO2 cameras are the basis for the retrieval of puff spreads. An example of such an image can be seen in Fig. 6 and the imaging technique will be described in the following Sect. 4.1. The puffs are detected automatically within the image using common image processing techniques (Sect. 4.2). This allows for calculating the CM and spread of the puff projected to the image plane. Making use of the tomographic setup of six cameras (see Figs. 2 and 5) and the previously measured, projected CMs, the 3-D trajectories are reconstructed (Sect. 4.3). The 3-D trajectories then allow for scaling the measured puff spreads to square metres.
4.1 SO2 camera imaging technique
The SO2 camera method (Mori and Burton, 2006) is based on the principle of absorption spectroscopy of backscattered sunlight. Gaseous SO2 molecules exhibit a distinct, wavelength-dependent absorption cross section in the ultraviolet σ(λ), where λ is the wavelength. The relationship between the light intensity before and after passing through a SO2 cloud – I0(λ) and I(λ) – is described by the Beer–Lambert law
where c(l) is the SO2 concentration at position l along the light path through the SO2 cloud and is the SO2 slant column density (SCD) along this light path. Generally, radiative transfer effects (e.g. multiple-scattering inside the SO2 cloud and light dilution Campion et al., 2015; Kern et al., 2013) have to be taken into account when translating the slant column density to the column-integrated concentration. However for this study, the effects are negligibly small due to the absence of aerosol and the small extension and short distance of the SO2 puffs to the cameras. Therefore, the slant column densities correspond nearly exactly to the column-integrated concentrations and are used as such throughout the publication.
The SO2 cameras record intensity images of the SO2 cloud I(λ). Images of the clear sky intensity I0(λ) can be measured in the same direction when the SO2 cloud is not present (i.e. before or after a release experiment). The SO2 slant column density S is proportional to the optical density τ(λ), which is retrieved from the two images by
Using a narrow bandpass filter in the ultraviolet (typically 310 nm), a narrow spectral band of strong SO2 absorption is selected. While high-precision laboratory measurements of the SO2 absorption cross section σ(λ) are available (Vandaele et al., 2009), calibration from τ(λ) to S is nevertheless necessary due to uncertainties of the exact filter function. The measured optical density images τ are approximated to SO2 SCDs by linear regression using absolute measurements of the SCDs
where a and b are calibration constants. Such measurements are available from images of gas cells containing a known amount of SO2 and/or from spectra of a built-in spectrometer (Lübcke et al., 2013). Making use of the differential optical absorption spectroscopy (DOAS) technique, a time series of precise point measurements of the SO2 SCD corresponding to a small pixel area within the camera images can be retrieved and correlated to the image time series.
Moving meteorological clouds behind the SO2 cloud can change the illumination of backscattered sunlight between the two images I0(λ) and I(λ). This leads to artefacts in the retrieved SCD images which can be of the same magnitude as the SO2 signal. While SO2 camera measurements under cloudy conditions should therefore be avoided if possible, we could obtain only such measurements due to the weather conditions during the experiments.
In this publication, the background images I0 were taken from the same direction between two puff releases and the images were calibrated using the built-in spectrometer. Note that, contrary to typical applications (Kern et al., 2015; Mori and Burton, 2006), measurements at only one wavelength (λ=310 nm) can be used for the analysis due to the absence of broadband absorption from additional aerosol in the SO2 cloud. More details on the retrieval steps used in this publication can be found in the Appendix B1.
4.2 Detection of individual puffs in image plane
The position and spread of individual SO2 puffs are tracked from the release point automatically. For that, rectangular ROIs containing the full puff need to be detected. Such a detection can be difficult for several reasons. (1) The images partly contain up to two puffs and artefacts from clouds, which can imitate SO2 absorption. (2) Small fractions of the puffs can separate completely from the puffs. (3) The images are noisy, making correct identification of pixels with low SO2 values at the edges of the puffs difficult. In consequence, the ROI has to be large enough to contain the full puff but small enough to exclude additional puffs and clouds.
To overcome these challenges, we choose an approach combining iterative tracking from the release point and applying signal thresholds to two noise-reduced versions of the original image. In this way, the ROI could be detected robustly and the total signal, CM and spread of the puff could be retrieved from the original image. Details of the detection algorithm can be found in Appendix B2. Further, this approach allows the tracking of several puffs in the same image frame as long as they are separable. Single clouds can be ignored if they are not at the same position as the puffs and even the position of a puff in front of an overcast sky can be constrained spatially, even if not fully detected.
4.3 3-D trajectories and pixel scaling
The previously retrieved CMs projected to the image planes of the cameras can be used to retrieve the 3-D trajectories of the CM in the global coordinate system. These allow for calculating the distances between a puff and the individual cameras at any given time. Subsequently, the scaling factor (Eq. 11) for the other moments of the PDF (Eqs. 12 and 13) can be determined.
The individual images of the six cameras are recorded at irregular time intervals due to differences in exposure and read-out times. Combining the irregular image times, the derived 3-D trajectories in the global coordinate system were retrieved on an arbitrary-chosen discrete, regular time grid. Here, 250 ms was chosen so that at least one image of every camera lies within each interval. The time series of the CM image coordinates of the six cameras are synchronised and interpolated to this common time grid.
For every time step and each camera, the line-of-sight line from the position of the camera through the detected CM in the image plane at (icm,jcm) is determined by calculating the azimuth and elevation angle. The azimuth angle of the CM is the sum of the camera's azimuth angle α of the optical axis and the relative azimuth angle of the CM to the optical axis
where icm is the pixel column of the CM, is the pixel column containing the optical axis (approximated by the central pixel), si is the physical pixel width on the CCD sensor and f is the focal length. The elevation angle is calculated analogously based on the camera's elevation angle and the pixel row jcm of the CM.
At every time step, the position of the CM in the global reference system is then calculated based on the line-of-sight lines of all available cameras using a least squares optimisation: the CM is the point in the global reference system which minimises the square distance to all lines. The CM can be calculated for every time step for which data from at least two cameras were available. However, in this analysis data from at least three cameras were used in order to reduce discontinuities caused by uncertainties in the cameras' position and pose. The reconstructed 3-D trajectories can then be used to determine the distances between the cameras and the puffs at any given, individual image time.
On July 20 between 10:24 and 10:47 UTC, a total of 140 puffs were released almost instantaneously, each puff containing between 0.8 and 1.2 g of SO2. The differences in mass originate from the manual opening and closing of the release valve. Due to the changing cloud cover, the analysis of the SO2 camera images requires that background images are selected manually every 30 to 40 s of data. Additionally, puffs overlapping with clouds or each other limit the analysis further. Hence, for this feasibility study, results for a continuous 1-minute interval (10:29:50 to 10:30:50 UTC), containing six subsequent puffs are presented.
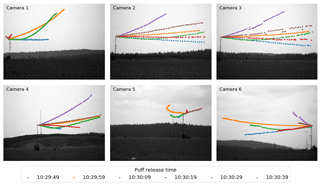
Figure 7Centre of mass coordinates of six subsequent puffs projected to the image planes of the six SO2 cameras. For cameras 4 and 5, a meteorological tower is visible in the image background. This tower is located a few hundred metres northwest of the release tower.
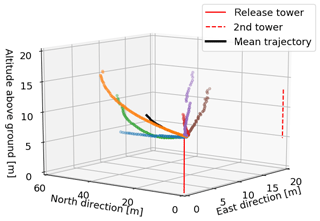
The six puffs can be tracked with all cameras in the image plane (Fig. 7) and the 3-D CM trajectories can be reconstructed successfully over up to 58 m (Figs. 8–10). Typical distance to extension ratios are around 100, justifying the assumption of constant scaling throughout the ROI. The puffs move in two dominant directions (approx. 0 ∘ and 30 ∘) in good agreement with the overall measured wind direction. Figure 11 displays the evolution of the moments of the spatial distribution (total mass, horizontal and vertical spread) of the six puffs. These are discussed in more detail in the following.
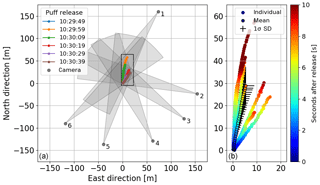
Figure 9Horizontal projection of the CM trajectories of the six puffs observed with six SO2 cameras. The left panel shows an overview of the camera positions relative to the reconstructed trajectories. The right panels shows a blow-up of the rectangular area marked in the left panel. The colour code represents the travel time since release. The mean trajectory and its standard deviation are displayed with black pluses.
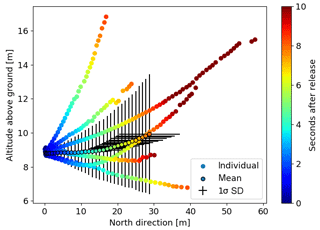
Figure 10Vertical projections of the CM trajectories to the altitude–north plane. The colour code represents the travel time since release. The mean trajectory and its standard deviation are displayed with black pluses. Note that the x axis scales 6× larger than the y axis.
5.1 Total SO2 mass
The total SO2 mass of the puffs is conserved, since loss mechanisms (e.g. dry deposition and oxidation of SO2) can be neglected on such short time scales as the ones observed. A change of the measured absolute mass and differences between the signals of different cameras are indications of measurement biases and limitations. These include besides others the cameras' detection limits, incomplete detection of the puff by the derived ROI, additional signals (both negative and positive) from cloud artefacts, uncertainties in the trajectory retrieval and thus the scaling parameter, and radiative transfer effects.
The upper panel in Fig. 11 shows the total mass of the puffs as observed by four of the six cameras. Cameras 5 and 6 were excluded due to overly pronounced additional signals from the cloudy sky. The background images including the cloud cover for each camera were optimised for the time of the second displayed puff (indicated by shaded area). For this puff, the retrieved total SO2 masses from the four cameras show good agreement: the mass first increases to circa 1.2 g SO2 while the puff is released and then stays constant for all cameras until the puff is no longer tracked. For the other puffs – and thus increasing time difference to the background images – the relative differences between the cameras increases (up to 50 %).
The total mass is strongly affected by clouds, which add both negative and positive signals to the total mass. For camera 3, single clouds are visible along the full pathway of the puff, resulting in a generally overestimated signal. For cameras 2 and 4, single clouds appear only from the middle of the image. Thus in this case an underestimation of the total mass starts only a few seconds after the release. Cameras 5 and 6 (not shown), however, fail to reproduce the released total mass even for the second puff. Camera 1 observes the puffs free of additional signal from clouds and hence catches the correct mass. However, due to it's frontal alignment to the puff's propagation direction, subsequent puffs might overlap. This was the case for the three puffs between 10:30:20 and 10:30:50 UTC. For these puffs no separate mass or spread information can be extracted.
As the mass cannot be retrieved accurately for all data points, it can be assumed that the puff spread would be affected in a similar way by the additional signal due to clouds or overlapping puffs. Therefore, such data points should be discarded from the analysis of the turbulent dispersion. Only measurements for which the total mass lies within a physically reasonable range (here, 1.0 to 1.3 gs−1) are included for further discussion.
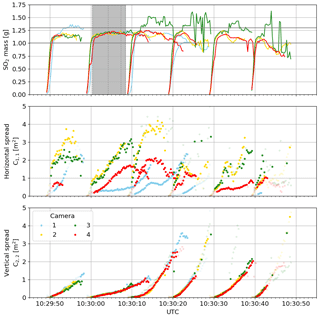
Figure 11Total mass, horizontal spread and vertical spread (lower panel) of six subsequent puffs. Only data from cameras 1–4 are shown due to significant cloud signals in camera 5 and 6. The background images, and thus cloud cover, were reconstructed from the shaded time period. The shaded data points are discarded because their corresponding mass lies outside the expected range (1.0–1.3 g).
5.2 Puff spread
Figure 11 shows the puff spread (Eqs. 10 and 13) in the image plane for four cameras. It is pointed out that these puff spreads are projected to the camera's object plane at the position of the puff. Hence only the puff spread perpendicular to the camera's optical axis is measured (see Fig. 5).
In the horizontal, the cameras' relative orientation lead to different projections and thus not directly comparable puff spreads. Camera 1 views the puffs almost frontal and thus the retrieved puff spreads are across-wind in first approximation. Cameras 2 and 3 view the puffs nearly perpendicular to their propagation direction, hence they measure approximately the along-wind spread and their results agree reasonably well. The limited comparability of the cameras and the short data set of only six puffs does not allow for a further analysis in terms of horizontal dispersion.
The elevation angles of the cameras are comparably small (2.3–3.9∘). The vertical projection to the image plane is negligibly small for these elevation angles (cos(3.9). Hence the measured vertical puff spreads correspond to the real vertical spread of the puff and thus are comparable between the cameras. The measured values of the four cameras agree with each other. In the following discussion only the vertical puff spread is considered for simplicity.
For the analysis of the turbulent dispersion it would be necessary to observe a large number of instantaneous releases under stationary atmospheric conditions. For this study, only six subsequent puffs were selected due to the limitations of the measurements under cloudy conditions. The total analysed time span is 60 s. Hence, the following discussion of the results should be considered as a demonstration of method rather than a robust estimate for parameterization of turbulent dispersion.
6.1 Meandering
The vertical meandering was calculated as the variance of the ensemble average of the CM trajectories. The shortest trajectory of the six puffs extended over 8 s after release. The ensemble average was calculated for every time step up to this time in order to give a constant weight to all detected trajectories (i.e. at every point in time, the same number of trajectories is averaged). Figure 12 shows the meandering for the six puffs and, additionally, it shows the meandering when additional puff trajectories from the full duration of the experiment are included.
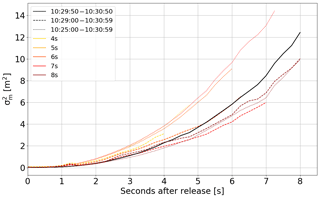
Figure 12Meandering in the vertical. The black curve shows the ensemble average over the six puffs. The meandering is sensitive to the chosen ensemble. The coloured dashed and dotted curves show the meandering calculated for different numbers of puffs, selected by varying the time interval (line style) and the minimum trajectory lengths (colour).
This enabled an assessment of the uncertainty of the meandering estimate. The number of included trajectories was varied by simultaneously reducing the minimum trajectory length and increasing the time interval. Including a different number of puffs can lead to both a higher and lower . The meandering is generally larger when more trajectories are included, particularly in the first few seconds all values lie above the meandering for the six puffs only. The meandering calculated from the full time period at medium trajectory lengths (7 s) was up to two times higher. The increase might originate from atmospheric variability or from the poor statistics. Additionally, a decreasing trend with increasing minimum trajectory length can be observed. This might be explained by the experimental setup. Some trajectories could get discarded during the data processing due to, e.g. clouds in the background or the puff moving out of the field of view. This leads to an effective data reduction to only certain directions and therefore an underestimation of the vertical meandering. In conclusion, the meandering shows a high dependence on the included trajectories, which can be only resolved if a higher number of puffs is available.
6.2 Relative dispersion
The relative dispersion is the spread of the SO2 distribution around its centre of mass. It can therefore be estimated for each individual puff. The spread of the six puffs, averaged over cameras 1–4, and their ensemble average are plotted on a double logarithmic scale in Fig. 13. The observed relative dispersion does not show a clear transition from the t2 to the t3 regime. In facts, the slope suggests that only the initial t2 regime is observed. That means that the largest observed puff length scales are still affected by the initial separation and, consequently, the puff dispersion according to the Richardson–Obukhov scaling (t3 regime) could not be observed in this experiment. A wider field of view of the cameras would result in longer observation times, which enable an estimate of the Richardson–Obukhov constant by fitting Eq. (6) to the extended data using the measured value for the energy dissipation.
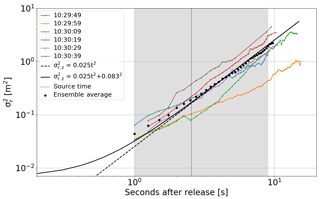
Figure 13Relative dispersion in the vertical on a log–log scale. The coloured curves show the dispersion of individual puffs and the black points show the ensemble average over these individual puffs. The source size was estimated by a linear fit to the ensemble average (dashed black line). The resulting source size was used to calculate the predicted curve by Eq. (4) (solid line) and estimate the source time (dotted black line).
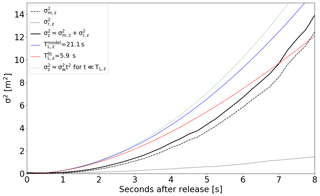
Figure 14Absolute dispersion in the vertical (solid black line). Relative dispersion and meandering are shown with dotted and dashed black lines, respectively. Two parameterizations of Taylor's theorem are plotted: modelled from the sonic anemometer data (blue) and fitted to the measured absolute dispersion (red). For dispersion times much smaller than the Lagrangian timescale, the absolute dispersion can be approximated by a t2-dependency (green).
The well-defined t2 expansion regime (the linear part with a slope of 2 in Fig. 13) allows for estimating the effective vertical source size. Following Eq. (5), the resulting vertical source size is fitted to cm and compares to the radius of the release outlet (6.25 cm). The increased number can be explained by the jet created at the source by the blower. Assuming an isotropic source, the source timescale was estimated to =2.6 s from the vertical source size and energy dissipation rate ϵ. The resulting time lies in the middle of the observed time period, making it possible to theoretically observe the onset of the transition to the inertial subrange.
6.3 Absolute dispersion
The absolute dispersion describes the spreading of particles relative to a fixed origin. It is calculated as the sum of meandering and relative dispersion (Eq. 3). In Fig. 14 the 1-D absolute dispersion in the vertical dimension is displayed. The figure contains two parameterizations (, TL) of Taylor's theorem (Eq. 1). In both cases, is taken from the sonic anemometer data close to the source. The estimate of the Lagrangian timescale differs: TL is either modelled from the measured Eulerian timescale TE,z=3.07 s from the same anemometer data using the empirical constant β=6.87 (Eq. 2) or fitted to the absolute dispersion retrieved from the image data. The modelled Lagrangian time is s and the fitted one is s. The fitted Lagrangian timescale relates to the measured Eulerian timescale with and lies within the previously reported range of 1 to 10 (Arya, 1999; Hay and Pasquill, 1959).
Here we report the absolute dispersion during the first 8 s after the release. Hence, all measurements were recorded at times below both the modelled and the measured Lagrangian timescales. For times much smaller than the true Lagrangian timescale, the absolute dispersion can be approximated by a quadratic relation, , independent of the Lagrangian timescale, hence making an estimation of the latter nearly impossible for short observation times. Therefore, even if a retrieval of the Lagrangian timescale from the current image data is possible, it is not reliable since the puff observation time does not exceed the Lagrangian timescale.
Further, the absolute dispersion was observed close to the source when it is dominated by the meandering (). The absolute dispersion has therefore an uncertainty similar to that of the meandering (see Sect. 6.1 above).
During the first Comtessa experiment, the passive tracer SO2 was released in the ABL to study its dispersion based on images from six UV SO2 cameras. As a proof-of-concept, the absolute dispersion, as well as the relative dispersion and meandering of an ensemble of six puffs could be retrieved by performing a reconstruction of the 3-D trajectories of the centre of mass positions of instantaneous puff releases. The measured absolute dispersion understates both the modelled and fitted parametrizations of Taylor's theorem due to underestimation of the puff meandering.
We showed that a tomographic setup of six cameras is in principle suited to measure the main statistical characteristics of the puff dispersion in the ABL. However, the data set was limited by several points: (1) Artefacts from clouds in the image are falsely interpreted as SO2 making an automatic SO2 retrieval difficult. For the data amounts necessary for a meaningful statistical analysis of puff releases, the data set should contain cloud free data to enable automatic retrieval. (2) Some propagation directions might get systematically discarded during the data processing. This would lead to an underestimation of the puff meandering. (3) The release of the SO2 puffs is only nearly instantaneous, leading to elongated puffs. This puts an uncertainty on the relative dispersion estimate, in particular for the along-wind coordinate.
It is desirable to determine a value for the Richardson–Obukhov constant and the higher moments of the concentration distribution in order to constrain atmospheric turbulence models. A robust estimate for the Richardson–Obukhov constant of relative dispersion and Lagrangian integral timescales could be obtained from a larger data set of longer tracked single puffs. Such a data set is planned to be produced during follow-up Comtessa field campaigns. The same concept as for the first campaign should be used but on a larger scale i.e. releasing larger amounts of SO2. Higher amounts of SO2 will increase the images' signal-to-noise ratio and facilitate observations at larger distances to the tower. Consequently, this increases the cameras' field-of-view enabling puff observations over longer distances and times.
Further, several conclusions regarding the camera placement could be drawn from the first campaign: (1) Cameras should not observe the puffs frontal as it is impossible to separate overlapping puffs in the analysis. Alternatively the time between two releases has to be sufficiently long to allow a clear puff separation. (2) If possible, release experiments should only be performed on cloud-free days or at least the cameras have to be positioned such that the clouds do not appear on the projected trajectories of the puffs. (3) Further, it should be possible to observe all propagation directions of the puffs to avoid biases in the meandering towards a certain direction. The used half-circle offers a good solution.
In the case of a cloud free data set, the presented method can be applied fully automatically. Hence, providing a larger and cloud free data set opens the door for statistical analysis of puff dispersion. Further under cloud free conditions, the underlying imagery can be used to conduct a complete tomographic reconstruction of SO2 concentration, which will be invaluable for constraining models of atmospheric boundary-layer dispersion.
The raw measurement data and the python code used for data analysis is available from the authors upon request. The code is based on the pyplis toolbox (Gliß et al., 2017).
A1 Reconstruction of the setup
Precise knowledge of the experimental setup is necessary for the reconstruction of 3-D trajectories. During the field campaign, the distances of the cameras to the release tower and the angle towards north were measured using a theodolite. Comparing the pixel coordinate of the top of the release tower in the camera image with the tower's position, the three angles defining the camera pose (azimuth, elevation and tilt) were extracted. The results are shown in Table A1.
A2 Camera temporal synchronisation
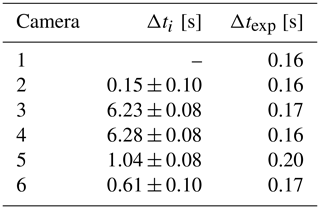
As no GPS time information was yet available during the experiment, the image time series of the six SO2 cameras had to be synchronised manually after the experiment. To this end, the release time of 18 subsequent puff releases between 10:29 and 10:31 UTC were detected for every camera. Due to the distinct movement of the puffs within the turbulent flow, the puffs could be clearly correlated in the images of all cameras. The relative temporal offset Δti between camera i to camera 1 was then calculated from the time difference of the first frame, on which a puff was visible.
The temporal offset was averaged over 18 observed puffs between 10:29 and 10:31 UTC and is given relative to camera 1 in Table A2. The accuracy of the temporal offset is limited by the discrete sampling frequency which in turns is constrained by the exposure and readout time.
A3 Data processing of the eddy covariance measurements
Meteorological measurements taken between 10:27 and 10:32 UTC have been used to obtain the parameters reported in Table 2. Before the actual post processing, the collected data was treated by the LICOR EddyPro software system for despiking (Mauder, 2013; Vickers and Mahrt, 1997) and for applying the triple rotation correction (Wilczak et al., 2001) that nullify the average vertical and across-wind components, and the Reynolds stress component. This means that the coordinate system is aligned with the measured mean wind direction; see also Burba (2013) for a description of the corrections applied in EddyPro.
The values for the mean wind and the three turbulent fluxes , , are reported at 8.7 m close to the source location. The energy spectrum Ei(k) of the ith velocity component, where k is the wavenumber, is the Fourier transform of the autocorrelation function of that velocity component and was calculated according to, e.g. Stull (1988) and using Taylor's hypothesis. The friction velocity u* was estimated by using the Reynolds stress component at two metres as . The Obukhov length L is defined as
where θv is the virtual potential temperature, κ≈0.4 is the von Kármán constant, g is the gravitational acceleration and is the vertical turbulent flux of virtual potential temperature. We used the sonic temperature as an approximation of virtual temperature as discussed in, e.g. Kaimal and Finnigran (1994). As a consistency check, the flux Richardson number was calculated at z=5.4 m using
In convective conditions, the flux Richardson number has a similar value to z∕L (here, −0.868) (Stull, 1988) and our measurements () are in good agreement.
The mean dissipation of turbulent kinetic energy ϵ was obtained by fitting a Kolmogorov spectrum to the inertial range of the measured spectrum for the along-wind component of velocity using the method discussed in detail by Stull (1988). The value of the Kolmogorov constant Ck=0.49 was taken according to measurements and theory of homogeneous isotropic turbulence (Pope, 2000; Stull, 1988). We observe a well-developed inertial subrange starting at a length scale of about 9 m and the differences between estimates of ϵ based on the three different velocity components are limited to about 30 %. The Eulerian integral timescale of the vertical velocity component TE,w was obtained by fitting an exponential decay to the autocorrelation function for the measured 5 min time series. The Lagrangian integral scale TL,w was estimated from the Eulerian one by using the empirical fixed ratio proposed by Hanna (1981) and Pasquill and Smith (1983), see Eq. (2) of the main paper.
Comtessa SO2 slant column density retrieval
The raw intensity images have to go through several retrieval steps to get the final product, the SO2 slant column densities. For a detailed, general description; see, e.g. Kantzas et al. (2010) or Lübcke et al. (2013). In the following all images are corrected for the dark signal, which was recorded daily after the release experiments.
Sky masks are defined for every camera based on local intensity thresholds. The sky masks separate the images in two regions according to whether the intensity contains a reflected component or only backscattered sunlight. Sunlight can be reflected from the ground, topography in the background, and structures such as the release tower and antennas. This reflected region is completely ignored in the further analysis.
The optical density images of the SO2 puffs are calculated according to Eq. (16) from a SO2-containing and SO2-free background image. The SO2-free background image is selected from the time series of puff releases. Typically, this image is cloud-free and can be scaled to the base intensity of an individual SO2-containing image recorded at a later time (Gliß et al., 2017). However, due to the partly strong cloud cover, a background image containing the exact cloud structures but no SO2 is necessary for the analysis. Such an image cannot be scaled to the changing base intensity with time and is thus constrained to a short analysis period of few tens of seconds for quantitative analysis. Therefore, a “patchwork” image from the same time series during the puff release between 10:30:00 and 10:30:10 UTC was selected for every camera. If a puff was present in this image, the respective image area was cut and replaced by the same area of an image several seconds later without the puff present in this area.The calibration from optical densities to SCDs is performed using the built-in DOAS spectrometer.
B2 Algorithm description: tracking of individual puffs in image plane
Figure B1 depicts the tracking algorithm schematically. The algorithm is based on three copies of the original image (see Fig. B2): (1) the original high-resolution image, (2) an image which was blurred with a 2-D Gaussian function (mean: 1, sigma: 5) and (3) a low-resolution image which was sub-sampled to (87×65 pixel) using image pyramids. The images are increasingly noise-reduced and have consequently lower detection limits for SO2. The average standard deviations for the three image types are (1) 2.4e16 molec cm−2, (2) 1.75e16 molec cm−2, and (3) 5.0e15 molec cm−2.
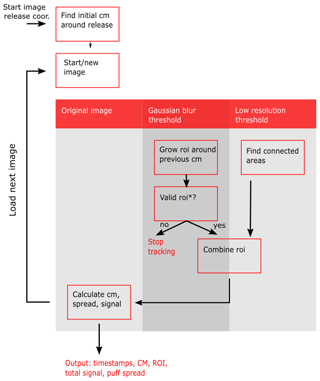
Figure B1Flow diagram of the tracking algorithm. The puffs are detected iteratively based on the previous detection and two noise-reduced versions of the original image. The conditions for a valid ROI can be found in the text.
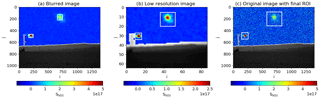
Figure B2Puff detection based on noise-reduced images, here for camera 1 at 10:30:12. The ROI is detected in a blurred image based on the position of the CM in the previous image (a). A low resolution image is used to detect connected areas above a threshold (b). The combination of both detections gives the resulting ROI, which is used to calculate the CM, total signal and spread in the original image (c).
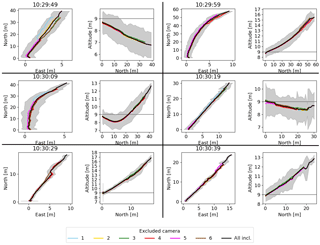
Figure B3Sensitivity of the reconstructed trajectories to the removal of data from a single camera. The trajectory colour indicates which camera was removed from the calculation, the black trajectory is based on data from all cameras. The time indicates the release time of the puff. In the altitude–north plots, the horizontal line represents the release altitude.
The puffs are tracked iteratively from the release point. Therefore, the image coordinates of the release point and the start image of the individual puffs have to be provided manually. The tracking will start from this image. After every successful detection of the ROI, the next image will be loaded. First the ROI is detected within the blurred image around the last-known position of the puff. That is the release point for the first image, and the CM of the previous image for all other images. A 50×50 ROI is set around this point. Then the ROI is increased incrementally by single image rows and columns. New pixel rows or columns are added to the ROI if they contain at least 5 % pixel above a threshold of 3.5e16 molec cm−2. The threshold is chosen as the double of the standard deviation to suppress noise and cloud artefacts effectively. The ROI contains the central part of the puffs but not necessarily separated fractions and weak tails. Weak tails and separated fractions can be detected within the low-resolution image which suppresses noise 4 times more compared to the blurred image. The image is separated into connected regions containing a significant signal. A pixel is considered to contain a signal if 25 % of the pixels in a 5×5 neighbourhood are above a threshold. This methods detects the SO2 puffs and clouds alike, thus a separate selection is necessary to identify the puffs. The detected ROIs are rescaled to the original resolution and compared to the previously detected ROI from the blurred image. If the previously found ROI immerses completely in a new ROI, it will be replaced by the larger ROI. In this way, the full area of puffs including tails close to the detection limit and separated SO2 patches are included. When the final ROI of a puff is determined, the total signal, CM and spread of the puff are calculated within this ROI based on the original image.
For the next image, the CM of the previous image is used as a starting point for the ROI which is determined equivalently. The procedure is repeated until an invalid ROI is detected. This is the case when the puff touches the image borders or moves in front of non-sky areas such as the ground or vegetation and topography on the horizon. In these cases, the ROI would no longer contain the complete puff. Further, the tracking stops when it is likely that cloud artefacts are tracked instead of the puff. This can be indicated by jumps in the CM or a sudden increase or decrease of the ROI.
B3 Sensitivity of trajectory retrieval to single camera
The 3-D CM trajectories are calculated by triangulation based on the individual 2-D CM trajectories of the six cameras. While using a least-square method including all six cameras reduces effects from uncertain camera position and pose and clouds, data from only two cameras would be in principle sufficient for reconstructing the 3-D trajectory. To determine the sensitivity to possibly inaccurate data obtained from certain cameras, we repeated the trajectory retrievals excluding systematically information from one camera (Fig. B3). The retrieved 3-D trajectories show no particular sensitivity to a single camera view, suggesting that none of the cameras adds crucial or false information to the reconstruction. Excluding the data from the cameras containing the most pronounced cloud cover (3,5,6) does not shift the retrieved trajectories outside the 1σ-range of the trajectory including all cameras. Hence, we argue that information from such cameras can be used for the trajectory reconstruction even if they fail to fully detect and separate the puff from cloud artefacts.
The online supplement contains videos of the six puff releases recorded with the six cameras. The videos are available at the online repository Zenodo: https://doi.org/10.5281/zenodo.1299638 (Dinger, 2018).
The detected ROI and CM are indicated on every image frame. The images were noise-reduced (Gaussian filter with σ=5) to increase the visibility of the puffs for the human eye. Note that the influence of cloud cover becomes more evident as the time difference between background image and image frame increases. Further, the times of the background images can be seen in the video: the image background noise cancels to zero for this time according to Eq. (16). In some videos, additional absorption from small insects flying through the cameras' field of view are visible in the form of straight lines.
ASD, AS and MC wrote the manuscript. KS, MC, AK, AS and IP contributed with discussion to the manuscript. ASD analysed the camera data and developed the methodology. MC, HA, and SYP analysed the eddy-covariance measurements towards turbulence. AS, MC and KS designed the Comtessa experiment. IP modelled the optimal setup of the UV cameras. ASD, KS, MC, HA, SYP, NS, JW and AS contributed to the field experiment. The SO2 cameras have been designed by CB, KS and developed by KS, ASD and CB.
The authors declare that they have no conflict of interest.
The Comtessa project has received funding from the European Research Council
(ERC) under the European Union's Horizon 2020 research and innovation programme under grant agreement no. 670462.
Edited by: Huilin Chen
Reviewed by: Jean-François Smekens and one anonymous referee
Arya, S. P.: Air pollution meteorology and dispersion, Oxford University Press, New York, 1999. a, b, c
Barad, M. L.: Project Prairie Grass, a Field Program in Diffusion, Geophysical Research Papers, 59, 1958. a
Batchelor, G. K.: Diffusion in a field of homogeneous turbulence, Math. Proc. Cambridge, 48, 345–362, https://doi.org/10.1017/S0305004100027687, 1952. a
Brown, R. J. and Bilger, R. W.: An experimental study of a reactive plume in grid turbulence, J. Fluid Mech., 312, 373–407, https://doi.org/10.1017/S0022112096002054, 1996. a
Burba, G.: Eddy Covariance Method for Scientific, Industrial, Agricultural, and Regulatory Apllications: A Field Book on Measuring Ecosystem Gas Exchange and Areal Emission Rates, LI-COR Biosciences, Lincoln, NE, USA, 2013. a
Burton, M. R., Prata, F., and Platt, U.: Volcanological applications of SO2 cameras, J. Volcanol. Geoth. Res., 300, 2–6, https://doi.org/10.1016/j.jvolgeores.2014.09.008, 2015. a
Campion, R., Delgado-Granados, H., and Mori, T.: Image-based correction of the light dilution effect for SO2 camera measurements, J. Volcanol. Geoth. Res., 300, 48–57, https://doi.org/10.1016/j.jvolgeores.2015.01.004, 2015. a
Cassiani, M.: The Volumetric Particle Approach for Concentration Fluctuations and Chemical Reactions in Lagrangian Particle and Particle-grid Models, Bounda.-Lay. Meteorol., 146, 207–233, https://doi.org/10.1007/s10546-012-9752-3, 2013. a
Cassiani, M. and Giostra, U.: A simple and fast model to compute concentration moments in a convective boundary layer, Atmos. Environ., 36, 4717–4724, https://doi.org/10.1016/S1352-2310(02)00564-2, 2002. a
Cassiani, M., Franzese, P., and Giostra, U.: A PDF micromixing model of dispersion for atmospheric flow. Part I: development of the model, application to homogeneous turbulence and to neutral boundary layer, Atmos. Environ., 39, 1457–1469, https://doi.org/10.1016/j.atmosenv.2004.11.020, 2005. a, b
Csanady, G. T.: Turbulent Diffusion in the Environment, Springer Netherlands, Dordrecht, https://doi.org/10.1007/978-94-010-2527-0, 1973. a
de Arellano, V.-G., Dosio, A., Vinuesa, J.-F., Holtslag, A. A. M., and Galmarini, S.: The dispersion of chemically reactive species in the atmospheric boundary layer, Meteorol. Atmos. Phys., 87, https://doi.org/10.1007/s00703-003-0059-2, 2004. a
Dimotakis, P. E.: The mixing transition in turbulent flows, J. Fluid Mech., 409, 69–98, https://doi.org/10.1017/S0022112099007946, 2000. a
Dinger, A. S.: Videos of artificially released SO2 puffs recorded simultaneously with six UV SO2 cameras, Zenodo, https://doi.org/10.5281/zenodo.1299638, 2018.
Franzese, P. and Cassiani, M.: A statistical theory of turbulent relative dispersion, J. Fluid Mech., 571, 391–417, https://doi.org/10.1017/S0022112006003375, 2007. a, b, c
Gant, S. and Kelsey, A.: Accounting for the effect of concentration fluctuations on toxic load for gaseous releases of carbon dioxide, Journal of Loss Prevention in the Process Industries, 25, 52–59, https://doi.org/10.1016/j.jlp.2011.06.028, 2012. a
Gifford, F. A.: Statistical Properties of A Fluctuating Plume Dispersion Model, Adv. Geophys., 6, 117–137, https://doi.org/10.1016/S0065-2687(08)60099-0, 1959. a
Gifford, F. A.: Use of Routine Meteorological Observations for Estimating Atmospheric Dispersion, Nucl. Safety, 2, 47–51, 1961. a
Gliß, J., Stebel, K., Kylling, A., Dinger, A. S., Sihler, H., and Sudbø, A.: Pyplis-A Python Software Toolbox for the Analysis of SO2 Camera Images for Emission Rate Retrievals from Point Sources, Geosciences, 7, 134, https://doi.org/10.3390/geosciences7040134, 2017. a, b
Hanna, S.: A history of classic atmospheric dispersion field experiments, in: 90th Amer. Meteorol. Soc. Ann. Meeting, Atlanta (GA), 2010. a
Hanna, S. R.: Lagrangian and Eulerian Time-Scale Relations in the Daytime Boundary Layer, J. Appl. Meteorol., 20, 242–249, 1981. a, b
Hanna, S. R.: Applications in Air Pollution Modeling, in: Atmospheric Turbulence and Air Pollution Modelling. Atmospheric Sciences Library, edited by: Nieuwstadt, F. and van Dop, H., 275–310, Springer Netherlands, Dordrecht, https://doi.org/10.1007/978-94-010-9112-1_7, 1984. a
Hay, J. and Pasquill, F.: Diffusion from a Continuous Source in Relation to the Spectrum and Scale of Turbulence, Adv. Geophys., 6, 345–365, https://doi.org/10.1016/S0065-2687(08)60122-3, 1959. a, b
Hilderman, T. L., Hrudey, S. E., and Wilson, D. J.: A model for effective toxic load from fluctuating gas concentrations, J. Hazard. Mater., 64, 115–134, https://doi.org/10.1016/S0304-3894(98)00247-7, 1999. a
Jørgensen, H. E. and Mikkelsen, T.: Lidar measurements of plume statistics, Bound.-Lay. Meteorol., 62, 361–378, https://doi.org/10.1007/BF00705565, 1993. a
Jørgensen, H. E., Mikkelsen, T., and Pécseli, H. L.: Concentration Fluctuations in Smoke Plumes Released Near the Ground, Bound.-Lay. Meteorol., 137, 345–372, https://doi.org/10.1007/s10546-010-9532-x, 2010. a
Kaimal, J. C. and Finnigran, J. J.: Atmopheric Boundary Layer Flows, Oxford University Press, Oxford, England, 1994. a
Kantzas, E. P., McGonigle, A. J. S., Tamburello, G., Aiuppa, A., and Bryant, R. G.: Protocols for UV camera volcanic SO2 measurements, J. Volcanol. Geoth. Res., 194, 55–60, https://doi.org/10.1016/j.jvolgeores.2010.05.003, 2010. a, b
Kern, C., Kick, F., Lübcke, P., Vogel, L., Wöhrbach, M., and Platt, U.: Theoretical description of functionality, applications, and limitations of SO2 cameras for the remote sensing of volcanic plumes, Atmos. Meas. Tech., 3, 733–749, https://doi.org/10.5194/amt-3-733-2010, 2010. a, b, c
Kern, C., Werner, C., Elias, T., Sutton, A. J., and Lübcke, P.: Applying UV cameras for SO2 detection to distant or optically thick volcanic plumes, J. Volcanol. Geoth. Res., 262, 80–89, https://doi.org/10.1016/j.jvolgeores.2013.06.009, 2013. a
Kern, C., Lübcke, P., Bobrowski, N., Campion, R., Mori, T., Smekens, J. F., Stebel, K., Tamburello, G., Burton, M., Platt, U., and Prata, F.: Intercomparison of SO2 camera systems for imaging volcanic gas plumes, J. Volcanol. Geoth. Res., 300, 22–36, https://doi.org/10.1016/j.jvolgeores.2014.08.026, 2015. a
Lübcke, P., Bobrowski, N., Illing, S., Kern, C., Alvarez Nieves, J. M., Vogel, L., Zielcke, J., Delgado Granados, H., and Platt, U.: On the absolute calibration of SO2 cameras, Atmos. Meas. Tech., 6, 677–696, https://doi.org/10.5194/amt-6-677-2013, 2013. a, b, c
Luhar, A. K., Hibberd, M. F., and Borgas, M. S.: A skewed meandering plume model for concentration statistics in the convective boundary layer, Atmos. Environ., 34, 3599–3616, https://doi.org/10.1016/S1352-2310(00)00111-4, 2000. a
Marro, M., Nironi, C., Salizzoni, P., and Soulhac, L.: Dispersion of a Passive Scalar Fluctuating Plume in a Turbulent Boundary Layer. Part II: Analytical Modelling, Bound.-Lay. Meteorol., 156, 447–469, https://doi.org/10.1007/s10546-015-0041-9, 2015. a
Marro, M., Salizzoni, P., Soulhac, L., and Cassiani, M.: Dispersion of a Passive Scalar Fluctuating Plume in a Turbulent Boundary Layer. Part III: Stochastic Modelling, Bound.-Lay. Meteorol., 167, 349–369, https://doi.org/10.1007/s10546-017-0330-6, 2018. a, b
Mauder, M.: A Comment on “How Well Can We Measure the Vertical Wind Speed? Implications for Fluxes of Energy and Mass” by Kochendorfer et al., Bound.-Lay. Meteorol., 147, 329–335, https://doi.org/10.1007/s10546-012-9794-6, 2013. a
McElhoe, H. B. and Conner, W. D.: Remote Measurement of Sulfur Dioxide Emissions Using an Ultraviolet Light Sensitive Video System, JAPCA J. Air Waste Ma., 36, 42–47, https://doi.org/10.1080/00022470.1986.10466043, 1986. a
Mikkelsen, T., Jørgensen, H. E., Nielsen, M., and Ott, S.: Similarity Scaling Of Surface-Released Smoke Plumes, Bound.-Lay. Meteorol., 105, 483–505, https://doi.org/10.1023/A:1020380820526, 2002. a
Monin, A. S. and Yaglom, A. M.: Statistical Fluid Mechanics, Volume II: Mechanics of Turbulence, MIT Press, Cambridge, 1975. a, b, c
Mori, T. and Burton, M.: The SO2 camera: A simple, fast and cheap method for ground-based imaging of SO2 in volcanic plumes, Geophys. Res. Lett., 33, 1–5, https://doi.org/10.1029/2006GL027916, 2006. a, b
Mylne, K. R.: Concentration fluctuation measurements in a plume dispersing in a stable surface layer, Bound.-Lay. Meteorol., 60, 15–48, https://doi.org/10.1007/BF00122060, 1992. a
Mylne, K. R. and Mason, P. J.: Concentration fluctuation measurements in a dispersing plume at a range of up to 1000 m, Q. J. Roy. Meteor. Soc., 117, 177–206, https://doi.org/10.1002/qj.49711749709, 1991. a, b
Nappo, C. J.: Atmospheric turbulence and diffusion estimates derived from observations of a smoke plume, Atmos. Environ., 15, 541–547, https://doi.org/10.1016/0004-6981(81)90184-0, 1981. a
Orszag, S. A. and Patterson, G. S.: Numerical simulation of three-dimensional homogeneous isotropic turbulence, Phys. Rev. Lett., 28, 76–79, https://doi.org/10.1103/PhysRevLett.28.76, 1972. a
Osorio, M., Casaballe, N., Belsterli, G., Barreto, M., Gómez, A., Ferrari, J. A., and Frins, E.: Plume segmentation from UV camera images for SO2emission rate quantification on cloud days, Remote Sensing, 9, 517, https://doi.org/10.3390/rs9060517, 2017. a
Ouellette, N. T., Xu, H., Bourgoin, M., and Bodenschatz, E.: An experimental study of turbulent relative dispersion models, New J. Phys., 8, https://doi.org/10.1088/1367-2630/8/6/109, 2006. a
Pasquill, F.: The Estimation of the Dispersion of Windborne Material, Meteorol. Mag., 90, 33–49, 1961. a
Pasquill, F. and Smith, F. B.: Atmospheric Diffusion (3rd edition), Ellis Hordwood, Ltd, Chichester, England, 1983. a
Pinsky, M., Khain, A., and Korolev, A.: Theoretical analysis of mixing in liquid clouds – Part 3: Inhomogeneous mixing, Atmos. Chem. Phys., 16, 9273–9297, https://doi.org/10.5194/acp-16-9273-2016, 2016. a
Pope, S. B.: Turbulent Flows, Cambridge University Press, Cambridge, https://doi.org/10.1017/CBO9780511840531, 2000. a
Prata, A. J.: Measuring SO2 ship emissions with an ultraviolet imaging camera, Atmos. Meas. Tech., 7, 1213–1229, https://doi.org/10.5194/amt-7-1213-2014, 2014. a
Roberts, O. F. T.: The Theoretical Scattering of Smoke in a Turbulent Atmosphere, P. R. Soc. A, 104, 640–654, https://doi.org/10.1098/rspa.1923.0132, 1923. a
Sawford, B.: Micro-Mixing Modelling of Scalar Fluctuations for Plumes in Homogeneous Turbulence, Flow Turbul. Combust., 72, 133–160, https://doi.org/10.1023/B:APPL.0000044409.74300.db, 2004. a, b
Schauberger, G., Piringer, M., Schmitzer, R., Kamp, M., Sowa, A., Koch, R., Eckhof, W., Grimm, E., Kypke, J., and Hartung, E.: Concept to assess the human perception of odour by estimating short-time peak concentrations from one-hour mean values. Reply to a comment by Janicke et al., Atmos. Environ., 54, 624–628, https://doi.org/10.1016/j.atmosenv.2012.02.017, 2012. a
Schröter, M., Obermeier, A., Brüggemann, D., Plechschmidt, M., and Klemm, O.: Remote monitoring of air pollutant emissions from point sources by a mobile lidar/sodar system, J. Air Waste Manage. Assoc., 53, 716–23, 2003. a
Shraiman, B. I. and Siggia, E. D.: Scalar turbulence, Nature, 405, 639–646, https://doi.org/10.1038/35015000, 2000. a
Smekens, J. F., Burton, M. R., and Clarke, A. B.: Validation of the SO2 camera for high temporal and spatial resolution monitoring of SO2 emissions, J. Volcanol. Geoth. Res., 300, 37–47, https://doi.org/10.1016/j.jvolgeores.2014.10.014, 2015. a
Stull, R. B.: An Introduction to Boundary Layer Meteorology, Kluwer Academic Publisher, Boston, https://doi.org/10.1007/978-94-009-3027-8, 1988. a, b, c, d
Taylor, G. I.: Diffusion by continuous movements, P. Lond. Math. Soc., 20, 196–212, https://doi.org/10.1112/plms/s2-20.1.196, 1921. a
van Heerwaarden, C. C. and Mellado, J. P.: Growth and Decay of a Convective Boundary Layer over a Surface with a Constant Temperature, J. Atmos. Sci., 73, 2165–2177, https://doi.org/10.1175/JAS-D-15-0315.1, 2016. a
Vandaele, A., Hermans, C., and Fally, S.: Fourier transform measurements of SO2 absorption cross sections: II, J. Quant. Spectrosc. Ra., 110, 2115–2126, https://doi.org/10.1016/j.jqsrt.2009.05.006, 2009. a
Vickers, D. and Mahrt, L.: Quality Control and Flux Sampling Problems for Tower and Aircraft Data, J. Atmos. Ocean. Tech., 14, 512–526, https://doi.org/10.1175/1520-0426(1997)014<0512:QCAFSP>2.0.CO;2, 1997. a
Wilczak, J. M., Oncley, S. P., and Stage, S. A.: Sonic anemometer tilt correction algorithms, Bound.-Lay. Meteorol., 99, 127–150, 2001. a
Yee, E. and Wilson, D. J.: A Comparison Of The Detailed Structure In Dispersing Tracer Plumes Measured In Grid-Generated Turbulence With A Meandering Plume Model Incorporating Internal Fluctuations, Bound.-Lay. Meteorol., 94, 253–296, https://doi.org/10.1023/A:1002457317568, 2000. a
Yee, E., Wilson, D. J., and Zelt, B. W.: Probability distributions of concentration fluctuations of a weakly diffusive passive plume in a turbulent boundary layer, Bound.-Lay. Meteorol., 64, 321–354, https://doi.org/10.1007/BF00711704, 1993. a
Yee, E., Chan, R., Kosteniuk, P. R., Chandler, G. M., Biltoft, C. A., Bowers, J. F., Yee, E., Chan, R., Kosteniuk, P. R., Chandler, G. M., Biltoft, C. A., and Bowers, J. F.: Experimental Measurements of Concentration Fluctuations and Scales in a Dispersing Plume in the Atmospheric Surface Layer Obtained Using a Very Fast Response Concentration Detector, J. Appl. Meteorol., 33, 996–1016, https://doi.org/10.1175/1520-0450(1994)033<0996:EMOCFA>2.0.CO;2, 1994. a
Yeung, P. K.: Lagrangian Investigations of Turbulence, Ann. Rev. Fluid Mech., 34, 115–142, https://doi.org/10.1146/annurev.fluid.34.082101.170725, 2002. a
Yeung, P. K., Pope, S. B., and Sawford, B. L.: Reynolds number dependence of Lagrangian statistics in large numerical simulations of isotropic turbulence, J. Turbul., 7, 1–12, https://doi.org/10.1080/14685240600868272, 2006. a
- Abstract
- Introduction
- Artificial release experiment
- Turbulent dispersion
- Retrieval of CM trajectories and spread of artificially released puffs using a tomographic setup of SO2 cameras
- Results
- Turbulent dispersion in the vertical
- Conclusions and future work
- Code and data availability
- Appendix A: Details on the artificial release experiment
- Appendix B: Details on image processing methods
- Appendix C: Videos of puff releases
- Author contributions
- Competing interests
- Acknowledgements
- References
- Abstract
- Introduction
- Artificial release experiment
- Turbulent dispersion
- Retrieval of CM trajectories and spread of artificially released puffs using a tomographic setup of SO2 cameras
- Results
- Turbulent dispersion in the vertical
- Conclusions and future work
- Code and data availability
- Appendix A: Details on the artificial release experiment
- Appendix B: Details on image processing methods
- Appendix C: Videos of puff releases
- Author contributions
- Competing interests
- Acknowledgements
- References