the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Pre-launch calibration results of the TROPOMI payload on-board the Sentinel-5 Precursor satellite
Quintus Kleipool
Antje Ludewig
Ljubiša Babić
Rolf Bartstra
Remco Braak
Werner Dierssen
Pieter-Jan Dewitte
Pepijn Kenter
Robin Landzaat
Jonatan Leloux
Erwin Loots
Peter Meijering
Emiel van der Plas
Nico Rozemeijer
Dinand Schepers
Daniel Schiavini
Joost Smeets
Giuseppe Vacanti
Frank Vonk
Pepijn Veefkind
The Sentinel-5 Precursor satellite was successfully launched on 13 October 2017, carrying the Tropospheric Monitoring Instrument (TROPOMI) as its single payload. TROPOMI is the next-generation atmospheric sounding instrument, continuing the successes of GOME, SCIAMACHY, OMI, and OMPS, with higher spatial resolution, improved sensitivity, and extended wavelength range. The instrument contains four spectrometers, divided over two modules sharing a common telescope, measuring the ultraviolet, visible, near-infrared, and shortwave infrared reflectance of the Earth. The imaging system enables daily global coverage using a push-broom configuration, with a spatial resolution as low as 7×3.5 km2 in nadir from a Sun-synchronous orbit at 824 km and an Equator crossing time of 13:30 local solar time.
This article reports the pre-launch calibration status of the TROPOMI payload as derived from the on-ground calibration effort. Stringent requirements are imposed on the quality of on-ground calibration in order to match the high sensitivity of the instrument.
A new methodology has been employed during the analysis of the obtained calibration measurements to ensure the consistency and validity of the calibration. This was achieved by using the production-grade Level 0 to 1b data processor in a closed-loop validation set-up. Using this approach the consistency between the calibration and the L1b product, as well as confidence in the obtained calibration result, could be established.
This article introduces this novel calibration approach and describes all relevant calibrated instrument properties as they were derived before launch of the mission. For most of the relevant properties compliance with the calibration requirements could be established, including the knowledge of the instrument spectral and spatial response functions. Partial compliance was established for the straylight correction; especially the out-of-spectral-band correction for the near-infrared channel needs future validation. The absolute radiometric calibration of the radiance and irradiance responsivity is compliant with the high-level mission requirements, but not with the stricter calibration requirements as the available on-ground validation shows. The relative radiometric calibration of the Sun port was non-compliant. The non-compliant subjects will be addressed during the in-flight commissioning phase in the first 6 months following launch.
- Article
(25413 KB) - Full-text XML
- BibTeX
- EndNote
The Sentinel-5 Precursor (S5P) mission represents the first in a series of atmospheric observing systems within Copernicus (Ingmann et al., 2012). Copernicus is the European Union's Earth observation programme, looking at our planet and its environment for the ultimate benefit of all European citizens. The programme is coordinated and managed by the European Commission. It is implemented in partnership with the member states, the European Space Agency (ESA), the European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT), the European Centre for Medium-Range Weather Forecasts (ECMWF), EU agencies, and Mercator Ocean.
The S5P mission is a single-payload satellite in a low Earth orbit that provides daily global information on concentrations of trace gases and aerosols important for air quality, climate forcing, and the ozone layer. The payload of the mission is the TROPOspheric Monitoring Instrument (TROPOMI), which is jointly developed by the Netherlands and ESA, and consists of a spectrometer with spectral bands in the ultraviolet (UV), the visible, the near-infrared (NIR), and the shortwave infrared (SWIR) wavelengths (Veefkind et al., 2012). The selected wavelength range for TROPOMI allows observation of key atmospheric constituents, including ozone (O3), nitrogen dioxide (NO2), carbon monoxide (CO), sulfur dioxide (SO2), methane (CH4), formaldehyde (CH2O), aerosols, and clouds.
With its launch on 13 October 2017 the S5P mission will avoid large gaps in the availability of global atmospheric products among its predecessors SCIAMACHY (Bovensmann et al., 1999), GOME-2 (Munro et al., 2016), and OMI (Levelt et al., 2006) and the future missions Sentinel-4 and Sentinel-5, scheduled for launch in 2022 and 2021 respectively.
There is a synergy between TROPOMI and the NOAA/NASA Suomi NPP (National Polar-orbiting Partnership) satellite. Identified synergies include the use of the VIIRS (Visible Infrared Imaging Radiometer Suite) for highly spatially resolved cloud information and OMPS (Ozone Mapping and Profiler Suite) for high vertically resolved stratospheric ozone profiles. It is planned to fly the S5P mission within approximately 5 min of NPP, thus building upon the successes of the A-Train constellation of Earth observation satellites.
The S5P satellite has been injected into a near-polar, near-Sun-synchronous orbit by a Rockot launcher. The initial 6 months of in-orbit operation will cover spacecraft, TROPOMI, and ground segment level commissioning activities (phase E1). The E1 phase will be followed by a 6.5-year exploitation E2 phase during which the spacecraft will be operated according to a stable, fully repetitive scenario, with systematic processing and archiving of data products within the S5P Payload Data Ground Segment (PDGS). The mission products will be disseminated to both operational users (e.g. Copernicus services, national Numerical Weather Prediction (NWP) centres, value adding industry) and the scientific user community.
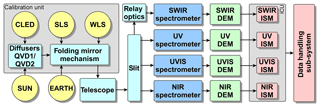
Figure 1Schematic overview of the TROPOMI instrument. Shown are the different light paths from the Earth, Sun, and internal sources CLED, WLS, and SLS to the TROPOMI spectrometers. The detector read-out is performed by DEMs, and the DEM control and data acquisition are performed by the ISMs.
2.1 Instrument overview
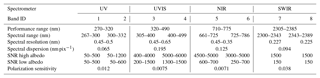
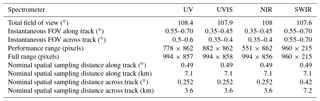
Table 1Main spectral characteristics of the four TROPOMI spectrometers and the definition of the TROPOMI spectral bands with identifiers 1–8. The listed values are based on on-ground calibration measurements and valid at the detector centre. The performance range is the range over which the requirements are validated; the full range in general is larger. The listed signal-to-noise ratio (SNR) values are given for the nominal measurement configuration for a mid-latitude reference spectrum. Both the high- and low-albedo SNR values over the spectral range including absorption lines are given.
The TROPOMI instrument is a space-borne nadir-viewing push-broom imaging spectrometer which was designed with OMI heritage. It has four separate spectrometers covering wavelength bands between the UV and the SWIR wavelengths. Using passive remote-sensing techniques the instrument measures the solar radiation reflected by and radiated from the Earth at the top of the atmosphere. It operates in a push-broom configuration with a wide swath of 108∘. Combined with a polar circular orbit of 824 km in altitude, the wide swath allows TROPOMI to achieve complete daily global surface coverage. Light from the entire swath is recorded simultaneously and dispersed onto two-dimensional imaging detectors: the position along the swath is projected onto one direction of the detectors, and the spectral information for each position is projected onto the other direction.
TROPOMI utilizes a single telescope to image the target area onto a rectangular slit that acts as the entrance slit of the spectrometer system. There are four different spectrometers, each with its own optics and detector: medium-wave UV, longwave UV combined with visible (UVIS), NIR, and SWIR. The spectrometers for UV, UVIS, and NIR are jointly referred to as UVN. The detectors for the UVN spectrometers are charge-coupled devices (CCDs). The SWIR part of the instrument is much colder than the UVN part and uses a complementary metal-oxide semiconductor (CMOS) detector. An optical relay separates the SWIR part thermally from the rest of the instrument. The interface is the pupil stop for the SWIR spectrometer.
TROPOMI has calibration light sources on-board: a spectral line source (SLS) consisting of five laser diodes in the SWIR range, a white light source (WLS), a common light-emitting diode (CLED), and detector LEDs (DLEDs). The DLEDs are situated close to each of the detectors, while the other sources are located in a calibration unit. A schematic overview of TROPOMI is shown in Fig. 1. Via different settings of the calibration unit, the telescope receives light from different sources: the Earth, the Sun, and the on-board calibration light sources. Additionally, the telescope can be closed off.
Each of the detectors is divided into two halves, which yields a total of eight spectral bands. Table 1 summarizes the main characteristics of each of the TROPOMI optical spectrometers and the definition of the spectral bands.
2.2 Telescope
Table 2Main geometrical performance parameters of each TROPOMI spectrometer. The listed nominal values are given at nadir for 1080 ms of co-addition time and a row binning factor of 2 for bands 2–6. Band 1 is not shown; it has a row binning factor of 16 and the across-track sampling distance is 8 times higher than for bands 2 to 6. The pixel dimensions (spectral × spatial) include the spectral smile.
The telescope is a two-mirror reflective telecentric telescope that follows an f–θ law; i.e. it has the property of creating a flat image field at the plane of interest, with a focused beam that is always perpendicular to that plane. It has a large field of view (108∘) in the across-track (swath, across-flight, or spatial) direction, and a small field of view in the along-track (along-flight or spectral) direction. The two telescope mirrors are referred to as the primary and secondary mirrors, in the order in which light from the Earth passes through the telescope. A strip on the Earth's surface is imaged by the primary mirror. The intermediate image, located close to the primary mirror, is re-imaged by the secondary mirror on the entrance slit of the spectrometer system. At the same time, the entrance pupil is imaged to infinity. Both mirrors are concave and aspherical. In the optical path between the two mirrors, coincident with the intermediate pupil, there is a polarization scrambler preceded by a rectangular aperture. It is this aperture that determines the telescope's throughput. The polarization scrambler comprises two wedge pairs. The edges are optimized in thickness to cancel out the birefringence of each wedge pair along the optical axis.
The width of the entrance slit defines the field of view in the spectral (along-track) direction. The light for the UVIS and NIR spectrometers passes through the slit, while light destined for the UV and the SWIR spectrometers is reflected from the side of the slit. Both the SWIR and the UV spectrometers have their own slit. A consequence of this arrangement is that the UV and the SWIR spectrometers are not co-registered with the UVIS and the NIR spectrometers. The light detected in the UV and SWIR ranges originates from another ground position than the light detected in the UVIS and NIR ranges. The difference is around 15 km in nadir and can be as high as 35 km at the edge of the swath; this corresponds to approximately 2 s in flight time or two scan lines in the baseline operational configuration. Some of the key geometrical performance parameters of the instrument are given per spectrometer in Table 2.
2.3 UVN module
The three UVN spectrometers are conceptually almost the same: each images a slit on a detector, dispersing the light by means of a grating. The UVIS and NIR spectrometers share the same 280 µm wide slit. Light for the UV and SWIR spectrometers first reflects off the UVIS–NIR slit and then passes through a dichroic that directs the SWIR component of the light towards the SWIR relay optics. The UV light is imaged on a second slit on a conjugate plane to the focal plane of the telescope. This slit is 696 µm wide on its conjugate plane, which corresponds to a virtual slit with a width of 560 µm. Using cylindrical optics, the slit is imaged only in the spectral dimension. This removes the strict requirement on the sharpness of the slit edges in the spatial dimension.
At the end of the spectrometer, the light falls onto a CCD. One direction of the CCD corresponds to the spatial (across-track) dimension; the other direction corresponds to the spectral (along-track or flight) dimension. The CCD pixel size is 26 µm × 26 µm, and the total number of pixels in the imaging area is 1024 × 1024. The image of the slit in the across-track direction is about 862 pixels wide, the remaining pixels being used for calibration and monitoring purposes. The dimensions of the slit image on the detectors are also given in Table 2. During data acquisition, UVN pixels can be binned in the spatial direction to decrease noise at the cost of resolution.
2.3.1 UVN spectrometers
The beam from the telescope is imaged on the slit telecentrically, as mentioned above. Light for the UV spectrometer actually reflects off the slit; therefore this first slit is not yet the limiting slit for the spectrometer. The reflected image is re-imaged by a collimator and a folding mirror to the actual entrance slit (UV slit) of the spectrometer. A dichroic separates the SWIR band from the UV band. Folding mirrors, one of them out of plane, guide the light onto the grating. The diffracted light passes through the imaging optics. The imaging optics consist of three lenses, all three de-centred and tilted with respect to the optical axis in order to obtain a good co-registration performance and to remove unwanted specular reflections (“ghosts”) from the system. The last lens and the CCD plane are tilted in order to correct for axial colour aberrations. To reduce the amount of spectral straylight that could reach the detector, a spatially varying coating is used on the last surface before the detector. This surface is the flat side of the last lens. At each location on the lens the coating transmits light of the expected wavelength, and it reflects light whose wavelength is 15 nm larger.
For the UVIS spectrometer, the light is collimated after passing through a dichroic. Via four folding mirrors the light is guided to the grating. Just as in the UV spectrometer, there is an out-of-plane folding mirror. The grating disperses the light, and the subsequent imaging system images the slit on the detector. The imager consists of five lenses, the last one has a flat side facing the detector.
For the NIR spectrometer, the slit image is guided via a dichroic and three folding mirrors and a collimating lens onto the grating. The dispersed light is imaged on the detector by three de-centred lenses.
Each UVN spectrometer contains LEDs to illuminate the detectors directly. These DLEDs are used for calibration and performance monitoring purposes. The DLEDs emit green light with a wavelength of 570 nm. The response of the individual UVN detectors to the DLED is not identical, as the optical coatings differ per spectrometer.
2.4 SWIR relay optics
Relay optics are necessary to be able to thermally separate the SWIR spectrometer from the UVN spectrometers. The SWIR spectrometer is cooled to around 205 K and its detector to 140 K, while the common telescope, calibration unit, and UVN optics are much warmer (290 K). The light from the telescope is imaged onto a pupil at the entrance of the SWIR spectrometer. The reflective slit, the collimator lens, and the front surface of the dichroic are shared with the UV spectrometer. The dichroic is made of silicon, providing a good filter function for a wide range of wavelengths. The pupil stop of 9 × 18 mm2 is at the end of the relay optics. This stop deliberately vignettes the beam, as this is the stop for the SWIR spectrometer. There is some amount of chromatic aberration, leading to a small magnification error of 0.008 %.
2.5 SWIR module
Functionally, the SWIR spectrometer is similar to the UVN spectrometers. The optical system is divided into six sections: SWIR entrance pupil, telescope, slit prism, collimator, grating, and imager. The imager interfaces with the focal plane array within the detector module.
The SWIR entrance pupil is formed by the UVN telescope and SWIR relay optics, and it forms the optical interface between the UVN and SWIR subsystems. The SWIR telescope receives its input from the main UVN optics and focuses it on a slit prism. The slit delimits the spatial extent of the image, defining the along-track field of view, as well as the spectral resolution (in combination with the collimator and the grating). The collimator then transfers the image of the slit to a grating that causes spectral separation. A final imager forms an image of the scene on the SWIR detector. The DLED for SWIR is located close to the detector and emits light at around 2200 nm.
2.6 Calibration unit
The calibration unit contains two rotation mechanisms: one diffuser carousel and one folding mirror. The diffuser carousel includes two quasi volume diffusers (QVDs) and has six defined positions: one position for each of the two Sun diffusers (QVD1 and QVD2), one position for the WLS, one position for the SLS (laser diodes), and two positions for the CLED. When the diffuser carousel is in the WLS position, the calibration port towards the Sun is closed, so that when the WLS is switched off, a dark measurement can be performed. One of the two Sun diffusers (QVD2) is used to monitor optical degradation and is employed only occasionally for Sun measurements during nominal operation.
The second rotation mechanism deploys a folding mirror in front of the telescope. This folding mirror directs the light from the Sun or the calibration sources towards the primary mirror of the telescope. The folding mirror is curved such that the large field of view of the telescope can be completely illuminated. When the folding mirror is deployed, the nadir view is blocked. This means that this mechanism can also function as an instrument shutter.
When the telescope looks directly to Earth, the diffuser carousel is in the closed position to block off the Sun port. For a Sun calibration, the diffuser carousel is rotated such that it opens the Sun port and directs the light towards the deployed folding mirror. The folding mirror itself closes the nadir port. In the monitoring diffuser mode (QVD2), the carousel is rotated by 180∘ with respect to the other diffuser mode. For the measurements with Sun and CLED the light passes through the diffusers, for WLS and SLS the light is reflected off the side of QVD1 and QVD2 respectively. For calibration with the WLS the diffuser carousel is placed in the same position as when closed. The difference is that the folding mirror is deployed so that the telescope receives light from the calibration source. A curved mirror on the back of the Sun diffuser reflects light from the WLS towards the folding mirror. The monitoring diffuser has a flat diffusing surface to reflect the light from the SLS towards the telescope. The optical path of the CLED can be chosen to be through either the Sun or the monitoring diffuser. The CLED light passes through the same optical elements as the Sun, but then in the opposite direction. In CLED mode, the light of the Sun is closed off.
2.7 UVN detectors and electronics
The three UVN spectrometers are equipped with separate but identical detector modules (DEMs) of the same type and configuration. Each UVN–DEM is equipped with a CCD sensor and front-end electronics, providing the raw digitized measurement data to the instrument control unit (ICU). The SWIR module has a CMOS detector and a different DEM than the one used in the UVN module, and a description can be found in Hoogeveen et al. (2013).
2.7.1 DEM construction
The main structure of each of the UVN–DEMs is the detector-side housing, which is an aluminium frame. It is the interface to the optical bench on the outside of the UVN–DEM. The support for the focal plane assembly, including the detector circuit and the thermal bus unit (TBU) side housing, is mounted onto the detector housing. The walls near the CCD are designed with an increased thickness in order to maximize radiation shielding. The focal plane assembly consists of the detector circuit including detector, the heat sink, the detector mount, and the thermal strap. Its functions are to provide mechanical, thermal, and electrical connections between the detector and the respective interfaces. The TBU-side housing acts as the closing lid of the UVN–DEM and is also the mechanical interface for the main circuit card and for the thermal strap and acts as the thermal interface to the warm TBU stage.
One of the main difficulties of the UVN–DEM thermal design is that the CCD has to remain at a much colder temperature than the electronics boards, which are in the same housing. This creates temperature gradients and the main task of the thermal design is to control these gradients so that both CCD and electronics can be operated in their own temperature range, which is 208 K for the three UVN CCDs and 294 K for the three UVN–DEMs. Critical to the scientific performance is the insulation of the detector from the electronics because their operating temperatures differ so much. This is achieved by encapsulating the CCD in a box-shaped multilayer insulation. As the CCD has to be operated at cold temperatures, it is thermally linked to a cold finger interface. Additionally, the detector is mounted on a hexapod whose legs provide the required thermal insulation from the rest of the housing.
2.7.2 CCD layout
The UVN CCDs are constructed with two sections, namely an image section in which the light flux is accumulated during exposure and a storage section in which the signal is stored for read-out, while the next image is accumulated in the image section. The storage section is shielded from incident light by a mask but is otherwise identical to the image section. The detectors are frame-transfer-type CCDs, which means that the pixels of the image and storage sections and the read-out register are connected into vertical shift chains; i.e. the charges of the pixel cells can be shifted down line by line. A frame transfer moves the contents of the image section into the storage section. The transfer is an operation in which 1026 line shifts are performed in quick succession, shifting in zero-charge lines from the top and shifting the charge of the bottom lines into the read-out register. At the end of the frame transfer, the entire image section, as well as the topmost line of the storage section, is emptied of charge and the old image section contents are moved to the 1024 bottom-most lines of the storage section. After the frame transfer, a new exposure starts in the image section, while the finished exposure is read out from the storage section. The frame transfer operation is handled internally by the UVN–DEM upon reception of a command to initiate a frame transfer. A two-phase clocking scheme is used to achieve a frame transfer time of ≤800 µs.
Once the frame is transferred to the storage section, the read-out starts. Only the charge in the storage section is shifted down one line at a time, leaving the contents of the image section unaffected. The operation shifts a zero-charge line into the topmost line of the storage section and the charge of the bottom-most line is shifted into the read-out register. The charge shifted into the read-out register is added to the charge already there. The process of shifting multiple lines into the read-out register before it is read out (and thereby emptied) is called binning or row binning. The capacity of the read-out register is larger than the pixel full well (PFW) to allow binning with a factor of 2–4.
The advantages of row binning are that it decreases the data rate and increases the signal-to-noise ratio (SNR). The disadvantage of binning is that resolution (information) is lost, as it is an irreversible process. The row binning factor is not necessarily the same across the CCD, but can be varied through instrument configuration. The binning can only be performed in the row direction, corresponding to the spatial dimension. This allows us to, for example, influence the ground pixel size across track or to bin all the rows from shielded rows of the image section into a single row. Spectral binning in the column direction is not possible.
Once the charge is shifted into the read-out register, it can be read out by shifting the charge pixel by pixel (column by column) onto the output node(s) of the detector. The TROPOMI UVN CCD uses two output nodes, one at each side of the register, effectively dividing each detector into two bands. The read-out register has 4 pixels on each side in addition to the 1024 pixels (columns) of the image and storage sections of the detector. These pixels, referred to as pre-scan and post-scan pixels, can be read out and used for calibration or monitoring purposes. In fact, it is possible to even read past the post-scan pixels; the resulting pixels are referred to as over-scan pixels and can be used for calibration or monitoring purposes as well.
2.7.3 CCD video chain
Figure 2 shows the different elements of the read-out chain for the UVN detectors. The output amplifier, which is connected to the output node, provides two gain settings: these are programmable according to the expected signal strength.
The main characteristics of the electronic circuitry associated with the sensor are summarized in Table 5. The individual pixels' full-well capacity amounts to about 0.8 × 106 electrons (e−). The register pixels' full-well capacity amounts to about 1.7 × 106 electrons (e−) varying per band. After the output node of the register, the signal of each of the detector bands is passed through a video amplifier with a fixed gain and then processed by a National Semiconductor LM9864QML integrated circuit. This circuit contains a correlated double sampling unit (CDS), a unit in which a digital programmable analog offset can be added (DAC), an 8-bit programmable gain amplifier (PGA), and a 14-bit analog-to-digital converter (ADC). The CDS can amplify the signal by a factor of 2. Apart from the CDS gain, all values can be set per detector band.

Figure 2Schematic of the read-out chain of the UVN detectors. In the output node charge is converted to a voltage, the analog video chain amplifies the signal with a fixed gain, the signal is detected in the correlated double sampling unit (CDS), an analog offset can be added (DAC), and the signal can be amplified by the programmable gain amplifier (PGA) before its conversion to digital units by an analog-to-digital converter (ADC).
2.8 Instrument control unit
The ICU is a unit consisting of eight boards with software running on a LEON processor. The main interfaces to the satellite platform are Mil-Bus for command and control and SpaceWire for science data output.
The ICU hardware includes the following parts: the processing function for the SpaceWire bus; on-board time, synchronization, and clock functionality; image processing and packetization, implemented in one field-programmable gate array (FPGA) per DEM; an ICU interface to the four DEMs; thermal control hardware drivers; and a power supply providing ICU internal power and secondary power to the DEMs. The ICU hardware is fully redundant except for the DEM interfaces and image processing, which are implemented as one non-redundant block per detector. The ICU is powered using two redundant power lines.
The ICU software performs the following main tasks: command and control, including command reception, scheduling, and execution; parameter management; thermal control; internal and external data acquisition and generation of housekeeping and engineering data packets; science data management; and on-board time synchronization control. The ICU is equipped with four identical, instrument-specific modules (ISMs), each controlling one DEM. For the three UVN–DEMs, the ICU controls the details of each frame transfer, line transfer, and line read-out. The UVN detectors are synchronized to minimize electromagnetic compatibility (EMC) effects, such that no frame transfer can occur while a measurement is read from the register. In the case of the SWIR DEM, the ICU only provides a signal to start the image acquisition, the details being left to the SWIR DEM itself. For the UVN CCD detectors, each detector is split into two halves as dictated by the detector design. This corresponds with the two bands per CCD detector, for consistency, the SWIR CMOS detector and spectral range is divided into two halves and bands as well.
The received pixel data arrive row by row; i.e. all pixels of the first row are received first, followed by all pixels of the next row, and so on. Depending on the binning scheme used (applicable to UVN only), a read-out of an entire exposure might consist of any number of rows from 0 to 1024 for each detector half. Image processing in the ICU is performed independently for the halves of a detector.
Up to 800 pixels (columns) can be read out from each UVN detector half. The SWIR detector has 500 columns per band and 256 rows. One additional virtual row can be read-out for SWIR for monitoring purposes. The co-addition factor can be set for all bands to be between 0 and 512, and it can be programmed separately per band. It is possible to co-add up to 256 consecutive images.
Information concerning the individual signals of a pixel that contribute (i.e. add up to) to a co-addition is lost, with one exception. One configurable detector column per band is also stored separately for every exposure and co-addition of an image. The data for these “small-pixel columns” are included in the science data and provide information on a higher spatial resolution than the data for other columns.
3.1 Purpose of calibration
For the retrieval of absolute densities of atmospheric constituents, the TROPOMI instrument needs to be calibrated prior to launch with respect to known radiometric sources. During the operational phase relative calibrations using the Sun as a source are performed. Calibration measurements are used to derive calibration key data (CKD) that are required by the L01b processor to compute absolute geolocated radiance values from the raw instrument L0 data (KNMI, 2017). From the calibration of OMI (Dobber et al., 2006), the precursor of TROPOMI, several lessons were learned with respect to how to validate the results obtained. The most important improvement with respect to OMI is the use of the production-grade L01b processor during the calibration campaign and in the analysis of all measurement data.
3.2 Use of the L01b processor
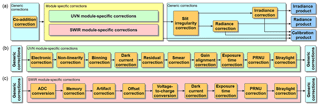
Figure 3(a) High-level overview of the different processing steps in the L01b processor. For the output products “radiance”, “irradiance”, and “calibration”, different algorithms are applied. The generic corrections are applied to all detectors. Panels (b) and (c) show the module-specific correction steps that differ between the UVN and SWIR modules. Note that not all processing steps are shown. In this paper all generic and UVN-specific corrections are discussed as well as the SWIR pixel response non-uniformity (PRNU). The other SWIR-specific corrections are presented in Hoogeveen et al. (2013) and Tol et al. (2018).
During the on-ground calibration of the TROPOMI instrument the production-grade L01b processor is directly employed to preprocess the calibration measurement data to every desired processing level, which is then used to calculate the CKD for the next step. Figure 3 gives a high-level overview of the different processing steps in the L01b processor for the generic instrument and UVN-specific corrections. Furthermore the processor is used to both verify and validate the CKD by reprocessing the measurement data, analysing the remaining uncorrected effects, and determining the CKD independently from different datasets. The use of the L01b processor ensures that the same algorithms are used in the correct order for all data and no additional sources for errors and inconsistencies are introduced.
The L01b processor also computes the error and the noise associated with the processed signal, which has the advantage that an error margin is provided for all CKD. At each individual processing step the noise and error of the signal are established. The noise is calculated quadratically from the read-out noise and the shot noise and converted along with the signal at each processing level. Similarly, the error at each processing level is established through formal error propagation including all error sources that enter the equation. One important error source are the CKD themselves used in the specific step; here the error supplied along with the CKD is used. Note that this latter error may stem from measurement noise in the original calibration measurements that becomes a systematic error in CKD and thus the L1b product. This is a novel approach to be implemented in a L01b data processor and not straightforward. The L1b product consists of separate irradiance and radiance data files, the more important product, reflectance, must be calculated by the user themselves. In order to ensure that the error in the reflectance is realistic, tailoring may be needed in the error calculations at each step. For example, the error in the pixel response non-uniformity (PRNU) CKD is not propagated because the PRNU effect itself will cancel out in the reflectance and so should its systematic error. All errors in this paper are given as 1σ values.
The advantage of using the production-grade processor over a separate prototype processor is that the former is intended to be used for systematic data processing in an production environment (the PDGS) and therefore is capable of digesting large volumes of data. In addition, a production-grade processor must meet all sorts of requirements on reliability and accuracy, which have to be validated before the software is accepted. A disadvantage is that such a processor is more difficult to operate and configure than a prototype processor, which calls for additional software to harness it; for TROPOMI this was implemented as the calibration framework.
The L01b data processor itself was developed by a collaborative software lead by KNMI. The correction and annotation algorithms that are implemented in the processor are described in the Algorithm Theoretical Basis Document (ATBD) (KNMI, 2017) and were subject to extensive software validation. This latter testing is performed by comparing the output of a compiled executable of the L01b processor against the output of an independent software implementation, in a different computer language, of the algorithms in the ATBD. From now on, this validated executable of the L01b processor is integrated in the calibration framework, which manages the configuration, production, and validation of the CKD. With this novel approach it is assured that the L01b processor and its CKD are consistent and validated and that the configuration is reproducible.
It is noteworthy that approximately equal effort was spent on the derivation on one side and the validation of the CKD on the other side. In this paper we will show the validation of the CKD for a few topics only to demonstrate the methodology. To show all validation results is not feasible within the limited space, and we will therefore only mention important validation results where needed.
The measurements and requirements for the used sources for the on-ground calibration of TROPOMI were devised by the science team under the lead of the Royal Netherlands Meteorological Institute (KNMI) and assisted by the Netherlands Institute for Space Research (SRON) for the SWIR part. These measurements were designed in such a way that they seamlessly integrated with the validation objectives in the calibration framework. The implementation and execution of the calibration measurements were performed by the industry team under the lead of Airbus Defence and Space Netherlands (ADSNL).
3.3 Calibration ground support equipment
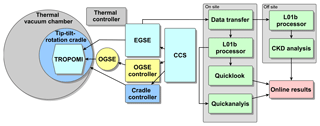
Figure 4Calibration facilities. The instrument TROPOMI is placed on a tip–tilt–rotation stage (“cradle”) inside a thermal vacuum chamber. The optical ground support equipment (OGSE), the cradle, and the electric ground support equipment (EGSE) are all commanded from the the central checkout system (CCS). The measurement data and ancillary data from the cradle and OGSE are transferred to an on-site server. Locally quick look and quick analysis is performed; the derivation of the CKD is performed off-site. Preliminary results and the quick look data are made available online for all parties concerned.
A high-level overview of the different subsystems which are part of the calibration set-up are shown in Fig. 4. From the TROPOMI central checkout system (CCS) all systems can be controlled manually or via scripts. All operations of the instrument, optical, electrical, and mechanical ground support equipment (OGSE, EGSE, MGSE) were performed by ADSNL and subcontractors. The CCS was manned 24/7, allowing for a 24/7 measurement campaign. The CCS also shows the raw data in near-real time and allows for functional checks of the equipment. The instruments are controlled via the EGSE.
The measurement data and ancillary data from the cradle and OGSE are transferred to an on-site server (PRISM). The L01b processor runs locally on the measurement data and dedicated software combines the ancillary data from the set-up with the measurement data. In parallel, the L0 data are transferred to off-site premises at the KNMI. Locally, quick look and quick analysis is performed; the derivation of the CKD is performed off-site. Preliminary results and the quick-look data are made available online for all parties concerned. Changes to set-ups and individual measurement sessions are recorded in a an online logbook.
From the EGSE the data are directly transferred to and processed on-site by the L01b processor by KNMI. Together with dedicated quick look and analysis tools, this provides the opportunity to perform on-site near-real-time analysis on the quality of the measurement. Also the L01b processor is tested in an operational scenario. During the calibration campaign there is not enough time to carry out the whole CKD derivation to assess whether the measurement is successful. Instead, pre-processing with the L01b processor is used by the on-site science team to assess the quality of the measurement itself in terms of SNR and illumination homogeneity, for example, to be able to derive the CKD with sufficient accuracy. The capability of performing this quality assessment in parallel with the commissioning of a new measurement set-up by the industry team was a key driver to success for completing the calibration campaign within the given time frame. The calibration key data themselves were derived on separate processing infrastructure by separate off-site science teams at KNMI (for UVN and instrument key data) and SRON (for SWIR-specific key data).
3.4 Calibration facility
The on-ground calibration for TROPOMI was performed in a 6.5 m diameter thermal vacuum tank located in a class 10000 (ISO7) clean room at the Centre Spatial de Liège (CSL) in Belgium. The campaign started at the end of December 2014 and lasted until the beginning of May 2015. A thermal shroud cooled by liquid nitrogen ensured that the instrument was kept at operational temperatures during the entire calibration campaign. The instrument was mounted on a tip–tilt stage stacked on top of a rotation stage. This cradle allowed us to calibrate the full instrument swath (108∘) under operational conditions. The thermal vacuum chamber has a single 30 cm diameter window. By moving the instrument with the cradle in front of the window, all swath angles can be illuminated one by one. Prior to the calibration campaign, pre- and post-environmental tests were performed to assess the instrument's stability with respect to vibrations and thermal cycling. The on-ground calibration was split into two parts: the Earth port configuration and the Sun port configuration. During a vacuum break between the two parts, the instrument was repositioned on the cradle to be able to perform the Sun port calibration. For the repositioning the area around the thermal vacuum chamber was kept at clean room class 100 (ISO5).
In this section we will discuss the calibration of the CCD detectors of the UVN module. All these calibrations are performed with the internal sources of the instrument or dark measurements. All detector calibration results of the CMOS SWIR detector are reported in Hoogeveen et al. (2013). The PRNU calibration of both the UVN and SWIR detectors is excluded here because it was derived as part of the total radiometric response calibration using an external WLS measurement. The results of the PRNU analysis are reported in Sect. 6.4.
4.1 Detector dark current calibration
Dark current is defined as the dark current flux times the elapsed time during which signal is acquired. The dark current flux itself can vary from pixel to pixel and also depends on detector temperature. The temperature is constant over the entire detector, and therefore over all detector pixels. The detector temperature is actively thermally controlled. According to theory, each additional kelvin causes an increase in the dark current of less than 3 %. Since the expected temperature fluctuations are far smaller, the temperature dependence is ignored in the L01b correction.
The dark current is modelled as the sum of both the image section dark current and storage section dark current. The elapsed time associated with the image dark current is the net exposure time. During the transfer of the frame in the CCD image section to the CCD storage section, additional dark current is formed similar to smear. The storage dark current built up during the storage time is a function of the row number.
Unbinned background measurements are used in this analysis, for at least two different exposure times. These are preprocessed up to and including binning correction. The image section dark current per pixel is derived as the slope of the graph of pixel signal against exposure time. The intercept of this graph contains a row dependency because of the residence time of the charge in the storage section. Therefore, the (smear-corrected) intercepts of one detector column form a linear function of the residence time; the slope of this function is the storage section dark current.
Specific dark current measurements were obtained with three different exposure times, the longest being more than 500 s, and are only taken at nominal temperature. The signals are amplified with a factor of approximately 15 using the CCD and PGA electronic gains.
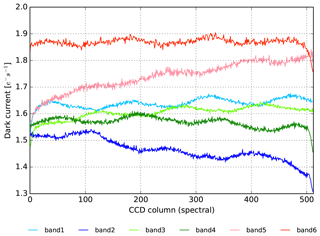
Per pixel, a standard linear regression least-squares fit is made; the image area dark current is now the linear coefficient. Figure 5 shows the row-averaged dark current in the image section for all UVN bands. The average dark current is lower than 2 , and thus very low. The average per band is shown in Table 5.
4.2 Detector smear
The purpose of the smear correction algorithm is to negate the effect of frame transfer smear, which is the added contribution of the signal due to the finite transfer time. The smear is always positive and the correction consists of a subtraction. With detailed knowledge of the row transfer process it is possible to compute the exact amount of smear generated. The detector smear algorithm is therefore an analytical correction in the L01b data processing chain that requires no calibration key data. For more detail the reader is referred to L01b data processor ATBD (KNMI, 2017).
4.3 Electronic conversion
The L01b processing chain contains numerous multiplicative factors that, taking into account the appropriate offset corrections, scale the measured signal from digital numbers (DNs) to radiance or irradiance. These factors are DN-to-voltage conversion, electronic gain, PRNU, slit irregularity, radiance, and irradiance responsivity.
Here, we concentrate on the electronic gain that converts a signal in volts back to the detected charge in a pixel. In the forward direction, there are, among others, the CCD output node, the CDS amplifiers, and the PGA. The CCD output node converts the signal from electrons to volts and has two gain settings.
A reference, or neutral gain setting is defined using the low CCD gain. The factor between a particular PGA, CDS, or CCD setting and the neutral gain setting is called the relative gain. The absolute charge-to-voltage factor is a design value, directly derived from the industry specifications of approximately 0.80 µV (e−)−1 for the low CCD gain. This value does not have to be directly calibrated, as any deviation from it will automatically be absorbed by consecutive multiplicative calibrations.
The charge-to-voltage factor defined per band leads to alignment problems between any two detector halves. Thus, only the relation between the two conversion factors has been calibrated, but not their absolute value. The observed shot noise is a means to indirectly calibrate this absolute gain.
Since the noise of each signal consists of read-out noise and shot noise, and shot noise is a function of signal magnitude, it is possible to draw a graph of signal versus total noise (as variance). This graph is a straight line, and the intercept is the read-out noise. We use repeated DLED measurements with different exposure times and high repetitions to confirm the shot noise law. In Fig. 6 the result is shown, clearly indicating that the shot noise law applies. The slope is not exactly 1, so we have to conclude that the design value for the voltage-to-charge conversion is not entirely correct. This is hardly surprising since the factor is difficult to establish directly.
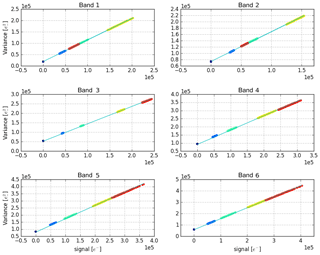
Figure 6Signal versus variance for all UVN bands: signals and corresponding temporal variances, sorted and block-wise averaged for several dark and illuminated instrument settings. The shot noise law is clearly visible: all points are close to the overall regression line. Only slight residuals as functions of the signal magnitudes seem to remain.
4.4 Detector non-linearity
The charge-to-voltage conversion at each CCD output is not entirely linear. Therefore, in the TROPOMI L01b processor, the voltage-to-charge conversion algorithm is followed by a non-linearity correction algorithm. The non-linearity is defined as the difference between the expected linear behaviour and the actually measured read-out register charges.
The non-linearity can be a non-trivial function of the measured register charge and is therefore provided to the L01b processor in the form of a number of Chebyshev expansion coefficients. This parametrized non-linearity function depends on the detector band and the CCD gain setting (high or low). A Chebyshev approximation is valid only on a particular signal interval; above that interval the correction is carried out, but the data are flagged as saturated. The Chebyshev polynomial function is evaluated for the measured pixel signal and subtracted from the signal.
DLED measurements are used with the same settings but varying exposure times. To distinguish between the register and the pixel non-linearity, binned measurements are used to determine the former. The binning factor is 5 for the register non-linearity measurements. Per pixel, the measured signal values lie on a curve. The expected linear behaviour is that the signals lie on a straight line between the origin and a point Lmax that is predefined and has the same value for all pixels in a band. Lmax is reached at different exposure times, depending on the response of each pixel. As a rule of thumb, Lmax is chosen such that for a pixel with average response. The difference between the constructed straight line and the curve of measured points is converted to non-linearity as a function of the measured charge. The combined set of the non-linearities of all pixels can be modelled by a low-order polynomial curve. The 1σ width of the cloud of points (of which the non-linearity curve is the least-squares approach) forms the greater part of the CKD error.
There is 1 degree of freedom in establishing the non-linearity: at a charge of Lmax, the CCD responds with a certain deviation d (not necessarily zero) of the linear behaviour. Together with the constraint that the non-linearity for a zero signal is zero (otherwise an additional offset would exist), there are thus two defined points of a straight line: the “linearity”.
Now, for each pixel we can draw a graph of signal versus exposure time from the available measurements. If the response of the pixel is moderate (i.e. the pixel is not dead or shielded), the maximum exposure time tmax corresponding to the signal value Lmax can be defined. The line through the origin and the point is the expected linear signal. The difference between the measured curve and the straight line of the expected signal is the non-linearity. The set of all non-linearity pairs of all pixels, depicted as a cloud in Fig. 7, can be approximated by a low-order polynomial curve. The curve is constrained to intersect the origin and the point [Lmax,d], these two parameters are chosen per band. For bands 4–6, Lmax is 1 million; for bands 1–3, the pivoting points are 320, 500 and 820 ke− respectively.
A closed-loop test was performed with the calibration framework such that the measurements were processed once more, but now up to and including the recently computed non-linearity correction. The framework then repeats the analysis of the non-linearity on that data. Because the data have now been corrected for non-linearity by the L01b processor, the analysis outcome should be that there is no non-linearity remaining, only noise. Figure 8 shows the re-computed non-linearity and its fitted curve. The curve is indeed more or less a straight horizontal line with a deviation of about 30 electrons near the highest charges. This amounts to less than 0.2 % at the highest charge. The obtained error curve is also calculated again by the framework and is very similar to the single-loop error curve (not shown here).
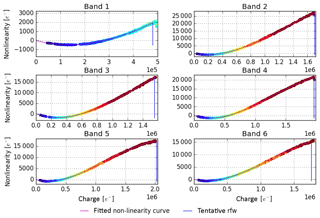
Figure 7For each UVN band the obtained non-linearity curve (purple line) together with the scatter plot of the individual non-linearity tuples (coloured dots) are shown. The horizontal axis represents the measured charge and the vertical axis the obtained non-linearity. Each colour indicates a sub-cloud from the pixels of an individual measurement with a certain exposure time. The blue vertical line indicates the limit chosen for the validity of the correction; this is the value for register full well.
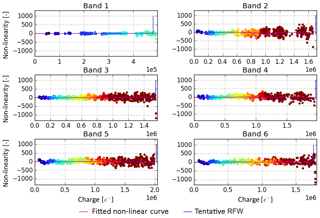
Figure 8The obtained non-linearity curve for all bands (purple line) together with the scatter plot of the individual non-linearity tuples after double processing. Each colour indicates a sub-cloud from the pixels of an individual measurement with a certain exposure time. The blue vertical line indicates the limit chosen for the validity of the correction; this is the value for register full well. The double-processed data show that the non-linearity correction removes the non-linearity from Fig. 7.
4.5 Pixel full-well capacity
In addition to the register non-linearity, which was investigated by using measurements of an average binning factor of 5, the pixel non-linearity was assessed. Although not CKD, it is important to know the maximum amount of charge that an individual pixel can hold (PFW). This is measured with unbinned measurements. However, any non-linearity at the pixel level cannot be distinguished from the register non-linearity since the charge inevitably passes through this register. Therefore the assumption is that the pixel signal behaves perfectly linearly up to some fraction of its PFW; unbinned measurements should not surpass this level.
The PFW capacity varies per CCD but is more or less equal for all detector pixels on a CCD. The electronic gain in each band is chosen such that register full well (RFW) occurs before ADC saturation. The only exception is band 1, in which the fixed gain is so high that ADC saturation is reached before PFW.
The PFW is visible as a flattening of the graph of pixel charge versus exposure time and indicates pixel saturation. However, even detector pixels that receive a lower signal flux can still be affected by saturation because the superfluous electrons spread over the detector and cause so-called blooming.
The analysis yields a minimum saturation level for each pixel that shows direct saturation. The result per band is shown in Table 3, in which over the set of all relevant pixels the minimum and some percentile values are shown. The values in this table can be used to set a threshold value for pixel saturation flagging. The SWIR PFW was calibrated on a unit level by SRON, and the values are repeated here for completeness.
Table 3The UVN saturation thresholds, measured in electrons, as obtained from unbinned measurements. Shown here are the minimum and three percentiles of the set of pixels that become directly saturated. Signal values above these thresholds should be flagged as “saturated” by the L01b processor; signal values below these thresholds can safely be regarded as behaving linearly, unless saturation occurs in neighbouring pixels.

4.6 Detector pixel quality calibration
The L01b algorithm labels individual defective image pixels by raising a flag in the corresponding L01b product map if the quality factor of a pixel is below a certain threshold. This quality factor is calculated by the analysis algorithm and distinguishes between bad and dead pixels. The L01b processor only labels pixels as bad, meaning either bad or dead. The detector pixel quality flagging (DPQF) key data are a per pixel map of floating point values (quality factors) between 0.0 and 1.0, which correspond to the lowest and highest quality. The floating point threshold used in the L01b processor is currently set to 0.8. This means that the L01b processor will flag every pixel as bad when its quality factor value in the CKD is lower then 0.8. No key data can be calculated for the read-out register (ROR) pixels. These pixels are assigned a quality factor of 1.0.
A UVN pixel is flagged as bad (dead) if it has less than 90 % (10 %) quantum efficiency (QE) compared to its neighbours, or shows darkness noise that is 10 (50) times higher than the CCD average, or creates dark current which is 10 (50) times higher than the CCD average. Pixels which display no large positive correlation between exposure time and signal response are declared dead.
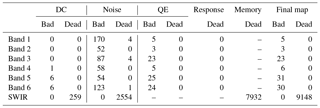
The marked pixels based on dark and illuminated measurements are merged together to form the final DPQF map. The SWIR DPQF was calibrated on a unit level with tests covering the dark flux, the noise, and the memory effect. Table 4 shows the number of bad and dead pixels that were marked by the calibration algorithms. It is clear that most UVN pixels have been flagged based on a deviating darkness noise. It was validated that all pixels, which were flagged based on darkness noise, were false positives by using a prototype sigma clipping implementation. For now, the darkness noise criterion is switched off, so the total column and final map do not contain these flagged pixels. The number of flagged UVN pixels is less than 0.04 % with the current thresholds and with the darkness noise criterion. The SWIR DPQF map shows 9148 dead pixels (3.560 % of the total number of pixels) of which a large fraction correspond to pixels under the cold shield and in the last row (approximately 2.4 % of the total number of pixels). The number of operational pixels is 250 880 for SWIR, and the final DPQF map shows 3028 dead operational pixels (1.2 % of the number of operational pixels).
Electronic calibration covers the offset and gain introduced in the the read-out chain of the front-end electronics. Here we treat the UVN electronic calibration; the SWIR calibration is described in Hoogeveen et al. (2013). Table 5 gives a summary of the UVN calibrated electronic and detector properties which are part of the CKD in the L01b data processor. In addition the SWIR values are reproduced for completeness.
Table 5The main characteristics of the detectors and front end electronics. Unless stated otherwise, the values for UVN are given for offset =0 (DAC), even parity, PGA =1 (code 97), CCD gain low, and CDS gain low. The UVN dark current is based on the maximum column average value. The register full-well value is based on the maximum value at which the non-linearity correction is valid.
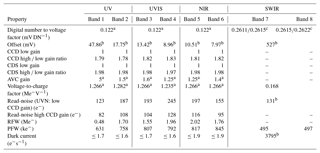
a Design value. b Shown are the average for UVN and median for SWIR. The correction is per pixel. c For SWIR this conversion is per half band.
5.1 Electronic offset
The definition of the electronic offset is the measured output signal when the input signal is zero and in absence of dark current. Each TROPOMI CCD detector has two distinct electronic detection chains, one for each band. Each chain itself has two separate CDS “lanes” that alternatively sample the sequence of pixels as they are read out, causing an artificial odd–even effect in the offset. The measured offset does however depend on the instrument settings for gain and offset, albeit not in an exactly linear way. The offset is thus defined as a single quantity per band and per parity (even or odd pixel). If a single pixel shows a deviation in offset from this general offset, this is called the offset residual. The residual is an image per band that differs per instrument configuration.
There are eight ways to determine a value for the electronic offset; to treat them all is out of the scope for this paper, but the important conclusion is that these methods do not yield the same answer within their precision. During the on-ground calibration it was observed that the offsets were not static as expected but show drifts in time of over several minutes. In addition, the offset shows patterns during a frame read-out, which causes spatial variations referred to as pixel offset non-uniformity (PONU).
To reduce the impact on the L1b product, the electronic offset correction is implemented in the L01b data processor as a dynamic correction; the CKD are retrieved per measurement frame. The preferred order is to first apply a dynamic correction using over-scan rows. The CCD gain should be set to the same value as the science data area. Secondly a dynamic correction using the ROR can be used. The CCD gain of the ROR should be set to the same value as the science data area. The least preferred option is to use the static offset based on dark images; in this case the temporal drift in offset will introduce an additive error component.
5.2 Electronic amplification
The front-end electronics of the UVN detector modules consists of six separate electronic chains, one for each band. All pixels in a band are read out sequentially through one of those chains. In each of these electronic chains several component gains must be calibrated. These individual gains must be multiplied to yield to the so-called system gain. This system gain (and offset) is thus equal for all pixels in a band by design, and therefore no pixel-dependent behaviour is expected. Some of these component gains can be actively controlled by changing the instrument settings. These gain settings are chosen to optimize SNRs while avoiding saturation. The CKD to be determined here are the actual system gain as a function of individual settings for gains. As shown in Fig. 2, the components between the detector and the ADC that yield the electronic gain are the CCD output node, with two possible settings (switchable per image row); the analog video chain amplifier (AVC) with a fixed gain; the CDS, with two possible settings; and the PGA, with 256 possible settings.
The goal of the calibration is to determine gain ratios, i.e. ratios of the gain resulting from a certain gain setting and the gain resulting from the so-called reference setting. The total instrument gain itself or absolute radiometric calibration is addressed in a separate process which relates a known incoming photon flux to the instrument response at the reference gain setting.
The gain ratios must thus be determined for all potential combinations of the possible gain settings: . In addition, the gain ratio can differ between odd and even columns due to the CDS lanes, referred to as parity. The reference setting is defined as PGA gain setting 97, low CDS gain, low CCD gain, and even parity.
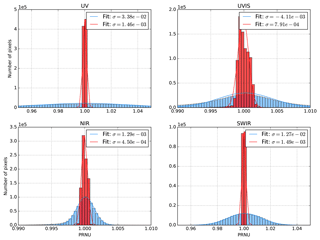
The four-dimensional CKD are derived from unbinned DLED measurements at various exposure times and multiple combinations of prevalent gain settings. In Fig. 9 the histograms of the derived gain ratio per detector pixel in each band are given. In this example the gain setting is chosen such that it would result in a gain ratio of about 2. Although there is a considerable spread in individual gain ratios, the mean of the histogram is rather accurate because of the large number of pixels involved.
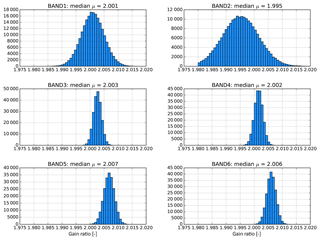
Figure 9The histogram of the obtained pixel gain ratios for PGA gain =2 and reference settings otherwise, for all UVN bands.
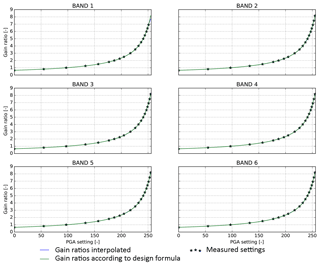
In Fig. 10 the obtained gain ratios are shown for all calibrated PGA settings indicated with dots. The interpolated curve for all possible 256 PGA settings, as well as the gain ratio according to the design formula from the supplier, is also given.
In this section the radiometric calibration of the UVN and SWIR spectrometers is described. The calibration aims at establishing the response of the instrument with respect to known radiometric standards for both the Earth and the Sun ports, for all wavelengths and viewing angles. This is accomplished through the combination of various calibration measurements, each targeting a different topic of the instrument's response function. The optical geometric properties of the instrument, in combination with the limitations of the calibration facility, dictate a certain approach to the overall calibration. Moreover, the logical flow in the L01b data processor requires CKD to be available for each correction step in the processing chain, and thus the calibration set-ups and measurements were optimized to deliver these CKD. The philosophy chosen is as follows.
The absolute radiometry for the Earth port absolute radiance responsivity calibration (ABSRAD) is calibrated using NIST traceable FEL lamps, in combination with external diffuser plates, independently commissioned at two calibration houses under a separate subcontract.
The Sun port has built-in QVDs, and the absolute radiometry ABSIRR is established directly from the same NIST traceable FEL lamps that are used for the Earth port.
The bidirectional scattering distribution function (BSDF) of the instrument was originally planned to be established independently using a Sun simulator stimulus in combination with the calibrated external diffusers (for the Earth port set-up). Due to problems with the Sun simulator this calibration could not be performed, and the BSDF had to be calculated from the obtained absolute radiance and absolute irradiance calibration data.
The absolute radiometry for the Earth port can only be established for a limited number of rows on the detector because the FEL lamps have a limited calibration lifetime. The established ABSRAD for the nadir row can be extended to all other detector pixels by the relative radiometry calibration RELRAD. Measurements with an integrating sphere yield the difference in response for all detector pixels relative to the response of the pixels on the nadir row. It is expected that the radiometric response due to optical and geometric effects is smooth in wavelength and viewing angle, and therefore only low-frequency effects are attributed to RELRAD. The remaining high-frequency effects are attributed to the PRNU, which is basically a detector effect that could have been calibrated separately. It was chosen to derive them together to ensure consistency in the total radiometric response of the instrument.
The absolute radiometric response of the Sun port is valid for all detector pixels, but only valid for a single angle of incidence on the internal diffuser. Under flight conditions, however, the angle of incidence of the Sun on the diffuser continuously changes in azimuth due to seasonal effects and in elevation due to orbital effects. This angular dependency RELIRR is calibrated using a Sun simulator. Due to stimulus failure only one of the two internal diffusers could be successfully calibrated.
The straylight in the instrument is dominated by near-field straylight. This is corrected for in the L01b data processor using a convolution method. The required CKD for this correction are derived with laser measurements over the full wavelength range.
For the NIR channel an additional straylight correction was needed to reach compliance with the requirements. Due to scattering at the inside of one of the lens mounts in the imager, the NIR channels suffer from out-of-spectral-range straylight for which a separate correction algorithm is needed in the L01b processor. The required CKD for this were obtained from dedicated measurements with a laser source in a dedicated delta-calibration campaign in ambient temperature and pressure.
In the following subsections we will present the results of these calibrations in more detail, including how the error on each CKD was established and justified through validation. The latter is important as the error in the CKD is propagated in the L01b data processor and will thus enter into the error of the final L1b data product.
6.1 Absolute radiance
ABSRAD is the determination of the relation between the electron generation rate in the detector and the absolute spectral radiance at the Earth port. It is derived from measurements of the instrument responsivity using a calibrated FEL lamp that illuminates a calibrated diffuser. Light reflected off the diffuser travels through ambient air and passes the window in the thermal vacuum chamber before it enters the Earth port in vacuum.
ABSRAD is determined for one reference across-track line of sight (swath angle) only. The calibration depends on wavelength and is only valid for this reference swath angle corresponding to a reference detector row. The ABSRAD CKD in the L01b data processor however need calibration data for all detector pixels, and therefore the ABSRAD result obtained for the reference row is duplicated to all other detector rows that take into account the spectral smile. This ignores the fact that the (spectral) radiometric response of the instrument is not the same for all detector rows. To address this, the RELRAD CKD (see Sect. 6.4) provide the relation between the electron generation rate for any swath angle and that for the reference angle.
Together RELRAD and ABSRAD provide the absolute radiance responsivity calibration for the instrument Earth port. ABSRAD measurements were performed for various combinations of two calibrated lamps (FEL1 and FEL2), two calibrated diffusers (DIF1 and DIF2), three lamp–diffuser distances, and three cradle rotation angles. For each measurement a corresponding background measurement was included in the session. The background measurement was performed by shuttering off the direct illumination of the diffuser. The used lamps were NIST calibrated 1000 W quartz tungsten halogen (QTH) FEL lamps with a colour temperature of 3200 K. The diffusers were 300 × 300 mm large plates made of sintered PTFE. The diffusers were calibrated both before and after the calibration campaign for the entire TROPOMI wavelength range. The lamp emits light in all directions, and baffling is placed at a distance from the lamp to prevent set-up straylight reaching the instrument, while avoiding overheating of the lamps. Lamp irradiance calibration data, diffuser calibration data of the bidirectional reflectance distribution function (BRDF), and thermal vacuum chamber (TVC) window transmission calibration data were supplied by industry.
For each experimental condition, a series of repeated images (typically 20–40) is available. These images are averaged to obtain a mean image, and a pixel-wise standard deviation is calculated and divided by the square root of the number of repetitions to obtain the standard deviation of the mean signal. Mean images and standard deviations of the mean are calculated for all illuminated and background measurements, which are then processed in the L01b data processor up to and including the RELRAD correction. Background images are subtracted from the corresponding illuminated images, and results are corrected for the spectral smile.
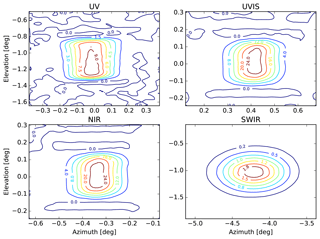
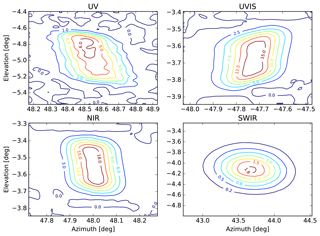
In the smile-corrected images, the row with line of sight (LOS) closest to the optical axis is selected for further processing. This row is referred to as the “optical axis row”. It is assumed that the nominal diffuser angles of incidence and reflection which apply for the “true” optical axis also apply for the optical axis row. Obviously, the maximum possible misalignment between the optical axis row and the true optical axis is half a row. This corresponds to an estimated difference of at most 50 % of the local signal gradient per row between the measured signal and the signal that would have been obtained if the alignment would have been perfect. This difference is estimated from measured spatial signal profiles and included as a contribution to the overall absolute ABSRAD CKD error. Rows other than the optical axis row are only used to obtain signal profiles and are not included in the ABSRAD CKD assessment. These rows are illuminated under non-nominal angles of incidence or reflection. Both the BRDF and lamp calibration data are potentially inaccurate for non-nominal angles.
Measured signals are assumed to represent radiance along each pixel's LOS, thus ignoring possible effects of finite pixel footprint on the diffuser. The relative error associated with this assumption is estimated to be 0.02 % for UVN and 0.1 % for SWIR. The relative error is included in the overall absolute ABSRAD CKD error.
Measurements obtained for nominal lamp–diffuser distances d1, d2, or d3 are tested for compatibility with the 1∕r2 law. For each nominal distance, the corresponding physical (i.e. real) lamp–diffuser distance is calculated taking into account corrections for the lamp filament position offset and average diffuser penetration depth. Compatibility with the 1∕r2 law is tested by multiplying each signal by the square of the corresponding physical distance, also taking into account a further geometrical correction for vertical diffuser off-centre distance. This vertical distance has an effect on the lamp–diffuser distance as well as on the angle of incidence. Distance effects related to inhomogeneous irradiance of the field of view of detector pixels in the optical axis row are less than 0.02 % and are therefore ignored. Results are then expected to be independent of lamp–diffuser distance: taking the ratio of each result and that obtained for distance d1 should equal unity. As shown in Fig. 11 results obtained for distance d2 are generally 0.1 %–0.5 % higher than expected, whereas for distance d3 discrepancies up to 1 % are obtained in all detectors. The high-frequency component visible in all plots is not measurement noise but diffuser features.
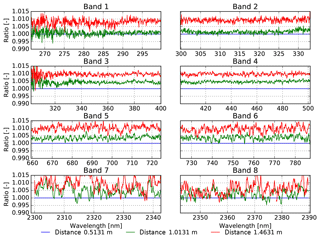
Figure 11Results obtained for bands 1–8 for different lamp–diffuser distances d1, d2, or d3, for lamp FEL1, diffuser DIF1, and cradle rotation angle 0∘. The radiance signals were multiplied by the square of the distance and then divided by the ABSRAD result obtained for distance d1; thus, roughly unity results are expected for distances d2 and d3. Results obtained for distance d2 (green lines) are generally 0.1 %–0.5 % higher than expected, whereas for distance d3 (red lines) discrepancies up to 1 % are obtained in all detectors. The high-frequency component visible in all plots is not measurement noise but diffuser features.
Averaged results obtained for each of the four lamp–diffuser combinations are corrected for spectral features: spectral anomalies were observed in detectors 1–3, which were identified as oxygen A-band absorption (at ≈ 760 nm), or various emission or absorption lines in the lamp output spectra. The spectral range of each anomaly is determined by inspection, and the corresponding area is invalidated and interpolated by a third-order Chebyshev fit of the data in two regions flanking the invalidated area. Maximum regions are selected that still yielded a good fit result. If no satisfactory fit can be obtained for any reasonably sized fit region, no interpolation is performed, leaving the anomalous area invalidated. Some features comprise closely spaced double spectral lines; these are interpolated using a joint fourth-order Chebyshev fit that includes the region between the two lines.
After invalidation or interpolation of spectral anomalies, results for each of the four lamp–diffuser combinations are spectrally smoothed in each band separately by low-pass Fourier filtering in order to remove the speckle caused by the external diffuser plates. This is not accomplished by traditional Fourier transforms but by fitting a series of sines to the signal that also included half-wave sines as well as linear and constant terms. The linear term is introduced to account for overall signal gradient (note that this is not possible using mere Fourier transforms, which implicitly assume a periodic signal). The number of terms minus two thus equals the maximum number of half sines used to describe the signal. A minimum number of terms is included that appeared necessary to obtain a good fit: fit residues were inspected for lack of fit, which then would call for a larger number of fit terms. If only high-frequency residues remain, the fit result is taken as the filtered signal. Results of the smoothing are shown in Fig. 12.
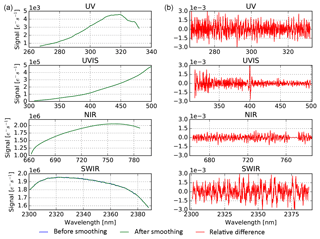
Figure 12Typical results of spectral smoothing. (a) For each detector, signals before (blue lines) and after smoothing (green lines); except for SWIR, differences between both signals are hardly visible on these scales. (b) Corresponding (relative) residuals as a ratio to the original signal, showing mainly highly frequent differences between the unfiltered and filtered signals. Somewhat lower-frequency features may be observed in the residuals for SWIR (e.g. between columns 850 and 900), but there is no correlation between these and similar features obtained for diffuser DIF2 (not shown), indicating that the effects are diffuser-borne. The “gap” in the NIR residuals between columns 800 and 900 corresponds to the interpolated oxygen A band.
For each of the four combinations of lamps FEL1 or FEL2 and diffusers DIF1 or DIF2, the absolute radiance at the Earth port is calculated from the (interpolated) calibration data of the lamps, diffusers, and TVC window transmission and by applying the appropriate geometrical correction factor. The ABSRAD calibration results for the optical axis row as shown in Fig. 13 are obtained by dividing absolute radiance at the Earth port by the smoothed results for the corresponding lamp–diffuser combination. Results are then compared pair-wise for each combination obtained with an identical lamp or diffuser, and an averaging procedure is applied. For the final ABSRAD CKD the ABSRAD result obtained for the optical axis row is duplicated to all remaining detector rows and the spectral smile is reapplied.
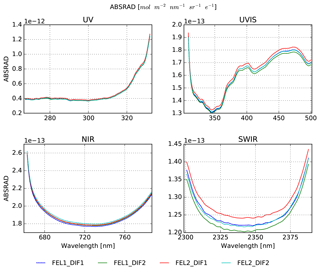
Figure 13ABSRAD calibration for the optical axis row for all spectrometers. Shown are data for lamps FEL1 and FEL2 for both diffusers DIF1 and DIF2. For UVIS, stronger gradients are observed than for the other spectrometers. The calibration curves are the combination of response of the detectors and the wavelength-dependent optical throughput of the spectrometers.
Figure 14 shows the estimated ABSRAD pixel-to-pixel uncertainty, and the corresponding variance is the square of this quantity. Wave-like patterns are observed in all detectors. They appear to be correlated with the number of terms included in the spectral smoothing procedure. Therefore, the patterns are probably an artefact of the smoothing procedure and the results should be used only as a general indication of order of magnitude. The relative uncertainty is on the order of 10−4–10−5. This is (much) lower than the measurement noise obtained in the ABSRAD measurements. Indeed, noise is effectively suppressed by the spectral smoothing procedure.
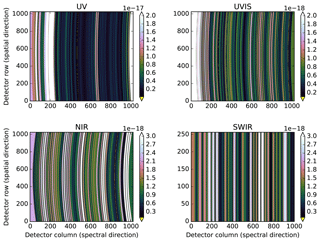
Figure 14Pseudo-colour image of the ABSRAD CKD error, defined as the uncertainty in CKD pixel-to-pixel variation. The colour scale unit is ( (e−)−1). The corresponding variance, , is the square of this quantity. The wave-like patterns observed in all detectors are an artefact of the spectral smoothing procedure. Note that this figure shows the final ABSRAD CKD in which the ABSRAD result obtained for the optical axis row is duplicated to all remaining detector rows and the spectral smile is reapplied; RELRAD is not included here.
Various effects have been identified that contribute to the absolute ABSRAD uncertainty and are summarized in Table 6. As the effects causing the uncertainty are considered to be mostly statistically independent, the individual contributions are added quadratically to obtain the overall absolute ABSRAD CKD uncertainty.
The ABSRAD CKD are calculated as an average of results obtained for different lamps, diffusers, and cradle rotation angles. The independent commissioning data available for each external diffuser, from both calibration institutes, have been combined to improve the overall accuracy of ABSRAD. The CKD have been derived from measurement data obtained for nominal diffuser angles of incidence or reflection only (i.e. pertaining to the diffuser centre). For angles of incidence or reflection other than the nominal angles, the calibration of diffusers and lamps is potentially inadequate.
The CKD are determined with a small (< 0.01 %) pixel-to-pixel uncertainty, but a much larger absolute pixel uncertainty is obtained. The latter is 1.9 % for UV, 1.2 % for UVIS, 1.0 % for NIR, and 1.6 % for SWIR. These values are within the mission requirements on Level 1b but not within the stricter calibration requirements.
The uncertainty mainly reflects discrepancies between the results obtained for the various combinations of lamps and diffusers. These discrepancies can in part be attributed to lamp or diffuser calibration uncertainty, and the remaining differences (0.5 %–1.5 %) are unexplained. The contributions to the uncertainty are listed in Table 6. In all detectors, results obtained for different cradle rotation angles, and results obtained for different lamp–diffuser distances, all agree to within 1 %.
6.2 Absolute irradiance
The absolute irradiance CKD are the ratio of the spectral irradiance at the internal diffuser (QVD) to the response that is measured. The preferred calibration approach is to use Sun simulator measurements to calculate the instrument BSDF and use this to convert the ABSRAD CKD to absolute irradiance values. The benefit of this is a better SNR since both the Sun simulator and the FEL lamp over the Earth port give a higher response than the FEL lamp over the Sun port. Moreover, a Sun simulator has the advantage of having a narrow field, similar to that of the Sun, resulting in a more realistic illumination geometry and lower set-up straylight. Unfortunately, the output of the available Sun simulator was highly unstable and could not be used to calculate the BSDF, and therefore the absolute irradiance CKD are based on FEL lamp Sun port measurements only as described hereafter.
To calculate the irradiance at the diffuser, the irradiance of a FEL lamp, which has been calibrated by NIST at a distance of 50 cm, must be converted to the irradiance at the distance between the Sun diffuser and the FEL lamp. The same lamps are used as for the absolute radiance described in Sect. 6.1. The FEL lamp is – in first order – considered to be a point source in this set-up so that the inverse-square law can be used for the conversion. For this, the distance between the FEL lamp and the diffuser must be determined accurately since an error in the distance will be propagated squared into the irradiance. For instance, at a distance of 1.5 m, an error of 1 cm on the determined distance (0.67 %) will result in an error of 1.33 % in the irradiance.
With the instrument in the closed vacuum chamber it is difficult to accurately measure the mechanical distance between the FEL lamp and the diffuser. The coil of the FEL lamp also extends over a few millimetres, which makes it impossible to designate a single distance needed to treat it as a point source. In addition, because the internal diffusers are volume diffusers, there is not just a single surface within the diffuser where the light is scattered, so the distance is not as well defined as it would be for a reflecting diffuser. Therefore, another approach is necessary to determine the distance: a distance offset is calculated from the measurements and added to the measured distance. Such an alternative approach is unavoidable when using a volume diffuser. It is noted that the aforementioned geometric restrictions affect the absolute irradiance calibration such that the introduced error is hard to quantify in absence of an independent validation measurement.
Measurements were performed with the FEL lamp placed in three positions: at approximately 1.5, 2.0, and 2.5 m from the Sun diffuser, labelled d1, d2, and d3 respectively. The FEL lamp is moved to these positions on a rail, which means that the relative distances between those three positions are known with a high accuracy. This gives, for each detector pixel, three equations with two unknowns: irradiance and lamp position. In principle this could be solved with a (non-linear) fit; however, instead of calculating millions of fits through three data points (one fit per detector pixel), we can also calculate the distance offset analytically for two FEL positions. The three FEL positions can be paired in three combinations (d1 and d2, d1 and d3, d2 and d3) and the distance offsets calculated from these pairs can be compared to each other. If they yield similar values their average can be used as the final distance offset. If the values are not similar this can be due to set-up straylight but also due to the fact that the point source assumption does not hold for the FEL lamp as used in the set-up. A disagreement in the obtained distance offset must be included in the calibration error budget.
An additional complication of this calibration approach lies in the fact that the QVDs are tilted with respect to the optical axis. During the absolute irradiance measurements the angle between the diffuser normal and the optical axis is about 25∘ in line with the in-flight solar measurement configuration. Given that the QVD has a width of approximately 5 cm, the optical path length to the diffuser parts that illuminate the upper and lower rows on the detector differ by about 2 cm. Here the FEL lamp is considered to be a point source, and thus, due to the inverse-squared law, one diffuser side will receive a lower irradiance than the other. If the diffuser is perfect, i.e. light falling on a spot on the diffuser is uniformly spread out over all detector rows, the derived distance offset will be independent of detector row. For an imperfect diffuser, which spreads the light over a limited number of rows, a row dependency with a maximum of 2 cm will be present in the distance offset. The data show a variation over the rows of 1 to 2 cm. In orbit no variation in irradiance is expected since the Sun is a better point source than the FEL lamp. The Sun illuminates the QVD with nearly parallel beams. Therefore on the ground this effect is corrected for by using a row-dependent distance offset. The distance offset is calculated for each detector pixel separately and subsequently averaged per row. Then a line is fitted, which yields a linear function that maps each row to a distance offset. The three linear functions, calculated from the three distance pairs, are averaged to give one distance offset function per detector.
Measurements were executed for both internal diffusers (QVD1 and QVD2) at three distances (d1, d2, and d3). All measurements were repeated with a second FEL lamp. In addition, a validation measurement was performed with FEL1 at distance d3 with the same instrument settings as at distance d1. The validation measurement is used to exclude measurement artefacts and not included in the CKD analysis. All measurements were carried out at cradle rotation 0∘ and tilt −1.28∘, the same cradle position that was used as the reference during the relative irradiance measurements.
The analytical derivation of the ABSIRR CKD is less complicated than RELRAD. The latter requires stitching of multiple measurements and subsequently a separation into RELRAD and PRNU without smoothing. For ABSIRR no separation is needed, only a smoothing to remove diffuser features due to speckle, as described further on. The ABSIRR CKD derived here are the mean of the absolute irradiance values calculated from the FEL1 and FEL2 measurements at the shortest distance d1. The absolute irradiance CKD for the optical axis rows are shown in Fig. 15. The absolute irradiance for QVD2 is about 5 % to 10 % higher than the QVD1 absolute irradiance, which means that the response via QVD2 is 5 % to 10 % lower given the same amount of light. The absolute irradiance increases at the edges of the detectors where the responsivity of the spectrometers decreases. For detector pixels that do not have an associated wavelength it is not possible to calculate an absolute irradiance. For those pixels the values have been calculated by extrapolation of the nearest valid pixel.
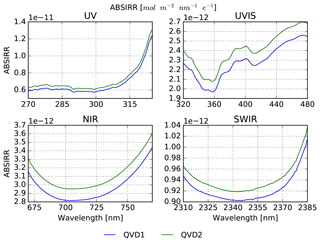
Figure 15Absolute irradiance CKD at the optical axis row (QVD1 in blue, QVD2 in green) for all spectrometers over their performance range. For each QVD the CKD are the mean of the absolute irradiance calculated from FEL1 and FEL2 at distance d1.
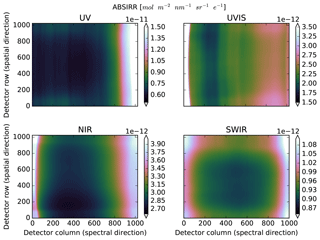
Figure 16Image plots of absolute irradiance CKD of QVD1 for all spectrometers. The dark blue pixels are where the ABSIRR is off the scale, which corresponds to a responsivity close to zero. The values at the edge of the detectors are calculated with nearest-neighbour extrapolation.
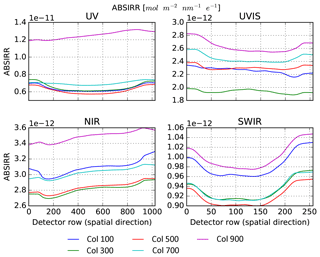
Figure 17The absolute irradiance CKD for QVD1 is shown for each detector in columns 100 (blue line), 300 (green), 500 (red), 700 (turquoise), and 900 (magenta) for each detector.
Figures 16 and 17 give an impression of the row dependence of the absolute irradiance CKD. The former shows the absolute irradiance of QVD1 as image plots; the latter shows a cross section for a few selected columns. Only the graphs of QVD1 are reported as QVD2 gives similar results. The absolute irradiance varies slowly over the rows, as expected. In the UVN detector the absolute irradiance stays at a similar level for all illuminated detector rows and it increases sharply at rows that are not illuminated. This contrasts with the SWIR detector for which the absolute irradiance of the illuminated rows increases slowly for rows closer to the edge.
The roughness of the diffuser surfaces causes interference patterns (speckle) that are dependent on the wavelength, viewing angle, and location on the diffuser. They are hard to characterize because of the many factors that influence them, so they are smoothed out. The diffuser features in the SWIR follow a normal distribution with a standard deviation of 0.4 % for both QVDs. With the UVN detectors no diffuser features could be observed. Under flight conditions the SWIR diffuser features will be reduced by averaging over 150 measurements in the elevation direction, thus effectively scrambling these patterns. Optionally, if the solar spectrum is assumed to be stable over a certain time period, the features can be reduced even further by averaging the solar irradiance of orbits that are measured at different azimuth angles.
To test the repeatability of the analysis, the FEL1 measurements at the longest distance (d3) were performed twice, using the same instrument settings. Even though the baffling of the validation measurement was placed incorrectly, it differs less than 0.2 % from the regular measurement. As a validation, the absolute irradiances calculated from the measurements at the three distances are compared. After applying the distance offset, the differences are within 0.5 %. As a further validation, the absolute irradiances calculated with FEL1 and FEL2 are compared: they show differences of up to 1.5 %. The established uncertainty for ABSIRR is 1.2 % for the UV, 1.3 % UVIS, 0.8 % NIR, and 1.0 % SWIR ranges. These values are within the requirements on Level 1b; however, this uncertainty does not include the geometric and fundamental problems associated with this specific measurement set-up, which is less optimal than using the BSDF method. The different known contributions to the uncertainty are given in Table 6.
6.3 Instrument BSDF
The instrument BSDF is not directly used in the L01b data processor. It can be expressed as the ratio of the total radiance responsivity (ABSRAD plus RELRAD) to the irradiance responsivity (ABSIRR), which are quantities used by the L01b data processor to calculate the solar irradiance and Earth-shine radiance respectively. Level 2 algorithms such as DOAS indirectly take the ratio of these two quantities when calculating the reflectivity, which makes the instrument BSDF an important parameter in many Level 2 algorithms.
The instrument BSDF was initially planned to be determined from measurements using the Sun simulator. However, this stimulus was not sufficiently stable for this purpose, resulting in uncertainties from 5 % up to 30 %. As a backup, measurements with an integrating sphere as described in Sect. 6.4 were performed. These measurements resulted in a too low SNR for bands 1 and 3, suffered from severe set-up straylight, and will not be considered further in this paper. Therefore the instrument BSDF has been derived from measurements for the calibration of absolute radiance and irradiance with the absolute calibrated FEL lamps and external calibrated diffusers (see Sect. 6.1). The FEL stimulus for the irradiance measurements is not collimated and suffers from a low SNR in the UV and UVIS ranges, in addition to an unknown speckle behaviour.
In Fig. 18 the instrument BSDF over both diffusers is given for the optical axis row, where RELRAD is unity. The curves are derived from the ABSRAD and ABSIRR CKD. ABSRAD and ABSIRR are similar for each spectrometer, but the shapes of the curves differ strongly per spectrometer. These are real instrument properties defined by mirror reflectances, dichroic transmission curves, (graded) coatings, and detector coatings. When calculating the BSDF these features do not all cancel out as can be seen in the figure. This could be caused by folding mirror properties or residual speckle on the internal or external diffusers, or artefacts of the optical stimulus. These features are not understood, and no further validation is possible due to the lack of proper independent on-ground measurements. This constitutes a known source of unknown errors, which cannot be quantified without independent validation measurements.
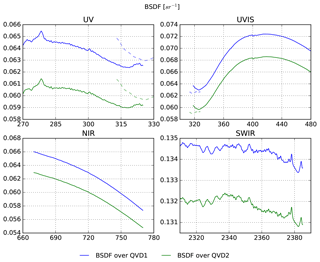
Figure 18The instrument BSDF plotted versus wavelength for both QVDs as calculated from the ABSRAD and ABSIRR calibration key data, which in turn are calculated from the FEL lamp measurements. Shown is the optical axis row over the performance range. The BSDFs for QVD1 and QVD2 have the same shape but are shifted due to the different throughput. The dashed lines in the UV and UVIS panels indicate the overlap region between the two spectrometers. Note that the solid and dashed lines do not coincide, which is expected because the optical paths of the spectrometers differ. The high-frequency structures are not understood and could be caused by the stimuli used.
The different contributions to the BSDF uncertainty are listed in Table 6. The relative uncertainty is found to be 1.9 % for the UV, 1.4 % for the UVIS, 1.2 % for the NIR, and 1.8 % for the SWIR ranges. The aforementioned unknown errors are not included in Table 6, and therefore the reported uncertainty is potentially underestimated.
Apart from SWIR, the reported values are within the requirements on calibration. The values supplied are 1σ values that are propagated within the L01b data processor to yield the formal error in the L1b data products' radiance and irradiance. In order to assure that errors do not enter double in the calculation of reflectance, the error propagation in the L01b processor has been tuned; see also Sect. 3.2.
Note that the BSDF of QVD1 is about 5 % to 10 % higher than the QVD2 BSDF, which is due to the fact that the absolute irradiance is the same amount lower for QVD1 as for QVD2. This means that the instrument response via QVD2 will be 5 % to 10 % lower given the same amount of light.
Table 6Summary of the relative standard uncertainty components per detector for the ABSRAD, RELRAD, ABSIRR CKD, and ensuing instrument BSDF. The quantities marked with * are not part of the BSDF calibration uncertainty because they cancel out. The uncertainties in this table only reflect the CKD errors; the final error in L1b products is calculated using these and all other CKD in the processing chain; see also the discussion on L01b error propagation in Sect. 3.2. Note that set-up straylight cannot be reasonably estimated and might be included in the components “Unexplained FEL lamp discrepancy” and “Unexplained measurement discrepancy”. This error budget excludes the known issues with the stimuli, which can not be quantified due to the lack of independent validation measurements. The reported uncertainty is therefore potentially underestimated. The total 1σ uncertainty was obtained by quadratically adding each individual contribution.
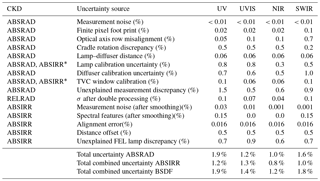
6.4 Relative radiance and PRNU
The total radiometric response of the instrument consists of several components including both electronic and optical effects. Sometimes it is not possible to attribute a component solely to one of the two. This is especially true for the PRNU and the relative radiometric response (RELRAD). The RELRAD can only be calibrated using an external source; the PRNU must therefore also be obtained from the same measurement.
The PRNU relates a pixel's individual response to that of its direct neighbours, whereas the RELRAD relates the radiometric response for every pixel to the pixel that is illuminated by light of the same wavelength on the detector row that corresponds to illumination from a source on the instrument's optical axis. The absolute radiance responsivity (ABSRAD) and the relative radiance responsivity (RELRAD) CKD together provide the total radiance responsivity calibration for all viewing angles of the instrument Earth port.
The pixel response non-uniformity in the detector is corrected in the L01b data processor by multiplying by a pixel-dependent map of values. Each detector has its own specific pattern, stemming from the way the detector was produced (coatings, back-thinning) as well as the specific response of the detector surface per wavelength. The PRNU is defined as a correction of a small deviation from the mean, which can vary from pixel to pixel. Therefore, the average value of this correction should be close to unity and display a variation of the order of a few percent with a potentially very high pixel grid frequency.
The RELRAD and PRNU analysis consists of two separate instances of the same algorithm, which separates essentially three different constituents of the signal: a spectral contribution, a spatially slowly varying part, and a spatially fast varying part. First, the algorithm processes the measurements to produce the fast varying part, the PRNU. Then the straylight correction algorithm is applied. When the signal has been corrected for PRNU and straylight, it is subjected to the same algorithm as used for the PRNU, but now to only produce the slowly varying part, the relative radiometric response.
In order to perform the analysis, a complete detector image is needed to separate the high- and low-frequency residual patterns from the signal. The measurement that is used for the derivation of the CKD uses an integrating sphere stimulus that only illuminates ≈33 rows for the UVN and ≈8 rows for the SWIR at a time. This illumination pattern is scanned over the detector by varying the cradle rotation angle with 1∘ at a time (this corresponds to ≈8 rows in UVN, 2 rows for SWIR). Between each two measurements a reference measurement at cradle rotation angle is performed. To arrive at a full detector image the partially overlapping measurements need to be combined in a process referred to as stitching; care must be taken here to avoid artefacts that could end up in the calibration.
The total scanning sequence over all swath angles takes a considerable amount of time, during which the output light source may vary. The reference measurements at cradle rotation angle must all have the same PRNU and absolute radiometric response, and therefore any change in the observed signal must stem from the stimulus itself. By comparing all reference measurements over time to the initial first measurement, the drift of the stimulus can be obtained. The measurements are corrected for this wavelength-dependent drift, which otherwise would end up falsely in the relative radiometric response.
The output spectrum of the light source is – per definition – independent of the instrument viewing angle or cradle rotation. Any variation in the observed signal in the azimuth (row) direction must thus be attributed to either the optical properties of the instrument (relative radiometric response) or the detector (PRNU). Therefore, if we divide each observed spectrum in each row by the stimulus spectrum, the PRNU and radiometric response remain. The stimulus spectrum, or the amplitude of the signal per wavelength for all detector pixels, is obtained by using the data from all rows.
The slow variations in the image after removal of the stimulus spectrum are ascribed to the relative radiometric response. They are separated from the high-frequency variations by means of performing a two-dimensional Chebyshev fit to the signal from the illuminated area of the detector. The desired relative radiometric response is now given by the combination of the one-dimensional Chebyshev low-pass result and these two-dimensional filtered data. This combination is then projected upon a wavelength grid and is subsequently column-wise normalized with respect to the value at the reference row for the corresponding wavelength to ensure that it reflects the relative radiometric response. This normalized quantity is projected back to the detector grid and then returned as the final CKD.
The results for the RELRAD are shown in Fig. 19. The relative radiance in the NIR channel does not display large features. For UVIS there is an asymmetric feature visible around column 400. Both the UV and SWIR channels show a similar decrease in intensity in the detector row direction. The relative uncertainty on the relative radiance in Table 6 has been estimated as the standard deviation σ of the residuals after double processing.
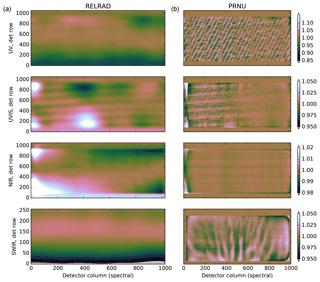
Figure 19(a) The relative radiance response as a function of the detector pixels (horizontal axis the detector column, vertical axis the detector row) for each detector. At the reference row the response is set to unity. (b) The PRNU for each detector as a function of the detector pixels.
Figure 19 shows how the PRNU pattern depends on the wavelength and becomes smoother for larger wavelengths going from the UV to UVIS and NIR ranges respectively. The SWIR detector has a very different hardware architecture. This leads to, amongst other effects, an articulated even–odd effect in the rows of the SWIR channel.
The pixel response non-uniformity after double processing is shown as histograms in Fig. 20. This validation shows that remaining PRNU effects are reduced with a factor of 41, 4, 2, and 70 for the UV, UVIS, NIR, and SWIR ranges respectively. The strongest reduction appears in the UV and SWIR detectors because these have strong PRNU signatures.
6.5 Relative irradiance
The relative irradiance factor is the correction of the signal for the angle under which the Sun port is illuminated. A range of measurements with the Sun simulator were performed for different azimuth (seasonal variation, φ) and elevation (ϵ) angles. The Sun simulator is a collimated and homogenized 1000 W Xe lamp. These measurements are normalized with measurements taken at the reference angle φ0,ϵ0, an angle close to the nominal Sun angle. The reference measurements were taken at regular intervals to also monitor possible drifts in the output of the stimulus.
The CKD are a correction factor for all detector pixels and for each azimuth–elevation angle pair, with which irradiance measurements are to be multiplied in order to remove the angular dependence of the Sun port. The CKD are defined as coefficients of a polynomial for pixels on a reduced grid, so that the L01b processor interpolates between the pixels to cover the whole detector and expands the polynomial to cover all possible azimuth and elevation angles within the valid range.
The signal for each φ,ϵ is averaged over the valid measurements and the corresponding background (dark) image is subtracted. The relative irradiance is the ratio of the signal image with respect to the signal image at the nominal angle.
The reference measurements are pixel-wise interpolated over time to provide a reference close in time with which normalization can be performed for each measurement. In this way, both the relative irradiance is calculated and the stimulus drift is taken care of.
For each detector pixel the irradiance can be retrieved as a function of discrete values of the azimuth and elevation angle. However, this yields a large dataset with high uncertainty due to noise in the measurements. Therefore, a coarse detector grid rc,cc is used for the computation. For these selected detector pixels the measurements are averaged over an area of typically 10 pixels to reduce variability. Then a low-order (4 × 4-dimensional) Chebyshev fit is made by extrapolation of the fit. This fit is valid between azimuth angle and elevation angle . The parameters of this fit are the key data used in the L01b processor. The measurements that suffer from vignetting are excluded in the construction of the polynomial fit by inspection.
The relative irradiance as a function of azimuth and elevation angle (φ, ϵ) is given in Fig. 21 for a number of pixels. The signal shows a smooth dependence on the azimuth and elevation angle per pixel and that the maximal signal is attained for the azimuth and elevation angles . The relative irradiance displays no large (qualitative) variability as a function of the detector pixel.
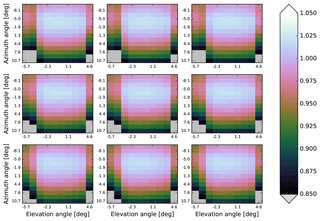
Figure 21The relative irradiance response of the instrument as a function of azimuth angle φ and elevation ϵ at a number of pixels (figures correspond to different pixel locations on the detector) for the NIR detector. The signal shows a smooth dependence on the azimuth and elevation angle per pixel and is similar for all pixels.
In Fig. 22 the dependency of the relative irradiance on the elevation angle (Fig. 22a) and azimuth angles (Fig. 22b) is given for different detector pixels. It is a reasonably smooth function for the azimuth angles tested (−9.7–10.7∘) and for elevation angles between −3.4 and 3.4∘. For larger elevation angles the images are visibly vignetted because the Sun port baffle is blocking the stimulus. This is a characteristic of the instrument, so the same range of elevation angles will be covered in flight.
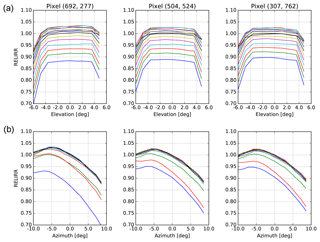
Figure 22Line plots for selected pixels from Fig. 21. (a) For varying elevation angles; (b) for varying azimuth angles. Lines in each plot are for different azimuth and elevation angles. The relative irradiance as a function of the azimuth angle is smooth and well behaved.
The calibration of the relative irradiance yields key data that largely remove the dependency of the Sun port measurements on the azimuth and elevation angles under which they were performed.
The order of the polynomial with which the dependency on the azimuth and elevation angles is fitted does not seem to influence the success of the calibration much. The residuals after using fourth-order Chebyshev polynomials show a slight visible pattern, but care must be taken not to overfit the signal. Double processing yields good results, effectively removing relative irradiance from the measurements using QVD2. The standard deviation of the signal decreases, with a remaining deviation from unity within 0.002 for the NIR and SWIR channels, 0.004 for UVIS, and 0.008 for the UV detector for pixels averaged over a small detector area.
The measurements using the nominal diffuser QVD1 suffered from stimulus stability issues, and it was not possible to derive reliable CKD. The calibration of both diffusers will be recovered with additional in-flight measurements during the E1 commissioning period after launch.
6.6 In-band straylight calibration
Straylight is any light that falls on a detector pixel which by optical design is not intended to detect that light. As opposed to intended or direct light, straylight is also referred to as unintended or indirect light. Scattering from surface roughness, unwanted specular reflections (ghosts), and unwanted diffraction effects (e.g. diffraction at obstacles, Rowland ghosts, and unwanted grating orders) causes the light to follow different paths from those intended by optical design. The redirected light that reaches the detector, i.e. straylight, gives rise to spurious signals at the detector.
Straylight in a hyper-spectral imager using two-dimensional detectors can be complex because light can scatter in both the spectral and the spatial dimensions and the source of the straylight may lie outside the intended spatial or spectral range. For TROPOMI we define the following types of straylight:
-
Out-of-field straylight is light that originates outside the intended spatial field of view of the telescope.
-
Out-of-spectral-range straylight is light that originates outside the intended spectral range of each spectrometer.
-
In-band straylight, in contrast to out-of-spectral-range straylight, is light that originates inside the intended spectral range of each spectrometer.
-
Near-field in-band straylight is light that originates within the intended field of view and spectral range of the detector and that causes spurious signal in the proximity of the pixels that were intended to receive the signal.
-
Far-field in-band straylight is similar to near-field straylight, but it causes straylight further away – but still on – the same detector.
-
Ghosts originate in the optics due to reflection from optical or mechanical components and come in both types, out-of-spectral-range and in-band.
All of the above listed types of straylight have in general both a spatial and a spectral component when they arrive at the detector. For some of the straylight types – the in-band straylight types – a correction is possible when the intensity of the source of the straylight is measured by the instrument. This is typically not possible for out-of-spectral-range and out-of-field straylight. For these, only a characterization is possible, which can be included in the specified radiometric error. To characterize and correct for TROPOMI straylight, a set of straylight tests were designed. The in-field-in-spectral-range straylight in the SWIR detector was characterized by SRON and is reported in Tol et al. (2018); this paper will continue with the straylight results for the UVN module. The TROPOMI instrument was designed for low ghosting, and all observed ghosts were sufficiently small to disregard them in the L1b correction. The spectral and spatial components of the out-of-spectral-range straylight are covered in Sect. 6.7. In this section we address the out-of-field and in-band spectral and spatial straylight.
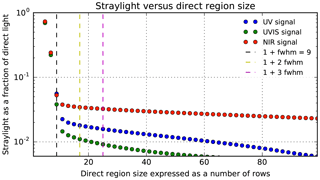
Figure 23Shown is the integrated straylight fraction received per UVN detector as a function of the direct region size. The illumination is via the Earth port. The NIR detector (red dots) displays the most straylight followed by the UV (blue dots) and the UVIS (green dots). The vertical dashed lines indicate the direct illumination in rows for three region sizes expressed in multiples of the FWHM of the direct signal. Shown are FWHM (black dashes), FWHM (yellow dashes), and FWHM (red dashes). The offset of one row is the centre of mass of the column average of the direct signal.
The straylight from outside the field of view of a spectrometer (out-of-field straylight) is characterized with an external white light source (EWLS), which is homogenized by a small integrating sphere and then shaped into a narrow field of (across × along flight). Baffles and low-reflectance materials reduce the straylight caused by the set-up. With the instrument itself the final set-up was commissioned and the observed features could be attributed to instrument internal ghosts.
This source is also used to construct straylight validation scenes and to determine the spatial part of the in-field straylight. The measurements show that the observed out-of-field straylight is 8.7, 30.8, and 28.7 times smaller than the measured total in-field in-band straylight, for the UV, UVIS, and NIR spectrometers respectively. This WLS, in combination with optical bandpass filters with a full width at half maximum (FWHM) of about 10 nm, is used to quantify the far-field straylight within the spectral range of each UVN spectrometer. Also for the out-of-spectral-range straylight characterization this WLS was used, but now together with long-pass and short-pass filters.
The main straylight correction in the L01b processing chain is based on measurements with a pulsed laser stimulus. This correction addresses all near-field spectral and spatial straylight. No other corrections were necessary, apart from the out-of-spectral-range correction described in the next section. The laser light is homogenized by a small integrating sphere and has a field of (across × along flight). The output of the laser can be tuned in the range of 210–2600 nm with step sizes between 0.05 nm for the short wavelengths and 1 nm for the long wavelengths.
Table 7Integrated straylight for the UVN detectors calculated from the measurements with the EWLS via the Earth port. Shown are data for three different sizes of the direct region (DR). Straylight is expressed as a percentage of the direct light.
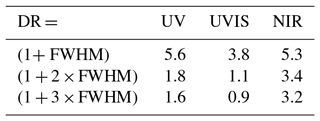
The UVN in-field, in-spectral-range straylight correction algorithm is implemented using a convolution, which first calculates a straylight signal for a given input signal and then subtracts the calculated straylight signal from the input signal. The main ingredient of the L01b straylight algorithm is the convolution between an input signal and a straylight convolution kernel to obtain a straylight signal. In this sense, this algorithm is similar to convolution algorithms used in common commercial image processing to sharpen or to smooth images. There, images are smoothed or sharpened depending on which convolution kernel is used. In the straylight correction, a special straylight convolution kernel, called a straylight response function (SLRF), is used to calculate the straylight signal for a given input signal. The SLRF describes the relative straylight response of the system and is derived from the on-ground calibration measurements obtained with the laser set-up.
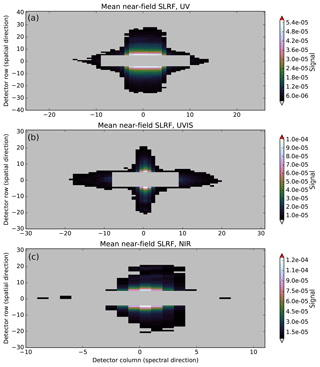
Figure 24Mean near-field straylight response function, shown for the UV (a), UVIS (b), and NIR (c) spectrometers. Each response function is displayed as a two-dimensional pseudo-colour plot, as a function of the relative distance in the spectral and spatial directions. The unit for the straylight response function is 1. The rectangle in the centre is the excluded direct region. The direct region in the spatial direction is 9 pixels wide for all UVN spectrometers; the width in the spectral dimension is optimized for each spectrometer to match the instrument spectral response function (ISRF).
To make a distinction between straylight near the directly illuminated region (direct region, DR) and straylight far away from the direct region, we call the former near-field straylight and the latter far-field straylight. It is clear that the straylight calculated as a fraction of the direct signal depends on the choice of the size of the direct region. The direct region should of course be larger than the FWHM of the direct signal. Otherwise, the reported straylight level would be exaggerated. Figure 23 shows how the calculated relative straylight depends on the choice of the direct region size, which is expressed as a number of detector rows. Three vertical lines in Fig. 23 denote direct region sizes of , 2 ×, and 3 × the direct signal FWHM. The offset of one row is the centre of mass of the column average of the direct signal. Table 7 summarizes straylight values calculated for the three direct region sizes.
Table 8Average straylight before and after the straylight correction together with the corresponding error estimates, as well as the average straylight correction factor. Listed is the total integrated (straylight) signal outside the direct region divided by the integrated signal inside the direct region. The values for UVN were obtained from EWLS measurement data via the Earth port. The error estimates for UVN are valid only if the systematic errors are negligible with respect to the random noise. The results shown for SWIR were obtained from laser measurements and are reproduced from Tol et al. (2018).
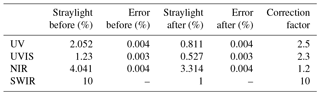
One single average near-field SLRF was derived from the laser measurements for each spectrometer of the UVN module. The obtained mean near-field SLRFs are shown in Fig. 24.
The rectangle in the centre is the excluded direct region. The algorithm used direct region sizes of 9 × 17, 9 × 17, and 9 × 13 (spatial × spectral) detector pixels, for the UV, UVIS, and NIR spectrometers respectively. The direct region sizes were chosen in such a manner to ensure that the straylight response does not include what is included in the instrument response. The direct region size in the spatial direction of 9 detector pixels was used to achieve consistency with the pixel response function analysis, which uses 7 detector pixels in the spatial direction. Similarly, the direct region sizes in the spectral direction were chosen to achieve consistency with the non-zero instrument spectral response function (ISRF) spectral ranges of [−0.5, 0.5], [−1.2, 1.2], and [−0.6, 06] nm, for the UV, UVIS, and NIR spectrometers respectively. After the near-field straylight response functions had been calculated, the far-field components were added to obtain the mean extended straylight response functions.
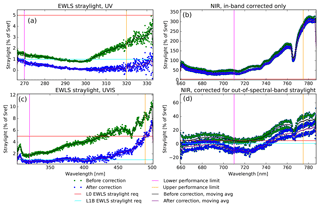
Figure 25Straylight in the middle of the hole of the EWLS hole-in-the-cloud scene, divided by the EWLS signal, before (green dots) and after (blue dots) the straylight correction with the straylight convolution algorithm. Solid black and blue lines respectively denote moving average of the straylight before and after the correction. In each panel, the two vertical lines denote the limits of the spectral performance range. The horizontal red line denotes the EWLS spatial straylight requirement at L0, and the horizontal cyan line denotes EWLS spatial straylight requirement at L1b. Data are shown for the UV (a) and UVIS (c) spectrometers. Data for the NIR spectrometer are shown without (b) and with an ad hoc out-of-band straylight correction (d). Note that this ad hoc correction differs from the out-of-band correction described in Sect. 6.7.
For the case of the EWLS measurements via the Earth port as a function of azimuth angle, the convolution algorithm reduces straylight outside the direct region by the factors shown in Table 8. Worse straylight performance in the case of the NIR spectrometer is due to a very strong out-of-spectral-range straylight contribution caused by light at wavelengths longer than 795 nm, which accounts for about 75 % of the observed straylight. This contribution is expected to be smaller in flight than it is in the on-ground calibration measurements. Unlike the Sun, the xenon lamp used as the source in the EWLS measurements has strong emission lines in the wavelength range between 800 and 1000 nm, which are the reason for the observed dominant out-of-spectral-range straylight contribution.
Compliance with the requirements on straylight for a pre-defined hole-in-the-cloud scene was established using measurements with an external WLS. This performance scene describes a worst-case radiance observation in which the full swath of the instrument is illuminated by pure white clouds, apart from a small gap around the nadir. Because the full swath of the instrument in the vacuum chamber cannot be illuminated simultaneously during on-ground validation, this scene is constructed from EWLS measurements, and the L0 and L1b requirements are expressed in terms of the signals from the EWLS. The spectrum of the source differs from in-flight Earth radiance, so the scene represents a EWLS hole in the cloud. The convolution algorithm reduces straylight in the middle of the hole of the EWLS hole-in-the-cloud scene as given in Fig. 25. The correction factor exceeds 10 for some wavelengths in the case of the UV spectrometer, and it reaches a value of 5 and 1.4 for the UVIS and NIR spectrometers respectively. Further validation with more realistic Earth scenes could not be established due to the lack of opportunity of performing zenith sky measurements, for example, in the calibration facility. For real Earth scenes and in deep absorption lines like the oxygen A band, the relative fraction of straylight versus useful signal could be higher as near-field straylight from the spectral dimension would fill the absorption lines. This effect is similar to the effect a hole-in-the-cloud scene has, but further validation can only be established during in-flight conditions. The top panel in Fig. 25b shows the straylight in the NIR range reaching levels up to 300 % of the reference signal with the external WLS employed. Figure 25d of the same figure shows the effect of an ad hoc out-of-band correction based on measurements with a long-pass filter. Due to the cut-off wavelength of the filter straylight, this correction removes signal from wavelengths longer than the NIR detector range. However, the overall signal of this ad hoc correction signal is not matched to the in-band signal due to a different stimulus setting. This causes an overcorrection and the negative signal in the plot.
Note that this EWLS hole-in-the-cloud-scene validation does not provide information on the spectral component of the straylight. The calibration of the instrument has shown that the straylight is dominated by near-field straylight, which has both a spatial and a spectral component. As indicated, the near-field straylight was calibrated with a laser source, and this is the basis of the current correction in the L01b processor. The ghosts were sufficiently small to be not corrected.
The UV spectrometer is compliant with both the L0 and L1b EWLS spatial straylight requirement, the UVIS spectrometer is partially compliant with both EWLS spatial straylight requirements, and the NIR spectrometer is not compliant with either of the EWLS spatial straylight requirements. In order to achieve compliance of the NIR spectrometer with the EWLS L1b spatial straylight requirement, it is necessary to correct for the out-of-spectral-range straylight. This correction has been determined for the NIR spectrometer as described in the next section.
6.7 Out-of-spectral-range straylight
During the calibration effort unexpected signal was encountered in the NIR spectrometer as mentioned in the previous section. This signal was tentatively attributed to out-of-spectral-band straylight. At that time no means were available for a full calibration and the topic was postponed. At a later point in the program, after integration of the instrument into the satellite, the opportunity arose to perform additional measurements. The out-of-band straylight campaign for the NIR detector at Airbus UK in Stevenage in December 2016 and January 2017 consisted of relative measurements.
A dedicated set-up was designed that could characterize the straylight at ambient temperature and pressure using the instrument already integrated on the platform. Because the measurements had to be performed under ambient conditions, the detectors could not be cooled to their nominal operational temperatures of 206 K. It was chosen to set the temperature for the NIR detector to 297 K, which is slightly above room temperature, which allows for the thermal control loop to stabilize the CCD temperature and thus its dark current. The latter point is essential because this dark current is approximately 100 000 electrons per second, and any variation herein could swamp the straylight signal under investigation. A dedicated correction algorithm was developed for the L01b processor to address the ambient dark current.
Due to the nature of the out-of-band straylight, no direct correction is possible in flight. The out-of-band signal is not measured in flight and therefore a correction must be based on an assumed out-of-band spectrum. Depending on the illumination, via the Sun port, the Earth port, or from internal sources, the spectra can differ. To weigh the out-of-band spectrum according to the instrument's response the source wavelengths and directions of the out-of-band straylight need to be characterized.
As a source, two narrow linewidth tunable continuous-wave lasers are used. The two lasers cover different wavelength ranges: 710–945 nm for the red laser and 592–683 nm for the blue laser. The instrument response is measured first for in-band wavelengths and then for out-of-band wavelengths. These in-band measurements are needed to normalize the power of the out-of-band measurements; the in-band measurements themselves give no information on straylight. In order to perform this normalization, the out-of-band power versus wavelength of the lasers is also needed. Because this is not known, the power in band and out of band is monitored with a photodiode. When spectral dependencies of the source and set-up are included, the in-band signal strength and swath position can be related to an expected out-of-band signal. To avoid long integration times, the out-of-band wavelengths are measured with a higher laser input power than the in-band wavelengths. The necessary attenuation is achieved with calibrated neutral density (ND) filters. Using this increased power during the out-of-band measurements, useful SNRs exceeding 500 could be achieved for the observed (in-band) straylight for all wavelengths and cross-track positions.
The set-up to measure the NIR out-of-band straylight in ambient temperature and pressure consists of the so-called Earth port adapter which is attached to the Earth port of TROPOMI, an optical assembly with neutral density (ND) filters and light sources. The Earth port adapter is connected directly to the Earth port; attached to the EPA are 11 fibre collimators. They are aligned to illuminate different swath angles (rows) of the NIR detector. The output of the light sources is coupled via a small integrating sphere and optical fibres to the collimators.
During the campaign, the short wavelength side of the NIR detector was referred to as the blue side and the long wavelength side as the red side. For both red and blue sides, the raw data consist of 11 sets of NIR-detector images, one set for each separate fibre.
During the the laser measurements the out-of-band power is monitored using a photodiode and current meter. The current is directly connected to the laser output including ND filter transmission. In other words, the evolution of the number of photons (caused by laser output drift, ND filter drift, and wavelength dependency of both) reaching the instrument is completely reflected in the observed photodiode current.
The typical behaviour of the spatial straylight distribution is shown in Fig. 26 for fibre 4. The straylight “blob” is most prominent at the associated detector row (i.e. row 668) of this fibre and is somewhat skewed towards the nadir row. In general, as could be expected from the total straylight magnitude, the blob grows when the laser illuminates the wavelengths from 808 to 818 nm and then decreases in size and strength. From 830 nm onward, no more out-of-band straylight is visible up to the highest laser wavelength of 945 nm. For the blue side the blob was visible between 623 and 645 nm, and no straylight was further measured for wavelengths down to 595 nm.
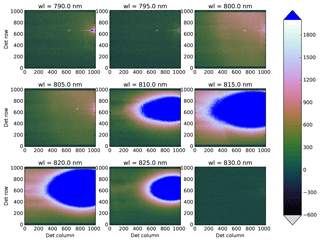
Figure 26The straylight image of the NIR detector for a range of laser wavelengths λlaser on the red side for fibre 4 before normalization. Detector columns are in the spectral direction, and detector rows are in the spatial direction. The colour scale is the same for all images.
After smoothing and normalization, the absolute straylight fractions from both sides can be compared. In Fig. 27 it can be seen that the absolute straylight fraction on the blue side is smaller than on the red side. The assumption is that the measured in-band signals at 666 nm (blue side) and at 780 nm (red side) are equal and that the extrapolation toward the out-of-band wavelengths is constant. Under this assumption of an entirely flat spectral density, the integrated straylight signal from the red side is about 6 times larger than the integrated signal from the blue side. More precisely. the ratio of the areas defined by the red and blue lines is 6. Note that the normalized fraction is difficult to interpret: it is the signal sum over all pixels at a given out-of-band laser wavelength relative to the associated total signal in the direct in-band region (and, in fact, in the entire detector) at a chosen in-band wavelength.
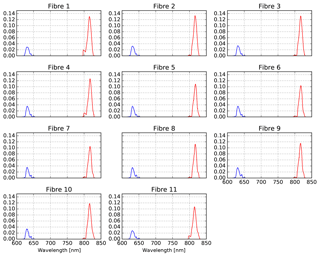
Figure 27Overview of the normalized and integrated contributions to straylight (SL) from both the red long wavelength side (red line) and the blue short wavelength side (blue line) for a flat spectrum. The figures for all fibres show that the contribution to the total straylight on the detector is dominated by signal originating from the long wavelength side and that there is no strong across-track variation.
Initial validation measurements were performed at the end of the campaign, with one or more fibres connected to a 12” Spectralon integrating sphere with 3 × 5 W QTH lamps. This QTH is a different stimulus than the one used during the regular calibration campaign for straylight, and therefore no direct comparison can be made between the two due to lack of knowledge about the spectral output of the EWLS. For the prediction of the out-of-range QTH signal, a direct extrapolation from the signal measured by TROPOMI (corrected for absolute radiance) is used, instead of information from the integrating sphere data sheets. The out-of-band straylight correction is carried out in two steps: first for straylight from the red side, then for straylight from the blue side (Fig. 28). The latter correction is smaller in magnitude.
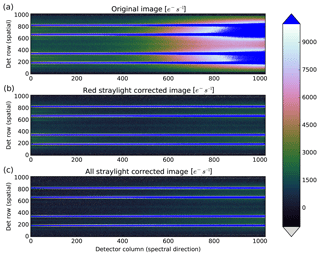
Figure 28Validation measurement with fibres 2, 4, 8, and 10 illuminated by the integrating sphere. (a) NIR detector image before correction. (b) Image after correction for straylight from the red (long wavelength) side only. (c) Image after out-of-band straylight correction for both sides.
The overall straylight reduction is shown in Fig. 29a. Note that no in-band (near-field) straylight correction has been applied here. Only in a later step, is remaining straylight partially removed by the regular in-band straylight L01b processor algorithm. In the second panel of the same figure, the expected out-of-band spectral behaviour is shown. In this case, it is a simple linear extrapolation from the in-band signal since the signal measured by TROPOMI itself was considered more reliable than external sources. In Fig. 29c, the evolution of low signals in the image is shown: in general, after correction a Gaussian curve with a mean of zero or slightly positive values is to be expected. The reason is that, after all straylight removal, a pixel signal is either very high (in the rows directly illuminated by the fibre) or zero (all other rows that are not directly illuminated).
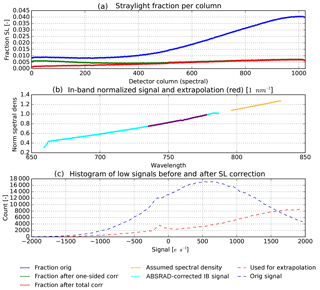
Figure 29(a) The total straylight fraction per NIR detector column, before (blue line) and after out-of-band straylight correction for the red side (green line) and both sides (red line). (b) The spectral extrapolation as based on the in-band signal (shown in turquoise). The in-band signal is corrected for absolute radiance and normalized to a characteristic in-band wavelength. The thin blue line denotes the region (roughly between 730 and 780 nm) on which the extrapolation is based. The extrapolation is linear in this case and shown as an orange line. (c) Histogram of the low signals below 2000 , before (blue dashes) and after (red dashes) out-of-band straylight correction.
All potential methods to validate the out-of-band straylight correction in the in-flight phase have to be considered. For the irradiance, the in-flight solar measurements will be used to construct optimally processed out-of-band correction CKD. For the radiance, construction of the processed CKD is more complex because input from L2 algorithms is needed to analyse the residuals; it may be necessary to analyse and correct for separate scene characteristics, water vapour dependence might be included by adjusting the non-linear scaling configuration parameter, and the impact of under-correction has to be analysed.
7.1 Pixel response function
The pixel response function (PRF) defines for each pixel the amount of light received from all directions. As the direction of the light can be defined by two angles, azimuth and elevation, this is a two-dimensional function. The barycentre of this distribution, i.e. its centre of mass, defines the centre-point direction from where the detector pixel receives light and is called the LOS.
To be able to determine the PRF per pixel, a star stimulus, which produces a collimated white light beam, is pointed at the Earth port of the instrument. The star stimulus is a 1000 W Xe source. It is homogenized and collimated to a field of 0.011∘. The beam is aligned co-linearly with an alignment cube on the collimating mirror. The relative orientation of this alignment cube to to the instrument alignment cube is determined with a theodolite.
The instrument is mounted on a cradle, which can rotate and tilt. These cradle angles are converted to LOS angles in the instrument reference frame (IRF). For each detector a number of cradle angle settings are measured, covering at least all angle combinations from which any light is received at the detector.
The IRF azimuth and elevation angle of the barycentre of the PRF distribution are not known a priori for each detector pixel. One can, however, make an initial guess for the 2-D azimuth–elevation window around this barycentre, which will hold relevant PRF information.
All star stimulus Earth port measurements are processed and annotated with the cradle to IRF alignment correction. Then for all measurements and for each pixel it is checked whether the azimuth and elevation angles of this measurement are within the azimuth–elevation window determined for that pixel. If it is within the window, the signal value for that pixel is stored with its azimuth and elevation angle. This way, a PRF data product results with dimensions row × column × measurement × variable , the last three items being the three variables signal, azimuth, and elevation angle.
When this process was completed for the first time, contour and surface plots were made for a number of pixels. The elevation–azimuth window was now checked and adjusted to tightly fit around the useful data but still including a large enough area for the entire PRF to fit within the window. In this way, the size of the data product was minimized.
Double measurements are removed such that each azimuth–elevation combination within the measurement grid with a step size of 0.05 ∘ is present once. Intermediate NaN (not-a-number) values are removed, and the volume of each PRF is normalized to 1.
For 1 pixel in the middle of each detector and 1 in a corner, a contour plot with 15 isolines and a tri-surface plot is shown in Figs. 30–31. The contour plot is made from a cubic interpolation of the data to a fine grid. The tri-surface plot draws a node at each data point and then connects to the closest data points in 3-D space to form triangular tiles that form a surface.
7.2 Line-of-sight annotation
A measurement of a single TROPOMI ground pixel consists of multiple spectral pixels, and the ground pixel location associated with it thus depends on the direction of observed light by all detector pixels involved. The CKD needed to determine this ground pixel location are the so-called LOS angles azimuth and elevation. The geometrical CKD, for each pixel on each detector, contain an elevation and an azimuth angle defined in the IRF.
The geolocation algorithm in the L01b data processor determines, for any measurement time instance, from which area on the Earth's surface light was received at a certain TROPOMI detector pixel, using the position and orientation of the spacecraft and the geometrical CKD. For a more rigorous explanation of the geolocation L01b algorithm the reader is referred to Sects. 26 and 27 of the L01b ATBD (KNMI, 2017).
Because the L01b processor only processes 1 ground pixel per detector row, the average of the LOS angles per detector row is taken. Then, to smooth out measurement uncertainties, a polynomial fit is made of each LOS angle with respect to the detector rows. Part of the detector rows do not receive light during this measurement, while LOS angles of these rows might be required for L01b processing. Therefore, the polynomial expressions are used to extrapolate the LOS angles over all rows of the detector.
To determine these LOS angles from the calibration measurements, a weighted mean method is used. For a certain cradle angle combination, the signal received from the detector will be highest at certain rows and or pixels. This signal for each pixel and each measurement is multiplied with one of the cradle angles corresponding to that measurement and subsequently summed for all measurements. Furthermore, the signal for each pixel is also summed over all measurements separately. The former image is then divided by the latter image, resulting in a weighted mean of the cradle angle for each pixel.
7.2.1 Intra-band spatial co-registration
The LOS angles for different detector pixels vary slightly within a single row. A measured spectrum is defined as the data sampled by the detector pixels within a single (binned) row. Because these individual detector pixels all look at slightly different scenes, the wavelengths within a measurement will also stem from slightly different scenes. A chromatic error is thus introduced when averaging these individual detector pixel LOS angles over the row. This effect is referred to as intra-band spatial co-registration.
To quantify the intra-band co-registration error, the minimum and maximum elevation and azimuth of each row are determined. The difference between these extremes can be converted to a distance at the location of the correlating ground pixel. This distance is plotted versus row number in Fig. 32, for both the LOS angles separately and their combination. The figure shows that the intra-band co-registration error increases strongly towards the edge of the swath; this is a geometric effect mainly caused by the curvature of the Earth. Because the spatial sampling distance also increases due to this effect by a factor of 4 towards the edge of the swath, the error remains sufficiently small with respect to the nominal ground pixel size as given in Table 1.
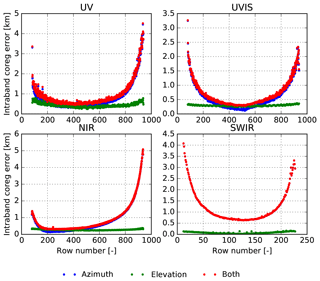
Figure 32Intra-band co-registration error as distance on the surface of the Earth (km) versus row number (spatial direction), for all detectors. For each row, the maximum difference between the elevation (green), azimuth (blue), and the combination of elevation and azimuth (red) is shown for any pixel pair in that row.
7.2.2 Inter-band spatial co-registration
For the inter-band co-registration, the ground pixel barycentre locations of different detectors are compared. As the SWIR detector has fewer rows, the azimuth and elevations values for the 1024 relevant detector rows of the UVN detectors are averaged per four rows. This results in 256 rows, exactly the number of significant SWIR rows.
The detectors are aligned with respect to the defined nadir rows, and the difference of all detector pairs in azimuth and elevation angles can be determined and converted to a distance on the ground at the location of the correlating ground pixel.
This distance is shown for both azimuth and elevation angle and the combination of both in Fig. 33 for all detector pair combinations. The distances increase at the edge of the swath due to the combined effect of the LOS not being orthogonal to the Earth and the curvature of the Earth. The inter-band co-registration error is – as expected from design – large for UV–SWIR and UVIS–NIR. Between UVIS and NIR the differences are very small. Both the UV and the SWIR spectrometer have an internal slit, which can explain the significant inter-band co-registration error in the elevation (along-track) direction between the two. This misregistration is a design feature of the instrument that cannot be solved at L1b. When data from multiple spectrometers are combined, the geolocation annotation, which is provided per detector, should be used to match ground pixels for each row and detector such that the signal stems from the same geolocation.
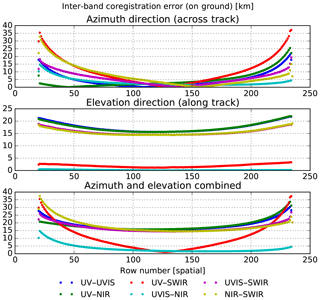
Figure 33Inter-band co-registration error as distance on the surface of the Earth (km) versus row number (spatial direction), for all detector combinations. For UVN, the average of four adjacent rows is taken for comparison to one SWIR row. The large differences between UVIS–NIR and UV–SWIR in the elevation direction are as expected from the slit design.
The spectral calibration consists of the determination of the ISRF and the wavelength calibration. For the SWIR spectrometer the results from the spectral calibration are reported in van Hees et al. (2018).
For the UVN spectrometers for both CKD, measurements were performed with SLS and a slit function stimulus (SFS).
A SLS produces a limited number of spectral features with a well-known wavelength (accuracy ≪ 0.01 nm) and low spectral bandwidth (≪ 0.01 nm). Measurements using an SLS yield very accurate knowledge on pixel wavelengths near the wavelengths of the spectral lines used. However the characteristic wavelength for detector pixels with wavelengths in between available spectral lines must be estimated by interpolation, which may lead to interpolation errors. For detector pixels beyond the first or last available spectral line within the detector spectral range, the situation is worse, as for these pixels extrapolation is required. In addition, the estimation of the centre of mass of the response for a spectral line may be distorted in case the SLS produces additional spectral lines with a wavelength near the spectral line wavelength. Hence the selection of suitable spectral lines must be performed with care. Two types of spectral line sources were used: a platinum–chromium–neon–argon hollow cathode (PtCrNeAr) lamp and a mercury–cadmium (HgCd) lamp.
A SFS consists of an echelle grating monochromator, producing several spectral lines simultaneously at typically several nanometres in distance. The absolute wavelength of the lines is only known with limited accuracy, but the relative spectral distances between the lines are well defined. By rotating the echelle grating, the wavelengths of the produced lines can be shifted in steps of a few hundredths (0.01) of a nanometre. The measurements from the SFS can be used to yield a wavelength calibration for spectral ranges that are not sufficiently covered by the SLSs.
For the ISRF, a pulsed laser produces spectral lines at different wavelengths. The output of the laser can be tuned in the range of 210–2600 nm with step sizes between 0.05 nm for the short wavelengths and 1 nm for the long wavelengths. The bandwidth of the laser increases towards longer wavelengths. For the NIR the bandwidth is too wide to determine the ISRF; there the SFS is used.
Measurements were performed for both Earth port and Sun port (internal diffuser QVD1 only). The stimuli were designed such that for the Earth port a homogeneous field was observed by TROPOMI for at least a number of detector rows per measurement (typically 5 to 7). For the Sun port the field was collimated to mimic the field from the Sun as observed by TROPOMI.
8.1 Instrument spectral response function
The ISRF (also known as slit function) characterizes each pixel's spectral response for different wavelengths.
The ISRF is modelled by a function Rb[ximg](dλ), where ximg represents a detector pixel and dλ represents the difference between the observed source wavelength and the pixel characteristic wavelength in nanometres. The latter wavelength has been defined as the source wavelength for which the centre of mass of the instrument response is at the specified pixel. The shape of the ISRF is determined by the instrument optics, dispersive elements, and entrance slits and thus differs per spectrometer. To obtain the ISRF for the UVN spectrometers, measurements were executed with the tunable laser and the SFS. Measurements with the SLSs are used to validate the ISRF. Measurements were performed for both the Earth port and the Sun port. By default, the scenes observed by TROPOMI for the Earth port ISRF measurements were homogeneous within the TROPOMI field of view in the flight direction. Some additional measurements were performed to study the influence of inhomogeneous scenes in the flight direction on the ISRF.
The ISRF parametrization step aims at obtaining the ISRF shape for each delta wavelength. Hence it should accurately interpolate the ISRF shape to the delta-wavelength grid and in addition remove any influence of noise in the data points on the obtained ISRF.
The objective for the fit function design is to find a function R that inherently satisfies a priori constraints such as edge values of 0 and provides enough flexibility to describe the actual ISRF with sufficient accuracy, i.e. below 1 %. Finding such a function is not trivial, in particular in the case the ISRF is asymmetric. The function eventually used for the UV and NIR detectors is described by the difference between two advanced sigmoid functions that are shifted in wavelength. The resulting function resembles a convolved Gaussian with additional flexibility in the tails. The function RUV,NIR is described by the following equation for UV and NIR (the a2 parameter indicates the wavelength shift between both sigmoids):
with (nm), the fitted amplitude a0 (nm−1), the double sigmoid centre location a1 (nm), and width a2 (nm). First-order (a3,a4; nm−1) and third-order (a5,a6; nm−3) scaling factors for both sigmoids, the skewness of the double sigmoid function (nm−1) and the offset a8 (nm−1) are included. All parameters ai are fitted.
For NIR the skewness parameter a7 was not used in the fit (set to 0). In addition, the parametrization of the ISRFs for NIR from SFS measurements involved an additional convolution step with a modelled SFS line shape: the spectral line shape of spectral lines produced by the SFS is expected to significantly affect the retrieved ISRF shape, which can be checked by comparing differences between ISRFs obtained from the SFS measurements and ISRFs obtained from SLS measurements.
For UVIS a convolved triangle function was used for the v0.1.0 CKD, consisting of a base triangle function that is integrated over a certain window around dλ. The width of the window could vary with dλ. Further analysis revealed that a sixth-order generalized exponential function showed slightly lower lack of fit; hence this function was used in the v1.0.0 analysis. It is described by
with (nm), the fitted amplitude a0 (nm−1), the centre location of the ISRF a1 (nm), generalized exponential order parameters of the order of 2–6, a2–a6 (nm−2–nm−6), and the fitted offset a7 (nm−1).
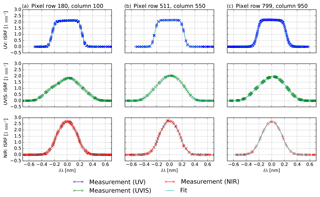
Figure 34Extracted data and parametrized instrument spectral response functions (ISRFs) for several pixels on the UVN detectors. For each detector two pixels at diagonal opposite corners (left and right columns) and a pixel in the middle of the detector (middle column) are shown. The data for the UV and UVIS ranges are derived from laser measurements, and the data for NIR are from SFS measurements.
The ISRF calibration analysis has been performed for the two main stimuli, the SLS and the tunable laser, and validated using two additional SLSs, PtCrNeAr and HgCd. The analysis included both Sun port and Earth port measurements. The use of two distinct stimuli has enabled cross-validation and provided redundancy, which has proven to be essential during the calibration campaign, as laser reliability and SNR issues for the SFS reduced the number of usable measurements. The following results were found.
For UV the ISRF shapes via the Earth port are flat-topped, block-like shaped, with a FWHM between 0.45 and 0.5 nm; see Fig. 34. Due to a higher SNR and better detector coverage, the laser measurements via the Earth port have been selected as the baseline for the CKD for the UV range.
For the UVIS range the ISRF shapes via the Earth port seem to be a mixture of triangular and Gaussian, with a slight asymmetry, and they have a FWHM between 0.45 and 0.65 nm; see Fig. 34. Towards higher UVIS wavelengths the FWHM of the laser measurements seems to increase with respect to the SFS measurements, which may indicate a broadening of the measured response bandwidth by the bandwidth of the produced laser line. Due to this potential broadening, the SFS measurements via the Earth port have been selected as the baseline for the CKD for the UVIS range.
For the NIR range the ISRF shapes via the Earth port resemble a Gaussian distribution with a rounded top, with a FWHM of 0.34–0.35 nm for the SFS measurements. The laser-derived ISRFs suffer from the expected broadening of lines produced by the stimulus, which increases FWHM to 0.355–0.365 nm; see Fig. 34. Due to this line broadening, the SFS measurements via the Earth port have been selected as a baseline for the CKD for the NIR range.
The accuracy of the parametrized ISRF measured via the Earth port is of the order of 1 % or less for a major part (but not all) of the delta-wavelength grid points and detector pixels. ISRF shapes obtained from the Sun port resemble shapes obtained for the Earth port, and average differences in Sun port vs. Earth port FWHM are within 0.6 %.
By changing the cradle tilt angle inhomogeneous illumination fields were created in the along-track direction (across-spectrometer slit) observed by TROPOMI. The results showed large changes (>10 %) in ISRF shape and centre of mass that resemble a cut-off of part of the response by a missing part of the field. As a consequence the use of the ISRF CKD on scenes with a large scene inhomogeneity as observed by individual pixels may lead to large errors in analysis results. Possible mitigation is marking results from such inhomogeneous scenes as invalid and/or additional modelling of the impact of the scene homogeneity on the ISRF.
8.2 Wavelength calibration
For the wavelength calibration a characteristic wavelength is established for each detector pixel xdet by means of measurement. This is yields a wavelength map λb[xdet]. The characteristic wavelength for a pixel is the wavelength for which the centre of mass of the instrument response is at the centre of the specified pixel. The wavelength calibration depends on external conditions, such as instrument temperature, scene uniformity, and instrument stability. The temperature dependency of the spectral calibration has not been studied during the on-ground calibration campaign, primarily due to timing constraints and the expected performance of the active thermal control of TROPOMI. Some investigative measurements on scene uniformity have been performed, but the spectral calibration is only valid for homogeneous scenes as observed by a detector pixel. The instrument stability has been studied by comparing results for the various measurement series, which were up to 2 months apart.
Figure 35Earth port wavelength maps for the UVN detectors, including interpolated and extrapolated areas, with a colour scale in nanometres. The spectral smile is visible in all spectrometers.
The spectral calibration measurements performed during the TROPOMI calibration campaign have enabled a wavelength calibration that is accurate over a large area of the detector, thanks to the possibility of cross-calibration and cross-validation of SFS measurements that provide a large spectral coverage and measurements using two SLSs that provide accurate absolute knowledge on wavelengths. The following results were found.
The full spectral range, including the range without performance requirements and the spectral smile, is 266 to 333 nm for the UV detector, 300 to 502 nm for the UVIS detector, and 656 to 787 nm for the NIR detector. Dispersions are 0.065 nm pixel−1 for the UV, 0.195 nm pixel−1 for the UVIS, and 0.125 nm pixel−1 for the NIR detectors, values that are constant within 5 % over the detector. The wavelength map for the UVN detectors is shown in Fig. 35.
From both unintentional issues in field alignment and intentional misalignment to simulate field inhomogeneity in Earth port measurements, it was found that wavelength shifts of up to 0.1 nm can occur due to inhomogeneous slit illumination. Inhomogeneous scenes can occur in orbit, for example due to the presence of clouds.
Measurements with the SFS via the Sun port have a poor SNR in the UV range, making the wavelength calibration for the UV range infeasible. The mitigation for this issue is to obtain the Sun port wavelength calibration for the UV range by adapting (scaling) the Earth port wavelength calibration for the UV range to the results of the Sun port HgCd SLS measurements in the UV range.
A comparison of Earth port and Sun port measurements shows agreement of both calibrations to within 0.025 nm for >80 % of the illuminated detector area. The Earth port SFS measurements yield a wavelength calibration with fit residuals that are 5, 6, and 4 pm for the UV, UVIS, and NIR detectors respectively.
The overall uncertainty of the wavelength calibration is estimated to be of the order of 0.009 nm standard deviation for the Earth port and 0.016 nm for the Sun port. The accuracy of the calibration is thus approximately two-thirds of the observed difference between the Earth and Sun ports, which theoretically should be the same. Depending on whether the systematic nature of the observed differences is confirmed during the E1 commissioning phase, a separate set of Sun port wavelength CKD might be justified.
We have presented the analysis method and ensuing results from the on-ground calibration of the TROPOMI payload on the Sentinel-5 Precursor satellite that was launched on 13 October 2017. A novel approach has been used in the analysis of the calibration measurements, which involved the use of the production-grade operational L01b data processor. The rationale for this approach was to ensure consistency of the processor with the required calibration key data (CKD). Previous experience with OMI had shown that this consistency is not always guaranteed using a prototype processor for the required preprocessing of the measurements. In addition, the large number of data required high-performance processing to finish the analysis in a timely manner. The methodology even went one step further as the L01b data processor was also used for the validation of calibration, and a physical sanity check whether the observations, and the calibration analysis thereon, match the implemented correction algorithm in the processor itself was included. A software framework was developed that brought the measurements, the CKD analysis software, the L01b processor, the validation tests, the logical dependencies, and the reporting of all obtained results together. We have shown for a few topics the benefits of this approach and feel that this methodology could be beneficial for future missions.
In general most calibration topics were successful and compliant with requirements. The geolocation annotation went very well, the ISRF is known within 1 %, and the wavelength assignment has at most 0.016 nm uncertainty. For the straylight correction, initially two potential correction schemes were foreseen. Early performance tests showed that the straylight is dominated by near-field straylight and that the convolution method would be the most suitable candidate as a correction algorithm. The required CKD were successfully obtained with laser measurements despite large problems with the stimuli for the UVN. This in-band correction reduces the straylight by a factor of 2.5 and 2.3 for the UV and UVIS spectrometers respectively and 1.2 for the NIR spectrometer. During the initial calibration campaign, evidence was found for out-of-spectral-range straylight in the NIR detector, which explains the lower aforementioned reduction factor in the NIR. Additional measurements in ambient conditions were executed approximately 2 years later with the instrument already integrated into the satellite. This recovery was successful, and a dedicated correction algorithm and CKD could be derived, which achieves an out-of-spectral-range straylight reduction of up to a factor of 8 in addition to the in-band correction. The absolute radiometric calibration of the Earth port was good and further improved to 1.0 % to 1.9 % by a post-calibration of the employed external diffuser.
Stability problems with the Sun simulator jeopardized the calibration of the two internal diffusers, as well as the calibration of the instruments' BSDF. As a consequence, the usually preferred method of deriving the absolute radiometric calibration of the Sun port from ABSRAD and the BSDF was not possible, and the Sun port was radiometrically calibrated using a FEL lamp directly. Proof was found for geometric uncertainties that could lead to larger errors than reported (0.8 % to 1.3 %) for ABSIRR, but no further on-ground validation was possible. The same holds for the BSDF calibration accuracy for which we can only account for 1.2 % to 1.9 %. Due to the problems with the Sun simulator the angular dependence calibration RELIRR of the internal diffusers was hampered. For one diffuser acceptable but non-compliant results were obtained, and for the other no results could be obtained.
During the E1 commissioning phase in the first 6 months after launch, the angular dependence of the internal solar diffusers will be recalibrated. In addition, the suspect BSDF and ABSIRR calibration will be validated using Sun measurements and reference solar spectra from other missions. The final validation of the out-of-spectral-range straylight in the NIR detector will be performed with additional measurements. Many other topics will be validated and verified as well, e.g. the accuracy of the geolocation annotation, but special attention is planned to be given to the problematic topics mentioned in this paper. Despite the problems presented in this paper, the overall calibration status of the TROPOMI instrument is good, and the results reported here are accepted as the launch configuration.
The calibration key data described in this paper can be downloaded from http://www.tropomi.eu/tropdata/l01b_ckd/trl01b_01.00.00_2018-04-01_ckd.tar.gz (last access: 29 november 2018).
AL is the optical expert and acted as the on-site lead for the KNMI calibration team in Liège; she also planned all the calibration activities. EL is the mathematical consultant and was responsible for all algorithm definitions, and he analysed and reported on most electronic calibrations. LB performed the modelling and analysis of the UVN in-band straylight correction. The analysis of the absolute radiometric radiance response was performed by RB, while the absolute radiometric response of the irradiance and BSDF was measured by PK. The relative radiometric response of the radiance and irradiance, which also included the detectors' PRNU, was measured by EvdP. RB was responsible for the development of the tools required for algorithm implementation in the L01b processor. WD was in charge of the calibration data processing chain and developed the calibration framework together with PK. RL took over the function of WD in a later stage. JS was responsible for the wavelength calibration analysis and the derivation of the UVN ISRF. PJD and DS were part of the on-site calibration team and responsible for the inspection of all measurement data. JL developed all geometric calibration analysis software and is responsible for the geolocation annotation in the L01b data processor. PM is responsible for all database engineering required for the calibration processing. DS developed part of the correction algorithms in the L01b data processor. NR is system architect and acting lead of the L01b data processing development team. FV is system engineer for the overall software development and responsible for the release management. GV derived the calibration accuracy requirements from the higher-level system requirements. QK is the instrument scientist and project lead of the L01b data processing and calibration development. PV is acting principal investigator for the TROPOMI payload on-board the Sentinel-5 Precursor satellite.
The authors declare that they have no conflict of interest.
This article is part of the special issue “TROPOMI on Sentinel-5 Precursor: data products and algorithms”. It is not associated with a conference.
The authors wish to thank the ADSNL calibration team in Liège for the excellent collaboration: Dirk Slootweg, Alexander van Heukelum, Jelle Beetstra, Cees de Haan, Piet Vriend, Barend Ording, Matthijs van der Kooij, Daniel ten Bloemendal, Jan Doornink, Jos Dingjan, Robert Voors, Johan de Vries, Tineke Bakker-van der Veen, and Bart Remmerswaal. The authors acknowledge the on-site support by NSO and ESA in Liège by Harry Förster, Rob Hamann, Sten Ekholm, Charlotte Pachot, and Berit Ahlers. We also acknowledge the support of the CSL team by Nathalie Ninane, Marie-Laure Hellin, Fabian Languy, Pascal Blain, Sylvie Liebecq, Christophe Grodent, Pierre Jamotton, Isabelle Domken, and Clément Merlin. We also would like to thank the two anonymous referees for their valuable review of the paper. The work presented in this paper was funded by NSO and ESA. Edited by: Jhoon Kim Reviewed by: two anonymous referees
Bovensmann, H., Burrows, J. P., Buchwitz, M., Frerick, J., Noël, S., Rozanov, V. V., Chance, K. V., and Goede, A. P. H.: SCIAMACHY: Mission Objectives and Measurement Modes, J. Amos Sci., 56, 127–150, https://doi.org/10.1175/1520-0469(1999)056<0127:SMOAMM>2.0.CO;2, 1999. a
Dobber, M. R., Dirksen, R. J., Levelt, P. F., van den Oord, G. H. J., Voors, R. H. M., Kleipool, Q., Jaross, G., Kowalewski, M., Hilsenrath, E., Leppelmeier, G. W., de Vries, J., Dierssen, W., and Rozemeijer, N. C.: Ozone monitoring instrument calibration, IEEE T. Geosci. Remote, 44, 1209–1238, https://doi.org/10.1109/TGRS.2006.869987, 2006. a
Hoogeveen, R. W. M., Voors, R., Robbins, M. S., Tol, P. J. J., and Ivanov, T. I.: Characterization results of the TROPOMI Short Wave InfraRed detector, Proc. SPIE, 8889, 888913, https://doi.org/10.1117/12.2028759, 2013. a, b, c, d
Ingmann, P., Veihelmann, B., Langen, J., Lamarre, D., Stark, H., and Courrèges-Lacoste, G. B.: Requirements for the GMES Atmosphere Service and ESA's implementation concept: Sentinels-4/-5 and -5p, Remote Sens. Environ., 120, 58–69, https://doi.org/10.1016/j.rse.2012.01.023, 2012. a
KNMI: Algorithm theoretical basis document for the TROPOMI L01b data processor, S5P-KNMI-L01B-0009-SD Issue 8.0.0, Royal Netherlands Meteorological Institute (KNMI), available at: http://www.tropomi.eu/document/tropomi-l01b-atbd (last access: 28 november 2018), 2017. a, b, c, d
Levelt, P. F., van den Oord, G. H., Dobber, M. R., Malkki, A., Visser, H., de Vries, J., Stammes, P., Lundell, J. O., and Saari, H.: The ozone monitoring instrument, IEEE T. Geosci. Remote, 44, 1093–1101, https://doi.org/10.1109/TGRS.2006.872333, 2006. a
Munro, R., Lang, R., Klaes, D., Poli, G., Retscher, C., Lindstrot, R., Huckle, R., Lacan, A., Grzegorski, M., Holdak, A., Kokhanovsky, A., Livschitz, J., and Eisinger, M.: The GOME-2 instrument on the Metop series of satellites: instrument design, calibration, and level 1 data processing – an overview, Atmos. Meas. Tech., 9, 1279–1301, https://doi.org/10.5194/amt-9-1279-2016, 2016. a
Tol, P. J. J., van Kempen, T. A., van Hees, R. M., Krijger, M., Cadot, S., Snel, R., Persijn, S. T., Aben, I., and Hoogeveen, R. W. M.: Characterization and correction of stray light in TROPOMI-SWIR, Atmos. Meas. Tech., 11, 4493–4507, https://doi.org/10.5194/amt-11-4493-2018, 2018. a, b, c
van Hees, R. M., Tol, P. J. J., Cadot, S., Krijger, M., Persijn, S. T., van Kempen, T. A., Snel, R., Aben, I., and Hoogeveen, Ruud, W. M.: Determination of the TROPOMI-SWIR instrument spectral response function, Atmos. Meas. Tech., 11, 3917–3933, https://doi.org/10.5194/amt-11-3917-2018, 2018. a
Veefkind, J., Aben, I., McMullan, K., Förster, H., de Vries, J., Otter, G., Claas, J., Eskes, H., de Haan, J., Kleipool, Q., van Weele, M., Hasekamp, O., Hoogeveen, R., Landgraf, J., Snel, R., Tol, P., Ingmann, P., Voors, R., Kruizinga, B., Vink, R., Visser, H., and Levelt, P.: TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications, Remote Sens. Environ., 120, 70–83, https://doi.org/10.1016/j.rse.2011.09.027, 2012. a