the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Metrology of solar spectral irradiance at the top of the atmosphere in the near infrared measured at Mauna Loa Observatory: the PYR-ILIOS campaign
Nuno Pereira
David Bolsée
Peter Sperfeld
Sven Pape
Dominique Sluse
Gaël Cessateur
The near-infrared (NIR) part of the solar spectrum is of prime importance for solar physics and climatology, directly intervening in the Earth's radiation budget. Despite its major role, available solar spectral irradiance (SSI) NIR datasets, space-borne or ground-based, present discrepancies caused by instrumental or methodological reasons. We present new results obtained from the PYR-ILIOS SSI NIR ground-based campaign, which is a replication of the previous IRSPERAD campaign which took place in 2011 at the Izaña Atmospheric Observatory (IZO). We used the same instrument and primary calibration source of spectral irradiance. A new site was chosen for PYR-ILIOS: the Mauna Loa Observatory (MLO) in Hawaii (3397 m a.s.l.), approximately 1000 m higher than IZO. Relatively to IRSPERAD, the methodology of monitoring the traceability to the primary calibration source was improved. The results as well as a detailed error budget are presented. We demonstrate that the most recent results, from PYR-ILIOS and other space-borne and ground-based experiments, show an NIR SSI lower than the previous reference spectrum, ATLAS3, for wavelengths above 1.6 µm.
- Article
(782 KB) -
Supplement
(156 KB) - BibTeX
- EndNote
An accurate knowledge of solar spectral irradiance (SSI) remains central to the study of the climate on Earth. The variability in the ultraviolet (UV) part of the spectrum and its influence on climate via the mechanisms of solar–terrestrial interactions, simulated by chemistry–climate models (Ermolli et al., 2013; Gray et al., 2010), constitutes most of the research in SSI measurements. Despite its extremely low variability, <0.05 % over a solar cycle (Harder et al., 2009; Lean, 1991), the near-infrared (NIR) part of the spectrum plays a major role in the Earth's radiative budget due to its quasi-total absorption by water vapour (Collins et al., 2006). The determination of its absolute level remains challenging (Meftah et al., 2017): the measurement of the top-of-atmosphere (TOA) SSI started nearly 50 years ago and evolved both with ground-based and space-borne instruments, and a consensus on the absolute level in the NIR part is still to be achieved (Bolsée et al., 2014; Hilbig et al., 2018).
Aircraft-borne instrumentation at an altitude of 12 km provided the first TOA SSI measurement dataset in 1969 (Arvesen et al., 1969) with an on-board standard of spectral irradiance.
Several ground-based measurement campaigns in the UV, visible and NIR have been conducted from the top two mountain-top reference sites since then:
-
At Izaña Atmospheric Observatory (IZO), the IRSPERAD dataset was obtained (Bolsée et al., 2014) with a NIR (0.6–2.3 µm) spectroradiometer and the QASUMEFTS (Gröbner et al., 2017) instrument, providing a high-resolution UV spectrum; both were calibrated against the Physikalisch-Technische Bundesanstalt (PTB) BB3200pg black body (Sapritsky et al., 1997; Sperfeld et al., 1998, 2000).
-
At Mauna Loa Observatory (MLO), Shaw (1982) conducted a campaign with a 10-channel (UV, visible and NIR) filter radiometer and Gröbner and Kerr (2001) with a double Brewer spectrophotometer measuring in the range 300–355 nm. Kindel et al. (2001) provided TOA SSI in the range 350 to 2500 nm, measured with a spectroradiometer. All of these measurement campaigns used different types of 1000 W lamps, traceable to National Institute of Standards and Technology (NIST) standards as calibration sources.
Finally, the CAVIAR (Menang et al., 2013) and CAVIAR2 (Elsey et al., 2017) spectra were obtained with an infrared Fourier spectrometer (FTIR) calibrated against National Physical Laboratory (NPL) standards at the UK Met Office observation site in Camborne, in the range 1–2.5 µm.
TOA SSI values from all the above-mentioned ground-based campaigns were obtained using the Langley plot technique that permits extrapolation to the TOA irradiance in atmospheric windows chosen according to criteria detailed in Sect. 2.2. The monitoring of the absolute spectral calibrations is secured through comparisons with relative stable secondary standards. The reliability of the traceability to primary irradiance standards is an advantage for ground-based measurement. Performing these measurements based on world reference sites for the determination of TOA physical quantities, such as IZO and MLO, on days with often pristine conditions, ensures a high accuracy of the TOA extrapolations (Kiedron and Michalsky, 2016; Shaw, 1975, 1976; Toledano et al., 2018).
On the other hand, space-borne SSI measurements covering the NIR range started in the 1990s, though these were limited to wavelengths shorter than 2.4 µm. From the SOLSPEC instrument family, the instrument SOSP (SOlar SPectrum) on board EURECA (Thuillier et al., 1981) that pioneered the space-borne NIR absolute solar spectroscopy released the ATLAS3 reference spectrum (Thuillier et al., 2003). An upgraded version of the SOLSPEC instrument, SOLAR/SOLSPEC, including a fully refurbished NIR channel, readout electronics and extended wavelength range up to 3 µm of SOLSPEC, flew from 2008 to 2017 on board the International Space Station (ISS) (Thuillier et al., 2009), releasing the SOLAR2 (Bolsée, 2012; Thuillier et al., 2014) and SOLAR-ISS(IR) (Meftah et al., 2017); SOLSPEC is the space-borne instrument that measured SSI farther in the NIR. The instrument providing the longest time series of SSI measurements in the NIR is the SIM (Spectral Irradiance Monitor) prism spectrometer on SORCE (Solar Radiation and Climate Experiment) launched in 2003 (Harder et al., 2000, 2005) and still on orbit but with infrequent operational time, due to the end of battery life. Another instrument contributing to NIR SSI measurements is SCIAMACHY (Scanning Imaging Absorption Spectrometer for Atmospheric Chartography) (Burrows et al., 1995; Noël et al., 1998), a remote sensing spectrometer adapted to measure SSI. The latest data release is SCIAMACHY V9 (Hilbig et al., 2018).
All above-mentioned NIR datasets reasonably agree up to 1.3 µm. When comparing SORCE and ATLAS3, the difference between both does not exceed 2 % in the NIR range, which is a consequence of SORCE being scaled up to ATLAS3, due to incompatibilities of fractional TSI (total solar irradiance) between both datasets (Harder et al., 2010).
At 1.6 µm, corresponding to the minimum opacity value of the solar photosphere, differences up to 8 % (reaching 10 % at 2.2 µm) were observed between ATLAS3 and SOLAR2 (Thuillier et al., 2014). This bias motivated the development of new ground-based instrumentation measuring the SSI NIR: CAVIAR and IRSPERAD (Bolsée et al., 2014; Menang et al., 2013). The data of both experiments confirmed this bias, both showing a level closer to that of SOLAR2. Posteriorly, SOLSPEC and SCIAMACHY data reprocessing processes tend to intermediate values between ATLAS3 and SOLAR2 (Hilbig et al., 2018; Meftah et al., 2017).
In this paper we present a rerun of the IRSPERAD experiment, named PYR-ILIOS, carried out in July 2016. While still using the Langley plot technique and calibration against the PTB black body, this new experiment differs from IRSPERAD in three aspects: first, the observation site is MLO instead of IZO; second, possible sources of systematic uncertainties have been identified and fixed (see Sect. 2.1); third, the traceability of the calibration to the primary standard was improved (see Sect. 2.6). A detailed estimation of the uncertainty budget will be presented in Sect. 3, followed by the presentation of the obtained spectrum and its comparison with space-borne and ground-based spectra described in this section, along with a discussion on the status of the NIR SSI measurement.
2.1 Instrumentation
The core of the direct Sun measurement instrumentation is a Bentham NIR spectrometer: it consists of a double monochromator placed inside a thermally stabilized container, with light detection by a PbS cell. An optical fiber guides the sunlight between the entrance slit of the spectrometer and the diffusor of a 7.2∘ field-of-view (FOV) sunlight-collecting optics (telescope). The telescope is connected to an EKO Sun tracker that provides a tracking accuracy (https://eko-eu.com/products/solar-energy/sun-trackers/str-22g-sun-trackers, last access: 12 December 2018) of 0.01∘. The working wavelength range is from 0.6 to 2.3 µm, with a nominal 10 nm bandpass. The instrument characteristics are given in depth in Bolsée et al. (2014) and have remained unchanged since. No modifications have been made either to the telescope or to the spectrometer. Nevertheless, a factory defect in the assemblage of the components was detected and rectified: the lens focusing the light collected in the optic fiber into the spectrometer entrance slit was properly fixed into its barrel support for the PYR-ILIOS campaign, which was not previously the case for the IRSPERAD campaign at IZO. Another change relative to the IRSPERAD campaign was that the thermally stabilized spectrometer container was placed indoors in a thermally stabilized environment, which reduced thermal stress due to outdoor exposure and improved the stability of the spectrometer's response.
2.2 Langley plot method
The wavelength-dependent direct transmitted solar irradiance in the atmosphere is described by the Beer–Bouguer–Lambert (BBL) law. For spectral regions where molecular absorption is negligible and only Rayleigh and aerosol scattering are present, the BBL law is written in the following form:
where E0 is the irradiance at the top of the atmosphere (TOA), m is the air mass factor (AMF) as a function of the solar zenith angle (SZA) θ and τ is the optical depth that depends on λ. D is the ratio between the Earth–Sun distance at the moment of the measurement and the mean Earth–Sun distance; subscripts R and A stand for Rayleigh and aerosol, respectively. Because the aerosol vertical profile over the measurement site at the moment of the measurement is unknown, aerosol AMF is approximated to Rayleigh AMF (Schmid and Wehrli, 1995); considering , defining and taking the logarithm of Eq. (1), it can be rewritten as
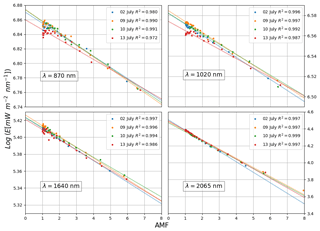
Provided that τ(λ) remains constant for a series of measurements of E0(λ) taken over a given range of m(θ) (spreading over a half day), the TOA value of E0(λ) is thus the intercept at the origin (m=0) of the least-squares regression to the data series E(λ) as a function of m(θ).
Solar zenith angles (SZAs) are calculated with the NOAA Solar Position Calculator (https://www.esrl.noaa.gov/gmd/grad/solcalc/index.html, last access: 12 December 2018) that implements Meeus (1998) algorithms and are subsequently corrected for atmospheric refraction effects according to Bennett (1982). AMFs are calculated using the Kasten and Young algorithm (Kasten and Young, 1989).
2.3 Atmospheric windows
The wavelength domains for which the Langley plot method described in Sect. 2.2 is valid, i.e. atmospheric windows, were determined through the model using a procedure developed in Kindel et al. (2001) and also used in Bolsée et al. (2014): using a TOA reference spectrum as input, the MODTRAN (MODerate resolution atmospheric TRANsmission) (Berk et al., 2014) RTM (radiative transfer model) was used to simulate irradiances measured at the ground, as a function of the measurement site parameters, for a series of AMFs. The Langley plot method was applied to these simulated irradiances, and the wavelengths for which the synthetic E0 recreated the input TOA within 0.5 % were kept as valuable wavelengths for the Langley plot; these set of wavelengths were grouped in contiguous windows called atmospheric windows.
2.4 Absolute calibration
The absolute calibration was performed against a primary standard of spectral irradiance, the BB3200pg black body of the PTB. It has been extensively described in Sapritsky et al. (1997) and Sperfeld et al. (1998, 2000). The spectral irradiance equation describing the black body emission is calculated using Planck's law:
where εBB and ABB stand, respectively, for the effective emissivity and the aperture of the BB3200pg, dBB for the distance between the black body aperture and the optic centre of the telescope and n for the refractive index of air; c1 and c2 are the first and second radiation constants.
The fundamental parameter, the temperature of the cavity TBB, is known with a standard uncertainty of 0.5 K (∼0.02 % for a nominal temperature of 3000 K) with a drift lower than 0.5 Kh−1 (Friedrich et al., 1995; Taubert et al., 2003; Werner et al., 2000). The uncertainties on εBB and ABB are ) and 0.04 mm (0.03 %), respectively (Woolliams et al., 2006). The distance between the black body aperture and the telescope optical active surface, the diffuser dBB, is the sum of two distances: , where dS is the distance between the black body and the first optical surface of the telescope, the quartz plate, and dT is the distance between the quartz plate and the diffuser. The uncertainties on ds and dT are 0.05 mm (Woolliams et al., 2006) and 0.5 mm, respectively; the combined uncertainty on dBB is 0.5 mm, 0.04 % at the nominal distance of 1384.05 mm.
The absolute calibration coefficient R, that converts the spectrometer signal into irradiance, is given by Eq. (4):
with SBB being the signal recorded by the spectrometer and EBB, the emission of the black body, given by Eq. (3). During the calibration campaign at PTB, two different temperature set points, 3016.5 and 2847.6 K, were used to build the response curve, RBB. The distance dBB was kept fixed at 1384.05 mm so that the black body aperture was seen by the entrance optics with an angular extension of 0.5∘.
2.5 Radiometric characterization
The spectrometer was characterized at the laboratory of the Belgian Institute for Space Aeronomy (BIRA-IASB) for the uncertainty on the measured signal, the detector sensitivity to temperature and for the wavelength scale. The flat field of the detector was measured during the ground-based campaign at MLO and the linearity was verified during the calibrations at the PTB laboratory:
-
The flat field of the entrance optics was measured during the ground-based campaign. The telescope was angularly displaced from the normal Sun direction thanks to an angular fine-tuning mechanism, for a series of angular positions for two orthogonal directions. The agreement between both directions' data curves allows an insensitivity of the signal to solar depointing better than 0.05∘ to be estimated, although a finer angular sampling would be necessary to accurately determine the angular limits of this insensitivity. Given the 0.01∘ pointing accuracy of the Sun tracker, the response of the instrument is considered to be insensitive to pointing during the campaign.
-
The temperature sensitivity of the spectrometer was determined in the laboratory (Bolsée et al., 2014). During the campaign, the spectrometer box was placed indoors with its temperature being constant within 0.1 ∘C, equivalent to the resolution of the temperature probe readout; no temperature correction on the signal was thus applied.
-
For the verification of the linearity of the detector, the telescope was placed at several different distances from a stable 200 W lamp. The measured signal as a function of distance was successfully fitted to an inverse square law function, demonstrating the detector linearity within a 2-decade dynamic range.
2.6 Relative calibration
A set of six FEL lamps (F102, F104, F417, F418, F545, F546) were used as relative calibration standards, to monitor a possible change of response of the spectrometer during the measurement campaign. Taking as reference the lamps' signal measured at the PTB (27 April 2016), ), four additional relative calibrations were performed:
-
Immediately before the start of the measurement campaign on 29 June (i=1), the signal of the six lamps, , was measured on site. This first MLO relative calibration was valuable to monitor the spectrometers' response change between the calibration at PTB and the beginning of the field measurements. During this 2-month period that included the transportation of the equipment, a decrease of response varying between 1 % and 3 % in the 1000 to 2200 nm range was detected.
-
During the 20-day measurement campaign, three relative calibrations were performed: on 7 July (i=2), 14 July (i=3) and 19 July (i=4). The cumulated loss of response between 29 June and July varied from 1.5 % to 0.5 % in the 800 nm to 1.8 µm domain.
The corresponding correction factor for each relative calibration is
where N stands for the total number of lamps, j for the lamp number and i for the calibration day index. K(λ) was obtained by linear interpolation for all days of the campaign.
2.7 Ground-based campaign
The PYR-ILIOS campaign took place during the first 20 days of July 2016 at the Mauna Loa Observatory (MLO) on the island of Hawaii. The MLO (19.53∘ N, 155.58∘ W) is situated at 3397 m a.s.l.; it is the leading long-term atmospheric monitoring facility on Earth, a primary calibration site for the AErosol Robotic NETwork (AERONET; https://aeronet.gsfc.nasa.gov/, last access: 12 December 2018), a global station for the Global Atmosphere Watch (GAW) of the World Meteorological Organization (WMO) and the premier site (https://www.esrl.noaa.gov/gmd/obop/mlo/programs/esrl/co2/co2.html, last access: 12 December 2018) for the measurement of the concentration of atmospheric carbon dioxide. It is considered a world reference site to accurately determine extraterrestrial constants via the Langley plot method (Kiedron and Michalsky, 2016; Shaw, 1975, 1976).
2.8 Data selection and analysis
From the 20-day campaign, 12 high-quality half-days, all during morning time, were kept for analysis. The selection criteria were verification of cloudless clear skies and a Langley plot correlation coefficient R2>0.9. The morning data of the days 2, 3, 5, 7, 8, 9, 10, 11, 13, 14, 16 and 17 July 2016 were kept for analysis; a subset of these selected Langley plots is shown in Fig. 1, for four different wavelengths.
3.1 Uncertainty on the spectrometer signal
The raw uncertainty of a spectrometer measured signal, , regardless of its source, either solar (SS), black body (SBB) or lamp signal, is a function of the intrinsic noise of the measured physical signal convolved by the spectrometer's transmission and detector's response. The uncertainty on a measured signal ) was determined in the laboratory by calculating the standard deviation for a sample of measured signals at several intensities from a 1000 W stable lamp (Bolsée et al., 2014). This uncertainty is shown in Fig. A1.
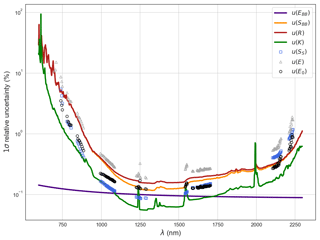
Figure 2Individual uncertainties contributing to the combined uncertainty in the TOA SSI, u(E0). Black-body-associated quantities (u(EBB), u(SBB) and u(R)) and lamp-associated quantities (u(K)) are plotted for the full wavelength working range, while solar-measurement-associated quantities (u(Ss), u(E) and u(E0)) are plotted in the atmospheric windows' wavelengths.
Additionally, all measured signals, ), are affected by an uncertainty term due to the finite bandpass of the instrument, u(CΔλ), and the uncertainty on the determination of the true wavelength scale, u(Cλ) (Obaton et al., 2007).
where δ(λ) stands for the maximum deviation in the determination of the real wavelength scale of the spectrometer. δ(λ) was determined in the laboratory by measuring the deviation between the measured and the corresponding nominal peak values of a series of well-known emission rays of Xe, Ar and Kr lamps as well as of lasers and Pen-Ray lamps, δ(λ)<0.2 nm for the working wavelength range. BW stands for the spectrometer bandpass of 10.63 nm, measured in the laboratory.
Table 1List of relative uncertainties terms expressed as percentages. The coverage factor is k=1 for all terms. A and B stand respectively for type A and type B uncertainties, while C stands for combined uncertainty according to GUM (2008). u(Cλ) and u(CΔλ) are calculated for a solar signal. The prefix u, for uncertainty, is omitted for each term of the first row, for the sake of clarity.

3.2 Langley plot sensitivity to aerosol daily variation
3.3 Uncertainty on a calibrated direct Sun measurement
The expression for a calibrated solar measurement, E(λ) is
with SS(λ), R(λ) and K(λ) being expressed by Eqs. (6), (4) and (5), respectively.
The uncertainties associated with the factors in Eq. (7) were calculated using the law of propagation of uncertainties (LPU) and are represented in Fig. 2. The similarity of shapes of the curves of the individual uncertainties reflects the convolution of the measured signals by the spectrometer's response. The largest contribution to the calibrated solar signal comes from the uncertainty on the absolute calibration which is dominated by the uncertainty u(SBB) of the measured signal, SBB, of the black body, whereas the uncertainty on the emission of the black body, u(EBB), is known within 0.2 % for the totality of the wavelength range.
3.4 Uncertainty on the determination of the TOA irradiance
The uncertainty in the determination of the TOA irradiance via the Langley plot method, ), corresponds to the uncertainty on the determination of the intercept at origin, P0, when applying a linear regression on Eq. (2). The uncertainty on the measured E in the Langley plot method logarithmic space, u(log(E)), and the uncertainty in the ) irradiance value are given by
where ) gives the irradiance TOA value. The uncertainty in P0 was estimated using two independent methods.
-
A Monte Carlo method was employed. Given a measured Langley plot dataset consisting of (mi,log(Ei)) points, a new synthetic dataset ) is created, where each ) is affected by a random normal distributed quantity, with a standard uncertainty given by Eq. (8), and each mi is affected by an uncertainty defined in Sect. 3.6. The standard deviation in the distribution of the N>>1 retrieved P0 values corresponds to u(P0), with ) given by Eq. (9).
-
The weighted total least-squares algorithm developed by Krystek and Anton (2007) was used. It computes the uncertainty in the determination for both linear regression parameters using the uncertainties on the measured quantities as inputs, i.e. the uncertainties on E (Sect. 3.3) and AMF (Sect. 3.6).
The uncertainty on the determination of the TOA irradiance, u(E0), matches perfectly for both methods; it is below 1 % for the central wavelength range of 0.9 to 2.2 µm. Figure 2 shows the contribution of all the uncertainty terms detailed in Sect. 3. In Table 1 a list of the uncertainty types and values at key wavelengths is presented.
3.5 Quantification of the circumsolar radiation
An ideal sunlight-collecting optic device should ideally have an acceptance angle equal to that of the solar disk seen on Earth, . In practice the FOV is much larger than 0.5∘ such that Sun- and sky-scattered radiation enters the FOV of the sunlight-collecting optics, affecting the direct normal Sun measurement. Circumsolar radiation is strongly dependent on aerosols' size and their abundance, increasing with AMF and decreasing with wavelength due to Rayleigh scattering (Blanc et al., 2014). The estimation of circumsolar radiation was done with the aid of the LibRadtran (Mayer and Kylling, 2005) RTM. LibRadtran computes the radiance field of the Sun- and sky-scattered radiation. The integral of this radiance field over the solid angle of the acceptance cone of the entrance optics is the amount of circumsolar irradiance (CSI) measured by the spectrometer in excess of the normal direct Sun irradiance (DNI) (Gueymard, 2001). For standard clear-sky atmospheric conditions observed at MLO and for typical aerosol charges values measured during the mission, the quantification of CSI is shown in Fig. A2. Given the uncertainty budget, the impact of the circumsolar radiation can be considered negligible.
3.6 Estimation of air mass factors' uncertainty
As referred to in Sect. 2.2, the absence of knowledge of the vertical profile of the relevant species, namely aerosols, is a limiting factor for accurately calculating the AMF. The uncertainty in the AMF calculation is based on the approach of Schmid and Wehrli (1995), who considered that mA, due to the presence of stratospheric aerosols, could take the form , with and standing for the ozone air mass. Assuming a rectangular distribution of mA delimited by k1=1 and a k1=0.2, the standard deviation of mA can be calculated as , to be used as input for the determination of the Langley plot parameters' uncertainty (Sect. 3.4).
The possible bias introduced at the Langley plot's intercept at origin by a realistic non-constant aerosol concentration during the measurement was estimated considering a measured aerosol optical depth (AOD) profile. For a given measured Langley plot consisting of (mi,log(Ei)) and regression parameters and τ, a synthetic Langley plot ) is determined. The synthetic values are calculated with the expression ), where ); τAOD(λ,ti) stands for the real diurnal aerosol optical depth profile measured with AERONET (available at λ=870, 1020, 1640 nm) and τR(λ,ti) the Rayleigh optical depth calculated according to Bodhaine et al. (1999). This bias at the intercept at origin, expressed as a ratio, , averaged over the selected days is −0.2 %, +0.4 % and +0.1 % for 870, 1020 and 1640 nm, respectively. The signal of the bias replicates the signal of the AOD morning trend measured at MLO, and the larger negative bias at 1020 nm relative to 1640 nm is due to the more pronounced AOD negative trend at 1640 nm. Assuming that the interval comprises the true value of the intercept at origin, E0, within a rectangular distribution, the corresponding uncertainty amounts to 0.06 % at 870 and 1640 nm and 0.1 % at 1020 nm, which is added quadratically to the uncertainty on (Sect. 3.4) to determine the uncertainty on E0. is interpolated linearly to the working wavelength range.
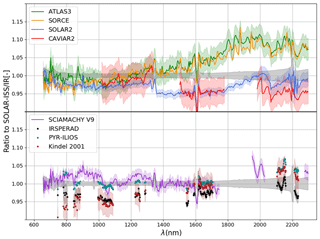
The PYR-ILIOS TOA SSI results are obtained by averaging the Eλ(0) obtained by the Langley plot method for the 12 half-days that satisfied the data selection criteria detailed in Sect. 2.8. PYR-ILIOS and other space-borne and ground-based instruments' datasets described in the Introduction are compared to the SOLAR-ISS(IR) from Meftah et al. (2017) in Fig. 3.
The mismatch between the PYR-ILIOS and IRSPERAD dataset varies between 2 % and 4.5 % in the central wavelength range between 1.0 and 1.8 µm, attaining 5 % in the 2.1 µm window and peaking to a maximum of 6 % in the 1.5 and 2.2 µm windows. Except for the shorter wavelengths' (λ<900 nm) region, uncertainties do not explain the observed mismatch between both. The higher disagreement is observed in the far end of the spectrum, with discrepancies of up to 13 % between CAVIAR2 and ATLAS3 and SORCE. Below 1.3 µm all the datasets are compatible within the uncertainties bars.
The difference observed between IRSPERAD and PYR-ILIOS is not explained by the uncertainties of both datasets. An atmospheric bias is not considered because MLO and IZO are world reference sites for the determination of extraterrestrial constants (Kiedron and Michalsky, 2016; Shaw, 1976; Toledano et al., 2018) and the atmospheric perturbations in ground-based SSI measurements are negligible (Bolsée et al., 2016; Elsey et al., 2017; Weber, 2015). By carrying out the new PYR-ILIOS experiment, we unveiled a defect of fixation of the focusing lens. Due to the fact that the instrument was moved between the IRSPERAD pre-campaign relative calibration (31 May 2011) and the start of the Sun measurement campaign (1 June 2011 onwards), the effect of the lens' eventual movement was not considered and therefore not monitored; this defect likely biased the SSI obtained during the IRSPERAD campaign in a non-reproducible way. This defect was detected and corrected for the PYR-ILIOS campaign and the relative calibration strategy adapted to identify possible similar issues: the instrument was installed and powered on and the lamps were measured; the solar measurements began immediately afterwards, without displacing or powering off the instrument. The PYR-ILIOS relative calibration procedure highlights the importance of monitoring ground-based pre-campaign instruments' response with secondary standards. Additionally it justifies the choice of PYR-ILIOS as a more reliable measurement than IRSPERAD, due to the higher confidence in the traceability of the instrument's calibration to the black body primary standard.
In the higher disagreement region around 1.6 µm, the most recent data versions of SOLAR/SOLSPEC and SCIAMACHY instruments, SOLSPEC-ISS and SCIAMACHY V9, respectively, as well as PYR-ILIOS converge to an intermediate level between SOLAR2 and ATLAS3. This convergence is also observed for longer wavelengths: in the 2 µm region PYR-ILIOS and Kindel et al. are in reasonable agreement, while the level of the two SCIAMACHY V9 adjacent bands (1.9–2.05 and 2.2–2.4 µm) suggests that it is also in agreement with the two ground-based datasets; on the other hand, in this region, both data versions of the SOLSPEC/SOLAR still retain the 8 % difference to ATLAS3 and SORCE.
A rerun of the measurement campaign at IZO would be crucial to understand the observed discrepancy between PYR-ILIOS and IRSPERAD datasets. Data from the SORCE successor, TSIS, which has been on board ISS since December 2017, are expected to further increase the understanding of SSI in the NIR.
The PYR-ILIOS NIR SSI dataset can be downloaded at ftp://ftp-ae.oma.be/dist/PYRILIOS_NIR_SSI/ (last access: 12 December 2018).
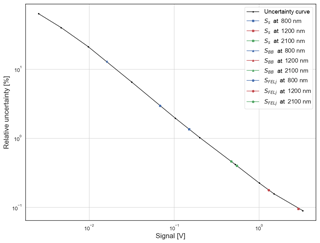
Figure A1Spectrometer's uncertainty curve as a function of the measured signal as determined in the laboratory. For reference, the uncertainty values for solar, black body and lamp signals at specific wavelengths are also shown.
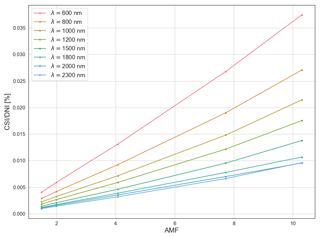
Figure A2Modelled percentage of circumsolar irradiance relative to normal direct irradiance, entering the detector as a function of wavelength and AMF. Circumsolar irradiance has a negligible effect on the measured irradiance, even for the highest circumsolar conditions (shorter wavelengths and high AMF).
The supplement related to this article is available online at: https://doi.org/10.5194/amt-11-6605-2018-supplement.
The authors declare that they have no conflict of interest.
The authors wish to thank the staff of the Mauna Loa Observatory for kindly supporting the campaign
and especially Paul Fukumura-Sawada of the NOAA Earth System Research Laboratory. We thank Brent Holben,
PI of the MLO AERONET site, for his efforts in establishing and maintaining the MLO site.
The authors acknowledge support from the Belgian Federal Science Policy Office (BELSPO) through
the ESA-PRODEX program (contract 4000110593 extension of PEA for 2016–2017) and the funding of the
Solar-Terrestrial Centre of Excellence (STCE).
Edited by: Mark Weber
Reviewed by: two anonymous referees
Arvesen, J. C., Griffin, R. N., and Pearson, D. J.: Determination of extraterrestrial solar spectral irradiance from a research aircraft, Appl. Opt., 8, 2215–2232, 1969. a
Bennett, G. G.: The Calculation of Astronomical Refraction in Marine Navigation, J. Navigation, 35, 255–259, https://doi.org/10.1017/s0373463300022037, 1982. a
Berk, A., Conforti, P., Kennett, R., Perkins, T., Hawes, F., and van den Bosch, J.: MODTRAN6: a major upgrade of the MODTRAN radiative transfer code, in: Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XX, edited by: Velez-Reyes, M. and Kruse, F. A., SPIE, https://doi.org/10.1117/12.2050433, 2014. a
Blanc, P., Espinar, B., Geuder, N., Gueymard, C., Meyer, R., Pitz-Paal, R., Reinhardt, B., Renné, D., Sengupta, M., Wald, L., and Wilbert, S.: Direct normal irradiance related definitions and applications: The circumsolar issue, Sol. Energy, 110, 561–577, https://doi.org/10.1016/j.solener.2014.10.001, 2014. a
Bodhaine, B. A., Wood, N. B., Dutton, E. G., and Slusser, J. R.: On Rayleigh Optical Depth Calculations, J. Atmos. Ocean. Tech., 16, 1854–1861, https://doi.org/10.1175/1520-0426(1999)016<1854:orodc>2.0.co;2, 1999. a
Bolsée, D.: Métrologie de la spectrophotométrie solaire absolue. Principes, mise en oeuvre et résultats. Instrument SOLSPEC à bord de la Station Spatiale Internationale, PhD thesis, Free University of Brussels, 2012. a
Bolsée, D., Pereira, N., Decuyper, W., Gillotay, D., Yu, H., Sperfeld, P., Pape, S., Cuevas, E., Redondas, A., Hernandéz, Y., and Weber, M.: Accurate Determination of the TOA Solar Spectral NIR Irradiance Using a Primary Standard Source and the Bouguer-Langley Technique, Sol. Phys., 289, 2433–2457, https://doi.org/10.1007/s11207-014-0474-1, 2014. a, b, c, d, e, f, g
Bolsée, D., Pereira, N., Cuevas, E., García, R., and Redondas, A.: Comments to the Article by Thuillier et al. “The Infrared Solar Spectrum Measured by the SOLSPEC Spectrometer Onboard the International Space Station” on the Interpretation of Ground-based Measurements at the Izaña Site, Sol. Phys., 291, 2473–2477, https://doi.org/10.1007/s11207-016-0914-1, 2016. a
Burrows, J., Hölzle, E., Goede, A., Visser, H., and Fricke, W.: SCIAMACHY-scanning imaging absorption spectrometer for atmospheric chartography, Acta Astronaut., 35, 445–451, https://doi.org/10.1016/0094-5765(94)00278-t, 1995. a
Collins, W. D., Lee-Taylor, J. M., Edwards, D. P., and Francis, G. L.: Effects of increased near-infrared absorption by water vapor on the climate system, J. Geophys. Res., 111, D18109, https://doi.org/10.1029/2005jd006796, 2006. a
Elsey, J., Coleman, M. D., Gardiner, T., and Shine, K. P.: Can Measurements of the Near-Infrared Solar Spectral Irradiance be Reconciled? A New Ground-Based Assessment Between 4000 and 10 000 cm-1, Geophys. Res. Lett., 44, 10071–10080, https://doi.org/10.1002/2017gl073902, 2017. a, b
Ermolli, I., Matthes, K., Dudok de Wit, T., Krivova, N. A., Tourpali, K., Weber, M., Unruh, Y. C., Gray, L., Langematz, U., Pilewskie, P., Rozanov, E., Schmutz, W., Shapiro, A., Solanki, S. K., and Woods, T. N.: Recent variability of the solar spectral irradiance and its impact on climate modelling, Atmos. Chem. Phys., 13, 3945–3977, https://doi.org/10.5194/acp-13-3945-2013, 2013. a
Friedrich, R., Fischer, J., and Strock, M.: Accurate calibration of filter radiometers against a cryogenic radiometer using a trap detector, Metrologia, 32, 509–513, 1995. a
Gray, L. J., Beer, J., Geller, M., Haigh, J. D., Lockwood, M., Matthes, K., Cubasch, U., Fleitmann, D., Harrison, G., Hood, L., Luterbacher, J., Meehl, G. A., Shindell, D., van Geel, B., and White, W.: Solar influences on climate, Rev. Geophys., 48, RG4001, https://doi.org/10.1029/2009RG000282, 2010. a
Gröbner, J. and Kerr, J. B.: Ground-based determination of the spectral ultraviolet extraterrestrial solar irradiance: Providing a link between space-based and ground-based solar UV measurements, J. Geophys. Res.-Atmos., 106, 7211–7217, https://doi.org/10.1029/2000JD900756, 2001. a
Gröbner, J., Kröger, I., Egli, L., Hülsen, G., Riechelmann, S., and Sperfeld, P.: The high-resolution extraterrestrial solar spectrum (QASUMEFTS) determined from ground-based solar irradiance measurements, Atmos. Meas. Tech., 10, 3375–3383, https://doi.org/10.5194/amt-10-3375-2017, 2017. a
Gueymard, C. A.: Parameterized transmittance model for direct beam and circumsolar spectral irradiance, Sol. Energy, 71, 325–346, https://doi.org/10.1016/s0038-092x(01)00054-8, 2001. a
GUM: Evaluation of Measurement Data – Guide to the Expression of Uncertainty in Measurement, BIPM, Paris, 2008. a
Harder, J., Lawrence, G., Rottman, G. J., and Woods, T. N.: The Spectral Irradiance Monitor (SIM) for the SORCE mission, in: Earth Observing Systems V., edited by: Barnes, W. L., Proc. SPIE, 4135, 204–214, 2000. a
Harder, J., Lawrence, G. M., Fontenla, J. M., Rottman, G., and Woods, T. N.: The Spectral Irradiance Monitor: Scientific requirements, instrument design, and operation modes, Sol. Phys., 230, 141–167, 2005. a
Harder, J. W., Fontenla, J. M., Pilewskie, P., Richard, E. C., and Woods, T. N.: Trends in solar spectral irradiance variability in the visible and infrared, Geophys. Res. Lett, 36, L07801, https://doi.org/10.1029/2008GL036797, 2009. a
Harder, J. W., Thuillier, G., Richard, E. C., Brown, S. W., Lykke, K. R., Snow, M., McClintock, W. E., Fontenla, J. M., Woods, T. N., and Pilewskie, P.: The SORCE SIM solar spectrum: Comparison with recent observations, Sol. Phys., 263, 3–24, 2010. a
Hilbig, T., Weber, M., Bramstedt, K., Noël, S., Burrows, J. P., Krijger, J. M., Snel, R., Meftah, M., Damé, L., Bekki, S., Bolsée, D., Pereira, N., and Sluse, D.: The New SCIAMACHY Reference Solar Spectral Irradiance and Its Validation, Sol. Phys., 293, 121, https://doi.org/10.1007/s11207-018-1339-9, 2018. a, b, c
Kasten, F. and Young, A. T.: Revised optical air mass tables and approximation formula, Appl. Opt., 28, 4735, https://doi.org/10.1364/ao.28.004735, 1989. a
Kiedron, P. W. and Michalsky, J. J.: Non-parametric and least squares Langley plot methods, Atmos. Meas. Tech., 9, 215–225, https://doi.org/10.5194/amt-9-215-2016, 2016. a, b, c
Kindel, B. C., Qu, Z., and Goetz, A. F. H.: Direct solar spectral irradiance and transmittance measurements from 350 to 2500 nm, Appl. Opt., 40, 3483–3494, 2001. a, b
Krystek, M. and Anton, M.: A weighted total least-squares algortihm fot fitting a straight line, Meas. Sci. Technol., 18, 3438–3442, 2007. a
Lean, J.: Variations in the Sun's radiative output, Rev. Geophys., 29, 505–535, https://doi.org/10.1029/91RG01895, 1991. a
Mayer, B. and Kylling, A.: Technical note: The libRadtran software package for radiative transfer calculations – description and examples of use, Atmos. Chem. Phys., 5, 1855–1877, https://doi.org/10.5194/acp-5-1855-2005, 2005. a
Meeus, J.: Astronomical Algorithms, Willmann-Bell, 1998. a
Meftah, M., Damé, L., Bolsée, D., Pereira, N., Sluse, D., Cessateur, G., Irbah, A., Sarkissian, A., Djafer, D., Hauchecorne, A., and Bekki, S.: A New Solar Spectrum from 656 to 3088 nm, Sol. Phys., 292, 101, https://doi.org/10.1007/s11207-017-1115-2, 2017. a, b, c, d
Menang, K. P., Ptashnik, I. V., Coleman, M., Gardiner, T., and Shine, K.: A high-resolution near-infrared extraterrestrial solar spectrum derived from ground-based Fourier transform spectrometer measurements, J. Geophys. Res., 118, 1–13, 2013. a, b
Noël, S., Bovensmann, H., Burrows, J. P., Frerick, J., Chance, K. V., Goede, A. P., and Muller, C.: SCIAMACHY instrument on ENVISAT-1, Sensors, Systems, and Next-Generation Satellites II., edited by: Fujisada, H., Proc. SPIE, 3498, 94–104, 1998. a
Obaton, A. F., Ledenberg, J., Fischer, N., Guimier, S., and Dubard, J.: Two procedures for the estimation of the uncertainty of spectral irradiance measurement for UV source calibration, Metrologia, 44, 152–160, 2007. a
Sapritsky, V. I., Khlevnoy, B. B., Khromchenko, V. B., Lisiansky, B. E., Mekhontsev, S. N., Melenevsky, U. A., Morozova, S. P., Prokhorov, A. V., Samoilov, L. N., Shapoval, V. I., Sudarev, K. A., and Zelener, M. F.: Precision blackbody sources for radiometric standards, Appl. Opt, 36, 5403–5408, 1997. a, b
Schmid, B. and Wehrli, C.: Comparison of Sun photometer calibration by use of the Langley technique and the standard lamp, Appl. Opt., 34, 4500–4512, 1995. a, b
Shaw, G. E.: Solar Spectral Irradiance: The Role of Earth-Based Measurements, in: The Solar Constant and the Earth's Atmosphere, Proceedings of the Workshop held at Big Bear Solar Observatory, Big Bear City, CA, 19–21 May 1975, Big Bear Solar Observatory, edited by: Zirin, E. H. and Walter, J., 210–231 1975. a, b
Shaw, G. E.: Error analysis of multi-wavelength sun photometry, Pure Appl. Geophys., 114, 1–14, https://doi.org/10.1007/BF00875487, 1976. a, b, c
Shaw, G. E.: Solar spectral irradiance and atmospheric transmission at Mauna Loa Observatory, Appl. Opt., 21, 2006, https://doi.org/10.1364/ao.21.002006, 1982. a
Sperfeld, P., Metzdorf, J., Galal Yousef, S., Stock, K. D., and Müller, W.: Improvement and extension of the black-body-based spectral irradiance scale, Metrologia, 35, 267–271, 1998. a, b
Sperfeld, P., Galal Yousef, S., Metzdorf, J., N., B., and Müller, W.: The use of self-consistent calibrations to recover absorption bands in the black-body spectrum, Metrologia, 37, 373–376, 2000. a, b
Taubert, D., Friedrich, R., Hartmann, J., and Hollandt, J.: Improved calibration of the spectral responsivity of Interference Filter Radiometers in the visible and near infrared spectral range at PTB, Metrologia, 40, S35–38, 2003. a
Thuillier, G., Simon, P. C., Labs, D., Pastiels, R., and Neckel, H.: An instrument to measure the solar spectrum from 170 to 3200 nm on board Spacelab, Sol. Phys., 74, 531–537, 1981. a
Thuillier, G., Hersé, M., Labs, D., Foujols, T., Peetermans, W., Gillotay, D., Simon, P. C., and Mandel, H.: The solar spectral irradiance from 200 to 2400 nm as measured by the SOLSPEC spectrometer from the ATLAS and EURECA missions, Sol. Phys., 214, 1–22, 2003. a
Thuillier, G., Foujols, T., Bolsée, D., Gillotay, D., Hersé, M., Peetermans, W., Decuyper, W., Mandel, H., Sperfeld, P., Pape, S., Taubert, D. R., and Hartmann, J.: SOLAR/SOLSPEC: Scientific objectives, instrument performance and its absolute calibration using a blackbody as primary standard source, Sol. Phys., 257, 185–213, 2009. a
Thuillier, G., Bolsée, D., Schmidtke, G., Foujols, T., Nikutowski, B., Shapiro, A. I., Brunner, R.,Weber, M., Erhardt, C., Hersé, M., Gillotay, D., Peetermans, W., Decuyper, W., Pereira, N., Haberreiter, M., Mandel, H., and Schmutz, W.: The Solar Irradiance Spectrum at Solar 30 Activity Minimum Between Solar Cycles 23 and 24, Sol. Phys., 289, 1931–1958, https://doi.org/10.1007/s11207-013-0461-y, 2014. a, b
Toledano, C., González, R., Fuertes, D., Cuevas, E., Eck, T. F., Kazadzis, S., Kouremeti, N., Gröbner, J., Goloub, P., Blarel, L., Román, R., Barreto, Á., Berjón, A., Holben, B. N., and Cachorro, V. E.: Assessment of Sun photometer Langley calibration at the high-elevation sites Mauna Loa and Izaña, Atmos. Chem. Phys., 18, 14555–14567, https://doi.org/10.5194/acp-18-14555-2018, 2018. a, b
Weber, M.: Comment on the Article by Thuillier et al. “The Infrared Solar Spectrum Measured by the SOLSPEC Spectrometer onboard the International Space Station”, Sol. Phys., 290, 1601–1605, https://doi.org/10.1007/s11207-015-0707-y, 2015. a
Werner, L., Fischer, J., Johannsen, U., and Hartmann, J.: Accurate determination of the spectral responsivity of silicon trap detectors between 238 and 1015 nm, Metrologia, 37, 279–284, 2000. a
Woolliams, E. R., Fox, N. P., Cox, M. G., Harris, P. M., and Harrison, N. J.: Final report on CCPR K1-a: Spectral irradiance from 250 nm to 2500 nm, Metrologia, 43, 02003, https://doi.org/10.1088/0026-1394/43/1A/02003, 2006. a, b