the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Albedo-Ice Regression method for determining ice water content of polar mesospheric clouds using ultraviolet observations from space
Gary E. Thomas
Jerry Lumpe
Charles Bardeen
Cora E. Randall
High spatial resolution images of polar mesospheric clouds (PMCs) from a camera array on board the Aeronomy of Ice in the Mesosphere (AIM) satellite have been obtained since 2007. The Cloud Imaging and Particle Size Experiment (CIPS) detects scattered ultraviolet (UV) radiance at a variety of scattering angles, allowing the scattering phase function to be measured for every image pixel. With well-established scattering theory, the mean particle size and ice water content (IWC) are derived. In the nominal mode of operation, approximately seven scattering angles are measured per cloud pixel. However, because of a change in the orbital geometry in 2016, a new mode of operation was implemented such that one scattering angle, or at most two, per pixel are now available. Thus particle size and IWC can no longer be derived from the standard CIPS algorithm. The Albedo-Ice Regression (AIR) method was devised to overcome this obstacle. Using data from both a microphysical model and from CIPS in its normal mode, we show that the AIR method provides sufficiently accurate average IWC so that PMC IWC can be retrieved from CIPS data into the future, even when albedo is not measured at multiple scattering angles. We also show from the model that 265 nm UV scattering is sensitive only to ice particle sizes greater than about 20–25 nm in (effective) radius and that the operational CIPS algorithm has an average error in retrieving IWC of %.
Polar mesospheric clouds (PMCs, known as noctilucent clouds in the ground-based literature) have been studied for over a century from high-latitude ground observations, but only since the space age have we understood their physical nature as water-ice particles occurring in the extremely cold summertime mesopause region. Their seasonal and latitudinal variations have now been well documented (DeLand et al., 2006). Interest in these clouds “at the edge of space” has been stimulated by suggestions that they are sensitive to global change in the mesosphere (Thomas et al., 1989). This expectation has been supported recently by a time series analysis of solar backscattered ultraviolet measurements of PMCs (Hervig et al., 2016) and by model calculations (Lübken et al., 2018).
The Aeronomy of Ice in the Mesosphere (AIM) satellite (Russell III et al., 2009) was designed to provide a deeper understanding of the basic processes affecting PMCs, through remote sensing of both the clouds and their physical environment (temperature, water vapor, and meteor smoke density, among other constituents). One of the two active experiments on board AIM is a camera array, the Cloud Imaging and Particle Size (CIPS) experiment, which provides high spatial resolution images of PMCs (McClintock et al., 2009). CIPS measures scattered ultraviolet (UV) sunlight in the nadir in a spectral region centered at 265 nm, where ozone absorption allows the optically thin ice particles to be visible above the Rayleigh scattering background issuing from the ∼50 km region (Rusch et al., 2009; Bailey et al., 2009). Because of its wide field of view and 43 s image cadence, CIPS views a cloud element multiple times in its sun-synchronous orbital passage over the polar region, thus providing consecutive measurements of the same location at multiple (typically seven) scattering angles (SAs). Together with scattering theory, the brightness of the cloud (albedo) at multiple angles provides constraints needed to estimate the mean ice particle size (Lumpe et al., 2013). From the particle size and albedo measurements, the ice water content is calculated for each cloud element (7.5 km × 7.5 km in the most recent CIPS retrieval algorithm). However, over time, the AIM orbit plane has drifted from its nominal noon–midnight orientation to the point where the satellite is currently operating in a terminator orbit. Responding to this altered geometry and the desire to broaden the scope of AIM, new measurement sequences were implemented to provide observations of the entire sunlit hemisphere, rather than just the summertime high-latitude region. Because the total number of images per orbit is fixed by data storage limitations, a new mode (the “continuous imaging mode”) of observations, with a reduced 3 min image cadence, was implemented in February 2016. The present sampling in a single Level 2 pixel contains far fewer scattering angles (often only one). To maintain consistency in the study of interannual variations of PMCs, this necessitates a revised method of retrieving ice water content (IWC) when only a single albedo measurement is available. IWC is a valuable measure of the physical properties of PMCs since it largely removes the effects of scattering-angle geometry, is a convenient PMC climate variable when averaged over season, and can be used in comparing with contemporaneous measurements of PMCs that use different observational techniques.
The Albedo-Ice Regression (AIR) method was developed to fill the need to retrieve PMC IWC with only a single measurement of albedo. Based on the simple notions that both albedo and IWC depend linearly upon the ice particle column density, multiple linear relationships are established between IWC and cloud directional albedo, depending upon scattering angle. The regressions are derived from three data sources: (1) the Specified Dynamics version of the Whole Atmosphere Community Climate Model (SD-WACCM) combined with the Community Aerosol and Radiation Model for Atmospheres (CARMA); (2) CIPS data for the years 2007–2013, when multiple scattering angles were available to derive IWC; and (3) Solar Occultation For Ice Experiment (SOFIE), which provides IWC and particle sizes. These three sources provide many thousands of albedo–IWC–particle size combinations, from which the AIR regressions are derived. Although the AIR method may be inaccurate for a single retrieval of IWC, averages over many observations result in close agreement as the number of data points increases. The utility of AIR thus depends upon the availability of large data sets that apply to roughly the same atmospheric conditions. For example, we will show CIPS results for July and January averages for ascending and descending portions of the orbit.
In this paper we first describe the theoretical framework relating the scattered radiance to mesospheric ice particles. It is desirable to use model data to test the AIR method, without the complications of cloud heterogeneity and viewing geometry. We utilized a first-principles microphysical model that accurately simulates large numbers of cloud properties (number density and particle size distribution). The processes treated by the model include nucleation on meteor “smoke” particles, growth, and sedimentation, occurring in a saturated environment at density and temperature conditions provided by the main global climate model (Bardeen et al., 2010). Several runs for 1-day and multiple-day periods during summer solstice conditions for solar conditions applying to 1995 were analyzed. Cloud radiances (albedos) at 265 nm were calculated for the SA range encountered by the CIPS experiment. We chose a set of cloud simulations to derive a single set of two AIR coefficients through linear regression. The accuracy of the AIR approximation was then tested on the same data, and on other model runs, using averages as a function of SA and increasing IWC threshold values. Thresholding is necessary to account for the fact that different measurement techniques have different detection sensitivities. This is not a signal or noise issue, rather the ability to discriminate PMCs against a background that is usually larger than the PMC signal itself. We show in particular how seasonal means of IWC can be derived from Solar Backscatter Ultraviolet Spectrometer (SBUV) radiance data, without the need to derive particle size.
Having tested the technique for model data, we use the same approach with real-life PMC data collected from CIPS in the normal pre-2016 operating mode. This mode provided scattering angles needed to define an ice scattering phase function, from which mean particle size was derived based on assumed properties of the underlying size distribution (Lumpe et al., 2013). The regressions were run for a period of 40 days in each of the four seasons, each comprising millions of separate cloud measurements, and from both summertime hemispheres. The results were combined into a single set of AIR coefficients, and again the AIR technique was tested on monthly averages. These averages were constructed over all years of nominal spacecraft operations (2007–2013 in the Northern Hemisphere and 2007–2008 through 2013–2014 in the Southern Hemisphere). Note that testing the accuracy of the AIR technique during the nominal mission period allows the method to be used even during the continuous imaging mode of CIPS operation.
We then employed highly accurate data from SOFIE for ice column density and mean particle size. Since the SOFIE technique uses near-IR solar extinction in water–ice absorption bands, the primary measurement is ice water content. As shown in Sect. 2.3, we inverted the retrieved SOFIE IWC to derive the equivalent 265 nm albedo and then applied the regression method described above to the results.
After describing the AIR method, we discuss briefly the application of the method to a third contemporaneous experiment, the SBUV satellite experiment, which has in common the same limitations as CIPS in its continuous-imaging mode, namely that measurements of nadir albedo are made at a single scattering angle. This has already resulted in a publication (DeLand and Thomas, 2015) in which we provided a time series of PMC IWC from the AIR method extending back to the first SBUV experiment in 1979.
Here we provide a brief overview of the theoretical basis of the IWC retrieval technique, referring to previous publications for more detail (Thomas and McKay, 1985; Rusch et al., 2009; Bailey et al., 2009; Lumpe et al., 2013). The basic measurement is PMC cloud radiance I(Φ,θ), where Φ is the scattering angle (angle between the sun and observation vectors) and θ is the view angle, which is the angle subtended by the nadir and observation direction, measured from the point of scattering. Since the ice layer is optically thin, and secondary scattering is negligible, the albedo is described by first-order scattering. The ratio of scattered (detected) radiance to the incoming solar irradiance Fλ is the albedo Aλ, where
Here z′ and r′ are the height and particle radius variables, and zb and zt define the height limits of the ice layer, with the majority of the integrand extending between 83 and 85 km. rmin and rmax are particle radii which span the particle size regime responsible for scattering (from ∼20 to ∼150 nm). As shown by Rapp and Thomas (2006), particles with sizes <20 nm are not detectable by UV measurements because of their small cross-section values – hence we refer to “UV-visible” clouds. σλ is the differential scattering cross section (cm2 sr−1) at wavelength λ and scattering angle Φ. is the number density of ice particles (cm−2) in the ranges r′, and z′, . For CIPS measurements, each camera has a finite bandpass, centered at 265 nm, and is characterized by a function with an effective width of 10 nm (McClintock et al., 2009). The albedo derived from this instrument is given by
In the model, the ice particles are assumed spherical, but the scattering theory should take account of the nonspherical nature of ice crystals. The best agreement of theory with near-IR mesospheric ice extinction occurs for a randomly rotating oblate-spheroid shape, of axial ratio 2 (Hervig and Gordley, 2010). This shape is assumed in the calculation of the cross section, which is accomplished through a generalization of Mie–Debye scattering theory, the T-matrix method (Mishchenko and Travis, 1998). The radius in the T-matrix approach is defined as the radius of the volume-equivalent sphere. In the model calculations, we will ignore the view angle effect. In the reported CIPS data, the secθ factor is applied to the reported albedos, so that A always refers to the nadir albedo (θ=0∘).
The ice water content (IWC) is the integrated mass of ice particles over a vertical column through the layer. Its definition is
ρ denotes the density of water ice at low temperature (0.92 g cm−3). Anticipating the results of this study that IWC is linearly related to the column density of ice particles, , we explore the physical basis of this result. As pointed out by Englert and Stevens (2007) and Hultgren and Gumbel (2014) such a relationship exists for certain SA values, for which σλ∼r3, in which case it is easily seen that Eq. (2) is proportional to IWC. However, we find that a linear approximation is valid for a much wider range of scattering angles. To understand this result, we imagine that all particles have the same radius, so that , where δ is the Dirac δ function. Then Eqs. (1) and (3) “collapse” to a simpler result:
Here N(rc)=ncΔz, where Δz is the effective vertical layer thickness. Eliminating the column density, N(rc) IWC is written
V(rc) denotes the particle volume. Thus in this special case, . A superposition of the effects of all participating particle sizes will exhibit a similar proportionality. When IWC(r) is integrated over all r values, the contributions from each size are straight lines, each having different intercepts and slopes.
As previously discussed, the value of the AIR method is in evaluating average IWC (denoted by 〈IWC〉) over many albedo observations made at numerous scattering angles. The accuracy of the method should be assessed primarily on this basis, not on how well an individual albedo measurement yields the correct value of IWC. However we also address the error of using individual albedo measurements in estimating IWC. An additional issue is the differing detection thresholds for IWC among the various experiments. In the case of the scattered-light experiments, the detection threshold depends upon how well the cloud radiance data can be separated from the bright Rayleigh-scattered background. The CIPS experiment retrieval method relies upon high spatial resolution over a large field of view and the differing scattering-angle dependence of PMCs and the Rayleigh-scattering background (Lumpe et al., 2013). The SBUV retrieval relies upon differing wavelength dependence of PMCs and background but primarily on the PMC radiance residuals being higher (2σ) than fluctuations from a smoothly varying sky background (Thomas et al., 1991; DeLand and Thomas, 2015). The AIM SOFIE method is very different, being a near-IR solar extinction measurement in multiple wavelength bands. SOFIE can detect much weaker clouds with smaller effective sizes than either CIPS or SBUV. Particle radii values as small as 10 nm can be retrieved from the SOFIE data (Hervig et al., 2009). To compare the various experiments, it is necessary to “threshold” the data from more sensitive experiments with a cutoff value of IWC.
In the next three sections, we present the AIR results from the model, CIPS and SOFIE, using averages over many cloud occurrences. It is not our intention to compare the different “thresholded” data sets to one another (this task will be relegated to a separate publication) but to illustrate how even measurements made at a single scattering angle (e.g., SBUV) can yield averaged IWC values that are sufficiently accurate to assess variations in daily and seasonal averages. These variations are of crucial value to determining solar cycle and long-term trends in the atmospheric variables (mainly temperature and water vapor) that control ice properties in the cold summertime PMC region. We examine the accuracy of AIR through simulations of scattered radiance from the model, and from CIPS and SOFIE data. Since these data sources yield particle radii, they can provide both the actual and approximate values of IWC from the regression formulas. Hervig and Stevens (2014) used the spectral content of the SBUV data to provide limited information on particle size. Together with the albedos themselves, they used this information to derive seasonally averaged ice water content. They showed that the variation of mean particle size over the 1979–2013 time period was relatively low (standard deviation of ±1 nm). They also found a very small systematic increase with time, as discussed in Sect. 3.
2.1 Model results
Using a microphysical model as a reference source of IWC data is useful, in the following ways. (1) In contrast to the CIPS and SOFIE retrieval algorithms, no artificial assumptions are needed concerning the size distribution of ice particles. (2) Limitations due to background removal are absent. (3) Radiance and IWC may be calculated accurately, so that effects of cloud inhomogeneity are absent. With regard to the latter point, we describe in more detail the model calculations. The model grid is 4∘ in latitude, 5∘ in longitude and variable in the vertical. Ice particles of varying sizes fill many of these cells, but the density of particles within each cell is, by definition, constant. For a given model cloud, the integration is made through a vertical “stack” of all ice-filled cells generated in a given computer run and within each particle size grid. The total radiance is the sum of contributions from the size range 20 to 150 nm. The observation angles are always assumed to be zero; in other words, the integration is performed in the vertical only. Thus cloud “boundaries” in the horizontal plane are not an issue. This contrasts with real heterogeneous clouds for which these approximations would not hold. The model contains variability due to waves of various sorts, including tides and gravity waves. However, it does not capture all known details of PMCs, such as double layers. Since we are dealing with integrated quantities, this should not be an important issue. Furthermore, we do not place full reliance on the model, which is why we also use two independent data sets.
To gain insight into the accuracy of the AIR approach, it is sufficient to work with monochromatic radiance at the central wavelength of the various passbands. The integrations of Eqs. (1) and (3) were approximated by sums over variable increments of radius and over all sub-layers within the model ice cloud (a typical ice layer is several kilometers thick.). The model height grid is variable, so that the smallest layer thickness is 0.26 km, which resolves the narrow ice layers (see Bardeen et al., 2010, for more details). We then performed the linear regression for SA values over which CIPS observations are made.
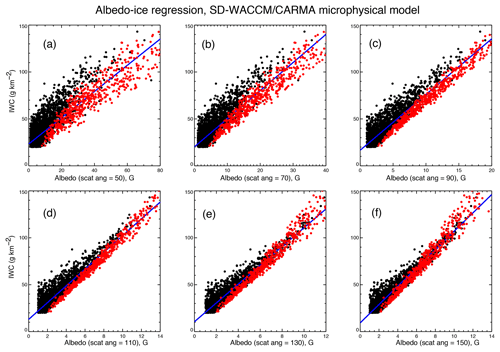
Figure 1Linear regressions of model PMC albedo versus model PMC ice water content. The black points represent model clouds with reff<40 nm. The red points apply to reff>40 nm. The blue line is the linear least-squares fit to all points. Panels (a) through (f) are for different scattering angles. The lower limit for the albedo (SA=90∘) is 1 G, which is the detection limit of the CIPS experiment.
Figure 1 displays the regressions for six scattering angles and 2514 individual model clouds. The units of IWC are g km−2, or equivalently µg m−2, which are commonly used in the literature. Each plot is divided into two groups according to the effective radii reff for each cloud. reff is defined in the literature (Hansen and Travis, 1974) as
Figure 1 clearly illustrates that particle size contributes to the scatter from the linear fits. For the conditions in Fig. 1c, the mean error of AIR for a single model simulation is 19 %. The error can be reduced substantially by averaging. For example, for 100 measurements, the AIR error in the average IWC is only 2 %. Figure 1 also shows the existence of a nonzero intercept of IWC versus albedo. The nonzero intercept was at first surprising since we expected that for an albedo of zero, IWC should also be zero. In fact, we found that the linear relationship breaks down for very small albedo, and the points in the plot narrow down in this limit (not shown). In albedo units of 10−6 sr−1 (hereafter referred to as 1 G) this departure from linearity occurs for A<1 G and IWC<10 g km−2, conditions which fortunately are below the detection threshold of CIPS and SBUV and are a result of the very faint small particles. For more sensitive detection techniques, this limitation must be kept in mind. A limitation of the present model (not necessarily all models) is that it does not simulate the largest particles in PMCs and the largest values of IWC, as seen in both AIM SOFIE and CIPS experiments. The largest model IWC value is 180 g km−2 and the largest effective radius is 66 nm, whereas CIPS and SOFIE find particle radii up to 100 nm and IWC up to 300 g km−2. This limitation is irrelevant for the AIR CIPS results (to be discussed) but could limit the application of the AIR technique to SBUV data. In Sect. 3 we will return to the issue of the AIR accuracy, as applied to SBUV data.
We chose to use averages for the entire model run, which includes different latitudes, longitudes, and UT, but the data can be divided in many different ways. It is certainly preferable in data sets to choose a small time and space interval over which temperature and water vapor are not expected to vary, but this is not necessary for the model. All that we ask of the model is whether the AIR results provide an accurate estimate of 〈IWC〉, taken over the ensemble of model cloud albedos calculated at a variety of scattering angles.
As discussed above, we are also interested in the accuracy of AIR in the thresholded data, that is, how AIR represents 〈IWC〉 in comparisons of data sets with varying detection sensitivities to PMCs. Figure 2 displays the error in the ensemble average (2488 model clouds) as a function of the IWC threshold and scattering angle. Despite the large data scatter from the linear fit shown in Fig. 1, the averaging removes almost all the influence of the random error. In this case, the overall error is less than 3 %. The influence of particle size is of course not a random error but acts like one in the averaging process. However, the AIR coefficients also depend weakly upon the mean effective radius, defined in Eq. (6) for a single cloud, which varies from one latitude to another and from year to year. The effect of variable reff on the AIR error is discussed in Sect. 3.
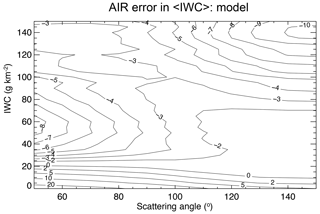
Figure 2Relative errors of ensemble averages, 〈IWC〉 using the AIR approximation, taken over all cloud model simulations for conditions of summer solstice. 〈IWC〉 is thresholded by the variable IWC in the vertical axis, so that 〈IWC〉 applies to all values above IWC. Contour lines are labeled as percent errors relative to the accurate model values.
2.2 AIR results from CIPS
A detailed description of the Version 4.20 CIPS algorithm, together with an error analysis of individual cloud observations, was presented in Lumpe et al. (2013). Here we describe only what is necessary to understand how IWC is derived from the data. Even though an accurate determination of the scattering-angle dependence of radiance (often called the scattering phase function) is obtained by seven independent measurements, this does not fully define the distribution of particle sizes. Instead, additional constraints need to be introduced to derive the mean particle size. The particles are assumed to be the same oblate-spheroidal shape as defined for the model calculations and to have a Gaussian size distribution (see Eq. 11 in Rapp and Thomas, 2006). A relationship between the Gaussian width s and the mean particle radius rm is derived from that found in vertically integrated lidar data (Baumgarten et al., 2010). The net result is that two parameters, the mean particle size and the Gaussian width, are retrieved from a given scattering phase function. However, there is only one independent variable, since the two are related by s(rm). Thus Eq. (3) simplifies to
V denotes the ice particle volume, averaged over the Gaussian distribution with a mean particle radius value rm. Aλ refers to the retrieved albedo, corrected to view angle θ=0∘ and interpolated to scattering angle Φ=90∘. Note the resemblance of Eq. (7) to Eq. (5). , along with rm and IWC, are products reported in the CIPS PMC database, found at http://lasp.colorado.edu/aim/ (last access: 12 March 2019). is the mean scattering cross section, integrated over the assumed Gaussian distribution with mean radius rm and distribution width s.
Before discussing the AIR results, we first apply the CIPS algorithm to the model data to test how well it works on a set of realistic particle sizes. As mentioned earlier, UV measurements of ice particles are not sensitive to particle radii <20–25 nm. We applied the CIPS algorithm to 6672 model clouds, using seven scattering-angle points, spanning the range 50–150∘ (the results are insensitive to the values chosen). We then calculated the percent difference between the exact model calculation of IWC and the simulated CIPS retrieved IWC for every model cloud. Figure 3 shows the result as a function of . Assuming the microphysical model is accurate, the accuracy of the CIPS UV measurements ranges from over +100 % for very small albedo to −60 % for high albedos. We emphasize that this is not an AIR result but is an attempt to assess how particles that are too small to be visible to UV measurements affect the accuracy of the CIPS IWC results. The mean difference and standard deviation for the (albedo) bin averages for two model days is %. With the caveat that not all ice is retrieved, a large subset of CIPS IWC data thus has an acceptable accuracy (an average of 84 % of the modeled ice mass is contained in particles with radii exceeding 23 nm). We note that IWC in the model used to derive the AIR approximation refers to all particle sizes.
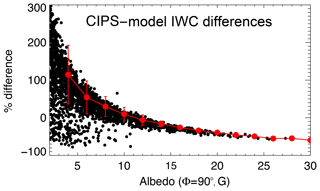
Figure 3Differences of IWC derived from the model cloud data and the accurate IWC from the model, plotted against the 265 nm albedo (in G units; see text), evaluated at SA=90∘. The error bars are the standard deviations in intervals of 2 G.
The procedure for deriving AIR coefficients from the CIPS data is as follows. (1) Regression coefficients were derived from data pertaining to 0–40 days from summer solstice (day from solstice, DFS=0 to 40) on every third orbit. This meant that ∼200 orbits per season were used. The regression analysis was performed on 4 years of data (2010–2013). The data were binned in 5∘ SA bins and only the best quality pixels with six or more points in the phase function were used. (2) Data from each northern and southern summer season were treated separately. The coefficients and standard deviations of the fit were then interpolated to a finer SA grid from 22 to 180∘ in increments of 1∘. (3) The coefficients from each hemisphere were averaged, and these coefficients were then used to create an AIR IWC database to accompany the normal CIPS products. As previously shown, the AIR data apply to the ice mass of UV-visible clouds, not to their total ice mass.
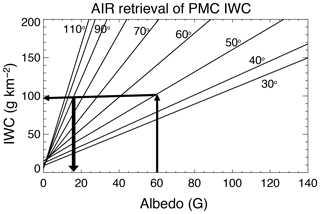
Figure 4Illustration showing how IWC=98 g km−2 (horizontal arrow) and G (thick downward arrow) are derived from the AIR method from a single measurement of cloud albedo at 60 G and SA=50∘ (upward arrow). Each straight-line plot is calculated from Eq. (9).
We emphasize that using the AIR data is unnecessary for seasons prior to the northern summer season of 2016 – however the AIR data have had great importance since that time because the observing mode was changed, resulting in measured phase functions that contain far fewer (and often only one) scattering angles. As illustrated in Fig. 4, it is trivial to infer both IWC and A(90∘) from a single measurement of albedo. This alternative 90∘ albedo value, ALB_AIR, is now included along with IWC AIR in the CIPS Level 2 data files. Figure 5 shows the AIR results for monthly-averaged IWC (July and January) compared to the same averages of the more accurate results from the operational (OP) retrieval described in Lumpe et al. (2013). The data have been separated into different hemispheres and into ascending and descending nodes of the sun-synchronous orbit and apply to the years of the nominal operating mode. The ALB_AIR results are systematically higher than the operationally retrieved 90∘ albedo, whereas there is no consistent bias in the IWC (AIR) value compared to the operational product. However, for both quantities the interannual changes between the AIR and OP results agree very well. This is reflected in the very high correlation coefficients of the two sets of values. A more stringent test of the AIR method comes from daily values of CIPS IWC. Shown in Figs. 6 and 7 are polar projections of IWC (AIR) and the more accurate operational IWC data product. These “daily daisies” are taken from overlapping orbit strips pertaining to 28 June of two different years. Figure 6 shows data from 2012, when CIPS was still in normal mode. The AIR result shows remarkable agreement with the operational IWC data. By 2016 (see Fig. 7) CIPS is in continuous imaging mode and the standard IWC retrieval is limited due to the scarcity of pixels with three or more scattering angles. Here the AIR approach is clearly superior and does a good job of filling in the polar region where CIPS detects high-albedo clouds. The differences in patterns are due primarily to variations of particle size rather than errors in the AIR method.
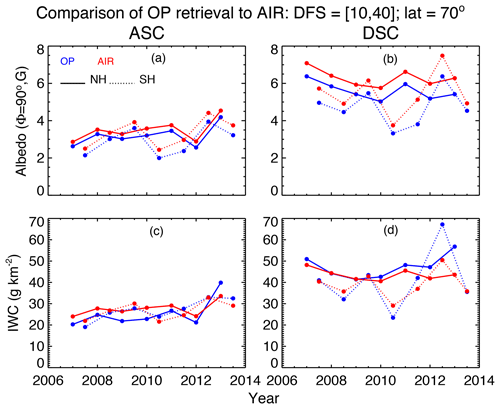
Figure 5Comparison of CIPS A(90∘) (a, b) and 〈IWC〉 (c, d) calculated from the operational (OP) and AIR algorithms. Data points correspond to July Northern Hemisphere (NH) and January Southern Hemisphere (SH) averages in a 5∘ latitude bin centered at 70∘. Panels (a, c) and (b, d) are for ascending (ASC) and descending (DSC) legs' data, respectively.
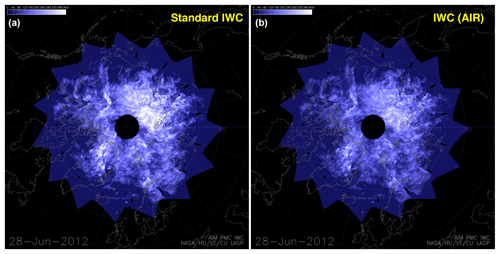
Figure 6Polar projection map of IWC from CIPS, day 180 (28 June 2012). Panels (a) and (b) show the operational IWC product and the AIR result, respectively.
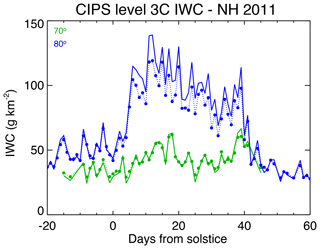
AIR accuracy can also be tested in the study of latitudinal variations. Figure 8 compares daily-averaged IWC from the CIPS Level 3C data, for both the standard and AIR algorithms, for the Northern Hemisphere 2011 season. It is clear that AIR is adequate, even for 24 h averages. For example, it is capable of defining the beginning and ending of the PMC season, a metric that has valuable scientific value (e.g., Benze et al., 2012).
2.3 AIR results from SOFIE
A third independent data set of IWC and particle size is available from the AIM SOFIE experiment (Gordley et al., 2009). SOFIE provides very accurate values of IWC, through precise near-IR extinction measurements, independent of particle size. It assumes the same Gaussian distribution of particle sizes as CIPS, so that the reported value of mean particle radius rm is consistently defined. SOFIE data are useful to investigate the extent to which the AIR approximation can be applied to an independent data set. To do so, it is necessary to calculate 265 nm albedo at various SA values, given the values of rm, ice column density N from the database, and the mean cross section, σλ(rmΦ). The latter quantity is averaged over the assumed Gaussian distribution. The equation for the albedo is
Given Aλ(Φ,0) and IWC for each PMC measurement (one occultation per orbit), we can once again perform regressions and find AIR coefficients for the SOFIE data set. The comparison of AIR results from all three data sets is shown in Fig. 9, where the constant term C is the y intercept and S is the slope in the AIR regression:
Figure 10 displays the results from the three data sets, expressed as contour plots of AIR-derived IWC as functions of SA and albedo. This comparison shows that the three sets of IWC resemble one another far better than would be anticipated from the AIR coefficients in Fig. 9, where the constant coefficient differs significantly between data sets. Since the result of the regression in yielding IWC is more significant than the coefficients themselves, the comparisons of Fig. 10 are the more appropriate diagnostic. The fact that the IWC derived from AIR is more accurate than would be expected from the differing coefficients is due to the fact that the errors of the constant and slope coefficients are anti-correlated. The agreement between the three results will be even better when taken over a large data set with variable SA and albedo. The comparisons of IWC from different satellite experiments as a function of year and hemisphere will be the subject of a separate publication.
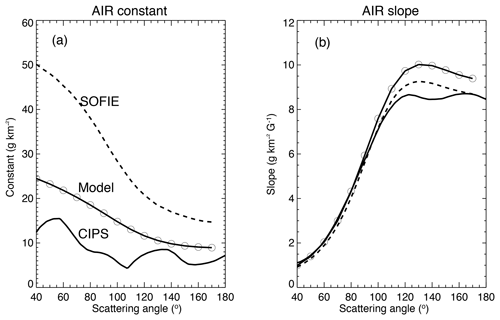
Figure 9AIR coefficients for three different sources of IWC and particle size: model (solid line with open circles), CIPS (solid line), and SOFIE (dashed line).
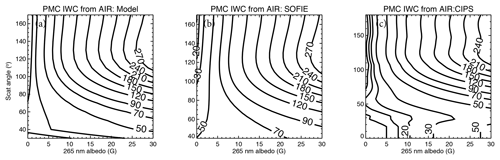
Figure 10Contour plots of the AIR approximations for IWC versus cloud albedo (G) for the three data sources: (a) model, (b) SOFIE, and (c) CIPS.
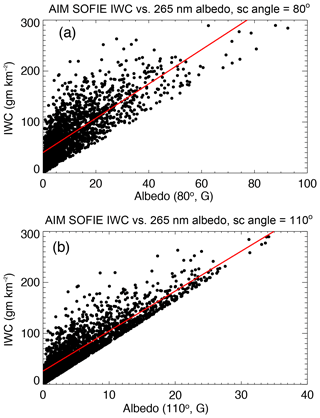
Figure 11 shows that the regressions with AIM SOFIE data obey a linear relationship between IWC and albedo for IWC <220 g km−2, but for SA values <90∘, AIR overestimates IWC by up to 15 %, depending upon the SA. For SA=110∘ the regressions are still linear up to 300 g km−2, values above which are seldom encountered in the data.
2.4 SBUV data
The AIR coefficients from the model have been used by DeLand and Thomas (2015) to derive mean IWC from SBUV data, which span the largest time interval of any satellite data set (1979–present). The 273 nm wavelength used in the SBUV Version 3 analysis is sufficiently close to the effective wavelength of the broader passband of the CIPS cameras (Benze et al., 2009) that the same coefficients may be applied to both data sets. The accuracy of the average IWC results was estimated by removing half the data by random sampling from an entire season and comparing the two results. For a highly populated region (more than 1000 clouds per season at latitudes higher than 70∘), the differences in IWC ranged between ±3 and 5 g km−2; thus they can be considered typical systematic errors. For a less populated region (50–64∘ latitude) where there were far fewer clouds (<50), the differences were larger, ±5–10 g km−2. Even the larger errors are sufficiently small for intercomparison of SBUV and contemporaneous PMC measurements. Figure 12 shows a comparison of SBUV IWC, using the model AIR coefficients, to the results of a more accurate determination of IWC derived from particle size determinations using SBUV spectral information (Hervig and Stevens, 2014). The comparison is for data residuals from July averages over the time series 1979–2017. Given the different assumptions underlying the two data sets, the agreement is very good (with an rms difference of 3 % for the residuals and 5 % for the actual values of 〈IWC〉).
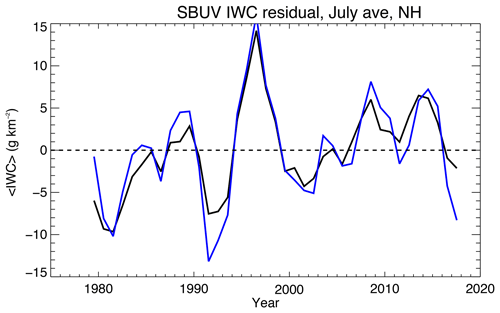
Figure 12Comparison of annually-averaged Northern Hemisphere July-averaged residuals (〈IWC〉 long-term mean) derived by two independent methods from SBUV 273 nm albedo data. Black curve: 〈IWC〉 derived from the AIR approximation. Blue curve: 〈IWC〉 derived from the same SBUV albedo data but including mean particle size variations (see text). 3-year smoothing has also been applied.
The AIR approximation is based on the notion that particle size effects can be ignored in retrieving IWC from albedo measurements; that is, they contribute in a sense to the “noise” of the measurement, which can be minimized by averaging. In fact, the particle size (or more accurately, the term r3) is a principal “driver” of 〈IWC〉 itself, so it is not obvious that particle size effects play a minor role in deriving IWC. The dependence of albedo on column density adequately captures this part of the variability (albedo is strictly linear in column density). The AIR slope term is averaged over a distribution of particle sizes, r. The size dependence of the cross section varies as a power of r, within two limits, the geometric-optics limit, r2, and the small-particle (Rayleigh) limit, r6. In the intermediate and realistic conditions of PMCs, the exponent has an intermediate value. Fortunately, there is a “sweet spot” (or better, a “sweet region” of the r domain) in which the r dependence of σλ is ∼r3, so that the slope term is constant (for fixed SAs). This behavior occurs for all relevant values of SA and for the albedo values typical of CIPS. It accounts mainly for the effectiveness of the AIR method. The other aspect favorable to AIR is the steep fall-off of the particle size distribution at the largest sizes, which contributes to the sharpness of the lower boundaries in the spread of points in Fig. 1. Averaging over many values of r results in the AIR slope term that, in the limit of large numbers, the term depends predominantly on Φ. This is an example of “regression to the mean” and illustrates how the approximation is designed to work for large numbers of clouds. In a fictitious case in which the mean cloud particle size is larger in one year than another, but the cloud column number remains the same, the mean albedo would increase according to Eq. (8), resulting in an increase of 〈IWC〉. We might expect that the slope term would be different in the two cases. Our study with three different data sets shows that the regression slope itself remains almost the same among the three data sets, despite their differing in mean particle size.
In fact, from SBUV spectral data, Hervig and Stevens (2014) found a small long-term trend in 〈IWC〉 and in addition a trend in the mean particle size ( nm decade−1). This contributed an additional 20 % to the overall long-term trend in 〈IWC〉. The ignored dependence on mean particle size using the AIR method thus adds a systematic uncertainty in derived 〈IWC〉 trends, which can be as large as 20 %, according to their analysis. This error undoubtedly varies inversely with the number of clouds in the averaging process. For example, the number of CIPS observations per PMC season greatly exceeds that of SBUV; therefore the error in 〈IWC〉 should be correspondingly smaller.
We have described the theoretical basis and accuracy for an approximation for retrieving the average ice water content (IWC) of polar mesospheric clouds (PMCs) from measurements of UV albedo at a single scattering angle. This approach provides a continuous set of consistent CIPS measurements of IWC from year to year, regardless of the number of scattering angles for which albedo at a single location is measured. The consistent AIR IWC database enables robust IWC comparisons throughout the AIM mission, from 2007 to the present. A comparison of IWC derived from the microphysical model and from the CIPS algorithm suggests that CIPS is capable of measuring 84 % of the total ice content of PMCs (for particle sizes exceeding ∼23 nm). Assuming the microphysical model is accurate, the accuracy of the CIPS UV measurements ranges from over +100 % for very small albedo to −60 % for high albedos. The overall accuracy of IWC (averaging over all albedo bins) is %. The CIPS algorithm overestimates the small-particle population (20–30 nm) as a result of the Gauss approximation when the mean particle size is small, and the opposite is true when the mean size is large. These errors are a result of the CIPS approximations and the invisibility of small particles and are irrelevant to the AIR approximation.
Distinct from the more fundamental errors due to the invisibility of very small ice particles and the Gaussian approximation, we also estimated the errors in the AIR approximation, relative to the AIM SOFIE data which apply to larger values of IWC than the model. AIR is less accurate for high IWC (>220 g km−2), but very high mass clouds (IWC >300 g km−2) are infrequent and do not influence seasonal averages of IWC. For the dimmer and more frequent clouds, Fig. 2 shows that the error in ensemble averages is of the order of 3 %. The accuracy of the AIR results for ensemble averages has a small systematic dependence on mean particle size – the error depends inversely on the size of the ensemble. The interannual and hemispheric variations of IWC derived from CIPS and SBUV measurements throughout an entire 11-year period (2007–2018) will provide detailed information on PMC variability over the recent solar cycle 24.
The CIPS operational PMC data, along with the AIR data, can be found in AIM CIPS Science Team (2019) at http://lasp.colorado.edu/aim/ (last access: 12 March 2019).
GET formulated the AIR approximation and derived the AIR coefficients from the microphysical model (provided by CB) and from the AIM SOFIE data (http://sofie.gats-inc.com/sofie/index.php, last access: 14 March 2019). JL and CER calculated the AIR coefficients from the CIPS data.
The authors declare that they have no conflict of interest.
We thank Matthew DeLand and Mark Hervig for providing us with the data used in Fig. 12. We gratefully acknowledge the tremendous effort of the engineering, mission operation, and data system teams whose dedication and skill resulted in the success of the CIPS instrument. The contributions of two anonymous reviewers greatly enhanced the clarity of the paper. AIM is funded by NASA's Small Explorers Program under contract NAS5-03132.
This paper was edited by Markus Rapp and reviewed by two anonymous referees.
AIM CIPS Science Team: Cloud Imaging and Particle Size (CIPS) Instrument Overview, available at: http://lasp.colorado.edu/aim/, last access: 12 March 2019.
Bailey, S. M., Thomas, G. E., Rusch, D. W., Merkel, A. W., Jeppesen, C., Carstens, J. N., Randall, C. E., McClintock, W. E., and Russell III, J. M.: Phase functions of polar mesospheric cloud ice as observed by the CIPS instrument on the AIM satellite, J. Atmos. Sol.-Terr. Phy., 71, 373–380, https://doi.org/10.1016/j.jastp.2008.09.039, 2009.
Bardeen, C. G., Toon, O. B., Jensen, E. J., Hervig, M. E., Randall, C. E., Benze, S., Marsh, D. R., and Merkel, A.: Numerical simulations of the three-dimensional distribution of polar mesospheric clouds and comparisons with Cloud Imaging and Particle Size (CIPS) experiment and the Solar Occultation For Ice Experiment (SOFIE) observations, J. Geophys. Res., 115, D10204, https://doi.org/10.1029/2009JD012451, 2010.
Baumgarten, G., Fiedler, J., and Rapp, M.: On microphysical processes of noctilucent clouds (NLC): observations and modeling of mean and width of the particle size-distribution, Atmos. Chem. Phys., 10, 6661–6668, https://doi.org/10.5194/acp-10-6661-2010, 2010.
Benze, S., Randall, C. E., DeLand, M. T., Thomas, G. E., Rusch, D. W., Bailey, S. M., Russell III, J. M., McClintock, W., Merkel, A. W., and Jeppesen, C.: Comparison of polar mesospheric cloud measurements from the Cloud Imaging and Particle Size experiment and the Solar Backscatter Ultraviolet instrument in 2007, J. Atmos. Sol.-Terr. Phy., 71, 365–372, 2009.
Benze, S., Randall, C. E., Karlsson, B., Harvey, V. L., DeLand, M. T., Thomas, G. E., and Shettle, E. P.: On the onset of polar mesospheric cloud seasons as observed by SBUV, J. Geophys. Res., 117, D07104, https://doi.org/10.1029/2011JD017350, 2012.
DeLand, M. T. and Thomas, G. E.: Updated PMC trends derived from SBUV data, J. Geophys. Res.-Atmos., 120, 2140–2166, https://doi.org/10.1002/2014JD022253, 2015.
DeLand, M. T., Shettle, E. P., Thomas, G. E., and Olivero, J. J.: A quarter-century of satellite PMC observations, J. Atmos. Sol.-Terr. Phy., 68, 9–29, 2006.
Englert, C. R. and Stevens, M. H.: Polar mesospheric cloud mass and the ice budget: 1. Quantitative interpretation of mid-UV cloud brightness observations, J. Geophys. Res., 112, D08204, https://doi.org/10.1029/2006JD007533, 2007.
Gordley, L. L., Hervig, M. E., Fish, C., Russell III, J. M., Bailey, S. M., Cook, J., Hansen, J., Shumway, A., Paxton, G., Deaver, L., Marshall, T., Burton, J., Magill, B., Brown, C., Thompson, E., and Kemp, J.: The solar occultation for ice experiment, J. Atmos. Sol.-Terr. Phy., 71, 300–315, 2009.
Hansen, J. E. and Travis, L. D.: Light scattering in planetary atmospheres, Space Sci. Rev., 16, 527–610, 1974.
Hervig, M. E. and Gordley, L. L.: Temperature, shape, and phase of mesospheric ice from Solar Occultation for Ice Experiment observations, J. Geophys. Res., 115, D15208, https://doi.org/10.1029/2010JD013918, 2010.
Hervig, M. E. and Stevens, M. H.: Interpreting the 35-year SBUV PMC record with SOFIE observations, J. Geophys. Res.-Atmos., 119, 12689–12705, https://doi.org/10.1002/2014JD021923,2014.
Hervig, J. E., Gordley, L. L., Stevens, M. H., Russell III, J. M., Bailey, S. M., and Baumgarten, G.: Interpretation of SOFIE PMC measurements: Cloud identification and derivation of mass density, particle shape, and particle size, J. Atmos. Sol.-Terr. Phy., 71, 316–330, 2009.
Hervig, M. E., Berger, U., and Siskind, D. E.: Decadal variability in PMCs and implications for changing temperature and water vapor in the upper mesosphere, J. Geophys Res.-Atmos., 121, 2383–2392, https://doi.org/10.1002/2015JD024439, 2016.
Hultgren, K. and Gumbel, J.: Tomographic and spectral views on the lifecyle of polar mesospheric clouds from ODIN/OSIRIS, J. Geophys Res.-Atmos., 119, 14129–14143, https://doi.org/10.1002/2014JD022435, 2014.
Lübken, F.-J., Berger, U., and Baumgarten, G.: On the anthropogenic impact on long-term evolution of noctilucent clouds, Geophys. Res. Lett., 45, 6681–6689, https://doi.org/10.1029/2018GL077719, 2018.
Lumpe, J. D., Bailey, S. M., Carstens, J. N., Randall, C. E., Rusch, D. W., Thomas, G. E., Nielsen, K., Jeppesen, C., McClintock, W. E., Merkel, A. W., Riesberg, L., Templeman, B., Baumgarten, G., and Russell IlI, J. M.: Retrieval of polar mesospheric cloud properties from CIPS: algorithm description, error analysis and cloud detection sensitivity, J. Atmos. Sol.-Terr. Phy., 104, 167–196, https://doi.org/10.1016/j.jastp.2013.06.007, 2013.
McClintock, W. E., Rusch, D. W., Thomas, G. E., Merkel, A. W, Lankton, M. R., Drake, V. A., Bailey, S. M., and Russell III, J. M.: The cloud imaging and particle size experiment on the Aeronomy of Ice in the mesosphere mission: Instrument concept, design, calibration, and on-orbit performance, J. Atmos. Sol.-Terr. Phy., 71, 340–355, https://doi.org/10.1016/j.jastp.2008.10.011, 2009.
Mishchenko, M. I. and Travis, L. D.: Capabilities and limitations of a current Fortran implementation of the T-matrix method for randomly oriented, rotationally symmetric scatterers, J. Quant. Spectrosc. Ra., 60, 309–324, 1998.
Rapp, M. and Thomas, G. E.: Modeling the microphysics of mesospheric ice particles: Assessment of current capabilities and basic sensitivities, J. Atmos. Sol.-Terr. Phy., 68, 715–744, 2006.
Rusch, D. W., Thomas, G. E., McClintock, W., Merkel, A. W., Bailey, S. M., Russell III, J. M., Randall, C. E., Jeppesen, C., and Callan, M.: The cloud imaging and particle size experiment on the aeronomy of ice in the mesosphere mission: Cloud morphology for the northern 2007 season, J. Atmos. Sol.-Terr. Phy., 71, 356–364, 2009.
Russell III, J. M., Bailey, S. M., Gordley, L. L., Rusch, D. W., Horányi, M., Hervig, M. E., Thomas, G. E., Randall, C. E., Siskind, D. E., Stevens, M. H., Summers, M. E., Taylor, M. J., Englert, C. R., Espy, P. J., McClintock, W. E., and Merkel, A. W.: The Aeronomy of Ice in the Mesosphere (AIM) mission: Overview and early science results, J. Atmos. Sol.-Terr. Phy., 71, 289–299, 2009.
Thomas, G. E. and McKay, C. P.: On the mean particle size and water content of polar mesospheric clouds, Planet. Space Sci., 33, 1209–1224, 1985.
Thomas, G. E., Olivero, J. J., Jensen, E. J., Schröder, W., and Toon, O. B.: Relation between increasing methane and the presence of ice clouds at the mesopause, Nature, 338, 490–492, 1989.
Thomas, G. E., McPeters, R. D., and Jensen, E. J.: Satellite observations of polar mesospheric clouds by the Solar Backscattered Ultraviolet radiometer: Evidence of a solar cycle dependence, J. Geophys. Res., 96, 927–939, 1991.