2.1 Experimental data

We use 794 IMPROVE network PM_2.5 samples and 238 laboratory standard samples reported by Ruthenburg et al. (2014), and we focus on the quantification of four organic functional groups and one additional inorganic group which absorbs in the same region: alcohol COH (aCOH), carboxylic COH (COOH), alkane CH (aCH), total (carboxylic, ketonic, and aldehydic) carbonyl (tCO), and inorganic ammonium NH (iNH). We report the evaluation of predictions for urban and rural sites separately. The urban sites consist of two collocated measurement stations in Phoenix, AZ, while the rural sites consist of five locations: Mesa Verde, CO; Olympic, WA; Proctor Maple Research Facility, VT; Sac and Fox, KS; St. Marks, FL; Trapper Creek, AK, spread throughout the United States.

Ambient samples were collected every third day from midnight to midnight (local time) for 24 h. FTIR spectra are obtained for PM collected on 25 mm PTFE filters (Teflon, Pall Gelman – 3.53 cm² sample area) of the same type that are analyzed for gravimetric mass, elements and light absorption in the IMPROVE network. The nominal flow rate is 22.8 L min⁻¹, which yields a volume of 32.8 m³ for 24 h. A Tensor 27 FT-IR spectrometer (Bruker Optics, Billerica, MA) equipped with a liquid-nitrogen-cooled wide-band mercury cadmium telluride detector is used to analyze the PTFE samples in transmission mode, using the empty sample compartment as the background. The sample compartment is continuously purged with air containing low levels of water vapor and CO₂. Further details are provided by Ruthenburg et al. (2014) and Dillner and Takahama (2015a). TOR OC (and EC) mass is measured on quartz filters collected in parallel to the PTFE samples using the IMPROVE_A protocol (Chow et al., 2007). The TOR OC values are also adjusted for positive artifacts due to organic vapor adsorption onto quartz fiber by subtracting the monthly mean blank values. Sulfate and nitrate concentrations are measured on nylon filters also collected in parallel and analyzed by ion chromatography. Elemental composition is measured by X-ray fluorescence (XRF). The atmospheric concentrations of OC, nitrate, sulfate, and elemental composition provided by these techniques (obtained from the Federal Land Manager Environmental Database, FED, http://views.cira.colostate.edu/fed/Default.aspx, last access: 4 April 2019) are converted to equivalent areal mass densities on the PTFE filters using the filter collection area and actual sampled volume.

2.2 Spectral pretreatment

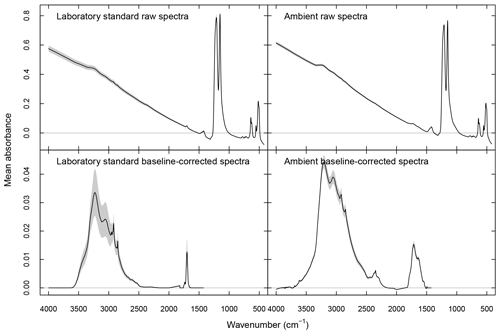
The baseline correction method of Kuzmiakova et al. (2016) is applied to both ambient and standard spectra for PF and PLS described below. This method uses smoothing splines (Reinsch, 1967) to model the baseline by regressing onto the background regions (where no analyte absorption is expected) as well as by interpolating through the analyte region. The calculated baseline is subtracted from the high-frequency region (>1500 cm⁻¹) where stretching or bending modes of aCOH, aCH, cCOH, carbonyl CO, and amine NH are present (Shurvell, 2006). A single parameter effectively controls the curvature of the fitted baseline, and we select the value which minimizes the negative absorbance fraction (NAF). NAF represents the contribution of negative analyte absorbance $\Vert {\mathit{a}}_{A-}{\Vert }_{\mathrm{1}}$ to the total analyte absorbance $\Vert {\mathit{a}}_A{\Vert }_{\mathrm{1}}$:

where $\Vert \cdot {\Vert }_{\mathrm{1}}$ denotes the one-norm magnitude of a vector (summation of all absolute values of vector elements). NAF is calculated across the entire wavenumber range in the analyte part of in a given segment, excluding the CO₂ absorbance band. Raw and baseline-corrected spectra are shown in Fig. 1.

Figure 1Laboratory and ambient sample spectra (raw and baseline corrected). Black lines denote mean absorbances, and dashed gray areas denote 95 % confidence intervals.

Download

2.3 Cluster analysis

Spectra similarities in baseline-corrected ambient sample spectra are used to group samples into clusters, as originally presented by Ruthenburg et al. (2014, appendix). We use Ward's hierarchical algorithm (Ward Jr., 1963), which has demonstrated useful categorizations in previous studies with FTIR spectra (e.g., Russell et al., 2009a; Takahama et al., 2011). Essentially, each baseline-corrected spectrum is normalized by its two-norm vector magnitude, and 20 clusters are selected to reduce the risk of grouping dissimilar samples together. Seven samples were excluded prior to cluster analysis and manually placed in three groups based on spectral similarity to known source profiles (Russell et al., 2011) (clusters 21 (n=2) and 22 (n=1)), or because the relative contribution of noise in low concentration samples would interfere with the clustering procedure (cluster 23 (n=4)). Clusters 19 (n=21) and 20 (n=19) were identified as being anomalous by Ruthenburg et al. (2014) when comparing FTIR-estimated OC to TOR OC. In this work, we identify two additional clusters which contain samples with anomalous predictions of organic FGs or iNH: clusters 7 (n=26) and 16 (n=12). Predictions and spectral characteristics for these four clusters are discussed separately, while the rest of the samples, classified as “rest” (n=706), are used for general evaluation.

2.4 Peak fitting

The method of PF constructs a physically based representation of absorbances based on Eq. (1), accounting for line shapes of spectral profiles resulting from absorption broadening. The fitted line shapes are constrained to be non-negative and within wavenumber limits derived from laboratory standards and ambient samples as described by Takahama et al. (2013b). To represent the essence of the PF algorithm in discretized notation, let s denote a line-shape function defined over wavenumbers $\stackrel{\mathrm{̃}}{\mathit{\nu }}$, and an arbitrary set of peak parameters θ for sample i and bond k. The parameters are collectively estimated by nonlinear least squares fitting of overlapping curves to x to minimize the residual e over specific regions of interest. The areal density of bond n^(a) is estimated as a product of the molar absorption coefficient and the integrated absorbance for each bond:

q denotes quadrature coefficients for numerical integration. $\mathrm{\Delta }\stackrel{\mathrm{̃}}{\mathit{\nu }}\equiv \mathrm{\Delta }{\stackrel{\mathrm{̃}}{\mathit{\nu }}}_j$ for FTIR, so this term has been taken out of the summation. $\stackrel{\mathrm{‾}}{\mathit{ϵ}}$ corresponds to the integrated absorption coefficient (which we report in units of ${\mathrm{cm}}^{\mathrm{2}}\mathrm{\mu }{\mathrm{mol}}^{-\mathrm{1}}\cdot {\mathrm{cm}}^{-\mathrm{1}}=\mathrm{cm}\mathrm{\mu }{\mathrm{mol}}^{-\mathrm{1}}$), which better characterizes the intensity of a dipole transition than ϵ when the absorption band spans a range of wavenumbers (Atkins and de Paula, 2006). We note that the use of these units marks a departure from previous convention of incorporating the filter collection area into the effective absorption coefficients (Maria et al., 2003; Gilardoni et al., 2007; Takahama et al., 2013b) ($\mathit{\pi }/\mathrm{4}\times {\mathrm{1.0}}^{\mathrm{2}}$ cm² in their work), but these units are preferred as they permit generalization across different filter sizes ($\mathit{\pi }/\mathrm{4}\times {\mathrm{2.12}}^{\mathrm{2}}$ cm² for Ruthenburg et al., 2014). For Gaussian line shapes used for both ambient and laboratory samples in this work, θ_ik corresponds to any number of relevant amplitude, location, and width parameters for each bond, and an analytical solution exists for its integral. For fixed absorbance profiles (e.g., cCOH), the peak parameter corresponds to a scaling coefficient.

Typically, calibration parameters are obtained from single-compound standards where attribution of absorption to individual functional groups is the least ambiguous. Prediction in more complex mixtures is enabled by the concurrent fitting of multiple absorption peaks and invocation of mixing rules to arrive at a representative absorption coefficient. In this work, we retain the algorithm for apportioning the absorbance spectrum to various functional groups (Takahama et al., 2013b) and re-evaluate absorption coefficients using the calibration standards prepared by Ruthenburg et al. (2014). The apportionment protocol is based on initial values and constraints set out by analysis of a large number of laboratory and ambient samples as described by Takahama et al. (2013b). While peaks for FGs in laboratory standards only include those present in the compound, all FGs are assumed to be present in each sample, which is a convenient approximation in atmospheric samples. Regressing integrated absorbance against areal density, we fit linear models without intercept to each compound or mixture of compounds in accordance with the Beer–Lambert law (the value of the slope is unaffected by the inclusion of an intercept in this data set). We retain coefficients only for regressions which the coefficient of determination (R²) is greater than 0.9 and combine values from each compound or mixture i into a single coefficient (to be applied to ambient samples) for each FG k using the fractional number of samples as weights:

These weights are selected to generate comparable models to PLS, and for this reason we also include estimates of absorption coefficients in multicomponent mixtures in addition to single-component standards when the fitting quality criterion is met. The estimates using the original absorption coefficients (Russell et al., 2009a, 2010; Liu et al., 2009) will be referred to as PFo, and estimates using the recalibrated absorption coefficients will be referred to as PFr.

2.5 Multivariate calibration

Multivariate calibration is an alternative approach that is typically formulated as a linear regression problem, with the analyte concentration as the regressand (response variable) and absorbances used as regressors. In scalar notation, this relationship is written as

n^(a) is the areal density for sample i and functional group k; x is the spectral absorbance, β is a wavenumber-specific regression coefficient, and e is the residual term. The number of wavenumbers at which absorbances are available exceeds the number of samples available for calibration (several thousand versus a few hundred), and the autocorrelation in absorbances due to the broadening leads to an underdetermined, collinear problem. Therefore, Eq. (4) must be solved by techniques other than classical least squares regression. PLS regression (Wold et al., 1984) is a generalization of multivariate multilinear regression and alleviates these problems by orthogonal projection and rank reduction (Geladi and Kowalski, 1986; Haaland and Thomas, 1988). Latent variables that maximize covariance with the response variable are found to model both the spectra matrix and response variables (FG abundances):

ℓ denotes the latent variable index, p and q are the loadings of x and n^a, respectively, and f and g are their residuals. The linear regression coefficients β in Eq. (4) are in turn derived from the loadings. In contrast to PF, multi-component reference standards that span the space of chemical composition are desired for PLS so that the ranges of composition – of both analytes and interferents – anticipated in prediction samples are available to train the model (Massart et al., 1988). As it is not possible to fully reproduce the high-dimensional chemical space of ambient samples, the amalgam of aerosol mixtures prepared in the laboratory targets the main features in this space.

A series of candidate models which satisfy Eqs. (4) and (5) is obtained by varying L, the maximum number of latent variables (LVs) or factors. The nonlinear iterative partial least squares (NIPALS) algorithm (Wold et al., 1983) is used to generate each model, and 10-fold Venetian blinds cross validation (Hastie et al., 2009; Arlot and Celisse, 2010) on the calibration set is applied to estimate corresponding root mean square of cross validation (RMSECV) values for the models. The minimum RMSECV solution is typically selected as the preferred model (defined by the value of L), but Takahama and Dillner (2015) found that this approach leads to overfitting with unrealistic results (i.e., extremely negative values) when extended to prediction of FGs in ambient samples. We therefore use the randomization test approach proposed by van der Voet (1994) to select the number of LVs. This method selects a model with fewer LVs for which the squared prediction error is not statistically greater than the reference (minimum RMSECV) model. This procedure is applied to each functional group separately such that each model is independent of one another (referred to as “PLS1” in chemometrics nomenclature). The number of LVs selected for PLSr and PLSbc are presented in Table S1 in the Supplement.

Though the interpretation of PLS models is less straightforward than PF, it is possible to examine how models are weighting spectral variables (wavenumbers) and calibration samples for making predictions. The regression coefficients are difficult to interpret directly as their magnitudes must be interpreted in combination with absorbances. In addition, the value of the regression coefficients can also be either positive or negative; the latter are associated with interfering species (Haaland and Thomas, 1988) or oscillations that increase with the number of LVs used (Gowen et al., 2011). Therefore, different approaches are used for estimating the contribution of specific wavenumbers to predictions. Takahama et al. (2016) used sparse calibration approaches that eliminated uninformative wavenumbers and used importance weighting to identify absorption bands used by PLS models. Wavenumbers highlighted by FG calibration models were associated with absorption bands of the target FGs while retaining similar prediction capability to the full wavenumber models presented here. The contribution of LVs to the explained variation and sum of squares of the spectra matrix and response variable are discussed in Sect. S4. The relationship between Eqs. (4) and (1) is illustrated in Sect. S1.

2.6 OC estimation from FG abundance

The constituent molar abundance n_a for atom a is calculated from the moles n_k of FG k through a coefficient λ_ak such that n_a=λ_akn_k. From n_a estimated for {C, O, H} in this work, the OC mass, OM∕OC mass ratio, and O∕C atomic ratios are obtained. While assignment of λ_ak for non-carbon atoms is unambiguous, λ_C⋅k depends on the assumed bonding configuration of polyfunctional carbon atoms (Takahama and Ruggeri, 2017). For instance, methylene (-CH₂-) carbon has a value of ${\mathit{\lambda }}_{\mathrm{C}\cdot \mathrm{aCH}}=\mathrm{0.5}$ (1 mol of carbon for two aCH groups), while methyl carbon (-CH₃) has a value of ${\mathit{\lambda }}_{\mathrm{C}\cdot \mathrm{aCH}}=\mathrm{0.33}$. It is also possible for the same carbon atoms to be associated with both aCH and aCOH, or other FGs, which makes the selection of λ less intuitive with increasing number of combinations; several statistical approaches are available for estimation in these instances. The only difference between Russell and coworkers (Russell, 2003; Takahama et al., 2013b) and Ruthenburg et al. (2014) is the value of λ_C⋅aCOH; the former authors define the value as 0.5 and the latter authors define it as 0. Overall, the choice of this value makes a ∼10 % difference in the carbon estimate for this data set. For this work we adopt the value of 0.5, which is also supported by a recent analysis of modeled α-pinene secondary organic aerosol (Ruggeri and Takahama, 2016; Takahama and Ruggeri, 2017) according to the Master Chemical Mechanism (Jenkin et al., 1997; Saunders et al., 2003). The full set of coefficients is provided in Sect. S1. We refer to the OC reconstructed through FG predictions as FG OC in this paper.

2.7 Quantification of carboxylic acid and non-acid carbonyl groups

While the carboxylic group comprises two molecular bonds, the abundances of carboxylic hydroxyl and carbonyl bonds are conventionally quantified separately with calibration models developed for their respective absorption bands. The carbonyl quantified in this way can include contributions from ketonic and aldehydic carbonyl because of their proximity in absorption bands that are difficult to resolve in environmental samples; the carboxylic hydroxyl cCOH and total carbonyl tCO are re-apportioned to estimate abundance of carboxylic COOH groups along with non-acid (ketonic, aldehyde, and ester) carbonyl CO (written as naCO). Stoichiometrically, n_COOH and n_cCOH are equivalent, while n_naCO is simply the difference between n_tCO and n_cCOH (Eq. S1 in the Supplement). In principle, the exact molar composition in a mixture should meet the condition that the tCO is in excess of the cCOH (n_tCO≥n_cCOH), with naCO content indicated by the tCO in excess of cCOH. To account for random errors, Takahama et al. (2013b) recommend the averaging of cCOH and tCO to estimate COOH when n_tCO∼n_cCOH. The estimated cCOH can be greater than tCO n_cCOH<n_tCO if the integrated absorption area or absorption coefficient is misspecified for either FG. In the absence of additional information, Takahama et al. (2013b) assume that the tCO is unmeasured due to shift in absorption frequency below that used in PF, and they base the COOH estimate on the cCOH. In such cases, an overall unmeasured fraction was assigned on a per-campaign basis to align tCO to cCOH abundances in previous studies, but in this work we apply this reasoning on a per-sample basis (i.e., n_COOH≡n_cCOH and $n_{\mathrm{naCO}}=max\mathit{\{}\mathrm{0},n_{\mathrm{tCO}}-n_{\mathrm{cCOH}}\mathit{\}}$).

One strategy to avoid the apportionment of tCO to COOH and naCO is to build an alternative PLS regression model to predict naCO directly, rather than tCO. The known concentrations in laboratory standards are transformed according to Eq. (S1) and provided as the response vectors to Eq. (4). In this work, the contributions to naCO in calibration standards are provided by 12-tricosanone and arachidyl dodecanoate, and therefore correspond to ketone and ester CO (i.e., no aldehyde CO). Previous studies atomizing dissolved aldehydic compounds found that they were transformed into alcohols by aldol condensation, which is also a possible but not a necessary outcome in the atmosphere (Takahama et al., 2013b) and depends on the presence of water and hydration constant of the compound. Nonetheless, we will refer to our new estimates as naCO under the assumption that aldehyde CO, if present in ambient samples, has a similar spectroscopic response to ketone and ester CO to the extent that we can quantify them. The COOH calibration remains identical to that for cCOH since n_COOH≡n_cCOH, and the stoichiometric consistencies for estimating OC, OM, OM∕OC, and O∕C ratios using different estimates of carbonyl are summarized in Sect. S1.

2.8 Evaluation metrics

Metrics such as mean error, mean bias, RMSE, and many others exist for intercomparison among measured and estimated values. In this work, to quantify overall bias we use total least squares slope (obtained via major axis regression), which accounts for uncertainties in both quantities being compared (Ripley and Thompson, 1987), and the Pearson's correlation coefficient (r) to quantify the strength of linear relationship between the two quantities. Values estimated with slopes and r close to unity among different methods are considered more robust. All evaluation metrics provided are for samples labeled as cluster “rest”, excluding clusters 7, 16, 19, and 20.

3.1 Estimation of absorption coefficients

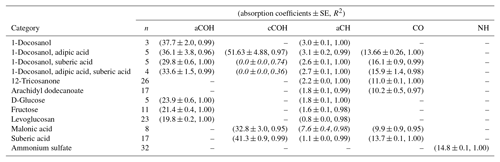
Calibration curves and predicted concentrations according to the PF strategy outlined in Sect. 2 are shown in Fig. 2. The top row refers to the calibration curves to compute the absorption coefficients (obtained using two-thirds of the 238 laboratory standards), and the bottom row refers to the evaluation of derived absorption coefficients on predicted concentrations for test set compounds not used in the calibration. Regression parameters including the number of samples used in each category, n, are included in Table 2. Absorption coefficients are estimated for cCOH by two mixtures (italic values in Table 2): (1) 1-docosanol and suberic acid, and (2) 1-docosanol, suberic acid, and adipic acid are not included in the calibration because of their low R² values. Malonic acid samples are additionally excluded in the estimation of aCH as its concentration range is far below the rest of the laboratory standards (below typical loadings of atmospheric samples) and the slope is twice greater than the next highest value (italic values in Table 2). This difference biases the weighted absorption coefficient in a way that does not reflect the weighting of the PLS regression (including this value makes a 19.9 % difference in the absorption coefficient). Overall, we used 97 % of the laboratory standard samples, of which two-thirds were reserved for the calibration (Figs. S1–S4 in Sect. S5). We can see that when the absorption coefficient for each respective category is applied to corresponding test set samples not used in the calibration (the remaining one-third of samples), predictions are within 6 % of the reference values (Fig. 2, bottom row).

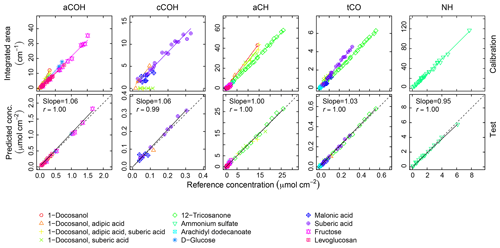
Figure 2Top row: integrated absorption as a function of known molar abundance used to derive molar absorption coefficients. Bottom row: evaluation of derived absorption coefficients on predicted concentrations for test set compounds not used in the fitting.

Download

Table 2Recalibrated absorption coefficients and fit statistics for each FG and compound. Italicized texts denote the compounds not used in the computation of cCOH and aCH absorption coefficients averages.

Download Print Version | Download XLSX

In Fig. 3, we compare the new absorption coefficients with those summarized by Takahama et al. (2013b) (specific citations described in figure caption) adjusted for filter collection area. aCOH for 1-docosanol is the only FG and organic compound for which we have a direct comparison; the value estimated for the absorption coefficient in this work is 3.6 times greater. This is due to different baseline correction methods and fitting procedures used by Gilardoni et al. (2007). When the same spectra preparation (smoothing spline baseline correction) is applied, the difference is 2 times greater but occurs in the same proportion for aCH absorption – i.e., both aCOH and aCH absorption coefficients for 1-docosanol spectra (n=3) acquired by Ruthenburg et al. (2014) are twice that for spectra acquired by Gilardoni et al. (2007) (n=6) when processed in the same way, but the ratio of aCOH to aCH absorbances for each method is within 4 %. This bias may partially be due to the fact that the slope of the calibration curve is determined by a single influential point for the few pure 1-docosanol samples collected by Ruthenburg et al. (2014). However, the consistency of the single-point estimate with aCOH coefficients for other mixtures containing 1-docosanol (Fig. 3) may suggest other differences that need to be investigated. For instance, the refractive index of the substrate may also affect the apparent absorbance in the limit of thin films (Hasegawa, 2017); similarity in optical properties of the filter type may have to be considered in future studies. Single measurements of fructose, glucose, as well as nine other sugars, were combined to derive an overall absorption coefficient for saccharides by Takahama et al. (2013b) (point estimates for fructose are effectively the same as the combined estimate, and glucose is 70 % smaller; Russell et al., 2010, Table S2). We observe that the absorption coefficients for individual compounds in this work are higher than the previous collective estimate. While there was previously no calibration performed for ammonium sulfate for its quantification by PF, the single ammonium sulfate sample used for removal of ammonium interference in the fitting procedure (introduced by Russell et al., 2009a) carried a mass of 6.0 µg over a $a=\mathit{\pi }/\mathrm{4}\times {\mathrm{1.0}}^{\mathrm{2}}$ cm² collection area (Takahama et al., 2013b), so this value is used to calculate a point estimate for its absorption coefficient. The recalibrated absorption coefficient is greater by a factor of 1.7. This is likely due to the combination of using a single-point value for estimating the coefficient.

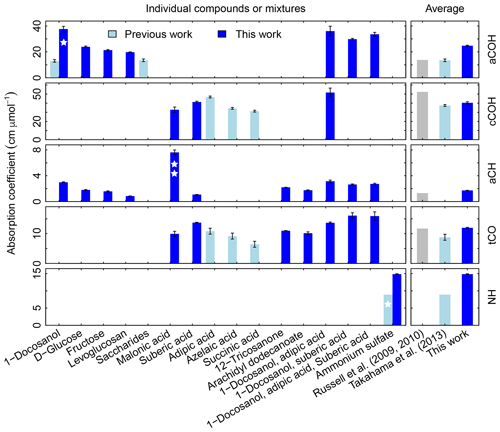
Figure 3Summary of molar absorption coefficients reported in the literature. The single star for 1-docosanol aCOH indicates that there are only three points – one of which is an influential point – so this is effectively a single-point estimate. The single star for ammonium sulfate indicates that it based on a single value. The double star is used to indicate that the absorption coefficient for malonic acid cCOH is estimated for a concentration range order of magnitude lower than the rest. Previous studies are summarized by Takahama et al. (2013b), which also compiled coefficients from Gilardoni et al. (2007) and Russell et al. (2010). The error bars represent plus/minus one standard error of the molar absorption coefficients.

Download

Absorption coefficients for aCH vary by a factor of 3.2 (between 1.0 and 3.2, over 10 compounds), for aCOH by a factor of 1.9 (between 19.8 and 37.7, over seven compounds), for cCOH by a factor of 1.6 (between 32.8 and 51.6, over three compounds), and for tCO by a factor 1.6 (between 10.0 and 16.1, over seven standards; Fig. S11). Without informed strategies for parameter selection, the range of valid possibilities for these absorption coefficients imparts uncertainty in FG calibration.

Shown on the right side of the Fig. 3 are averaged values reported by Russell and coworkers (Gilardoni et al., 2007; Russell et al., 2009a, 2010; Takahama et al., 2013b) and this work. Both sets will be compared in the following sections. The FG absorption coefficients for aCOH and aCH estimated in this work are higher by a factor of 1.8 and 1.3 respectively, which leads to lower estimates for FG abundances. In contrast, the FG absorption coefficient for cCOH is lower than that reported by Russell et al. (2009a) (factor of 0.8) and comparable to the one reported by Takahama et al. (2013b). The FG absorption coefficient for tCO is comparable with the one of Russell et al. (2009a) and 1.4 times greater than the one reported by Takahama et al. (2013b).

3.2 Comparison of estimated OC and ammonium to external measurements

We first compare quantities for which we have an independent estimate (TOR OC and ammonium) to place our predictions in context. Individual contributions of FGs used to estimate OC are discussed in Sect. 3.3. Comparisons are stated for regular samples not belonging to anomalous clusters (Sect. 2) unless otherwise noted. Evaluation of anomalous clusters is discussed separately in Sect. 3.6.

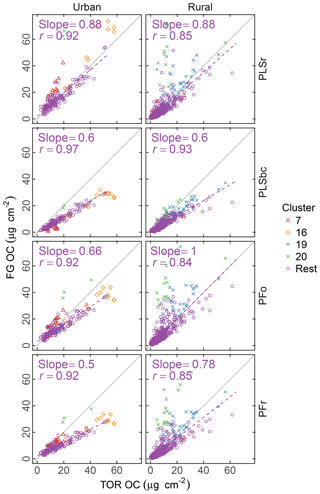
Figure 4Comparison of estimated OC (FG OC) against OC measured by TOR method (TOR OC). PFo refers to peak fitting using the original parameters. PLSr refers to partial least square using raw spectra. PFr refers to peak fitting using the recalibrated absorption coefficients. PLSbc refers to partial least square using baseline-corrected spectra.

Download

Figure 4 summarizes the comparison of predicted concentrations of OC using different sets of absorption coefficients (for PF – PFo and PFr refer to PF using the original and the recalibrated absorbance coefficients respectively) or different spectra pretreatment (for PLS – PLSbc and PLSr refer to PLS using the baseline-corrected and unprocessed spectra respectively). In general, the correlation between TOR OC and FG OC is high (r= 0.84–0.97) and typically greater for urban sites than for rural ones. In the urban samples, OC estimated by PLSr is closer to TOR OC with an underprediction of 12 %, while the other methods underpredict TOR OC by 34 %–50 %. In the rural sites, the agreement with TOR OC is more varied with three models underpredicting TOR OC by 0 %–22 % and PLSbc by 40 %. In general, the consistent underprediction is expected on account of the undetectable carbon atoms by FTIR due to lack of functionalization or association solely with bonds we do not measure.

The difference between PFo and PFr is due to the systematic increase in absorption coefficients used by PFr compared with PFo, which decreases the molar abundance of FGs and, consequently, the FG OC. This difference is particularly articulated by the absorption coefficient for aCH (1.73 against 1.31) as its mole fraction is over 60 % regardless of estimation method used.

The differences between PLSr and PLSbc are more difficult to understand, but some interpretations can be made. First, systematic differences can occur in the way that laboratory standard and ambient sample spectra are baseline corrected as the absorbance regions are different. Also, baseline correction used in the PLSbc does not include frequency lower than 1500 cm⁻¹, thus excluding the alkane peak around 1450 cm⁻¹ that is likely being used for aCH estimation by the PLSr model (Takahama et al., 2016). As FG abundances in laboratory samples are reproduced with minimal error, we anticipate that PTFE interferences to predictions are minimal with PLSr. However, PLSr may be erroneously incorporating some information regarding the scattering by supermicron particles in its prediction (Sect. 3.6). Notably, the samples labeled as anomalous by Ruthenburg et al. (2014) (clusters 19 and 20) are predicted more consistently in relation to TOR OC with PLSbc than PLSr, suggesting the baseline correction has partially removed spectral features from the raw spectra that lead to unexpected deviations in predictions. For the remaining samples, it is generally possible to find models – using raw or baseline-corrected spectra – with different parameters (e.g., a different number of LVs) that produce similar predictions and also models in which FG OC agrees better with TOR OC. While we do not explore all possible combinations of parameters exhaustively in this paper, an example of how comparisons of FG OC predictions vary with number of LVs of aCH for PLS with baseline corrected is given in Fig. S16. The solution that best matches TOR OC (referred to as PLSbc*) from this evaluation is shown in Fig. 5.

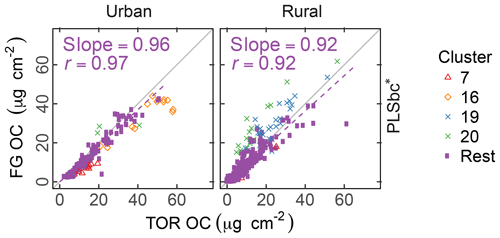
Figure 5Comparison of estimated OC (FG OC) gainst OC measured by TOR method (TOR OC). PLSbc* refers to partial least square using baseline-corrected spectra and a heuristic choice for the aCH LVs number (13) based on agreement between FG OC and TOR OC (Fig. S16).

Download

The solutions in the neighborhood (±3 LVs) of the PLSbc models for each FG are highly correlated, but they vary in their slope by a factor of approximately 1.5 (Sect. S8). PLSbc* varies from PLSbc for aCH by only 2 LVs.

PLSbc* is only one of many possible models that show improved agreement with TOR OC to be explored in future work; for this paper we restrict our evaluation of results primarily to those obtained by the protocols described in Sect. 2.

Figure 6 summarizes the comparison of ammonium concentrations predicted by FTIR with the value estimated as the cation counterpart of sulfate and nitrate. The correlation in comparisons is strong for rural sites (r>0.89) and moderately strong (r= 0.47–0.71) in urban sites for all models. Part of this difference may be that the dynamic range of ammonium in rural sites is twice the value of urban sites. While our estimated reference values are thought to be the upper bound of ammonium concentrations (on account of our assumptions that (i) there is neither evaporation loss of ammonium nitrate from PTFE nor (ii) nitrate association with dust instead of ammonium), the reference ammonium is overpredicted by the PSLr model at urban sites and by the PFo model at both urban and rural sites. The PFo overpredictions can be explained by the uncertainty on the absorption coefficient estimated using a single value. The overprediction in urban sites only by PLSr is less simple to interpret. One possibility is the scattering contribution to the FTIR spectra by large particles may be more significant for these samples, and this effect is reduced by baseline correction.

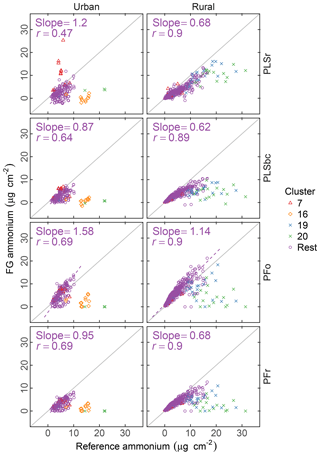
Figure 6Comparison of estimated ammonium (FG ammonium) against ammonium measured using ion chromatography (IC ammonium). PFo refers to peak fitting using the original parameters. PLSr refers to partial least square using raw spectra. PFr refers to peak fitting using the recalibrated absorption coefficients. PLSbc refers to partial least square using baseline-corrected spectra.

Download

While ammonium quantification by FTIR has been the focus of past researchers (Johnson et al., 1981; McClenny et al., 1985; Allen et al., 1994; Krost and McClenny, 1994; Reff et al., 2007), the recent work of Russell, Dillner, and co-workers focused on organic FG quantification, and an extensive evaluation for ammonium has not been performed. However, as the absorption bands of iNH overlap with aCOH, cCOH, and aCH, it is useful to know whether the fitted ammonium scales with an external measurement. Such a simultaneous evaluation of bonds is important for PF, since the IR absorption in each spectrum is apportioned to contributions from various bonds; overapportionment for one bond can lead to underapportionment for another. Based on the assessment with PFr using a better-characterized absorption coefficient, comparisons with the reference ammonium values suggest that neither gross overestimation nor underestimation of the fitting is likely. Calibration models for PLSr and PLSbc used in this work are developed independently of one another (the “PLS1” approach); therefore, the predictive capability of one species is not strongly tied to another as with PF. In summary, the LVs in the ammonium calibration model are not necessarily the same as the organic FGs; the over- or underprediction of ammonium is less consequential to how we interpret the FG quantifications. An alternative, multimodel formulation (“PLS2”) can provide estimates of both analyte and interferents using the same set of LVs. The current decision to use PLS1 is based on the knowledge that PLS1 typically outperforms PLS2 as it is optimized for each target analyte (Martens and Næs, 1991), but in extrapolation (as in our use case) the physically consistency offered by PLS2 may confer benefits not conventionally recognized with such models.

3.3 Variations in estimated FGs

Figure 7 summarizes pairwise correlation coefficients and regression slopes (excluding anomalous clusters 7, 16, 19, and 20) of FG abundances estimated using the methods discussed in Sect. 3.2. Individual scatter plots can be found in the Supplement (Figs. S5–S9). Overall, aCH, iNH, and tCO, agree with fairly high correlation r>0.75, but the agreement of aCOH and cCOH – two FGs with broad absorption regions on account of the OH stretch – varies more significantly. The strong agreement of iNH predicted by PLS and PF is particularly notable. While the calibration models for PLSr and PLSbc are formulated to predict ammonium iNH, they are technically equivalent to a calibration model for ammonium sulfate as this is the only substance with this bond in the calibration set. However, the comparison of predictions against PF, which only uses the NH stretching peak – which are spectroscopically similar between ammonium nitrate and sulfate – suggests that the PLS models are likely using features that are specific to this absorption band that is common to both ammonium salts.

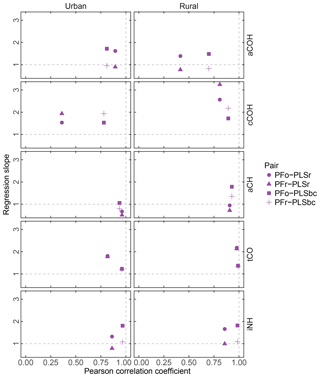
Figure 7FG comparison summary. Pearson correlation coefficient PFo refers to peak fitting using the original parameters. PLSr refers to partial least square using raw spectra. PFr refers to peak fitting using the recalibrated absorption coefficients. PLSbc refers to partial least square using baseline-corrected spectra.

Download

First, we focus on the comparison between PFo and PLSr. In urban samples, aCH presents the highest correlation (r=0.96) of all FGs, presumably, because the aCH absorption is unambiguous on account of the high abundance of hydrocarbon compounds in urban areas. However, the slope (0.68) reveals a systematic difference between the two. For the rest of the organic FGs in both urban and rural sites, PFo estimates are higher than PLSr; the regression slopes vary between 1.39 (aCOH in rural samples) and 2.57 (cCOH in rural samples).

Correlation coefficients in the PFr–PLSr comparison for any organic FG are similar to the PFo–PLSr comparison; the only notable difference is the larger regression slope for cCOH (1.94 and 3.25 for urban and rural samples against 1.53 and 2.57 respectively), due to the lower absorption coefficient applied to PFr than PFo (Table 2). The cCOH and tCO estimated by PFr are still higher than PLSr (by 1.78 to 3.25). However, the underprediction of FG OC relative to TOR OC (Sect. 3.2) can be explained by the lower concentrations of aCH and aCOH estimated with the recalibrated absorption coefficients as they compose more than 70 % of the organic aerosol mass according to PF analysis (Sect. 3.5).

PFo and PFr predictions agree closely with PLSbc, likely because they use the same portion of the spectra. The organic FG correlations vary between 0.7 (aCOH – rural samples) and 0.99 (tCO – rural sample). PFr predictions are closer to PLSbc than PFo, with the exception of cCOH, since they use the same laboratory standard compounds.

The correlation for iNH is greater than 0.97 with slope close to one in the case of PFr and greater than 1.8 in the case of PFo, which indicates a systematic bias due to the different absorption coefficients used (14.84 and 8.89 for PFr and PFo respectively).

The correlations in tCO between PF and PLS are high (r>0.81), potentially because of the narrow absorption band of the carbonyl FG. PF estimates of tCO for urban samples increase in correlation with PLS estimates from 0.82 to 0.96 (with the slope approaching unity) when baseline-corrected spectra are used for PLS, suggesting that signal contributions (presumably from PTFE) interfering from the quantification are effectively removed.

Within the broader scope of assessing uncertainty for each FG, we can consider that the estimated slopes can vary according to the selection of absorption coefficient value for PF and the number of LVs for PLS. The range of absorption coefficients is given in Sect. 3.1, with aCH having the largest range. If we examine the set of PLSbc solutions (varying only in number of LVs) with a correlation coefficient greater than 0.95 with the selected solutions presented here, we find that the largest variability is also in the aCH (ranges are shown in Fig. S11 and differences among models in Fig. S12). Models with different number of LVs reflect different weighting of calibration samples and their responses, so it is not surprising to find that the magnitude of uncertainties (reported in Sect. 3.1) is similar between PLS and PF for the same set of calibration standards.

3.4 Quantification of carboxylic acid and non-acid carbonyl

Figure 8 compares the abundance of tCO and cCOH predicted by the four methods. Both PLSr and PLSbc predict similar abundances of tCO as cCOH, suggesting that most of the carbonyl is associated with carboxylic acid groups, and the non-acid fraction is small to negligible. While it is possible for both models to use the carbonyl absorption band, Takahama et al. (2016) suggest that the wavenumbers are weighted differently by the two models.

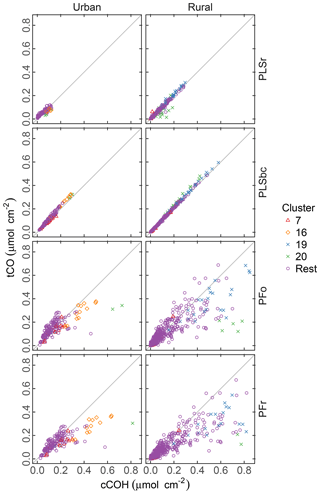
Figure 8Comparison of quantified abundance of tCO and cCOH. PFo refers to peak fitting using the original parameters. PLSr refers to partial least square using raw spectra. PFr refers to peak fitting using the recalibrated absorption coefficients. PLSbc refers to partial least square using baseline-corrected spectra.

Download

There is noticeably more scatter in the relationship between tCO and cCOH from the PF predictions, with the presence of naCO difficult to identify in these samples. Furthermore, tCO abundance is systematically lower than cCOH for many samples (discernable beyond the extent of scatter). Takahama et al. (2013b) hypothesized that this discrepancy could be due to underestimation of carbonyl in samples where the absorption band is shifted to lower frequencies. However, given that (1) the constraint n_tCO≥n_cCOH is met for the PLS estimates, and (2) the relative overprediction by PF in comparison to PLS is greater for cCOH than tCO in these samples, it is likely that it is cCOH that is overestimated by PF for these samples. This may be due to the peak profile for cCOH or baseline correction artifacts. For clusters 19 and 20 in which the overestimation is more severe, the baseline correction artifact is the most probable reason as discussed in Sect. 3.6.

Figure 9 compares the estimated naCO for two methods of calibration: one estimated through the difference of tCO and COOH (the canonical approach) and by direct calibration (alternate approach). We find that, on average, the naCO is close to zero using both estimates (and within the differences of cCOH and tCO). For predictions with raw spectra, the range of predictions is smaller for naCO estimated directly than as a difference of cCOH and tCO. naCO estimates from PLS with baseline-corrected spectra are notably less variable than for those using raw spectra. Moreover, the canonical and alternate estimates are strongly correlated (r=0.99 for urban and r=0.95 for rural samples) even for these low concentrations, despite the fact that the two models use wavenumbers and latent variables differently (Fig. S13). These results suggest that baseline correction can reduce interferences that may impart uncertainties in the estimation of FGs in this region for most samples, including clusters 7, 16, and 20.

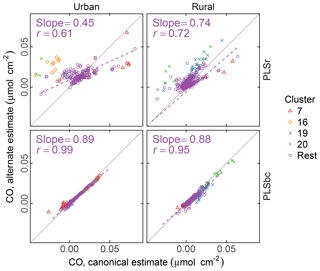
Figure 9Comparison of estimated CO according to canonical calibration (as difference between molar abundance of cCOH and tCO), and alternate calibration (direct calibration to non-acid CO). PLSr refers to partial least square using raw spectra. PLSbc refers to partial least square using baseline-corrected spectra.

Download

High abundances of naCO have been reported in biomass burning and biogenic secondary OM in past studies (using PF), either due to ketones present in photochemical reaction products (Schwartz et al., 2010) or esterification in the condensed phase (Russell et al., 2011). Therefore, it is surprising to find such low abundances of naCO especially in rural sites with biogenic influences and samples influenced by residential wood burning (Kuzmiakova, 2019). This finding may point to a differences in sample types between this and previous work, as well as possible artifacts due to long PM collection times, storage, and transport protocols in monitoring network samples. For instance, more opportunities for conversion of naCO to aCOH by aldol condensation in the condensed phase may be possible in these samples.

3.5 Evaluation of estimated OM, OM∕OC, and O∕C

Figure 10 (left column) summarizes estimates of OM, OM∕OC, and O∕C obtained by FTIR (distributions are shown in Fig. S14). On average, concentrations of OM are higher in urban samples than rural ones, while the OM∕OC ratio and O∕C ratio shows the opposite pattern, as expected from previous studies. These trends are in agreement with measurements by GC-MS and AMS (Turpin and Lim, 2001; Aiken et al., 2008), and they are in accordance with our understanding of atmospheric processes by which condensation of functionalized molecules (Ziemann, 2005; Kroll and Seinfeld, 2008) and heterogeneous reactions (Smith et al., 2009; Lim et al., 2010) lead to chemical aging.

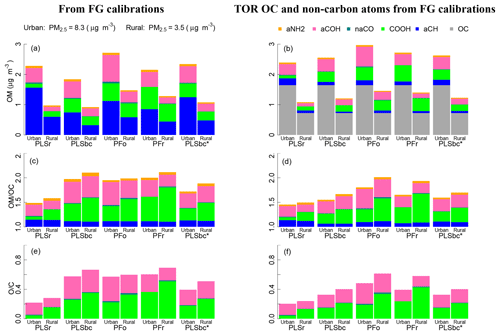
Figure 10(a, b) bar plots of OM mass fractions from quantified FGs. (c, d) bar plots of OM∕OC ratio and associated non-carbon atoms. (e, f) O∕C. In the left panels (a), (c), and (e) OM, OM∕OC and O∕C ratios use OC estimated by FG calibrations (FG OC). In the right panels (b), (d), and (f) the OM, OM∕OC and O∕C ratios use OC measured by TOR. PLSr and PLSbc refer to partial least square using raw and baseline-corrected spectra respectively. PFo and PFr refers to peak fitting using the original recalibrated absorption coefficients. PLSbc* is the same as PLSbc except that the number of LVs for aCH has been selected heuristically (Sect. 3.2).

Download

The absolute magnitudes, however, require further consideration. The mean OM∕OC values estimated by PLSr (Ruthenburg et al., 2014) of 1.5 and 1.6 for urban and rural sites, respectively, are within range of values previously reported by GC-MS and AMS (Turpin and Lim, 2001; Aiken et al., 2008). However, the mean O∕C ratio of 0.25 for rural sites is particularly low and corresponds to values for hydrocarbon-like components derived from AMS PMF analysis (e.g., Aiken et al., 2008; de Gouw et al., 2009; Canagaratna et al., 2015). These results suggest that PLSr may be underestimating the oxygenated FGs (COOH and aCOH), especially for rural sites. The mean OM∕OC ratios for PLSbc, PFo and PFr are higher than PLSr and range from 2.0 (urban) up to 2.1 (rural), with O∕C ratios from 0.5 (urban) and 0.7 (rural). The surprisingly high values of OM∕OC and O∕C for urban samples can be attributed to an underestimation of FG OC, which inflates the OM∕OC estimates. However, the mass fractions of FGs (shown as conventional pie graphs in Fig. S10 in the Supplement) suggest relative proportions estimated by PFo, PFr, and PLSbc are similar to urban aerosol composition previously reported by Russell and co-workers (Russell et al., 2011; Takahama et al., 2013a). The proportion of aCH mass is estimated above 40 % and COOH and aCOH approximately one-quarter each; primary amine and carbonyl comprise the rest of the average OM mass for the urban samples (between 3 % and 6 %). In contrast, PLSr estimates the aCH fraction to be 71 % for urban samples and 64 % for rural (whereas the other models estimate between 35 % and 40 % for rural sites).

To improve these carbon-normalized metrics, the undetected carbon moieties can be corrected by incorporating an assumed carbon mass recovery fraction (Takahama and Ruggeri, 2017). Alternatively, an available OC reference measurement can instead be used for normalization – this can be TOR OC, which we use here, or TOR-equivalent OC estimated from FTIR spectra (Dillner and Takahama, 2015a; Reggente et al., 2016). This latter procedure leaves FTIR FG measurements to provide only the non-carbon atom content, which can be estimated with less uncertainty than the carbon content by using FG analysis (Sect. 2.6). The uncertainty in aCH abundance plays a critical role in estimation of carbon and OM mass, as nearly half of the total carbon is attributed to that associated with aCH. When using FG OC for normalization, contribution of this FG to the non-carbon portion of OM∕OC is 0.17 at most (Sect. S2), but this belies the substantial role in governing the overall magnitude of the ratio through its contribution to the OC estimate. However, if an external OC value is provided, the non-carbon contribution of aCH to OM is due to only hydrogen and the OM∕OC (and O∕C) is primarily dependent on estimates of the oxygenated fraction.

Figure 10 (right column) summarizes estimates of OM, OM∕OC, and O∕C obtained by using FTIR estimates for non-carbon atom abundance, and TOR OC for carbon content. The adjustments reflect the extent of underestimation of TOR OC by each of the models, and, predictably, the PLSr mean rural OM∕OC is reduced with respect to its urban counterpart while the mean urban OM∕OC is reduced with respect to the rural counterparts for the rest of the models. In the case of urban samples, the mean OM∕OC varies between 1.5 (PLSr) and 1.8 (PFo), and the mean O∕C varies between 0.20 (PLSr) and 0.48 (PFo). In the case of rural samples, the mean OM∕OC varies between 1.5 (PLSr) and 2.0 (PFo), and the mean O∕C varies between 0.21 (PLSr) and 0.61 (PFr).

When we heuristically adjust the PLSbc aCH model parameters to match TOR OC concentrations within 10 % on average (PLSbc* introduced in Sect. 3.2), estimated OM, OM∕OC, and O∕C values fall within the extremes spanned by the various models. While laboratory calibrations can generate models that give reasonable predictions for ambient samples (to the extent that they can be evaluated), this comparison underscores the challenge in selecting the most appropriate model for ambient samples based on laboratory data. More experience in evaluating different model selection criterion on extrapolation is necessary to improve the calibration strategy for FG estimation.

3.6 Anomalous samples

We examine and summarize in Fig. 11 a few of the anomalous clusters. Cluster 7 (first row in Fig. 11) samples have significant overprediction in both OC and ammonium for the calibration model using raw spectra (PLSr) but less in the baseline-corrected models. These samples are found in almost all sites and are primarily influenced by dust (Kuzmiakova, 2019). This conclusion is evidenced by the FTIR spectra having two sharp peaks above 3000 cm⁻¹ and a broader peak between 950 and 1100 cm⁻¹ indicative of Si–O bonds; resemblance of spectral features to hydroxyl groups from organic compounds or bound water in hydrates associated with dust is also observed. Accompanying XRF measurements also indicate high abundance of mineral dust elements in these samples. Larger atmospheric particles are likely to scatter infrared radiation, with increasing contributions above ∼200 nm (Signorell and Reid, 2010), and non-negligible contributions above 1  µm (Allen and Palen, 1989). While the primary purpose of the baseline correction is to remove the scattering from the PTFE fibers, it is also likely that there is a scattering contribution from the particles, which confers a positive artifact to the estimate of OC in the raw spectra calibration model. Baseline correction appears to reduce these artifacts through the removal of the particle scattering contribution to the observed absorbance.

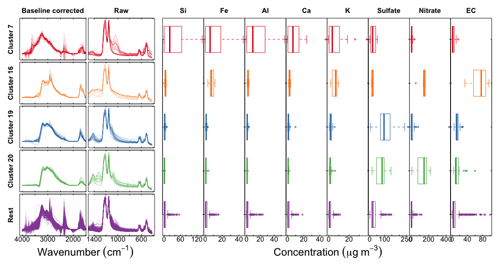
Figure 11Left column shows scaled baseline-corrected spectra between 4000 and 1500 cm⁻¹; middle column shows scaled raw spectra below 1500 cm⁻¹, and concentrations of PM constituents measured in the IMPROVE network: trace elements from X-ray fluorescence, inorganic ions (sulfate and nitrate) from ion chromatography, and elemental carbon from TOR analysis.

Download

Cluster 16 (second row in Fig. 11) consists of wintertime Phoenix, AZ, samples which are associated with residential wood burning (Kuzmiakova, 2019). The consistent disagreement of the reference ammonium concentrations with all models suggests that the error may be attributed to the estimation of reference values rather than the calibrations. We expect gas–particle partitioning to favor the condensed phase for ammonium nitrate for wintertime temperatures in Phoenix, so an evaporation artifact from Teflon is not anticipated to be the most significant factor. However, potassium nitrate is a well-known product of biomass burning, and the offset in ammonium equivalently formulated in the magnitude of potassium matches the reported concentrations by XRF.

The atypical predictions for clusters 19 and 20 (third and fourth row in Fig. 11) are likely due to the abundance of large ammonium sulfate (cluster 19) and ammonium nitrate (cluster 20) particles in the samples, leading to anomalous transmission of infrared radiation (Christiansen peak effect) (Christiansen, 1885; Barnes and Bonner, 1936; Henry, 1948; Prost, 1973) through the sample (Fig. S15). The Christiansen peak effect occurs under two limiting conditions: the refractive index approaches that of the surrounding medium (air in this case), and the size of the particle(s) approaches the wavelength of the incident radiation. The refractive indices of ammonium sulfate and ammonium nitrate both exhibit a local minimum below 1.3 at 3.0 µm (3300 cm⁻¹) (Jarzembski et al., 2003). PM_2.5 can include some particles above 2.5 µm as the cut point corresponds to the median diameter of any particle efficiency curve of a size-selective inlet (cyclone for IMPROVE samples). However, another reason that the Christiansen effect plays a role in these samples is that its magnitude can still be significant for particles smaller than this diameter (Carlon, 1979). The result of this phenomenon is that the transmittance increases near this wavelength, though never approaching 100 % on account of co-absorbing substances and inhomogeneities in atmospheric particles (Shelyubskii, 1993; Pollard et al., 2007). The corresponding absorbance spectrum displays a sharp decrease at the Christiansen wavelength relative to its neighboring absorbances and spectral distortions in its vicinity. This optical artifact can affect both baseline correction and direct calibration (without baseline correction) if these effects are not taken into account, and our unexpected predictions can most certainly be attributed to this phenomenon. Remedies for this artifact may entail explicit modeling of the anomalous transmittance peak in the baseline correction or inclusion of samples which have this effect in the calibration samples. As both of these effects are nonlinear to absorbance, their treatment by a linear model may lead to a suboptimal representation of their contributions across multiple latent variables (including cross-over with contributions to the signal such as instrument noise; Zupan and Gasteiger, 1991). Nonetheless, the demonstrated performance of calibration models for TOR-equivalent OC prepared from the regression of FTIR spectra to collocated TOR OC measurements (Dillner and Takahama, 2015a) suggests that PLS can handle these irregularities (scattering, Christiansen effect) as long as samples which exhibit them are included in the calibration samples, with or without baseline correction.