the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Assessing the impact of clouds on ground-based UV–visible total column ozone measurements in the high Arctic
Xiaoyi Zhao
Kristof Bognar
Vitali Fioletov
Andrea Pazmino
Florence Goutail
Luis Millán
Gloria Manney
Cristen Adams
Kimberly Strong
Zenith-Sky scattered light Differential Optical Absorption Spectroscopy (ZS-DOAS) has been used widely to retrieve total column ozone (TCO). ZS-DOAS measurements have the advantage of being less sensitive to clouds than direct-sun measurements. However, the presence of clouds still affects the quality of ZS-DOAS TCO. Clouds are thought to be the largest contributor to random uncertainty in ZS-DOAS TCO, but their impact on data quality still needs to be quantified. This study has two goals: (1) to investigate whether clouds have a significant impact on ZS-DOAS TCO, and (2) to develop a cloud-screening algorithm to improve ZS-DOAS measurements in the Arctic under cloudy conditions. To quantify the impact of weather, 8 years of measured and modelled TCO have been used, along with information about weather conditions at Eureka, Canada (80.05∘ N, 86.41∘ W). Relative to direct-sun TCO measurements by Brewer spectrophotometers and modelled TCO, a positive bias is found in ZS-DOAS TCO measured in cloudy weather, and a negative bias is found for clear conditions, with differences of up to 5 % between clear and cloudy conditions. A cloud-screening algorithm is developed for high latitudes using the colour index calculated from ZS-DOAS spectra. The quality of ZS-DOAS TCO datasets is assessed using a statistical uncertainty estimation model, which suggests a 3 %–4 % random uncertainty. The new cloud-screening algorithm reduces the random uncertainty by 0.6 %. If all measurements collected during cloudy conditions, as identified using the weather station observations, are removed, the random uncertainty is reduced by 1.3 %. This work demonstrates that clouds are a significant contributor to uncertainty in ZS-DOAS TCO and proposes a method that can be used to screen clouds in high-latitude spectra.
- Article
(6027 KB) - Full-text XML
- BibTeX
- EndNote
Ozone is one of the most widely monitored trace gases in the atmosphere. It can be measured via its strong absorption bands in the ultraviolet (UV), visible (Vis) and infrared (IR) portions of the spectrum. Remote sensing measurements of total column ozone (TCO) started in the 1920s with the Dobson instrument (Dobson, 1968), which measures the UV spectrum (the so-called Huggins bands). During the International Geophysical Year, 1957–1958, the worldwide Dobson ozone-monitoring network was established. Stratospheric ozone has been a focus of scientific study since the 1970s and became a matter of intense interest with the discovery and subsequent studies of the Antarctic ozone hole (Farman et al., 1985; Solomon et al., 1986; Stolarski et al., 1986) and depletion on the global scale (Ramaswamy et al., 1992; Stolarski et al., 1991).
To improve the accuracy of, and to automate, TCO measurements, the Brewer spectrophotometer was developed in the early 1980s (Kerr et al., 1981, 1988). In 1988, the Brewer was designated (in addition to the Dobson) as the World Meteorological Organization (WMO) Global Atmosphere Watch (GAW) standard for TCO measurement. By 2017, there were more than 230 Brewer instruments installed around the world. Brewer instruments can provide TCO values via four types of observations: direct-sun, direct-moon, zenith-sky, and spectral UV irradiance (De Backer and De Muer, 1991; Fioletov et al., 1997, 1999; Labow et al., 2013). The most accurate ozone data products from Brewer instruments are their direct-sun (DS) measurements, which have a typical accuracy of 1 % (Fioletov et al., 2005). One limitation of Dobson or Brewer UV instruments is the so-called stray-light effect (Fioletov et al., 2000; Kerr et al., 1981; Van Roozendael et al., 1998), which prevents the use of Dobson or Brewer instruments to retrieve TCO at large solar zenith angles (SZAs, above 80∘).
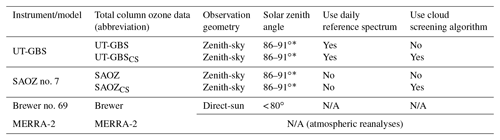
Since the 1990s, a zenith-sky UV–visible ozone monitoring group has been operating within the Network for the Detection of Atmospheric Composition Change (NDACC) (Hendrick et al., 2011; Sarkissian et al., 1995; Van Roozendael et al., 1998; Van Roozendael and Hendrick, 2009; Vaughan et al., 1997). Unlike Dobson or Brewer instruments, NDACC UV–visible instruments use the zenith-sky visible spectrum (Chappuis bands) to retrieve TCO. The use of visible spectroscopy makes it possible to measure TCO at higher SZAs (up to 91∘), which allows for the collection of data at high latitudes during polar sunrise and sunset. The NDACC UV–visible network consists of more than 35 instruments that have provided more than 2 decades of measurements of total column amounts of ozone, NO2, BrO, and OClO retrieved using the zenith-sky scattered sunlight differential optical absorption spectroscopy (ZS-DOAS) technique (Hendrick et al., 2011; Van Roozendael et al., 1998; Vaughan et al., 1997). A UV–visible ZS-DOAS instrument, the University of Toronto Ground-based Spectrometer (UT-GBS), has been deployed in Eureka, Nunavut, Canada (80.05∘ N, 86.41∘ W), during springtime from 1999 to 2009 and year-round since 2010 and is part of the NDACC UV–visible network. In addition, an NDACC-certified Système D'Analyse par Observations Zénithales (SAOZ) instrument has been deployed at the same site since 2005. Both UT-GBS and SAOZ data analyses follow the NDACC retrieval protocols (Van Roozendael and Hendrick, 2009) and use the NDACC ozone air mass factor (AMF) lookup table (LUT) in the TCO retrieval.
Many studies have compared WMO–GAW Dobson or Brewer TCO (hereafter referred to as DB TCO) with NDACC UV–visible zenith-sky TCO (referred to as ZS TCO) (Fraser et al., 2007; Hendrick et al., 2011; Høiskar et al., 1997; Kyrö, 1993; Roscoe et al., 1994, 2001; Van Roozendael et al., 1998; Vaughan et al., 1997). In general, it has been found that ZS TCO retrievals have advantages, such as weak temperature dependence of ozone cross sections (in the visible band), the ability to measure at large SZAs (e.g., during polar sunrise and sunset), and limited sensitivity to clouds compared to DB TCO (Daumont et al., 1992; Hendrick et al., 2011; Scarnato et al., 2009; Van Roozendael and Hendrick, 2009). However, ZS TCO also has negative characteristics, such as low temporal coverage (twice per day), low total accuracy (6 %, compared to 1 % for DB TCO), and dependency on the AMF calculated using a radiative transfer model (RTM) (Hendrick et al., 2011; Van Roozendael et al., 1998; Van Roozendael and Hendrick, 2009; Wardle, 1997; Zhao et al., 2016b). Van Roozendael et al. (1998) reported that the sensitivity of ZS ozone AMFs to multiple scattering in tropospheric clouds could lead to occasional positive bias in ZS TCO retrieved from SAOZ instruments. Erle et al. (1995) found that tropospheric clouds may severely affect ZS TCO, leading to overestimation of the ozone column by 12 %–30 % at SZAs of 90–60∘. Hendrick et al. (2011) concluded that the main sources of uncertainties in the ZS ozone AMF calculation are (1) inaccurate ozone profiles and surface albedo, (2) the choice of aerosol extinction profile and RTM, and (3) the presence of clouds.
However, clouds are not accounted for in the NDACC ozone AMF calculations (Hendrick et al., 2011). This is because the twilight zenith-sky measurements are strongly weighted by the contribution of the stratospheric ozone and therefore show limited sensitivity to the uncertainties in parameters affecting tropospheric ozone (e.g., Mie scattering in a cloud layer; Hendrick et al., 2011). Hendrick et al. (2011) reported that cloudy AMFs are systematically larger than non-cloudy AMFs by about 5 %–8 % at 86∘ SZA and 2 % at 91∘ SZA. This leads to a random uncertainty of 3.3 % for TCO calculated using the NDACC ozone AMF LUT between 86 and 91∘ SZA. In fact, clouds are the largest source of random uncertainty in ZS TCO. The second largest source, the climatological ozone profile, only accounts for 1 %, and the third largest source, aerosols, only accounts for 0.6 %. Based on the uncertainty budget (Table 4) in Hendrick et al. (2011), ZS TCO precision is 4.7 %. Theoretically, it could be improved to 3.4 % if the uncertainty due to cloud was removed. Sarkissian et al. (1997) found that low-altitude clouds have a very small effect on ozone AMFs, and there was no systematic deviation of the TCOs measured by SAOZ relative to ozonesondes when total cloud cover was observed. Pfeilsticker et al. (1998) categorized cloud effects on the basis of three processes (geometry effect, multiple reflection effect, and photon diffusion) and quantified their magnitudes using RTM calculations. They reported that these processes may introduce significant errors in ZS TCO. Pfeilsticker et al. (1998) shows that the enhanced ozone absorption due to photon diffusion in the cloud may increase the ZS TCO by as much as 9 %. It is clear that different types of clouds (different cloud optical depth, height, water or ice content, etc.) can have different impacts on ZS-DOAS TCO accuracy.
While ZS-DOAS measurements are affected by clouds, the Multi-Axis DOAS (MAX-DOAS) technique (Hönninger et al., 2004; Platt, 1994; Platt and Stutz, 2008; Sanders et al., 1993) is even more sensitive to clouds. Unlike ZS-DOAS, which measures at a 90∘ elevation viewing angle, MAX-DOAS measures over a range of elevation angles (typically 3–10 different angles, from 0 to 90∘). At low elevation angles, sunlight arriving at the instrument has typically taken a long path through the troposphere and hence has greater sensitivity to tropospheric trace gases (Platt and Stutz, 2008). This enhanced tropospheric sensitivity also creates an urgent need for a cloud and aerosol detection and classification algorithm for MAX-DOAS measurements (Gielen et al., 2014; Wagner et al., 2014, 2016; Wang et al., 2015). In general, these algorithms are based on the colour index (CI, the intensity ratio of two measured wavelengths) and O4 absorption derived from ZS–MAX-DOAS measurements at mid-latitudes (more details are provided in Sect. 3.1). However, at this time, there is no cloud-screening (detection) algorithm developed specifically for ZS-DOAS measurements at high latitudes, where the limited SZA range makes it challenging to apply any of the previously developed algorithms. For example, the algorithm developed by Wagner et al. (2016) needs measurements with SZA < 60∘, whereas these small SZA measurements only account for about 7 % of UT-GBS year-round measurements at Eureka, located at 80∘ N, where the lowest SZA is about 56∘.
The objective of this work is to develop a cloud detection algorithm for high-latitude measurements using data collected by ZS-DOAS instruments deployed at Eureka to improve TCO data quality. This paper is organized as follows. Section 2 describes the measured and modelled TCO data used in this study, with additional information about Eureka weather records. In Sect. 3, by adapting and improving some cloud-screen algorithms from MAX-DOAS instruments, a new algorithm for high-latitude ZS-DOAS measurements is introduced. This algorithm is applied to UT-GBS and SAOZ TCO retrievals to help identify the weather conditions during the measurements and to improve measurement accuracy. In Sect. 4, both the standard and cloud-screened ZS-DOAS TCO data are compared to Brewer direct-sun and modelled TCO data. Random uncertainties are estimated for all ZS-DOAS TCO datasets using a statistical uncertainty estimation model. A discussion of scientific significance and conclusions is given in Sect. 5. In short, by generating long-term ozone time series that are unbiased by meteorological conditions, this work will help the validation of satellite algorithms for cloudy scenes (Fioletov et al., 2011). In the future, this high-quality ground-based TCO dataset will be used for satellite validation in the high Arctic.
2.1 UT-GBS
The UT-GBS is a Triax-180 grating spectrometer, built by HORIBA Jobin-Yvon. The Triax-180 is a crossed Czerny-Turner triple grating imaging spectrometer. Light is directed by a collimating mirror to a grating and is then focused by a focusing mirror onto a charge-coupled device (CCD) detector. This instrument was assembled in 1998 and has been involved in numerous field campaigns, summarized in Zhao (2017). These include the MANTRA 1998 balloon campaigns in Vanscoy, Saskatchewan (Bassford et al., 2001, 2005), and the 2009 CINDI campaign (Roscoe et al., 2010) at Cabauw, the Netherlands. When it is not travelling, the UT-GBS takes measurements in the University of Toronto Atmospheric Observatory or stays at the Polar Environment Atmospheric Research Laboratory (PEARL) at Eureka (Fogal et al., 2013; Zhao et al., 2016a).
Over the last 18 years, several components of the instrument have been changed. The field of view (FOV) of the instrument was changed from 2 to 0.2∘ in 2012 after an upgrade to the input optics (Zhao, 2017). The instrument was upgraded to a ZS–MAX-DOAS system by coupling with a solar-tracker system in 2015 (Franklin, 2015; Zhao, 2017). The details of instrument changes and history are summarized in Zhao (2017). In 2011, a reprocessed TCO dataset (1999–2011) with the NDACC AMF LUT version 1.0 was used for satellite validation (Adams et al., 2012). In the current work, the latest NDACC AMF LUT (version 2.0) is used in the TCO retrieval.
In this work, UT-GBS measurements made at the PEARL Ridge Lab from 2010 to 2017 are used. For this period, the UT-GBS was operated with a 600 groove-per-millimetre grating and recorded spectra between 350 and 560 nm with resolution of 0.4–2 nm (Adams, 2012; Zhao, 2017). The UV–visible spectra were processed using the QDOAS software (Danckaert et al., 2015) using daily reference spectra. Due to the decreased resolution at the edge of CCD, the ozone differential slant column densities (dSCDs) were retrieved in the 450–545 nm window instead of the NDACC-recommended 450–550 nm window. Following the NDACC recommendations (Van Roozendael and Hendrick, 2009), cross sections of ozone (Burrows et al., 1999), NO2 (Vandaele et al., 1998), H2O (Rothman et al., 2005), O4 (Greenblatt et al., 1990), and Ring (Chance and Spurr, 1997) were all fitted, and a third-order polynomial was included in the DOAS analysis. The accuracy of UT-GBS TCO data in the high Arctic (2003–2011) is 6.2 % (Adams, 2012; Adams et al., 2012).
A new cloud-screening TCO retrieval package was developed for UT-GBS ZS-DOAS measurements to convert ozone dSCDs to vertical column densities (VCDs). Two versions of UT-GBS data are discussed in this work: (1) NDACC standard ZS-DOAS TCO data (referred to as UT-GBS data), and (2) cloud-screened ZS-DOAS TCO data (UT-GBSCS data). Details of the data processing are provided in Sect. 3.
2.2 SAOZ
The first SAOZ instrument was constructed in the late 1980s and designed as a ZS-DOAS instrument (Pommereau and Goutail, 1988). SAOZ records spectra between 270 and 620 nm with a resolution of 1 nm. Two SAOZ instruments have performed measurements at Eureka since 2005. SAOZ no. 15 was deployed at the PEARL Ridge Lab from 2005 to 2009 for springtime measurements, and SAOZ no. 7 has been deployed since 2010 for year-round sunlit measurements. SAOZ and UT-GBS TCO data have been compared during several mid-latitude and Arctic campaigns (Adams et al., 2012; Fraser et al., 2007, 2008, 2009; Roscoe et al., 2010).
In this work, the UT-GBS cloud-screening TCO retrieval algorithm was used to retrieve SAOZ TCO. Two versions of SAOZ data were generated: (1) NDACC standard ZS-DOAS TCO data (referred to as SAOZ) and (2) cloud-screened data (SAOZCS). The SAOZ and SAOZCS data all used the same ozone dSCDs provided by LATMOS (Laboratoire Atmosphères, Milieux, Observations Spatiales) in the NDACC-recommended 450–550 nm window.
The accuracy of SAOZ TCO was estimated to be 0 %–9 % (Roscoe et al., 1994, 2001; Sarkissian et al., 1997) before the standardized NDACC ozone retrieval protocol was implemented. The accuracy of NDACC/SAOZ TCO data at mid-latitudes is reported to be 5.9 % (Hendrick et al., 2011). Details of the SAOZ data processing can be found in Sect. 3.
2.3 Brewer
The Brewer instruments use a holographic grating in combination with a slit mask to select six channels in the UV (303.2, 306.3, 310.1, 313.5, 316.8, and 320 nm) to be detected by a photomultiplier (Kerr, 2002). The first and second wavelengths are used for internal calibration and measuring SO2, respectively. The four longer wavelengths are used for the ozone retrieval. The TCO is calculated by analyzing the relative intensities at these different wavelengths using the Bass and Paur (1985) ozone cross section.
Four Brewer instruments (nos. 21, 69, 111, and 192) have been deployed at Eureka since 1992 by Environment and Climate Change Canada (ECCC). Brewer no. 69, an MKV monochromator, took measurements from 1992 to 2017 (the longest Brewer TCO record at Eureka). During the time of this study, Brewer no. 69 was located on the roof of the Eureka Weather Station main building, which is 15 km away from the PEARL Ridge Lab. In this work, Brewer no. 69 direct-sun spectra were analyzed using the standard Brewer algorithm (Kerr et al., 1981) with small changes to the analysis parameters due to the high latitude of the measurements (Adams et al., 2012). This Brewer TCO dataset is referred to as Brewer. The random uncertainty of Brewer data is typically less than 1 % (Fioletov et al., 2005) and for high-quality data (e.g., SZA < 71∘) it is less than 0.6 % (Zhao et al., 2016b).
2.4 MERRA-2
The second Modern-Era Retrospective analysis for Research and Applications (MERRA-2) is an atmospheric reanalysis from NASA's Global Modeling and Assimilation Office (GMAO) that provides high-resolution globally gridded meteorological fields using the Goddard Earth Observing System-Version 5 data assimilation system (Bosilovich et al., 2015; Fujiwara et al., 2017; Gelaro et al., 2017). MERRA-2 has a horizontal resolution of 0.625∘ × 0.5∘ (longitude × latitude). In this work, vertical profiles of MERRA-2 ozone (Wargan et al., 2017), temperature, pressure, and scaled potential vorticity (sPV) over Eureka were computed using the Jet and Tropopause Products for Analysis and Characterization (JETPAC) package described by Manney et al. (2011, 2017). The sPV is potential vorticity scaled in “vorticity units” to give a similar range of values at each level (Dunkerton and Delisi, 1986; Manney et al., 1994), which can be used to identify the location of the polar vortex (e.g., Adams et al., 2013; Manney et al., 2007; Zhao et al., 2017). The profile data are on 72 model levels with a 3 h temporal resolution and approximately 1 km vertical spacing near the tropopause.
MERRA-2 TCO assimilates ozone profile and total column data from the Microwave Limb Sounder (MLS) and the Ozone Monitoring Instrument (OMI), respectively, starting in late 2004 (Wargan et al., 2017). The MERRA-2 TCO at Eureka has been used in a previous study by Zhao et al. (2017) to supplement Brewer TCO. In that study, the MERRA-2 TCO (2005–2015) for Eureka has a strong correlation (R=0.99) and a small positive bias (1.6 %) compared to Brewer TCO. For the current work, the use of MERRA-2 TCO provides important information because (1) MERRA-2 has a 3 h temporal resolution and therefore MERRA-2 TCO can match ZS TCO (observations made when the SZA is in range 86–91∘) more closely in time than DB TCO (Brewer observes TCO when SZA < 82∘), and (2) MERRA-2 has continuous TCO data, which is not limited by sunlight or weather (cloud) conditions (whereas, Brewer data start in late March and are limited to cloud-free conditions). Thus, MERRA-2 TCO can be used to assess the cloud impact on ZS TCO and to estimate the resulting statistical uncertainty (which requires a large sample size; more details are provided in Sect. 4.2). In this study, MERRA-2 TCO data from 2010 to 2017 have been used.
The MERRA-2 data were also used to identify the location of the polar vortex, as it can have a non-negligible impact on the TCO measurements. For example, when the polar vortex is present, it is possible that the zenith-sky observations sampled ozone-depleted air within the vortex, while the direct-sun observations measured ozone-rich air outside the vortex (e.g., Adams et al., 2012) or vice versa. Following Adams (2012), the MERRA-2 sPV profile was interpolated to the 490 K potential temperature level (near the altitude of the lower stratospheric ozone maximum for Eureka, about 17–21 km) and is referred to here as sPV490 K. Following Manney et al. (2007), the inner and outer vortex edges are identified at sPV490 K values of s−1 and s−1, respectively. For the 8-year period of this study (2010–2017), about 10 % of ZS TCO measurements were made when the polar vortex was above Eureka. However, only 1 % of the coincident ZS and DB TCO measurements were made when the vortex was above Eureka. Further details about the impact of the polar vortex are presented in Sect. 4.1.
2.5 Eureka Weather Station meteorological record
The Eureka Weather Station, operated by ECCC, has long-term records collected since 1947. In this work, Eureka hourly weather reports for 2010–2017 have been used to classify measured and modelled TCO data on the basis of weather conditions (http://climate.weather.gc.ca/, last access: 16 April 2019). Details of the observing, recording, and reporting of weather conditions can be found in MANOBS (Meteorological Service of Canada, 2015). For example, when no weather or obstructions to visibility occur, weather conditions are reported as clear (0∕10), mainly clear (1∕10 to 4∕10), mostly cloudy (5∕10 to 9∕10), and cloudy (10∕10), based on the amount (in tenths) of cloud covering the dome of the sky.
2.6 Radiative transfer simulations
The radiative transfer model SCIATRAN (Rozanov et al., 2005; http://www.iup.uni-bremen.de/sciatran/, last access: 16 April 2019) has been used to simulate the intensity of the scattered solar radiation observed on the ground. The model is designed to be used in any standard observation geometry (e.g., limb, nadir, zenith, or off-axis) by satellite, ground-based, or airborne instruments in ultraviolet, visible, and near-infrared spectral regions.
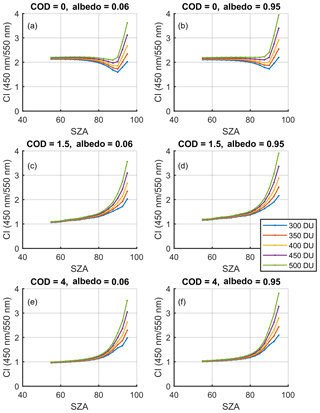
In this work, simulations of radiance have been performed for ground-based zenith-sky viewing observations in the visible band with varying aerosol and cloud optical depths. In the simulations, SCIATRAN standard trace gas volume mixing ratio (O3, NO2, SO2 and etc.), pressure, and temperature profile scenarios are used, which are obtained from a 2-D chemical–dynamical model developed at the Max Planck Institute for Chemistry (MPIC, Brühl and Crutzen, 1993). Aerosol scattering is simulated using the Henyey–Greenstein phase function with aerosol scenarios taken from LOW-resolution TRANsmission (LOWTRAN) 7. Rayleigh scattering and ozone absorption are included. Different surface albedos (0.95 for winter conditions and 0.06 for summer conditions) are also assumed for different seasons.
The cloud-screening algorithm has three steps and uses the calibrated CI, temporal smoothness of the CI, and temporal smoothness of O4 dSCDs as proxies in cloud screening. In the first step, the measured CI is calibrated using a statistical method and a threshold for clear-sky conditions is determined based on RTM simulations (described in below). Next, the temporal smoothness of CI and O4 dSCDs measured each day are labelled by a high-frequency filter (local regression method). Third, ozone dSCDs that passed the first two steps (identified as not cloud contaminated) are used in the so-called cloud-screen Langley plot method and converted to VCDs.
3.1 Colour index calibration
The CI is the ratio of the intensity of sunlight at two different wavelengths. For radiometrically calibrated instruments (such as Brewer instruments and sun photometers), their measured intensity can be used as a good indication of sky condition (Fioletov et al., 2002, 2011). However, DOAS instruments are normally uncalibrated (Platt and Stutz, 2008) and their measured spectral intensity cannot be directly used to infer sky conditions (Gielen et al., 2014; Wagner et al., 2014, 2016; Wang et al., 2015). Wagner et al. (2016) proposed a statistical method to perform absolute calibration of the CI and O4 measured by MAX-DOAS instruments. In the current work, following Wagner et al. (2016), an absolute calibration is performed on ZS-DOAS CI, but the method is modified for use under high Arctic conditions.
The CI we use here is defined as the intensity ratio of two measured wavelengths (shorter to the longer wavelength). For example, UT-GBS spectra extend from about 350 to 560 nm and intensities of 450 and 550 nm were selected to calculate the CI as follows:
Other pairs of intensities proposed in other studies, such as 360 and 385, 360 and 550, 405 and 550, and 425 and 490 (Gielen et al., 2014; Hendrick et al., 2011; Sarkissian et al., 1991; Wagner et al., 1998, 2014, 2016) were all tested for UT-GBS. The 450 and 550 pair was found to be the most reliable one for the ZS-DOAS instruments used in this work. The 450 and 550 intensity pair was chosen to obtain the largest spectral contrast (in the NDACC-recommended ozone retrieval window) and also to avoid the influence of strong atmospheric absorption features, such as those of ozone.
As pointed out in previous studies (Gielen et al., 2014; Wagner et al., 2014, 2016), the zenith-sky CI measured in cloudy conditions is smaller than that in clear-sky conditions. This is because the cloud enhances the scattering at the longer wavelength, due to enhanced Mie scattering. Figure 1 shows the measured CI from the UT-GBS in 2011. The plot is colour-coded by the density of the scattering points, and the coloured lines are examples of the CI simulated by the radiative transfer model under different sky conditions. Two distinct branches of the CI are revealed: the upper branch (measured CI value about 2) indicates clear-sky conditions, while the lower branch (measured CI value about 1.2) indicates cloudy-sky conditions. The CI can efficiently distinguish cloudy and clear conditions only when the SZA is smaller than about 85∘; the two CI branches merge at SZAs close to 90∘.
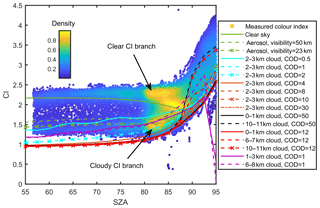
Figure 1Colour index as a function of solar zenith angle. The measurements are from the UT-GBS in 2011, colour-coded by the normalized density of the points. Colour lines are examples of radiative transfer model CI simulations, using a surface albedo of 0.06 and the MPIC climatology ozone profile (total column ozone = 425 DU), and twelve sub-layers within each cloud layer. Cloud height and cloud optical density (COD) are indicated in the legend.
From Fig. 1, it appears that the determination of a threshold to separate cloudy CI and clear-sky CI is straightforward. However, this type of CI density plot varies from instrument to instrument and even from year to year (e.g., if the instrument optics change). Thus, the threshold is not a constant. To determine the threshold, the simple solution would be to compare the measured CI with RTM simulations. However, Fig. 1 also shows a clear offset between the measured and simulated CI curves. For example, the lowest measured CI at SZA = 60∘ is about 1.3, while the RTM shows the lowest value could be about 1. Thus, the calibration of CI is necessary to correct this offset.
Following Wagner et al. (2016), the calibrated CI (CIcal) is given by the multiplication of measured CI (CImeas) by a constant factor β:
To adapt the method of Wagner et al. (2016) (which is based on SZA < 55∘) to high-latitude conditions, CI data with SZA < 85∘ are used in this work.
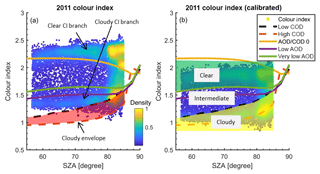
Figure 2UT-GBS 2011 colour index before and after calibration, colour-coded by the normalized density of the points. Colour lines are SCIATRAN radiative transfer model CI results, with cloud optical depth (COD) and aerosol optical depth (AOD) conditions indicated in the legend. Panel (a) shows the measured CI and panel (b) shows the calibrated CI. Note that any measurements with solar zenith angle (SZA) > 85∘ have been removed in this calibration process and are not shown here.
The process used to calibrate the data is illustrated in the example in Fig. 2. First, we define a so-called cloudy envelope (see the red shaded area in Fig. 2a) based on RTM simulations. The top of the cloudy envelope is defined as simulated CI with cloud optical depth (COD) = 1.5, whereas the bottom of the envelope is defined by the lowest simulated CI from all RTM simulations (more information about the RTM simulations is provided in Appendix A). Next, we assume the best estimated β should make most of CIs of the cloudy branch fall into this cloudy envelope (as shown in Fig. 2a as before calibration and Fig. 2b as after calibration) using the method described in the paragraph below. Following Gielen et al. (2014), we also categorize the calibrated CI values into three regimes as shown in Fig. 2b: (1) cloudy, when CIcal(SZA) < CICOD=1.5(SZA), (2) clear, when CIcal(SZA) > CIvisibility=50 km(SZA), and (3) intermediate, when , which represents sky conditions with slightly decreased visibility, typically due to thin clouds or moderate aerosol.
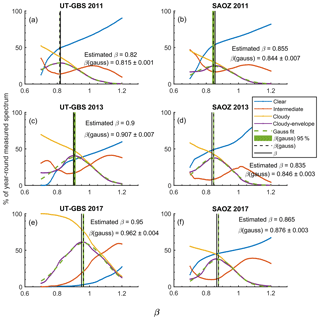
Figure 3Examples of colour index calibration factor (β) determination. The y axis is the percentage of year-round measured spectra, the x axis is the β value used in the calibration. Solid lines represent measurements under different weather categories (blue for clear, red for intermediate, yellow for cloudy, and purple for cloudy envelope). Estimated values for β and the Gaussian fit, β (gauss), are shown by the vertical solid black line and dashed black lines, respectively. The vertical green shaded area is the 95 % confidence bound on β (gauss). The instrument name and measurement year are indicated on each panel. Note that any measurements with solar zenith angle (SZA) > 85∘ have been removed in this calibration process.
Figure 3 shows examples of the estimation of β values for both UT-GBS and SAOZ in various years. For example, in Fig. 3a, the percentage of measurements that fall into the cloudy branch envelope is shown by the purple line for various β (partially hidden by the dashed green line), and the corresponding maximum is for β=0.82. For quality control purposes, a Gaussian fit (dashed green line) is applied to the β estimation curve (solid purple line), which gives β (gauss) (vertical dashed black line) with 95 % confidence bounds (green shading). For years when there are enough cloudy measurements, the β (gauss) value is close to the estimated β value, indicating the good reliability of the calibration result for that year. The estimated β values for SAOZ were more stable than those for UT-GBS. This is because this SAOZ instrument was almost untouched after it was first deployed at Eureka. However, the UT-GBS, as a travelling instrument, has been disassembled and reassembled several times over the 8 years covered in this work. The shifting of the calibration factor in 2013 is due to the fact that a 10 m spot to slit fibre bundle replaced the old 1 m single fibre. The shift in 2017 is due to a 200-grit UV diffuser that was used to attenuate the light signal (to enable MAX-DOAS measurements). Details about all instrument upgrades are provided in Zhao (2017).
In Fig. 3, the blue, red, and yellow lines indicate the percentage of measurements categorized into those three sky-condition regimes (clear, intermediate, and cloudy). For UT-GBS 2011 measurements (Fig. 3a), about 49 % of measured spectra are labelled as clear, 14 % as intermediate, and 37 % as cloudy. In short, after this CI calibration, a CI sky condition label (clear, intermediate, or cloudy) is generated for each spectrum. Spectra with CI sky condition labelled as cloudy can be filtered out.
3.2 Smoothness of CI and O4 dSCDs
As shown in previous publications, the measured CI and O4 dSCDs vary smoothly during the day if there are no rapidly changing clouds (Gielen et al., 2014; Wagner et al., 2014, 2016; Wang et al., 2015). Thus, the temporal smoothness of CI and O4 dSCDs can be used as complementary sky condition labels. Details of how the smoothness of CI and O4 dSCDs were quantified are presented in Appendix B.
3.3 Langley plot method
Following Hendrick et al. (2011), the ozone dSCDs are converted to ozone VCDs (TCO) using the following equation:
where the VCD, dSCD, and AMF are all functions of SZA. The reference column density (RCD) is the residual ozone amount in the reference spectrum that is used in the DOAS analysis. The dSCD is directly obtained by DOAS analysis (using the QDOAS software). The AMF is extracted from the NDACC ozone AMF LUT, based on the latitude and elevation of the PEARL Ridge Lab, day of the year, sunrise or sunset conditions, wavelength, SZA, surface albedo, and ozone column (daily TCOs interpolated from daily or weekly Eureka ozonesonde data). Following the NDACC recommendation (Van Roozendael et al., 2009), the Eureka ozonesonde profiles are integrated to generate TCO values that are used to create the “Day_SZA_O3_col.dat” file, which is used by the NDACC LUT to interpolate daily AMFs for Eureka. The inclusion of ozonesonde TCO data in the AMF calculations improves the results, especially under vortex conditions (Bassford et al., 2001). The RCD value is retrieved using the so-called Langley plot method (Hendrick et al., 2011).
In general, by rearranging Eq. (3), a linear fit of dSCDs vs. AMFs is made for each twilight period, from which the RCD is given by the intercept value (AMF = 0). In this work, ozone dSCDs in the NDACC-recommended SZA range (86 to 91∘) were selected for each twilight, when those dSCDs were available. Otherwise, to adapt to the high-latitude conditions, the nearest available 5∘ SZA range was used (Adams, 2012). For quality control purposes, any fit with less than eight measurements or with a coefficient of determination (R2) less than 0.9 was discarded.
For the UT-GBS, a daily average RCD was calculated from the morning and evening twilight RCDs because a daily reference spectrum (recorded at high sun around local noon) was used in the DOAS analysis. Applying this daily RCD in Eq. (3), a group of VCDs (at different SZA) can be retrieved for that day. Next, sunrise and sunset VCDs were produced from the weighted mean of the VCD(SZA) (weighted by the DOAS fitting error divided by the AMF; Adams, 2012). These sunrise and sunset VCDs are the final product of ZS-DOAS TCO data, referred to as UT-GBS data.
The difference between SAOZ and UT-GBS TCO data processing is that SAOZ uses a fixed reference spectrum in its DOAS analysis. For SAOZ 2010–2017 observations, only three fixed reference spectra were used: from day 94 of the year 2010, day 126 of the year 2011, and day 101 of the year 2016. Thus, for SAOZ, three fixed RCDs were used for 2010 (5.0×1019 molec. cm−2), 2011 (1.6×1019 molec. cm−2), and 2012–2017 (4.4×1019 molec. cm−2) measurements. Other settings in the SAOZ TCO retrieval (such as SZA range, quality control) are the same as for the UT-GBS data.
3.4 Cloud-screened Langley plot method
The cloud-screened Langley plot method is widely used for ground-based AOD measurements using sun photometers (Dayou et al., 2014). In general, this method is based on an objective cloud-screening algorithm, which is used to select cloudless data from a continuous time series that is needed for the regression. With the information from the CI value label (Sect. 3.1, assigned for spectra with SZA < 85∘) and CI and O4 smoothness labels (Sect. 3.2, assigned for spectra with SZA < 91∘), we assigned a sky condition flag to each spectrum. If any of the three labels indicate cloudy conditions, the corresponding spectrum is flagged as cloudy and it is excluded from the cloud-screened Langley plot. When cloud-affected spectra have been removed, the same criteria are applied to the cloud-screened Langley plot as were applied for the conventional Langley plot (e.g., requiring nine data points and R2 > 0.9). The resulting cloud-screened UT-GBS (SAOZ) TCO data are referred to as UT-GBSCS (SAOZCS). Table 1 summarizes the measured and modelled ozone data products.
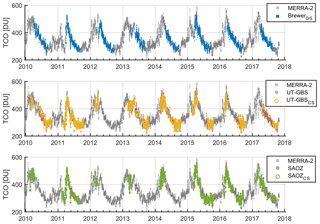
TCO time series (2010–2017) from all instruments and MERRA-2 are shown in Fig. 4. In general, the seasonal cycles of the TCO from all ground-based instruments and the model track well with each other. The Brewer instrument at Eureka typically makes measurements from April to August, while UT-GBS and SAOZ can provide measurements from March to September. The Brewer TCO has a 3–5 min temporal resolution; to pair with UT-GBS and SAOZ data, the Brewer TCO is resampled semi-daily by averaging data collected for each half of the day. MERRA-2 TCO has a 3 h temporal resolution, thus MERRA-2 TCO from the provided time nearest to that of UT-GBS and SAOZ measurements is used. The hourly weather records are resampled semi-daily by using the “median weather type” for each half of the day. For example, a weather condition (semi-daily) is cloudy if most hourly weather records in that half day are cloudy. From 2010 to 2017, UT-GBS and Brewer had 916 coincident measurements, of which 172 coincident measurements were made in clear-sky conditions and 101 coincident measurements were made in cloudy conditions. Other major weather conditions for UT-GBS and Brewer coincident measurements include mainly clear (226), mostly cloudy (303), ice crystals (47), rain (11), and snow (38). Measurements made in other minor weather conditions such as blowing snow, fog, and rain showers only account for 2 %–3 % and are neglected.
4.1 Weather impacts on TCO accuracy
Following Adams et al. (2012), the agreement between sets of coincident measurements (M1 and M2) was evaluated using the mean relative difference, defined as follows:
where N is the number of measurements. Without categorizing TCO measurements by weather conditions, the UT-GBS dataset has a 0.05±0.25 % mean relative difference from the Brewer dataset, where the uncertainty is the standard error of the mean. Similarly, SAOZ has % mean relative difference from Brewer. These results are slightly better than those of Adams et al. (2012), who reported the mean relative difference between the UT-GBS (SAOZ) and Brewer TCO measurements at Eureka as −1.4 % (0.4 %) for 2005–2011. These results (at Eureka) are better than the high-latitude agreement reported by Hendrick et al. (2011), who found that SAOZ TCO (1990–2008) was systematically lower than Brewer TCO at Sodankylä (67∘ N, 27∘ E) by 3 %–4 %, with the largest discrepancies in the spring and fall. Hendrick et al. (2011) suggested that this bias was due to the temperature dependence (Kerr, 2002; Kerr et al., 1988; Scarnato et al., 2009; Van Roozendael et al., 1998; Zhao et al., 2016b) and uncertainty in the ozone cross section (Bass and Paur, 1985) used in Brewer measurements.
The agreement between the UT-GBS, SAOZ, and Brewer in Adams et al. (2012) (and this study) is notable given the challenges of taking ZS-DOAS measurements at 80∘ N, particularly in the summer when measurements within the NDACC-recommended SZA range are not available. With help from the Eureka weather record, we can further explore the datasets to quantify the impact of weather and improve our understanding of these comparison results.
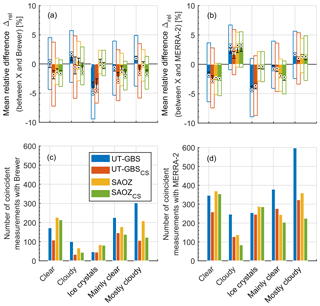
Figure 5The impact of sky conditions on total column ozone measurements at Eureka: (a) mean relative difference between UT-GBS (SAOZ) TCO and Brewer TCO, (b) mean relative difference between UT-GBS (SAOZ) TCO and MERRA-2 TCO. (c) The number of coincident measurements corresponding to (a) and (d) the number of coincident measurements corresponding to (b). Different colours represent different datasets, as indicated in the legend. In (a) and (b), the hollow box represents the 75th to 25th percentile of the dataset, the target symbol (black dot with coloured circle around) represents the median value, the solid bar represents the mean value, and the error bars represent the standard error on the mean. In all panels, the x axis represents weather types reported at the Eureka Weather Station.
In order to quantify the effects of weather on the ZS-DOAS data, coincident measurements were characterized according to the five major weather conditions from the Eureka weather record observations. Box plots for percent differences between the datasets were produced, as shown in Fig. 5. Overall, the box plots demonstrate that biases between the ZS-DOAS and reference datasets are dependent on weather conditions. This is discussed in more detail below.
4.1.1 Weather impacts without the cloud-screening algorithm applied
The effect of weather on the UT-GBS and SAOZ datasets is clear in the comparisons with the Brewer datasets (Fig. 5a). The weather classification used here and in Fig. 5 is based on hourly observations of sky conditions made by a meteorological technician at Eureka. For clear conditions, UT-GBS (SAOZ) has % ( %) mean relative difference from the Brewer, while for cloudy conditions this difference increases to 1.25±0.67 % (0.38±0.62 %). Therefore, there is a 1.3 % (1.5 %) difference (statistically significant) between UT-GBS (SAOZ) clear-sky measurements and cloudy-sky measurements; this difference is referred to as the clear–cloudy difference in the rest of this work.
This demonstrates that the good general agreement (low bias) between UT-GBS (SAOZ) TCO and Brewer TCO reported in Sect. 4.1 arises from a combination of a negative bias in clear-sky conditions and a positive bias in cloudy conditions. Thus, if only clear-sky measurements are selected, ZS-DOAS measurements have a negative bias compared to Brewer measurements, which agrees with previous findings (Hendrick et al., 2011; Van Roozendael et al., 1998).
Measurements during other precipitation conditions (snow and rain) are relatively sparse (less than 50 coincident measurements, not shown here) since Brewer direct-sun measurements need a clear view toward the sun. The UT-GBS TCO has a large negative bias ( %) in ice crystal conditions, while SAOZ TCO is almost unaffected (0.24±0.56 %). One possible explanation for this discrepancy is that the UT-GBS has a much narrower field of view (0.2–2∘) than SAOZ instruments (4∘). However, with the limited coincident measurements, it is difficult to fully understand this feature.
To further study the impact of weather on ZS-DOAS TCO, we use a reference TCO dataset (other than Brewer), whose data quality is not affected by the weather. As described in Sect. 2.4, MERRA-2 TCO data have been used in previous studies, and agrees well with Brewer data at Eureka. Comparison results are shown in Fig. 5b and d. There are approximately twice as many coincident measurements for MERRA-2 as for Brewer.
Figure 5b shows that in clear conditions, UT-GBS (SAOZ) has a % ( %) mean relative difference compared to the MERRA-2 dataset, while in cloudy conditions this difference shifted to a positive value, 2.34±0.44 % (2.46±0.45 %). Therefore, the clear–cloudy difference for UT-GBS (SAOZ) TCO is 4.1 % (4.9 %) and it is statistically significant. This difference is larger than the clear–cloudy difference relative to the Brewer TCO. This may be because there are more coincident data points with MERRA-2 in early spring (late February to March); the ZS-DOAS TCO measurements in early spring are not as accurate as in late spring and early summer (late March to early May), mainly due to the lack of high sun reference spectra. Furthermore, Brewer has no measurements in heavy cloud conditions and so Brewer TCO may be clear-sky biased.
Using MERRA-2 sPV490k, for the 2010–2017 period, 7.8 % (11.0 %) of UT-GBS (SAOZ) TCO measurements were made when the polar vortex was above Eureka. Measurements inside the polar vortex (not shown here) were filtered out to assess whether the location of the polar vortex relative to the instrument line-of-sight and model sampling is the cause of this large clear–cloudy difference. However, the clear–cloudy differences for both UT-GBS and SAOZ are almost unchanged (5.4 % for UT-GBS, 5.0 % for SAOZ). During clear conditions, UT-GBS (SAOZ) has % ( %) mean relative difference compared to the MERRA-2 dataset, while during cloudy conditions, the mean relative difference is 2.44±0.44 % (2.54±0.48 %).
4.1.2 Weather impacts with cloud-screening algorithm applied
Comparisons between the cloud-screened ZS-DOAS measurements and the reference datasets are also shown in Fig. 5. This algorithm successfully filtered more of the measurements made when clouds had been observed at the Eureka Weather Station. For example, Fig. 5c shows that the number of coincident measurements between SAOZ and Brewer decreased from 227 to 214 for clear conditions. For mostly cloudy conditions, this number decreased from 209 to 122. Note that this algorithm is not designed to simply discard all TCO measurements made on cloudy days but only to remove individual spectra that are cloud contaminated. For example, even for a cloudy day, if clouds cleared up during part of the twilight period, this algorithm may produce ZS-DOAS TCO data (if other criteria are also met, as described in Sect. 3.3 and 3.4).
Figure 5a shows that the UT-GBSCS (SAOZCS) has a % ( %) mean relative difference with respect to Brewer while during cloudy conditions the mean relative difference is % ( %). Therefore, the UT-GBSCS (SAOZCS) data have a negative bias compared to Brewer, even during cloudy conditions, which is expected for high-quality cloud-free measurements (see Sect. 4.1.1). The clear–cloudy difference for UT-GBSCS (SAOZCS) TCO is 1.59 % (0.84 %), which is not statistically significant, suggesting that a larger sample size is needed to infer this difference. Similarly, if MERRA-2 TCO data are used as the reference (see Fig. 5b), during clear conditions, UT-GBSCS (SAOZCS) has % ( %) mean relative difference, while during cloudy conditions the mean relative difference is 1.61±0.59 % (2.78±0.58 %). Since cloudy days mostly appear in the summertime, sensitivity tests were performed with the dataset divided into summer and spring/autumn periods to assess whether there was any seasonal bias. In general, we found that the clear–cloudy difference is still statistically significant in summer, no matter which reference is selected (Brewer or MERRA-2). For spring/autumn, the clear–cloudy difference is statistically significant only when MERRA-2 is used as the reference but not if Brewer is used as the reference due to the limited number of Brewer measurements given the large SZAs in spring and autumn.
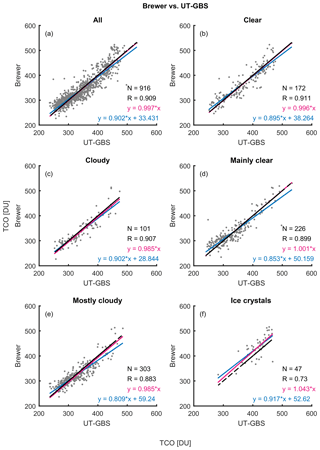
Figure 6Scatter plots of Brewer total column ozone vs. UT-GBS TCO. Panel (a) shows the scatter plot of all coincident measurements of Brewer and UT-GBS. Panels (b) to (f) show scatter plots with weather conditions indicated in their titles. On each scatter plot, the red line is the linear fit with intercept set to 0, the blue line is a simple linear fit, and the black line is the one-to-one line.
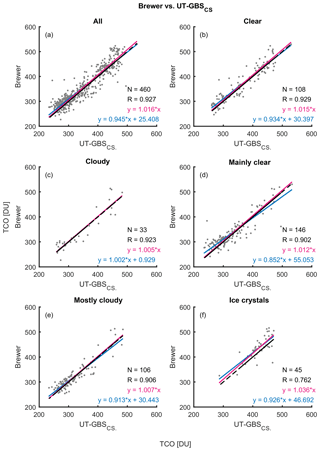
Figure 7Scatter plots of Brewer total column ozone vs. UT-GBS cloud-screened TCO (UT-GBSCS). Panel (a) shows the scatter plot of all coincident measurements of Brewer and UT-GBSCS. Panel (b) to (f) show scatter plots with weather conditions indicated in their titles. On each scatter plot, the red line is the linear fit with intercept set to 0, the blue line is a simple linear fit, and the black line is the one-to-one line.
The effectiveness of the cloud-screening algorithm is further demonstrated by scatter plots for Brewer vs. UT-GBS and UT-GBSCS shown in Figs. 6 and 7. When data for all weather conditions are considered together (Figs. 6a and 7a) after applying the cloud-screening algorithm, the slope of the linear fit improved from 0.90 to 0.95, the intercept decreased from 33.43 to 25.41 DU, and R increased from 0.91 to 0.93. The effectiveness of the algorithm is most apparent for cloudy conditions (Figs. 6c and 7c), for which the slope of the linear fit improved from 0.90 to 1.00, the intercept decreased from 28.84 to 0.93 DU, and R increased from 0.91 to 0.92, although the number of coincident measurements decreased from 101 to 33. Similar improvements can be found for other weather types, especially for most cloudy condition (Figs. 6e and 7e).
Correlations were also examined for other pairs of measurements such as Brewer vs. SAOZ and SAOZCS, MERRA-2 vs. UT-GBS and UT-GBSCS, etc. These results are summarized in Fig. 8, which shows the correlation coefficients for all pairs of TCO datasets. Most pairs of data have R value greater than 0.9, and the R values are larger for the cloud-screened datasets (crosses) than for the unscreened (circles).
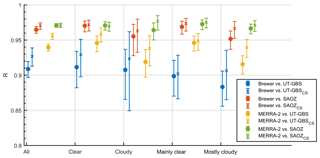
Figure 8Correlation coefficients (R) of pairs of measured and modelled total column ozone datasets. The comparisons with UT-GBS or SAOZ TCO datasets are shown by circles, and those with cloud-screened TCO datasets (UT-GBSCS or SAOZCS) are shown by crosses. The error bars are the 95 % confidence interval for each coefficient.
In addition to the accuracy studied in Sect. 4.1, another important aspect of the TCO datasets is their precision. By comparing the same quantity retrieved from different remote sensing instruments, the random uncertainties can be characterized from the measurements themselves (Fioletov et al., 2006; Grubbs, 1948; Toohey and Strong, 2007; Zhao et al., 2016b). Following the method of Fioletov et al. (2006), briefly explained in Appendix C, a statistical uncertainty estimation model is used to estimate random uncertainties for ZS-DOAS instruments (UT-GBS and SAOZ).
Figure 9a shows the resulting estimated random uncertainties. The first blue column in Fig. 9a represents the estimated random uncertainty for UT-GBS TCO when using Brewer TCO as reference (see description in Appendix C). The number of coincident measurements is shown in Fig. 9b. In general, UT-GBS (SAOZ) has a random uncertainty of 4.04±0.21 % (3.19±0.17 %), when using the Brewer as the reference. If MERRA-2 is used as a reference, the random uncertainty for UT-GBS and SAOZ is 3.86±0.11 % and 2.80±0.09 %, respectively. Thus, SAOZ TCO has about 1 % lower random uncertainty than UT-GBS TCO. The estimated random uncertainties for UT-GBS and SAOZ are both lower than 4.7 %, the precision value reported by Hendrick et al. (2011).
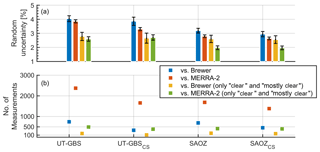
Figure 9Statistical uncertainty estimation results. Panel (a) shows the estimated random uncertainties (%) and panel (b) shows the number of coincident measurements used. The x axis indicates names of TCO datasets that have been assessed. Colours represents different reference datasets (shown in legend).
Theoretically, the cloud-screened TCO datasets (UT-GBSCS and SAOZCS) should have lower random uncertainties than the conventional TCO datasets (UT-GBS and SAOZ). The UT-GBSCS (SAOZCS) has random uncertainty 3.86±0.29 % (2.94±0.19 %), when using Brewer as the reference. With MERRA-2 as the reference, UT-GBSCS (SAOZCS) has a random uncertainty of 3.30±0.11 % (2.64±0.10 %). Although UT-GBSCS and SAOZCS have lower random uncertainties compared to UT-GBS and SAOZ, the only significant improvement on random uncertainty is for UT-GBS, which decreased from 3.86±0.11 % to 3.30±0.11 % (red bar on UT-GBS and UT-GBSCS columns), when using MERRA-2 as reference. This improvement is most likely significant because the sample size is sufficient (2370 coincident measurements; see Fig. 9b).
To further illustrate the cloud effect, the Eureka weather record is used as an extra filter to strengthen the cloud filtering. Measurements are preserved and used in uncertainty estimation only if they were made in clear or mostly clear recorded weather conditions. The yellow and green symbols represent the precision calculated with this extra filter applied. Filtering out all measurements made in non-ideal weather, the UT-GBS random uncertainty improved from 4.04±0.21 % to 2.78±0.29 % when using Brewer as a reference (see the blue and yellow bars on the UT-GBS column). For SAOZ, random uncertainty improved from 3.19±0.17 % to 2.60±0.26 % (blue and yellow bars on the SAOZ column). These improvements are both statistically significant. This result is close to the uncertainty budget table in Hendrick et al. (2011), in which ZS-DOAS TCO total precision can be improved by about 1 % in cloud-free conditions.
Clouds are the largest source of random uncertainty in ZS-DOAS TCO retrievals. This work provides a measurement-based evaluation of the effect of cloud conditions on ZS-DOAS TCO. A cloud-screening algorithm was developed to improve TCO data quality under cloudy conditions, one which could potentially be applied to the NDACC UV–visible network. With ozone measurements, weather observations, and models, this study helps answer the following questions.
-
What is the effect of cloudy-sky conditions on ZS-DOAS TCO data? For the Eureka datasets, there is a statistically significant difference of 1 %–5 % between ZS-DOAS TCO measurements made under cloudy and clear-sky conditions.
-
It has been estimated that clouds contribute up to 3.3 % random uncertainty in the NDACC ZS-DOAS TCO retrieval (Hendrick et al., 2011). Thus, by removing the cloud term from the error budget, ZS-DOAS TCO datasets should have their random uncertainty lowered by about 1.3 %. Can this value be verified by field measurements? After removing cloudy measurements using weather records, the Eureka ZS-DOAS TCO random uncertainties are reduced by 0.6 %–1.3 %. Note that the 3.3 % random uncertainty in Hendrick et al. (2011) is an upper limit of the impact of clouds on ozone AMFs, since it is based on sensitivity tests using parameter values for rather large stratus cloud (Shettle, 1989). Thus, the findings in this work agree with the results in Hendrick et al. (2011).
-
TCO measurements in the high Arctic are challenging (e.g., because of low sun and large SZA in early spring). What is the general quality of ZS-DOAS TCO measured at Eureka? Using a statistical uncertainty estimation model, TCO datasets from two ZS-DOAS instruments located at Eureka have been evaluated. UT-GBS TCO has a random uncertainty of 3.9 %–4.0 %, while SAOZ TCO has a random uncertainty of 2.8 %–3.2 %. Both instruments have random uncertainties that are lower than the 4.7 % reported by Hendrick et al. (2011).
-
Adams et al. (2012) and this work both found that the mean relative difference between the ZS-DOAS and Brewer TCO measurements at Eureka (e.g., 0.4 % for SAOZ 2005–2011, in Adams et al., 2012) is better than the high-latitude agreement reported by Hendrick et al. (2011), who found a negative bias of 3 %–4 % in SAOZ TCO (1990–2008) compared with Brewer TCO at Sodankylä (67∘ N). Given the challenges of taking ZS-DOAS measurements in the high Arctic (Eureka, 80∘ N), why do measurements at Eureka have such good agreement with Brewer data? This good agreement is a combination of a positive bias during cloudy conditions and a negative bias during clear conditions. For measurements under clear conditions only, UT-GBS (SAOZ) has a % ( %) mean relative difference compared with Brewer, while for cloudy conditions only this mean relative difference is positive at 1.25±0.67 % (0.38±0.62 %). However, if Brewer TCO is replaced by MERRA-2 TCO during clear conditions, UT-GBS (SAOZ) has a % ( %) mean relative difference, while during cloudy conditions this mean relative difference is 2.34±0.44 % (2.46±0.45 %). In addition, in the high Arctic, Brewer TCO measurements are only available for relatively short portions of the year (from April to September), and thus the temperature effect (seasonal bias) in the Brewer TCO dataset is smaller compared to that in datasets collected at mid-latitudes and low latitudes (Zhao et al., 2016b). Thus, it is likely the good agreement between ZS-DOAS and Brewer at Eureka is due to a combination of temperature, cloud, and other effects. Answering this type of question about consistency between datasets is important for the NDACC UV–visible network to provide globally harmonized ZS-DOAS TCO datasets.
In addition to answering the scientific questions above, this work also provides the following contributions to ZS-DOAS measurements and data processing. (1) A cloud-screening algorithm for ZS-DOAS ozone measurements at high-latitude sites has been developed. This algorithm can be modified and applied to low- and mid-latitude ZS-DOAS measurements. (2) Cloud-screened long-term (2010–2017) ZS-DOAS TCO datasets in Eureka have been produced, implementing the latest NDACC UV–visible network ozone retrieval protocol. These TCO datasets will be used for validation of space-based ozone measurements by the Optical Spectrograph and InfraRed Imager System (OSIRIS) and the Atmospheric Chemistry Experiment (ACE) in a future paper.
The UT-GBS data are available from the Canadian Network for the Detection of Atmospheric Change (CANDAC, http://www.candac.ca/candacweb/index.php, last access: 16 April 2019) and the Network for the Detection of Atmospheric Composition Change (NDACC, ftp://ftp.cpc.ncep.noaa.gov/ndacc/station/eureka/, last access: 16 April 2019). SAOZ data are available from the Canadian Arctic ACE/OSIRIS Validation Campaign (https://eureka.physics.utoronto.ca/, last access: 16 April 2019). Brewer and ozonesonde data are available from the World Ozone and UV Data Centre (https://woudc.org/, last access: 16 April 2019). Eureka Weather Station records are available from Environment and Natural Resources in Canada (https://www.canada.ca/en/services/environment.html, last access: 16 April 2019). Any additional data may be obtained from Xiaoyi Zhao (xizhao@atmosp.physics.utoronto.ca).
Several factors, in addition to cloud optical depth and cloud height, can introduce systematic changes in the colour index simulated using a radiative transfer model. In this work, the impact of total column ozone and surface albedo were examined. In general, we found that changing the TCO and surface albedo has a systematic but limited impact on the CI calculated using the 450 and 550 nm intensity pair, when the SZA is limited to values less than 85∘. Figure A1 shows the colour index simulated using different values of TCO and surface albedo. Here we refer to the variation in CI with TCO as the “TCO effect”, and the variation in CI with surface albedo as the “albedo effect”. In general, in these simulations, increasing the TCO or surface albedo resulted in a larger CI. This can be explained by enhanced ozone absorption and surface reflection at the longer wavelength (550 nm) relative to 450 nm. However, these changes in CI depend strongly on SZA. In the presence of clouds, a 200 DU TCO increment (from 300 to 500 DU) will only lead to an increase in the CI by less than 0.2 at SZA = 80∘. However, at SZA = 90∘, a 200 DU ozone increment will lead to an increase of about 0.7. These simulation results also explain why in Fig. 1 the two branches of CI values merge at around SZA = 90∘. With clouds present, if surface albedo increased from 0.06 (typical of soil and water) to 0.95 (typical of snow), the CI increased by only 0.04 at SZA = 80∘. However, at SZA = 90∘, the same surface albedo change increases the CI by 0.1–0.2. In general, this shows that the albedo effect is smaller than the TCO effect, and both of them depend strongly on SZA. Thus, the CI label, proposed in Sect. 3.1, is only used to identify cloud conditions when SZA < 85∘.
To determine the smoothness of the calibrated colour index, following Gielen et al. (2014) we define a temporal smoothness label (TSL) for CI as follows:
where t is local time, LOWESS(t,x) is the fitted daily CI curve using the LOcally WEighted Scatterplot Smoothing (LOWESS) fit based on local least-squares fitting applied to a specified x fraction of the data (Cleveland and Devlin, 1988). The local fitting fraction x is selected as 50 %. Only CIs measured with SZA < 92∘ are used in the daily curve fitting. If TSLCI > 0.1, we label the spectrum as cloudy (referred to as CI smoothness label).
Similarly, we define a TSL for O4 absorption as follows:
where t is local time, LOWESS(t,x) is the fitted daily O4 dSCDs using the LOWESS fit, and the local fitting fraction x is selected as 50 %. Only O4 dSCDs measured with SZA < 92∘ are used in the daily curve fitting. If TSL > 0.2, we label the spectrum as cloudy (referred to as the O4 smoothness label).
These thresholds for TSL and TSLCI both follow Gielen et al. (2014) but, instead of using LOWESS fit, they used a double sine function to simulate the low-frequency variation in CI and O4.
Random uncertainties for ZS-DOAS measurements can be determined using a statistical estimation method (Fioletov et al., 2006; Grubbs, 1948; Toohey and Strong, 2007; Zhao et al., 2016b). As an example, we define the two types of measured TCO (denoted as M1 and M2, for Brewer and ZS-DOAS measurements, respectively) as simple linear functions of the true TCO value (X) and instrument random uncertainties (δ1 and δ2) and assume that there is no multiplicative or additive bias between ZS-DOAS and Brewer, giving
If we assume that the instrument random uncertainties are independent of the measured TCO, the variance of M is the sum of the variances of X (around the mean of the dataset) and δ:
If the difference between ZS-DOAS and Brewer does not depend on X (no multiplicative bias), and the random uncertainties of the two instruments are not correlated, then the variance of the difference is equal to the sum of the variance of the random uncertainties:
Since we have the measured TCO and the difference between the ZS-DOAS and Brewer datasets, the variance of the instrument random uncertainties can be solved by
Equation (C1) can be used to estimate the standard deviation of instrument random uncertainties ( and ). The variances and can be estimated from the available measurements (with some uncertainty). The uncertainties in the and estimates depend on the sum of all three variances , , and and can be high even if the estimated variance itself is low (but one or more of the variances , , and are high). Thus, the estimates are only as accurate as the least accurate of these parameters. Following the method in Zhao et al. (2016b), the variance estimates can be improved by increasing the number of data points or by reducing variances of X by removing some of its natural variability. Thus, the M1 and M2 used in the statistical uncertainty estimation are replaced by so-called residual ozone, which is defined as the difference between the semi-daily measured TCO and its weekly mean.
XZ analyzed the data and prepared the manuscript with significant conceptual input from KB and KS and critical feedback from all co-authors. VF, AP, and FG provided support in Brewer and SAOZ data processing and data analysis. LM and GM performed and analyzed the MERRA-2 simulations. CA, XZ, and KB operated the UT-GBS and performed subsequent data analysis.
The authors declare that they have no conflict of interest.
CANDAC/PEARL funding partners are the Arctic Research Infrastructure Fund, Atlantic Innovation Fund/Nova Scotia Research Innovation Trust, Canadian Foundation for Climate and Atmospheric Science, Canada Foundation for Innovation, Canadian Space Agency (CSA), Environment and Climate Change Canada (ECCC), Government of Canada International Polar Year, Natural Sciences and Engineering Research Council (NSERC), Ontario Innovation Trust, Ontario Research Fund, Indian and Northern Affairs Canada, and the Polar Continental Shelf Program. The spring 2010–2017 measurements were also supported by the Canadian Arctic ACE/OSIRIS Validation Campaigns funded by CSA, ECCC, NSERC, and the Northern Scientific Training Program. MERRA-2 work at the Jet Propulsion Laboratory, California Institute of Technology, was done under contract with the National Aeronautics and Space Administration. Xiaoyi Zhao was supported by the NSERC CREATE Training Program in Arctic Atmospheric Science, the Probing Atmosphere in the High Arctic (PAHA) project, and the Visiting Fellowships in Canadian Government Laboratories program. We thank CANDAC/PEARL/PAHA PI James Drummond, ACE Validation Campaign PI Kaley Walker, PEARL Site Manager Pierre Fogal, the CANDAC operators, and the staff at ECCC's Eureka Weather Station for their contributions to data acquisition, and logistical and on-site support. We thank Jonathan Davies and David Tarasick from ECCC for providing ozonesonde data. We thank Thomas Danckaert, Caroline Fayt, Michel Van Roozendael, and others from IASB-BIRA for providing QDOAS software and the NDACC UV–visible working group for providing NDACC UV–visible ozone AMF LUT. We thank Alexei Rozanov and the SCIATRAN radiative transfer model development team at the Institute of Environmental Physics (IUP), University of Bremen, for providing the model and the support.
This paper was edited by Michel Van Roozendael and reviewed by three anonymous referees.
Adams, C.: Measurements of atmospheric ozone, NO2, OClO, and BrO at 80∘ N using UV-visible spectroscopy, Ph.D Thesis, University of Toronto, Canada, 2012.
Adams, C., Strong, K., Batchelor, R. L., Bernath, P. F., Brohede, S., Boone, C., Degenstein, D., Daffer, W. H., Drummond, J. R., Fogal, P. F., Farahani, E., Fayt, C., Fraser, A., Goutail, F., Hendrick, F., Kolonjari, F., Lindenmaier, R., Manney, G., McElroy, C. T., McLinden, C. A., Mendonca, J., Park, J.-H., Pavlovic, B., Pazmino, A., Roth, C., Savastiouk, V., Walker, K. A., Weaver, D., and Zhao, X.: Validation of ACE and OSIRIS ozone and NO2 measurements using ground-based instruments at 80∘ N, Atmos. Meas. Tech., 5, 927–953, https://doi.org/10.5194/amt-5-927-2012, 2012.
Adams, C., Strong, K., Zhao, X., Bourassa, A. E., Daffer, W. H., Degenstein, D., Drummond, J. R., Farahani, E. E., Fraser, A., Lloyd, N. D., Manney, G. L., McLinden, C. A., Rex, M., Roth, C., Strahan, S. E., Walker, K. A., and Wohltmann, I.: The spring 2011 final stratospheric warming above Eureka: anomalous dynamics and chemistry, Atmos. Chem. Phys., 13, 611–624, https://doi.org/10.5194/acp-13-611-2013, 2013.
Bass, A. M. and Paur, R. J.: The ultraviolet cross-sections of ozone: I, The measurements, in: Atmospheric Ozone, 606–610, Springer, Germany, 1985.
Bassford, M. R., McLinden, C. A., and Strong, K.: Zenith-sky observations of stratospheric gases: the sensitivity of air mass factors to geophysical parameters and the influence of tropospheric clouds, J. Quant. Spectrosc. Ra., 68, 657–677, https://doi.org/10.1016/S0022-4073(00)00052-2, 2001.
Bassford, M. R., Strong, K., McLinden, C. A., and McElroy, C. T.: Ground-based measurements of ozone and NO2 during MANTRA 1998 using a Zenith-sky spectrometer, Atmos.-Ocean, 43, 325–338, https://doi.org/10.3137/ao.430404, 2005.
Bosilovich, M. G., Lucchesi, R., and Suarez, M.: MERRA-2: File specification, NASA, Global Modeling and Assimilation Office, Greenbelt, Maryland, 2015.
Brühl, C. and Crutzen, P. J.: MPIC two-dimensional mode, in: The atmospheric effects of stratospheric aircraft, vol. 1292 of NASA Ref. Publ., 103–104, 1993.
Burrows, J. P., Richter, A., Dehn, A., Deters, B., Himmelmann, S., Voigt, S., and Orphal, J.: Atmosperic remote-sensing reference data from GOME-2 temperature-dependent absorption cross sections of O3 in the 231–794 nm range, J. Quant. Spectrosc. Ra., 61, 509–517, https://doi.org/10.1016/s0022-4073(98)00037-5, 1999.
Chance, K. V. and Spurr, R. J. D.: Ring effect studies: Rayleigh scattering, including molecular parameters for rotational Raman scattering, and the Fraunhofer spectrum, Appl. Opt., 36, 5224–5230, https://doi.org/10.1364/AO.36.005224, 1997.
Cleveland, W. S. and Devlin, S. J.: Locally weighted regression: an approach to regression analysis by local fitting, J. Am. Stat. Assoc., 83, 596–610, 1988.
Danckaert, T., Fayt, C., Van Roozendael, M., de Smedt, I., Letocart, V., Merlaud, A., and Pinardi, G.: QDOAS Software user manual version 2.109, Software user manual, Belgian Institute for Space Aeronomy, Brussels, 2015.
Daumont, D., Brion, J., Charbonnier, J., and Malicet, J.: Ozone UV spectroscopy I: Absorption cross-sections at room temperature, J. Atmos. Chem., 15, 145–155, https://doi.org/10.1007/bf00053756, 1992.
Dayou, J., Chang, J. H. W., and Sentian, J.: Ground-Based Aerosol Optical Depth Measurements, in: Ground-Based Aerosol Optical Depth Measurement Using Sunphotometers, 9–30, Springer, Singapore, 2014.
De Backer, H. and De Muer, D.: Intercomparison of total ozone data measured with Dobson and Brewer ozone spectrophotometers at Uccle (Belgium) from January 1984 to March 1991, including zenith sky observations, J. Geophys. Res.-Atmos., 96, 20711–20719, https://doi.org/10.1029/91JD02159, 1991.
Dobson, G. M. B.: Exploring the atmosphere, 2nd edn., Clarendon Press, UK, Oxford, 1968.
Dunkerton, T. J. and Delisi, D. P.: Evolution of Potential Vorticity in the Winter Stratosphere of January–February 1979, J. Geophys. Res., 91, 1199–1208, https://doi.org/10.1029/JD091iD01p01199, 1986.
Erle, F., Pfeilsticker, K., and Platt, U.: On the influence of tropospheric clouds on zenith-scattered-light measurements of stratospheric species, Geophys. Res. Lett., 22, 2725–2728, https://doi.org/10.1029/95GL02789, 1995.
Farman, J. C., Gardiner, B. G., and Shanklin, J. D.: Large losses of total ozone in Antarctica reveal seasonal ClOx∕NOx interaction, Nature, 315, 207–210, https://doi.org/10.1038/315207a0, 1985.
Fioletov, V. E., Kerr, J. B., and Wardle, D. I.: The relationship between total ozone and spectral UV irradiance from Brewer observations and its use for derivation of total ozone from UV measurements, Geophys. Res. Lett., 24, 2997–3000, https://doi.org/10.1029/97GL53153, 1997.
Fioletov, V. E., Kerr, J. B., Hare, E. W., Labow, G. J., and McPeters, R. D.: An assessment of the world ground-based total ozone network performance from the comparison with satellite data, J. Geophys. Res., 104, 1737–1747, https://doi.org/10.1029/1998JD100046, 1999.
Fioletov, V. E., Kerr, J. B., Wardle, D. I., and Wu, E.: Correction of stray light for the Brewer single monochromator, in: Proceedings of the Quadrennial Ozone Symposium, 37, Sapporo, Japan, 2000.
Fioletov, V. E., Kerr, J. B., Wardle, D. I., Krotkov, N. A., and Herman, J. R.: Comparison of Brewer ultraviolet irradiance measurements with total ozone mapping spectrometer satellite retrievals, Opt. Eng., 41, 3051–3062, https://doi.org/10.1117/1.1516818, 2002.
Fioletov, V. E., Kerr, J. B., McElroy, C. T., Wardle, D. I., Savastiouk, V., and Grajnar, T. S.: The Brewer reference triad, Geophys. Res. Lett., 32, L20805, https://doi.org/10.1029/2005GL024244, 2005.
Fioletov, V. E., Tarasick, D. W., and Petropavlovskikh, I.: Estimating ozone variability and instrument uncertainties from SBUV (/2), ozonesonde, Umkehr, and SAGE II measurements: Short-term variations, J. Geophys. Res., 111, D02305, https://doi.org/10.1029/2005jd006340, 2006.
Fioletov, V. E., McLinden, C. A., McElroy, C. T., and Savastiouk, V.: New method for deriving total ozone from Brewer zenith sky observations, J. Geophys. Res., 116, D08301, https://doi.org/10.1029/2010JD015399, 2011.
Fogal, P. F., LeBlanc, L. M., and Drummond, J. R.: The Polar Environment Atmospheric Research Laboratory (PEARL): Sounding the Atmosphere at 80∘ North, Arctic, 66, 337–386, 2013.
Franklin, J. E.: Solar absorption spectroscopy at the Dalhousie Atmospheric Observatory, Ph.D Thesis, Dalhousie University, Canada, 2015.
Fraser, A., Bernath, P. F., Blatherwick, R. D., Drummond, J. R., Fogal, P. F., Fu, D., Goutail, F., Kerzenmacher, T. E., McElroy, C. T., Midwinter, C., Olson, J. R., Strong, K., Walker, K. A., Wunch, D., and Young, I. J.: Intercomparison of ground-based ozone and NO2 measurements during the MANTRA 2004 campaign, Atmos. Chem. Phys., 7, 5489–5499, https://doi.org/10.5194/acp-7-5489-2007, 2007.
Fraser, A., Goutail, F., Strong, K., Bernath, P. F., Boone, C., Daffer, W. H., Drummond, J. R., Dufour, D. G., Kerzenmacher, T. E., Manney, G. L., McElroy, C. T., Midwinter, C., McLinden, C. A., Nichitiu, F., Nowlan, C. R., Walker, J., Walker, K. A., Wu, H., and Zou, J.: Intercomparison of UV-visible measurements of ozone and NO2 during the Canadian Arctic ACE validation campaigns: 2004–2006, Atmos. Chem. Phys., 8, 1763–1788, https://doi.org/10.5194/acp-8-1763-2008, 2008.
Fraser, A., Adams, C., Drummond, J. R., Goutail, F., Manney, G., and Strong, K.: The Polar Environment Atmospheric Research Laboratory UV-visible Ground-Based Spectrometer: First measurements of O3, NO2, BrO, and OClO columns, J. Quant. Spectrosc. Ra., 110, 986–1004, https://doi.org/10.1016/j.jqsrt.2009.02.034, 2009.
Fujiwara, M., Wright, J. S., Manney, G. L., Gray, L. J., Anstey, J., Birner, T., Davis, S., Gerber, E. P., Harvey, V. L., Hegglin, M. I., Homeyer, C. R., Knox, J. A., Krüger, K., Lambert, A., Long, C. S., Martineau, P., Molod, A., Monge-Sanz, B. M., Santee, M. L., Tegtmeier, S., Chabrillat, S., Tan, D. G. H., Jackson, D. R., Polavarapu, S., Compo, G. P., Dragani, R., Ebisuzaki, W., Harada, Y., Kobayashi, C., McCarty, W., Onogi, K., Pawson, S., Simmons, A., Wargan, K., Whitaker, J. S., and Zou, C.-Z.: Introduction to the SPARC Reanalysis Intercomparison Project (S-RIP) and overview of the reanalysis systems, Atmos. Chem. Phys., 17, 1417–1452, https://doi.org/10.5194/acp-17-1417-2017, 2017.
Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., Darmenov, A., Bosilovich, M. G., Reichle, R., Wargan, K., Coy, L., Cullather, R., Draper, C., Akella, S., Buchard, V., Conaty, A., da Silva, A. M., Gu, W., Kim, G.-K., Koster, R., Lucchesi, R., Merkova, D., Nielsen, J. E., Partyka, G., Pawson, S., Putman, W., Rienecker, M., Schubert, S. D., Sienkiewicz, M., and Zhao, B.: The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2), J. Climate, 30, 5419–5454, https://doi.org/10.1175/JCLI-D-16-0758.1, 2017.
Gielen, C., Van Roozendael, M., Hendrick, F., Pinardi, G., Vlemmix, T., De Bock, V., De Backer, H., Fayt, C., Hermans, C., Gillotay, D., and Wang, P.: A simple and versatile cloud-screening method for MAX-DOAS retrievals, Atmos. Meas. Tech., 7, 3509–3527, https://doi.org/10.5194/amt-7-3509-2014, 2014.
Greenblatt, G. D., Orlando, J. J., Burkholder, J. B., and Ravishankara, A. R.: Absorption measurements of oxygen between 330 and 1140 nm, J. Geophys. Res., 95, 18577–18582, https://doi.org/10.1029/JD095iD11p18577, 1990.
Grubbs, F. E.: On estimating precision of measuring instruments and product variability, J. Am. Stat. Assoc., 43, 243–264, https://doi.org/10.1080/01621459.1948.10483261, 1948.
Hendrick, F., Pommereau, J.-P., Goutail, F., Evans, R. D., Ionov, D., Pazmino, A., Kyrö, E., Held, G., Eriksen, P., Dorokhov, V., Gil, M., and Van Roozendael, M.: NDACC/SAOZ UV-visible total ozone measurements: improved retrieval and comparison with correlative ground-based and satellite observations, Atmos. Chem. Phys., 11, 5975–5995, https://doi.org/10.5194/acp-11-5975-2011, 2011.
Høiskar, B. A. K., Dahlback, A., Vaughan, G., Braathen, G. O., Goutail, F., Pommereau, J.-P., and Kivi, R.: Interpretation of ozone measurements by ground-based visible spectroscopy – a study of the seasonal dependence of airmass factors for ozone based on climatology data, J. Quant. Spectrosc. Ra., 57, 569–579, https://doi.org/10.1016/S0022-4073(96)00084-2, 1997.
Hönninger, G., von Friedeburg, C., and Platt, U.: Multi axis differential optical absorption spectroscopy (MAX-DOAS), Atmos. Chem. Phys., 4, 231–254, https://doi.org/10.5194/acp-4-231-2004, 2004.
Kerr, J. B.: New methodology for deriving total ozone and other atmospheric variables from Brewer spectrophotometer direct sun spectra, J. Geophys. Res., 107, 4731, https://doi.org/10.1029/2001JD001227, 2002.
Kerr, J. B., McElroy, C. T., and Olafson, R. A.: Measurements of ozone with the Brewer ozone spectrophotometer, in: Proceedings of the Quadrennial Ozone Symposium, 74–79, 4–9 August, Boulder, USA, 1981.
Kerr, J. B., Asbridge, I. A., and Evans, W. F. J.: Intercomparison of total ozone measured by the Brewer and Dobson spectrophotometers at Toronto, J. Geophys. Res., 93, 11129–11140, https://doi.org/10.1029/JD093iD09p11129, 1988.
Kyrö, E.: Intercomparison of total ozone data from Nimbus 7 TOMS, the Brewer UV Spectrophotometer and SAOZ UV-Visible Spectrophotometer at High Latitudes Observatory, Sodankylä, Geophys. Res. Lett., 20, 571–574, https://doi.org/10.1029/93GL00806, 1993.
Labow, G. J., McPeters, R. D., Bhartia, P. K., and Kramarova, N.: A comparison of 40 years of SBUV measurements of column ozone with data from the Dobson/Brewer network, J. Geophys. Res., 118, 7370–7378, https://doi.org/10.1002/jgrd.50503, 2013.
Manney, G. L., Zurek, R. W., Gelman, M. E., Miller, A. J., and Nagatani, R.: The anomalous Arctic lower stratospheric polar vortex of 1992-1993, Geophys. Res. Lett., 21, 2405–2408, https://doi.org/10.1029/94gl02368, 1994.
Manney, G. L., Daffer, W. H., Zawodny, J. M., Bernath, P. F., Hoppel, K. W., Walker, K. A., Knosp, B. W., Boone, C., Remsberg, E. E., Santee, M. L., Harvey, V. L., Pawson, S., Jackson, D. R., Deaver, L., McElroy, C. T., McLinden, C. A., Drummond, J. R., Pumphrey, H. C., Lambert, A., Schwartz, M. J., Froidevaux, L., McLeod, S., Takacs, L. L., Suarez, M. J., Trepte, C. R., Cuddy, D. C., Livesey, N. J., Harwood, R. S., and Waters, J. W.: Solar occultation satellite data and derived meteorological products: Sampling issues and comparisons with Aura Microwave Limb Sounder, J. Geophys. Res., 112, D24S50, https://doi.org/10.1029/2007JD008709, 2007.
Manney, G. L., Hegglin, M. I., Daffer, W. H., Santee, M. L., Ray, E. A., Pawson, S., Schwartz, M. J., Boone, C. D., Froidevaux, L., Livesey, N. J., Read, W. G., and Walker, K. A.: Jet characterization in the upper troposphere/lower stratosphere (UTLS): applications to climatology and transport studies, Atmos. Chem. Phys., 11, 6115–6137, https://doi.org/10.5194/acp-11-6115-2011, 2011.
Manney, G. L., Hegglin, M. I., Lawrence, Z. D., Wargan, K., Millán, L. F., Schwartz, M. J., Santee, M. L., Lambert, A., Pawson, S., Knosp, B. W., Fuller, R. A., and Daffer, W. H.: Reanalysis comparisons of upper tropospheric-lower stratospheric jets and multiple tropopauses, Atmos. Chem. Phys., 17, 11541–11566, https://doi.org/10.5194/acp-17-11541-2017, 2017.
Meteorological Service of Canada: MANOBS: manual of surface weather observations, Meteorological Service of Canada, Ottawa, Ontario, 2015.
Pfeilsticker, K., Erle, F., Funk, O., Marquard, L., Wagner, T., and Platt, U.: Optical Path Modifications Due to Tropospheric Clouds: Implications for Zenith Sky Measurements of Stratospheric Gases, J. Geophys. Res., 103, 25323–25335, https://doi.org/10.1029/98JD01803, 1998.
Platt, U.: Differential optical absorption spectroscopy (DOAS), in: Air Monitoring by Spectroscopic Techniques, 27–84, John Wiley, New York, 1994.
Platt, U. and Stutz, J.: Differential Optical Absorption Spectroscopy: Principles and Applications, Springer, Germany, Berlin, 2008.
Pommereau, J. P. and Goutail, F.: O3 and NO2 ground-based measurements by visible spectrometry during Arctic winter and spring 1988, Geophys. Res. Lett., 15, 891–894, https://doi.org/10.1029/GL015i008p00891, 1988.
Ramaswamy, V., Schwarzkopf, M. D., and Shine, K. P.: Radiative forcing of climate from halocarbon-induced global stratospheric ozone loss, Nature, 355, 810–812, 1992.
Roscoe, H. K., Squires, J. A. C., Oldham, D. J., Sarkissian, A., Pommereau, J.-P., and Goutail, F.: Improvements to the accuracy of zenith-sky measurements of total ozone by visible spectrometers, J. Quant. Spectrosc. Ra., 52, 639–648, https://doi.org/10.1016/0022-4073(94)90030-2, 1994.
Roscoe, H. K., Hill, J. G. T., Jones, A. E., and Sarkissian, A.: Improvements to the accuracy of zenith-sky measurements of total ozone by visible spectrometers II: use of daily air-mass factors, J. Quant. Spectrosc. Ra., 68, 327–336, https://doi.org/10.1016/S0022-4073(00)00057-1, 2001.
Roscoe, H. K., Van Roozendael, M., Fayt, C., du Piesanie, A., Abuhassan, N., Adams, C., Akrami, M., Cede, A., Chong, J., Clémer, K., Friess, U., Gil Ojeda, M., Goutail, F., Graves, R., Griesfeller, A., Grossmann, K., Hemerijckx, G., Hendrick, F., Herman, J., Hermans, C., Irie, H., Johnston, P. V., Kanaya, Y., Kreher, K., Leigh, R., Merlaud, A., Mount, G. H., Navarro, M., Oetjen, H., Pazmino, A., Perez-Camacho, M., Peters, E., Pinardi, G., Puentedura, O., Richter, A., Schönhardt, A., Shaiganfar, R., Spinei, E., Strong, K., Takashima, H., Vlemmix, T., Vrekoussis, M., Wagner, T., Wittrock, F., Yela, M., Yilmaz, S., Boersma, F., Hains, J., Kroon, M., Piters, A., and Kim, Y. J.: Intercomparison of slant column measurements of NO2 and O4 by MAX-DOAS and zenith-sky UV and visible spectrometers, Atmos. Meas. Tech., 3, 1629–1646, https://doi.org/10.5194/amt-3-1629-2010, 2010.
Rothman, L. S., Jacquemart, D., Barbe, A., Chris Benner, D., Birk, M., Brown, L. R., Carleer, M. R., Chackerian, J. C., Chance, K., Coudert, L. H., Dana, V., Devi, V. M., Flaud, J. M., Gamache, R. R., Goldman, A., Hartmann, J. M., Jucks, K. W., Maki, A. G., Mandin, J. Y., Massie, S. T., Orphal, J., Perrin, A., Rinsland, C. P., Smith, M. A. H., Tennyson, J., Tolchenov, R. N., Toth, R. A., Vander Auwera, J., Varanasi, P., and Wagner, G.: The HITRAN 2004 molecular spectroscopic database, J. Quant. Spectrosc. Ra., 96, 139–204, https://doi.org/10.1016/j.jqsrt.2004.10.008, 2005.
Rozanov, A., Rozanov, V., Buchwitz, M., Kokhanovsky, A., and Burrows, J. P.: SCIATRAN 2.0 – A new radiative transfer model for geophysical applications in the 175–2400 nm spectral region, Adv. Space Res., 36, 1015–1019, https://doi.org/10.1016/j.asr.2005.03.012, 2005.
Sanders, R. W., Solomon, S., Smith, J. P., Perliski, L., Miller, H. L., Mount, G. H., Keys, J. G., and Schmeltekopf, A. L.: Visible and Near-Ultraviolet spectroscopy at McMurdo station, Antarctica 9 Observations of OClO from April to October 1991, J. Geophys. Res., 98, 7219–7228, https://doi.org/10.1029/93jd00042, 1993.
Sarkissian, A., Pommereau, J. P., and Goutail, F.: Identification of polar stratospheric clouds from the ground by visible spectrometry, Geophys. Res. Lett., 18, 779–782, https://doi.org/10.1029/91GL00769, 1991.
Sarkissian, A., Roscoe, H. K., Fish, D., Van Roozendael, M., Gil, M., Chen, H. B., Wang, P., Pommereau, J. P., and Lenoble, J.: Ozone and NO2 Air-Mass Factors for Zenith-Sky Spectrometers – Intercomparison of Calculations with Different Radiative-Transfer Models, Geophys. Res. Lett., 22, 1113–1116, 1995.
Sarkissian, A., Vaughan, G., Roscoe, H. K., Bartlett, L. M., O'Connor, F. M., Drew, D. G., Hughes, P. A., and Moore, D. M.: Accuracy of measurements of total ozone by a SAOZ ground-based zenith sky visible spectrometer, J. Geophys. Res., 102, 1379–1390, https://doi.org/10.1029/95JD03836, 1997.
Scarnato, B., Staehelin, J., Peter, T., Gröbner, J., and Stübi, R.: Temperature and slant path effects in Dobson and Brewer total ozone measurements, J. Geophys. Res., 114, D24303, https://doi.org/10.1029/2009JD012349, 2009.
Shettle, E. P.: Models of aerosols, clouds, and precipitation for atmospheric propagation studies, Neuilly sur Seine, France, 1989.
Solomon, S., Garcia, R. R., Rowland, F. S., and Wuebbles, D. J.: On the depletion of Antarctic ozone, Nature, 321, 755–758, https://doi.org/10.1038/321755a0, 1986.
Stolarski, R. S., Krueger, A. J., Schoeberl, M. R., McPeters, R. D., Newman, P. A., and Alpert, J. C.: Nimbus 7 satellite measurements of the springtime Antarctic ozone decrease, Nature, 322, 808–811, https://doi.org/10.1038/322808a0, 1986.
Stolarski, R. S., Bloomfield, P., McPeters, R. D., and Herman, J. R.: Total Ozone trends deduced from Nimbus 7 Toms data, Geophys. Res. Lett., 18, 1015–1018, https://doi.org/10.1029/91gl01302, 1991.
Toohey, M. and Strong, K.: Estimating biases and error variances through the comparison of coincident satellite measurements, J. Geophys. Res., 112, D13306, https://doi.org/10.1029/2006JD008192, 2007.
Van Roozendael, M. and Hendrick, F.: Recommendations for total ozone retrieval from NDACC zenith-sky UV-VIS spectrometers, Belgian Institute for Space Aeronomy, Brussels, 2009.
Van Roozendael, M., Peeters, P., Roscoe, H. K., De Backer, H., Jones, A. E., Bartlett, L., Vaughan, G., Goutail, F., Pommereau, J.-P., and Kyro, E.: Validation of ground-based visible measurements of total ozone by comparison with Dobson and Brewer spectrophotometers, J. Atmos. Chem., 29, 55–83, https://doi.org/10.1023/A:1005815902581, 1998.
Vandaele, A. C., Hermans, C., Simon, P. C., Carleer, M., Colin, R., Fally, S., Mérienne, M. F., Jenouvrier, A., and Coquart, B.: Measurements of the NO2 absorption cross-section from 42 000 cm−1 to 10 000 cm−1 (238–1000 nm) at 220 K and 294 K, J. Quant. Spectrosc. Ra., 59, 171–184, https://doi.org/10.1016/s0022-4073(97)00168-4, 1998.
Vaughan, G., Roscoe, H. K., Bartlett, L. M., OConnor, F. M., Sarkissian, A., Van Roozendael, M., Lambert, J. C., Simon, P. C., Karlsen, K., Hoiskar, B. A. K., Fish, D. J., Jones, R. L., Freshwater, R. A., Pommereau, J. P., Goutail, F., Andersen, S. B., Drew, D. G., Hughes, P. A., Moore, D., Mellqvist, J., Hegels, E., Klupfel, T., Erle, F., Pfeilsticker, K., and Platt, U.: An intercomparison of ground-based UV-visible sensors of ozone and NO2, J. Geophys. Res., 102, 1411–1422, https://doi.org/10.1029/96JD00515, 1997.
Wagner, T., Erle, F., Marquard, L., Otten, C., Pfeilsticker, K., Senne, T., Stutz, J., and Platt, U.: Cloudy sky optical paths as derived from differential optical absorption spectroscopy observations, J. Geophys. Res., 103, 25307–25321, https://doi.org/10.1029/98jd01021, 1998.
Wagner, T., Apituley, A., Beirle, S., Dörner, S., Friess, U., Remmers, J., and Shaiganfar, R.: Cloud detection and classification based on MAX-DOAS observations, Atmos. Meas. Tech., 7, 1289–1320, https://doi.org/10.5194/amt-7-1289-2014, 2014.
Wagner, T., Beirle, S., Remmers, J., Shaiganfar, R., and Wang, Y.: Absolute calibration of the colour index and O4 absorption derived from Multi AXis (MAX-)DOAS measurements and their application to a standardised cloud classification algorithm, Atmos. Meas. Tech., 9, 4803–4823, https://doi.org/10.5194/amt-9-4803-2016, 2016.
Wang, Y., Penning de Vries, M., Xie, P. H., Beirle, S., Dörner, S., Remmers, J., Li, A., and Wagner, T.: Cloud and aerosol classification for 2.5 years of MAX-DOAS observations in Wuxi (China) and comparison to independent data sets, Atmos. Meas. Tech., 8, 5133–5156, https://doi.org/10.5194/amt-8-5133-2015, 2015.
Wardle, D. I.: The relationship between total ozone and spectral UV irradiance from Brewer observations and its use for derivation of total ozone from UV measurements, Geophys. Res. Lett., 24, 2997–3000, https://doi.org/10.1029/97GL53153, 1997.
Wargan, K., Labow, G., Frith, S., Pawson, S., Livesey, N., and Partyka, G.: Evaluation of the Ozone Fields in NASA's MERRA-2 Reanalysis, J. Climate, 30, 2961–2988, https://doi.org/10.1175/JCLI-D-16-0699.1, 2017.
Zhao, X.: Studies of Atmospheric Ozone and Related Constituents in the Arctic and at Mid-latitudes, Ph.D Thesis, University of Toronto, Canada, 2017.
Zhao, X., Strong, K., Adams, C., Schofield, R., Yang, X., Richter, A., Friess, U., Blechschmidt, A.-M., and Koo, J.-H.: A case study of a transported bromine explosion event in the Canadian high arctic, J. Geophys. Res., 121, 457–477, https://doi.org/10.1002/2015JD023711, 2016a.
Zhao, X., Fioletov, V., Cede, A., Davies, J., and Strong, K.: Accuracy, precision, and temperature dependence of Pandora total ozone measurements estimated from a comparison with the Brewer triad in Toronto, Atmos. Meas. Tech., 9, 5747–5761, https://doi.org/10.5194/amt-9-5747-2016, 2016b.
Zhao, X., Weaver, D., Bognar, K., Manney, G., Millán, L., Yang, X., Eloranta, E., Schneider, M., and Strong, K.: Cyclone-induced surface ozone and HDO depletion in the Arctic, Atmos. Chem. Phys., 17, 14955–14974, https://doi.org/10.5194/acp-17-14955-2017, 2017.
- Abstract
- Introduction
- Datasets and models
- Cloud screening
- Weather impacts and statistical uncertainty estimation
- Statistical uncertainty estimation
- Conclusions
- Data availability
- Appendix A: RTM simulations
- Appendix B: Smoothness of CI and O4 dSCDs
- Appendix C: Statistical uncertainty estimation
- Author contributions
- Competing interests
- Acknowledgements
- Review statement
- References
- Abstract
- Introduction
- Datasets and models
- Cloud screening
- Weather impacts and statistical uncertainty estimation
- Statistical uncertainty estimation
- Conclusions
- Data availability
- Appendix A: RTM simulations
- Appendix B: Smoothness of CI and O4 dSCDs
- Appendix C: Statistical uncertainty estimation
- Author contributions
- Competing interests
- Acknowledgements
- Review statement
- References