the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A novel approach to calibrating a photoacoustic absorption spectrometer using polydisperse absorbing aerosol
Katie Foster
Rudra Pokhrel
Matthew Burkhart
Shane Murphy
A new technique for calibrating photoacoustic aerosol absorption spectrometers with multiple laser passes in the acoustic cavity (multi-pass PAS) has been developed utilizing polydisperse and highly absorbing aerosol. This is the first calibration technique for multi-pass PAS instruments that utilizes particles instead of reactive gases and does not require knowledge of the exact size or refractive index of the absorbing aerosol. In this new method, highly absorbing materials are aerosolized into a polydisperse distribution and measured simultaneously with a multi-pass PAS and a cavity-attenuated phase shift particulate matter single-scattering albedo (CAPS PMSSA, Aerodyne Inc.) instrument. The CAPS PMSSA measures the bulk absorption coefficient through the subtraction of the scattering coefficient from the extinction coefficient. While this approach can have significant errors in ambient aerosol, the accuracy and precision of the CAPS PMSSA are high when the measured aerosol has a low single-scattering albedo (SSA) and particles are less than 300 nm in size, in which case truncation errors are small. To confirm the precision and accuracy of the new calibration approach, a range of aerosol concentrations were sent to the multi-pass PAS and CAPS PMSSA instruments using three different absorbing substances: Aquadag, Regal Black, and Nigrosin. Six repetitions with each of the three substances produced stable calibrations, with the standard deviation of the calibration slopes being less than 2 % at 660 nm and less than 5 % at 405 nm for a given calibration substance. Calibrations were also consistent across the different calibration substances (standard deviation of 2 % at 660 nm and 10 % at 405 nm) except for Nigrosin at 405 nm. The accuracy of the calibration approach is dependent on the SSA of the calibration substance but is roughly 6 % for the calibration substances used here, which all have an SSA near 0.4 at 405 nm. This calibration technique is easily deployed in the field as it involves no toxic or reactive gases and it does not require generation of a monodisperse aerosol. Advantages to this particle-based calibration technique versus techniques based on ozone or nitrogen dioxide absorption include no reactive losses or impact from carrier gases and the broad absorption characteristics of the particles, which eliminate potentially significant errors in calibration that come with small errors in the peak wavelength of the laser light when utilizing gas-phase standards.
- Article
(3214 KB) -
Supplement
(395 KB) - BibTeX
- EndNote
Absorbing aerosols represent a significant uncertainty in estimates of global radiative forcing. Black carbon (BC) aerosols, which absorb at all visible wavelengths (Bond et al., 2013), are emitted into the atmosphere as a byproduct of incomplete combustion of biomass and fossil fuels (Bond and Bergstrom, 2006; Jacobson, 2004, 2010). Brown carbon refers to organic aerosol that absorbs much more strongly in the high-energy (blue) portion of the visible spectrum than the low-energy (red) portion (Bahadur et al., 2012; Barnard et al., 2008; Kirchstetter and Thatcher, 2012; McMeeking et al., 2014). Bond et al. (2013) estimated the global top of the atmosphere radiative forcing of BC to be 1.1 [0.17–2.1] W m−2, compared to the radiative forcing from CO2 of +1.68 [1.5–1.86] W m−2 and CH4 at +0.97 [0.80–1.14] W m−2 [2013]. This estimate that BC is the second most radiatively significant emission does not include the radiative effects of brown carbon, which is potentially a significant category of absorbing aerosol but which has a larger uncertainty in its optical properties and abundance. Modeling studies indicate that the direct radiative forcing of brown carbon could range up to +0.12 or +0.57 W m−2 (Lin et al., 2014; Saleh et al., 2015). Much of the uncertainty stems from the dependence on mixing state (Brown et al., 2018; Cappa et al., 2012; Feng et al., 2013; Liu et al., 2015) and from a wide range of reported refractive indices (Chakrabarty et al., 2010; Lack et al., 2012b; Nakayama et al., 2013; Saleh et al., 2013, 2014). The actual radiative forcing of brown carbon is significantly less if it bleaches quickly, but the extent and timeframe of bleaching remain uncertain (Forrister et al., 2015; Lee et al., 2014; Liu et al., 2016).
Given the significance and uncertainty of absorbing aerosol radiative forcing, it is critical to have accurate and unbiased measurements of aerosol absorption. There are several ways to measure aerosol absorption. Most commonly, absorption is measured by filter-based techniques such as the aethalometer (Hansen et al., 1984), particle soot absorption photometer (PSAP) (Bond et al., 1999), or continuous light absorption photometer (CLAP) (Ogren et al., 2017). These approaches utilize measurement of the attenuation of light intensity (typically from an LED) due to absorption by aerosols that are captured on a filter, but these techniques are prone to a variety of biases from multiple scattering within the filter itself, variability in backscatter based on the size distribution of the particles, and issues with nonlinear responses to loading as the filter becomes saturated (Bond et al., 1999; Collaud Coen et al., 2010; Kondo et al., 2009; Lack et al., 2014; Müller et al., 2011; Weingartner et al., 2003). While filter-based measurements can be high precision, absorption measurements made by filter-based measurements are typically only accurate to within roughly 30 %–35 % (Bond et al., 2013). An alternate way to measure absorption is via the difference of extinction and scattering (Wei et al., 2013). The difference method is nonideal for many types of ambient aerosol due to small measurement errors in extinction and scattering having large impacts on measured absorption levels when the particles are mostly scattering (single-scattering albedo, SSA, is high) (Singh et al., 2014). Scattering measurements are prone to truncation errors for aerosols larger than ∼300 nm (when measuring scattering in the visible), due to the high fraction of forward-scattered light for particles with larger size parameters (Onasch et al., 2015).
Photoacoustic spectrometry has emerged as an unbiased and sensitive method for measuring absorption of dry aerosol (Arnott et al., 1999; Lack et al., 2006, 2014; Petzold and Niessner, 1996). A photoacoustic aerosol absorption spectrometer (PAS) with a single laser pass can be calibrated based on first principles if the resonant cell area, resonant frequency, quality factor of resonator, and the laser beam power at the resonant frequency are known (Rosencwaig, 1980). This approach was implemented by Arnott et al. (1999, 2000) and was validated by passing a known concentration of nitrogen dioxide through the instrument. However, the sensitivity of the photoacoustic technique is strongly related to the laser power inside the acoustic cell and increased sensitivity can be achieved through implementation of an acoustic cell where the laser passes through the cell many times (Lack et al., 2006). Unfortunately, implementation of a multi-pass cell prevents straightforward calibration of the instrument. Theoretically, the absorption coefficient (babs) can be determined from a PAS as a function of absolute laser power (PLaser), pressure at the microphone (PMic), resonator cross sectional area (ARes), resonant frequency FR, and quality factor (Q).
For multi-pass instruments it is difficult (Fischer and Smith, 2018b) or not feasible, given the instrument setup (Lack et al., 2012b), to know all of these terms accurately. This means the first principles approach of Arnott et al. (1999) is not possible for many instruments. The issue with a fundamental calibration is that the overlap integral of the laser, acoustic mode, and aerosol is not known accurately enough for calibrations. Additionally, the microphone sensitivity and laser power are not known accurately enough for calibration purposes in the design of Lack et al. (2012b). Therefore, another calibration approach must be utilized. Lack et al. (2012b) adopted an approach where ozone-enriched air is passed in parallel through a photoacoustic cell and a cavity ring-down cell that is operated at the same wavelength. While this approach has advantages, such as the ease of forming ozone in situ, there are also significant drawbacks. These drawbacks include (1) a very small absorption cross section of ozone at 405 nm wavelength ( cm2 per molecule; Axson et al., 2011) necessitating very high ozone concentrations, (2) the need to exactly match the laser wavelengths of the PAS and cavity ring-down spectrometer (CRDS), (3) potential reactions or differential wall loss of the ozone between instruments, and (4) an apparent dependence of the calibration on the bath gas, with a nitrogen bath gas yielding incorrect slopes (Fischer and Smith, 2018a). Even when accounting for these known potential issues with ozone calibration, unresolved discrepancies between calibrations performed by different research groups remain (Bluvshtein et al., 2017; Davies et al., 2018; Fischer and Smith, 2018a). Another option is to calibrate with known concentrations of nitrogen dioxide (instead of ozone) running through both the PAS and CRDS. The primary problem with using NO2 to calibrate is that NO2 photolyzes at 405 nm and the magnitude of photolysis depends on the laser power in the instrument (Jones and Bayes, 1973; Lack et al., 2012a), so while it would be a good calibration standard at 532 nm, it is a poor standard near or below 405 nm. Even for 532 nm cells, calibration with NO2 requires exact matching of laser wavelengths between the PAS and CRDS, has the potential for reactive loss, and requires the use of a toxic substance. While the NO2 concentrations are often small enough not to pose a significant health hazard, NO2 use on airborne platforms still requires significant additional safety precautions. Given the issues with gas-phase calibration, it would be desirable to have a particle-based calibration method. In addition to avoiding the issues with reactive gases, a particle-based calibration would enable detection of particle losses in the system. Calibration using particles has been attempted by several groups to assess the validity of their PAS calibration (Lack et al., 2006, 2014; Bluvshtein et al., 2017; Fischer and Smith, 2018). All of these groups generated absorbing particles from nigrosin dye and then size-selected monodisperse aerosols with a differential mobility analyzer (DMA). The aim of this approach is to determine the absorption through Mie theory based on knowledge of the refractive index and size of a monodisperse distribution of spherical particles being sent to the instrument. However, size selection via DMA causes two major issues. First, the concentration of particles is dramatically reduced because only a small fraction of the size distribution passes through the instrument and because uncharged particles are lost. Second, large particles with multiple charges will be passed through the DMA, along with the monodisperse particles of interest, which causes significant errors in the calibration because these particles have roughly 8 (doubly charged) or more (triply charged) times the mass of the target particles, and absorption is roughly proportional to mass. The only way to accurately account for these multiply charged particles is to be confident that there are very few particles in the larger size ranges or to add a second DMA to measure the size distribution generated. Adding a second DMA is expensive, adds complexity, and may not accurately detect a very small number of multiply charged particles that would result in significant error. In addition to the issues of generating a monodisperse distribution, this approach to particle-based calibration requires exact knowledge of the real and imaginary refractive index of the calibration particles. The refractive index of nigrosin dye has been tested by several groups as an aerosol calibration standard, and three different groups have published estimates of the complex refractive index (RI) of nigrosin at 405 nm (Bluvshtein et al., 2017; Ugelow et al., 2017; Washenfelder et al., 2013). The three studies differ in the retrieved imaginary RI at a given wavelength by 15 %, indicating that nigrosin does not have consistent optical properties between different batches and is probably not an ideal candidate for an absorption calibration standard. In fact, there has been a desire for a substance that can be atomized that absorbs in the visible and that has had a known constant refractive index for several years. Zangmeister and Radney (2018) have found a substance that can be atomized from aqueous solution that has a relatively constant refractive index and could eventually be an aerosol absorption standard, but this approach still requires selection of a monodisperse aerosol distribution, which has the limitations discussed above.
This paper presents a novel calibration technique that utilizes polydisperse absorbing aerosol and does not require a substance with a known refractive index. The technique allows measurement of concentrations spanning from a few Mm−1 to several hundred Mm−1, gives consistent results for several different substances across many laboratory calibrations, and has been used successfully in the field.
2.1 University of Wyoming photoacoustic absorption spectrometer
The photoacoustic absorption spectrometer utilized in this study (referred to from here on as the University of Wyoming PAS or UW PAS) is based on the design of Lack et al. (2012b), with identical cell construction, lasers, mirrors, microphones, speakers, and analog signal conditioning. Some important differences are that the Lack et al. (2012b) PAS has five cells, while the UW PAS has four: two cells operating at a wavelength of 660 nm and two at 405 nm. One cell at each wavelength is configured to sample dry air, while the other two are typically plumbed to the outlet of a thermodenuder. For the calibrations presented in this study, the thermodenuded cells are run in a bypass mode and represent a duplicate measurement at each wavelength. The UW PAS has custom data-acquisition software and significantly different vibration isolation and cooling systems than the Lack et al. (2012b) PAS. While these modifications provide utility and noise suppression, they do not fundamentally alter the operation of the instrument. A brief instrument description follows. Ambient air is pulled through two half-wavelength resonant cells which consist of two cylinders (11 cm in length and 1.9 cm diameter) with quarter-wavelength caps. The primary eigenmode of this instrument consists of one full wavelength across the two cells, such that the antinodes are at the center of each cell and 180∘ out of phase. One cell is illuminated with laser light while the other is not. The signal from the two cells is subtracted in an attempt to remove background noise. Cells are sealed with antireflective coated windows to pass laser light, and outside of this enclosed cell are two cylindrical mirrors rotated 90∘ out of phase. The front mirror has a 2 mm hole to pass a collimated laser beam and radius of curvature of 430 mm, while the back mirror cylindrical radius is 470 mm. The mirrors are treated with a dielectric coating to be 99.5 % reflective. When appropriately aligned, the end result is an astigmatic pattern that produces many (theoretically 182) passes of the laser light, with energy lost from scattering off the mirrors and windows at each pass and several potential versions of the astigmatic pattern, each with different numbers of passes. The light loss depends on how clean the system is and the system alignment, and, for this reason, quantification of laser power in the cell is not possible without a significant amount of additional equipment. The laser power is modulated at the resonant frequency of the cell and interacts with absorbing aerosol in the cell, which heat and expand the air around them at the frequency of modulation. The resulting acoustic wave is measured by two microphones (Knowles Corp. EK-23132-000) placed at each antinode (one in the cell with laser light passing through it and one in the dark cell). The subtraction and amplification of the two microphone signals is done on a signal-processing board identical to that described in Lack et al. (2012b). The analog signal is then digitized and converted via a Fourier transform into frequency space. The power at the peak resonant frequency is summed with the power 1 Hz to either side of the peak so that the total signal is an integrated area across three points that each are 1 Hz apart. Thus, the signal from each PAS cell is referred to as integrated area (IA).
To obtain the maximum and consistent signal the lasers must be modulated at each cell's resonant frequency, which is dependent on temperature and pressure in the cell. Accordingly, a resonant frequency calibration is performed at regular intervals (typically at least every 5 min) to account for any drifts in temperature or pressure. There is a speaker (Knowles Corp. EP-24075-000) in each cell for this purpose. This resonant frequency calibration is performed in a different way than Lack et al. (2012b). The speaker output is swept over range of frequencies at constant output power and the frequency that gives the maximum integrated area is found. The first calibration is done over a wide range of frequencies (1640–1370 Hz), then subsequent calibrations are done over ∼5 Hz ranges given that the resonant frequency has never been observed to vary by more than this between frequency calibrations.
2.2 CAPS PMSSA
The Aerodyne CAPS PMSSA instrument combines a cavity-attenuated phase shift (CAPS) measurement of extinction with an integrating nephelometer measurement of scattering. The instrument uses a form of cavity-enhanced spectroscopy by which a square wave modulated light emission from an LED is detected as a phase-shifted signal from which extinction can be calculated (Kebabian et al., 2007). At the same time, scattered light from particles in the CAPS cavity is integrated across all angles minus the extreme forward and backward directions. The details of the CAPS PMSSA design, principles of operation, calibration, sensitivity, and measurement uncertainty are presented in Onasch et al. (2015). The advantage of a single instrument that can measure the single-scattering albedo of bulk aerosols in real time is that it minimizes potential sampling issues that can cause error between the scattering and extinction measurement. The extinction measurement is absolute (similar to cavity ring-down spectroscopy) and therefore does not require routine calibration. The scattering channel is calibrated by linking it to the extinction measurement through measurements of a purely scattering aerosol, as discussed in Sect. 3.1. The main difficulty with using a CAPS PMSSA to measure the scattering coefficient of ambient aerosols is the truncation of light scattered from larger particles that tend to have a phase function, where a large fraction of light is scattered in the forward direction. Onasch et al. (2015) calculated the truncation as a function of polystyrene latex (PSL) sphere diameter for 660 and 450 nm wavelength instruments and demonstrated that the truncation only becomes significant for particles larger than 300 nm in diameter.
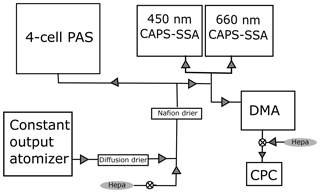
Figure 1Schematic of the calibration setup. Flow begins in the bottom left at the constant output atomizer, and the aerosols are diluted and dried before being distributed to each instrument. The DMA is a TSI differential mobility analyzer, and the CPC is a TSI 3010 condensation particle counter. When combined, these two instruments are referred to as a scanning mobility particle sizer.
2.3 Generation of absorbing aerosol for PAS calibration
Three different absorbing substances were used in this study: Aquadag, Nigrosin, and Regal Black. All three are commonly used to generate absorbing aerosol for optical measurements by photoacoustic absorption spectrometers, and Aquadag is commonly used for calibration of the single particle soot photometer (SP2) (Baumgardner et al., 2012; Gysel et al., 2011; Jordan et al., 2015; McMeeking et al., 2014; Saleh et al., 2013). Aquadag (lot no. ON03616890) is a high-viscosity slurry while Nigrosin (lot no. BCBR0628V) and Regal Black (batch no. 400R GP-3901) are solid crystals. For all three substances, the method of generating a solution was the same. The exact concentration of the solution is not critical because atomized particles are diluted with particle-free air, but the size distribution is important due to the need to have particles smaller than 300 nm to limit truncation in the scattering channel of the CAPS PMSSA. A few crystals (solids) or a quarter spatula (slurry) of the given substance is mixed with Milli-Q water (Millipore system SimPak2) and progressively diluted (starting with a couple hundred milliliters of water) until the size distribution of the atomized aerosols is such that 99 % of the mass is below 300 nm. More diluted solutions tend to yield aerosol with smaller sizes. After generating a reasonable solution that has a peak in its number size distribution from 40 to 70 nm, the solutions are sonicated for 15 min to ensure they are completely dissolved or well-mixed with the water.
Figure 1 shows a schematic of the experimental setup. Absorbing aerosols are generated from solution using a constant output atomizer (TSI) fed with particle-free (pulled through a HEPA filter) air at 140 kPa. The aerosol is then passed through a silica gel diffusion drier (TSI) and further diluted with particle-free air to achieve the desired concentration. The dilution is varied so that a range of concentrations can be measured. The aerosols are dried a second time with a Nafion tube drier (Purma Pure PD-100T) that is a permanent part of the UW PAS inlet before the flow is split to four different instruments – the four-cell PAS, two different wavelength (450, 660 nm) CAPS PMSSA instruments, and a TSI scanning mobility particle analyzer (SMPS), which is a combination of a differential mobility analyzer (DMA) and condensation particle counter (CPC). The SMPS is set up with a 10:1 ratio of sheath to sample flow, using flow rates of 3 L min−1 for the sheath and 0.3 L min−1 for the sample. The output from the DMA is diluted with 0.7 L min−1 of filtered air to achieve a 1 L min−1 flow rate for the CPC.
The concept of the calibration method is to calibrate a multi-pass PAS based on the absorption of small, highly absorbing (SSA < 0.5) particles for which the absorption can be accurately measured by the CAPS PMSSA. To ensure accurate results, the performance, accuracy, and precision of the CAPS PMSSA measurement of absorption, through the difference between extinction and scattering, must first be verified.
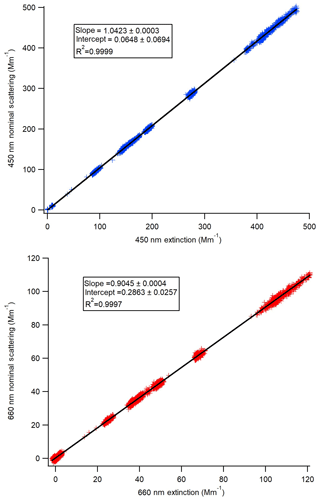
Figure 2Scattering calibration curves for each of the Aerodyne CAPS PMSSA instruments. The scattering channel is calibrated based on the relationship to the extinction channel across a range of concentrations. The slope of the resulting linear fit gives the ratio that scattering must be corrected by.
3.1 Calibration of the CAPS PMSSA scattering channel
The scattering channel for the CAPS PMSSA is calibrated relative to the extinction channel because the extinction does not require calibration (Onasch et al., 2015). To calibrate the scattering channel, polydisperse ammonium sulfate was atomized, dried, and diluted following the methods described in Sect. 2.3. The mean geometric diameter of the atomized solution was tuned (through dilution of the atomized liquid) to be close to 55 nm, with less than 1 % of the mass at diameters greater than 300 nm, as verified by the SMPS. The concentration of the purely scattering ammonium sulfate aerosol is varied to achieve extinction coefficient values ranging from ∼5 to 600 Mm−1. A linear fit to the resulting data gives the relationship between the scattering coefficient and extinction coefficient derived by a particular instrument. Figure 2 shows an example of one calibration. The intercept in all cases is very close to zero and is not used because baseline corrections with a filter are made at regular intervals automatically by both instruments. In Fig. 2a the 660 nm instrument has a ratio of scattering to extinction of 0.9045, so the true scattering coefficient is the reported scattering coefficient divided by this slope. Similarly, in Fig. 2b, the scattering signal must be divided by 1.0423. Across six calibrations performed in this manner, the 450 nm CAPS PMSSA calibration slope was 1.0439±0.0073 (0.7 % standard deviation of the mean). For the 660 nm instrument, the ratio of scattering to extinction averaged over six calibrations is 0.890±0.018 (2 % standard deviation from the mean). The errors in this calibration are included in the error estimate for the accuracy of this calibration technique.
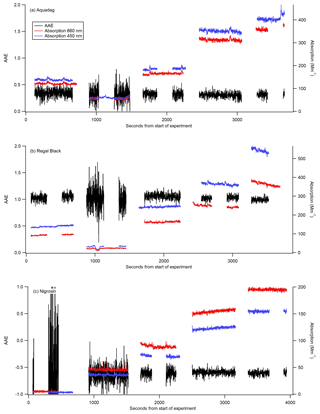
Figure 3AAE (black) calculated from 1 Hz data from the CAPS PMSSA data for three different substances: Aquadag (a), Regal Black (b), and Nigrosin (c). The 450 nm (blue) and 660 nm absorption (red) coefficients are taken from the CAPS PMSSA instrument. The absorption coefficients are shown for context, as the AAE becomes significantly more noisy at low concentrations. Gaps in data occur when the CAPS is conducting a baseline period, and the instruments are switched to filter for several minutes between each concentration.
Tests were also performed to verify the accuracy of the extinction measurement in the CAPS PMSSA. In these tests, PSLs of various sizes were size-selected by an SMPS, then the flow from the SMPS was split between a TSI 3010 CPC and the CAPS PMSSA. It was found that the extinction measured by the CAPS PMSSA was within 5 % of the extinction calculated based on Mie theory using the PSL size and the number of particles measured by the CPC. The error between the Mie calculations and the CAPS PMSSA is within what is expected based on the size range stated for the PSLs, the counting accuracy of the CPC, and the stated accuracy of the CAPS PMSSA.
3.2 Calculation of absorption Ångström exponent for each substance
The UW PAS has two cells that operate at a wavelength of 405 nm and two that operate at a wavelength of 660 nm. While the red LED CAPS PMSSA instrument also operates at 660 nm, the blue LED CAPS PMSSA operates at 450 nm, a mismatch with the PAS wavelength. Initially a 405 nm CAPS PMSSA instrument was built, but the 405 nm mirrors rapidly degraded, requiring a return to the 450 nm wavelength. We demonstrate here that accurate calibration with the proposed method is feasible even when the instruments are ∼50 nm separated in wavelength. This suggests that one could calibrate PAS instruments at different wavelengths without having to have a CAPS PMSSA instrument to exactly match every PAS wavelength. Currently, CAPS DPMSSA are available at 630, 660, 530, and 450 nm.
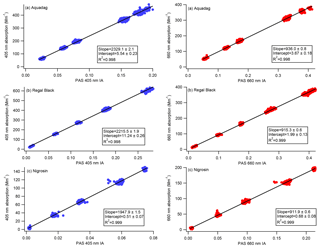
Figure 5Calibration curves representing CAPS PMSSA absorption versus PAS integrated area (IA). The PAS 405 nm cell is on the left, and the 660 nm cell is on the right. A line is fit to the data, the slope of which gives the relationship between absorption and IA. Intercepts are allowed to vary in order to achieve the most accurate slopes based on higher absorption levels where the accuracy of the CAPS PMSSA is highest. During operation in the field, both instruments are frequently zeroed based on filter measurements, meaning the intercept of the calibration slope is not needed.
To account for the wavelength difference between the CAPS PMSSA (450 nm) and the UW PAS (405 nm), the absorption Ångström exponent (AAE) was calculated based on the 660 and 450 nm CAPS PMSSA measurements of absorption for each calibration and substance. This calculated AAE can then be used to convert the 450 nm absorption coefficient measured by the CAPS PMSSA into an estimate of the 405 nm absorption coefficient needed to calibrate the multi-pass PAS. Equation (2) shows how AAE is calculated from the two different wavelength CAPS PMSSA measurements of absorption coefficient, and the same relationship is used to convert absorption at 450 nm to absorption at 405 nm.
The experimentally derived AAE is different for each of the three substances used in this study, allowing for an assessment of the accuracy of utilizing AAE derived from measurements at 660 and 450 nm to convert from absorption at 450 nm to absorption at 405 nm. Six different calibrations were conducted with each substance to assess the stability of the estimated AAE. For Aquadag the average AAE (±1σ) was 0.3423±0.0357, for Regal Black it was 1.053±0.022, and for Nigrosin it was . The standard deviation expressed as a percentage for each of the substances is as follows: 2 % for Regal Black, 10 % for Aquadag, and 24 % for Nigrosin. These results suggest that, of these substances, Regal Black may be the best choice for this calibration technique because it has a very stable AAE and the AAE is close to 1, which is often the assumption made for black carbon (Bergstrom et al., 2002; Lack et al., 2012b; Moosmüller et al., 2009, 2011). Aquadag is also a good choice because, while it has slightly more variability in its AAE, the AAE itself is smaller than that of Regal Black meaning the accuracy of its value is mathematically less critical. Nigrosin had a higher standard deviation than either Regal Black or Aquadag, perhaps suggesting that even within a single batch the substance does not have consistent optical properties. Additionally, the Nigrosin tested here yielded a negative AAE, which is inconsistent with Fig. 4 of Bluvshtein et al. (2017) in the wavelength range of 400–450 nm that shows a positive AAE. Nigrosin has been shown to have an index of refraction that varies across the visible wavelengths (Bluvshtein et al., 2017) and does not have a relationship between absorption and wavelength that is perfectly modeled by AAE. However, given that the adjustment is only over a small wavelength range, the error introduced by adjusting absorption measurements from 450 to 405 nm with the AAE technique is still assessed here. Nigrosin has the largest variation in calculated AAE from the different calibrations, but the difference in absorption at 405 nm calculated from the highest AAE (−0.3) to the lowest (−0.6), a factor of 2 in AAE, is only 3 %. This demonstrates that even with significant variation in AAE the calibration method is still robust and this adjustment in wavelength causes minimal error. The errors introduced by AAE for Regal Black and Aquadag are significantly smaller than that for Nigrosin. Figure 3 shows 1 Hz data from one of the six calibrations with each substance. The AAE for a given substance is fairly stable but does grow noisy when absorption values are < 10 Mm−1. This noise is particularly pronounced in Fig. 3c, when small (∼5 Mm−1 absorption) concentrations of Nigrosin do not produce a stable enough signal in the two CAPS PMSSA instruments to accurately calculate AAE.
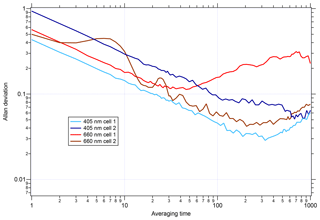
3.3 UW PAS stability
Before applying the CAPS PMSSA calibration to the UW PAS, the noise level of the UW PAS was assessed by plotting the Allan deviation as a function of time. A similar analysis for the CAPS PMSSA can be found in Onasch et al. (2015). The Allan deviation, as a function of averaging time, is displayed for each cell in the instrument in Fig. 4. While the behavior of each cell is slightly different, on average, across the four cells of the instrument, the 1 s Allan variance is 0.6 Mm−1 and is 0.5 Mm−1 for the best performing cell. After 60 s of averaging, the noise drops nearly an order of magnitude to 0.09 Mm−1 on average and 0.06 Mm−1 in the lowest noise cell. As an alternative noise assessment to the Allan deviation, the standard deviation of 1, 30, and 60 s average data are listed for all cells in Table S1 in the Supplement. The 1 s data standard deviation varies between channels, from 0.01 to 0.12 Mm−1, while at 30 s the range is 0.004 to 0.02 Mm−1, and 60 s averaging has little change from 30 s.
3.4 Precision of calibration results
As described in Sect. 2.3, Nigrosin, Aquadag, and Regal Black were aerosolized and passed to the four PAS cells (two 405 nm cells, two 660 nm cells), two CAPS PMSSA cells (660 and 450 nm), and an SMPS. The purpose of measuring with an SMPS was to confirm that only a negligible fraction of the polydisperse aerosol mass was at diameters > 300 nm. Aerosol size distributions for each substance are displayed in Fig. S1 in the Supplement. Absorption was determined at 450 and 660 nm by subtracting the CAPS PMSSA measurement of scattering from CAPS PMSSA measurements of extinction. The absorption at 405 nm, where the PAS operates, was determined via measurements of the AAE as outlined in Sect. 3.3. The resulting calibration slopes for each channel across six calibrations are shown in Fig. 5 and Table 1. The standard deviation of the six different calibration slopes at 660 nm have a maximum standard deviation of 1.2 % of the mean (Regal Black has this largest standard deviation). At 405 nm, the variation is larger, with Nigrosin having the largest standard deviation between the calibrations of 4 %. In practice, the calibration slopes are applied to the PAS microphone signal to convert from integrated area to absorption (as outlined in Sect. 2.1). Filter periods are frequently conducted to determine the background absorption, and the PAS data are zeroed to this background. Large (on the order of several hundred Mm−1) concentrations are used to generate a slope that can be applied over significant concentrations in field measurements of smoke particles. Therefore, intercepts can be on the order of 10 Mm−1. The intercepts from the calibrations are not used.
Table 1Summary of AAE and calibration slopes for each substance, reported as average and standard deviation from six calibrations.

Variations over the six calibrations using a single substance are quite small and for the 660 nm data variation between the substances is also small (4 %). However, there is more variation between the three different substances in the blue wavelength and up to a 17 % difference between Nigrosin and Aquadag, though the results for Aquadag and Regal Black are within 5 % of one another. We hypothesize that the optical properties of Nigrosin may vary in such a way that assuming an AAE between 450 and 405 nm may be inappropriate.
3.5 Accuracy of calibration
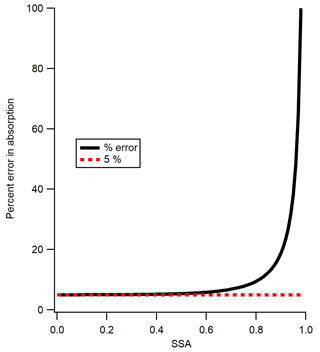
The previous section demonstrated that the precision of the calibration method is ∼5 %, based on the variation in the average of six calibration runs or between the results from different substances (other than Nigrosin at 405 nm, which appears to be an outlier). Next, the accuracy of the method is assessed. The fractional accuracy of the extinction coefficient measured by the CAPS PMSSA is found by Onasch et al. (2015) to be ±0.05 or 5 %. The fractional error in SSA is reported by Onasch et al. (2015) to be 0.01 or 1 %, but we find that it is slightly larger for our instrumental setup at 0.02 or 2 %. We derive this slightly larger error in SSA from the variability in our six repetitions of the scattering to extinction calibration for the CAPS PMSSA. One way to find the absorption coefficient from CAPS PMSSA data is via Eq. (3).
We utilize this equation because it allows the error to be couched in terms of SSA. Given this, the fractional error in the absorption coefficient, defined here to be σabs, is found by adding the fractional errors in extinction and the fractional error in the term (1–SSA) in quadrature. This can only be done if the errors are independent. In this case independence is a reasonable assumption because the error in extinction is caused by the accuracy of interpreting the phase-shifted signal in the CAPS, while the error in SSA is caused by the ability to match the scattering signal to the extinction signal, as discussed in Sect. 3.1. Given this, the error in the extinction does not depend on the error in the SSA and vice versa. The error in the term (1–SSA) is simply two percent of the SSA because the integer 1 has no error. This yields an equation for the fractional error in the absorption coefficient of
where σabs is the fractional error in absorption and σext is the fractional error in extinction. The fractional error in absorption (σabs) is displayed (as a percent) as a function of SSA in Fig. 6. As SSA reaches 0, the error in absorption approaches the 5 % limit which is the error in extinction alone, but as SSA approaches 1 the error reaches infinity. The SSA of the three calibration substances in the current study are all close to 0.4, which yields an error of approximately ±5.2 %. The high error above an SSA of ∼0.85 is a good indicator of the limits of using the CAPS PMSSA for measuring absorption in ambient conditions, and one of the main motivations for making absorption measurements with the PAS instrument. Figure 6 also gives guidance into the highest SSA substances that one might consider using to calibrate a multi-pass PAS with the CAPS PMSSA, based on the level of accuracy desired. Finally, at very low levels of extinction, the errors are not defined by Eq. (4) but are dominated by the detection limits of the CAPS PMSSA. Despite this, Eq. (4) is a good representation of the calibration error for the technique presented here because the slope of the calibration line is controlled by measurements with sufficient extinction (see Fig. 5).
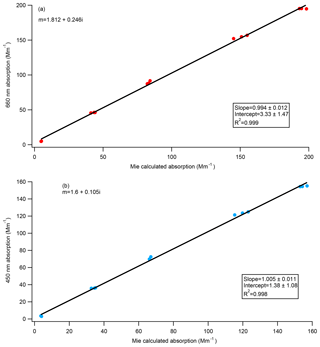
3.6 Mie theory applied to the Nigrosin calibration
The refractive index of Nigrosin dye was derived by Bluvshtein et al. (2017) through ellipsometry at both 405 nm () and 660 nm (). The theoretical absorption of the polydisperse Nigrosin particles used during the calibrations done in this paper was calculated from Mie theory assuming these refractive indices and compared to the absorption measured by the CAPS PMSSA. Size distributions were measured by the SMPS, and absorption estimates were made for every SMPS scan yielding three independent calculations of absorption for every concentration level. We also performed this calculation for other indices of refraction that have been previously published in the literature. Figure 7a shows measured CAPS absorption versus calculated absorption from Mie theory at 660 nm using the RI derived by Bluvshtein et al. (2017) () and demonstrates good agreement. The same calculations were done at 405 and 450 nm using the Bluvshtein et al. (2017) values ( at 405 nm, at 450 nm), but in this case the ratio of measured CAPS absorption to calculated absorption from Mie theory is ∼0.58 for both the 405 nm comparison and the 450 nm comparison. The RI that gives the best agreement between the 450 nm CAPS PMSSA measured absorption and Mie theory, shown in Fig. 7b, is . This refractive index is similar to the result given in Liu et al. (2013) of . The discrepancy between the current result and that from Bluvshtein et al. (2017) and different refractive indices found in the literature at 405 nm for Nigrosin (Washenfelder et al., 2015; ; Ugelow et al., 2017; ) suggest that different batches of Nigrosin have different absorptivity and that Nigrosin may not be a good calibration substance at shorter visible wavelengths.
A new calibration method for multi-pass photoacoustic absorption spectrometers that uses polydisperse absorbing aerosol and an accompanying measurement of absorption from the CAPS PMSSA instrument has been presented. This method is demonstrated to be consistent over repeated trials and across three different aerosol types, namely Aquadag, Regal Black, and Nigrosin. The calibration curve represents the relationship between absorption as measured by the CAPS PMSSA to integrated area as measured by the PAS and is demonstrated to be linear over 3 orders of magnitude in absorption, up to ∼600 Mm−1. The method is found to have an absolute accuracy of less than ±6 % for the substances tested. This aerosol-based method of calibration is simple and easy to utilize in both the laboratory and the field and does not require size selection. By using absorbing particles, we eliminate several potential concerns from gas-phase calibrations using nitrogen dioxide or ozone. Namely, there is no potential for reactive losses and concentrations on the order of hundreds of Mm−1 of absorption are easily and safely attained. Additionally, small differences in wavelength between instruments are of negligible consequence. To accommodate for a wavelength difference between 405 nm PAS cells and the 450 nm CAPS PMSSA, we calculate the AAE of each species based on the relationship between 660 and 450 nm measured absorption coefficients from the CAPS PMSSA and apply this to convert the 450 nm absorption coefficient to the absorption coefficient at 405 nm. This is also shown to have small uncertainties, < 3 %. Finally, we derive the refractive index of a particular batch of Nigrosin at 450 nm to be and confirm a previous result at 660 nm of .
All data are available from the corresponding authors upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/amt-12-3351-2019-supplement.
MB, KF, RP, and SM all aided in the construction of the PAS. SM designed the experiments. KF and RP performed the experiments and data analysis. KF synthesized the data and wrote the manuscript with input from all authors.
The authors declare that they have no conflict of interest.
The authors thank Ernie Lewis for providing his Mie theory code. This material is based upon work supported by the United States Environmental Protection Agency (US EPA) under grant no. R835883.
This paper was edited by Troy Thornberry and reviewed by two anonymous referees.
Arnott, W. P., Moosmüller, H., Rogers, C. F., Jin, T., and Bruch, R.: Photoacoustic spectrometer for measuring light absorption by aerosol: Instrument description, Atmos. Environ., 33, 2845–2852, https://doi.org/10.1016/S1352-2310(98)00361-6, 1999.
Arnott, W. P., Moosmüller, H., and Walker, J. W.: Nitrogen dioxide and kerosene-flame soot calibration of photoacoustic instruments for measurement of light absorption by aerosols, Rev. Sci. Instrum., 71, 4545–4552, https://doi.org/10.1063/1.1322585, 2000.
Axson, J. L., Washenfelder, R. A., Kahan, T. F., Young, C. J., Vaida, V., and Brown, S. S.: Absolute ozone absorption cross section in the Huggins Chappuis minimum (350–470 nm) at 296 K, Atmos. Chem. Phys., 11, 11581–11590, https://doi.org/10.5194/acp-11-11581-2011, 2011.
Bahadur, R., Praveen, P. S., Xu, Y., and Ramanathan, V.: Solar absorption by elemental and brown carbon determined from spectral observations, P. Natl. Acad. Sci. USA, 109, 17366–17371, https://doi.org/10.1073/pnas.1205910109, 2012.
Barnard, J. C., Volkamer, R., and Kassianov, E. I.: Estimation of the mass absorption cross section of the organic carbon component of aerosols in the Mexico City Metropolitan Area, Atmos. Chem. Phys., 8, 6665–6679, https://doi.org/10.5194/acp-8-6665-2008, 2008.
Baumgardner, D., Popovicheva, O., Allan, J., Bernardoni, V., Cao, J., Cavalli, F., Cozic, J., Diapouli, E., Eleftheriadis, K., Genberg, P. J., Gonzalez, C., Gysel, M., John, A., Kirchstetter, T. W., Kuhlbusch, T. A. J., Laborde, M., Lack, D., Müller, T., Niessner, R., Petzold, A., Piazzalunga, A., Putaud, J. P., Schwarz, J., Sheridan, P., Subramanian, R., Swietlicki, E., Valli, G., Vecchi, R., and Viana, M.: Soot reference materials for instrument calibration and intercomparisons: a workshop summary with recommendations, Atmos. Meas. Tech., 5, 1869–1887, https://doi.org/10.5194/amt-5-1869-2012, 2012.
Bergstrom, R. W., Russell, P. B., and Hignett, P.: Wavelength Dependence of the Absorption of Black Carbon Particles: Predictions and Results from the TARFOX Experiment and Implications for the Aerosol Single Scattering Albedo, J. Atmos. Sci., 59, 567–577, https://doi.org/10.1175/1520-0469(2002)059<0567:WDOTAO>2.0.CO;2, 2002.
Bluvshtein, N., Flores, J. M., He, Q., Segre, E., Segev, L., Hong, N., Donohue, A., Hilfiker, J. N., and Rudich, Y.: Calibration of a multi-pass photoacoustic spectrometer cell using light-absorbing aerosols, Atmos. Meas. Tech., 10, 1203–1213, https://doi.org/10.5194/amt-10-1203-2017, 2017.
Bond, T. C. and Bergstrom, R. W.: Light Absorption by Carbonaceous Particles: An Investigative Review, Aerosol Sci. Technol., 40, 27–67, https://doi.org/10.1080/02786820500421521, 2006.
Bond, T. C., Anderson, T. L., and Campbell, D.: Calibration and Intercomparison of Filter-Based Measurements of Visible Light Absorption by Aerosols, Aerosol Sci. Technol., 30, 582–600, https://doi.org/10.1080/027868299304435, 1999.
Bond, T. C., Doherty, S. J., Fahey, D. W., Forster, P. M., Berntsen, T., Deangelo, B. J., Flanner, M. G., Ghan, S., Karcher, B., Koch, D., Kinne, S., Kondo, Y., Quinn, P. K., Sarofim, M. C., Schultz, M. G., Schulz, M., Venkataraman, C., Zhang, H., Zhang, S., Bellouin, N., Guttikunda, S. K., Hopke, P. K., Jacobson, M. Z., Kaiser, J. W., Klimont, Z., Lohmann, U., Schwarz, J. P., Shindell, D., Storelvmo, T., Warren, S. G., and Zender, C. S.: Bounding the role of black carbon in the climate system: A scientific assessment, J. Geophys. Res.-Atmos., 118, 5380–5552, https://doi.org/10.1002/jgrd.50171, 2013.
Brown, H., Liu, X., Feng, Y., Jiang, Y., Wu, M., Lu, Z., Wu, C., Murphy, S., and Pokhrel, R.: Radiative effect and climate impacts of brown carbon with the Community Atmosphere Model (CAM5), Atmos. Chem. Phys., 18, 17745–17768, https://doi.org/10.5194/acp-18-17745-2018, 2018.
Cappa, C. D., Onasch, T. B., Massoli, P., Worsnop, D. R., Bates, T. S., Cross, E. S., Davidovits, P., Hakala, J., Hayden, K. L., Jobson, B. T., Kolesar, K. R., Lack, D. A., Lerner, B. M., Li, S.-M., Mellon, D., Nuaaman, I., Olfert, J. S., Petaja, T., Quinn, P. K., Song, C., Subramanian, R., Williams, E. J., and Zaveri, R. A.: Radiative Absorption Enhancements Due to the Mixing State of Atmospheric Black Carbon, Science, 337, 1078–1081, https://doi.org/10.1126/science.1223447, 2012.
Chakrabarty, R. K., Moosmüller, H., Chen, L.-W. A., Lewis, K., Arnott, W. P., Mazzoleni, C., Dubey, M. K., Wold, C. E., Hao, W. M., and Kreidenweis, S. M.: Brown carbon in tar balls from smoldering biomass combustion, Atmos. Chem. Phys., 10, 6363–6370, https://doi.org/10.5194/acp-10-6363-2010, 2010.
Collaud Coen, M., Weingartner, E., Apituley, A., Ceburnis, D., Fierz-Schmidhauser, R., Flentje, H., Henzing, J. S., Jennings, S. G., Moerman, M., Petzold, A., Schmid, O., and Baltensperger, U.: Minimizing light absorption measurement artifacts of the Aethalometer: evaluation of five correction algorithms, Atmos. Meas. Tech., 3, 457–474, https://doi.org/10.5194/amt-3-457-2010, 2010.
Davies, N. W., Cotterell, M. I., Fox, C., Szpek, K., Haywood, J. M., and Langridge, J. M.: On the accuracy of aerosol photoacoustic spectrometer calibrations using absorption by ozone, Atmos. Meas. Tech., 11, 2313–2324, https://doi.org/10.5194/amt-11-2313-2018, 2018.
Feng, Y., Ramanathan, V., and Kotamarthi, V. R.: Brown carbon: a significant atmospheric absorber of solar radiation?, Atmos. Chem. Phys., 13, 8607–8621, https://doi.org/10.5194/acp-13-8607-2013, 2013.
Fischer, D. A. and Smith, G. D.: Can ozone be used to calibrate aerosol photoacoustic spectrometers?, Atmos. Meas. Tech., 11, 6419–6427, https://doi.org/10.5194/amt-11-6419-2018, 2018a.
Fischer, D. A. and Smith, G. D.: A portable, four-wavelength, single-cell photoacoustic spectrometer for ambient aerosol absorption, Aerosol Sci. Technol., 52, 393–406, https://doi.org/10.1080/02786826.2017.1413231, 2018b.
Forrister, H., Liu, J., Scheuer, E., Dibb, J., Ziemba, L., Thornhill, K. L., Anderson, B., Diskin, G., Perring, A. E., Schwarz, J. P., Campuzano-Jost, P., Day, D. A., Palm, B. B., Jimenez, J. L., Nenes, A., and Weber, R. J.: Evolution of brown carbon in wildfire plumes, Geophys. Res. Lett., 42, 4623–4630, https://doi.org/10.1002/2015GL063897, 2015.
Gysel, M., Laborde, M., Olfert, J. S., Subramanian, R., and Gröhn, A. J.: Effective density of Aquadag and fullerene soot black carbon reference materials used for SP2 calibration, Atmos. Meas. Tech., 4, 2851–2858, https://doi.org/10.5194/amt-4-2851-2011, 2011.
Hansen, A. D. A., Rosen, H., and Novakov, T.: The aethalometer – an instrument for the real-time measurement of optical absorption by aerosol particles, Sci. Total Environ., 36, 191–196, 1984.
Jacobson, M. Z.: The short-term cooling but long-term global warming due to biomass burning, J. Climate, 17, 2909–2926, https://doi.org/10.1175/1520-0442(2004)017<2909:TSCBLG>2.0.CO;2, 2004.
Jacobson, M. Z.: Short-term effects of controlling fossil-fuel soot, biofuel soot and gases, and methane on climate, Arctic ice, and air pollution health, J. Geophys. Res.-Atmos., 115, 14, https://doi.org/10.1029/2009JD013795, 2010.
Jones, I. T. N. and Bayes, K.: Photolysis of nitrogen dioxide, J. Chem. Phys., 59, 4836, https://doi.org/10.1063/1.1680696, 1973.
Jordan, C. E., Anderson, B. E., Beyersdorf, A. J., Corr, C. A., Dibb, J. E., Greenslade, M. E., Martin, R. F., Moore, R. H., Scheuer, E., Shook, M. A., Thornhill, K. L., Troop, D., Winstead, E. L., and Ziemba, L. D.: Spectral aerosol extinction (SpEx): a new instrument for in situ ambient aerosol extinction measurements across the UV/visible wavelength range, Atmos. Meas. Tech., 8, 4755–4771, https://doi.org/10.5194/amt-8-4755-2015, 2015.
Kebabian, P. L., Robinson, W. A., and Freedman, A.: Optical extinction monitor using cw cavity enhanced detection, Rev. Sci. Instrum., 78, 063102, https://doi.org/10.1063/1.2744223, 2007.
Kirchstetter, T. W. and Thatcher, T. L.: Contribution of organic carbon to wood smoke particulate matter absorption of solar radiation, Atmos. Chem. Phys., 12, 6067–6072, https://doi.org/10.5194/acp-12-6067-2012, 2012.
Kondo, Y., Sahu, L., Kuwata, M., Miyazaki, Y., Takegawa, N., Moteki, N., Imaru, J., Han, S., Nakayama, T., Oanh, N. T. K., Hu, M., Kim, Y. J., and Kita, K.: Stabilization of the mass absorption cross section of black carbon for filter-based absorption photometry by the use of a heated inlet, Aerosol Sci. Technol., 43, 741–756, https://doi.org/10.1080/02786820902889879, 2009.
Lack, D. A., Lovejoy, E. R., Baynard, T., Pettersson, A., and Ravishankara, A. R.: Aerosol Absorption Measurement using Photoacoustic Spectroscopy: Sensitivity, Calibration, and Uncertainty Developments, Aerosol Sci. Technol., 40, 697–708, https://doi.org/10.1080/02786820600803917, 2006.
Lack, D. A., Richardson, M. S., Law, D., Langridge, J. M., Cappa, C. D., McLaughlin, R. J., and Murphy, D. M.: Aircraft Instrument for Comprehensive Characterization of Aerosol Optical Properties, Part 2: Black and Brown Carbon Absorption and Absorption Enhancement Measured with Photo Acoustic Spectroscopy, Aerosol Sci. Technol., 46, 555–568, https://doi.org/10.1080/02786826.2011.645955, 2012a.
Lack, D. A., Langridge, J. M., Bahreini, R., Cappa, C. D., Middlebrook, A. M., and Schwarz, J. P.: Brown carbon and internal mixing in biomass burning particles, P. Natl. Acad. Sci. USA, 109, 14802–14807, https://doi.org/10.1073/pnas.1206575109, 2012b.
Lack, D. A., Moosmüller, H., McMeeking, G. R., Chakrabarty, R. K., and Baumgardner, D.: Characterizing elemental, equivalent black, and refractory black carbon aerosol particles: A review of techniques, their limitations and uncertainties, Anal. Bioanal. Chem., 406, 99–122, https://doi.org/10.1007/s00216-013-7402-3, 2014.
Lee, H. J., Aiona, P. K., Laskin, A., Laskin, J., and Nizkorodov, S. A.: Effect of Solar Radiation on the Optical Properties and Molecular Composition of Laboratory Proxies of Atmospheric Brown Carbon, Environ. Sci. Technol., 48, 10217–10226, https://doi.org/10.1021/es502515r, 2014.
Lin, G., Penner, J. E., Flanner, M. G., Sillman, S., Xu, L., and Zhou, C.: Radiative forcing of organic aerosol in the atmosphere and on snow: Effects of SOA and brown carbon, J. Geophys. Res.-Atmos., 119, 7453–7476, https://doi.org/10.1002/2013JD021186, 2014.
Liu, J., Lin, P., Laskin, A., Laskin, J., Kathmann, S. M., Wise, M., Caylor, R., Imholt, F., Selimovic, V., and Shilling, J. E.: Optical properties and aging of light-absorbing secondary organic aerosol, Atmos. Chem. Phys., 16, 12815–12827, https://doi.org/10.5194/acp-16-12815-2016, 2016.
Liu, S., Aiken, A. C., Gorkowski, K., Dubey, M. K., Cappa, C. D., Williams, L. R., Herndon, S. C., Massoli, P., Fortner, E. C., Chhabra, P. S., Brooks, W. A., Onasch, T. B., Jayne, J. T., Worsnop, D. R., China, S., Sharma, N., Mazzoleni, C., Xu, L., Ng, N. L., Liu, D., Allan, J. D., Lee, J. D., Fleming, Z. L., Mohr, C., Zotter, P., Szidat, S., and Prévôt, A. S. H.: Enhanced light absorption by mixed source black and brown carbon particles in UK winter, Nat. Commun., 6, 1–11, https://doi.org/10.1038/ncomms9435, 2015.
McMeeking, G. R., Fortner, E., Onasch, T. B., Taylor, J. W., Flynn, M., Coe, H., and Kreidenweis, S. M.: Impacts of nonrefractory material on light absorption by aerosols emitted from biomass burning, J. Geophys. Res.-Atmos., 119, 12272–12286, https://doi.org/10.1002/2014JD021750, 2014.
Moosmüller, H., Chakrabarty, R. K., and Arnott, W. P.: Aerosol light absorption and its measurement: A review, J. Quant. Spectrosc. Ra., 110, 844–878, https://doi.org/10.1016/j.jqsrt.2009.02.035, 2009.
Moosmüller, H., Chakrabarty, R. K., Ehlers, K. M., and Arnott, W. P.: Absorption Ångström coefficient, brown carbon, and aerosols: basic concepts, bulk matter, and spherical particles, Atmos. Chem. Phys., 11, 1217–1225, https://doi.org/10.5194/acp-11-1217-2011, 2011.
Müller, T., Henzing, J. S., de Leeuw, G., Wiedensohler, A., Alastuey, A., Angelov, H., Bizjak, M., Collaud Coen, M., Engström, J. E., Gruening, C., Hillamo, R., Hoffer, A., Imre, K., Ivanow, P., Jennings, G., Sun, J. Y., Kalivitis, N., Karlsson, H., Komppula, M., Laj, P., Li, S.-M., Lunder, C., Marinoni, A., Martins dos Santos, S., Moerman, M., Nowak, A., Ogren, J. A., Petzold, A., Pichon, J. M., Rodriquez, S., Sharma, S., Sheridan, P. J., Teinilä, K., Tuch, T., Viana, M., Virkkula, A., Weingartner, E., Wilhelm, R., and Wang, Y. Q.: Characterization and intercomparison of aerosol absorption photometers: result of two intercomparison workshops, Atmos. Meas. Tech., 4, 245–268, https://doi.org/10.5194/amt-4-245-2011, 2011.
Nakayama, T., Sato, K., Matsumi, Y., Imamura, T., Yamazaki, A., and Uchiyama, A.: Wavelength and NOx dependent complex refractive index of SOAs generated from the photooxidation of toluene, Atmos. Chem. Phys., 13, 531–545, https://doi.org/10.5194/acp-13-531-2013, 2013.
Ogren, J. A., Wendell, J., Andrews, E., and Sheridan, P. J.: Continuous light absorption photometer for long-term studies, Atmos. Meas. Tech., 10, 4805–4818, https://doi.org/10.5194/amt-10-4805-2017, 2017.
Onasch, T. B., Massoli, P., Kebabian, P. L., Hills, F. B., Bacon, F. W., and Freedman, A.: Single Scattering Albedo Monitor for Airborne Particulates, Aerosol Sci. Technol., 49, 267–279, https://doi.org/10.1080/02786826.2015.1022248, 2015.
Petzold, A. and Niessner, R.: Photoacoustic soot sensor for in-situ black carbon monitoring, Appl. Phys., 63, 191–197, https://doi.org/10.1007/BF01095272, 1996.
Rosencwaig, A.: Photoacoustic Spectroscopy, Ann. Rev. Biophys. Bioeng., 46, 207–311, https://doi.org/10.1016/S0065-2539(08)60413-8, 1980.
Saleh, R., Hennigan, C. J., McMeeking, G. R., Chuang, W. K., Robinson, E. S., Coe, H., Donahue, N. M., and Robinson, A. L.: Absorptivity of brown carbon in fresh and photo-chemically aged biomass-burning emissions, Atmos. Chem. Phys., 13, 7683–7693, https://doi.org/10.5194/acp-13-7683-2013, 2013.
Saleh, R., Robinson, E. S., Tkacik, D. S., Ahern, A. T., Liu, S., Aiken, A. C., Sullivan, R. C., Presto, A. a., Dubey, M. K., Yokelson, R. J., Donahue, N. M., and Robinson, A. L.: Brownness of organics in aerosols from biomass burning linked to their black carbon content, Nat. Geosci., 7, 1–4, https://doi.org/10.1038/ngeo2220, 2014.
Saleh, R., Marks, M., Heo, J., Adams, P. J., Donahue, N. M., and Robinson, A. L.: Contribution of brown carbon and lensing to the direct radiative effect of carbonaceous aerosols from biomass and biofuel burning emissions, J. Geophys. Res.-Atmos., 120, 10285–10296, https://doi.org/10.1002/2015JD023697, 2015.
Singh, S., Fiddler, M. N., Smith, D., and Bililign, S.: Error analysis and uncertainty in the determination of aerosol optical properties using cavity ring-down spectroscopy, integrating nephelometry, and the extinction-minus-scattering method, Aerosol Sci. Technol., 48, 1345–1359, https://doi.org/10.1080/02786826.2014.984062, 2014.
Ugelow, M. S., Zarzana, K. J., Day, D. A., Jimenez, J. L., and Tolbert, M. A.: The optical and chemical properties of discharge generated organic haze using in-situ real-time techniques, Icarus, 294, 1–13, https://doi.org/10.1016/j.icarus.2017.04.028, 2017.
Washenfelder, R. A., Flores, J. M., Brock, C. A., Brown, S. S., and Rudich, Y.: Broadband measurements of aerosol extinction in the ultraviolet spectral region, Atmos. Meas. Tech., 6, 861–877, https://doi.org/10.5194/amt-6-861-2013, 2013.
Wei, Y., Ma, L., Cao, T., Zhang, Q., Wu, J., Buseck, P. R., and Thompson, J. E.: Light Scattering and Extinction Measurements Combined with Laser-Induced Incandescence for the Real-Time Determination of Soot Mass Absorption Cross Section, Anal. Chem., 85, 9181–9188, https://doi.org/10.1021/ac401901b, 2013.
Weingartner, E., Saathoff, H., Schnaiter, M., Streit, N., Bitnar, B., and Baltensperger, U.: Absorption of light by soot particles: Determination of the absorption coefficient by means of aethalometers, J. Aerosol Sci., 34, 1445–1463, https://doi.org/10.1016/S0021-8502(03)00359-8, 2003.
Zangmeister, C. D. and Radney, J. G.: NIST interlaboratory study of aerosol absorption measurements using photoacoustic spectroscopy, Tech. Note 1989, https://doi.org/10.6028/NIST.TN.1989, 2018.