the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A novel approach for simple statistical analysis of high-resolution mass spectra
Otso Peräkylä
Liine Heikkinen
Mikko Äijälä
Kaspar R. Daellenbach
Qiaozhi Zha
Matthieu Riva
Olga Garmash
Heikki Junninen
Pentti Paatero
Douglas Worsnop
Mikael Ehn
Recent advancements in atmospheric mass spectrometry provide huge amounts of new information but at the same time present considerable challenges for the data analysts. High-resolution (HR) peak identification and separation can be effort- and time-consuming yet still tricky and inaccurate due to the complexity of overlapping peaks, especially at larger mass-to-charge ratios. This study presents a simple and novel method, mass spectral binning combined with positive matrix factorization (binPMF), to address these problems. Different from unit mass resolution (UMR) analysis or HR peak fitting, which represent the routine data analysis approaches for mass spectrometry datasets, binPMF divides the mass spectra into small bins and takes advantage of the positive matrix factorization's (PMF) strength in separating different sources or processes based on different temporal patterns. In this study, we applied the novel approach to both ambient and synthetic datasets to evaluate its performance. It not only succeeded in separating overlapping ions but was found to be sensitive to subtle variations as well. Being fast and reliable, binPMF has no requirement for a priori peak information and can save much time and effort from conventional HR peak fitting, while still utilizing nearly the full potential of HR mass spectra. In addition, we identify several future improvements and applications for binPMF and believe it will become a powerful approach in the data analysis of mass spectra.
- Article
(5553 KB) -
Supplement
(722 KB) - BibTeX
- EndNote
Volatile organic compounds (VOCs) are emitted to the atmosphere both from biogenic and anthropogenic sources (Guenther et al., 1995; Wei et al., 2008). After oxidation, these gaseous species can partition to the particle phase and contribute to atmospheric organic aerosol (OA), a major component of tropospheric particulate matter (Zhang et al., 2007). The chemical components, both in particulate (OA) and gaseous phase (VOC and their oxidation products), play important roles in many atmospheric physical and chemical processes. They can deteriorate air quality causing adverse health effects, and aerosol particles can influence Earth's climate by altering the radiative balance, as well as decrease visibility (Stocker et al., 2013; Zhang et al., 2016; Pope III et al., 2009; Shiraiwa et al., 2017).
Recent instrumental advances in mass spectrometry have greatly enhanced our capability to investigate the chemical composition and evolution of aerosol particles and their precursors. The Aerodyne aerosol mass spectrometer (AMS) is widely applied in atmospheric research (Canagaratna et al., 2007), measuring the bulk composition and temporal behavior of the nonrefractory aerosol, and has successfully identified different/unique OA sources utilizing factor analysis (Jimenez et al., 2009; Zhang et al., 2011). With the development of gas-phase chemical ionization mass spectrometry (CIMS) (Huey, 2007) and the commercially available time-of-flight (TOF)-CIMS (Bertram et al., 2011) and CI-APi-TOF (chemical ionization atmospheric pressure interface time-of-flight mass spectrometer; Jokinen et al., 2012), these instruments are becoming more popular in atmospheric chemistry research. Due to these new advances, the detection methods for aerosol precursor vapors and the understanding of their formation mechanisms have been greatly improved. For example, the discovery of highly oxygenated molecules (HOM) by the CI-APi-TOF has led to increased knowledge regarding atmospheric oxidation pathways, with large implications on secondary organic aerosol (SOA) and new particle formation (Ehn et al., 2014; Jokinen et al., 2015; Kirkby et al., 2016; Yan et al., 2016). In particular, biogenic VOCs such as monoterpenes (C10H16) promptly produce HOM upon ozonolysis, e.g., C10H16O7 and C10H16O9.
While a mass spectrum can contain large amounts of information representing the highly complex nature of the atmospheric sample, it also presents considerable challenges for the analysis and interpretation of the data. One example of such a challenge is the identification and separation of peaks with similar but not identical masses. A single integer mass can contain tens of distinct ions, with mass-to-charge ratios (m∕z) close to each other. In all cases, specific spectral fitting techniques are needed to resolve the overlapping peaks at the same integer mass. Typically, a least squares fit is made to the spectrum, using analysis software such as Squirrel/PIKA (http://cires1.colorado.edu/jimenez-group/ToFAMSResources/ToFSoftware/, last access: June 2019), tofTools (Junninen et al., 2010) or Tofware (https://www.tofwerk.com/software/tofware/, last access: June 2019). However, these techniques require a predefined list of ions. This makes the analysis resource-intensive, and it can easily introduce subjective bias in determining the peak list.
Figure 1 depicts a concrete example, measured by a nitrate-based CI-APi-TOF, where peak separation is not large enough to allow unambiguous fitting of all the ions, and the final result will depend on which ions the analyst chooses to include. As the m∕z increases, the number of possible ions at a certain unit mass increases rapidly (Kroll et al., 2011; Stark et al., 2015). Too closely overlapping peaks will sometimes lead to ambiguously fitted peaks and arbitrarily resolved ions, resulting in unreliable separation of signals. Additionally, mass calibration errors can also affect correct peak assignment or fitting. A few recent studies discuss in more detail the uncertainties of ion identification and separation in high-resolution (HR) mass spectra (Stark et al., 2015; Corbin et al., 2015; Cubison and Jimenez, 2015).
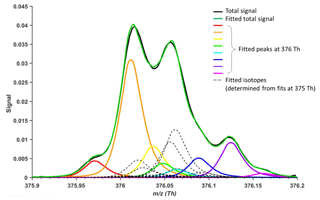
Figure 1Example of traditional HR peak fitting. Potential peak fitting at m∕z 376 Th (10 h average) in an atmospheric simulation chamber during a monoterpene ozonolysis experiment, utilizing a nitrate-based CI-APi-TOF (resolving power of 13 000 Th Th−1). Even a minor shift in the mass axis calibration could cause the signals of especially the yellow, green and blue peaks to change dramatically. Similarly, adding or removing an ion would alter the amount of signal attributed to the other fitted peaks.
Another typical analysis approach is to utilize only the unit mass resolution, or UMR, data. As opposed to high-resolution fitting, where the signals of individual ions are separated from the total measured signal, in UMR analysis all signals at a given integer mass are integrated and treated together. This approach is more straightforward and less subjective than HR fitting but loses all possible high-resolution details in the spectrum (see Fig. 2).
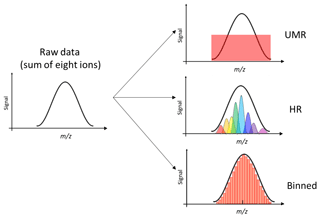
Figure 2Conceptual comparison of traditional methods (UMR and HR) and binned mass spectra for PMF analysis. The raw data signal is shown in the left and contains eight ions. By UMR analysis, the information of the eight ions is totally lost. Using an analyst-determined peak list, HR analysis attempts to separate signals at this mass by fitting selected ions. By binning the spectra, we utilize the HR information without any a priori information required.
Even with perfect high-resolution peak fits, a spectrum typically contains information of hundreds, if not thousands, of ions, many of which come from similar sources. This wealth of data itself presents a challenge for data analysis. Factor analysis enables the reduction of data dimensions and can help to apportion the signals to factors. These factors may correspond to different sources or formation processes. Positive matrix factorization (PMF) (Paatero and Tapper, 1994) has been widely utilized in environmental sciences, applied to UMR and HR AMS data, succeeding in identifying multiple OA sources (Lanz et al., 2008; Ulbrich et al., 2009; Sun et al., 2011; Zhang et al., 2011). Compared to AMS data, PMF has been applied to CIMS data analysis much less frequently. To our knowledge, only Yan et al. (2016) and Massoli et al. (2018) have reported PMF analysis on nitrate-based CI-APi-TOF, utilizing UMR and HR data, respectively.
UMR-PMF cannot utilize the full information content provided by HR mass spectrometers but is more straightforward to apply. In contrast, accurate HR peak fitting can better preserve the information content of the raw data than UMR and thus provide more information to PMF, resulting in more interpretable results. However, incorrectly fitted peaks can severely disturb the PMF modeling and the factor interpretation. In addition, mass spectra from iodide-adduct TOF-CIMS (Lee et al., 2014) often contain more peaks per mass than the -CI-APi-TOF, making HR fitting much more complex (or, in some cases, even unmanageable), severely limiting the potential of HR PMF.
In this study, a novel, yet simple and reliable, data analysis method, binned mass spectra combined with PMF (binPMF), is proposed to try to tackle the abovementioned problems in both HR and UMR PMF. Instead of using traditional UMR or HR fitting techniques for the mass spectra, we binned the mass spectra prior to PMF analysis (Fig. 2). We applied binPMF to both ambient and synthetic datasets, succeeding in separating the key components of different sources/processes. Compared to UMR PMF, binPMF preserves more of the high-resolution information content of the mass spectra, without the immense effort and subjectivity associated with high-resolution peak fitting. As a result, this novel method can improve our understanding of sources/formation processes governing the particulate and gaseous phases in more detail and in a less subjective manner.
We divided the mass spectra into narrow bins as presented in Fig. 2 and carried out PMF analysis to extract more information from the dataset. Details on the data preparation (binning the mass spectra) and error estimation for the PMF input are discussed in the Sect. 2.2 and 2.3. To test the performance of binPMF under different scenarios, we first constructed synthetic datasets, using a simple one-/two-mass system (Sect. 2.4.1). In the second step, we applied binPMF to an ambient dataset measured with a -CI-APi-TOF in a boreal forest site located in southern Finland (Sect. 2.4.2).
2.1 Positive matrix factorization
The PMF model was developed by Paatero and Tapper (Paatero and Tapper, 1994) in the 1990s and has been widely applied in the analysis of various types of environmental data ever since (Zhang et al., 2017; Yan et al., 2016; Ulbrich et al., 2009; Song et al., 2007). By decomposing the observed dataset into different factors, PMF helps to simplify the complex data matrix and extract useful information contained within it. Compared to other common source apportionment tools, like chemical mass balance (CMB) (Schauer et al., 1996), PMF requires no prior knowledge of source information as essential input. Nevertheless, as a statistical method, PMF does require more data as input, which is typically not a problem for environmental mass spectrometry datasets. The main distinction of PMF from other factor analysis techniques is that PMF utilizes a least squares minimization scheme weighted with data uncertainties, as well as nonnegative constrains, to minimize the ambiguity caused by rotation of the factors (Huang et al., 1999; Paatero and Tapper, 1994).
In PMF modeling, a measurement of chemical species is assumed to be a sum of contributions from several relatively fixed sources/processes. The measured data matrix is broken down to two smaller matrices and a residual term as follows:
where X represents an m×n data matrix of original measurement for species n (e.g., m∕z) at time point m, TS is the m×p time series matrix of factor contributions, MS is the p×n matrix of factor profiles or the factor mass spectra, and R is the residual between the modeled and the measured data. p is the number of factors, which needs to be determined based on the interpretability of the PMF results, among other criteria. Thus, in PMF, the original data matrix is approximated in terms of p factors, each of which has a distinct mass spectrum and time series.
To find the solution, the PMF model utilizes uncertainty estimates for each element in the data matrix X. These uncertainty estimates are used to weight the residuals (R), in order to calculate the Q value as
where Sij is the estimated uncertainty of species/mass j at time point i, and Rij is the residual of that mass at the same time. Q is then minimized iteratively to find the mathematically optimal solution. An expected Q value (Qexp) can be calculated as the number of non-down-weighted data values in X minus the sum of elements in TS and MS. If the data follow the requirements of PMF, the solution with the correct number of factors should have a Q∕Qexp value near unity. When this is true, the residuals on average fall within the expected uncertainties for each time point and variable. More details about uncertainty estimation will be discussed in Sect. 2.3. The PMF analysis in this study was performed with the toolkit of Source Finder (SoFi, v6.3) (Canonaco et al., 2013) using the multilinear engine (ME-2) (Paatero, 1999). Masses with low signal-to-noise ratio (SNR<0.2; see Sect. 2.3 on error estimation) were down-weighted by a factor of 10, and masses with were down-weighted by a factor of 2, as suggested by Paatero and Hopke (2003). The down-weighting effect was considered in the Qexp calculation. In this study, PMF was operated in robust mode, where outliers () were dynamically down-weighted (Paatero, 1997).
One of the problems in any factorization analysis is rotational ambiguity, which is caused by an infinite number of similar solutions generated by PMF (Paatero et al., 2002; Henry, 1987). Generally, the nonnegativity constraint alone is not sufficient for solution uniqueness. Rotating a certain solution and assessing the rotated results is one possible way to determine the most physically reasonable solution. Known source profiles or source contributions can also serve as constrains. In addition, if there is a sufficient number of time points when the contribution of a source is nearly zero, independent of other sources, rotational uniqueness of solutions can be achieved (Paatero et al., 2002). The same is true if specific variables in the profiles go to zero. Otherwise, the correct solution (correct rotation) may only be obtained by skillful use of rotational tools. Ambient measurement data can often contain zero values in most sources/processes, greatly reducing rotational ambiguity of the PMF results. The issue of rotational ambiguity is not explored in detail in this paper, as it is common to all PMF approaches, and the main purpose here is to illustrate the new methodology of binPMF. All the solutions shown in this study were achieved without considering their rotational uniqueness. Finally, we note that, in addition to rotational ambiguity, binPMF also inherits all other fundamental limitations and strengths of the underlying PMF method.
2.2 binPMF data matrix preparation
Instead of UMR or HR fitting of the mass spectra, the mass spectra were divided into small bins after mass calibration (Figs. 2 and S1 in the Supplement). Data were first linearly interpolated to a mass interval of 0.001 Th and then divided into bins of 0.02 Th width. At an integer mass N, only the signals between N−0.2 and N+0.3 Th (the signal region) were binned to avoid unnecessary computation of masses without any signal. With the binning, there were 25 data points for each nominal mass, instead of only one signal in UMR or several fitted peaks in HR analysis. All the parameters mentioned above, e.g., bin width and signal region size, should be adjusted to suit the mass spectrometer and the data being analyzed. Further details on binning procedures are discussed in Sect. 3.3.
2.3 binPMF error matrix preparation
Besides the data matrix, an error matrix describing the expected uncertainty for each element in the data matrix is also required as input in PMF analysis. Here, the error matrix (Polissar et al., 1998) is estimated as
where the uncertainty of mass j at time point i, Sij, is composed of analytical uncertainty σij and instrument noise σnoise. σij is the uncertainty arising from counting statistics and is estimated as
in which I is the signal intensity in counts per second, ts is the averaging time in seconds and a is an empirical parameter incorporated to include unaccounted uncertainties (Allan et al., 2003; Yan et al., 2016). In our study, we applied binPMF with CI-APi-TOF data as an example, and the same a value of 1.28 was utilized as estimated previously from laboratory experiments in the work of Yan et al. (2016). The σnoise is calculated as the median of the standard deviation of instrument noise, calculated from the bins between two nominal masses that should be least influenced by real signals (the noise region), i.e., N+0.5–N+0.8 Th (see Fig. S1).
2.4 Data sources and description
This study utilized both ambient and synthetic datasets to test the performance of binPMF. The ambient data were collected at the SMEAR II station (Station for Measuring Ecosystem–Atmosphere Relations; Hari and Kulmala, 2005) in the boreal forest in Hyytiälä, southern Finland. Located in a rural forest area, the station has a wide range of continuous measurements of meteorology, aerosol and gas-phase properties year-round. There are no strong anthropogenic sources close to the site but two sawmills 5 km to southeast and the city of Tampere 60 km to the southwest. Detailed meteorological parameters and concentrations of trace gases during this campaign have been presented earlier (Zha et al., 2018). Before the application to ambient data, we constructed a simple synthetic dataset to examine how well binPMF can separate overlapping ions under different conditions.
2.4.1 Synthetic dataset
As a first test of the performance of binPMF, we generated a series of synthetic datasets based on two distinct sources. Each synthetic dataset Y was created by summing up the signals of the two sources. Each source consisted of a constant source profile (represented as the matrix MS) and had a unique temporal behavior (represented as the matrix TS). Each source was the multiplication of MS (mass spectra/source profile) and TS (time series). The two TS values for the two sources were generated randomly and independently from each other, as shown in Fig. S2 (correlation coefficient R=0.375). To avoid rotational ambiguity (see Sect. 2.1) in these tests, we added zero values to the time series of the two sources, independently of each other.
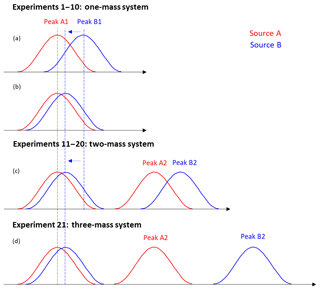
Figure 3Conceptual schematic diagram for the synthetic datasets. Panels (a) and (b) describe experiments 1–10 in the one-mass system; panel (c) describes experiments 11–20 in the two-mass system. Panel (d) shows experiment 21, with peaks A2 and B2 at separate integer masses (see text for details).
As shown in Fig. 3, each source profile (MS) was generated to consist of either one or two separate peaks, covering either one or two unit masses, respectively. The peaks were generated as Gaussians of known width and centroid position. The peaks of the different sources/profiles were partially overlapping, with the exact overlap, i.e., the distance (m∕z difference) between the overlapping peaks, being varied from one experiment to another.
Peaks in the synthetic MS profiles were first generated as perfect smooth peaks (fine m∕z interval of 0.00001 Th), with mass resolution of 5000 Th Th−1. We define the resolution R of a peak as , where M is the mass of the ion, and ΔM is the full width at half maximum signal intensity, FWHM. As an example, with R=5000 Th Th−1, an ion at m∕z of 300 Th will have a FWHM of 0.06 Th, corresponding to 200 ppm. Multiplying the source profiles and the time series, we generated an ideal data matrix. From this ideal matrix, we sampled with a m∕z interval of 0.015 Th to simulate the real measurement data. The interval selected was close to that typically used for the high-mass-resolution (HTOF; Junninen et al., 2010) mass analyzer on a CI-APi-TOF. After the sampling, Gaussian distributed noise, both from background random noise and signal-dependent noise, was added to make up the data matrix Y′, point by point, as shown in Eq. (6) below. The variance of the Gaussian distributed noise was estimated as one-hundredth of the coefficient c, which is the average value of Y.
Finally, random m∕z shift within ±10 ppm was added to simulate mass calibration error, spectrum by spectrum. This error, resulting from inaccurate conversion of the time of flight into the mass-to-charge ratio, is one of the main causes of ambiguous or incorrect peak assignment or fitting. In our study, with the bin width of 0.02 Th and the mass calibration error of 10 ppm, a maximum of 15 % of one bin's signal may incorrectly shift to the adjacent bin, for a mass at 300 Th ( %). The impact of this mass shift will effectively be smaller, due to the high temporal correlation of adjacent bins, as the signal from an ion will spread to several adjacent bins (the FWHM is ∼3 times the bin width). In the case of HR fitting of peaks, a 10 ppm mass calibration error may cause much more dramatic changes than merely shifting 15 % of the signal. There is also no reason for ions from a given source to selectively end up at the same integer mass, meaning that the signal is likely to be shifted to another ion from a completely different source.
Twenty-one synthetic experiments were designed, varying the mass difference between peaks (m∕z difference) and number of unit masses included in the MS, as shown in Table S1 in the Supplement and Fig. 3. For experiments 1–10, each of the two source profiles consisted of one peak (A1 and B1), both located at the same unit mass (chosen to be 310 Th in this study), with varying separation of the peak centroids. In experiments 11–20, we added one more peak to each profile (peaks A2 and B2), in addition to peaks A1 and B1. The additional peaks were added at another unit mass (311 Th) and their m∕z difference was fixed at 0.05 Th (161 ppm), while the position of peak B1 was varied as in experiments 1–10. For experiment 21, peaks A2 and B2 were added at two different masses (311 and 312 Th), corresponding to a m∕z difference sufficiently large that there was no meaningful overlap between them. In the MS (i.e., mass spectra profiles), all peaks had the same intensity level initially. The variation of the peak intensity ratio comes from variations in the time series (Fig. S2). The same time series for each of the two sources was used in all experiments 1–21.
With this approach of only using two masses, we purposefully provide a challenging dataset for binPMF, as in most real datasets there would be many more masses to help constrain the final solutions. Nevertheless, as we will show, this simple synthetic dataset already provided a wealth of useful information in the results attainable with binPMF and provided a good comparison to the traditional HR fitting approach.
2.4.2 Ambient dataset
The ambient dataset was measured at ground level during the Influence of Biosphere-Atmosphere Interactions on the Reactive Nitrogen budget (IBAIRN) campaign (Zha et al., 2018) in September 2016. The measurements were conducted using a -CI-APi-TOF that has been described in detail elsewhere (Jokinen et al., 2012; Junninen et al., 2010; Yan et al., 2016). Here, the ambient gas-phase molecules clustered with the nitrate ion were measured with about 4000 Th Th−1 mass resolving power. Data from 1 to 26 September, averaged to 1 h time resolution, in the mass range of 300–350 Th (a typical monoterpene HOM monomer range, Ehn et al., 2014) were utilized for the binPMF analysis. A baseline subtraction was applied to the mass spectra, which caused some small signals next to large peaks to become negative. In our analysis, any m∕z bin where the median signal was negative was excluded from the data matrix.
3.1 Synthetic dataset
3.1.1 Experiment settings
As introduced in Sect. 2.4.1, the synthetic datasets were constructed to assess the response of binPMF to varied m∕z difference, peak intensity ratios and number of masses included, as shown in Table S1 and Fig. 3. The smaller the distance between the two peaks, the harder it is to accurately separate them with traditional HR peak identification and fitting. In our experiments, the m∕z difference was decreased stepwise from 0.050 Th (161 ppm) to 0.001 Th (3 ppm), in a system where the FWHM was roughly 200 ppm.
The analysis procedure of the synthetic dataset is briefly described here. In all cases, the parameter of interest is to see how well binPMF is able to deconvolve the adjacent peaks A1 and B1 at m∕z 310 Th. First, binPMF was applied to the synthetic datasets, and factors profiles (mass spectra) were extracted. The optimal number of factors for the synthetic dataset is two, the same as the number of sources, so only the two-factor solution was studied with binPMF. The results of the diagnostic parameter Q∕Qexp for each experiment are included in Table S1. Gaussian fitting was then performed on the factor profiles to retrieve the locations of peaks A1 and B1 and thereby assess how well binPMF was able to retrieve the original peak positions.
In addition to applying binPMF to the synthetic datasets, traditional HR peak fitting was also conducted as comparison (by tofTools in our study). For the tofTools fits, we constrained the peak locations and widths to those originally used for generating the data (Table S1). Peaks fitted by tofTools and peaks fitted to the binPMF factors were compared, as well as the retrieved time series correlation with the original datasets. More details are presented and discussed in the following sections.
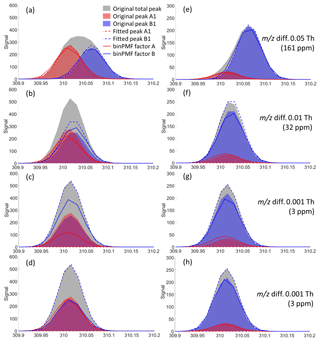
Figure 4Peak separation results by a traditional HR fitting method (dashed lines) and binPMF (solid lines), at the 79th time point (a–d) and at the 21st time point (e–h) for experiment numbers 1 (a, e), 5 (b, f), 10 (c, g), and 20 (d, h). The signal intensity ratios of peaks A1 and B1 were about 1:1 and 1:6, respectively, at the 79th and the 21st time points. Panels (a)–(c) and (e)–(g) are for the one-mass system, while panels (d) and (h) are for the two-mass system.
3.1.2 Comparison of peak fitting
We examined the performance of traditional HR fitting and binPMF by comparing their results to the original input data. In Fig. 4, the shaded areas depict the original data, the dashed lines the traditional HR peak fitting result and the solid lines the binPMF factors. Red and blue represent source/factor A and B, respectively. Panels (a)–(d) (in Fig. 4) show four scenarios of peak fitting results from experiments 1, 5, 10 and 20 at the 79th time point, where the two peaks had similar signal intensities. When the two peaks were separated by 0.05 Th (Fig. 4a), both methods captured the peak intensities quite well. However, as the m∕z difference narrowed, the performance of both methods declined, with the HR fitting results deteriorating faster than those from binPMF. As m∕z difference reached 0.001 Th (3 ppm), the traditional HR fitting method completely failed to fit the two peaks (panels c and d), instead attributing all the signal to just one fitted mass. In panels (e)–(h), the peak fitting results at the 21st time point are displayed, where the ratio of the two peaks was roughly 1:6. Here, the traditional fitting method failed to extract the two peaks already at a m∕z difference of 0.01 Th (30 ppm), attributing all signal to peak B1 (panels g and h). As shown in panels (d) and (h), when a second set of peaks, separated by 0.05 Th, was introduced for the two sources in the datasets, binPMF was able to utilize the temporal behavior of peaks A2 and B2, performing much better, even in the extremely difficult cases when the m∕z difference for the two peaks was only 0.001 Th (3 ppm). It is an inherent advantage of binPMF over traditional peak fitting methods that the temporal behavior and the correlations between different variables can be utilized.
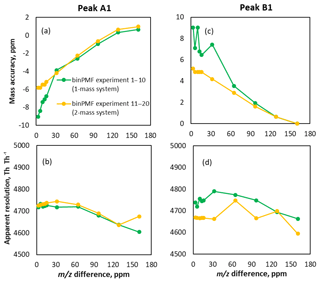
Figure 5Characteristics of peaks fitted to binPMF factors. Panels (a) and (b) show results for peak A1 and (c) and (d) for peak B1. In panels (a) and (c), the mass accuracy of peaks resolved by binPMF is compared to the original data. Panels (b) and (d) depict the resolution of the two fitted peaks. The original resolution of the input data was 5000 Th Th−1.
Figure 5 shows an overview of all the results of peaks fitted with binPMF. Experiments 1–10 for the one-mass system are shown with green lines and experiments 11–20 for the two-mass system in yellow. Mass accuracy was calculated as the difference between fitted peak center mass and the original mass, divided by the original mass, in parts per million. When the m∕z difference got smaller, the mass accuracy of peaks fitted to binPMF factors declined (Fig. 5a and c). At a m∕z difference of 0.01 Th (32 ppm), the mass accuracy was and 7±2 ppm for peaks A1 and B1, respectively. The uncertainties were estimated by repeating the analysis with 10 different random time series for the two sources (Brown et al., 2015). For comparison, this separation approximately corresponds to that between (310.0780 Th) and (310.0892 Th). With the m∕z difference decreasing, the position of peak A1 (the left red peak in Fig. 3), as identified by binPMF, shifted gradually to the left, while peak B1 (the right blue peak) shifted to the right. When peaks A2 and B2 were introduced to the sources, the mass accuracy improved (<6 ppm). The resolution of the peaks fitted to binPMF factor profiles stayed fairly constant but had degraded compared to the original input data (5000 Th Th−1), explained at least partially by the data binning (Fig. 5b and d). Overall, binPMF performs relatively well in peak separation, with reasonable mass accuracy and peak resolution compared to the original datasets.
3.1.3 Correlation of time series
In addition to the peak positions, we also compared the temporal behavior of both the binPMF factors and the time series obtained through traditional fitting to the original time series. When the m∕z difference was larger than 0.02 Th (65 ppm), both methods worked similarly well in reproducing the original time series (Fig. 6). As the m∕z difference decreased below 0.02 Th (65 ppm), correlations decreased rapidly (panels a and c), with that of the traditional method decreasing faster. However, as shown by the yellow lines, when peaks A2 and B2 were added to each source profile, the time series correlation coefficients between original data and peaks extracted by binPMF were close to unity in experiments 11–20. The coefficients stayed similar to that from the experiment with a m∕z difference of 0.05 Th (161 ppm), which was the fixed m∕z difference for the two new peaks added at 311 Th in experiments 11–20. This means that the separation of the factor time series was mainly driven by the additional, better-separated peaks. Again, the traditional HR fitting method could not utilize the information at 311 Th, and therefore no improvement to the peak deconvolution at 310 Th was seen. In addition to the correlation analysis, also the assignment of absolute signal to peaks A1 and B1 was evaluated. This was done by a linear fit (through zero) to the data points retrieved by the different methods as a function of the original input data. The slopes of the fitted lines are plotted in Fig. 6b and d and show that the signal was for the most part correctly attributed to within a few percent. The largest scatter in the determined slopes was observed for binPMF experiments with only one mass, at low peak separations.
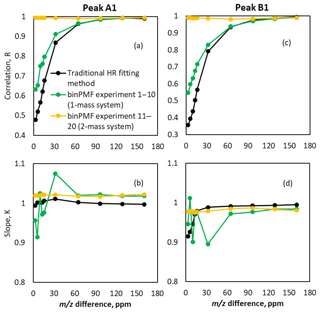
Figure 6Comparison of time series of binPMF and HR fitting. Panels (a) and (b) show results for peak A1 and (c) and (d) for peak B1. Correlation of time series (a, c) retrieved by binPMF (green lines for experiments 1–10, yellow for 11–20) and traditional HR fitting (black lines) compared to original input data. Panels (b) and (d) depict the slope K of the linear fit , where y is the signal retrieved from the synthetic data by either binPMF or the HR fitting, and x is the original input signals.
3.1.4 Summary and discussion
Based on the results shown above, binPMF was found to be as capable of separating different peaks as traditional peak fitting techniques when the two peaks were separated by more than the mass calibration uncertainty (yet still in all cases by less than the FWHM of the peaks). As the m∕z difference of the two overlapping peaks decreased, the performance of the traditional method declined faster than that of binPMF. This was shown for signal attribution of fitted peaks and time series correlation with original data. When masses with covaried temporal behavior of the targeted overlapping peaks were introduced in the dataset, the performance of binPMF improved significantly.
The peak fitting principles of the traditional method and binPMF are very different. For example, tofTools fits peaks based on predetermined instrument parameters (e.g., peak shape and peak width), as well as the peak location, either as a numeric value or a chemical composition from which the location is calculated (Junninen et al., 2010). HR peak fitting by tofTools can be effective if the majority of the components (peaks) are known and provided in a peak list, which is valuable information for peak separation that was not provided to binPMF in this study. However, this information can be hard to achieve due to unknown numbers and/or identities of all the ions at a given mass, in combination with the limited mass resolving power of the mass spectrometer. HR peak fitting is also sensitive to mass calibration error, increasingly so when many ions in close proximity to each other need to be fit. On the contrary, in binPMF, peaks are separated based on the temporal variation of masses, which is an inherent advantage of PMF, though no information of the peaks is provided beforehand. To be more specific, a conceptual illustration is shown in Fig. S3. The red peaks belong to source A and the blue peaks to source B. As mentioned before, the time series of sources A and B were totally independent and random. The shaded areas (the tails of the peaks), e.g., red shaded area in Fig. S3a, contained masses that only had significant signal from peak A1 (left red peak). Similarly, the blue shaded area in Fig. S3a was mostly from peak B1. The different temporal behaviors of the red and blue shaded areas helped the separation and correct attribution also in the regions with overlapped signals. When the m∕z difference of peaks A1 and B1 decreased, shown in Fig. S3b, the two shaded areas also became smaller. This is the main reason why the fitted masses of binPMF had lower mass accuracy and lower correlation coefficients compared to the original data, as the m∕z difference decreased.
When peaks A2 and B2 (m∕z difference of 0.05 Th) were added in the dataset, peaks A1 and B1 were better separated and fitted by binPMF compared to the scenarios with only one mass. This is because, as shown in Fig. S3c, the red and blue shaded areas became larger due to the addition of two more peaks. In this case, it was peaks A2 and B2 that dominated the separation of sources A and B. In experiment 21, three integer masses were included in the dataset. Though it was still equally difficult for the traditional HR method to separate and fit peaks A1 and B1 with a m∕z difference of 0.001 Th (3 ppm), it was the easiest experiment for binPMF out of all the experiments because of the large m∕z difference of peaks A2 and B2 (1.000 Th, 3225 ppm). In experiment 21, the mass accuracies for peaks A1 and B1 were −3.2 and 2.6 ppm, respectively, and the time series correlation with original data was 1.000 and 0.999, respectively. In most real-world applications, individual sources typically contain multiple peaks, and the correlations of these can be utilized by binPMF.
We note once more that the results of binPMF and traditional HR peak fitting are not totally comparable. Information about the peaks, like the exact peak centroid position, peak width (resolution) and number of peaks, was provided to the traditional fitting method. For binPMF, no prior information about the peaks was given, except for the optimal number of factors, i.e., two.
3.2 Ambient dataset
With the success of binPMF for the synthetic datasets, we applied the new method to a real ambient dataset. Here we used data collected in September 2016, from Hyytiälä in Finland. The SMEAR II station is a forest site dominated by monoterpene (C10H16) emissions (Hakola et al., 2006). Previous CI-APi-TOF measurements of HOM at the site (Ehn et al., 2014; Yan et al., 2016) have presented bimodal distributions, with one mode corresponding to HOM monomers (range 300–400 Th) and the second to HOM dimers (450–650 Th). For testing the binPMF analysis on our ambient dataset, we selected the HOM monomer range of 300–350 Th. While the synthetic dataset primarily compared binPMF to traditional HR fitting analysis, in this section, we compare the binPMF results with that of traditional UMR-PMF, as employed by Yan et al. (2016). HR fitting was not performed for the ambient dataset, for all reasons mentioned in earlier sections, including the difficulty and efforts of producing a proper unambiguous peak list, as well the limitations of overlapping peaks.
As mentioned above, no prior knowledge was provided to PMF before the analysis. To determine the number of factors for further analysis, we conducted runs with two to eight factors. As the number of factors increased, more information could be extracted from the raw data. However, after the optimal number of factors, the additional factors may split the physically reasonable factors into meaningless fragments. There have been many studies on evaluations of PMF runs and selections of PMF factor number (Zhang et al., 2011; Craven et al., 2012). This is an inherent challenge in any PMF analysis, and not specific to binPMF, and therefore we do not put emphasis on this here. In this study, based on commonly used mathematical parameters and physical interpretation, we chose the seven-factor result, as presented below. Our main aim with this work is to present a proof of concept for the binPMF methodology, and we will therefore not provide a detailed interpretation of all the factors (though several of the factors are easily validated based on earlier studies). The factor evolution from two to eight factors is briefly discussed below.
From two to six factors, Q∕Qexp showed a dramatic decrease from 6.5 to 2.7. Then for seven and eight factors, Q∕Qexp decreased to 2.3 and 2.0, respectively. The unexplained variation also declined from 14 % to 8.8 %, going from two to six factors, and then reached 8.0 % for seven factors and 7.6 % for eight factors. The two-factor solution first split the data into a daytime factor and a nighttime factor, with very distinct mass spectral profiles. The daytime factor was characterized by signals at 307, 311, 323, 339 Th and other odd masses, while the nighttime factor was dominated by 308, 325, 340 and 342 Th. The odd masses are typical signatures of daytime monoterpene-derived organonitrates at the site, while the even masses, and specific odd masses e.g., a radical at 325 Th, have been identified as monoterpene ozonolysis products (Ehn et al., 2014; Yan et al., 2016). As the number of factors increased, the daytime factor was further split into new daytime factors, with diurnal profiles having various peak times around noon or early afternoon. When the number of factors increased to seven, a clear sawtooth shape in the diurnal trend was resolved with marker masses at 308, 324, 325 and 339 Th. Many of the profiles resolved in the seven-factor solution are similar to those found by Yan et al. (2016), and separating more factors did not yield new factors that we could interpret. Therefore, we opted to use this seven-factor result for the main discussion below, as it provided us with enough information to evaluate the binPMF method for this dataset.
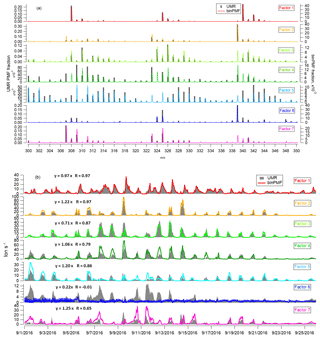
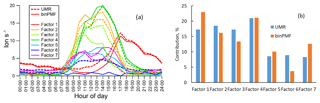
Figure 7Comparison of binPMF and UMR-PMF for factor mass spectral profiles (a) and time series (b). The equations in each panel describe how signals from binPMF (y) compare with the UMR-PMF solution (x). R is the correlation coefficient between the time series.
Figure 7 shows the mass spectral profiles and factor time series for the seven-factor result, while Fig. 8 displays the diurnal trends and factor contributions to the total signal. As shown in Fig. 8a, the seven factors separated by binPMF consist of one nighttime factor (Factor 1), five daytime factors (Factor 2, 3, 4, 5 and 7) and a sawtooth-pattern factor (Factor 6). The same dataset was also analyzed by UMR-PMF, and the corresponding seven-factor results are also included in Figs. 7 and 8 for comparison.
Overall, the results between UMR-PMF and binPMF are very similar. UMR-PMF also resolved one clear nighttime factor and additionally six daytime factors. For the nighttime factor, both binPMF and UMR-PMF showed comparable temporal behavior, diurnal trend (peak at 17:00; all times are given in Finnish winter time, UTC+2), mass spectral profiles (peaks at 340, 308, 325, 342 Th) and factor contribution (∼20 %). This factor has been validated in both chamber and ambient studies to be formed from monoterpene ozonolysis (Ehn et al., 2014; Yan et al., 2016). As shown in Fig. 7a, both methods also resolved similar, though not identical, mass spectral profiles for the other six factors, with mostly comparable time series (Fig. 7b) and peak times in the diurnal trends (Fig. 8a).
Despite the similarities, there also existed distinct differences between the results from binPMF and UMR-PMF. As the most distinctive dissimilarity, binPMF Factor 6 revealed a contamination factor. This factor was found to be related to automated instrument zeroing every 3 h, giving rise to the distinct 3 h sawtooth pattern. The zeroing system introduced some additional compounds into the sampling lines, and the semivolatile nature of these compounds caused them to linger, and slowly decay, in the tubing even after the instrument had returned to sampling ambient air. binPMF accurately retrieved the 3 h interval of the zero measurements. However, with the same mass range (300–350 Th), UMR-PMF failed to extract the contamination factor, regardless of the number of factors retrieved (up to 20 factor solutions were evaluated). Instead, these contamination signals were always mixed into the other factors. Factor 6 from UMR-PMF contributed almost twice as much as that estimated by binPMF due to the inaccurate factor separation (Fig. 8b). The time series of other factors, e.g., Factor 5 and 7 in UMR-PMF, were clearly influenced by Factor 6. Compared to UMR-PMF, binPMF thus showed a clear advantage in providing more information out of the data by being more sensitive to subtle variations.
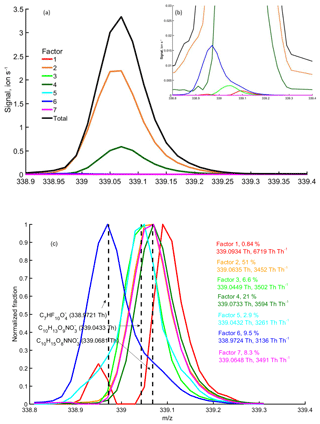
Figure 9binPMF factor profiles at m∕z 339 Th at 12:00 on 9 September. Panels (a) and (b) show the absolute concentrations of each factor, while in panel (c) the factor profiles are normalized to the same maximum peak heights. The fitted peak location (Th) and the apparent resolution (Th Th−1) for each factor are given in panel (c). The contribution of different factors to the integer m∕z 339 Th is shown as a percentage. Three potential chemical compositions were marked with black vertical dashed lines.
In addition to better resolving certain factors from the data, the binPMF mass spectral profiles will still contain more information than visible in Fig. 7, due to the multiple bins at each unit mass. As an example, binPMF Factor 6 showed masses with clear negative mass defects, e.g., at 324 and 339 Th (Fig. 9). We identified many ions in this factor as different fluorinated carboxylic acids, which are common interference signals in negative ion CIMS, outgassing from, e.g., Teflon tubing (Brown et al., 2015; Ehn et al., 2012; Heinritzi et al., 2016). The exact source of these products in our setup was not established, but it is not surprising that the additional valves, filters and/or tubing in the zeroing line could have caused this type of signal to be introduced to the instrument with the zero air. In general, this finding highlights the usefulness of the binPMF approach, where factor separation can be performed first, and the specific factor profiles can be utilized in interpreting the physical meaning of the different factors. This is in complete contrast to the more traditional approach, where all ions need to be identified first, and only then can HR PMF be attempted. As not all ions are going to be observable at all times, many ions may remain unidentified. For example, if peak identification would only have been done during periods when the HOM signals were high, as in the case shown in Fig. 9a, the fluorinated ion at 339 Th would not have been found (contributing only 0.45 % to the total signal at this time point), even though it on average contributes nearly 10 % of the signal at this mass over the entire campaign. binPMF, on the other hand, utilized the full dataset for the identification and was able to separate several ions at 339 Th. By fitting Gaussian signals to the factor profiles, similar to the synthetic data in Sect. 3.1.2, we see that the two major peaks were fitted with decent resolution (Fig. 9). Also the contamination factor (Factor 6) was clearly separated and fitted, and the resolution (3136 Th Th−1) is slightly underestimated by the fit, as only one Gaussian was fitted to each profile, yet there is clearly more than one ion at 339 Th in Factor 6. As shown in Fig. 9c, there is also a clear indication that Factor 3 and 5, which together make up as much signal at 339 Th as the contamination Factor 6, mainly contain signals from another molecule (C10H13O9) rather than the dominant signals at this mass (C10H15NO8). However, further work will be needed to validate this. Factor 1 has marginal contribution to the signal at 339 Th (as seen in Fig. 9b) throughout the campaign, and we expect it does not contain a useful signal, as is suggested by the unreasonably high resolution, i.e., narrow peak width, of the fitted peak. The resolving power of the instrument was around 4000 Th Th−1, and thus any apparent peak resolution above that will be unrealistic. However, as this factor contains signal at the outer edges of the main peaks at this m∕z, it is possible that this factor relates to some instrumental variability affecting the peak shape. This is highly speculative, but such a phenomenon may be worth looking into in later studies utilizing binPMF. In summary, resolving multiple overlapping peaks by traditional methods is time-consuming and can be tricky and ambiguous. Here, binPMF greatly simplified this problem by providing additional separation between the ions.
3.3 Future improvements and applications
The new technique for mass spectra analysis, binPMF, as presented above, shows clear promise in utilizing HR information while saving time and effort, as well as decreasing ambiguity related to conventional HR peak fitting. It is also more sensitive to subtle variation than standard UMR analysis. We consider this study a successful proof of concept and note that several future improvements and applications are still foreseeable. We list some of these below.
-
Varied bin width. The full width at half maximum of an individual peak in a mass spectrometer is mass-dependent, with peaks getting wider at higher masses. In binning the mass spectrum with a constant bin width, like in this study, the average number of bins per peak increases as a function of mass. To represent the peaks in a comparable manner, the bin width should thus be dependent on the mass. Varying the bin width as a function of the mass, and the mass resolution of the instrument, would enable a constant number of bins (e.g., seven) per peak. Too few bins per peak would mean that we may lose valuable information in the binning, and potentially risk introducing aliasing effects, while too many points per peak would lead to an unnecessarily high number of variables, without noticeable gain in information content. This would also result in high computational cost. If targeting seven bins per peak, then the function for determining bin width based on m∕z and resolution (R, which is mass-dependent) could be
Δm is the full peak width at half maximum signal intensity. If we consider an instrument with approximate constant resolution of 5000 Th Th−1 for masses from 200 to 600 Th, the bin width at 200 and 600 Th should be around 0.01 and 0.03 Th, respectively.
-
Optimization of binning region. Similarly to bin width, the binning region, i.e., the signal region ( in this study, introduced in Sect. 2.2), should also be mass-dependent. Due to the widening of the peaks with increasing mass, the binning region should also get wider. In addition, the typical mass defect of measured ions typically varies with mass. This means that the binning regions should not necessarily be defined with respect to the integer masses but to some chosen mass defect. Another approach would be to bin all the data and remove the bins not meeting a certain criterion, such as one related to the signal-to-noise ratio in that bin, afterwards. In this case, there would be no need for a predefined mass defect or region width, and one could utilize the signals that do not fall within the expected regions.
-
Error estimation. Good error estimation is crucial to PMF calculation. Uncertainty in PMF analyses arises from three main causes, random errors in data values, rotational ambiguity and modeling errors (Paatero et al., 2014). Variations in mass calibration are one example of a modeling error. It is common practice to increase uncertainty values Sij specified for data values disturbed by modeling errors. This increase does not account for the mass calibration error in the sense that the effect of mass calibration variation would disappear. The increase simply balances residuals in different data values so that the best possible result may be obtained. In addition to the two error estimation terms discussed in Sect. 2.3, σij and σnoise, a third form of error, to balance the mass calibration variation, could also be considered for error estimation. Similarly, although generally rare and suggestive of some instrumental problem, if the peak shape or resolution shift over time, this would also require an improved error estimation in order to account for increased variability.
-
Multipeak fitting. As discussed, peak identification is one of the most time-consuming and potentially ambiguous tasks in HR analysis, and with binPMF this may not always be a necessary task. However, as binPMF often resolves several peaks (chemical components) at each integer mass, peak identification can be made easier if peak identification is constrained to several binPMF factor profiles rather than just the initial HR spectrum. The optimal approach for this will be the target of a future study.
Most likely several other improvements to the approach will be identified in future studies, and simplicity of the analysis remains a critical consideration. We propose that binPMF is a good tool for initial exploration of new datasets, at which stage optimizing all parameters is not necessarily crucial, if the results can help guide further analysis directions. However, for maximizing the information content that can be extracted from a given dataset, optimized routines are important.
While recent advances in mass spectrometry have greatly enhanced our understanding of atmospheric chemistry, the increased information content in mass spectra also brings difficulties and challenges to the data analysis. Peak identification and separation can be challenging and ambiguous, as well as extremely time-consuming and involving large uncertainties. Constructing peak lists, i.e. deciding which ions to fit to the mass spectra, and validating the results are becoming one of the most labor-intensive parts of the entire work. In this study, we propose a simple and reliable method, binPMF, to try to avoid many of these problems, while still being able to distinguish different chemical pathways/sources in the atmosphere.
Different from traditional analysis, binned positive matrix factorization (binPMF), divides the mass spectra into smaller bins, before applying PMF to distinguish different types of factors and behavior in the data. This method utilizes more available information than classical UMR-PMF and requires no prior peak information as in the case of traditional HR-PMF. We applied binPMF successfully to both ambient and synthetic datasets to test its usefulness under different circumstances.
Traditional HR analysis fits peaks to each mass according to a predefined list and is not able to utilize any information across masses or time. In our analysis of a simple synthetic dataset with two overlapping ions at a single integer mass, we found that binPMF was able to separate the contributions of each ion even in cases where the HR analysis failed completely. This was the case for overlapping ions where binPMF had help in constraining the time series from another integer mass. When applied to an ambient dataset of HOM measured by a CI-APi-TOF, binPMF identified more physically meaningful factors than UMR-PMF. Additionally, for factors where the two PMF approaches agreed, binPMF still contained more mass spectral information for ion identification, as compared to UMR-PMF.
We provide a proof of concept for the utility of binPMF, showing that it can outperform the two traditional analysis approaches, UMR and HR. We identify several future improvements and applications for binPMF, including an approach to greatly facilitate the time-consuming process of peak list construction. We expect binPMF to become a powerful tool in the data exploration and analysis of mass spectra.
The data used in this study are available from the first author upon request: please contact Yanjun Zhang (yanjun.zhang@helsinki.fi).
The supplement related to this article is available online at: https://doi.org/10.5194/amt-12-3761-2019-supplement.
ME, YZ, OP and CY designed the study. QZ and MR collected the data; data analysis was done by YZ and OP. YZ wrote the paper. All coauthors discussed the results and commented the manuscript.
The authors declare that they have no conflict of interest.
This research was supported by the European Research Council (grant 638703-COALA); the Academy of Finland (grants 317380 and 320094); and the Vilho, Yrjö and Kalle Väisälä Foundation. Kaspar R. Daellenbach acknowledges support by the Swiss National Science postdoc mobility grant P2EZP2_181599. We thank the tofTools team for providing tools for mass spectrometry data analysis. The personnel of the Hyytiälä forestry field station are acknowledged for help during field measurements.
Open access funding provided by Helsinki University Library.
This paper was edited by Jonathan Abbatt and reviewed by two anonymous referees.
Allan, J. D., Jimenez, J. L., Williams, P. I., Alfarra, M. R., Bower, K. N., Jayne, J. T., Coe, H., and Worsnop, D. R.: Quantitative sampling using an Aerodyne aerosol mass spectrometer 1. Techniques of data interpretation and error analysis, J. Geophys. Res.-Atmos., 108, 4090, https://doi.org/10.1029/2002JD002358, 2003.
Bertram, T. H., Kimmel, J. R., Crisp, T. A., Ryder, O. S., Yatavelli, R. L. N., Thornton, J. A., Cubison, M. J., Gonin, M., and Worsnop, D. R.: A field-deployable, chemical ionization time-of-flight mass spectrometer, Atmos. Meas. Tech., 4, 1471–1479, https://doi.org/10.5194/amt-4-1471-2011, 2011.
Brown, S. G., Eberly, S., Paatero, P., and Norris, G. A.: Methods for estimating uncertainty in PMF solutions: Examples with ambient air and water quality data and guidance on reporting PMF results, Sci. Total Environ., 518–519, 626–635, https://doi.org/10.1016/j.scitotenv.2015.01.022, 2015.
Canagaratna, M., Jayne, J., Jimenez, J., Allan, J., Alfarra, M., Zhang, Q., Onasch, T., Drewnick, F., Coe, H., and Middlebrook, A.: Chemical and microphysical characterization of ambient aerosols with the aerodyne aerosol mass spectrometer, Mass Spectrom. Rev., 26, 185–222, 2007.
Canonaco, F., Crippa, M., Slowik, J. G., Baltensperger, U., and Prévôt, A. S. H.: SoFi, an IGOR-based interface for the efficient use of the generalized multilinear engine (ME-2) for the source apportionment: ME-2 application to aerosol mass spectrometer data, Atmos. Meas. Tech., 6, 3649–3661, https://doi.org/10.5194/amt-6-3649-2013, 2013.
Corbin, J. C., Othman, A., Allan, J. D., Worsnop, D. R., Haskins, J. D., Sierau, B., Lohmann, U., and Mensah, A. A.: Peak-fitting and integration imprecision in the Aerodyne aerosol mass spectrometer: effects of mass accuracy on location-constrained fits, Atmos. Meas. Tech., 8, 4615–4636, https://doi.org/10.5194/amt-8-4615-2015, 2015.
Craven, J. S., Yee, L. D., Ng, N. L., Canagaratna, M. R., Loza, C. L., Schilling, K. A., Yatavelli, R. L. N., Thornton, J. A., Ziemann, P. J., Flagan, R. C., and Seinfeld, J. H.: Analysis of secondary organic aerosol formation and aging using positive matrix factorization of high-resolution aerosol mass spectra: application to the dodecane low-NOx system, Atmos. Chem. Phys., 12, 11795–11817, https://doi.org/10.5194/acp-12-11795-2012, 2012.
Cubison, M. J. and Jimenez, J. L.: Statistical precision of the intensities retrieved from constrained fitting of overlapping peaks in high-resolution mass spectra, Atmos. Meas. Tech., 8, 2333–2345, https://doi.org/10.5194/amt-8-2333-2015, 2015.
Ehn, M., Kleist, E., Junninen, H., Petäjä, T., Lönn, G., Schobesberger, S., Dal Maso, M., Trimborn, A., Kulmala, M., Worsnop, D. R., Wahner, A., Wildt, J., and Mentel, Th. F.: Gas phase formation of extremely oxidized pinene reaction products in chamber and ambient air, Atmos. Chem. Phys., 12, 5113–5127, https://doi.org/10.5194/acp-12-5113-2012, 2012.
Ehn, M., Thornton, J. A., Kleist, E., Sipila, M., Junninen, H., Pullinen, I., Springer, M., Rubach, F., Tillmann, R., Lee, B., Lopez-Hilfiker, F., Andres, S., Acir, I.-H., Rissanen, M., Jokinen, T., Schobesberger, S., Kangasluoma, J., Kontkanen, J., Nieminen, T., Kurten, T., Nielsen, L. B., Jorgensen, S., Kjaergaard, H. G., Canagaratna, M., Dal Maso, M., Berndt, T., Petaja, T., Wahner, A., Kerminen, V.-M., Kulmala, M., Worsnop, D. R., Wildt, J., and Mentel, T. F.: A large source of low-volatility secondary organic aerosol, Nature, 506, 476, https://doi.org/10.1038/nature13032, 2014.
Guenther, A., Hewitt, C. N., Erickson, D., Fall, R., Geron, C., Graedel, T., Harley, P., Klinger, L., Lerdau, M., McKay, W. A., Pierce, T., Scholes, B., Steinbrecher, R., Tallamraju, R., Taylor, J., and Zimmerman, P.: A GLOBAL-MODEL OF NATURAL VOLATILE ORGANIC-COMPOUND EMISSIONS, J. Geophys. Res.-Atmos., 100, 8873–8892, https://doi.org/10.1029/94jd02950, 1995.
Hakola, H., Tarvainen, V., Bäck, J., Ranta, H., Bonn, B., Rinne, J., and Kulmala, M.: Seasonal variation of mono- and sesquiterpene emission rates of Scots pine, Biogeosciences, 3, 93–101, https://doi.org/10.5194/bg-3-93-2006, 2006.
Hari, P. and Kulmala, M.: Station for Measuring Ecosystem–Atmosphere Relations (SMEAR II), Boreal Environ. Res., 10, 315–322, 2005.
Heinritzi, M., Simon, M., Steiner, G., Wagner, A. C., Kürten, A., Hansel, A., and Curtius, J.: Characterization of the mass-dependent transmission efficiency of a CIMS, Atmos. Meas. Tech., 9, 1449–1460, https://doi.org/10.5194/amt-9-1449-2016, 2016.
Henry, R. C.: Current factor analysis receptor models are ill-posed, Atmos. Environ., 21, 1815–1820, https://doi.org/10.1016/0004-6981(87)90122-3, 1987.
Huang, S., Rahn, K. A., and Arimoto, R.: Testing and optimizing two factor-analysis techniques on aerosol at Narragansett, Rhode Island, Atmos. Environ., 33, 2169–2185, https://doi.org/10.1016/S1352-2310(98)00324-0, 1999.
Huey, L. G.: Measurement of trace atmospheric species by chemical ionization mass spectrometry: Speciation of reactive nitrogen and future directions, Mass Spectrom. Rev., 26, 166–184, https://doi.org/10.1002/mas.20118, 2007.
Jimenez, J. L., Canagaratna, M. R., Donahue, N. M., Prevot, A. S. H., Zhang, Q., Kroll, J. H., DeCarlo, P. F., Allan, J. D., Coe, H., Ng, N. L., Aiken, A. C., Docherty, K. S., Ulbrich, I. M., Grieshop, A. P., Robinson, A. L., Duplissy, J., Smith, J. D., Wilson, K. R., Lanz, V. A., Hueglin, C., Sun, Y. L., Tian, J., Laaksonen, A., Raatikainen, T., Rautiainen, J., Vaattovaara, P., Ehn, M., Kulmala, M., Tomlinson, J. M., Collins, D. R., Cubison, M. J., Dunlea, J., Huffman, J. A., Onasch, T. B., Alfarra, M. R., Williams, P. I., Bower, K., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Salcedo, D., Cottrell, L., Griffin, R., Takami, A., Miyoshi, T., Hatakeyama, S., Shimono, A., Sun, J. Y., Zhang, Y. M., Dzepina, K., Kimmel, J. R., Sueper, D., Jayne, J. T., Herndon, S. C., Trimborn, A. M., Williams, L. R., Wood, E. C., Middlebrook, A. M., Kolb, C. E., Baltensperger, U., and Worsnop, D. R.: Evolution of Organic Aerosols in the Atmosphere, Science, 326, 1525–1529, https://doi.org/10.1126/science.1180353, 2009.
Jokinen, T., Sipilä, M., Junninen, H., Ehn, M., Lönn, G., Hakala, J., Petäjä, T., Mauldin III, R. L., Kulmala, M., and Worsnop, D. R.: Atmospheric sulphuric acid and neutral cluster measurements using CI-APi-TOF, Atmos. Chem. Phys., 12, 4117–4125, https://doi.org/10.5194/acp-12-4117-2012, 2012.
Jokinen, T., Berndt, T., Makkonen, R., Kerminen, V.-M., Junninen, H., Paasonen, P., Stratmann, F., Herrmann, H., Guenther, A. B., Worsnop, D. R., Kulmala, M., Ehn, M., and Sipila, M.: Production of extremely low volatile organic compounds from biogenic emissions: Measured yields and atmospheric implications, P. Natl. Acad. Sci. USA, 112, 7123–7128, https://doi.org/10.1073/pnas.1423977112, 2015.
Junninen, H., Ehn, M., Petäjä, T., Luosujärvi, L., Kotiaho, T., Kostiainen, R., Rohner, U., Gonin, M., Fuhrer, K., Kulmala, M., and Worsnop, D. R.: A high-resolution mass spectrometer to measure atmospheric ion composition, Atmos. Meas. Tech., 3, 1039–1053, https://doi.org/10.5194/amt-3-1039-2010, 2010.
Kirkby, J., Duplissy, J., Sengupta, K., Frege, C., Gordon, H., Williamson, C., Heinritzi, M., Simon, M., Yan, C., Almeida, J., Troestl, J., Nieminen, T., Ortega, I. K., Wagner, R., Adamov, A., Amorim, A., Bernhammer, A.-K., Bianchi, F., Breitenlechner, M., Brilke, S., Chen, X., Craven, J., Dias, A., Ehrhart, S., Flagan, R. C., Franchin, A., Fuchs, C., Guida, R., Hakala, J., Hoyle, C. R., Jokinen, T., Junninen, H., Kangasluoma, J., Kim, J., Krapf, M., Kuerten, A., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Mathot, S., Molteni, U., Onnela, A., Peraekylae, O., Piel, F., Petaejae, T., Praplan, A. P., Pringle, K., Rap, A., Richards, N. A. D., Riipinen, I., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Scott, C. E., Seinfeld, J. H., Sipilae, M., Steiner, G., Stozhkov, Y., Stratmann, F., Tome, A., Virtanen, A., Vogel, A. L., Wagner, A. C., Wagner, P. E., Weingartner, E., Wimmer, D., Winkler, P. M., Ye, P., Zhang, X., Hansel, A., Dommen, J., Donahue, N. M., Worsnop, D. R., Baltensperger, U., Kulmala, M., Carslaw, K. S., and Curtius, J.: Ion-induced nucleation of pure biogenic particles, Nature, 533, 521, https://doi.org/10.1038/nature17953, 2016.
Kroll, J. H., Donahue, N. M., Jimenez, J. L., Kessler, S. H., Canagaratna, M. R., Wilson, K. R., Altieri, K. E., Mazzoleni, L. R., Wozniak, A. S., and Bluhm, H.: Carbon oxidation state as a metric for describing the chemistry of atmospheric organic aerosol, Nat. Chem., 3, 133–139, 2011.
Lanz, V. A., Alfarra, M. R., Baltensperger, U., Buchmann, B., Hueglin, C., Szidat, S., Wehrli, M. N., Wacker, L., Weimer, S., Caseiro, A., Puxbaum, H., and Prevot, A. S. H.: Source Attribution of Submicron Organic Aerosols during Wintertime Inversions by Advanced Factor Analysis of Aerosol Mass Spectra, Environ. Sci. Technol., 42, 214–220, https://doi.org/10.1021/es0707207, 2008.
Lee, B. H., Lopez-Hilfiker, F. D., Mohr, C., Kurtén, T., Worsnop, D. R., and Thornton, J. A.: An Iodide-Adduct High-Resolution Time-of-Flight Chemical-Ionization Mass Spectrometer: Application to Atmospheric Inorganic and Organic Compounds, Environ. Sci. Technol., 48, 6309–6317, https://doi.org/10.1021/es500362a, 2014.
Massoli, P., Stark, H., Canagaratna, M. R., Krechmer, J. E., Xu, L., Ng, N. L., Mauldin, R. L., Yan, C., Kimmel, J., Misztal, P. K., Jimenez, J. L., Jayne, J. T., and Worsnop, D. R.: Ambient Measurements of Highly Oxidized Gas-Phase Molecules during the Southern Oxidant and Aerosol Study (SOAS) 2013, ACS Earth and Space Chemistry, 2, 653–672, https://doi.org/10.1021/acsearthspacechem.8b00028, 2018.
Paatero, P.: Least squares formulation of robust non-negative factor analysis, Chemometr. Intell. Lab., 37, 23–35, https://doi.org/10.1016/S0169-7439(96)00044-5, 1997.
Paatero, P.: The Multilinear Engine – A Table-Driven, Least Squares Program for Solving Multilinear Problems, Including the n-Way Parallel Factor Analysis Model, J. Comput. Graph. Stat., 8, 854–888, https://doi.org/10.1080/10618600.1999.10474853, 1999.
Paatero, P. and Hopke, P. K.: Discarding or downweighting high-noise variables in factor analytic models, Anal. Chim. Acta, 490, 277–289, https://doi.org/10.1016/S0003-2670(02)01643-4, 2003.
Paatero, P. and Tapper, U.: Positive matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values, Environmetrics, 5, 111–126, 1994.
Paatero, P., Hopke, P. K., Song, X.-H., and Ramadan, Z.: Understanding and controlling rotations in factor analytic models, Chemometr. Intell. Lab., 60, 253–264, https://doi.org/10.1016/S0169-7439(01)00200-3, 2002.
Paatero, P., Eberly, S., Brown, S. G., and Norris, G. A.: Methods for estimating uncertainty in factor analytic solutions, Atmos. Meas. Tech., 7, 781–797, https://doi.org/10.5194/amt-7-781-2014, 2014.
Polissar, A. V., Hopke, P. K., Paatero, P., Malm, W. C., and Sisler, J. F.: Atmospheric aerosol over Alaska: 2. Elemental composition and sources, J. Geophys. Res.-Atmos., 103, 19045–19057, 1998.
Pope III, C. A., Ezzati, M., and Dockery, D. W.: Fine-particulate air pollution and life expectancy in the United States, New Engl. J. Med., 360, 376–386, 2009.
Schauer, J. J., Rogge, W. F., Hildemann, L. M., Mazurek, M. A., Cass, G. R., and Simoneit, B. R.: Source apportionment of airborne particulate matter using organic compounds as tracers, Atmos. Environ., 30, 3837–3855, 1996.
Shiraiwa, M., Ueda, K., Pozzer, A., Lammel, G., Kampf, C. J., Fushimi, A., Enami, S., Arangio, A. M., Fröhlich-Nowoisky, J., Fujitani, Y., Furuyama, A., Lakey, P. S. J., Lelieveld, J., Lucas, K., Morino, Y., Pöschl, U., Takahama, S., Takami, A., Tong, H., Weber, B., Yoshino, A., and Sato, K.: Aerosol Health Effects from Molecular to Global Scales, Environ. Sci. Technol., 51, 13545–13567, https://doi.org/10.1021/acs.est.7b04417, 2017.
Song, Y., Shao, M., Liu, Y., Lu, S., Kuster, W., Goldan, P., and Xie, S.: Source apportionment of ambient volatile organic compounds in Beijing, Environ. Sci. Technol., 41, 4348–4353, 2007.
Stark, H., Yatavelli, R. L. N., Thompson, S. L., Kimmel, J. R., Cubison, M. J., Chhabra, P. S., Canagaratna, M. R., Jayne, J. T., Worsnop, D. R., and Jimenez, J. L.: Methods to extract molecular and bulk chemical information from series of complex mass spectra with limited mass resolution, Int. J. Mass Spectr., 389, 26–38, https://doi.org/10.1016/j.ijms.2015.08.011, 2015.
Stocker, T., Qin, D., Plattner, G., Tignor, M., Allen, S., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P.: IPCC, 2013: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 1535 pp., Cambridge Univ. Press, Cambridge, UK, and New York, 2013.
Sun, Y.-L., Zhang, Q., Schwab, J. J., Demerjian, K. L., Chen, W.-N., Bae, M.-S., Hung, H.-M., Hogrefe, O., Frank, B., Rattigan, O. V., and Lin, Y.-C.: Characterization of the sources and processes of organic and inorganic aerosols in New York city with a high-resolution time-of-flight aerosol mass apectrometer, Atmos. Chem. Phys., 11, 1581–1602, https://doi.org/10.5194/acp-11-1581-2011, 2011.
Ulbrich, I. M., Canagaratna, M. R., Zhang, Q., Worsnop, D. R., and Jimenez, J. L.: Interpretation of organic components from Positive Matrix Factorization of aerosol mass spectrometric data, Atmos. Chem. Phys., 9, 2891–2918, https://doi.org/10.5194/acp-9-2891-2009, 2009.
Wei, W., Wang, S., Chatani, S., Klimont, Z., Cofala, J., and Hao, J.: Emission and speciation of non-methane volatile organic compounds from anthropogenic sources in China, Atmos. Environ., 42, 4976–4988, https://doi.org/10.1016/j.atmosenv.2008.02.044, 2008.
Yan, C., Nie, W., äijälä, M., Rissanen, M. P., Canagaratna, M. R., Massoli, P., Junninen, H., Jokinen, T., Sarnela, N., Häme, S. A. K., Schobesberger, S., Canonaco, F., Yao, L., Prévôt, A. S. H., Petäjä, T., Kulmala, M., Sipilä, M., Worsnop, D. R., and Ehn, M.: Source characterization of highly oxidized multifunctional compounds in a boreal forest environment using positive matrix factorization, Atmos. Chem. Phys., 16, 12715–12731, https://doi.org/10.5194/acp-16-12715-2016, 2016.
Zha, Q., Yan, C., Junninen, H., Riva, M., Sarnela, N., Aalto, J., Quéléver, L., Schallhart, S., Dada, L., Heikkinen, L., Peräkylä, O., Zou, J., Rose, C., Wang, Y., Mammarella, I., Katul, G., Vesala, T., Worsnop, D. R., Kulmala, M., Petäjä, T., Bianchi, F., and Ehn, M.: Vertical characterization of highly oxygenated molecules (HOMs) below and above a boreal forest canopy, Atmos. Chem. Phys., 18, 17437–17450, https://doi.org/10.5194/acp-18-17437-2018, 2018.
Zhang, Q., Jimenez, J. L., Canagaratna, M., Allan, J., Coe, H., Ulbrich, I., Alfarra, M., Takami, A., Middlebrook, A., and Sun, Y.: Ubiquity and dominance of oxygenated species in organic aerosols in anthropogenically-influenced Northern Hemisphere midlatitudes, Geophys. Res. Lett., 34, L13801, https://doi.org/10.1029/2007GL029979, 2007.
Zhang, Q., Jimenez, J. L., Canagaratna, M. R., Ulbrich, I. M., Ng, N. L., Worsnop, D. R., and Sun, Y.: Understanding atmospheric organic aerosols via factor analysis of aerosol mass spectrometry: a review, Anal. Bioanal. Chem., 401, 3045–3067, https://doi.org/10.1007/s00216-011-5355-y, 2011.
Zhang, Y., Lin, Y., Cai, J., Liu, Y., Hong, L., Qin, M., Zhao, Y., Ma, J., Wang, X., and Zhu, T.: Atmospheric PAHs in North China: spatial distribution and sources, Sci. Total Environ., 565, 994–1000, 2016.
Zhang, Y., Cai, J., Wang, S., He, K., and Zheng, M.: Review of receptor-based source apportionment research of fine particulate matter and its challenges in China, Sci. Total Environ., 586, 917–929, 2017.