the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
On the information content in linear horizontal delay gradients estimated from space geodesy observations
Gunnar Elgered
Tong Ning
Peter Forkman
Rüdiger Haas
We have studied linear horizontal gradients in the atmospheric propagation delay above ground-based stations receiving signals from the Global Positioning System (GPS). Gradients were estimated from 11 years of observations from five sites in Sweden. Comparing these gradients with the corresponding ones from the European Centre for Medium-Range Weather Forecasts (ECMWF) analyses shows that GPS gradients detect effects over different timescales caused by the hydrostatic and the wet components. The two stations equipped with microwave-absorbing material below the antenna, in general, show higher correlation coefficients with the ECMWF gradients compared to the other three stations. We also estimated gradients using 4 years of GPS data from two co-located antenna installations at the Onsala Space Observatory. Correlation coefficients for the east and the north wet gradients, estimated with a temporal resolution of 15 min from GPS data, can reach up to 0.8 for specific months when compared to simultaneously estimated wet gradients from microwave radiometry. The best agreement is obtained when an elevation cut-off angle of 3∘ is applied in the GPS data processing, in spite of the fact that the radiometer does not observe below 20∘. We also note a strong seasonal dependence in the correlation coefficients, from 0.3 during months with smaller gradients to 0.8 during months with larger gradients, typically during the warmer and more humid part of the year. Finally, a case study using a 15 d long continuous very-long-baseline interferometry (VLBI) campaign was carried out. The comparison of the gradients estimated from VLBI and GPS data indicates that a homogeneous and frequent sampling of the sky is a critical parameter.
Space geodetic techniques, where the fundamental observable is a radio signal's time of arrival at a station on the surface of the Earth, are affected by variations in the propagation velocity in the atmosphere. Because time measurements avoid problems related to accurate calibration, which are common for systems measuring different types of emissions, it is a common view that Global Navigation Satellite Systems (GNSSs) have a long-term stability and are well suited for climate monitoring, e.g. in terms of the atmospheric water vapour content. Estimates of the total propagation delay above a GNSS station can be used to determine the integrated amount of water vapour. It is also common practice to estimate two-dimensional horizontal linear gradients for each station in the GNSS data processing because they improve the reproducibility of estimated geodetic parameters; see, e.g. Bar-Sever et al. (1998).
We have studied estimated gradients primarily from Global Positioning System (GPS) data from Swedish GNSS stations by comparing these gradients to independent measurements. An important site is the Onsala Space Observatory where a geodetic very-long-baseline interferometry (VLBI) telescope and a water vapour radiometer (WVR) are installed and co-located with GNSS receiver stations. The overall goal was to study the usefulness of GPS-derived gradients in atmospheric and climate research. Previous studies have been carried out using GNSS data from Onsala. Comparing the gradients derived from VLBI, GPS, and a WVR, Gradinarsky et al. (2000) found that when varying the constraint for the gradient variability from 0.2 to 5.6 mm , the weighted root-mean-square (RMS) difference compared to the WVR gradients varied between 0.8 and 1.0 mm for both the GPS and the VLBI gradients. Using multi-GNSS observations, Li et al. (2015) found a significant increase in the correlation coefficient to about 0.6 when compared to ECMWF gradients, while the one for the GPS alone was typically below 0.5. In addition, they found that the RMS difference of the gradient was reduced to about 25 %–35 % by multi-GNSS processing.
There are some interesting questions actualized by previous work, which we tried to take further. Of specific interest in our study was to investigate if there is any systematic seasonal behaviour in the estimated gradients in Sweden and if they can be explained by the influence of regional-scale weather systems. The question about the seasonal changes of gradients was previously studied by Koulali et al. (2012). Another issue is that comparisons of estimated GPS gradients with a high temporal resolution are rather sparse and have, to our knowledge, so far not covered periods of many years. Here we report on comparisons between GPS and WVR gradients, with a temporal resolution of 15 min, over a more or less continuous 4-year period. With such a resolution it is, for example, possible to study convective systems (Brenot et al., 2013) and the relation between the temporal variability of the gradients and the zenith wet delay (ZWD) during the passage of weather fronts.
In Sect. 2 we give a short background on the cause of gradients that are sensed by the space geodetic techniques and the model used to estimate them. In Sect. 3 instruments, techniques, and their data are described. The results are presented in two sections. First, in Sect. 4, we compare 11 years of total gradients from five Swedish GNSS stations to gradients originating from the European Centre for Medium-Range Weather Forecasts (ECMWF) analyses. Here we study seasonal dependence. In Sect. 5, we use data from two co-located GNSS stations (with different antenna installations) and one WVR to assess the station performances and differences between different GPS processing variants. We also study the seasonal dependence of the estimated wet gradients over a 4-year period. Finally, within this 4-year period a 15 d long VLBI campaign occurred, which we use as a case study. In Sect. 6 we present our conclusions and suggest possible future studies of gradients.
The delay of space geodetic signals propagating through the atmosphere depends on the refractive index. For space geodetic applications it is meaningful to define one hydrostatic and one wet component (Davis et al., 1985). For a horizontally stratified atmosphere it is then common practice to use equivalent zenith values for these components. Additionally we may define a horizontal linear gradient that can be inferred from ground-based observations (Davis et al., 1993), consisting of one east and one north component, which in turn also can be separated into one hydrostatic and one wet component.
Hydrostatic gradients are determined by pressure and temperature gradients and exist mainly over regional scales (e.g. persistent high- and low-pressure systems) and synoptic scales (e.g. weather systems). Using a European and a global GPS network, including three of the GPS stations used in this study, Meindl et al. (2004) showed that the north gradient has a clear dependence on latitude when averaged over long timescales. For the area of interest in this study, we specifically mention the Icelandic low-pressure system that typically evolves in the winter and disappears in the summer (Hewson and Longley, 1944). This is a component in the North Atlantic Oscillation and the Arctic Oscillation (Thompson and Wallace, 1998; Sanchez-Franks et al., 2016).
Temperature and especially water vapour can show strong horizontal gradients over small (kilometre) scales and temporal variability is typically also much higher than that of the hydrostatic gradients; see, e.g. Li et al. (2015). Hence, the large local gradients over a station are mainly caused by the variability in water vapour and the wet refractivity. Gradients can be significant during a passage of a weather front; e.g. Kačmařík et al. (2019) report gradient amplitudes of up to 3–4 mm during the passage of an occlusion front over Germany. Nahmani et al. (2019) studied gradients during the passage of mesoscale convective systems in West Africa and Koulali et al. (2012) showed correlations between gradients and precipitation and moisture fluxes in Morocco. Other specific weather phenomena that can cause horizontal variability in the partial pressure of water vapour, and hence also the wet refractivity, are sea breeze (Craig et al., 1945; Miller et al., 2003), cloud rolls (Brown, 1970), and convection processes in general.
We note that none of the known processes is expected to be strictly horizontally linear, but the strength in the geometry, the distribution of the observations in the sky, and the GNSS data quality makes it difficult to determine additional atmospheric parameters of a higher order.
The atmospheric parameters that are normally estimated when processing space geodesy data are an equivalent zenith wet delay and linear horizontal delay gradients in the east and the north directions. The uncertainties of the estimates depend on the geometry of the observations and the accuracy of the so-called mapping functions, used to describe the estimated parameters dependence on the elevation angle, given the specific weather conditions at the site, at the time; see, e.g. Boehm et al. (2006) and Kačmařík et al. (2019). The common model used to relate the observed delay along the line-of-sight, ΔL(α,ε), and the estimated parameters (IERS Conventions, 2010) are also used in this study, i.e.
where mh, mw, and mg are the mapping functions, depending on the elevation angle ε, for the hydrostatic and wet delays and the gradients, respectively; ΔLhz and ΔLwz are the equivalent hydrostatic and wet delays in the zenith direction; α is the azimuth angle, measured clockwise from the north, implying that Ξe and Ξn are the gradients in the east and in the north directions. While total gradients are estimated, they can be interpreted as the sum of hydrostatic and wet components as well. In the following we will subtract the hydrostatic component computed from ECMWF from the total GPS gradient to get the GPS wet gradient.
In addition to the east and the north gradient components, we also studied the gradient amplitude, defined as follows:
The gradient amplitude is defined for the hydrostatic, wet, and total gradients.
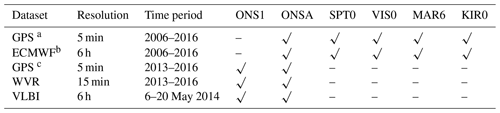
We compared gradients estimated from GPS observations acquired at five sites and six antenna and receiver installations: Kiruna (KIR0), Mårtsbo (MAR6), Borås (SPT0), Visby (VIS0), and Onsala (ONSA and ONS1) with respect to VLBI, WVR, and ECMWF estimates. These stations are also part of the EUREF network (Bruyninx et al., 2012). Their geographic locations are shown in Fig. 1. In this section, we first describe the different datasets. Thereafter, we summarize their use and characterize them in terms of formal errors, advantages, and disadvantages.
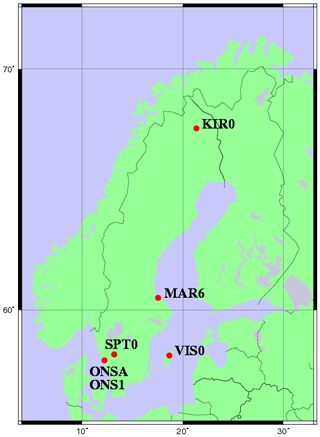
Figure 1The five sites used in the study. Two antenna installations, ONSA and ONS1, are co-located together with the VLBI telescope and the WVR at the Onsala site. An antenna installation is referred to as a station.
3.1 GPS
We used 11 years of GPS data (2006–2016) from the five Swedish GNSS sites mentioned above. Gradients in the east and the north directions were estimated with a temporal resolution of 5 min. Two GNSS stations are operating continuously at the Onsala Space Observatory on the western coast of Sweden. The primary station, ONSA, was established in 1987 and the other station, ONS1, was taken into operation in 2011. The six antenna installations are shown in Fig. 2. The antennas of ONSA and ONS1 are located within 100 m of each other and should observe almost identical atmospheric gradients. For the time period 2013–2016, we compared gradients from these two stations with simultaneously estimated gradients using data from a WVR located 10 m from the ONSA antenna.
The analysis of the GPS data followed the same lines as described by Ning et al. (2013) and is summarized in Table 1. Specifically we mention that each day was analysed independently after adding 3 h of data from the previous day and 3 h from the following day, i.e. in total 30 h. The reason was to avoid discontinuities at midnight in the estimated time series.
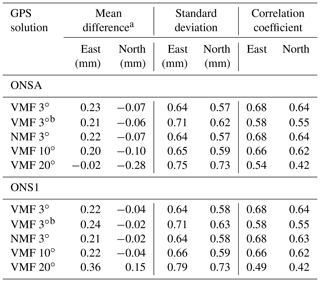
In order to investigate the impact of different constraints on the estimated gradients we also reprocessed two days of GPS data for ONSA, where large changes (2–3 mm) in both the east and the north gradient components were observed over a couple of hours by both the GPS and the WVR data. In addition to the constraint value of 0.3 mm suggested by Bar-Sever et al. (1998), the values 0.6, 0.9, and 1.2 mm were used. The use of these different values shows only small differences compared to the WVR in the daily averaged gradient amplitudes, from 0.02 to 0.12 mm, although the short-term variability in the GPS gradients increases when weaker constraints (larger values) are used. This is consistent with the result presented by Gradinarsky et al. (2000) for the same site. We note that by using a stronger constraint (small value) we remove the possibility of following rapid variations in the gradients but at the same time reduce unwanted noise being absorbed into the gradient estimates. This is a possible explanation why differences between GPS and WVR gradients are less sensitive to the constraint value used in the GPS processing. The impact of the constraint value is further discussed in Sects. 5.2 and 6.
Recent work by Kačmařík et al. (2019) compared estimated gradients with those from a numerical weather model using different gradient mapping functions and elevation cut-off angles. They found the best agreement for an elevation cut-off angle equal to 3∘. They also showed that the Bar-Sever et al. (1998) gradient mapping function resulted in 17 % smaller gradient amplitudes compared to the Chen and Herring (1997) mapping function. For the 11-year study presented in the next section, we used a 10∘ elevation cut-off angle only, whereas we used several different elevation cut-off angles in the comparison with the WVR data from the Onsala site for a 4-year period.
Based on the 5 min gradients, we calculated mean values over 15 min, 6 h, 1 d, and 1 month in order to match the temporal resolution of the comparison data and to study the variability of the wet and the hydrostatic gradients over different timescales.

Figure 2The six antenna installations used to acquire the GPS data. See Fig. 1 for their geographical location.
Table 1Processing of GPS data.
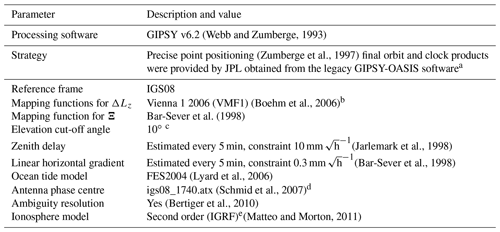
a For the 11-year dataset. For the 4-year dataset, the products were obtained from a new GipsyX software. We noted that the difference in the products due to the change of software is small (Sibois et al., 2017). b For the 11-year dataset. For the 4-year dataset the weighted (sin (ε)) VMF1 and the NMF (Niell, 1996) were also used. c For the 11-year dataset. For the 4-year dataset 3 and 20∘ were also used. d For the 11-year dataset. For the 4-year dataset igs08_1869.atx was used. e International Geomagnetic Reference Field.
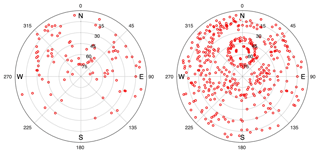
Examples of the sky coverage of the GPS observations are shown in Fig. 3 for the Onsala site. At this latitude there is a significant part of the sky that is never sampled, just north of the zenith direction. It is reasonable to assume that this will have a negative impact on the estimated gradients, especially in the north direction.
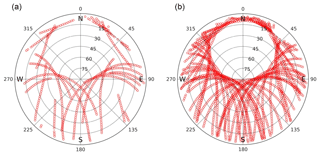
Figure 3Sky plots of GPS observations at Onsala from 06:00 to 12:00 UT (a) and from 00:00 to 24:00 UT (b) on 12 May 2014. This particular day was chosen because it is included in the CONT14 campaign presented in Sect. 5.3. The sky distribution of observations is very similar, although not identical, for all days.
3.2 Microwave radiometer
The microwave radiometer, shown in Fig. 4, was designed in order to provide independent estimates of the wet propagation delays for space geodetic applications. It measures the emission from the sky, on and off the water vapour line at 22.2 GHz. Its specifications are summarized in Table 2 and the data processing was carried out as was described for another WVR by Elgered and Jarlemark (1998).
During the time period 2013–2016 the WVR was observing in a sky mapping mode, as is illustrated in Fig. 5. A disadvantage of a WVR is that the algorithm for calculation of the wet propagation delay fails for data acquired during rain or when large liquid drops are present in the sensed atmosphere. Typically such conditions imply large positive errors in the wet delay and the water vapour content (Westwater and Guiraud, 1980). Therefore, data taken during rain, or when the estimated equivalent amount of liquid water in the zenith direction was >0.7 mm, were discarded from the gradient analysis. In addition there were also time periods when the WVR hardware failed. The amount of analysed data are shown in Fig. 6 as the number of individual observations per day. The first long data gap, in 2014–2015, was caused by a broken mechanical waveguide switch and the second long gap, in 2015–2016, was due to broken cables in the so-called cable wrap. As a consequence the cable wrap was redesigned to avoid similar failures in the future.
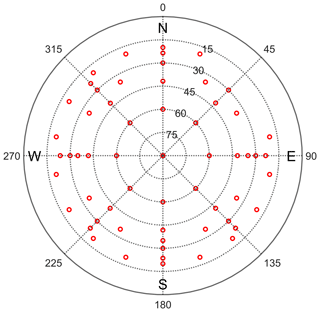
Figure 5A measurement cycle of the WVR begins with two azimuth scans. In order to avoid emission from the ground, the lowest elevation angle observed was 20∘. Starting in the north, first turning at an elevation angle of 20∘ clockwise to the north (excluding the azimuth angles of 40∘ and 60∘ due to a nearby radio telescope) and then turning anticlockwise at an elevation angle of 35∘. Thereafter, four tip curves were made over the zenith direction (implying four observations in the zenith direction during each cycle): from the north to the south, from the southwest to the northeast, from the east to the west, and from the northwest to the southeast. The cycle was about 8 min long and was repeated continuously, implying that almost two complete cycles with a total of ≈100 observations were used when estimating gradients every 15 min.
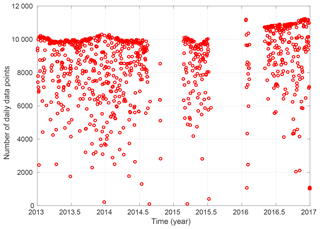
Figure 6Number of data points per day observed by the WVR. During days without data loss, e.g. due to rain, each estimated gradient was based on ≈100 observations in the directions illustrated in Fig. 5. Observations close to the sun were removed from the raw data before the data analysis was carried out, which causes the seasonal variation in the maximum number of observations per day. During the last year the measurement cycle was optimized by reducing some of the time delays inserted between samples, but the observational sequence shown in Fig. 5 was used during the whole period.
In order to avoid ground-noise pickup the WVR provided observations of the wet delay in the different directions above 20∘. Therefore, a simple sin (ε) mapping function was used to relate these slant wet delays to the equivalent ZWD. The WVR gradients were estimated based on all observations carried out during a period of 15 min using the method of least squares and the Bar-Sever gradient mapping function. We used a four-parameter model, fitting a ZWD, a ZWD rate, and an east and north gradient to the data (Davis et al., 1993). This means that the estimated gradients are independent of the successive estimates, which is different from the gradients estimated from the space geodetic techniques, where temporal constraints are applied.
3.3 Very-long-baseline interferometry
We used the VLBI data from the CONT14 campaign coordinated by the International VLBI Service (Nothnagel et al., 2017). The IVS organizes continuous (CONT) VLBI campaigns every third year in order to acquire state-of-the-art VLBI data over a time period of 2 weeks and to demonstrate the highest accuracy of which the current VLBI system is capable. The primary goal of these CONT campaigns is to support research concerning high-resolution Earth rotation (Haas et al., 2017), reference frame stability, and daily to sub-daily site motions but also other aspects. A concise overview of the IVS CONT campaigns is given by MacMillan (2017).
The CONT14 campaign was observed during 6–20 May 2014. The VLBI data were analysed with the Calc/Solve analysis software (Ma et al., 1990). Station positions, ZWD, atmospheric gradients, relative clock parameters with respect to a reference station, as well as earth rotation parameters were estimated. The relative clock parameters were estimated as piecewise linear functions every hour, with a constraint of s s−1 between clock rate segments. The ZWD and atmospheric gradients were estimated as piecewise linear functions (i.e. not stochastic processes) with a temporal resolution of 30 min and 6 h, respectively. Constraints for the variability of 15 mm h−1 for the ZWD rate segments and 2 mm d−1 for gradient rates were applied. The NMF (Niell, 1996) mapping functions for ZWD and the Chen and Herring (1997) mapping function for gradients were used in the analysis, together with meteorological information recorded at the VLBI stations. An elevation cut-off angle of 5∘ was used with no elevation-dependent weighting.
Figure 7 depicts the sampling of the sky for a 6 h period, which is the highest temporal resolution of the gradient estimates from VLBI, as well as all observations scheduled for a 24 h experiment. This schedule was repeated every day with only minor modifications.
3.4 ECMWF
The Technical University of Vienna provides hydrostatic and wet gradients based on ECMWF data for many space geodetic sites globally. The product used here is usually referred to as LHGs (linear horizontal gradients) and is described by Boehm and Schuh (2007). It is available during certain time periods from the middle of 2005 and is more continuous from 2006. It is computed from profiles of hydrostatic and wet refractivity with a temporal resolution of 6 h and a spatial resolution of 0.25∘ (∼30 km). The profile closest to the site is used together with one profile to the east and one profile to the north to calculate the refractivity gradient profiles. These are thereafter integrated to give the delay gradients. Because it was observed that, on average, the gradients computed in this way overestimate the more accurate gradients estimated from slant profiles, they are scaled by empirically derived factors, 0.53 for the hydrostatic gradients and 0.71 for the wet gradients (Boehm and Schuh, 2007). This computation method and rescaling provide gradient estimates of limited accuracy but they still represent a valuable and independent source of information that is used here for comparisons with estimated GPS gradients.
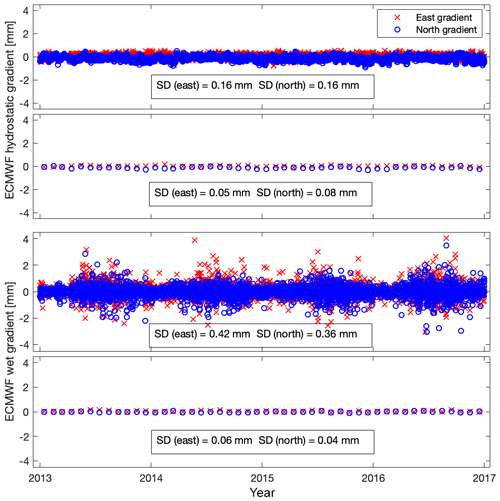
Figure 8The ECMWF gradients for the Onsala (ONSA) site during the 4-year time period studied in Sect. 5. From the top: hydrostatic gradients every 6 h, their monthly averages, wet gradients every 6 h, and their monthly averages.
There are alternative methods of deriving gradients from Numerical Weather Model data using ray tracing methods; see, e.g. Zus et al. (2015), and references therein. More recently the Technical University of Vienna also introduced a new gradient product based on a least-squares adjustment of the ERA-Interim analyses (Landskron and Böhm, 2018).
In this study we used the LHG data from 2006 to 2016, resulting in a time series of 11 years. As an introduction, examples of the ECMWF hydrostatic and wet gradients are illustrated in Fig. 8. Worth noting is that the wet gradients dominate for the temporal resolution of 6 h and vary with the season, whereas the wet and the hydrostatic gradients show similar standard deviations (SDs) for the monthly averages.
3.5 Summary of datasets
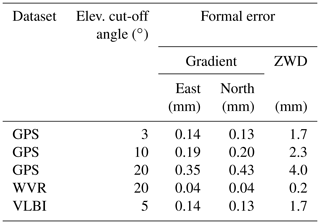
The results of comparisons between the gradients from these datasets are presented in the next two sections. The usage is defined in Table 3. In Sect. 4, GPS gradients estimated using the 10∘ elevation cut-off angle are compared to the ECMWF gradients. The temporal resolution is limited to 6 h in the ECMWF data. On the other hand, the time series are 11 years long. The results in Sect. 5 focus on comparisons of the wet gradients at the Onsala site. These have a temporal resolution of 15 min when comparing to WVR data and the ECMWF data are only used to subtract the hydrostatic gradients from the total gradients estimated by the GPS and the VLBI techniques. In Table 4 we summarize the typical formal errors of the remote-sensing techniques. Worth noting is the larger formal error for the north GPS gradient, compared to the east gradient, using the elevation cut-off angle of 20∘. The reason is that we lose many observations of satellites located in the north; see Fig. 3. Other important comments are that WVR gradients are not estimated during rain events and are not based on observations below 20∘ elevation angles but have a more homogeneous sky coverage compared to the GPS and the VLBI observations. Gradients from GPS and WVR have a superior temporal resolution, 5 and 15 min, respectively, compared to the 6 h resolution of the VLBI and the ECMWF gradients.
Table 3Summary of used datasets.
a The GPS data were processed with elevation cut-off angles equal to 10∘. b Boehm and Schuh (2007). c The GPS data were processed with elevation cut-off angles equal to 3, 10, and 20∘; different mapping functions; and elevation-angle-dependent weighting.
4.1 Seasonal variations in horizontal gradients
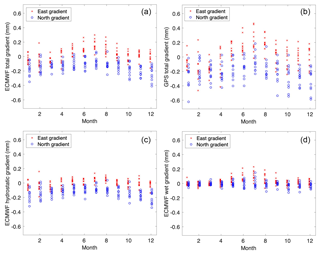
We start by investigating the characteristics of the gradients over the year. In Fig. 9 we present the monthly mean gradients for the time period 2006–2016 estimated from ECMWF data and GPS data from the Onsala (ONSA) station. In the top graphs, comparing ECMWF and GPS gradients, we note that the GPS gradients show a larger variability. There are also differences between the east and the north gradients both in the mean over the year and in the seasonal variations.
We can clearly see negative north gradients in the winter, with a mean value around −0.2 mm, both in the GPS and the ECMWF results. When the ECMWF gradients are separated into the hydrostatic and the wet components this variation appears in the hydrostatic component. We interpret this effect as the influence of the Icelandic low-pressure system mentioned in Sect. 2. The winter feature is clearly seen in the analyses of the mean sea level pressure in the ERA-40 Atlas (https://software.ecmwf.int/static/ERA-40_Atlas/docs/section_B/parameter_mslp.html, last access: 5 July 2019).
The results for the other four stations (KIR0, MAR6, SPT0, and VIS0) show similar systematic features. One exception is KIR0, which is at a higher latitude and has a less humid climate. At KIR0 the average monthly wet gradients are much smaller except during the summer months. Furthermore, the influence of the Icelandic low pressure in the winter is not as large as it is at the other four stations. Another exception is seen in the ECMWF wet gradients for ONSA in Fig. 9. They are larger in the summer when the wet refractivity is higher. This is also seen at the other stations but at ONSA there is a tendency of a positive east gradient in the summer. The ONSA GPS station is located a few hundred metres from the coastline (see Fig. 1), suggesting that the air, on average, is more humid over land compared to over the sea. One possible cause could be the sea breeze that occurs during the summer (Craig et al., 1945; Miller et al., 2003). The issue of wet gradients is studied further using a higher temporal resolution and comparisons with the WVR data in Sect. 5.
4.2 Comparing GPS and ECMWF gradients over different timescales at the five stations
We study the agreement, in terms of correlation coefficients, between the total GPS and ECMWF gradients from five GPS stations using data from 2006 to 2016. These are shown in Table 5.
Table 5Correlation coefficients for the total east and north gradients estimated from GPS data and compared to ECMWF data.
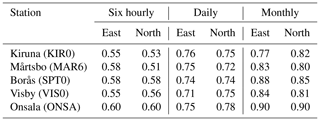
The correlations seen in all cases confirm that a consistent atmospheric signal in terms of gradients is detected by the GPS observations and ECMWF analyses. We note that the correlation coefficients increase for longer-averaging time periods. Our interpretation is that by long-term averaging we compare a larger fraction of the gradient that is caused by large-scale temperature and pressure gradients. Unfortunately, the temporal resolution of 6 h in the ECMWF data is not sufficient to resolve either rapid changes in the pressure related to moving weather systems or many of the short-lived small-scale gradients associated with the variability in the water vapour.
Another result worth noting is that the two stations with the highest correlation coefficients, especially for the monthly averages, are ONSA and SPT0. The 95 % confidence interval is for the correlation coefficient of 0.90 obtained at station ONSA, based on 131 data points (12 months over 11 years). These two stations are the only ones that are equipped with microwave-absorbing material below the antenna and above the metal plate used for the antenna mounting. This could reduce the impact from unwanted multipath effects. The phenomenon calls for further study.
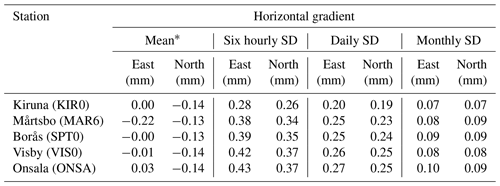
The mean values and the SD of the gradients, for the three different temporal resolutions, are presented in Tables 6 and 7 from GPS and ECMWF data, respectively. For the 6 h temporal resolution, the GPS gradients estimated at the same time epoch as the ECMWF gradients are included in the calculations. The daily and monthly values are averages using this 6 h data. When comparing the two tables it is clear that there are differences in the mean values of up 0.2 mm. These differences are mainly in the east component whereas there are consistent negative values for the north component. The SD of the GPS gradients is larger than the ECMWF gradients by a factor of 2. The differences may be explained using at least two reasons. First, the ECMWF gradient data used here have some intrinsic shortcomings (see Sect. 3.4). Second, not all variations in the water vapour content observed by the GPS receivers are actually represented in the ECMWF model, due to its rather coarse spatial and temporal resolutions (Bock and Parracho, 2019).
We note that the SD obtained for the KIR0 station for 6 h and 1 d is smaller. This is likely a consequence of the lower humidity at the station. For monthly averages, these differences are reduced and the SD for all stations is in the range 0.13–0.18 mm indicating that the hydrostatic gradients and other effects, e.g. signal multipath effects, become relatively more important. Variations in the electromagnetic environment that change the impact of the signal multipath at a station may be due to, e.g. snow, rain, vegetation, and soil moisture. The relative importance of hydrostatic and wet gradients was illustrated in Fig. 8 using 4 years of data from the ONSA station. Using all 11 years of ECMWF data, all stations have SDs of the hydrostatic east and north monthly gradients in the range from 0.05 to 0.07 mm, whereas the SDs for the monthly wet gradients show a dependence on latitude, from 0.03 mm at KIR0 in the north to 0.06 mm at ONSA in the south.
Table 6Mean values and standard deviations (SDs) over the 11 years of estimated total gradients from GPS data for different temporal resolutions.
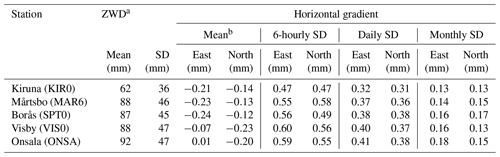
a The zenith wet delay (ZWD) is included to illustrate the amount of water vapour in the atmosphere above the station and its SD is based on the 6 h gradients. b The mean gradient values are based on the 6 h gradients.
For the Onsala site we study total gradients from the two GPS stations and one VLBI station and wet gradients from the WVR for the time period 2013–2016. We use the hydrostatic gradients from ECMWF to calculate wet gradients from GPS and VLBI total gradients. The designs of the two GPS stations are different (see Fig. 2), which motivates the inclusion of both of them in the comparisons. Three different studies are made using the following data: (1) assessment of the impact of using different processing of the GPS data, primarily varying the elevation cut-off angle, by comparison to the WVR gradients; (2) using the GPS gradients from the processing variant showing the best agreement with the WVR gradients, the seasonal variations in the wet gradient are characterized; and (3) a 15 d long period with VLBI data is used as a case study for comparisons with GPS and WVR wet gradients and the ZWD.
5.1 Test of GPS processing variants relative to WVR data
Gradients in the east and the north directions are estimated from the GPS data for five different solutions. We use three different elevation cut-off angles for the VMF1 zenith delay mapping functions. One additional solution is carried out with elevation-dependent weighting (sin (ε)), and in the fifth solution the VMF1 mapping functions are replaced by the NMF. As stated earlier, the gradient mapping function presented by Bar-Sever et al. (1998) is used in all cases.
The GPS wet gradients for ONSA and ONS1 are computed by subtracting the hydrostatic gradients from ECMWF (see Fig. 8), linearly interpolated to match the time epochs of the GPS gradients, from the total GPS gradients. Thereafter, we form 15 min averages for the east and the north wet gradients from GPS and compare them to the corresponding WVR results.
The results for the different GPS solutions are summarized in Tables 8 and 9. Because of the different gradient amplitudes from the WVR and GPS, we present mean values and SD of the differences as well as correlation coefficients. Table 8 shows the results when the total gradients from the stations ONSA and ONS1 are compared to each other. Table 9 shows the results when the wet gradients from ONSA and ONS1 are compared to the WVR gradients. We note that in both tables the best agreement between the gradients estimated is obtained for an elevation cut-off angle equal to 3∘. The 95 % confidence interval for correlation coefficients around 0.65 and approximately 80 000 data pairs is ±0.004. This result was not expected by us, given that the WVR has an elevation cut-off angle of 20∘ (in order to avoid ground-noise pickup) the GPS solution using the same cut-off angle would show a better agreement. Our interpretation is that for the temporal resolutions of 5–15 min, the low-elevation observations are important in order to distinguish the gradient parameters relative to other estimated parameters in the GPS analysis. A higher elevation cut-off angle will remove many observations towards the north, especially for a cut-off angle of 20∘; see Fig. 3 and Table 4 with the formal errors.
The solution giving the best agreement, when comparing gradients from ONSA and ONS1 data with each other, is the one with elevation-dependent weighting, whereas the comparisons with the WVR, for both ONSA and ONS1, give the best agreement without weighting. The choice of elevation cut-off angle is a compromise between having a good geometry and avoiding effects of signal multipath. Our interpretation is that the gradients from ONSA and ONS1 are estimated based on very similar observational directions and have common error sources, such as orbit errors, resulting in correlations around 0.9. In order to increase an already high correlation, the observations at the lowest elevation angles are not that important, since multipath effects will be increasingly different the closer to the horizon the observations are made. When ONSA and ONS1 gradients are compared to those from the WVR the situation is different because these gradients are independent and the geometry of the GPS observations becomes more important in order to estimate a more accurate gradient. Although we note that the correlation coefficients are reduced here to 0.68 and 0.64 for the east and the north component, respectively. Since the WVR provides independent gradients, we will in the following focus on the VMF 3∘ solution without elevation-dependent weighting.
Table 8Assessment of the different GPS solutions comparing total gradients from the two GPS stations ONSA and ONS1.
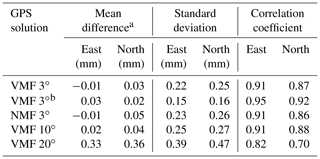
a The mean difference is ONS1−ONSA. b Elevation-dependent weighting, sin (ε).
5.2 Wet gradients from GPS and WVR
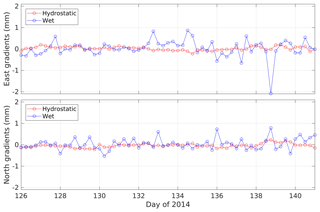
An overview of the data in terms of monthly means of the wet gradient amplitude and the ZWD is presented in Fig. 10. The GPS solution with a 3∘ elevation cut-off angle, no weighting, and the VMF1 mapping functions is used. When forming monthly means the correlations are obvious, both between GPS and WVR estimates and between the variability, in terms of the SD, and the gradient amplitudes and the ZWD. Here we also note that the WVR gives much larger gradients. Factors that can cause a difference in gradient amplitude are listed as follows.
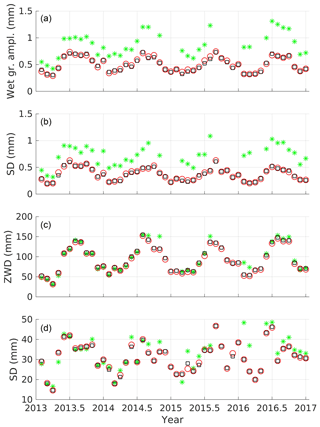
Figure 10Time series of (a) monthly means of wet gradient amplitudes (), (b) their SD, (c) monthly means of the ZWD, and (d) the ZWD SD from GPS and WVR. The GPS results are from the 3∘ solution without weighting and the temporal resolution in the time series used to calculate the monthly mean and the SD is 15 min. The green stars denote WVR data. The ONSA and ONS1 data are denoted by red circles and black squares, respectively.
(1) The WVR is sensitive to liquid water in the atmosphere. This is a cause for positive systematic errors in the ZWD, as well as occasional overestimates of gradient amplitudes. We investigated this possibility by deleting all WVR observations implying a liquid water content larger than 0.3 mm. However, the impact was insignificant. The average gradient amplitude decreased by 0.01 mm. The reason being that large liquid contents are rather infrequent, given that already data acquired during rain (which was assumed to occur when liquid water content was larger than 0.7 mm) have been removed.
(2) The WVR gradients for one 15 min period do not depend on earlier or later estimates, whereas the GPS gradients are estimated using constraints on the variability. A constraint has a similar impact as a low-pass filter (peaks with a short duration will be reduced).
(3) The fact that the WVR and the GPS gradients are computed for different elevation cut-off angles has two possible impacts: (i) the larger volume sensed by GPS (with a 3∘ cut-off angle) includes different air masses and introduces an averaging effect that reduces the mean amplitude and the variability of the gradients, similar to averaging over longer time periods as shown in Table 6 and (ii) the higher cut-off angle (20∘) results in larger formal errors and thus larger variability and larger gradient amplitudes. Table 10 shows the impact of changing the elevation cut-off angle for the GPS observations for ONSA and ONS1 over the 4-year period 2013–2016. We also note from Table 4 that the formal errors of the WVR gradients are significantly smaller than those for the GPS gradients.
We conclude that the constraints and the sampling of different air masses are the likely explanations for the differences in gradient amplitudes estimated from GPS and WVR data but cannot, based on these results, determine their relative importance.
Table 10The impact of the elevation cut-off angle on the estimated 15 min GPS gradient amplitude*.
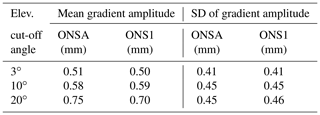
* The corresponding WVR values are only available for the 20∘ elevation cut-off angle: the mean is 0.87 mm and the SD is 0.78 mm.
A correlation plot for the total gradients from ONSA and ONS1 for the VMF1 solution with a 3∘ elevation cut-off angle is shown in Fig. 11. As in the previous section, we see a slightly higher correlation for the east gradients, possibly because of the poorer sampling of the sky north of the zenith direction due to the geometry of the GPS satellite constellation at this latitude (see Fig. 3). The two GPS stations share several error sources, such as clock and orbit errors of the observed satellites, and the use of the same mapping functions, meaning that the rather high correlation is overoptimistic due to a common mode suppression of errors.
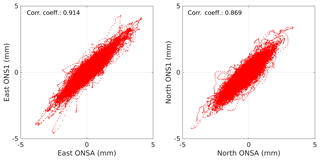
Figure 11Correlations between estimated total gradients from the GPS stations ONSA and ONS1 using all data with a 5 min resolution from the period 2013–2016.
Correlation plots for the wet gradients from ONSA, ONS1, and the WVR are presented in Fig. 12. As seen previously from total gradients, the correlations between the estimated gradients from the two GPS stations are significantly higher compared to when the GPS gradients are correlated with the gradients from the WVR. It is also not surprising that the correlation between the wet gradients from ONSA and ONS1 are slightly lower compared to the correlation between the total gradients (Fig. 11). When subtracting the hydrostatic gradients, a common signal is removed and the dynamic range is reduced, which affects the correlation coefficients.
The reasons for the lower correlation coefficients between the WVR and the GPS gradients are almost identical to the reasons listed above of why the WVR gradient amplitudes are higher: (1) they do not have common sources of errors; (2) the WVR data suffer both from white noise and algorithm errors, especially when liquid water is present; (3) the WVR data for each 15 min period are independent of the successive periods, whereas there are temporal constraints on the gradients estimated from the GPS data; (4) the sampling of the sky also agrees much better between the two GPS stations, assuming that, in general, the directions of the observations are towards the same satellites, whereas the WVR observations are evenly spread over the sky and above an elevation angle of 20∘.
Concerning the sampling of the atmosphere, the use of a multi-GNSS constellation has been shown to improve the agreement between GNSS gradients with those estimated from a WVR (Li et al., 2015). In this context it should be noted that with many more GNSS observations the optimum elevation cut-off angle may not be as low as 3∘ because of an improved sampling of the atmosphere.
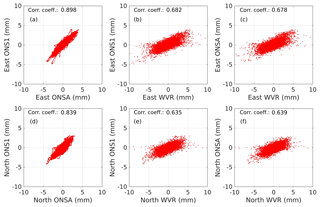
Figure 12Correlations between estimated wet gradients from the WVR, ONSA, and ONS1 using all data from the period 2013–2016. The data in the graphs with ONSA and ONS1 (a, d) have the original 5 min resolution, whereas the GPS data are averaged over 15 min when compared to the WVR data (b, e and c, f). The correlation coefficients obtained when the east gradients from the WVR were correlated with the original total gradients from GPS were 0.633 for ONSA and 0.637 for ONS1. The corresponding values for the north gradients were 0.575 for WVR-ONSA and 0.571 for WVR-ONS1. This supports our assumption that the ECMWF hydrostatic gradients are reasonably accurate when carrying out a linear interpolation between the 6 h samples.
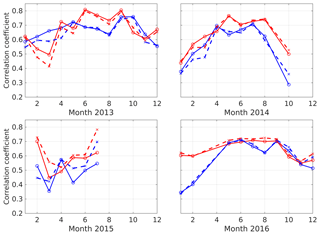
Figure 13Correlations between estimated wet gradients from the WVR data and the GPS data from ONSA (solid lines) and ONS1 (dotted lines), averaged over 15 min when the hydrostatic gradients are removed from the total GPS gradients for each month of the 4 years. The east gradients are presented with red lines and the north gradients with blue lines.
We investigated if an average of the wet gradients from both GPS stations, ONSA and ONS1, estimated at the same time epoch, will improve the agreement with the WVR. We see an overall small improvement. For the east gradient the individual correlation coefficients were improved from 0.678 (ONSA) and 0.682 (ONS1) to 0.698. The corresponding values for the north gradient were increased from 0.639 (ONSA) and 0.635 (ONS1) to 0.666. Our interpretation is that by averaging the GPS gradients from ONSA and ONS1 the stochastic noise is reduced.
Correlation plots are shown in Fig. 13 for each month of the 4 years. A clear seasonal dependence is seen because the variability in the wet refractivity is larger during the warmer time periods, resulting in larger gradients and a larger dynamic range. We note that during October 2014 there were problems with the WVR (see Fig. 6). During most of the days there is a significant data loss, likely due to rain, which could be the reason for the low correlation during this month. The other months with low correlations are March 2015 for both the east and the north component and January and February 2016 for the north component. In all these cases there were no large gradients detected and this has an impact on the correlations. In Fig. 8 of Lu et al. (2016), a correlation coefficient of 0.52 was reported for the months March–May 2014, between GPS and WVR gradients. Here we show that the variability from month to month is large, and therefore the choice of the time period for gradient comparison studies is a critical issue.
Comparing the results obtained for ONSA with those from ONS1 they are almost identical (in both Figs. 12 and 13) meaning that in this case there is no obvious improvement from the absorbing material below the antenna on ONSA. This is different to the previous finding where ONSA and SPT0, with microwave-absorbing material, showed a better agreement with ECMWF gradients compared to the KIR0, MAR6, and VIS0 stations. Our assumption is that the lack of a concrete pillar with a metal mounting plate just below the antenna on ONS1, or any other objects affecting the electromagnetic environment at the antenna, eliminates the need for an absorber (see Fig. 2).
5.3 GPS, VLBI, and WVR wet gradients during CONT14
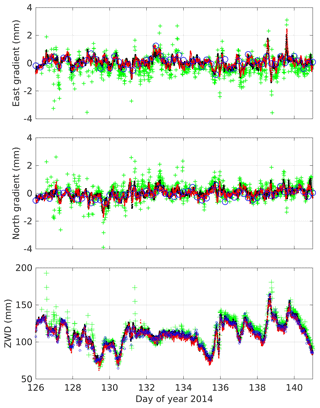
The wet gradients from the two space geodetic techniques GPS and VLBI are compared to each other and to the WVR during the CONT14 campaign. Observations from several earlier CONT campaigns have been analysed in terms of gradients, with different results depending on the station and the time of the campaign (Teke et al., 2013). We use this campaign as an example study of the short-term variability of the wet gradients. The GPS gradients are those obtained from the VMF1 solution, unweighted, with a 3∘ elevation cut-off angle. The ECMWF data (see Fig. 14) is only used to subtract the hydrostatic gradients from the total gradients estimated by VLBI and GPS. The time series of estimated gradients and ZWD are shown in Fig. 15.
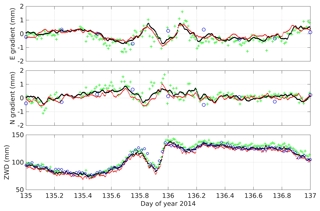
Figure 16Zoom in on the time series in Fig. 15. The symbols are as before: VLBI gradients (blue circles), GPS gradients for ONSA (red dots) and ONS1 (black dots), and WVR (green pluses).
Again we note that the size of the WVR gradients is larger compared to all other instruments. The VLBI gradients correlate with the gradients from the other instruments but their amplitudes are smaller. Given that the sampling of the atmosphere is much more sparse with the VLBI telescope, a short-lived gradient in combination with the assumption of linear functions in 6 h segments will probably reduce the variability in the estimated amplitude.
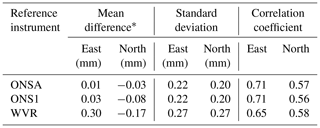
Table 11 summarizes the correlation coefficients for the east and the north VLBI wet gradients compared to those from the two GPS stations, ONSA and ONS1, and the WVR. Here we have correlated averages using data ±3 h around the VLBI gradient value every 6 h. In order to be consistent the interpolated data from continuous VLBI segments are also averaged in this way.
We note that the correlation coefficients are lower for the north component for all three comparisons, whereas the SDs are similar. The reason is that the size of the east gradients are larger compared to the north gradients during this 15 d period. Scatter plots (not shown) confirm what is indicated by the SDs: that the quality of the east and north components is similar.
Table 11Comparison of estimated wet gradients from VLBI relative to GPS and WVR data.
* The mean difference is VLBI−reference instrument.
We attribute the lower correlation coefficients obtained between VLBI-GPS and VLBI-WVR, using 6 h averages during the CONT14 campaign compared to GPS-WVR 15 min averages for the month of May 2014 in Fig. 13, to the sparse sequential sampling of the sky by the VLBI observations. On the other hand, averaging the WVR gradients over ±3 h reduces some of the noise seen in the 15 min values. The future use of the twin telescopes with faster slewing speeds at the site is likely to improve this situation. During CONT14 there were approximately 360 useful observations at Onsala per day. We expect this to increase by a factor of 6–7 when using the new VLBI Geodetic Observing System (VGOS) (Niell et al., 2018), which means that the use of twin telescopes could result in 200 observations per hour. This in turn makes it possible to improve the temporal resolution of the estimated atmospheric gradients.
Finally, we like to use this 15 d long time series for a discussion on gradient variability. At the end of day 135 (see the ZWD plot in Fig. 15) more humid air starts to enter over the site. We note a sudden decrease, followed by a rapid increase. In Fig. 16 we zoom in on the gradients and the ZWD during this period. Here we have an example with wet gradients from GPS and WVR gradients when a warm front passage occurs in the evening of day 135. During this passage there is also a smaller drier air mass present, causing a decrease followed by an increase in the ZWD. During this dip in ZWD the wind at the ground was from the west increasing from 7 m s−1 at 18:00 UT to 11 m s−1 at 24:00 UT. During the decrease in ZWD we see a clear positive east gradient and during the following increase in ZWD the east gradient has a negative peak. Also, during the first few hours of day 136 a decrease in the ZWD corresponds to positive values for the east gradient and the wind continued to come from the west. This is as expected, but there are also variations in the north gradient during this period, consistently detected by the WVR and the GPS data, showing that the wind at the ground was not fully representative for all altitudes.
We have estimated linear horizontal gradients from GPS data acquired at five sites in Sweden. Averaging gradients in the east and the north direction over 1 month gives correlation coefficients of up to 0.9 when compared to gradients calculated from meteorological analyses of the ECMWF (Boehm and Schuh, 2007). The hydrostatic component gives the largest contribution to the monthly averages of the gradients.
We studied wet gradients estimated with a temporal resolution of 15 min from GPS and WVR data. We found that an elevation cut-off angle of 3∘ implies a better agreement when comparing GPS gradients with those from the WVR, in spite of the fact that the WVR does not observe the atmosphere below elevation angles of 20∘. This confirms the result from Kačmařík et al. (2019) showing that low-elevation observations are important for the accuracy of the estimated GPS gradients, although none of us have shown that 3∘ is an optimum cut-off angle.
We also note that when using a 3∘ elevation cut-off angle in the GPS processing, the amplitude of the GPS gradients decreases by approximately 20 % compared to using a 20∘ cut-off angle. We interpret this decrease as the result of two combined effects: (1) the decrease in mean amplitude and variability at the lower cut-off angle results from the averaging of a larger air mass (similar to averaging over longer periods); (2) the increase in mean amplitude and variability at the higher cut-off angle results from the increase in uncertainty and thus larger scatter in the estimates. The relative importance of these two effects are recommended topics to be studied further, e.g. by using simulations based on high-resolution numerical weather models.
Correlation coefficients between wet gradients estimated from GPS and the WVR data can reach up to 0.8 for specific months. We note a strong seasonal dependence, from 0.3 during months with smaller gradients to 0.8 during months with larger gradients, typically during the warmer and more humid part of the year. Related to this we suggest further studies of large wet gradients estimated from GPS, again in combination with meteorological high-resolution models for verification of the quality of the gradients.
In general, we also note slightly higher correlation coefficients for the GPS-derived gradients in the east compared to the north direction. We interpret this difference to be caused by an inhomogeneous spatial sampling of the sky, which is important when we assume that the linear model describing horizontal gradients has deficiencies. The different sampling of the sky is an important issue for any comparison between different techniques. This question remains unresolved and is also recommended for further study.
Additional issues that deserve attention in future studies, in addition to similar studies in different climates, e.g. the tropics, include multi-GNSS observations. At latitudes similar to those in this study, the use of GNSS satellites with a higher orbit inclination will reduce the part of the sky not sampled by GPS.
For VLBI the use of VGOS (twin) telescopes will also dramatically improve the sampling of the atmosphere. When WVR data are used to evaluate gradients from the space geodetic techniques one may consider also applying different constraints on the temporal variability of these estimates. We suggest that future work on gradients should focus on the interplay between the elevation cut-off angle, the temporal resolution, and the constraint value using both single and multi-GNSS. Furthermore, we believe that the outcome of such studies will be weather- and site-dependent, which will make it difficult to arrive at just one optimal recommendation that is globally valid.
The input GNSS data, in RINEX format, are available from EUREF: https://igs.bkg.bund.de/dataandproducts/browse (last access: 8 July 2019). The input VLBI data are available from the IVS: ftp://ivs.bkg.bund.de/pub/vlbi/ivsdata/db/2014/ (last access: 8 July 2019). The ECMWF gradients are accessible from the Technical University of Vienna: http://vmf.geo.tuwien.ac.at/trop_products/GNSS/LHG/ (last access: 8 July 2019). The estimated gradients from GPS, VLBI, and WVR data have been registered and archived by the Swedish National Data Service (SND): https://doi.org/10.5878/nswt-yr39 (Elgered et al., 2019).
GE coordinated and wrote the major part of the manuscript and together with TN planned the different GNSS data analyses during the COST Action ES1206. TN performed the GNSS data analyses, resulting in the estimated gradients. PF and RH carried out the same task for WVR and VLBI data, respectively. All authors contributed in the writing process, to the sections presenting the results produced by each author in particular, and approved the entire paper before submission.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Advanced Global Navigation Satellite Systems tropospheric products for monitoring severe weather events and climate (GNSS4SWEC) (AMT/ACP/ANGEO inter-journal SI)”. It is not associated with a conference.
We appreciate the constructive comments and suggestions from the editor and the three referees. They resulted in a significantly improved paper, offering additional possible explanations for the obtained results as well as additional studies. For example, the use of a 3∘ elevation cut-off angle in the GPS data processing was not included in our original manuscript. The map in Fig. 1 was produced using Generic Mapping Tools (Wessel and Smith, 1998).
This paper was edited by Olivier Bock and reviewed by three anonymous referees.
Bar-Sever, Y.-E., Kroger, P. M., and Börjesson, J. A.: Estimating horizontal gradients of tropospheric path delay with a single GPS receiver, J. Geophys. Res., 103, 5019–5035, https://doi.org/10.1029/97jb03534, 1998. a, b, c, d, e, f
Bertiger, W., Desai, S. D., Haines, B., Harvey, N., Moore, A. W., Owen, S., and Weiss, J. P.: Single receiver phase ambiguity resolution with GPS data, J. Geod., 84, 327–337, https://doi.org/10.1007/s00190-010-0371-9, 2010. a
Bock, O. and Parracho, A. C.: Consistency and representativeness of integrated water vapour from ground-based GPS observations and ERA-Interim reanalysis, Atmos. Chem. Phys. Discuss., https://doi.org/10.5194/acp-2019-28, in review, 2019. a
Boehm, J., Werl, B., and Schuh, H.: Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data, J. Geophys. Res., 111, B02406, https://doi.org/10.1029/2005JB003629, 2006. a, b
Boehm, J. and Schuh, H.: Troposphere gradients from the ECMWF in VLBI analysis, J. Geod., 81, 403–408, https://doi.org/10.1007/s00190-007-0144-2, 2007. a, b, c, d
Brenot, H., Neméghaire, J., Delobbe, L., Clerbaux, N., De Meutter, P., Deckmyn, A., Delcloo, A., Frappez, L., and Van Roozendael, M.: Preliminary signs of the initiation of deep convection by GNSS, Atmos. Chem. Phys., 13, 5425–5449, https://doi.org/10.5194/acp-13-5425-2013, 2013. a
Brown, R. A.: A secondary flow model for the planetary boundary layer, J. Atmos. Sci., 27, 742–757, 1970. a
Bruyninx, C., Habrich, H., Söhne, W., Kenyeres, A., Stangl, G., and Völksen, C.: Enhancement of the EUREF Permanent Network Services and Products, Geodesy for Planet Earth, IAG Symposia Series, 136, 27–35, https://doi.org/10.1007/978-3-642-20338-1_4, 2012. a
Chen, G. and Herring, T. A.: Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data, J. Geophys. Res., 102, 20489–20502, https://doi.org/10.1029/97JB01739, 1997. a, b
Craig, R. A., Katz, I., and Harney, P. J.: Sea breeze cross sections from pyschrometric measurements, B. Am. Meteorol. Soc., 26, 405–410, 1945. a, b
Davis, J. L., Herring, T. A., Shapiro, I. I., Rogers, A. E. E., and Elgered, G.: Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length, Radio Sci., 20, 1593–1607, https://doi.org/10.1029/RS020i006p01593, 1985. a
Davis, J. L., Elgered, G., Niell, A. E., and Kuehn, C. E.: Ground-based measurement of gradients in the “wet” radio refractivity of air, Radio Sci., 28, 1003–1018, https://doi.org/10.1029/93RS01917, 1993. a, b
Elgered, G. and Jarlemark, P. O. J.: Ground-Based Microwave Radiometry and Long-Term Observations of Atmospheric Water Vapor, Radio Sci., 33, 707–717, https://doi.org/10.1029/98RS00488, 1998. a
Elgered, G., Forkman, P., Haas, R., and Ning, T.: Chalmers University of Technology, Department of Space, Earth and Environment, On the information content in linear horizontal delay gradients estimated from space geodesy observations, Swedish National Data Service, Version 1.0, https://doi.org/10.5878/nswt-yr39, 2019.
Gradinarsky, L. P., Haas, R., Elgered, G., and Johansson, J. M.: Wet path delay and delay gradients inferred from microwave radiometer, GPS and VLBI observations, Earth Planets Space, 52, 695–698, https://doi.org/10.1186/BF03352266, 2000. a, b
Haas, R., Hobiger, T., Kurihara S., and Hara, T.: Ultra-rapid earth rotation determination with VLBI during CONT11 and CONT14, J. Geod., 91, 831–837, https://doi.org/10.1007/s00190-016-0974-x, 2017. a
Hewson, E. W. and Longley, R. W.: Meteorology: Theoretical and Applied, John Wiley & Sons, New York, 1944. a
IERS Conventions: IERS Technical Note, edited by: Petit, G. and Luzum, B.; 36, Verlag des Bundesamts für Kartographie und Geodäsie, Frankfurt am Main, 179 pp., 2010. a
Jarlemark, P. O. J., Emardson, T. R., and Johansson, J. M.: Wet Delay Variability Calculated from Radiometric Measurements and Its Role in Space Geodetic Parameter Estimation, Radio Sci., 33, 719–730, https://doi.org/10.1029/98RS00551, 1998. a
Kačmařík, M., Douša, J., Zus, F., Václavovic, P., Balidakis, K., Dick, G., and Wickert, J.: Sensitivity of GNSS tropospheric gradients to processing options, Ann. Geophys., 37, 429–446, https://doi.org/10.5194/angeo-37-429-2019, 2019. a, b, c, d
Koulali, A., Ouazar, D., Bock, O., and Fadil, A.: Study of seasonal-scale atmospheric water cycle with ground-based GPS receivers, radiosondes and NWP models over Morocco, Atmos. Res., 104–105, 273–291, https://doi.org/10.1016/j.atmosres.2011.11.002, 2012. a, b
Landskron, D. and Böhm, J.: Refined discrete and empirical horizontal gradients in VLBI analysis, J. Geod., 92, 1387–1399, https://doi.org/10.1007/s00190-018-1127-1, 2018. a
Li, X., Zus, F., Lu, C., Ning, T., Dick, G., Ge, M., Wickert, J., and Schuh, H.: Retrieving high-resolution tropospheric gradients from multiconstellation GNSS observations, Geophys. Res. Lett., 42, 4173–4181, https://doi.org/10.1002/2015GL063856, 2015. a, b, c
Lu, C., Li, X., Li, Z., Heinkelmann, R., Nilsson, T., Dick, G., Ge, M., and Schuh, H.: GNSS tropospheric gradients with high temporal resolution and their effect on precise positioning, J. Geophys. Res.-Atmos., 121, 912–930, https://doi.org/10.1002/2015JD024255, 2016. a
Lyard, F., Lefevre, F., Letellier, T., and Francis, O.: Modelling the global ocean tides: Modern insights from FES2004, Ocean Dynam., 56, 394–415, https://doi.org/10.1007/s10236-006-0086-x, 2006. a
Ma, C., Sauber, J. M., Bell, L. J., Clark, T. A., Gordon, D., Himwich, W. E., and Ryan, J. W.: Measurement of horizontal motions in Alaska using very long baseline interferometry, J. Geophys. Res., 95, 21991–2011, https://doi.org/10.1029/JB095iB13p21991, 1990. a
MacMillan, D. S.: EOP and scale from continuous VLBI observing: CONT campaigns to future VGOS networks, J. Geod., 91, 819–829, https://doi.org/10.1007/s00190-017-1003-4, 2017. a
Matteo, N. A. and Morton, Y. T.: Ionosphere geomagnetic field: Comparison of IGRF model prediction and satellite measurements 1991–2010, Radio Sci., 46, RS4003, https://doi.org/10.1029/2010RS004529, 2011. a
Meindl, M., Schaer, S., Hugentobler, U., and Beutler, G.: Tropospheric Gradient Estimation at CODE: Results from Global Solutions, J. Meteorol. Soc. Jpn., 82, 331–338, https://doi.org/10.2151/jmsj.2004.331, 2004. a
Miller, S. T. K., Keim, B. D., Talbot, R. W., and Mao, H.: Sea breeze: Structure, forecasting, and impacts, Rev. Geophys., 41, 1011, https://doi.org/10.1029/2003RG000124, 2003. a, b
Nahmani, S., Bock, O., and Guichard, F.: Sensitivity of GPS tropospheric estimates to mesoscale convective systems in West Africa, Atmos. Chem. Phys. Discuss., https://doi.org/10.5194/acp-2018-1242, in review, 2019. a
Niell, A. E.: Global mapping functions for the atmosphere delay at radio wavelengths, J. Geophys. Res., 101, 3227–3246, https://doi.org/10.1029/95JB03048, 1996. a, b
Niell, A., Barrett, J., Burns, A., Cappallo, R., Corey, B., Derome, M., C. Eckert, C., Elosegui, P., McWhirter, R., Poirier, M., Rajagopalan, G., Rogers, A., Ruszczyk, C., SooHoo, J., Titus, M., Whitney, A., Behrend, D., Bolotin, S., Gipson, J., Gordon, D., Himwich, E., and Petrachenko, B.: Demonstration of a broadband very long baseline interferometer system: A new instrument for high-precision space geodesy, Radio Sci., 53, 1269–1291, https://doi.org/10.1029/2018RS006617, 2018. a
Ning, T., Elgered, G., Willén, U., and Johansson, J. M.: Evaluation of the atmospheric water vapor content in a regional climate model using ground-based GPS measurements, J. Geophys. Res., 118, 1–11, https://doi.org/10.1029/2012JD018053, 2013. a
Nothnagel, A., Artz, T., Behrend, D., and Malkin, Z.: International VLBI Service for Geodesy and Astrometry Delivering high-quality products and embarking on observations of the next generation, J. Geod., 91, 711–721, https://doi.org/10.1007/s00190-016-0950-5, 2017. a
Sanchez-Franks, A., Hameed, S., and Wilson, R. E.: The Icelandic Low as a Predictor of the Gulf Stream North Wall Position, J. Phys. Oceanogr., 46, 817–826, https://doi.org/10.1175/JPO-D-14-0244.1, 2016. a
Schmid, R., Steigenberger, P., Gendt, G., Ge, M., and Rothacher, M.: Generation of a consistent absolute phase center correction model for GPS receiver and satellite antennas, J. Geod., 81, 781–798, https://doi.org/10.1007/s00190-007-0148-y, 2007. a
Sibois, A., Amiri, N., Bertiger, W., Miller, M., Murphy, D., Ries, P., Sakamura, C., and Sibthorpe, A.: Ensuring a smooth operational transition from GIPSY-OASIS to GipsyX: product verification and validation overview, poster presented at the IGS Workshop, Paris, France, available at: http://www.igs.org/presents/workshop2017 (last access: 5 July 2019), 2017. a
Teke, K., Nilsson, T., Böhm, J., Hobiger, T., Steigenberger, P., Garcia-Espada, S., Haas, R., and Willis, P.: Troposphere delays from space geodetic techniques, water vapor radiometers, and numerical weather models over a series of continuous VLBI campaigns, J. Geod., 87, 981–1001, https://doi.org/10.1007/s00190-013-0662-z, 2013. a
Thompson, D. W. J. and Wallace, J. M.: The Arctic oscillation signature in the wintertime geopotential height and temperature fields, Geophys. Res. Lett., 25, 1297–1300, https://doi.org/10.1029/98GL00950, 1998. a
Webb, F. H. and Zumberge, J. F.: An Introduction to the GIPSY/OASIS-II, JPL Publ., D-11088, Jet Propulsion Laboratory, Pasadena, California, 1993. a
Wessel, P. and Smith, W. H. F.: New, improved version of generic mapping tools released, EOS T. Am. Geophys. U., 79, 579, https://doi.org/10.1029/98EO00426, 1998. a
Westwater, E. R. and Guiraud, F. O.: Ground-based microwave radiometric retrieval of precipitable water vapor in presence of clouds with high liquid content, Radio Sci., 15, 947–957, https://doi.org/10.1029/RS015i005p00947, 1980. a
Zumberge, J. F., Heflin, M. B., Jefferson, D. C., Watkins, M. M., and Webb, F. H.: Precise point positioning for the efficient and robust analysis of GPS data from large networks, J. Geophys. Res., 102, 5005–5017, https://doi.org/10.1029/96JB03860, 1997. a
Zus, F., Dick, G., Heise, S., and Wickert, J.: A forward operator and its adjoint for GPS slant total delays, Radio Sci., 50, 393–405, https://doi.org/10.1002/2014RS005584, 2015. a
- Abstract
- Introduction
- Cause of horizontal gradients and models
- Instrumentation and data
- Comparison of gradients from GPS and ECMWF data for the time period 2006–2016
- Wet gradients at the Onsala site
- Conclusions and suggestions for future work
- Data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Review statement
- References
- Abstract
- Introduction
- Cause of horizontal gradients and models
- Instrumentation and data
- Comparison of gradients from GPS and ECMWF data for the time period 2006–2016
- Wet gradients at the Onsala site
- Conclusions and suggestions for future work
- Data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Review statement
- References