the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Characterisation of the transfer of cluster ions through an atmospheric pressure interface time-of-flight mass spectrometer with hexapole ion guides
Markus Leiminger
Stefan Feil
Paul Mutschlechner
Arttu Ylisirniö
Daniel Gunsch
Lukas Fischer
Alfons Jordan
Siegfried Schobesberger
Gerhard Steiner
Here we present an alternative approach of an atmospheric pressure interface (APi) time-of-flight mass spectrometer for the study of atmospheric ions and cluster ions, the so-called ioniAPi-TOF. The novelty is the use of two hexapoles as ion guides within the APi. In our case, hexapoles can accept and transmit a broad mass range enabling the study of small precursor ions and heavy cluster ions at the same time. Weakly bound cluster ions can easily de-cluster during ion transfer depending on the voltages applied to the ion transfer optics. With the example system of , we estimate that cluster ions with higher binding energies than 17 kcal mol−1 can be transferred through the APi without significant fragmentation, which is considerably lower than about 25 kcal mol−1 estimated from the literature for APi-TOFs with quadrupole ion guides. In contrast to the low-fragmenting ion transfer, the hexapoles can be set to a high-fragmenting declustering mode for collision-induced dissociation (CID) experiments as well. The ion transmission efficiency over a broad mass range was determined to be on the order of 1 %, which is comparable to existing instrumentation. From measurements under well-controlled conditions during the CLOUD experiment, we demonstrate the instrument's performance and present results from an inter-comparison with a quadrupole-based APi-TOF.
- Article
(740 KB) -
Supplement
(766 KB) - BibTeX
- EndNote
The study of ion composition in the atmosphere has a long history, and mass spectrometers have been used as an important tool in elucidating their identity and concentrations since the early days. Galactic cosmic rays (GCRs) are the main ionisation source in the atmosphere, while radioactive decay (of radon) is more relevant at ground level. Minor entries originate from lightning, power lines and combustion sources (Curtius, 2006). Higher ion number concentrations are detected in the upper atmosphere and lower number concentrations at ground level. Typically, up to 10 000 ions per cubic centimetre can be observed within the troposphere having a lifetime of a few hundred seconds (Ferguson and Arnold, 1981; Hirsikko et al., 2011). Despite their low abundance, ions can play an important role in atmospheric new particle formation via ion–ion recombination and ion-induced nucleation (Kirkby et al., 2016) as well as in atmospheric electricity.
In the 1970s, Frank Arnold and co-workers were the first to study the composition of ions in the lower stratosphere and upper troposphere. In the positive ion spectrum, detected signals were mainly attributed to hydrated hydronium clusters and protonated organic vapours (Arnold et al., 1977, 1978). For negative ions, clusters of de-protonated acids like and were identified in the mass range of 1 to 280 amu (Viggiano and Arnold, 1981). At ground level, the composition of the main tropospheric ions was also studied by Fred Eisele and co-workers with a quadrupole mass spectrometer (Eisele, 1986; Perkins and Eisele, 1984). Using collision-induced dissociation (CID), they identified the “core” ions of hydrated clusters showing that positive core ions consist mainly of protonated amines. The latter were examined using tandem mass spectrometry, which helped to identify pyridine and its homologues (Eisele, 1988). Back then, Fred Eisele had already observed a manifold of tropospheric ions up to 700 amu in the positive ion mass spectrum, but the low mass resolving power of the quadrupole mass analyser was a bottleneck for revealing their sum formula. Tandem mass spectrometry was not performed for these heavy ions for several reasons like insufficient sensitivity and the natural variability (Eisele and Tanner, 1990).
The development of an atmospheric pressure interface time-of-flight mass spectrometer (APi-TOF MS, Aerodyne Research Inc. and Tofwerk AG) overcame the limitations of quadrupole mass analysers regarding mass resolving power, duty cycle and mass range. Junninen et al. (2010) demonstrated that this instrument is suitable to detect many unknown ions in the atmosphere and assign sum formulas to many mass peaks for the first time (Ehn et al., 2010; Junninen et al., 2010). Especially in the field of atmospheric new particle formation, the APi-TOF enabled the study of ion formation starting from single molecules such as sulfuric acid, ammonia, amines and highly oxygenated organic molecules (HOMs) and externally to the formation of molecular clusters of sizes with a mobility equivalent diameter of 1–2 nm (Almeida et al., 2013; Kirkby et al., 2016; Kürten et al., 2014; Schobesberger et al., 2013). In the last couple of years, the APi-TOF was the key instrument for many scientific studies of new particle formation in both laboratory and field settings (Bianchi et al., 2016; Kirkby et al., 2011; Sipilä et al., 2016).
However, questions arose about fragmentation of cluster ions inside the APi-TOF instrument during the ion transfer from ambient pressure through the two quadrupoles and the following lens system to the detector (Ehrhart et al., 2016). It remained unclear if additional ligands besides water molecules might be lost during the ion transfer as well. In a recent publication by Olenius et al. (2013), the authors concluded that fragmentation might be a reasonable explanation for the observed difference in measured and modelled cluster ion distributions of clusters (Olenius et al., 2013).
Few publications explicitly studied fragmentation inside the APi-TOF mass spectrometer (Bertram et al., 2011; Brophy and Farmer, 2016; Lopez-Hilfiker et al., 2016). Bertram et al. (2011) showed that fragmentation of cluster ions is strongly sensitive to the voltage settings in the APi. Lopez-Hilfiker et al. (2016) as well as Brophy and Farmer (2016) used two different types of chemical ionisation (CI) APi-TOF to study fragmentation of reagent–adduct cluster ions. Both found that the electric field inside the APi could be tuned to a low-fragmenting “clustered” setting and a high-fragmenting “declustering” setting. Even using the low-fragmenting setting, however, the transfer of weakly bound cluster ions was evidently affected by fragmentation inside the APi (Brophy and Farmer, 2016; Lopez-Hilfiker et al., 2016). Here, the question arises of which cluster bond strengths are affected by fragmentation and how strongly.
For the instrument configuration used by Lopez-Hilfiker et al. (2016), Iyer et al. (2016) found that for chemical ionisation using iodide (I−) as reagent ion, adduct–molecule clusters with binding energies above 25 kcal mol−1 are mostly detected with maximum sensitivity at the collisional limit by comparing experimentally measured sensitivities with modelled binding energies. Cluster ions below this threshold suffer from lower sensitivities, likely due to non-thermal dissociation during the ion transfer inside the mass spectrometer (i.e. partial fragmentation). It remains unclear if this threshold can be explained by fragmentation in the APi or by the loss of weakly bound ligands during the charging process of a neutral cluster by the reagent ion in the ion molecule region (IMR) of the TOF-CIMS (Kurtén et al., 2011). In the Supplement, however, the authors conclude that fragmentation in the APi of their TOF-CIMS is more reasonable. Furthermore, they also state that cluster ions with binding energies below 10 kcal mol−1 may not be detectable at all (Iyer et al., 2016). Consequently, there may be two threshold binding energies, one below which partial fragmentation of cluster ions can be expected and the other one below which the non-detection of cluster ions is almost certain. Quantifying these thresholds (e.g. around 10 and 25 kcal mol−1 for the APi configuration in Iyer et al., 2016) can help characterise the ion transfer of APi-TOF instruments.
In those previous studies, the APi's declustering strength was deliberately manipulated by varying the electric potential gradients between two ion optic parts in the APi, e.g. between the skimmer and the second quadrupole (Brophy and Farmer, 2016; Lopez-Hilfiker et al., 2016). This electric field is located at the transition from the first to the second pressure stage where the gas pressure drops from 200 to a few pascals. The cluster ions accelerated by the electrical field can therefore attain relatively high energies via collisions (Zapadinsky et al., 2019; at >100 Pa, collisions tend to be too frequent and hence low in collision energy, and at ≪1 Pa collisions tend to be too rare due to the increased mean free path). Hence, the transition region from the first pressure stage to the second one is also a transition from multi- to single-collision conditions.
The role of the quadrupoles in the fragmentation of cluster ions has not been investigated so far. From theory, there are some differences with regard to the ion transfer properties comparing the quadrupole to higher-order multipoles that can mainly be explained by the number of rods. To radially trap or guide ions of various mass-to-charge (m∕z) ratios through a multipole a radiofrequency (RF) with amplitude V0 is applied to alternating rods. Ions of low m∕z are efficiently trapped with higher frequencies and lower amplitudes while ions of high m∕z can be more efficiently transferred with lower frequencies and higher amplitudes. The time-averaged radial trapping field within a multipole of 2n electrodes can be described with the effective potential V∗ (Gerlich, 1992):
Here, we have the charge q, the ion mass m, the angular frequency Ω, the amplitude V0, the inner radius of the electrode arrangement r0 and the radial distance of the ion r inside the multipole. In general, the effective potential V∗ is high close to the rods and low close to the centre. The slope between multipole rods and its centre depends on the rod number; see Fig. S0 in the Supplement. A higher rod number further provides a more homogenous trapping field. The trapping fields of RF-only multipoles do not affect the axial kinetic energy of ions, but can affect the radial ion energy (Armentrout, 2000).
From Eq. (1), it can be seen that the effective potential varies with . A quadrupole (n=2) has a quadratic dependence (r∕r0)2 while a hexapole depends on (r∕r0)4. Consequently, the effective potential of a quadrupole increases much closer to the centre of the ion guide compared to a hexapole. On the one hand this results in an efficient focusing of the ions for a quadrupole, but on the other hand, this yields strong perturbations of ions in radial direction and thus the ion kinetic energies are not well defined. Here, a hexapole has a much lower impact on the radial energy due to a larger field free region, as the effective potential is flatter close to the centre and higher close to the rods. Compared to higher-order multipoles that have an even larger field free region, a hexapole still offers a more pronounced focusing power.
The n2 dependence of the effective potential further means that for the same RF settings, a hexapole has a stronger trapping field over a quadrupole of a factor of 9∕4. To transfer ions of high m∕z with the same efficiency, a quadrupole would require higher RF settings, which in turn would lead to an increased effective potential not only close to the rods but also in the centre according to the (r∕r0)2 dependence of the effective potential. From this, higher-order multipoles should in general show a lower impact on the stability of cluster ions.
Further, it is important to mention the mass discrimination properties of multipole ion guides (Heinritzi et al., 2016). Small ions can be lost due to unstable trajectories at higher RF settings on the multipole, which is known as the low mass cut-off. However, heavy ions typically need a stronger effective potential within the ion guide to be efficiently focused and transferred (see Eq. 1). Therefore, the efficient transmission of small and heavy ions in a multipole ion guide depends on the mass window of the multipole. Higher-order multipoles are recommended for the transfer of a broader mass window ranging from low to high masses (Gerlich, 2004). For quadrupole ion guides, the effect of a dramatic cut-off at low masses is especially pronounced due to the much narrower field free region within the quadrupole compared to higher-order multipoles (Gerlich, 1992). In general, multipoles can be tuned to a mass window of interest. In the field of atmospheric new particle formation, a broad mass range is essential to get a complete understanding of the nucleating ions. Primary ions like NO+, or H3O+ have different charging properties and the detection of small ions can therefore help to identify the composition of heavy cluster ions by revealing likely ionisation pathways. Thus, information could be lost due to mass discrimination effects for small and heavy ions. Here, hexapole ion guides show advantageous properties regarding the ion transfer.
Ion trajectory simulations through a quadrupole, a hexapole and an octopole by Hägg and Szabo (1986b) showed that higher multipoles (n≥3) are more suited for guiding ions while only the quadrupole can be used as a mass analyser. In an accompanying study, the authors found that the transmission through higher multipoles depends on the initial conditions of the ion beam, e.g. initial position or velocity (Hägg and Szabo, 1986a). The reason for this is that the x and y coordinates are no longer independent compared to the quadrupole. An overall lower transmission efficiency of ions could be a likely consequence. Hägg and Szabo (1986c) found in another study that the multipoles of an even order like the octopole have more stable trajectories because the opposing electrodes have the same sign whereas multipoles of an odd order like the hexapole have opposing electrodes of opposite sign (Hägg and Szabo, 1986c). This would be one benefit of using an octopole over a hexapole despite otherwise similar transfer properties. For further ion trajectory simulations in multipole ion guides with focus on phenomena like collisional cooling and radial stratification of different m∕z ions due to ion–ion and ion–neutral interactions, we refer the reader to Tolmachev et al. (2003) and references therein. The main properties of multipole ion guides are summarised in Table 1.
Table 1Qualitative comparison of the ion guide transfer properties of ideal multipoles with 2n poles (Gerlich, 1992).

In the present study, we introduce the ioniAPi-TOF with hexapole ion guides. We characterise the performance of the ioniAPi-TOF regarding ion transmission efficiency, mass range and the impact of electric fields in fragmenting cluster ions. Additionally, we present an inter-comparison with a state-of-the-art quadrupole-based APi-TOF during the CERN CLOUD experiment performed in autumn 2017 and discuss similarities as well as differences in the instrument's performance.
2.1 The ioniAPi-TOF
The ioniAPi-TOF mass spectrometer consists of a laminar flow inlet and an atmospheric pressure interface (APi) including two hexapole ion guides, an ion transfer optic and an orthogonal extraction, reflectron time-of-flight (TOF) mass analyser (see Fig. 1).
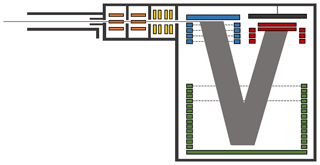
Figure 1Schematic of the ioniAPi-TOF mass spectrometer. The hexapoles are shown in orange and the ion optical lens system in yellow. The orthogonal extraction region is coloured in blue. The reflectron is coloured in green and the detection region with post acceleration and MCP in red.
The laminar flow inlet draws atmospheric ions from the ambient to the inlet of the mass spectrometer via an adjustable flow of 1 to 15 L min−1. The inlet is made of a stainless-steel tube with a length of 10 cm and a diameter of 1∕2 in. Within this tube, a core-sampling probe is placed in front of the entrance aperture of the ioniAPi-TOF with an inner diameter of 2.5 mm and a length of 25 mm as indicated in Fig. 1.
The entrance aperture has a diameter of 0.4 mm yielding an inlet flow of 1.1 L min−1 from ambient pressure into the mass spectrometer. Skimmers with bore diameters of 1.2 mm separate the different pressure stages. Two hexapole ion guides of the same length are installed in the first and second pressure stages of the atmospheric pressure interface. The first hexapole runs at a frequency of 1 MHz and an amplitude of 200 Vpp. The frequency of the second hexapole is about 5.5 MHz with an amplitude of 600 Vpp. The third pressure stage contains an ion transfer optical lens system consisting of two lens stacks. It focuses the ion beam coming from the hexapoles and transfers it to the orthogonal extraction region of the mass spectrometer.
As the time-of-flight mass analyser, we chose the ioniTOF1000 platform of Ionicon Analytik GmbH (Innsbruck, Austria). It is a compact time-of-flight mass spectrometer with a short ion flight path of roughly 0.5 m and therefore expected to have a sufficiently high ion transmission efficiency, which is important due to the low abundance of atmospheric ions. The same time-of-flight mass analyser was already presented in Müller et al. (2014). The ioniTOF1000 is made of a multistage orthogonal-extraction region consisting of a pusher and four mesh electrodes supplied with a reference, pull, grid, and a drift tube cage voltage.
Depending on the desired mass range of interest, the extraction frequency can be adjusted to measure ions of a mass-to-charge (m∕z) ratio of up to 10 000 Th (1 Thomson = 1 Da/e−). For the results presented herein, the extraction frequency is typically set to 30 kHz to measure ions up to 2000 Th.
A double-stage reflectron is used for an improved mass resolution leading to a V-shaped ion flight path. Ions are post-accelerated and detected with a multichannel plate (MCP) stack with a voltage of ∼2200 V. Compared to Müller et al. (2014) we achieved a mass resolution at full width at half maximum (FWHM) of ∼2000 for ions above m∕z 100; see Fig. 2.
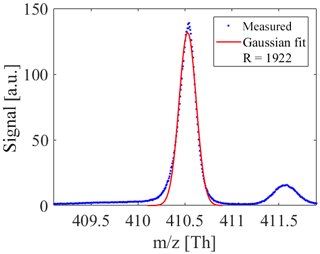
Figure 2The mass resolution of the ioniAPi-TOF is about 2000 at a nominal mass of 410 Th, which corresponds to C28H60N+, the THABr monomer.
A hyco four-cylinder diaphragm pump is used at ambient pressure to draw air through the laminar flow inlet. A Pfeiffer Vacuum ACP 40 roots pump is used as a fore pressure pump to reduce the pressure in the cell of the first hexapole in the ioniAPi-TOF to 2.3 mbar. Three Pfeiffer Vacuum HiPace 80 turbo-molecular pumps, which are connected to a MD1 diaphragm pump of Vacuubrand, evacuate the ion transfer optics region and the TOF mass analyser. Together they maintain a typical pressure of a few 10−3 mbar in the second hexapole of the ioniAPi, followed by 10−4 mbar within the lens stacks and a few 10−6 mbar in the TOF mass analyser.
As described in Müller et al. (2014) a time-to-digital converter (TDC) is used to convert the MCP signals into ion counts per time bin. The applied extraction frequency of 30 kHz results in about 280 000 time bins. The IONICON TOF 3.0 software is used for data acquisition. The data are stored in the HDF5 file format (HDF5-group). The ioniAPi-TOF allows detection of ions in positive and negative ion mode. In this work, we present results of the positive ion mode only.
2.2 Cluster calibration unit
The cluster calibration unit (CCU) allows the calibration of the mass axis over a broad mass range and of the mass-dependent transmission efficiency of (CI-)APi-TOF mass spectrometers (Heinritzi et al., 2016). For this purpose, the CCU consists of an electrospray ionisation source (ESI), a “Vienna”-type high-resolution differential mobility analyser (UDMA, Steiner et al., 2010) and a Faraday cup electrometer (FCE; Winklmayr et al., 1991); see Fig. 3.
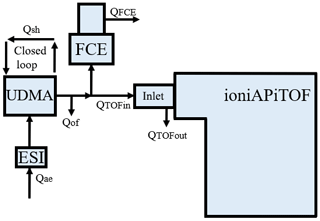
Figure 3Experimental setup of the cluster calibration unit consisting of an electrospray ionisation source (ESI), a differential mobility analyser (UDMA) and a Faraday cup electrometer (FCE) (Steiner et al., 2010; Winklmayr et al., 1991). Although not shown here, the flow to both detectors is split via a Y splitter with an angle of 20∘ for both sampling lines downstream to reduce inhomogeneities that might occur due to the flow separation.
Millimolar solutions of tetra-alkyl-ammonium halides dissolved in acetonitrile are used for the ESI; see Table 2 for details (Ude and Fernández de la Mora, 2005). By applying a high voltage of a few kilovolts, the ESI generates cluster ions of the desired polarity. A transport flow of typically 14 L min−1 transfers the ions over a distance of a few centimetres from the ESI directly into the UDMA. Within the UDMA, the ions are classified in terms of their electrical mobility. In this study, a filtered recirculating sheath flow of about 700 L min−1 was used. Under these conditions and the given geometry, the resolving power of the UDMA was around 10 to 15, which is sufficient to distinguish ionic monomers, dimers and trimers of one selected calibration compound within the ion mobility spectrum. An exemplary ion mobility spectrum is shown in Supplement Fig. S1. For details on the definition on the resolving power of DMAs, we refer to Flagan (1998).
Table 2Positive cluster ions, their corresponding mass-to-charge ratio m∕z and the mobility diameter dz of tetra-methyl-ammonium-iodine (TMAI), tetra-propyl-ammonium-iodine (TPrAI), tetra-butyl-ammonium-iodine (TBAI), tetra-heptyl-ammonium-bromide (THABr) and tributylmethylammonium-bis(trifluoromethylsulfonyl)imide (ionic liquid: IL) used in this work. A is the tetra-alkyl-ammonium part of the neutral molecule, while B can be I or Br in the case of the first four compounds.
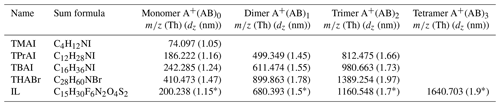
* The mobility diameters for the ionic liquid were determined in this study with an uncertainty of ±0.1 nm.
To retrieve the transmission at a desired mass-to-charge (m∕z) ratio in the mass spectrometer, the UDMA can be set to a constant voltage that corresponds to a specific electrical mobility. Consequently, only ions of the corresponding electrical mobility will pass the UDMA. The aerosol flow coming from the outlet of the UDMA is guided through an 8 mm stainless-steel tube of 10 cm length. After this length, the flow is separated via a Y-shaped flow splitter with an angle of 40∘ between the two outlet tubes to reduce inhomogeneities of the sample flow. For the same reason, the flow rates to both the FCE and the ioniAPi-TOF are set equally to 6 L min−1 resulting in an overflow of 2 L min−1.
2.3 Experiments with a corona ion source
For the comparison of a low-fragmenting (clustered) setting (voltage difference: dV = −1.4 V) and a high-fragmenting (declustering) setting (voltage difference: dV = −10.0 V) described in Sect. 3.2, ions were generated with a corona ion source. A 1∕2 in. T-piece was connected to the 1∕2 in. laminar flow inlet in front of the ioniAPi-TOF. Cleaned and dried lab air was drawn in a straight line through the T-piece. The corona needle was placed through a 1∕2 in. plug into the T-piece orthogonally to the flow direction. The needle tip sat below the air flow.
A voltage of +1.7 kV led to the ionisation of ambient air streaming into the direction of the entrance aperture of the mass spectrometer. Hereby, a large variety of ions was produced via ion–molecule reactions and charge transfer covering a mass range from 18 to 1000 Th. The reaction time within the laminar flow inlet was approximately 35 ms. In the course of the experiment, high amounts of H3O+(H2O)n were needed to study the fragmentation of these cluster ions. The corona ion source yielded sufficient and stable ion signals for constant flow conditions inside the inlet tube as will be shown in Sect. 3.2, Fig. 7.
2.4 CLOUD experiment
To test the performance of the ioniAPi-TOF under the highly demanding conditions of a long-term measurement campaign with the challenge of various experimental conditions and different chemical systems, we participated in the CLOUD 12 campaign in autumn 2017. The CLOUD (Cosmics Leaving OUtdoor Droplets) experiment at the European Centre for Nuclear Research (CERN) studies the influence of galactic cosmic rays (GCRs) on atmospheric new particle formation under very well-controlled conditions (Duplissy et al., 2016; Kirkby et al., 2011). This effect can be studied by comparing the experiments at ground level GCR ion pair production rates to experiments under neutral conditions inside the chamber where a high voltage field is turned on. Upper tropospheric ion pair production rates and ion number concentrations can be realised via a π-beam of 3.5 GeV/c from the CERN Proton Synchrotron. The chamber is made of electro-polished stainless steel with a volume of 26.1 m3. At the top and at the bottom of the chamber, two fans made of stainless steel are used for homogeneous mixing of the air yielding mixing times of a few minutes. To study a wide range of tropospheric conditions, a thermal housing allows experiments at temperatures ranging from 203 to 310 K with a stability of 0.1 K. A very clean atmosphere is obtained using cryogenic N2 and O2 in the natural ratio of 79:21 with a level of contaminant vapours in the sub-parts per trillion by volume range (Schnitzhofer et al., 2014). The effect of relative humidity can be studied by adjusting the flow rate of ultrapure de-ionised water being vaporised into the chamber. Ozone is produced via UV photolysis of O2. The volume mixing ratio of O3 can be controlled by the flow rate. Further trace gases like SO2, NH3, isoprene (C5H8) or α-pinene (C10H16) can be introduced separately via a gas handling system.
During the measurements at the CLOUD experiments, we used a critical orifice at the exhaust of the inlet to maintain a constant flow rate of 12.6 L min−1 as this was found to be the optimal setting regarding the total ion signal intensity. The ioniAPi-TOF inlet line was connected via a flow splitter with the PTR3 (Breitenlechner et al., 2017) to the same CLOUD sampling port. Due to reasons of limited space around the CLOUD chamber, the ioniAPi-TOF was mounted on top of the PTR3. Consequently, it could not be connected via a straight line to the flow splitter. We connected the instrument with two 30 cm long flexible well tubes and one additional straight tube. All tubes were made of stainless steel. In total, the sigmoidal-shaped inlet line to the flow splitter had a length of 1.2 m. Together with the length of the sampling probe that reached into the chamber; the total length of the inlet line was about 1.95 m and had a diameter of 1∕2 in. In addition to wall losses due to the length of the inlet line, the flexible well tubes might have resulted in an additional loss factor due to their rippled inner surface.
2.5 The APi-TOF
The operation principle of the APi-TOF of the University of Eastern Finland (UEF) is similar to what has been extensively reported in previous publications (Junninen et al., 2010; Schobesberger et al., 2013). The instrument was directly connected to the CLOUD chamber through a 30 cm long stainless-steel tubing with an outer diameter of 1 in. (25.4 mm), which was then reduced to 10 mm diameter in the last 10 cm of the tubing. The flow rate inside the sampling tube was in total 9 L min−1 all the way to the 0.3 mm diameter sampling pinhole of the instrument. From the 9 L min−1 total flow, 0.8 L min−1 entered the instrument. The UEF APi-TOF was operated in positive ion mode for the experiments shown here with ion guiding quadrupoles operating at pre-defined “high mass” settings having a mass range of about 100–2000 m∕z.
The main differences in the configuration of both instruments are listed in Table 3. The configuration of the ion transfer system in the APi shows major differences due to the use of segmented quadrupoles in the UEF APi-TOF while non-segmented hexapoles are used in the ioniAPi-TOF as well as other geometric factors like skimmer orifice diameters and distances.
Table 3Main technical differences of the ioniAPi-TOF UIBK compared to the UEF APi-TOF relevant for this study (Junninen et al., 2010). Mass resolution and extraction frequency are setting dependent. Shown values were used during the CLOUD 12 campaign and therefore valid for the inter-comparison in Sect. 3.3.

The different lengths of the TOF mass analysers explain differences in the mass resolving power and the extraction frequencies.
2.6 Data analysis and post-processing
The data of the UEF APi-TOF were processed using the MATLAB-based tofTools package version 6.11 (Junninen et al., 2010). We used the Ionicon PTR-MS Viewer 3.2 and TOF data processing scripts written by Lukas Fischer for data analysis of the UIBK ioniAPi-TOF (for TOF data processing scripts see Breitenlechner et al., 2017).
3.1 Characterisation of the transmission efficiency
The overall absolute transmission efficiency of the ioniAPi-TOF was determined with the cluster calibration unit for a mass range of 74 to 1640 Th. The transmission efficiency of a selected m∕z was determined by the ratio of ion count rates measured with the ioniAPi-TOF and the FCE. The substances listed in Table 2 were used as calibration standards. Monomer, dimer, trimer and tetramer cluster ions were produced with the ESI and selected each as a monodisperse aerosol via the UDMA. The smallest ion was the monomer of tetra-methyl-ammonium iodide at m∕z 74 and the heaviest cluster ion used was the tetramer of the ionic liquid with m∕z 1640.
The mass spectrum of a monodisperse aerosol typically has major counts at the m∕z peak of the mobility selected ion. Minor counts of ions of m∕z < 100 like , , and protonated acetonitrile clusters were also observed. Additionally, minor peaks of impurities or fragments were observed; see Fig. S2. In the case of dimers, their signal still showed the highest intensity. In addition, a peak at the m∕z of the monomer appeared with a relative abundance of less than 10 %. The observation of fragments was even more pronounced in the case of trimers. Here, the count rates of monomers and dimers reached in some cases similar intensities compared to the trimer, although only the trimer was expected.
This was not only observed for all mobility standards in Table 2, but also in different types of APi-TOF mass spectrometers using the CCU. We could observe the same fragmentation pattern with the ioniAPi-TOF as well as with the UEF APi-TOF in the course of the inter-comparison, and with an H-TOF, Tofwerk AG Thun Switzerland, without an APi interface in the laboratory at the University of Innsbruck (UIBK). This H-TOF was not equipped with a typical APi as it is part of a proton-transfer-reaction time-of-flight mass spectrometer (PTR-TOF MS; Graus et al., 2010). For the experiments with the UDMA, we mounted a simple single pressure stage. This single pressure stage consisted of a front plate with a critical orifice diameter of 0.3 mm and two electrode lenses that were connected to the sampler plate of the H-TOF. A pressure of 2 mbar in the single pressure stage was achieved with a pre-pressure pump. To our knowledge, there are only a few detailed reports of observations of such fragmentation patterns for the standards we used here. Heinritzi et al. (2016) reported fragmentation of iodide dimers in the negative ion mode. While Junninen et al. (2010) did not observe such fragmentation with the calibration standards, only at a mobility diameter of 1.6 nm was a fragment possibly due to an impurity reported.
The aforementioned observation can be interpreted as either fragments or the result of a broad tail of the UDMA's transfer function allowing ions of high abundance to be still partially transferred despite not having the expected ion mobility. Further, multiply charged ions with the same ion mobility could also pass the UDMA and evaporate or fragment afterwards, leading to the formation of monomers and dimers, which are then detected (Rus et al., 2010). No peaks of multiply charged ions were observed in the mass spectrum. So far, we exclude fragmentation inside the ioniAPi as an explanation, as we will show in Sect. 3.2. that when using the low-fragmenting setting in the ioniAPi (voltage difference: −1.4 V) the cluster ion H3O+(H2O)3 does not appear to fragment almost at all, even though it is relatively weakly bound (binding energy: BE(H3O+(H2O)3) H = 17 kcal mol−1; Meot-Ner, 1984). For much heavier cluster ions, such as produced with the calibration standards, even higher collision energies would be necessary for a fragmentation of the observed intensity. The relationship between the energy in the lab system Elab and the centre-of-mass energy ECM is shown in Eq. (2) (Armentrout, 2002). Here, m is the mass of the buffer gas (air) and mion the mass of the ion. ECM is proportional to the reciprocal of the ions' mass mion. With increasing mass, higher electric fields would be necessary to reach sufficient collision energies for heavy ions.
The conversion into the centre-of-mass frame of reference allows the estimation that for ions with a high m∕z, e.g. Th, the collision energy under low-fragmenting settings and air molecules as buffer gas should not be sufficient to explain the observed peak pattern by fragmentation.
However, the fractions of fragment signals can be corrected as done in Heinritzi et al. (2016). For this purpose, we assume that the fragmentation occurs outside the APi. Thus, the electrometer counts the fragments as well. In general, ions of different m∕z have different transmission efficiencies through an APi. To obtain the transmission of the monomer, solely the sum of count rates at the monomer mass and its isotope peaks was divided by the expected count rate that was determined from the current measured with the electrometer. With the obtained monomer transmission efficiency, the electrometer signal was corrected to determine the transmission for the dimer. Further, the transmission factor of the monomer and the corrected transmission factor of the dimer were used to determine the transmission of the trimer.
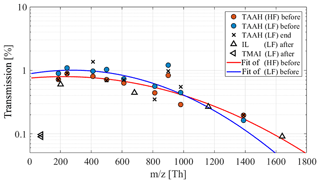
Figure 4Transmission efficiency for low-fragmenting (LF) and high-fragmenting (HF) ion transfer settings of the ioniAPi-TOF for ions of different tetra-alkyl-ammonium-halides (TAAH) and an ionic liquid (IL); see Table 2. A Gaussian fit was used to obtain the transmission curves. Calibrations were done before the CLOUD campaign, in the end and after the campaign in Innsbruck.
In the end, this leads to the overall absolute transmission efficiency shown in Fig. 4. An overall transmission efficiency of about 1 % was found. Considering the instruments' background noise, this corresponds to a detection limit of roughly ions cm−3 for 5 min integration time and ions cm−3 for 1 h integration time. The error in determining the transmission efficiency due to fragment peaks was found to be less than 10 %. In general, the transmission is highest in the mass range from 200 to 600 Th and decreases for heavier ions. The transmission of small ions was only determined in the course of one experiment where it seems to decrease sharply to values as low as for heavy ions. Nevertheless, we later observed that the highest individual ion count rates are under standard (low-fragmenting) settings and highest at ions below m∕z 100 (for example see Fig. 9). This may indicate that small natural ions are more than 1 order of magnitude more abundant than heavier ions or that the transmission at m∕z 74 is underestimated.
The transmission efficiency was determined for both the low-fragmenting (voltage difference: dV = −1.4 V) and the high-fragmenting (voltage difference: dV = −10.0 V) setting for comparison. As shown in Fig. 4, the low-fragmenting setting yields a higher transmission efficiency for most of the mass range. Despite an overall lower transmission, the high-fragmenting setting offers a slightly higher transmission for heavier ions, here m∕z 1391, due to the better focusing of heavier ions. This resembles a shift or a tilting of the transferred mass window. Overall, though, both settings offer a comparable high ion transmission. The data points (Fig. 4) determined after the CLOUD campaign for the low-fragmenting setting are comparable to the calibration done in the beginning of the campaign.
3.2 Characterisation of the ion transfer
In the following, we address the question of fragmentation inside the ioniAPi-TOF. As mentioned in the introduction, recent studies demonstrated that the electric potential difference between parts of the ion optics in the APi can be used to study collision-induced fragmentation of cluster ions, e.g. a voltage difference (dV) between the skimmer and the second multipole (Brophy and Farmer, 2016; Lopez-Hilfiker et al., 2016).
Further, it was shown for the APi-TOF that fragmentation of clusters is most likely for pressures between 1.0 and 0.01 mbar and elevated electric fields (Zapadinsky et al., 2019). Similar conditions can also be found and set in the ioniAPi-TOF. With regard to the conditions presented in Zapadinsky et al. (2019), the most critical region in the ioniAPi-TOF would be the transition from the first to the second pressure stage. In the current instrument configuration, it was not possible to apply any other electric fields to the first pressure stage aside from the RF frequency and amplitude. Therefore, we exclude fragmentation due to axial electric fields in this region. Downstream of the second pressure stage, ions can be accelerated to even higher energies compared to previous regions. However, at a pressure below 10−4 mbar the number of collisions is too low due to a mean free path of above 50 cm. In the present study, we focus on the second pressure stage where fragmentation is most likely.
3.2.1 Low- and high-fragmenting settings
To compare the aforementioned low- and high-fragmenting settings, hydrated hydronium clusters were used as a model system due to their well-known binding energies; see Table 4 (Meot-Ner, 1984). In Fig. 5, the distribution of the hydrated hydronium clusters is exemplarily shown for both settings. Ions were produced using a corona ion source in front of the inlet as introduced in Sect. 2.3. We used the fits of the ion transmission efficiency of the low- and high-fragmenting settings from Fig. 4 to correct the individual ion intensities for all the water clusters with respect to transmission effects.
Table 4Gibbs free energies, binding energies (BE() = -ΔH) and corresponding dV50 for clusters (Meot-Ner, 1984) determined for a dV scan shown in Figs. 7 and S5.

In the low-fragmenting setting, the higher-order and weakly bound hydrated hydronium clusters H3O+(H2O)2 and H3O+(H2O)3 show the highest abundance (Fig. 5). The high-fragmenting setting (highest dV) overall leads to the cluster distribution shifting to smaller and more strongly bound hydrated hydronium clusters, and H3O+(H2O)3 largely dissociates, thereby reducing its intensity by a factor of 10.
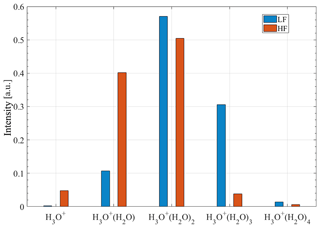
Figure 5Comparison of the low-fragmenting (LF, voltage difference: dV = −1.4 V) and the high-fragmenting (HF, voltage difference: dV = −10.0 V) settings. Ion counts are corrected for transmission effects and normalised for each setting.
The peak at m∕z 91.06, assumed to be H3O+(H2O)4, is also included in the figure. Its signal intensity seems to behave as expected for the low- and high-fragmenting settings because it shows a reduction for the latter setting.
The intensity of H3O+ increased by a factor of 25 for the high-fragmenting setting. Although this is a significant increase, the new cluster equilibrium ends with H3O+(H2O) and H3O+(H2O)2 showing the highest intensities. Evidently, a voltage difference of −10 V, which was the maximum adjustable voltage setting, is not enough to completely fragment H3O+(H2O) cluster ions (bound most strongly, -ΔH = 31.5 kcal mol−1; Table 4).
3.2.2 Declustering scan
A so-called declustering scan investigates the relation of voltage settings in the APi to the binding energy of cluster ions (Lopez-Hilfiker et al., 2016). In the current configuration of the ioniAPi-TOF, no axial electric fields can be applied to any parts of the first pressure stage as explained previously. Therefore, the dV scan is obtained in a slightly different way compared to the one described in Lopez-Hilfiker et al. (2016). In Lopez-Hilfiker et al. (2016), the whole first pressure stage is shifted towards a more negative dV while the voltages downstream remain constant. In our case, no shift of the first pressure stage is currently possible. Therefore, the first pressure stage remains at zero potential. The voltage difference between skimmer-1 and the second hexapole was stepwise increased, thereby reducing the DC offset of the hexapole (Fig. 6). The ion optics following the second hexapole were set to one setting during the declustering scan to maintain a high transmission efficiency with a constant voltage of −13 V at the first lens that follows the second hexapole. The declustering scan started from dV = 0 to −10 V in steps of 1 V, skimmer-1 being grounded. Ions were generated with a corona ion source as before.
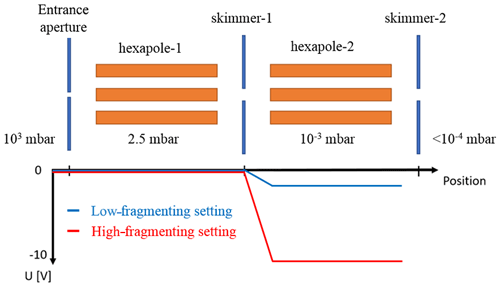
Figure 6Schematic of the region inside the ioniAPi-TOF mass spectrometer where fragmentation was studied in this work. Here, a low-fragmenting clustered setting and a high-fragmenting declustering setting can be used to identify cluster ions and to study their stability by adjusting the voltage difference (dV) between skimmer-1 and hexapole-2.
Figure 7 shows the dV scan for four hydronium cluster ions . The initial cluster distribution may look differently depending on the conditions in the first pressure stage like pressure or electric fields; e.g. different RF settings on the first hexapole can alter the mass-dependent transmission. The count rates of each ion are normalised to its initial count rate during the scan. Increasing the dV from 0 to −3 V increases the transmission of all four clusters.
Each increase in dV results in a higher collision energy. This explains why primarily the higher-order hydrated hydronium clusters show a decrease for the lowest voltage steps. First, H3O+(H2O)3 is collisionally fragmenting due to its low binding energy (-ΔH = 17 kcal mol−1; see Table 4). In the centre-of-mass system, the collision energy needed to break the cluster bond corresponds to the Gibbs free energy of the H3O+(H2O)3 cluster (ΔG = −9 kcal mol−1 at 298 K; see Table 4). Although the Gibbs free energy is more accurate in describing the energy of a cluster ion within this process, the estimation of the Gibbs free energy is not straightforward. This is due to the uncertainty of temperature in the transition from the first to the second pressure stages. Therefore, we exemplarily determined the ΔG values for the hydrated hydronium clusters at a temperature of 298 K in Table 4. In the following, we use the binding energy (-ΔH).
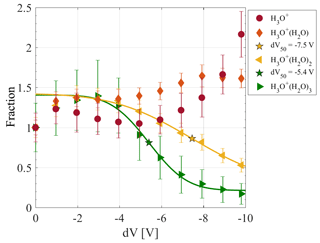
Figure 7Declustering (dV) scan between the skimmer-1 and the second hexapole using hydrated hydronium clusters. Peak intensities are normalised on each ion's initial signal. The dV50 of H3O+(H2O)3 is −5.4 V and that of H3O+(H2O)2 is −7.5 V. The low-fragmenting setting uses a dV of −1.4 V, whereas −10 V is used for the high-fragmenting setting.
Further increase in dV results in the fragmentation of H3O+(H2O)2, which has a slightly higher binding energy (-ΔH = 20 kcal mol−1). While larger clusters are fragmenting an increase is observed for H3O+(H2O). Above a dV of −8 to −9 V, the intensity of H3O+(H2O) also starts showing a decrease. Here, the collision energy is already high enough to partially fragment H3O+(H2O), which has a much higher binding energy (-ΔH = 31.5 kcal mol−1). H3O+ shows a steady increase which is pronounced for a higher dV. H3O+(H2O)2 shows no significant response to the decrease in the H3O+(H2O)3 ion. This can be attributed to an overall low count rate of H3O+(H2O)3 and a much higher count rate of H3O+(H2O)2. Fragmentation of H3O+(H2O)3 will therefore not significantly increase the H3O+(H2O)2 count rate.
For such a dV scanning procedure, Lopez-Hilfiker et al. (2016) found a linear relationship between the voltage corresponding to the half signal maximum of a cluster, the so-called dV50, and the binding energy (Lopez-Hilfiker et al., 2016). In accordance to that study, we used a non-linear least-square sigmoidal model to fit the data points. From the fit, we determined a dV50 of −5.4 and −7.5 V for H3O+(H2O)3 and H3O+(H2O)2, respectively. The higher dV50 obtained for H3O+(H2O)2 is consistent with its binding energy being higher than that of H3O+(H2O)3 (see Table 4).
As the voltage at the first lens is set to −13 V, fragmentation between the second hexapole and the following lens might dominate the first few voltage steps. To distinguish the role of the region from the skimmer to the entrance of the second hexapole and the region from the exit of the second hexapole to the following lens, we show additional experiments in the Supplement. With a high-resolution ioniAPi-TOF, we conducted the same experiments and show with Fig. S4 that both instruments show a good agreement in the responses of the hydronium ion distribution to the dV scanning procedure used in Fig. 7. Figure S5 shows a declustering scan between skimmer-1 and the second hexapole. Here, the second hexapole and the following lens are stepped synchronously with a constant voltage difference of −1 V between both ion optic parts. This is necessary to maintain sufficient transmission. From Fig. S6, it can be concluded that this small offset should not affect the fragmentation. The dV scan in Fig. S5 shows that the dV50 is shifted to lower values; see Table 4. This shows that the dV50 values in Fig. 7 are offset by the voltage at lens-1. In Fig. S6, a declustering scan between the exit of the second hexapole and the following first lens with lens-1 and lens-2 being stepped synchronously reveals that a dV below −9 V mainly increases the ion transmission. Only above −9 V is the voltage difference from lens-1 to the exit of the second hexapole high enough to induce fragmentation of the more weakly bound hydronium cluster ions. Figure S7 shows that a voltage scan between lens-1 and lens-2 has no effect on the hydronium cluster ion distribution. To conclude, the region between skimmer-1 and the second hexapole is the region where cluster ions are most likely affected by fragmentation depending on the voltage settings compared to the other probed regions.
A potential source of uncertainty on the experiments with hydronium cluster ions may be the fragmentation of larger hydrated hydronium clusters with n>3. Such clusters could potentially form on collisions with available water molecules during the expansion from ambient pressure into the first pressure stage due to the significant cooling. During this experiment, no larger water clusters were detected, likely due to the use of clean and dried air having a low relative humidity (RH) of approximately 2 %. Other experiments at higher RH showed hydronium clusters up to 1000 m∕z and higher. The impact of larger hydronium ions on the dV scan can be discarded in this study.
The high number of collisions in the first pressure stage leads to a thermodynamic equilibrium distribution of hydronium clusters. Consequently, a dV scan in the second pressure stage affects only the established hydronium cluster distribution coming from the first pressure stage.
3.2.3 Threshold binding energies
The results from Sect. 3.2.2 allow the establishment of an approximate threshold cluster binding energy for a fragment-free transfer through the mass spectrometer as an example for the applied conditions. These results may vary under different conditions. To estimate this threshold for the ioniAPi-TOF, we start with the H3O+(H2O)3 cluster ion. From the declustering scan in Fig. 7, the decrease in the ion signal of H3O+(H2O)3 starts at a voltage difference (dV) of −3 to −4 V. Below these dVs, fragmentation is not a significant issue between the skimmer-1 and the second hexapole. Therefore, we conservatively estimate that cluster ions with binding energies above 17 kcal mol−1 are likely to be transferred through the probed region of the ioniAPi without substantial fragmentation for a low-fragmenting setting. Cluster ions with binding energies below this threshold are partially affected by fragmentation with increasing degree. Assuming a linear relationship between the voltage difference and the binding energy according to Lopez-Hilfiker et al. (2016), we extrapolate a threshold binding energy of 8 to 11 kcal mol−1 using the dV50 values from Table 4 for the ion transfer between skimmer-1 and the second hexapole. Other regions were shown to be less critical. Below this threshold, cluster ions are not likely to be detected depending on other conditions in the ioniAPi.
It has to be noted that the ion transmission shows strong responses for even small voltage differences between ion optic parts. A DC offset of only 0.2 V on the second hexapole for example can significantly improve the ion transmission compared to no offset. To maintain a satisfying detection sensitivity the electric potentials of the second hexapole and the following lens should be set closely.
To compare the threshold binding energy of fragment-free cluster transfer of the ioniAPi-TOF to a quadrupole based APi-TOF, we only can give rough estimates based on existing literature. Via comparing modelled binding energies for adduct cluster ions and their sensitivity with a TOF-CIMS, Iyer et al. (2016) estimated that cluster ions with a binding energy below 25 kcal mol−1 can be expected to fragment at least partially during the ion transfer for the TOF-CIMS in Lopez-Hilfiker et al. (2016) and that cluster ions of binding energies below 10 kcal mol−1 are not likely to survive the transfer. Although it is not clear from their study if fragmentation can happen in the IMR or in the APi of the instrument, they conclude in the Supplement that fragmentation in the APi is more likely (Iyer et al., 2016).
In Brophy and Farmer (2016), a declustering (dV) scan of the acetate–acetic acid cluster () is shown. The voltage difference was also scanned between the skimmer and the front of the second multipole as done in this study (Fig. 4 in Brophy and Farmer). For this region, the authors determined a dV50 of 4.1 V for , which has a binding energy of 29.3 kcal mol−1 (Meot-Ner and Sieck, 1986). At a voltage difference of 0 V, this cluster did not completely reach a plateau, which must be considered as still partially fragmenting. From this, the threshold binding energy for their instrument seems to be even above the TOF-CIMS in Iyer et al. (2016). In contrast, Bertram et al. (2011) showed a mass spectrum of acetate–acetic acid cluster ions where under weak electric fields (15 V cm−1 throughout the APi) higher-order clusters () were also detectable with their TOF-CIMS instrument (Bertram et al., 2011). The binding energy of the trimer () is 19.6 kcal mol−1 (Meot-Ner and Sieck, 1986). From Bertram et al. (2016), a lower-fragmenting transfer of cluster ions for a quadrupole-based APi-TOF is also possible. While no quantitative threshold binding energy was determined, it can only be estimated to be in the order of the binding energy of the acetate–acetic acid trimer of 19.6 kcal mol−1.
The differences in thresholds of fragment-free cluster transfer for the mentioned instruments obviously depend on more factors than the applied voltage settings in the APi like instrument geometry, pressures and flows. Nevertheless, our data suggest that the critical region of the ioniAPi is between the skimmer and the entrance of the second hexapole and that it allows a slightly lower threshold binding energy for the transfer of cluster ions. From our data, it is still difficult to attribute the observed difference to the number of poles of the ion guides. In the case of RF-only ion guides, this difference could be explained only by the radial contribution of the multipoles. Here, more research is needed regarding the effect of RF frequency and amplitude on cluster ions at different pressures. For example, Rus et al. (2010) concluded that RF heating in the multipole was responsible for fragmentation of unstable cluster ions. Further, the successful fragmentation of a cluster via a collision with air as buffer gas depends also on the achieved collision energy in the centre-of-mass system. Heavier ions need higher electric fields to achieve the necessary collision energy. But they can also more readily accumulate the collision energy in a higher number of vibrational modes within the cluster compared to smaller ions reducing their chance of fragmentation (Zapadinsky et al., 2019).
3.3 Mass window and comparison to a quadrupole-based APi-TOF MS
In the course of the CLOUD 12 campaign, we conducted an inter-comparison with the quadrupole-based APi-TOF mass spectrometer of the University of Eastern Finland (UEF). The results of the transmission efficiency inter-comparison in positive ion mode made at the end of the campaign are shown in Fig. 8. The data points are corrected for cluster fragments as mentioned in Sect. 3.1. Here, inlet line losses are not accounted for as the calibration setup of the CCU allows nearly identical flow conditions for both detectors, electrometer and mass spectrometer. A transmission efficiency of overall about 1 % was found for both mass spectrometers. The overall ion transmission is a factor of 2 to 3 higher for the UEF APi-TOF. This factor can be attributed to various differences in the instrument configurations as described in Sect. 2.5, e.g. ion optic configuration, geometry as well as flows due to pumping. It can be noted that due to the compact size of the TOF mass analyser of the ioniAPi-TOF, it can be run at a higher duty cycle with an almost 3-fold higher extraction frequency. Due to the higher extraction, more ions are detected, leading to a comparable transmission efficiency with the UEF APi-TOF.
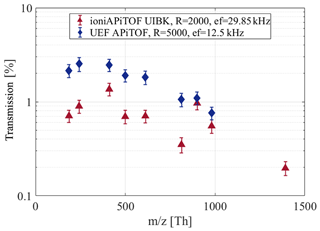
Figure 8Comparison of the ioniAPi-TOF and the UEF APi-TOF regarding the transmission efficiency. The UEF API-TOF is set to high-mass range settings (m∕z 100–2000 Th). The extraction frequencies (ef) vary with the length of the TOF mass analyser.
From Fig. 8, the UEF APi-TOF has a higher transmission for medium mass ions between 200 and 600 Th. At higher masses at about 1000 Th, the difference in the transmission efficiency of both instruments decreases. This can be explained with the different ion transfer properties of higher-order multipoles as shown in Table 1. In general, hexapole ion guides allow a poorer focusing compared to quadrupoles but are capable of transmitting a broader mass range. Examples below will demonstrate these properties using parallel measurements.
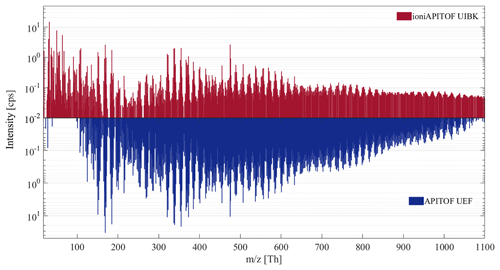
Figure 9Comparison of the mass spectra obtained during run 1963.15 at the CLOUD experiment at CERN of the ioniAPi-TOF and the UEF APi-TOF.
A qualitative inter-comparison was performed during a CLOUD experiment at CERN where the ozonolysis of a mixture of α-pinene and isoprene was studied at −50 ∘C. The experimental conditions for the inter-comparison of both APi-TOF instruments are noted in Table 5. This experiment was chosen because oxidation of α-pinene is expected to form highly oxygenated molecules (HOMs) (Ehn et al., 2010; Kirkby et al., 2016) and therefore high mass ions. Another reason was the use of the CERN π-beam, which yields increased ion concentrations inside the CLOUD chamber, leading to higher ion count rates with both APi-TOFs and a better signal-to-noise ratio (S∕N). The mass spectra obtained by the ioniAPi-TOF and the UEF APi-TOF are compared in Fig. 9. Ion count rates are corrected for diffusion losses with the Gormley–Kennedy equation (Bemgård et al., 1996) for both instruments.
Table 5Experimental conditions for the inter-comparison during run 1963.15 at the CLOUD experiment, CERN.

First, this inter-comparison shows that in general, the overall peak pattern for the experiment is comparable for both instruments. Several “bands” consisting of combinations of C5 and C10 HOM appear in both mass spectra and show a similar distribution, e.g. mass ranges 300 to 450, 450 to 650, 650 to 850 and 850 to 1050 Th. For example, the peaks at m∕z 151, 153, 169 and 185 correspond to C10H15O+, C10H17O+, and , respectively, showing the same relative intensity in the mass spectrum of the ioniAPi-TOF as well as in the APi-TOF. Further analysis of the mass spectral data is not included in the present study.
Second, comparing the peak intensities, a difference in the dynamic range between both instruments, the UEF APi-TOF and the UIBK ioniAPi-TOF, for ions above a m∕z of roughly 350 can be seen. This can mainly be attributed to the differences in mass resolution (for this experiment ∼5000 (APi-TOF) and ∼1600 (ioniAPi-TOF)), leading to a higher dynamic range for the UEF APi-TOF. Higher diffusion losses in the much longer inlet line during the experiment as well as differences in the ion transmission efficiency (see Fig. 8) can additionally contribute to the lower dynamic range of the ioniAPi-TOF. The apparent higher sensitivity of the ioniAPi-TOF for high mass ions can be explained with a higher background noise due to the lower mass resolution. The correction for inlet line losses and the 3-fold higher extraction frequency, values given in Fig. 8, of this compact TOF mass analyser compared to the medium-sized APi-TOF contribute as well.
Third, the mass spectra show large differences for ions of masses below 100 Th. As the UEF APi-TOF is set to the high mass range setting, the high-pass mass filter property of the quadrupole leads to the low-mass cut-off disabling the detection of small ions in exchange for an increase in ion transfer and detection of high mass ions. The use of hexapoles as ion guides in the ioniAPi-TOF allows the detection of small ions below 100 Th and of high mass ions up to 1100 Th simultaneously as shown for the tested experimental conditions. Here, only the mass range up to 1100 Th is shown as ion count rates at higher m∕z were too low in both instruments, setting a practical upper m∕z limit for this comparison.
However, the calibration results shown in Fig. 8 suggest that both instruments have a comparable level of transmission efficiency for ions above 100 Th. From this perspective, the hexapole ion guides show beneficial properties when measuring a broad mass range. The loss of information on one end of the mass window, as evident here for the quadrupole system, is not necessary. We note that this effect is not exclusively limited to comparing hexapole with quadrupole systems, as progression to even higher-order multipoles may further broaden the accessible mass range. However, this will be subject to a future study.
In the present study, we introduce an alternative type of atmospheric pressure interface time-of-flight mass spectrometer, the so-called ioniAPi-TOF, with the main difference of using hexapoles as ion guides in the APi. We characterised the ioniAPi-TOF regarding ion transmission efficiency, mass range transmission and the effect of ion transfer properties on the cluster ion stability. We found that the overall ion transmission efficiency (so far tested from m∕z 74 to 1640 Th) with hexapole ion guides is around 1 % and comparable to existing APi technology using quadrupole ion guides. The detection limit for 1 h integration time is around ions cm−3. The width of the transmitted mass range was found to be broader compared to a quadrupole-based APi-TOF, when each instrument was using just one single setting. In atmospheric nucleation studies, this has the advantage of simultaneously detecting very small precursor ions, which can harbour information on nucleation precursor compounds, and the much heavier cluster ions that form during nucleation. Further, the effect of the ion transfer through the ioniAPi on the cluster stability and its fragmentation was studied. Using the system of we were able to estimate that cluster ions with binding energies above 17 kcal mol−1 are not substantially fragmenting in the critical region between the skimmer and the second hexapole. From the literature, we estimated a threshold of roughly 20 to 25 kcal mol−1 for quadrupole-based APi-TOF instruments. Comparing these numbers, a slightly less-fragmenting ion transfer for the ioniAPi seems possible. Still, further work is needed to understand the differences in fragmentation inside various APi configurations and if the lower-fragmenting transfer suggested for the ioniAPi is due to the number of poles or if other differences (e.g. pumping, geometry, voltage settings) are responsible. The mass resolution of ∼2000 in the present study was limited by the use of a compact TOF mass analyser. Future focus lies on improving both mass resolution and the transmission efficiency.
Data related to this article are available upon request to the corresponding authors.
The supplement related to this article is available online at: https://doi.org/10.5194/amt-12-5231-2019-supplement.
PM, SF, GS and ML performed the measurements with the ioniAPi-TOF in Innsbruck while GS and ML performed the measurements at the CLOUD experiment. ML carried out the data analysis of the ioniAPi-TOF experiments. AY contributed with data obtained with the UEF API-TOF at the CLOUD experiment. ML wrote the paper and all authors contributed to the final paper development.
The authors declare the following competing financial interest: Ionicon Analytik GmbH plans to commercialise the ioniAPi-TOF.
This article is part of the special issue “The CERN CLOUD experiment (ACP/AMT inter-journal SI)”. It is not associated with a conference.
We thank Ionicon Analytik GmbH for providing an ioniTOF-1000 mass spectrometer and for the support in the development of the ioniAPi-TOF MS. Furthermore, we thank CERN for support of the CLOUD experiment as well as the CLOUD collaboration (http://cloud.web.cern.ch/, last access: 12 September 2019) for the opportunity to test the new instrument and for their support. We thank the tofTools team for providing tools for mass spectrometry analysis.
This work is funded by the Austrian Science Fund, FWF (project no. P27295-N20), the Tiroler Wissenschaftsfonds (nanoTOF-ICE), the University of Innsbruck promotion grant for young researchers, the Academy of Finland's Centre of Excellence programme (grant no. 307331) and the University of Eastern Finland doctoral programme in environmental physics, health and biology.
This paper was edited by Jonathan Abbatt and reviewed by three anonymous referees.
Almeida, J., Schobesberger, S., Kürten, A., Ortega, I. K., Kupiainen-Määttä, O., Praplan, A. P., Adamov, A., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Donahue, N. M., Downard, A., Dunne, E., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Henschel, H., Jokinen, T., Junninen, H., Kajos, M., Kangasluoma, J., Keskinen, H., Kupc, A., Kurtén, T., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Leiminger, M., Leppä, J., Loukonen, V., Makhmutov, V., Mathot, S., McGrath, M. J., Nieminen, T., Olenius, T., Onnela, A., Petäjä, T., Riccobono, F., Riipinen, I., Rissanen, M., Rondo, L., Ruuskanen, T., Santos, F. D., Sarnela, N., Schallhart, S., Schnitzhofer, R., Seinfeld, J. H., Simon, M., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Tröstl, J., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Virtanen, A., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Williamson, C., Wimmer, D., Ye, P., Yli-Juuti, T., Carslaw, K. S., Kulmala, M., Curtius, J., Baltensperger, U., Worsnop, D. R., Vehkamäki, H., and Kirkby, J.: Molecular understanding of sulphuric acid-amine particle nucleation in the atmosphere, Nature, 502, 359–363, https://doi.org/10.1038/nature12663, 2013.
Armentrout, P. B.: Kinetic energy dependence of ion-molecule reactions: Guided ion beams and threshold measurements, Int. J. Mass Spectrom., 200, 219–241, https://doi.org/10.1016/S1387-3806(00)00310-9, 2000.
Armentrout, P. B.: Mass spectrometry – Not just a structural tool: The use of guided ion beam tandem mass spectrometry to determine thermochemistry, J. Am. Soc. Mass Spectrom., 13, 419–434, https://doi.org/10.1016/S1044-0305(02)00347-1, 2002.
Arnold, F., Krankowsky, D., and Marien, K. H.: First mass spectrometric Measurements of Positive Ions in the Stratosphere, Nature, 267, 30–32, 1977.
Arnold, F., Böhringer, H., and Henschen, G.: Composition measurements of stratospheric positive ions, Geophys. Res. Lett., 5, 653–656, https://doi.org/10.1029/GL005i008p00653, 1978.
Bemgård, A., Colmsjö, A., and Melin, J.: Assessing breakthrough times for denuder samplers with emphasis on volatile organic compounds, J. Chromatogr. A, 723, 301–311, https://doi.org/10.1016/0021-9673(95)00878-0, 1996.
Bertram, T. H., Kimmel, J. R., Crisp, T. A., Ryder, O. S., Yatavelli, R. L. N., Thornton, J. A., Cubison, M. J., Gonin, M., and Worsnop, D. R.: A field-deployable, chemical ionization time-of-flight mass spectrometer, Atmos. Meas. Tech., 4, 1471–1479, https://doi.org/10.5194/amt-4-1471-2011, 2011.
Bianchi, F., Tröstl, J., Junninen, H., Frege, C., Henne, S., Hoyle, C. R., Molteni, U., Herrmann, E., Adamov, A., Bukowiecki, N., Chen, X., Duplissy, J., Gysel, M., Hutterli, M., Kangasluoma, J., Kontkanen, J., Kurten, A., Manninen, H. E., Munch, S., Perakyla, O., Petaja, T., Rondo, L., Williamson, C., Weingartner, E., Curtius, J., Worsnop, D. R., Kulmala, M., Dommen, J., and Baltensperger, U.: New particle formation in the free troposphere: A question of chemistry and timing, Science, 352, 1109–1112, https://doi.org/10.1126/science.aad5456, 2016.
Breitenlechner, M., Fischer, L., Hainer, M., Heinritzi, M., Curtius, J., and Hansel, A.: PTR3: An Instrument for Studying the Lifecycle of Reactive Organic Carbon in the Atmosphere, Anal. Chem., 89, 5824–5831, https://doi.org/10.1021/acs.analchem.6b05110, 2017.
Brophy, P. and Farmer, D. K.: Clustering, methodology, and mechanistic insights into acetate chemical ionization using high-resolution time-of-flight mass spectrometry, Atmos. Meas. Tech., 9, 3969–3986, https://doi.org/10.5194/amt-9-3969-2016, 2016.
Curtius, J.: Nucleation of atmospheric aerosol particles, Comptes Rendus Phys., 7, 1027–1045, https://doi.org/10.1016/j.crhy.2006.10.018, 2006.
Duplissy, J., Merikanto, J., Franchin, A., Tsagkogeorgas, G., Kangasluoma, J., Wimmer, D., Vuollekoski, H., Schobesberger, S., Lehtipalo, K., Flagan, R. C., Brus, D., Donahue, N. M., Vehkamäki, H., Almeida, J., Amorim, A., Barmet, P., Bianchi, F., Breitenlechner, M., Dunne, E. M., Guida, R., Henschel, H., Junninen, H., Kirkby, J., Kürten, A., Kupc, A., Määttänen, A., Makhmutov, V., Mathot, S., Nieminen, T., Onnela, A., Praplan, A. P., Riccobono, F., Rondo, L., Steiner, G., Tome, A., Walther, H., Baltensperger, U., Carslaw, K. S., Dommen, J., Hansel, A., Petäjä, T., Sipilä, M., Stratmann, F., Vrtala, A., Wagner, P. E., Worsnop, D. R., Curtius, J., and Kulmala, M.: Effect of ions on sulfuric acid-water binary particle formation: 2. Experimental data and comparison with QC-normalized classical nucleation theory, J. Geophys. Res.-Atmos., 121, 1752–1775, https://doi.org/10.1002/2015JD023538, 2016.
Ehn, M., Junninen, H., Petäjä, T., Kurtén, T., Kerminen, V.-M., Schobesberger, S., Manninen, H. E., Ortega, I. K., Vehkamäki, H., Kulmala, M., and Worsnop, D. R.: Composition and temporal behavior of ambient ions in the boreal forest, Atmos. Chem. Phys., 10, 8513–8530, https://doi.org/10.5194/acp-10-8513-2010, 2010.
Ehrhart, S., Ickes, L., Almeida, J., Amorim, A., Barmet, P., Bianchi, F., Dommen, J., Dunne, E. M., Duplissy, J., Franchin, A., Kangasluoma, J., Kirkby, J., Kürten, A., Kupc, A., Lehtipalo, K., Nieminen, T., Riccobono, F., Rondo, L., Schobesberger, S., Steiner, G., Tomé, A., Wimmer, D., Baltensperger, U., Wagner, P. E., and Curtius, J.: Comparison of the SAWNUC model with CLOUD measurements of sulphuric acid-water nucleation, J. Geophys. Res., 121, 12401–12414, https://doi.org/10.1002/2015JD023723, 2016.
Eisele, F.: First tandem mass spectrometric measurement of tropospheric ions, J. Geophys. Res. Atmos., 93, 716–724, https://doi.org/10.1029/JD093iD01p00716, 1988.
Eisele, F. and Tanner, D.: Identification of ions in continental air, J. Geophys. Res.-Atmos., 95, 539, https://doi.org/10.1029/Jd095id12p20539, 1990.
Eisele, F. L.: Identification of tropospheric ions, J. Geophys. Res.-Atmos., 91, 7897–7906, https://doi.org/10.1029/jd091id07p07897, 1986.
Ferguson, E. E. and Arnold, F.: Ion Chemistry of the Stratosphere, Acc. Chem. Res., 14, 327–334, https://doi.org/10.1021/ar00071a001, 1981.
Flagan, R. C.: History of Electrical Aerosol Measurements, Aerosol Sci. Technol., 28, 301–380, https://doi.org/10.1080/02786829808965530, 1998.
Gerlich, D.: Inhomogeneous RF Fields: A Versatile Tool for the Study of Processes with Slow Ions, Adv. Chem. Phys., 82, 1–176, 1992.
Gerlich, D.: Applications of rf fields and collision dynamics in atomic mass spectrometry, J. Anal. At. Spectrom., 19, 581–590, https://doi.org/10.1039/b404032p, 2004.
Graus, M., Müller, M., and Hansel, A.: High resolution PTR-TOF: Quantification and Formula Confirmation of VOC in Real Time, J. Am. Soc. Mass Spectrom., 21, 1037–1044, https://doi.org/10.1016/j.jasms.2010.02.006, 2010.
Hägg, C. and Szabo, I.: New ion-optical devices utilizing oscillatory electric fields, II, Stability of ion motion in a two-dimensional hexapole field, Int. J. Mass Spectrom. Ion Process., 73, 237–275, https://doi.org/10.1016/0168-1176(86)80002-7, 1986a.
Hägg, C. and Szabo, I.: New ion-optical devices utilizing oscillatory electric fields, IV, Computer simulations of the transport of an ion beam through an ideal quadrupole, hexapole, and octopole operating in the rf-only mode, Int. J. Mass Spectrom. Ion Process., 73, 295–312, https://doi.org/10.1016/0168-1176(86)80004-0, 1986b.
Hägg, C. and Szabo, I.: New ion-optical devices utilizing oscillatrory electric fields, III, stability of ion motion in two-dimensional octopole field, Int. J. Mass Spectrom. Ion Process., 13, 237–275, https://doi.org/10.1016/0168-1176(86)80003-9, 1986c.
Heinritzi, M., Simon, M., Steiner, G., Wagner, A. C., Kürten, A., Hansel, A., and Curtius, J.: Characterization of the mass-dependent transmission efficiency of a CIMS, Atmos. Meas. Tech., 9, 1449–1460, https://doi.org/10.5194/amt-9-1449-2016, 2016.
Hirsikko, A., Nieminen, T., Gagné, S., Lehtipalo, K., Manninen, H. E., Ehn, M., Hõrrak, U., Kerminen, V.-M., Laakso, L., McMurry, P. H., Mirme, A., Mirme, S., Petäjä, T., Tammet, H., Vakkari, V., Vana, M., and Kulmala, M.: Atmospheric ions and nucleation: a review of observations, Atmos. Chem. Phys., 11, 767–798, https://doi.org/10.5194/acp-11-767-2011, 2011.
Iyer, S., Lopez-Hilfiker, F., Lee, B. H., Thornton, J. A., and Kurtén, T.: Modeling the Detection of Organic and Inorganic Compounds Using Iodide-Based Chemical Ionization, J. Phys. Chem. A, 120, 576–587, https://doi.org/10.1021/acs.jpca.5b09837, 2016.
Junninen, H., Ehn, M., Petäjä, T., Luosujärvi, L., Kotiaho, T., Kostiainen, R., Rohner, U., Gonin, M., Fuhrer, K., Kulmala, M., and Worsnop, D. R.: A high-resolution mass spectrometer to measure atmospheric ion composition, Atmos. Meas. Tech., 3, 1039–1053, https://doi.org/10.5194/amt-3-1039-2010, 2010.
Kirkby, J., Curtius, J., Almeida, J., Dunne, E., Duplissy, J., Ehrhart, S., Franchin, A., Gagné, S., Ickes, L., Kürten, A., Kupc, A., Metzger, A., Riccobono, F., Rondo, L., Schobesberger, S., Tsagkogeorgas, G., Wimmer, D., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Downard, A., Ehn, M., Flagan, R. C., Haider, S., Hansel, A., Hauser, D., Jud, W., Junninen, H., Kreissl, F., Kvashin, A., Laaksonen, A., Lehtipalo, K., Lima, J., Lovejoy, E. R., Makhmutov, V., Mathot, S., Mikkilä, J., Minginette, P., Mogo, S., Nieminen, T., Onnela, A., Pereira, P., Petäjä, T., Schnitzhofer, R., Seinfeld, J. H., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Vanhanen, J., Viisanen, Y., Vrtala, A., Wagner, P. E., Walther, H., Weingartner, E., Wex, H., Winkler, P. M., Carslaw, K. S., Worsnop, D. R., Baltensperger, U. and Kulmala, M.: Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation, Nature, 476, 429–435, https://doi.org/10.1038/nature10343, 2011.
Kirkby, J., Duplissy, J., Sengupta, K., Frege, C., Gordon, H., Williamson, C., Heinritzi, M., Simon, M., Yan, C., Almeida, J., Trostl, J., Nieminen, T., Ortega, I. K., Wagner, R., Adamov, A., Amorim, A., Bernhammer, A. K., Bianchi, F., Breitenlechner, M., Brilke, S., Chen, X., Craven, J., Dias, A., Ehrhart, S., Flagan, R. C., Franchin, A., Fuchs, C., Guida, R., Hakala, J., Hoyle, C. R., Jokinen, T., Junninen, H., Kangasluoma, J., Kim, J., Krapf, M., Kurten, A., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Mathot, S., Molteni, U., Onnela, A., Perakyla, O., Piel, F., Petaja, T., Praplan, A. P., Pringle, K., Rap, A., Richards, N. A. D., Riipinen, I., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Scott, C. E., Seinfeld, J. H., Sipila, M., Steiner, G., Stozhkov, Y., Stratmann, F., Tomé, A., Virtanen, A., Vogel, A. L., Wagner, A. C., Wagner, P. E., Weingartner, E., Wimmer, D., Winkler, P. M., Ye, P., Zhang, X., Hansel, A., Dommen, J., Donahue, N. M., Worsnop, D. R., Baltensperger, U., Kulmala, M., Carslaw, K. S., and Curtius, J.: Ion-induced nucleation of pure biogenic particles, Nature, 533, 521–526, https://doi.org/10.1038/nature17953, 2016.
Kürten, A., Jokinen, T., Simon, M., Sipilä, M., Sarnela, N., Junninen, H., Adamov, A., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., Dommen, J., Donahue, N. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Hakala, J., Hansel, A., Heinritzi, M., Hutterli, M., Kangasluoma, J., Kirkby, J., Laaksonen, A., Lehtipalo, K., Leiminger, M., Makhmutov, V., Mathot, S., Onnela, A., Petäjä, T., Praplan, A. P., Riccobono, F., Rissanen, M. P., Rondo, L., Schobesberger, S., Seinfeld, J. H., Steiner, G., Tomé, A., Tröstl, J., Winkler, P. M., Williamson, C., Wimmer, D., Ye, P., Baltensperger, U., Carslaw, K. S., Kulmala, M., Worsnop, D. R., and Curtius, J.: Neutral molecular cluster formation of sulfuric acid–dimethylamine observed in real time under atmospheric conditions, Proc. Natl. Acad. Sci. USA, 111, 15019–15024, https://doi.org/10.1073/pnas.1404853111, 2014.
Kurtén, T., Petäjä, T., Smith, J., Ortega, I. K., Sipilä, M., Junninen, H., Ehn, M., Vehkamäki, H., Mauldin, L., Worsnop, D. R., and Kulmala, M.: The effect of H2SO4 – amine clustering on chemical ionization mass spectrometry (CIMS) measurements of gas-phase sulfuric acid, Atmos. Chem. Phys., 11, 3007–3019, https://doi.org/10.5194/acp-11-3007-2011, 2011.
Lopez-Hilfiker, F. D., Iyer, S., Mohr, C., Lee, B. H., D'Ambro, E. L., Kurtén, T., and Thornton, J. A.: Constraining the sensitivity of iodide adduct chemical ionization mass spectrometry to multifunctional organic molecules using the collision limit and thermodynamic stability of iodide ion adducts, Atmos. Meas. Tech., 9, 1505–1512, https://doi.org/10.5194/amt-9-1505-2016, 2016.
Meot-Ner, M. M.: The Ionic Hydrogen Bond and Ion Solvation, 2, Solvation of Onium Ions by One to Seven H2O Molecules, Relations between Monomolecular, Specific, and Bulk Hydration, J. Am. Chem. Soc., 106, 1265–1272, https://doi.org/10.1021/ja00317a016, 1984.
Meot-Ner, M. and Sieck, L. W.: The Ionic Hydrogen Bond and Ion Solvation, 5, OH…O- Bonds. Gas-Phase Solvation and Clustering of Alkoxide and Carboxylate Anions, J. Am. Chem. Soc., 108, 7525–7529, https://doi.org/10.1021/ja00284a014, 1986.
Müller, M., Mikoviny, T., Feil, S., Haidacher, S., Hanel, G., Hartungen, E., Jordan, A., Märk, L., Mutschlechner, P., Schottkowsky, R., Sulzer, P., Crawford, J. H., and Wisthaler, A.: A compact PTR-ToF-MS instrument for airborne measurements of volatile organic compounds at high spatiotemporal resolution, Atmos. Meas. Tech., 7, 3763–3772, https://doi.org/10.5194/amt-7-3763-2014, 2014.
Olenius, T., Schobesberger, S., Kupiainen-Määttä, O., Franchin, A., Junninen, H., Ortega, I. K., Kurtén, T., Loukonen, V., Worsnop, D. R., Kulmala, M., and Vehkamäki, H.: Comparing simulated and experimental molecular cluster distributions, Faraday Discuss., 165, 75–89, https://doi.org/10.1039/c3fd00031a, 2013.
Perkins, M. D. and Eisele, F. L.: First Mass Spectrometric Measurements of Atmospheric Ions At Ground Level., J. Geophys. Res., 89, 9649–9657, https://doi.org/10.1029/JD089iD06p09649, 1984.
Rus, J., Moro, D., Sillero, J. A., Royuela, J., Casado, A., Estevez-Molinero, F., and Fernández de la Mora, J.: IMS-MS studies based on coupling a differential mobility analyzer (DMA) to commercial API-MS systems, Int. J. Mass Spectrom., 298, 30–40, https://doi.org/10.1016/j.ijms.2010.05.008, 2010.
Schnitzhofer, R., Metzger, A., Breitenlechner, M., Jud, W., Heinritzi, M., De Menezes, L.-P., Duplissy, J., Guida, R., Haider, S., Kirkby, J., Mathot, S., Minginette, P., Onnela, A., Walther, H., Wasem, A., Hansel, A., and the CLOUD Team: Characterisation of organic contaminants in the CLOUD chamber at CERN, Atmos. Meas. Tech., 7, 2159–2168, https://doi.org/10.5194/amt-7-2159-2014, 2014.
Schobesberger, S., Junninen, H., Bianchi, F., Lonn, G., Ehn, M., Lehtipalo, K., Dommen, J., Ehrhart, S., Ortega, I. K., Franchin, A., Nieminen, T., Riccobono, F., Hutterli, M., Duplissy, J., Almeida, J., Amorim, A., Breitenlechner, M., Downard, A. J., Dunne, E. M., Flagan, R. C., Kajos, M., Keskinen, H., Kirkby, J., Kupc, A., Kurten, A., Kurten, T., Laaksonen, A., Mathot, S., Onnela, A., Praplan, A. P., Rondo, L., Santos, F. D., Schallhart, S., Schnitzhofer, R., Sipila, M., Tome, A., Tsagkogeorgas, G., Vehkamaki, H., Wimmer, D., Baltensperger, U., Carslaw, K. S., Curtius, J., Hansel, A., Petaja, T., Kulmala, M., Donahue, N. M., and Worsnop, D. R.: Molecular understanding of atmospheric particle formation from sulfuric acid and large oxidized organic molecules, Proc. Natl. Acad. Sci. USA, 110, 17223–17228, https://doi.org/10.1073/pnas.1306973110, 2013.
Sipilä, M., Sarnela, N., Jokinen, T., Henschel, H., Junninen, H., Kontkanen, J., Richters, S., Kangasluoma, J., Franchin, A., Peräkylä, O., Rissanen, M. P., Ehn, M., Vehkamäki, H., Kurten, T., Berndt, T., Petäjä, T., Worsnop, D., Ceburnis, D., Kerminen, V. M., Kulmala, M. and O'Dowd, C.: Molecular-scale evidence of aerosol particle formation via sequential addition of HIO3, Nature, 537, 532–534, https://doi.org/10.1038/nature19314, 2016.
Steiner, G., Attoui, M., Wimmer, D., and Reischl, G. P.: A medium flow, high-resolution Vienna DMA running in recirculating mode, Aerosol Sci. Technol., 44, 308–315, https://doi.org/10.1080/02786821003636763, 2010.
Tolmachev, A. V., Udseth, H. R., and Smith, R. D.: Modeling the ion density distribution in collisional cooling RF multipole ion guides, Int. J. Mass Spectrom., 222, 155–174, https://doi.org/10.1016/S1387-3806(02)00960-0, 2003.
Ude, S. and De La Mora, J. F.: Molecular monodisperse mobility and mass standards from electrosprays of tetra-alkyl ammonium halides, J. Aerosol Sci., 36, 1224–1237, https://doi.org/10.1016/j.jaerosci.2005.02.009, 2005.
Viggiano, A. A. and Arnold, F.: The first height measurements of the negative ion composition of the stratosphere, Planet. Space Sci., 29, 895–906, https://doi.org/10.1016/0032-0633(81)90079-9, 1981.
Winklmayr, W., Reischl, G. P., Lindner, A. O., and Berner, A.: A new electromobility spectrometer for the measurement of aerosol size distributions in the size range from 1 to 1000 nm, J. Aerosol Sci., 22, 289–296, https://doi.org/10.1016/S0021-8502(05)80007-2, 1991.
Zapadinsky, E., Passananti, M., Myllys, N., Kurtén, T., and Vehkamaki, H.: Modeling on Fragmentation of Clusters inside a Mass Spectrometer, J. Phys. Chem. A, 123, 611–624, https://doi.org/10.1021/acs.jpca.8b10744, 2019.





