the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Unified quantitative observation of coexisting volcanic sulfur dioxide and sulfate aerosols using ground-based Fourier transform infrared spectroscopy
Pasquale Sellitto
Henda Guermazi
Elisa Carboni
Richard Siddans
Mike Burton
We developed an optimal-estimation algorithm to simultaneously retrieve, for the first time, coexisting volcanic gaseous SO2 and sulfate aerosols (SA) from ground-based Fourier transform infrared (FTIR) observations. These effluents, both linked to magmatic degassing process and subsequent atmospheric evolution processes, have overlapping spectral signatures leading to mutual potential interferences when retrieving one species without considering the other. We show that significant overestimations may be introduced in SO2 retrievals if the radiative impact of coexistent SA is not accounted for, which may have impacted existing SO2 long-term series, e.g. from satellite platforms. The method was applied to proximal observations at Masaya volcano, where SO2 and SA concentrations, and SA acidity, were retrieved. A gas-to-particle sulfur partitioning of 400 and a strong SA acidity (sulfuric acid concentration: 65 %) were found, consistent with past in situ observations at this volcano. This method is easily exportable to other volcanoes to monitor magma extraction processes and the atmospheric sulfur cycle in the case of ash-free plumes.
- Article
(586 KB) -
Supplement
(77 KB) - BibTeX
- EndNote
Volcanic gas and particulate emissions affect tropospheric and stratospheric compositions, air quality and the environment, the distribution and optical properties of low and high clouds, the Earth radiation budget from the regional to the global scale, and therefore climate (e.g. von Glasow et al., 2009; Robock, 2000). One of the most important environmental pollutants and the main source of radiative forcing from volcanoes is long-lived acidic and highly reflective sulfate aerosols (SA), directly emitted (primary SA) or formed by gas-to-particle conversion of sulfur dioxide (SO2) emissions (secondary SA).
Observing these volcanic emissions and their atmospheric processes and variability in space and time using ground-based and satellite remote sensing is a crucial step towards understanding and quantifying their environmental and climatic impacts. Proximal integrated observations of different and interacting gaseous and particulate volcanic effluents is also important to gain insights into magmatic degassing processes and eruption forecasting. Fourier transform infrared (FTIR) spectroscopy (e.g. Oppenheimer et al., 1998; Francis et al., 1998; Duffell et al., 2003; Burton et al., 2007) is a powerful tool in this context. Ground-based FTIR is an ideal instrument for measuring magmatic degassing as it allows for remote quantification of the major magmatic gases, including H2O, CO2, SO2, HCl, HF and also trace gases such as SiF4, CO and OCS. Typically a radiation source is needed, and this may be an artificial infrared lamp or hot rock or lava (e.g. Allard et al., 2005). Correspondingly, open-path (OP) FTIR is based on an atmospheric path of a known distance between an artificial or natural source and an FTIR optical system. These spectrometers collect spectra over a large spectral range, which contains broad spectral features arising from volcanic aerosols as well as more finely structured molecular absorption signatures. However, until now, these broadband aerosol features have not been utilised as the research focus has been exclusively on magmatic gas emissions. This means a very rich resource of information on volcanic aerosols and their processes is potentially available in previously measured FTIR spectra from volcanoes worldwide.
The possibility of sporadic detection of SA, without specific physicochemical characterisation, from high-spectral-resolution infrared satellite instruments has been shown in the past for relatively strong volcanic eruptions with stratospheric injection (Haywood et al., 2010; Karagulian et al., 2010). In this work, we demonstrate that systematic detection, quantification and chemical characterisation of volcanic sulfate aerosols using OP-FTIR spectrometry is feasible. As SO2 and SA emissions are inter-connected by magmatic degassing processes and by the subsequent short-term and small-scale atmospheric processes (e.g. Sellitto et al., 2017a) and have absorption features in the same spectral range (e.g. Sellitto and Legras, 2016; Sellitto et al., 2017b), we explore the possibility of characterising simultaneously these two volcanic effluents. This co-retrieval is intended to limit mutual biases, which are expected if SO2 and SA are retrieved individually (e.g. Guermazi et al., 2017). In addition, this co-retrieval provides, in principle, simultaneous information on two interacting species, contributing a constraint to the inner volcanic and atmospheric sulfur cycle. This new inversion method (described in Sect. 3) is then applied to OP-FTIR observations taken at Masaya volcano during a measurement campaign conducted in 1998 (described in Sect. 2). Results are given and discussed in Sect. 4 and conclusions are drawn in Sect. 5.
Masaya volcano (11.98∘ N, 86.16∘ W) is located in the Central American volcanic belt, which runs from Guatemala to Costa Rica in the north–south direction. It is situated about 25 km south-east of Managua city, Nicaragua, with an elevation of about 600 m. It is structured as a basaltic-andesitic shield caldera. Masaya is one of the world's most persistent sources of passive magmatic degassing with a relatively stable degassing rate and episodic stronger events (Rymer et al., 1998). The active vent releases SO2, whose fluxes range from about 500 to 2500 t d−1 (Duffell et al., 2003; Mather et al., 2006; de Moor et al., 2013; Carn et al., 2017). Masaya is, therefore, one of the largest contributors of volcanic gas emissions in the Central American arc (de Moor et al., 2017). One of Masaya's most remarkable features is its accessibility; it is literally a drive-in volcano with a car park next to the main degassing crater. This means that it has been used as a natural laboratory to conduct investigations into magmatic degassing and aerosol evolution. In situ air mass sampling and subsequent laboratory analyses of Masaya's plume to investigate aerosol composition and burden were conducted during several campaigns (e.g. Allen et al., 2002; Martin et al., 2011).
The data used in this work were collected not with direct sampling but with OP-FTIR remote sensing during a two-year (1998–1999) measurement campaign. In particular, we focus on high-quality spectra collected during a measurement session from about 16:40 to 17:10 UTC on 15 March 1998. During these measurements, Masaya was not in an eruptive period and observations are therefore representative of the normal passive degassing activity. During the campaign, a MIDAC Corporation OP-FTIR spectrometer was deployed on the top of Santiago crater. The observation geometry for this instrumental set-up is depicted in Fig. 2 of Horrocks et al. (1999): an infrared lamp and an FTIR spectrometer were placed on two sides of the active Masaya crater so that the radiation of the lamp is observed by the FTIR after it is transmitted through the plume with a total distance of 518 m. More details on the FTIR system and its technical specifications, the campaign, and its major results can be found in (Horrocks et al., 1999; Burton et al., 2000).
With reference to Fig. 2 of Horrocks et al. (1999), the radiance spectrum measured by the spectrometer when the plume is in the line of sight is
where Ilamp(λ) is the radiance emitted by the lamp and the total optical depth is the combination of the total optical depth of the plume and of the background atmosphere. If an observation is taken when the plume is not in the line of sight of the spectrometer, a background reference spectrum is obtained:
By taking two observations with and without the plume in the line of sight, the plume optical depth can be isolated:
If the plume is considered homogeneous, its optical depth can be expressed as follows:
where L is the path length into the plume and is the spectral extinction coefficient of the plume, which encompasses both absorption by volcanic gases and absorption and scattering by particles. To avoid radiative interferences with volcanic gaseous effluents other than SO2, we (1) restricted our analyses to the spectral range 800–1170 cm−1, where only SO2 (roto-vibrational ν1 band (e.g. Carboni et al., 2012)) and water vapour have absorption bands, and (2) carefully selected spectral micro-windows within this interval to single out the spectral regions not affected by water vapour lines absorption. The water vapour continuum absorption, in this band, is very small and can be neglected (Shine et al., 2016). In the selected spectral micro-windows, the extinction coefficient of the plume can be expressed as follows:
In the previous equation, represents the extinction by particulate matter in the plume, i.e. sulfate aerosols, ash or condensed water. Ash emissions were not visually observed during the measurement session. In addition, the spectral signature of ash and pure condensed water, both very different and distinguishable from the SA spectral signature, is not observed in our dataset, so we exclude the presence of both types of particles.
We first selected a background reference spectrum based on the least amount of hydrochloric acid (HCl) measured in the plume, with an independent method, as done by Horrocks et al. (1999). The HCl is abundant in the plume. Then, using Eqs. (3) and (4), we derived the measured as follows:
Using an optimal estimation method based on the Levenberg–Marquardt minimisation algorithm (Rodgers, 2000, p. 92–93, and references therein) (more details on the set-up of this method are given in Appendix A), we fitted the measured and a modelled , parameterised as follows:
In Eq. (7), is the extinction coefficient of a target sulfate aerosol (SA) layer, calculated using a Mie code (http://eodg.atm.ox.ac.uk/MIE/, last access: 4 October 2019). We fixed the size distribution as a mono-modal log-normal distribution with 0.2 µm mean radius, 30 particles per cubic centimetre number concentration and 1.86 µm width. The SA layers have been taken as a dispersion of spherical droplets of a binary system solution, composed of water and sulfuric acid. The sulfuric acid mixing ratio- ([H2SO4]) and temperature-dependent complex refractive indices of these droplets have been taken from Biermann et al. (2000) for the temperature T of the plume, which was assumed to be atmospheric temperature. Each combination of the size distribution parameters and [H2SO4] corresponds to a total sulfate aerosol mass concentration. In the spectral region between about 800 and 1200 cm−1, a clear spectral signature of SA has been found by Sellitto and Legras (2016). Sellitto and Legras have also shown that the mass concentration, through a shift of the total absorption signature, and [H2SO4], through a modification of the shape of the spectral signature, mostly determine the extinction coefficient of sulfate aerosol layers, except for extreme values of the mean radius (e.g. mean radii greater than 0.4–0.5 µm). In this latter case, the scattering component of the total extinction may become important, leading to a stronger dependence of on the size distribution. Extreme values of the mean radius are unlikely for these proximal observations. Based on these considerations, in the fitting procedure we adjust the total mass concentration of the sulfate aerosols in the plume by adjusting a mass concentration ratio parameter , defined as the ratio between the total mass concentration and the mass concentration associated to the Mie-calculated extinction coefficient . In addition, the optimal estimation is run multiple times, using each time a different value of [H2SO4]. An optimal value of [H2SO4] is selected based on the deviation of the modelled and measured . As for the SO2 component, is the SO2 absorption cross section calculated at temperature T and pressure p of the plume, using HITRAN (high-resolution transmission molecular absorption database) spectroscopic data (position, shape and intensity of the absorption lines in the selected spectral region). Then, the number concentration is adjusted during the spectral fitting.
From the SA mass concentration ratio and the SO2 density , the total mass concentrations of sulfate aerosols and sulfur dioxide, and , are derived. Finally, the vector of the estimated plume's parameters is tri-dimensional and is composed of the SO2 and sulfate aerosol mass concentrations, and , and the sulfate aerosol acidity (in terms of their sulfuric acid mixing ratio [H2SO4]). The error content of the SO2 and sulfate aerosol mass concentrations can be derived using the Rodgers framework (Rodgers, 2000). These uncertainties are dominated by error components transferred from the spectral measurement radiometric noise and the information content correlations between these two retrieved parameters, and is typically smaller than 15 % for both parameters.
Figure 1a shows the measured and modelled (after spectral fitting) extinction coefficient for the Masaya volcano plume, as well as the spectral residuals, for one individual FTIR observation in our dataset. The raw FTIR observations for this spectrum are in the Supplement. In Fig. 1b, the individual contributions of the SA layer and of the SO2 to the fitted are also shown. A clear spectral signature of SA is visible in with the two peculiar absorption features (two combinations of bend–stretch vibrational modes) of the undissolved H2SO4 molecules (870–920 and 1150–1200 cm−1) and the symmetric stretch ν1 bisulfite ion vibrational mode around 1050 cm−1 (Biermann et al., 2000; Sellitto and Legras, 2016). These components of are isolated in the SA-only spectrum of Fig. 1b. Comparing the two panel, it is also apparent how an SA-only plume cannot completely explain the spectral shape of the measured spectrum. Adding the SO2 contribution, the spectrum is more satisfactorily fitted. The residuals are between near-zero, for wavenumbers <1080 cm−1, and about cm−1 (up to 20 %), for longer wavenumbers. The residuals are consistently contained in the ±1σresiduals interval, except for wavenumbers higher than 1100 cm−1. The higher residuals above 1100 cm−1 can be due to (a) the lack of fine-scale structures of the Biermann et al. (2000) refractive indices for SA (which are provided at a coarse spectral resolution), (b) uncertainties in the SO2 spectral absorption coefficient transferred from uncertainties in temperature and pressure used in their calculation, and/or (c) spectral drifts in the FTIR observations.
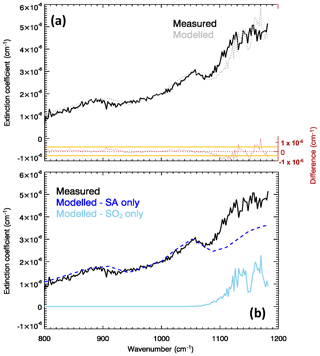
Figure 1(a) Measured (solid black line) and modelled/fitted (dotted grey line) extinction coefficient of the Masaya volcano plume for the observation of 15 March 1998 at 17:06 UTC. Residuals (modelled minus measured extinction coefficient) are also shown in red. Orange lines show the corresponding standard deviation interval (here, excluding specific systematic spectroscopic errors transmitted from the SA laboratory measurements, has been considered conservatively equal to ; details on the calculation of are given in Appendix A). (b) Individual components of the modelled extinction coefficient due to SA (blue line) and SO2 (sky blue line).
During the measurement session mentioned in Sect. 2, 38 in-plume spectral measurements are taken. In most cases, i.e. 25 spectra (66 % of the overall observations), coexistent SO2 and SA are detected. For 5 spectra (13 %) only SO2 is detected. For the remaining 8 spectra (21 %), no clear SA or SO2 signals are detected. For these latter cases, the measured plume's extinction coefficient is very small and we suppose that the plume was not or only partially in the line of sight of the FTIR. The mean values of the total mass concentrations of SA and SO2 and the mixing ratio of SA, calculated by averaging the mentioned 25 individual retrievals obtained during the measurement session, are summarised in Table 1. With an independent retrieval algorithm, using a different spectral range (between 2465 and 2550 cm−1), Horrocks et al. (1999) have found a SO2 concentration of 98.4±20.0 mg m−3 for the same observation set at Masaya. Our retrieved SO2 average total mass concentration (153.7±85.3 mg m−3), even if slightly higher, is consistent with the one obtained by Horrocks et al. (1999). The higher value in our average estimation can be due to the presence of volcanic fluorine compounds that might be present in the plume but are neglected in the present study. The retrieved average sulfate aerosol mass concentration is 0.4±0.2 mg m−3. The SO2∕SA ratio is then about 400. Due to the proximal observations, these aerosols can be considered primary emissions and are still not significantly processed by interaction with the atmosphere. The average H2SO4 mixing ratio is 65±18 %. This result reveals highly acidic sulfate aerosols as observed previously with direct sampling (Allen et al., 2002). These acidic aerosols have been shown to be formed by small particles (<2 µm), accounting for up to 80 % of the total mass of aerosol emissions at this volcano. The acidity comes from the rapid conversion of sulfuric acid and hydrofluoric acid to particles, initiated from the oxidation of SO2 (Mather et al., 2004). Thus, one important source of systematic error in our method is the possible presence of hydrofluoric acid dissolved in the aerosol droplets, that has been neglected in our radiative calculations. By considering the average SO2 and SA mass concentrations and the average mixing ratio, it results that the gas-to-particle partition of sulfur in the plume is about 400, which is very similar to what was found, in 2002, at Masaya by Allen et al. (2002) (about 450). In any case, the temporal evolution of the three parameters and the SO2∕SA ratio are very variable and different samples, taken at different times, can be significantly different. Masaya volcanic activity is very stable but the gas emission rates vary and, critically, the aerosol evolution is probably strongly dependent on highly variable atmospheric parameters such as relative humidity and temperature, as well as the plume age at the moment of detection, which depends partly on wind velocity. Notwithstanding this variability, the average sulfur partitioning seems very stable at longer timescales.
Table 1Mean SO2 and SA mass concentrations, and mean sulfuric acid mixing ratio in SA, for our retrieval session at Masaya volcano with associated standard deviations (due to their variability during the measurement session). These mean values are obtained by averaging 25 individual retrievals.

We tested the possibility that SA extinction could interfere with SO2 retrievals by retrieving SO2 only, with our optimal estimation method, in spectra where the coexistence of the two volcanic plume components is clear, like the one in Fig. 1. In this case, we obtain an overestimation of the SO2 total mass concentration of nearly 50 % with respect to the case of co-retrieval of SO2 and SA mass concentrations. Even if this is an extreme case and inversion methods can be developed to partially compensate broadband biases, like the one introduced by aerosols in the sampled air masses, this example shows how the radiative interferences between SO2 and SA may introduce overestimations in these retrievals. This is particularly important for the observation of volcanic plumes, with a potentially substantial impact in the case of aged plumes. For stratospheric eruptions, rapid formation of secondary SA has been recently observed, e.g. for the Kasatochi volcano (Alaska, USA, August 2008) (Krotkov et al., 2010) and Nabro volcano (Eritrea, June 2011) (Penning de Vries et al., 2014) eruptions, with SO2 lifetimes as short as a few hours. For volcanic eruptions with injection at lower altitudes (in the troposphere) or in persistent passive degassing regimes, the rapid gas and aqueous-phase oxidation and/or nucleation of SO2 can lead to radiatively active layers within a few hours after the initial SO2 emission (Sellitto et al., 2016; Guermazi et al., 2017), with potentially systematic volcanic signature on the regional aerosol optical properties downwind (Sellitto et al., 2017c). In general, the lifetime of SO2 and the inherent timescales of SA formation and evolution are complex and depend on various factors including the solar irradiation, humidity, temperature, pH and the presence of oxidants (e.g. Eatough et al., 1997). Then, we recommend to either co-retrieve SO2 and SA or to take explicitly into account these interferences when attempting to retrieve chemically, micro-physically, and radiatively interconnected pollutants. These considerations apply notably to satellite observations where the spectroscopic inversion problem can be even more severe than in the present ground-based OP-FTIR case, due to the strongly ill-posed problem linked to a longer atmospheric path and the inherent radiative transfer. We also highlight that to date the typical band used to quantify SO2 with ground-based OP-FTIR is that at 2500 cm−1, which is less affected by the aerosol extinction (e.g. Horrocks et al., 1999).
We developed a retrieval algorithm to observe volcanic SO2 and SA emissions using ground-based OP-FTIR spectrometry. To the best of our knowledge, this is the first time that SO2 and SA are simultaneously characterised using this or other ground-based or satellite-based remote-sensing techniques. The retrieval is based on a non-linear least square fitting algorithm, minimising the difference between modelled and measured spectral extinctions of volcanic plumes. A spectral micro-windows selection was performed in order to avoid the interference with water vapour absorption and to optimise the spectral fitting. The absorption of SO2 and the extinction of SA have been modelled by means of high-spectral-resolution temperature- and pressure-dependent spectroscopic data and a Mie code driven by state-of-the-art aerosol optical properties, respectively.
We applied this method to proximal ground-based FTIR observations at Masaya volcano. We retrieved SO2 and SA total mass concentrations and SA mixing ratio (linked to particle acidity). Average concentrations of SO2, SO2/SA ratios and acidity of aerosols are consistent with previous observations at Masaya. A gas-to-particle partition of sulfur of about 400 is found and a strong acidity ([H2SO4] of about 65 %), which is very consistent with past observations at Masaya, pointing to reasonable long-term stability of Masaya primary sulfate emissions. We also underline the importance of taking into account SA when attempting to retrieve volcanic SO2 from ground-based or satellite remote-sensing instruments around the 1200 cm−1 SO2 band. Neglecting the rapid formation (or even primary emission) of SA may lead to significant overestimation of SO2 (in our case up to about 50 %). This method can be fruitfully applied to the quite large library of previously collected FTIR spectra from volcanoes worldwide to constrain the magmatic and/or atmospheric processes that determine their sulfur emissions and gas-to-particle partitioning. This method can also be exported to thermal infrared (TIR) satellite observations, like those from IASI (Infrared Atmospheric Sounding Interferometer) or others, as long as the full radiative transfer through the longer atmospheric path to the satellite platform is taken into account.
The FTIR spectra used to produce Fig. 1 are available in the Supplement. The whole dataset can be provided on demand (pasquale.sellitto@lisa.u-pec.fr).
An ad hoc optimal estimation retrieval method is used in this work to retrieve and that are used to obtain the final tri-dimensional output vector composed of the SO2 and sulfate aerosol mass concentration and and the sulfate aerosol acidity [H2SO4] (see Sect. 3). The method is based on the minimisation of the following cost function J:
In the previous equation, is the state vector to be retrieved; xa is the a priori vector for x, with its associated covariance matrix Sa; and Sϵ is the measurement error covariance matrix (linked to the uncertainty in the measured extinction coefficient ). The measured and modelled extinction coefficients and are the same as in Sect. 3, with their implicit wavelength dependence and represented as vector.
The a priori values of and , elements of xa, are both taken as zero. In the a priori covariance matrix Sa, the diagonal elements describe the expected variability in the retrieved parameters, while off-diagonal elements express the possible covariances: in this work only diagonal elements are assigned non-zero values. The measurement noise covariance matrix Sϵ has been constructed to represent the measurement error on the measured extinction coefficient. Thus, for each diagonal element (measurement noise transferred to the extinction coefficient at a given wavelength), we have considered the following expression, with reference to Eq. (6):
Based on a conservative choice of a relative error of 1 % for both background and in-plume observations, we obtain a variance of about cm−2. Off-diagonal values of Sϵ are taken as zero.
The supplement related to this article is available online at: https://doi.org/10.5194/amt-12-5381-2019-supplement.
PS and EC conceived the method. PS and HG implemented the method and realised the inversions. RS developed the optimal-estimation software and EC, HG and PS contributed and adapted the software to the case study. MB collected and preprocessed the FTIR measurements at Masaya volcano. All authors discussed the results and contributed to the final article.
The authors declare that they have no conflict of interest.
This article is part of the special issue “StratoClim stratospheric and upper tropospheric processes for better climate predictions (ACP/AMT inter-journal SI)”. It is not associated with a conference.
Giuseppe Salerno and Alessandro La Spina are gratefully acknowledged for the discussions on sulfate aerosols inversion from FTIR measurements.
This research has been supported by the EC Seventh Framework Programme (STRATOCLIM (grant no. 603557)), the Agence Nationale de la Recherche (TTL-Xing), the Centre National d'Etudes Spatiales (TOSCA/IASI), and the Istituto Nazionale di Geofisica e Vulcanologia (SMED).
This paper was edited by Pierre Herckes and reviewed by Michael Fromm and one anonymous referee.
Allard, P., Burton, M., and Muré, F.: Spectroscopic evidence for a lava fountain driven by previously accumulated magmatic gas, Nature, 433, 407–410, 2005. a
Allen, A. G., Oppenheimer, C., Ferm, M., Baxter, P. J., Horrocks, L. A., Galle, B., McGonigle, A. J. S., and Duffell, H. J.: Primary sulfate aerosol and associated emissions from Masaya Volcano, Nicaragua, J. Geophys. Res., 107, 4682, https://doi.org/10.1029/2002JD002120, 2002. a, b, c
Biermann, U. M., Luo, B. P., and Peter, T.: Absorption Spectra and Optical Constants of Binary and Ternary Solutions of H2SO4, HNO3, and H2O in the Mid Infrared at Atmospheric Temperatures, J. Phys. Chem. A, 104, 783–793, https://doi.org/10.1021/jp992349i, 2000. a, b, c
Burton, M., Allard, P., Muré, F., and La Spina, A.: Magmatic Gas Composition Reveals the Source Depth of Slug-Driven Strombolian Explosive Activity, Science, 317, 227–230, https://doi.org/10.1126/science.1141900, 2007. a
Burton, M. R., Oppenheimer, C., Horrocks, L. A., and Francis, P. W.: Remote sensing of CO2 and H2O emission rates from Masaya volcano, Nicaragua, Geology, 28, 915–918, https://doi.org/10.1130/0091-7613(2000)28<915:RSOCAH>2.0.CO;2, 2000. a
Carboni, E., Grainger, R., Walker, J., Dudhia, A., and Siddans, R.: A new scheme for sulphur dioxide retrieval from IASI measurements: application to the Eyjafjallajökull eruption of April and May 2010, Atmos. Chem. Phys., 12, 11417–11434, https://doi.org/10.5194/acp-12-11417-2012, 2012. a
Carn, S. A., Fioletov, V. E., McLinden, C. A., Li, C., and Krotkov, N. A.: A decade of global volcanic SO2 emissions measured from space, Scientific Reports, 7, 44095, https://doi.org/10.1038/srep44095, 2017. a
de Moor, J. M., Fischer, T. P., Sharp, Z. D., King, P. L., Wilke, M., Botcharnikov, R. E., Cottrell, E., Zelenski, M., Marty, B., Klimm, K., Rivard, C., Ayalew, D., Ramirez, C., and Kelley, K. A.: Sulfur degassing at Erta Ale (Ethiopia) and Masaya (Nicaragua) volcanoes: Implications for degassing processes and oxygen fugacities of basaltic systems: Sulfur Degassing at Basaltic Volcanoes, Geochem. Geophy. Geosy., 14, 4076–4108, https://doi.org/10.1002/ggge.20255, 2013. a
de Moor, J. M., Kern, C., Avard, G., Muller, C., Aiuppa, A., Saballos, A., Ibarra, M., LaFemina, P., Protti, M., and Fischer, T. P.: A New Sulfur and Carbon Degassing Inventory for the Southern Central American Volcanic Arc: The Importance of Accurate Time-Series Data Sets and Possible Tectonic Processes Responsible for Temporal Variations in Arc-Scale Volatile Emissions: New volatile budget for Central America, Geochem. Geophy. Geosy., 18, 4437–4468, https://doi.org/10.1002/2017GC007141, 2017. a
Duffell, H. J., Oppenheimer, C., Pyle, D. M., Galle, B., McGonigle, A. J., and Burton, M. R.: Changes in gas composition prior to a minor explosive eruption at Masaya volcano, Nicaragua, J. Volcanol. Geoth. Res., 126, 327–339, https://doi.org/10.1016/S0377-0273(03)00156-2, 2003. a, b
Eatough, D., Caka, F., and Farber, R.: The Conversion of SO2 to Sulfate in the Atmosphere, Israel J. Chem., 34, 301–314, https://doi.org/10.1002/ijch.199400034, 1997. a
Francis, P., Burton, M. R., and Oppenheimer, C.: Remote measurements of volcanic gas compositions by solar occultation spectroscopy, Nature, 396, 567–570, 1998. a
Guermazi, H., Sellitto, P., Serbaji, M. M., Legras, B., and Rekhiss, F.: Assessment of the Combined Sensitivity of Nadir TIR Satellite Observations to Volcanic SO2 and Sulphate Aerosols after a Moderate Stratospheric Eruption, Geosciences, 7, 84, https://doi.org/10.3390/geosciences7030084, 2017. a, b
Haywood, J. M., Jones, A., Clarisse, L., Bourassa, A., Barnes, J., Telford, P., Bellouin, N., Boucher, O., Agnew, P., Clerbaux, C., Coheur, P., Degenstein, D., and Braesicke, P.: Observations of the eruption of the Sarychev volcano and simulations using the HadGEM2 climate model, J. Geophys. Res., 115, D21212, https://doi.org/10.1029/2010JD014447, 2010. a
Horrocks, L., Burton, M., Francis, P., and Oppenheimer, C.: Stable gas plume composition measured by OP‐FTIR spectroscopy at Masaya Volcano, Nicaragua, 1998–1999, Geophys. Res. Lett., 26, 3497–3500, https://doi.org/10.1029/1999GL008383, 1999. a, b, c, d, e, f, g
Karagulian, F., Clarisse, L., Clerbaux, C., Prata, A. J., Hurtmans, D., and Coheur, P. F.: Detection of volcanic SO2, ash, and H2SO4 using the Infrared Atmospheric Sounding Interferometer (IASI), J. Geophys. Res., 115, D00L02, https://doi.org/10.1029/2009JD012786, 2010. a
Krotkov, N. A., Schoeberl, M. R., Morris, G. A., Carn, S., and Yang, K.: Dispersion and lifetime of the SO2 cloud from the August 2008 Kasatochi eruption, J. Geophys. Res., 115, D00L20, https://doi.org/10.1029/2010JD013984, 2010. a
Martin, R., Ilyinskaya, E., Sawyer, G., Tsanev, V., and Oppenheimer, C.: A re-assessment of aerosol size distributions from Masaya volcano (Nicaragua), Atmos. Environ., 45, 547–560, https://doi.org/10.1016/j.atmosenv.2010.10.049, 2011. a
Mather, T., Pyle, D., Tsanev, V., McGonigle, A., Oppenheimer, C., and Allen, A.: A reassessment of current volcanic emissions from the Central American arc with specific examples from Nicaragua, J. Volcanol. Geoth. Res., 149, 297–311, https://doi.org/10.1016/j.jvolgeores.2005.07.021, 2006. a
Mather, T. A., Tsanev, V. I., Pyle, D. M., McGonigle, A. J. S., Oppenheimer, C., and Allen, A. G.: Characterization and evolution of tropospheric plumes from Lascar and Villarrica volcanoes, Chile: Vvolcanic emissions, J. Geophys. Res., 109, D21303, https://doi.org/10.1029/2004JD004934, 2004. a
Oppenheimer, C., Francis, P., Burton, M., Maciejewski, A., and Boardman, L.: Remote measurement of volcanic gases by Fourier transform infrared spectroscopy, Appl. Phys. B-Laser O., 67, 505–515, https://doi.org/10.1007/s003400050536, 1998. a
Penning de Vries, M. J. M., Dörner, S., Puḳīte, J., Hörmann, C., Fromm, M. D., and Wagner, T.: Characterisation of a stratospheric sulfate plume from the Nabro volcano using a combination of passive satellite measurements in nadir and limb geometry, Atmos. Chem. Phys., 14, 8149–8163, https://doi.org/10.5194/acp-14-8149-2014, 2014. a
Robock, A.: Volcanic eruptions and climate, Rev. Geophys., 38, 191–219, https://doi.org/10.1029/1998RG000054, 2000. a
Rodgers, C.: Inverse Methods For Atmospheric Sounding: Theory And Practice, Series On Atmospheric, Oceanic And Planetary Physics, World Scientific Publishing Company, London, UK, available at: https://books.google.fr/books?id=Xv7sCgAAQBAJ (last access: 4 October 2019), 2000. a, b
Rymer, H., van Wyk de Vries, B., Stix, J., and Williams-Jones, G.: Pit crater structure and processes governing persistent activity at Masaya Volcano, Nicaragua, B. Volcanol., 59, 345–355, https://doi.org/10.1007/s004450050196, 1998. a
Sellitto, P. and Legras, B.: Sensitivity of thermal infrared nadir instruments to the chemical and microphysical properties of UTLS secondary sulfate aerosols, Atmos. Meas. Tech., 9, 115–132, https://doi.org/10.5194/amt-9-115-2016, 2016. a, b, c
Sellitto, P., di Sarra, A., Corradini, S., Boichu, M., Herbin, H., Dubuisson, P., Sèze, G., Meloni, D., Monteleone, F., Merucci, L., Rusalem, J., Salerno, G., Briole, P., and Legras, B.: Synergistic use of Lagrangian dispersion and radiative transfer modelling with satellite and surface remote sensing measurements for the investigation of volcanic plumes: the Mount Etna eruption of 25–27 October 2013, Atmos. Chem. Phys., 16, 6841–6861, https://doi.org/10.5194/acp-16-6841-2016, 2016. a
Sellitto, P., Salerno, G., La Spina, A., Caltabiano, T., Terray, L., Gauthier, P.-J., and Briole, P.: A novel methodology to determine volcanic aerosols optical properties in the UV and NIR and Ångström parameters using Sun photometry, J. Geophys. Res.-Atmos., 122, 9803–9815, https://doi.org/10.1002/2017JD026723, 2017a. a
Sellitto, P., Sèze, G., and Legras, B.: Secondary sulphate aerosols and cirrus clouds detection with SEVIRI during Nabro volcano eruption, Int. J. Remote Sens., 38, 5657–5672, https://doi.org/10.1080/01431161.2017.1348635, 2017b. a
Sellitto, P., Zanetel, C., di Sarra, A., Salerno, G., Tapparo, A., Meloni, D., Pace, G., Caltabiano, T., Briole, P., and Legras, B.: The impact of Mount Etna sulfur emissions on the atmospheric composition and aerosol properties in the central Mediterranean: A statistical analysis over the period 2000–2013 based on observations and Lagrangian modelling, Atmos. Environ., 148, 77–88, https://doi.org/10.1016/j.atmosenv.2016.10.032, 2017c. a
Shine, K. P., Campargue, A., Mondelain, D., McPheat, R. A., Ptashnik, I. V., and Weidmann, D.: The water vapour continuum in near-infrared windows – Current understanding and prospects for its inclusion in spectroscopic databases, J. Mol. Spectrosc., 327, 193–208, https://doi.org/10.1016/j.jms.2016.04.011, 2016. a
von Glasow, R., Bobrowski, N., and Kern, C.: The effects of volcanic eruptions on atmospheric chemistry, Chem. Geol., 263, 131–142, https://doi.org/10.1016/j.chemgeo.2008.08.020, 2009. a
- Abstract
- Introduction
- The case study: Masaya volcano and the observation geometry
- Methodology
- Results and discussion
- Conclusions
- Data availability
- Appendix A: Optimal estimation set-up
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- The case study: Masaya volcano and the observation geometry
- Methodology
- Results and discussion
- Conclusions
- Data availability
- Appendix A: Optimal estimation set-up
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement





