the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Estimating solar irradiance using sky imagers
Soumyabrata Dev
Florian M. Savoy
Yee Hui Lee
Stefan Winkler
Ground-based whole-sky cameras are now extensively used for the localized monitoring of clouds. They capture hemispherical images of the sky at regular intervals using a fish-eye lens. In this paper, we propose a framework for estimating solar irradiance from pictures taken by those imagers. Unlike pyranometers, such sky images contain information about cloud coverage and can be used to derive cloud movement. An accurate estimation of solar irradiance using solely those images is thus a first step towards the short-term forecasting of solar energy generation based on cloud movement. We derive and validate our model using pyranometers colocated with our whole-sky imagers. We achieve a better performance in estimating solar irradiance and in particular its short-term variations compared to other related methods using ground-based observations.
Clouds have a significant impact on solar energy generation. They intermittently block the sun and significantly reduce the solar irradiance reaching solar panels. A short-term forecast of solar irradiance is needed for grid operators to mitigate the effects of a drop in power generation. With rapid developments in photogrammetric techniques, ground-based sky cameras are now widely used (Dev et al., 2016d). These cameras, known as whole-sky imagers (WSIs), are upward-looking devices that capture images of the sky at regular intervals of time. These images are subsequently used for automatic cloud coverage computation, cloud tracking, and cloud-base height estimation. In our research group, we use these imagers to study the effects of clouds on satellite communication links (Dev et al., 2017b, 2018b; Yuan et al., 2016).
The localized and short-term forecasting of cloud movements is an ongoing research topic (Shakya et al., 2017; Jiang et al., 2017; Feng et al., 2018). Optical flow techniques can be used to forecast images using anterior frames (Dev et al., 2016c). Similarly, cloud motion vectors are exploited for solar power prediction from satellite images (Jang et al., 2016). Our proposed method for estimating solar irradiance is thus a first step towards solar irradiance forecasting, as the input data used to estimate the irradiance are the same as those used to forecast the sky condition.
The accurate estimation and prediction of solar energy generation is a challenging task, as clouds greatly impact the total irradiance received on the earth's surface. In the event of clouds covering the sun for a short time, there is a sharp decline in the produced solar energy. Therefore, it is important to model the incoming solar radiation accurately. In this paper, we attempt to measure the rapid fluctuations of solar irradiance using ground-based sky cameras.
The analysis of clouds and several other atmospheric phenomena is traditionally done using satellite images. However, satellite images have either low temporal or low spatial resolutions. A popular instrument is the Moderate-resolution Imaging Spectroradiometer (MODIS) (Pagano and Durham, 1993), which is onboard the Terra and Aqua satellites and provides a large-scale view of cloud dynamics and various atmospheric phenomena. Data from MODIS are usually available only twice in a day for a particular location. This is useful for a macroanalysis of cloud formation on the earth's surface. Another illustrative example of such satellite data is the HelioClim-1 database from the Global Earth Observation System of Systems (GEOSS) (Lautenbacher, 2006). It provides hourly and daily averages of surface solar radiation received at ground level (Lefèvre et al., 2014). Ouarda et al. (2016) assessed the solar irradiance from six thermal channels obtained from the Spinning Enhanced Visible and Infrared Imager (SEVIRI) instrument. However, these are temporal and spatial averages. Solar energy applications require knowledge of the solar irradiance at specific locations and at all times throughout the day. Therefore, images obtained from satellites are generally not conducive for continuous analysis and prediction, especially in regions where cloud formation is highly localized.
1.1 Related work
Several existing works analyze ground-based images with different meteorological observations. Most of them correlate the cloud coverage obtained from sky images with meteorologist observations. Silva and Souza-Echer (2016) validated cloud coverage measurements obtained from ground-based automatic imagers and human observations for two meteorological stations in Brazil. Huo and Lu (2012) also performed such field experiments for three sites in China. The computation of such cloud coverage percentage is important in solar energy generation. It can hugely impact the amount of solar radiation arriving at a particular place.
The correct estimation of solar irradiance is particularly important in tropical countries like Singapore, where the amount of received solar irradiance is high. Rizwan et al. (2012) demonstrated that tropical countries are conducive for installing large central power stations powered by solar energy because of the large amount of incident sunlight throughout the year. Several attempts have been made to estimate the solar radiation from general meteorological measurements via temperature, humidity, and precipitation (Hargreaves and Samani, 1985; Donatelli and Campbell, 1998; Bristow and Campbell, 1984; Hunt et al., 1998). These existing models aim to provide global solar radiation using different sensors. Alsadi and Nassar (2017) demonstrated such estimation models from the perspective of a photovoltaic (PV) solar field, showing that successive rows of PV panels receive less solar radiation than the first row. They also provided an analytical solution by including the design parameters in the estimation model.
In addition to solar irradiance estimation, there have been several efforts to forecast solar irradiance, with a lead time of a few minutes. Baharin et al. (2016) proposed a machine-learning forecast model for PV power output using Malaysia as the case study. Similarly Chu et al. (2015) used a reforecasting method to improve the PV power output forecasts with a lead time of 5, 10, and 15 min. Satellite images have also been used in the realm of solar analytics. Mueller et al. (2004) proposed a clear-sky model that is based on radiative transfer models obtained from Meteosat's atmospheric parameters. However, satellite data have lower temporal and spatial resolutions.
Recently, with the development of low-cost photogrammetric techniques, sky cameras are being deployed for such purposes. These sky cameras have both high temporal and high spatial resolutions and are able to provide more localized information about atmospheric events. Alonso-Montesinos and Batlles (2015) used sky cameras to quantify total solar radiation. Yang and Chen (2015) studied solar irradiance variability using entropy and covariance. Dev et al. (2018a) used triple exponential smoothing for analyzing the seasonality of solar irradiance. However, these approaches do not model the sharp short-term variations of solar radiation.
1.2 Outline
In this paper, we use images obtained from WSIs to accurately model the fluctuations of solar radiation. There are several advantages of using a WSI for this instead of a pyranometer. Common weather stations generally use a solar sensor that measures total solar irradiance. It is a point measurement providing scalar information for a particular location and does not provide information on clouds and their evolution over time. On the other hand, the wide-angle view of a ground-based sky camera provides us with extensive information about the sky. It allows for the tracking of clouds over successive image frames and also the prediction of their future location. In this paper, we attempt to model solar irradiance from sky images. This can also help in solar energy forecasting, which is useful in photovoltaic systems (Lorenz et al., 2009).
The main contributions of this paper are as follows.
-
We develop a framework to accurately estimate and track rapid fluctuations of solar irradiance.
-
We propose a method for estimating solar irradiance using ground-based sky camera images.
-
We conduct extensive benchmarking of our proposed method with other solar irradiance estimation models.
The rest of the paper is organized as follows. Section 2 describes our experimental setup that captures the sky and/or cloud images and collects other meteorological sensor data. Our framework for estimating solar irradiance is presented in Sect. 3. Section 4 discusses the evaluation of our approach and its benchmarking with other existing solar estimation models. We discuss the possible applications of our approach in Sect. 5. We also point out a few limitations of our approach and ways to address them. Section 6 concludes the paper.
Our experimental setup consists of weather stations and ground-based WSIs. These devices are colocated on the rooftop of our university building in Singapore (1.34∘ N, 103.68∘ E). They continuously capture various meteorological data, and we archive them for subsequent analysis.
2.1 Whole-sky imager (WSI)
Commercial WSIs are available on the market. However, those imagers have high cost, low image resolution, and little flexibility in operation. In our research group, we have designed and built custom low-cost high-resolution sky imagers, which we call WAHRSIS, i.e., Wide-Angle High-Resolution Sky Imaging System (Dev et al., 2014). A WAHRSIS essentially consists of a high-resolution digital single-lens reflex (DSLR) camera with a fish-eye lens and an onboard microcomputer. The entire device is contained inside a weatherproof box with a transparent dome for the camera. Over the years, we have built several versions of WAHRSIS (Dev et al., 2014, 2015). They are now deployed at several locations around our university campus, capturing images of the sky at regular intervals.
Our WAHRSIS camera is calibrated with respect to white balancing, geometric distortions, and vignetting. The imaging system in WAHRSIS is modified so that it captures the near-infrared region of the spectrum. Hence, the red channel of the captured image is more prone to saturation, which renders the captured image reddish in nature. Therefore, we employ custom white balancing in the camera such that it compensates for the alteration resulting from the near-infrared capture. Figure 1 depicts the captured images obtained from automatic and custom white balancing.

Figure 1We use custom white balancing to correct the white balance using (a) automatic white balancing and (b) custom white balancing.
We use the popular toolbox by Scaramuzza et al. (2006) for the geometric calibration of WAHRSIS. This process involves the computation of the intrinsic parameters of the camera. We use a black-and-white regular checkerboard pattern and position it at various points around the camera. Figure 2 illustrates a few sample positions of the checkerboard in the calibration process. Using the corner points and the known dimensions of the pattern, we can estimate the intrinsic parameters of the camera.
Finally, we apply vignetting correction to the images captured by our sky camera. Owing to the fish-eye nature of the lens, the area around the center of the lens is brighter than at the sides. We use an integrating sphere to correct this variation of illumination. Figure 3 depicts an image captured inside an integrating sphere that provides a uniform illumination distribution in all directions. We use luminance characteristics from this reference image to correct the images captured by our sky camera.
2.2 Weather station
In addition to the sky imagers, we have also installed colocated weather stations. We use a Davis Instruments 7440 Weather Vantage Pro for our recordings. It measures rainfall, total solar radiation, temperature, and pressure at intervals of 1 min. The resolution of the tipping-bucket rain gauge is 0.2 mm per tip.
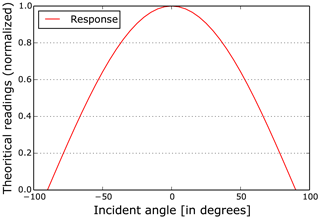
It also includes a solar pyranometer measuring the total solar irradiance flux density (W m−2). This consists of both direct and diffuse solar irradiance components. The solar sensor integrates the solar irradiance across all angles and provides the total solar irradiance. On a clear day with no occluding clouds, the solar sensor can be approximated by a typical cosine response, shown in Fig. 4, for varying degrees of solar incident angle. The solar sensor reading is highest around noon when the incident angle of sunrays is at the minimum, whilst the reading is low during morning and evening hours.
The solar radiation under a clear sky can be modeled using the solar zenith angle and the earth's eccentricity. Several clear-sky models have been developed for various regions. The best clear-sky model for Singapore is provided by Yang et al. (2012). We performed a comparison of various clear-sky models in Singapore (Dev et al., 2017a) and found that the Yang et al. (2012) model provides a good estimate of the clear-sky irradiance. It models clear-sky global horizontal irradiance (GHI) Gc as follows:
where E0 is the eccentricity correction factor for earth, Isc is the solar irradiance constant (1366.1 Watt m−2), and α is the solar zenith angle (measured in degrees). The factor E0 is calculated as
where is the day angle (measured in radians) and dn is the day number of the year.
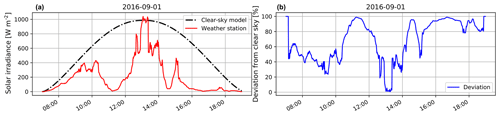
As an illustration, we show the clear-sky radiation for 1 September 2016 in Fig. 5 compared to the actual solar irradiance measured by our weather station. We also show the deviation of the measured solar radiation from the clear-sky model. We observe that there are rapid fluctuations in the measured readings. In our previous work (Dev et al., 2016), we observed that these rapid fluctuations are caused by incoming clouds that obstruct the sun from direct view. Such information about the cloud profile and its formation cannot be obtained from a point-source solar recording. Therefore, we aim to model these rapid fluctuations in the measured solar radiation from wide-angle images captured by our sky cameras.
This section presents our model for computing solar irradiance from images captured by a whole-sky imager. We sample pixels using a cosine-weighted hemispheric sampling to simulate the behavior of a pyranometer based on the fish-eye camera lens. We then compute the relative luminance using the image-capturing parameters after gamma correction. We finally derive an empirical fitting function to scale the computed luminance estimates to match measured irradiance values.
3.1 Cosine-weighted hemispheric sampling
The behavior of our fish-eye lens with focal length f is modeled by the equisolid equation , relating the distance (r) of any pixel from the center of the image to its incident light ray elevation angle (θ). This allows us to project a captured image onto the unit hemisphere, as shown in Fig. 6.
Solar irradiance is composed of a direct component relating the sunlight reaching the earth without interference, as well as diffuse and reflected components. Given the high resolution of our images, we consider randomly sampled pixel locations on the hemisphere as input to the luminance computation. We follow a cosine-weighted hemispheric distribution function, the center of which is at the location of the sun. This is because clouds in the circumsolar region have the highest impact on the total solar irradiance received on the earth's surface (Dev et al., 2016). We provide more emphasis to the clouds around the sun compared to those near the horizon. In our previous work (Dev et al., 2016), we used a cloud mask around the sun to estimate the solar irradiance. However, this requires the additional step of optimizing the size of the cropped image for the best results. Therefore, we adopt the strategy of cosine-weighted hemispheric sampling.
The first step is to compute the sampled locations from the top of the unit hemispheric dome. Each of the locations is computed as follows using two random floating points R1 and R2 as input, where .
This is represented in Fig. 6.
The second step is to detect the location of the sun using a thresholding method. This is needed to align the center of the previously computed distribution (i.e., the top of the hemispheric dome) to the actual sun location in the unit sphere. We choose a threshold of 240 in the red channel R of the red–green–blue (RGB) captured image and compute the centroid of the largest area above the threshold (Savoy et al., 2016). We then compute the rotation matrix transforming the z axis unit vector to the unit vector pointing towards the sky. We apply this rotation to all the sampled points, resulting in Fig. 6. This means that the number of sampled points in a region of the hemisphere is proportional to the cosine of the angle between the sun direction and the direction to that region. We experimentally concluded that this achieves a good balance between all irradiance components. We consider the pixel values of a total of 5000 points sampled using this method as input for the irradiance estimation.

Figure 6Cosine-weighted hemispheric sampling process. We plot the following: (a) a projection of the original image on a hemisphere, (b) cosine hemispheric sampling with the origin at the top, (c) a rotation matrix applied to the center at the sun location, (d) the original image with the detected sun location in red, (e) a projection of the sampled points onto the image, and (f) a projection of the rotated sampled points onto the image.
3.2 Relative luminance calculation
For each of the i sampled pixels in the RGB image, we compute its luminance value using the following formula. The formula is proposed in SMPTE Recommended Practice 177 (SMPTE, 1993) to compute the luminance of an image from the R, G, and B values of the RGB image.
The JPEG compression format encodes images after applying a gamma correction. This nonlinearity mimics the behavior of the human eye. This needs to be reversed in order to compute the irradiance. We use a gamma correction factor of 2.2, which is most commonly used in imaging systems (Poynton, 2003). We thus apply the following formula, assuming pixel values normalized between 0 and 255:
We then average the pixel values across all the i sampled points in the image and denote it by , the average luminance value of the sampled points from the image.
However, each image of the sky camera is captured with varying camera parameters such as ISO, F number, and shutter speed. These camera parameters can be read from the image metadata and are useful to estimate the scene luminance. The amount of brightness of the sampled points 𝒩 is proportional to the number of photons hitting the camera sensor. This relationship between scene luminance and pixel brightness is linear (Hiscocks and Eng, 2011) and can be modeled using the camera parameters:
where 𝒩 is the pixel value, Kc is a calibration constant, et the exposure time in seconds, fs the aperture number, S the ISO sensitivity, and ℒs the luminance of the scene.
We can thus compute the relative luminance ℒr as follows:
3.3 Modeling irradiance from luminance values
Using our hemispheric sampling and relative luminance computation, we have one relative luminance value ℒr per image. We use this relative luminance value to estimate the solar radiation. The usual sunrise time in Singapore is between 06:40 and 07:05, and sunset time is approximately between 18:50 and 19:10 local time. This information is obtained from the National Weather Agency of Singapore, the National Environment Agency (2019). Therefore, we consider images captured in the time interval of 07:00 until 19:00.
We use our ground-based whole-sky images captured during the period January 2016 to August 2016 to model the solar radiation. The solar irradiance is computed as the flux of radiant energy per unit area normal to the direction of flow. The first step in estimating irradiance from the luminance is thus to cosine-weight it according to its direction of flow. We weight our measurements according to the solar zenith angle α. This is based on empirical evidence from our experiments on solar irradiance estimation. The modeled luminance ℒ is expressed as
Let us assume that the actual solar radiation recorded by the weather station is 𝒮. We check the nearest weather station measurement for all the images captured by WAHRSIS between April 2016 and December 2016. Figure 7 shows the scatter plot between the image luminance and solar radiation. The majority of the data follow a linear relationship between the two. However, they deviate from linearity for higher values of luminance. This is mainly because of the fact that the mapping between scene luminance and the obtained pixel value in the camera sensor becomes nonlinear for large luminances. A more detailed discussion on this is provided in Sect. 5.
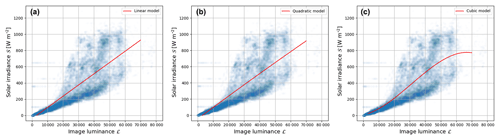
Figure 7Empirical fit between solar irradiance and image luminance computed with our proposed framework using (a) a linear model, (b) a quadratic model, and (c) a cubic model. We observe that it deviates from linearity at higher luminance values. Higher-order polynomials are ill-conditioned.
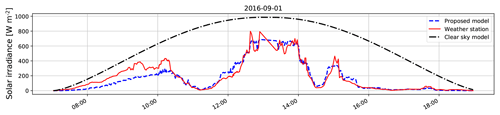
Figure 8Measured weather station data (in red) vs. clear-sky radiation (in black) on 1 September 2016. The sampling interval between two measurements is 2 min.
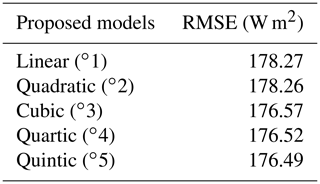
We attempt to fit a linear model and other higher-order polynomial regressors to model the relationship between image luminance from sky camera images and the measured solar radiation. Figure 7 shows the best-fit curve for several orders of polynomial function. In order to provide an objective evaluation of the different models, we also compute the root mean square error (RMSE) value between the actual and regressed values. Table 1 summarizes the performance of the different order polynomials. We observe that lower-order polynomials of degree 1 and 2 perform slightly inferior to those of higher-order polynomials. However, higher-order polynomial models are ill-conditioned. Therefore, we choose the cubic model to model the measured solar radiation 𝒮 from the image luminance ℒ. This is based on the assumption that the mapping from scene luminance to pixel values in the captured image is linear for lower luminance values, and it behaves in a nonlinear fashion for higher luminance values. We use this selected model in all our subsequent discussions and evaluations.
Table 1Performance evaluation of various polynomial order regressors. We measure the RMSE value for each of the models.
We model solar radiation as , with , , a1=0.00397, and a0=7.954 for our data. This model is derived specifically for equatorial regions like Singapore, and the regression constants are based on our WAHRSIS sky imaging system. They would have to be fine-tuned for other regions and different imaging systems using our methodology. To facilitate this, we make the source code of all the simulations in this paper available online at https://github.com/Soumyabrata/estimate-solar-irradiance (last access: 23 September 2019).
In this section, we evaluate the accuracy of our proposed approach. It is derived based on WAHRSIS images captured from January to August 2016. We also use these images to evaluate the accuracy of our proposed model. Furthermore, we benchmark our algorithm with other existing solar radiation estimation models.
4.1 Evaluation
One of the main advantages of our approach is that all rapid fluctuations of solar radiation can be accurately tracked from the image luminance. We illustrate this by providing the measured solar readings of 1 September 2016 in Fig. 8. The clear-sky model follows a cosine response and is shown in black, while the measured solar recordings are shown in red. We normalize our computed luminance in such a manner that it matches the measured solar readings. We multiply each data point with a conversion factor such that the distance between corresponding inter-samples of luminance and weather station recordings is minimized (see Appendix A for details). We use this normalization factor in order to map the computed image luminance to a similar scale as the cosine clear-sky model. We observe that our computed luminances from the whole-sky image and the measured solar radiation closely follow each other. We emphasize here that it is important to accurately track the rapid solar fluctuations. Unlike other solar estimation models based on meteorological sensor data, our proposed model can successfully estimate the peaks and troughs of solar readings.
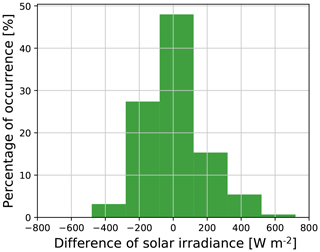
Using our proposed methodology, we compute the luminance of all the captured images. Subsequently, using our proposed cubic model, we estimate the corresponding solar radiation values. The estimated solar irradiance values are compared with the actual irradiance values obtained from the solar sensors in the colocated weather station, which serve as the ground-truth measurements. Figure 9 shows the histogram of differences between the estimated and actual solar radiation. We observe that the estimates do not deviate much from the actual solar radiation. Nearly half (47.9 %) of the data points are concentrated in the range [−100,+100] W m−2.
4.2 Benchmarking
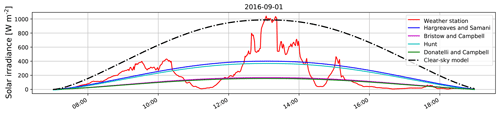
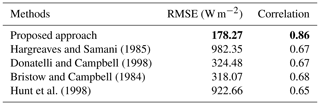
We benchmark our proposed approach with other existing solar estimation models. To the best of our knowledge, there are no proposed models to estimate short-term fluctuations of solar irradiance from ground-based images. However, most researchers have been using other meteorological sensor data, e.g., temperature, humidity, rainfall, and dew-point temperature, to estimate daily solar irradiance. One of the pioneer works was done by Hargreaves and Samani (1985), who proposed a model based on daily temperature variations. Donatelli and Campbell (1998) improved the model by including clear-sky transitivity as one of the factors. On the other hand, Bristow and Campbell (1984) proposed a model of solar radiation estimation by including the atmospheric transmission coefficient. Subsequently, Hunt et al. (1998) showed that the solar estimation model can be further improved by incorporating precipitation data in the model. We benchmark our proposed approach with these different existing models. We illustrate the various benchmarking models in Fig. 10. Unfortunately, most of these other approaches fail to capture the short-term variations of solar radiation.
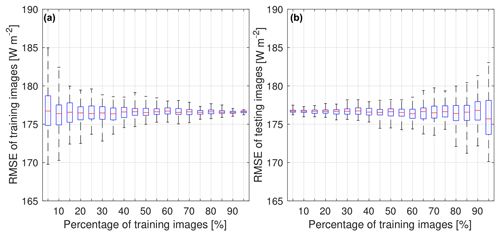
Figure 11Effect of the percentage of training images on RMSE values. We plot the (a) performance on the training set and the (b) performance on the test set. The lower and upper end of each box represents the 25th and 75th percentiles of the data, and the red line represents the median. Each experiment is conducted 100 times with a random choice of training and test sets.
We calculate the root mean square error (RMSE) of the estimated solar radiation and Spearman's rank correlation coefficient as evaluation metrics. The RMSE of an estimation algorithm represents the standard deviation of the actual and estimated solar radiation values. Spearman correlation is a nonparametric measure to characterize the relationship between measured and estimated solar radiation, which does not assume that the underlying datasets are derived from a normal distribution. We report both metrics in Table 2. Our proposed approach achieves the best results amongst all methods. Note that the training and testing set of images are identical, and all images are considered for benchmarking purposes.
Hargreaves and Samani (1985)Donatelli and Campbell (1998)Bristow and Campbell (1984)Hunt et al. (1998)Table 2Benchmarking of our proposed approach with other solar radiation estimation models. The best performance is indicated in bold font.
Furthermore, we check if our proposed model generalizes well with random samples of our captured sky camera images. We choose a random selection of images as the training set and fit our linear regressor on these selected training images. The RMSE values are then calculated on these training images. We perform this analysis for varying percentages of training images. Each experiment is performed 100 times to remove any selection bias.
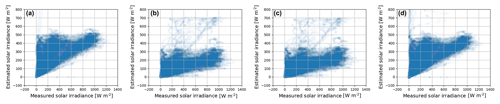
Figure 12Scatter plot between measured solar irradiance and estimated solar irradiance for the benchmarking algorithms. (a) Hargreaves and Samani (1985). (b) Donatelli and Campbell (1998). (c) Bristow and Campbell (1984). (d) Hunt et al. (1998).
Figure 11a shows the results on training images. We observe that the variation of the RMSE values gradually decreases as we increase the number of training images. Moreover, we check the variation of RMSE values when the test images are not identical to the training images. Once we choose a random selection of images as a training set, the remaining images are considered the test set. We show the RMSE on such images in Fig. 11b. As expected, the variation of RMSE values increases with a higher percentage of training images. The linear regressor model overfits the data and provides higher variation in the error when tested on fewer test images. However, the average RMSE does not vary much in all cases. Therefore, we conclude that our proposed model is free from selection bias and generalizes well with a random selection of training and testing images.
We show the scatter plot between the measured solar radiation and estimated solar radiation for the different benchmarking algorithms in Fig. 12. We observe that there is no strong correlation for most of these existing algorithms. This is because meteorological sensor data alone, with no cloud information, cannot determine the sharp fluctuations of solar radiation. This is an important limitation of these models, which we have attempted to address in this paper. Our model based on sky images has additional information about cloud movement and its evolution, which is the fundamental factor behind rapid solar radiation fluctuations. In our proposed model, most of these short-term variations are captured (see Fig. 8).
5.1 Short-term forecasts
Our proposed approach can estimate solar radiation accurately with the smallest RMSE compared to other models. The main advantage of our approach is that it can be used on predicted images as well, opening the potential for short-term solar irradiance forecasting, which is needed in the solar energy field. As an initial case study, we have exploited optical flow techniques to estimate the direction and flow of cloud motion vectors between two successive image frames. We use the ratio channel of the sky and/or cloud image, where B and R are the blue and red channels, respectively. We implement an optical flow technique (Optical Flow MATLAB, 2019) that uses a simpler conjugate gradient solver to obtain the flow field. Figure 13 illustrates the estimated flow field.
Using the images captured at t and t−2 min, we estimate the horizontal and vertical translation. Under the assumption that the flow of cloud motion vectors for the successive t+2 min is similar to that of previous frames, we estimate the future t+2 min frame and subsequently the t+4 min frame. Figure 14 illustrates this. We obtain a forecast accuracy of 70 % for a prediction lead time up to 6 min.
In future work, we plan to use our proposed methodology for estimating solar irradiance on this predicted sky–cloud image. This will enable us to provide more stable and reliable forecasts of solar irradiance.
5.2 Scope for improvement
There is still scope for improvement in our approach. First, we use JPEG images instead of uncompressed RAW images for the computation of scene luminance. The JPEG compression algorithm introduces nonlinearities in the pixel values, which affects the process of estimating solar irradiance. We can generate more consistent results by using only RAW format images. Nevertheless, we still use JPEG images, as they have a significantly smaller size, which is more practical from an operational point of view. In contrast, uncompressed RAW images are much larger in size, which makes it impossible to capture and store RAW images at short intervals due to the processing requirements. In our future work, we intend to explore the use of RAW format images for the computation of solar irradiance values from sky cameras.
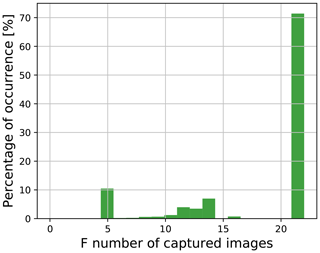
Secondly, our captured images have a wide range of camera settings with varying shutter speed, ISO, and aperture values. This is disadvantageous because the relationship between the pixel value and camera aperture value becomes nonlinear for larger F numbers. The relationship deviates from linearity for F numbers above 4.0 (Hiscocks and Eng, 2011). Figure 15 depicts the wide range of F numbers in the captured images used in deriving our proposed model. We observe that a significant percentage of images have large F numbers, whereby the nonlinearity sets in. This can be solved by using the aperture priority mode of the sky camera, whereby the F number is fixed and the exposure time varies dynamically to match the lighting conditions of the scene.
We presented a method for estimating the rapid fluctuations of solar irradiance using the luminance of images taken by a whole-sky imager. We are able to estimate the rapid short-term variations, which significantly improves on the state of the art. This approach is of interest for solar energy generation because these variations cause a sudden decrease in the electricity output from solar panels. Short-term predictions of such ramp-downs are needed to maintain the stability of a power grid.
Combining our solar irradiance estimation approach with cloud movement tracking in the input images could ultimately lead to better irradiance predictions. Such information on rapid fluctuations of solar irradiance can assist in establishing a high-reliability solar energy generation system. We also plan to explore methodologies from time series modeling (Dev et al., 2018a) to predict solar irradiance.
The source code of all simulations in this paper is available at https://github.com/Soumyabrata/estimate-solar-irradiance (Dev et al., 2019).
Let be the weather station records for t number of time stamps. The luminance values computed for each of the corresponding weather station points are represented by . We attempt to estimate the conversion factor x such that the objective function f(x) representing the inter-sample distances between the weather station and the computed luminance value is minimized. We represent the objective function f(x) as
We compute the derivative f′(x) and equate it to 0 to find the normalization factor x as
YHL and SW conceived of the presented idea. SD and FMS developed the theory and performed the computations and experiments. All authors discussed the results and contributed to the final paper.
The authors declare that they have no conflict of interest.
The authors thank the Defence Science and Technology Agency (DSTA), Singapore, for their support in the research. The ADAPT Centre for Digital Content Technology is funded under the SFI Research Centres Programme (grant 13/RC/2106) and co-funded under the European Regional Development Fund.
This paper was edited by Saulius Nevas and reviewed by two anonymous referees.
Alonso-Montesinos, J. and Batlles, F. J.: The use of a sky camera for solar radiation estimation based on digital image processing, Energy, 90, 377–386, 2015. a
Alsadi, S. Y. and Nassar, Y. F.: Estimation of Solar Irradiance on Solar Fields: An Analytical Approach and Experimental Results, IEEE T. Sustain. Energy, 8, 1601–1608, https://doi.org/10.1109/TSTE.2017.2697913, 2017. a
Baharin, K. A., Abdul Rahman, H., Hassan, M. Y., and Gan, C. K.: Short-term forecasting of solar photovoltaic output power for tropical climate using ground-based measurement data, J. Renew. Sustain. Ener., 8, 053701, https://doi.org/10.1063/1.4962412, 2016. a
Bristow, K. L. and Campbell, G. S.: On the relationship between incoming solar radiation and daily maximum and minimum temperature, Agr. Forest Meteorol., 31, 159–166, 1984. a, b, c, d
Chu, Y., Urquhart, B., Gohari, S. M., Pedro, H. T., Kleissl, J., and Coimbra, C. F.: Short-term reforecasting of power output from a 48 MWe solar PV plant, Sol. Energy, 112, 68–77, 2015. a
Dev, S., Savoy, F. M., Lee, Y. H., and Winkler, S.: WAHRSIS: A low-cost, high-resolution whole sky imager with near-infrared capabilities, in: Proc. IS&T/SPIE Infrared Imaging Systems, 9071, 90711L, https://doi.org/10.1117/12.2052982, 2014. a, b
Dev, S., Savoy, F. M., Lee, Y. H., and Winkler, S.: Design of low-cost, compact and weather-proof whole sky imagers for High-Dynamic-Range captures, in: Proc. International Geoscience and Remote Sensing Symposium (IGARSS), 26–31 July, Milan, 5359–5362, 2015. a
Dev, S., Savoy, F. M., Lee, Y. H., and Winkler, S.: Estimation of solar irradiance using ground-based whole sky imagers, in: Proc. International Geoscience and Remote Sensing Symposium (IGARSS), 10–15 July, Beijing, 7236–7239, 2016. a, b, c
Dev, S., Savoy, F. M., Lee, Y. H., and Winkler, S.: Short-term prediction of localized cloud motion using ground-based sky imagers, in: Proc. IEEE TENCON, Singapore, https://doi.org/10.1109/TENCON.2016.7848499, 2016c. a
Dev, S., Wen, B., Lee, Y. H., and Winkler, S.: Ground-Based Image Analysis: A Tutorial on Machine-Learning Techniques and Applications, IEEE Geosci. Remote Sens. Mag., 4, 79–93, 2016d. a
Dev, S., Manandhar, S., Lee, Y. H., and Winkler, S.: Study of clear sky models for Singapore, in: Progress in Electromagnetics Research Symposium-Fall (PIERS-FALL), 2017, IEEE, 19–22 November, Singapore, 1418–1420, 2017a. a
Dev, S., Lee, Y. H., and Winkler, S.: Color-Based Segmentation of Sky/Cloud Images From Ground-Based Cameras, IEEE J. Sel. Top. Appl., 10, 231–242, 2017b. a
Dev, S., AlSkaif, T., Hossari, M., Godina, R., Louwen, A., and van Sark, W.: Solar Irradiance Forecasting Using Triple Exponential Smoothing, in: 2018 International Conference on Smart Energy Systems and Technologies (SEST), IEEE, 10–12 September, Sevilla, 1–6, 2018a. a, b
Dev, S., Savoy, F. M., Lee, Y. H., and Winkler, S.: High-dynamic-range imaging for cloud segmentation, Atmos. Meas. Tech., 11, 2041–2049, https://doi.org/10.5194/amt-11-2041-2018, 2018b. a
Dev, S., Savoy, F. M., Lee, Y. H., and Winkler, S.: Estimating Solar Irradiance Using Sky Imagers, available at: https://github.com/Soumyabrata/estimate-solar-irradiance, last access: 23 September 2019.
Donatelli, M. and Campbell, G. S.: A simple model to estimate global solar radiation, in: Proc. 5th European Society of Agronomy Congress, 28 June–2 July, Nitra, 133–134, 1998. a, b, c, d
Feng, C., Cui, M., Hodge, B., Lu, S., Hamann, H., and Zhang, J.: Unsupervised Clustering-Based Short-Term Solar Forecasting, IEEE T. Sustain. En., 10, 2174–2185, https://doi.org/10.1109/TSTE.2018.2881531, 2018. a
Hargreaves, G. H. and Samani, Z. A.: Reference crop evapotranspiration from temperature, Appl. Eng. Agric., 1, 96–99, 1985. a, b, c, d
Hiscocks, P. D. and Eng, P.: Measuring Luminance with a digital camera, Syscomp Electronic Design Limited, 2011. a, b
Hunt, L. A., Kuchar, L., and Swanton, C. J.: Estimation of solar radiation for use in crop modelling, Agr. Forest Meteorol., 91, 293–300, 1998. a, b, c, d
Huo, J. and Lu, D.: Comparison of cloud cover from all-sky imager and meteorological observer, J. Atmos. Ocean. Tech., 29, 1093–1101, 2012. a
Jang, H. S., Bae, K. Y., Park, H., and Sung, D. K.: Solar Power Prediction Based on Satellite Images and Support Vector Machine, IEEE T. Sustain. En., 7, 1255–1263, https://doi.org/10.1109/TSTE.2016.2535466, 2016. a
Jiang, Y., Long, H., Zhang, Z., and Song, Z.: Day-Ahead Prediction of Bihourly Solar Radiance With a Markov Switch Approach, IEEE T. Sustain. En., 8, 1536–1547, https://doi.org/10.1109/TSTE.2017.2694551, 2017. a
Lautenbacher, C. C.: The global earth observation system of systems: Science serving society, Space Policy, 22, 8–11, 2006. a
Lefèvre, M., Blanc, P., Espinar, B., Gschwind, B., Ménard, L., Ranchin, T., Wald, L., Saboret, L., Thomas, C., and Wey, E.: The HelioClim-1 Database of Daily Solar Radiation at Earth Surface: An Example of the Benefits of GEOSS Data-CORE, IEEE J. Sel. Top. Appl., 7, 1745–1753, 2014. a
Lorenz, E., Hurka, J., Heinemann, D., and Beyer, H. G.: Irradiance Forecasting for the Power Prediction of Grid-Connected Photovoltaic Systems, IEEE J. Sel. Top. Appl., 2, 2–10, 2009. a
Mueller, R., Dagestad, K.-F., Ineichen, P., Schroedter-Homscheidt, M., Cros, S., Dumortier, D., Kuhlemann, R., Olseth, J., Piernavieja, G., Reise, C., Wald, L., and Heinemann, D.: Rethinking satellite-based solar irradiance modelling: The SOLIS clear-sky module, Remote Sens. Environ., 91, 160–174, 2004. a
National Environment Agency: Weather, available at: http://www.nea.gov.sg/weather-climate/forecasts, last access: 9 August 2019. a
Optical Flow MATLAB/C++ Code, https://people.csail.mit.edu/celiu/OpticalFlow/, last access: 9 August 2019. a
Ouarda, T. B. M. J., Charron, C., Marpu, P. R., and Chebana, F.: The Generalized Additive Model for the Assessment of the Direct, Diffuse, and Global Solar Irradiances Using SEVIRI Images, With Application to the UAE, IEEE J. Sel. Top. Appl., 9, 1553–1566, 2016. a
Pagano, T. S. and Durham, R. M.: Moderate resolution imaging spectroradiometer (MODIS), in: Proc. Sensor Systems for the Early Earth Observing System Platforms, International Society for Optics and Photonics, 1939, 2–17, 1993. a
Poynton, C.: Digital Video and HDTV Algorithms and Interfaces, Morgan Kaufmann Publishers Inc., San Francisco, 2003. a
Rizwan, M., Jamil, M., and Kothari, D. P.: Generalized Neural Network Approach for Global Solar Energy Estimation in India, IEEE T. Sustain. En., 3, 576–584, https://doi.org/10.1109/TSTE.2012.2193907, 2012. a
Savoy, F. M., Dev, S., Lee, Y. H., and Winkler, S.: Geo-referencing and stereo calibration of ground-based whole sky imagers using the sun trajectory, in: Proc. International Geoscience and Remote Sensing Symposium (IGARSS), 10–15 July, Beijing, 2016. a
Scaramuzza, D., Martinelli, A., and Siegwart, R.: A toolbox for easily calibrating omnidirectional cameras, in: Proc. IEEE/RSJ International Conference on Intelligent Robots and Systems, 9–15 October, Beijing, 5695–5701, 2006. a
Shakya, A., Michael, S., Saunders, C., Armstrong, D., Pandey, P., Chalise, S., and Tonkoski, R.: Solar Irradiance Forecasting in Remote Microgrids Using Markov Switching Model, IEEE T. Sustain. En., 8, 895–905, https://doi.org/10.1109/TSTE.2016.2629974, 2017. a
Silva, A. A. and Souza-Echer, M. P.: Ground-based observations of clouds through both an automatic imager and human observation, Meteorol. Appl., 23, 150–157, 2016. a
SMPTE Recommendation: RP 177-1993, Derivation of Basic Television Color Equations, https://doi.org/10.5594/SMPTE.RP177.1993, 1993. a
Yang, D. and Chen, N.: Expanding Existing Solar Irradiance Monitoring Network Using Entropy, IEEE T. Sustain. En., 6, 1208–1215, https://doi.org/10.1109/TSTE.2015.2421734, 2015. a
Yang, D., Jirutitijaroen, P., and Walsh, W. M.: The estimation of clear sky global horizontal irradiance at the equator, Energy Procedia, 25, 141–148, 2012. a, b
Yuan, F., Lee, Y. H., Meng, Y. S., and Ong, J. T.: Water Vapor Pressure Model for Cloud Vertical Structure Detection in Tropical Region, IEEE T. Geosci. Remote, 54, 5875–5883, 2016. a