the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A Gaussian mixture method for specific differential phase retrieval at X-band frequency
Guang Wen
Patrick S. Market
The specific differential phase Kdp is one of the most important polarimetric radar variables, but the variance σ2(Kdp), regarding the errors in the calculation of the range derivative of the differential phase shift Φdp, is not well characterized due to the lack of a data generation model. This paper presents a probabilistic method based on the Gaussian mixture model for Kdp estimation at X-band frequency. The Gaussian mixture method can not only estimate the expected values of Kdp by differentiating the expected values of Φdp, but also obtain σ2(Kdp) from the product of the square of the first derivative of Kdp and the variance of Φdp. Additionally, the ambiguous phase and backscattering differential phase shift are corrected via the mixture model. The method is qualitatively evaluated with a convective event of a bow echo observed by the X-band dual-polarization radar in the University of Missouri. It is concluded that Kdp estimates are highly consistent with the gradients of Φdp in the leading edge of the bow echo, and large σ2(Kdp) occurs with high variation of Kdp. Furthermore, the performance is quantitatively assessed by 2-year radar–gauge data, and the results are compared to linear regression model. It is clear that Kdp-based rain amounts have good agreement with the rain gauge data, while the Gaussian mixture method gives improvements over the linear regression model, particularly for far ranges.
Apart from radar reflectivity (ZH) and differential reflectivity (ZDR), polarimetric radars also obtain the differential phase shift (Φdp) to reflect the forward-scattering property of hydrometeor scatterers (Seliga and Bringi, 1978; Sachidananda and Zrnić, 1986). Its range derivative, also called the specific differential phase (Kdp), has some advantages over ZH and ZDR (Zrnić and Ryzhkov, 1996), including insensitivity to attenuation, clutter, partial beam blockage, and radar absolute calibration. The specific differential phase has played a key role in various meteorological applications – such as hydrometeor classification (Lim et al., 2005; Park et al., 2009), raindrop size distribution retrieval (Bringi et al., 2002; Williams et al., 2014), and quantitative precipitation estimation (Ryzhkov et al., 2005; Cifelli et al., 2011) – since Kdp is a phase variable independent of ZH and ZDR and almost linearly proportional to rain rate.
A linear regression model has been developed to derive Kdp from the slope of the range profile of Φdp measured by the polarimetric radars. In Hubbert et al. (1993), Φdp is first processed by a light filter that attenuates the Φdp magnitudes within a scale of 375 m by 10 dB, and it is then heavily smoothed in 1.5 km by 10 dB. An iterative filtering technique is used for eliminating nonzero backscattering differential phase shift (Hubbert and Bringi, 1995). The filtered Φdp measurements are finally fitted into a first-order polynomial to estimate the Φdp slope in a given window. Liu et al. (1993) supply the accuracy of mean Kdp as ±0.25∘ km−1 using 128 pulses, while Aydin et al. (1995) indicate that the accuracy is within ±0.5 ∘ km−1 for a heavy rainfall event using 64 pulses. On the other hand, Ryzhkov and Zrnić (1996) produce two kinds of Kdp for S-band radars: one is obtained over 16 range gates (2.4 km) for ZH≤40 dBZ, and the other is produced over 48 gates (7.2 km) for ZH>40 dBZ. Negative Kdp is incorporated into the rain rate algorithm to avoid bias in the low rain rate. The analyses of 15 storms show that the standard error of Kdp is 0.04–0.10 ∘ km−1 for heavily filtered Kdp and 0.12–0.30 ∘ km−1 for lightly filtered Kdp using either 128 or 64 pulses. Vulpiani et al. (2012) develop a multistep moving-window approach based on the linear regression model to handle the Φdp folding and other ambiguous data. This approach is applicable to the complex terrain but still valid for various topographical environments.
X-band dual-polarization radars have drawn increasing attention in the radar meteorology community in recent years on account of their low cost, fine resolution, and high sensitivity to light precipitation (Chandrasekar et al., 2012; Lim et al., 2013; Berne and Krajewski, 2013; Kalogiros et al., 2014; Oue et al., 2016). In the literature, X-band algorithms have been proposed for Kdp estimation. For example, the linear regression method is adapted for the X-band radar data and used to retrieve rainfall (Matrosov et al., 2006). The ambiguous Φdp is naturally corrected by examining the complex values of the range profiles of Φdp exponentials, and Kdp is then estimated by a regularization framework based on a cubic spline smoothing (Wang and Chandrasekar, 2009). In this method, the bias and variance are adjustable through the smoothing parameter, giving high spatial resolutions of Kdp estimates. Moreover, algorithms of linear programming (Giangrande et al., 2013) and Kalman filter (Schneebeli et al., 2014) have also been applied to the Kdp estimation, yielding good performance for rainfalls and snowfalls. It is noticeable that the Kalman filter method minimizes the Gaussian error function to obtain the mean profile of Kdp. It gives a significant improvement on the Kdp mean, particularly in the small-scale structure with high peaks. In addition, the Φdp measurements at X-band frequency are affected by the backscattering differential phase shift δco. The constraints of and δco−ZDR can be used to improve the estimation of Kdp and δco (Otto and Russchenberg, 2011; Reinoso-Rondinel et al., 2018), although these constraints are only valid in the rain regime.
The recent algorithms are focused on the improvement of estimating the mean Kdp, whereas its variance (σ2(Kdp)) is not well characterized due to the lack of a data generation model. The Kdp variance is often inherited from the Φdp variance (σ2(Φdp)), leading to large relative errors for low Kdp with a fixed path length. As noted by Gorgucci et al. (1999), the Kdp estimated by the linear regression has large errors in the nonuniform rain media, while the errors increase when the radar reflectivity presents large gradients in dimensions. In this study, we propose a probabilistic method based on the Gaussian mixture model for Kdp estimation at X-band frequency. The Gaussian mixture method can not only estimate the expected values of Kdp by differentiating the conditional expectation of Φdp, but also yield σ2(Kdp) by regarding the errors in the calculation of the first derivative of Φdp. It is found that σ2(Kdp) is closely related to the square of the first derivative of Kdp and σ2(Φdp), while a large σ2(Kdp) is associated with high variation of Kdp estimates. When compared to the existing methods, our method considers the joint probability density function of the data as the nonlinear Gaussian mixture, leading to better performance for the multimodal data. Since the Kdp variance is nonconstant, it leads to the variability in the Kdp error characteristics. We can then use the Kdp variance to calculate the variances of ZH and ZDR via the attenuation correction, as well as the variance of rain rate via the R–Kdp relation. These variances are useful for studying the propagation of uncertainty in the weather model and the streamflow trends in the hydrological model.
The paper is organized as follows. Section 2 provides background information about Kdp and the Gaussian mixture model. Section 3 describes the radar and gauge data. Section 4 presents the methodology. We first remove the residual clutter using data masks (Sect. 4.1) and then derive the joint probability density function to estimate the expected value of Φdp and σ2(Φdp) (Sect. 4.2). Next, we correct the ambiguous phase and δco via the mixture model (Sect. 4.3). Last, we calculate the expected value and variance of Kdp (Sect. 4.4) and improve the Kdp profile by reducing σ2(Kdp) (Sect. 4.5). To evaluate the algorithm, Sect. 5 gives a case study and a comparison between the radar and gauge. Section 6 summarizes the paper.
The specific differential phase is the first derivative of the differential phase shift Φdp along the radar range, giving a way to estimate Kdp by radar measurement of Φdp. Furthermore, the probability density function of Φdp can be modeled as a Gaussian mixture, which is often obtained via an expectation–maximization (EM) approach. The mean and variance of the Gaussian mixture may lead to the improvement of the Kdp estimation.
In this section, we introduce the physical interpretation of Kdp and the regression model for estimating Kdp. Since the Gaussian mixture is adopted as the data generation model, we also give a brief description of the mathematical definition of the Gaussian mixture model and the EM approach.
2.1 Specific differential phase (Kdp)
For linear polarization, Kdp is proportional to the integral of the raindrop size distribution and the real part of the difference of forward-scattering amplitudes at orthogonal polarizations. It is mathematically formulated as
where λ is radar wavelength in millimeters, D is raindrop size in millimeters, N(D) is size spectrum in cubic meters per millimeter (m3 mm−1), and is forward-scattering amplitudes at horizontal and vertical polarizations, respectively.
By considering the Rayleigh–Gans scattering from identical and horizontally oriented oblate spheroids, such as raindrops, the forward-scattering amplitudes are proportional to the inverse square of radar wavelength, i.e., , leading to the fact that Kdp is inversely proportional to radar wavelength, i.e., . Therefore, the values of Kdp at the X band are often larger than that at the S band by a factor of 3, indicating that X-band radar can provide better Kdp data than S-band radar when retrieving the rainfall rate. The conclusion is still valid even if the Mie effect is taken into account (Bringi and Chandrasekar, 2001; Chandrasekar et al., 2006).
However, Kdp cannot be detected by polarimetric radar directly, whereas its integral Φdp is measurable. Hence, Kdp can be estimated as the range derivative of the profile of Φdp, i.e., , where r is the radar range in kilometers. An alternative approach to estimating Kdp is to apply a regression fit to the profile of Φdp, and the first-order polynomial is usually considered as the fitting function (Balakrishnan and Zrnić, 1990; Ryzhkov and Zrnić, 1995). Subsequently, if the Φdp measurements are equally spaced in range by Δr, Kdp is then estimated by
where n is the number of gates. Equation (2) shows that the accuracy of Kdp estimates is determined by the number of gates (n) and the accuracy of Φdp. By assuming σ2(Φdp) is relatively stable for all gates along a ray and noting that Φdp(ri) is the only variable in Eq. (2), σ2(Kdp) is formulated as
In Eq. (3), σ2(Kdp) is proportional to σ2(Φdp), which is related to the spectrum width, cross-correlation coefficient, and the dwell time (Sachidananda and Zrnić, 1986; Hubbert et al., 1993), and inversely proportional to n3. This method has been widely used in the existing radar system (Cifelli et al., 2018; Chandrasekar et al., 2018; Chen et al., 2017b, c). The details of the regression-based estimation of Kdp are given in Bringi and Chandrasekar (2001) and Appendix A.
Moreover, it is notable that the backscattering phase shift is not negligible at the X band; thus the total propagation phase shift (Ψdp) consists of Φdp and the backscattering differential phase, δco; i.e., . The backscattering phase shift is often shown as a sudden jump over one or a few range gates in a monotonically increasing Ψdp profile of rain (May et al., 1999), with a value much larger than the standard deviation σ(Ψdp). The presence of δco over a small number of consecutive gates can be eliminated by a simple filter (Hubbert and Bringi, 1995).
The specific differential phase is a unique polarimetric variable in terms of statistical errors in the rain rate estimation, since it is the range derivative of the phase measurement Φdp. The errors in the calculation of the first derivative also need to be taken into account. In this study, we consider a Gaussian mixture as the data generation model, which plays an important role in the estimation of Kdp and σ2(Kdp).
2.2 Gaussian mixture model
The Gaussian mixture is a statistical model for data probability density estimation, assuming that the data points are generated by a mixture of a finite number of Gaussian distributions associated with their weights (McLachlan and Peel, 2000; Sung, 2004). Intuitively, it is used to model the multimodal data, with each Gaussian component corresponding to a subpopulation of the data. The mathematical formulation is given as
where m is the number of components in the Gaussian mixture, wi is a weight with , and is the ith Gaussian distribution with mean μi and covariance Σi; i.e., , where k is the data dimension.
It is prevalent to use an Expectation–Maximization (EM) algorithm to estimate the parameters, w, μ, and Σ, by constructing the lower bound of the log-likelihood based on Jensen's inequality (Dempster et al., 1977). The EM algorithm is divided into two steps, namely, an expectation (E) step and a maximization (M) step. In the E step, a degree of membership toward to the jth cluster is calculated; i.e.,
where i is the ith data with a total number of n data points, and y is a latent variable that determines the corresponding cluster. Here, Q gives a tight lower bound for the log-likelihood, equivalent to maximizing the expectation. In the M step, the exact form of the lower bound based on Jensen's inequality is expressed as
By maximizing the lower bound with respect to each parameter, wj, μj, and Σj are updated as (Petersen and Pedersen, 2012)
Notably, the M step increases the log-likelihood monotonically, if the covariance Σj is a positive-definite matrix. Finally, the E step and M step are iteratively operated until the log-likelihood converges to a value with the difference between two successive steps below a certain threshold. In addition, the EM algorithm requires a specification of the number of clusters, m, prior to the E and M steps, and an inappropriate choice of m may lead to meaningless values of the parameters. To tackle this problem, the Bayesian information criterion is often calculated to select the optimal m, while a Dirichlet process may also be used to model a prior probability to construct an infinite Gaussian mixture.
One of interpretations of the Gaussian mixture is to view each distribution as a cluster with a Gaussian probability density, while the individual data point is attributed to a specific cluster or a weight toward the cluster, regarded as unsupervised learning (Hastie et al., 2009). The clustering procedures based on the Gaussian mixture model have been applied to the identification of storm structure (Veneziano and Villani, 1996), as well as the particle identification at S-band (Wen et al., 2015, 2016b, 2017) and X-band (Wen et al., 2016a) frequencies. Furthermore, the Gaussian mixture model can be extended to fit a set of unknown parameters in the prior probability of the Bayesian framework, forming a Bayesian–Gaussian mixture model (Li et al., 2012). The prior is then multiplied with the known conditional probability of data given the parameters to be estimated, yielding the posterior probability with a new set of parameters. The expectation of the posterior is often used to retrieve the conditional mean of the new parameters based on least squares criteria.
For the regression problem, the characteristics of the Gaussian mixture imply that the direct modeling of a regression function is very difficult. Nevertheless, the joint probability of the measurements and the estimated parameters may be modeled as a Gaussian mixture, leading to a regression function derived from the joint density model. Due to the asymptotic consistency of a Gaussian mixture model, it is capable of estimating a general density function in ℝn in any shape (Sung, 2004). Moreover, the speed of calculating unknown parameters within a Gaussian mixture linearly depends on the number of the training data points, and the computation of the outputs is independent of the size of the training data. Consequently, regression based on a Gaussian mixture can be achieved very rapidly, compared to Gaussian process regression that grows with the data size. In addition, the Gaussian mixture can also be used to solve the regression problem with multiple dimensions, and a subset of dimensions can be selected to handle the missing data (Wen et al., 2015).
As part of the Missouri Experimental Project to Stimulate Competitive Research (EPSCoR), an X-band dual-polarization radar in the University of Missouri (MZZU) was deployed at the South Farm Research Center (38.906∘ N, 92.269∘ W) in the Midwest of America in the summer of 2015. The details of the radar characteristics are described in Simpson and Fox (2017). The primary objective is to provide the observations of precipitation near the surface by means of low-cost and fine-scale X-band radar and to fill the observational gaps of the S-band radar network in Saint Louis (KLSX), Kansas City (KEAX), and Springfield (KSGF). Within the MZZU radar coverage, the Hinkson Creek located near Columbia, MO, flows through a catchment basin and eventually merges into the Missouri River, forming a typical urban watershed (Hubbart and Zell, 2013). The radar can provide timely flash flooding warning for the Hinkson Creek watershed and surrounding areas.
In this study, we analyze the data collected by the X-band MZZU dual-polarization radar. The maximum unambiguous range of the MZZU radar is 94.64 km with a resolution of 260 m in range and 1∘ in azimuth. During the observational periods, the radar operates in a volumetric scanning mode of nine elevations at 0.8, 2, 3, 4, 5, 6, 7, 8.5, and 10∘, updated every 4 min. The raw radar data are organized and processed by an open-source software package called the Python ARM Radar Toolkit (Py-ART: Helmus and Collis, 2016). Moreover, to validate the Kdp estimation algorithm, we also use the data from tipping-bucket rain gauges in the Missouri Mesonet weather station network, including Bradford Farm (38.897∘ N, 92.218∘ W), Sanborn Field (38.942∘ N, 92.320∘ W), Auxvasse (39.089∘ N, 91.999∘ W), and Williamsburg (38.907∘ N, 91.734∘ W). The horizontal distances between the rain gauges and the radar center are 4.4, 6.0, 30.8, and 46.2 km, respectively. The first elevations at Bradford and Sanborn may be affected by ground clutter, since the radar beams are very close to the ground, with heights of 314.6 and 336.9 m a.s.l., respectively, including the radar tower. Therefore, the second elevation at 2∘ is selected for validation. In contrast, the first elevations at Auxvasse and Williamsburg reach about 723.8 and 999.0 m a.s.l., which are less contaminated by ground clutter. Furthermore, the point measurement of the rain gauge is different from the volumetric measurement of radar, imposing additional errors on the comparison between the radar and gauge (Anagnostou et al., 1999). The radar-based rain rate is then derived by averaging Kdp over three successive range gates and three successive azimuthal rays with a total of nine values centered over each gate in order to obtain good consistency between the instruments. In addition, the rain gauges are carefully calibrated in terms of instrumentation failure, clogging, and other discrepancies between the devices (Simpson and Fox, 2017) and are well documented to provide long-term data for rainfall observations.
Table 1Characteristics of hourly rain gauge data at Bradford, Sanborn, Auxvasse, and Williamsburg between April 2016 and June 2018. Mean: mean values, SD: standard deviation, Max: maximum values, Total: sums of rain amounts, and Duration: sum of rainfall time.
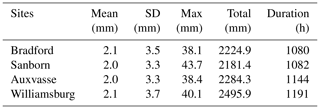
Table 1 summarizes the characteristics of rainfalls observed at Bradford, Sanborn, Auxvasse, and Williamsburg between April 2016 and June 2018. It is clear that the hourly rain amounts are dominated by light rain, with similar means of 2.0–2.1 mm at the four sites, indicating uniformly distributed rainfalls within the experimental region. On the other hand, the standard deviations of Bradford and Williamsburg are 3.5 and 3.7 mm, respectively, a little larger than that of 3.3 mm at Sanborn and Auxvasse. Moreover, Sanborn gives the highest hourly rain amount, the lowest total rain amount, and the second lowest duration out of the four sites, due to the effects of the urban heat island (Hubbart et al., 2014). The second highest maximum hourly rain amount is recorded at Williamsburg; however, the total rain amount and duration are also the highest among the four sites, implying that convective rain is the most frequent at Williamsburg. In contrast, stratiform rain is more common at Bradford, since the gauge records the lowest maximum hourly rain amount and duration, as well as the second total hourly rain amount. In addition, it can be seen that Auxvasse also provides useful data for the comparisons between gauges and between the radar and gauge, though the statistics are all ranked in the middle of the four sites. Overall, the rain gauge data at Bradford, Sanborn, Auxvasse, and Williamsburg are representative and sufficiently large, leading to a valid dataset for testing the Kdp and Kdp-based rain amounts.
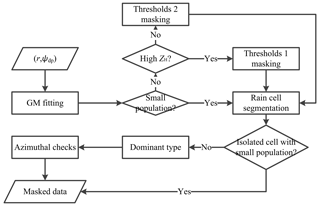
As discussed in Sect. 2, the joint probability density function (PDF) based on a Gaussian mixture can be used to derive the regression model for Kdp estimation. The Gaussian mixture method (GMM) not only estimates the expected values of Kdp by differentiating the conditional expectation of Φdp, but also gives an estimation of Kdp variance by regarding the errors in the calculation of the first derivative of Φdp. In this section, we describe GMM for the Kdp estimation using MZZU radar data. Figure 1 illustrates the flowchart of GMM (Fig. 1b), comparing to that of the linear regression model (LR; Fig. 1a).
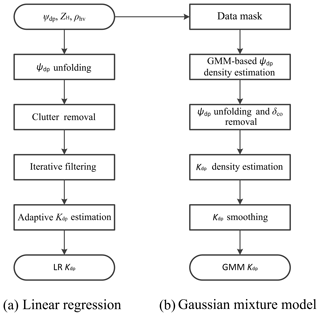
Figure 1Flowcharts of Kdp estimation algorithms used in the MZZU radar: (a) linear regression model and (b) Gaussian mixture method.
From the chart of LR in Fig. 1a, we can see that after the radar measurements are collected, the Ψdp is unfolded and then the clutter is removed. After these corrections, an iterative filtering method is applied to the Ψdp profile. An adaptive method is finally used to estimate the Kdp profile according to the values of ZH. The Gaussian mixture model, on the other hand, processes Ψdp differently. First of all, the clutter is masked out according to the thresholds of ZH and the variation of Ψdp. Secondly, the range r and Ψdp are fitted into a Gaussian mixture to yield the joint PDF, while the Ψdp mean and the Ψdp variance are obtained by taking the first raw and second central moments of the conditional PDF of Ψdp given r. Thirdly, some specific clusters in the Gaussian mixture PDF are adjusted to solve the problems of ambiguous Ψdp and backscattering differential phase shift δco in order to derive the PDF of Φdp. Fourthly, a raw Kdp profile is calculated from the first derivative of the expected values of Φdp, and the associated variances are obtained via a Taylor series expansion. Finally, the raw Kdp profile is smoothed, and, consequently, the variances are reduced. In addition, new Φdp with lower variances can be reconstructed from the Kdp estimates.
4.1 Data masking
The presence of clutter in the Ψdp measurements may severely affect the Kdp estimation, producing significantly large variations on the estimates. It is well known that the effect of clutter can be reduced by applying a spectrum filter to the time-series data (e.g., May and Strauch, 1998; Hubbert et al., 2009). However, some residual clutter echoes are still shown on the radar measurements including Ψdp (Wen et al., 2017). Therefore, the clutter needs to be well handled in GMM, prior to the deviation of the regression model based on the joint PDF.
In LR, the clutter is often eliminated by some criteria based on Ψdp or ρhv. For instance, we use the thresholds of the local standard deviation of Ψdp less than 10∘ to classify valid points. Further, 10 consecutive range gates of valid points signify the beginning of a rain cell, and 5 consecutive gates of invalid points finish the associated rain cell. Overall, the thresholds give a fairly good performance on the MZZU radar; however, the clutter may be incorrectly identified in the regions of high reflectivity or for the echoes mixed by weather and clutter, which are often associated with large Ψdp variation.
In contrast, GMM adopts sophisticated procedures, as depicted in Fig. 2. It is clear that there are five stages in the data masking, beginning with the input of raw Ψdp and ending with masked data. At the first stage, the raw data are fitted to a Gaussian mixture initialized by the k-means clustering, while the covariance is set to be diagonal for simplicity. The clusters with no more than five points are promptly masked out, before they pass to the second stage. Stages two, three, and four of the process all involve the clusters. At the second stage, the clusters are validated according to two sets of thresholds with respect to mean reflectivity. For the MZZU radar, the ratio of the standard deviations, σ(Ψdp)∕σ(r), less than 14.2∘ km−1 and σ(Ψdp) less than 4.1∘ (threshold 2) are used for ZH less than 41 dBZ. To reduce the misclassification in the hail regions, the thresholds are increased for higher ZH, resulting in ∘ km−1 and σ(Ψdp)<6.3∘ (threshold 1). Next, the entire Ψdp profile is divided into multiple rain cell segments by considering the gaps between two consecutive clusters. Similar to the first stage, the segments containing no more than five points are excluded from the output of masked data. Following this, the dominant one is determined for each segment by comparing the weight accumulations of weather and clutter clusters. For a clutter segment with mean height below 200 m, the clusters within the segment are reevaluated by thresholds of ∘ km−1 and σ(Ψdp)<0.8∘; on the other hand, the clusters in a weather segment are reexamined using ∘ km−1 and σ(Ψdp)<6.1∘. This step can efficiently identify the clutter-contaminated weather echoes, which are often associated with large variances. At the last stage, some isolated points along the azimuth are obscured in the final results.
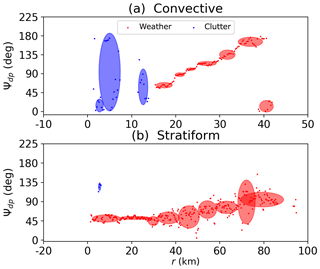
Figure 3Examples of data masking: (a) a convective case (azimuth 252∘) and (b) a stratiform case (azimuth 1∘). The blue points and ellipses represent the clutter data and clusters, respectively, while the red color corresponds to the weather echoes. The x axis is the radar range in kilometers.
Figure 3 illustrates two examples for data masking, including a convective case (Fig. 3a) and a stratiform case (Fig. 3b). The data points in the two cases show steadily increasing trends related to anisotropic media along the wave propagation path. However, between 1.3 and 15 km at an azimuth of 252∘ in the convective case (Fig. 3a), the data present significant fluctuations with the minimum value at about 0∘ but the maximum value at 180∘. Since the dynamic range of Ψdp is from 0 to 180∘ for the MZZU radar, the measurements near the ground are likely to be the clutter returns, verifying the results of data masking. After 15 km, the Ψdp points start from about 50∘ and go all the way up to 180∘. Notwithstanding this trend, the points sharply decrease to about 10∘ at about 40 km, indicating the occurrence of phase folding. The data masking can effectively detect the phase folding and provide valid masked data for deriving the joint PDF. On the other hand, the weather echoes are more frequently observed at 1∘ in azimuth in the stratiform case (Fig. 3b). By taking a closer look at the Ψdp data, we can discern that the points largely fluctuate between 40 and 80 km due to low signal-to-noise ratio. In LR, these points may be incorrectly discarded based on σ(Ψdp) thresholds, leading to some missing data in the stratiform regions. In contrast, the data masking accurately identifies weather echoes characterized by a number of vertically oriented density ellipses. The continuous and uniformly distributed regimes are consistent with the physical interpretation of stratiform precipitation. In addition, the data masking is also sensitive to sudden jumps at the beginning of the Ψdp data, which may be caused by δco.
4.2 Ψdp density estimation
In the previous section, it is shown that the Ψdp profile varies along the range r. It rises quickly for horizontally oriented anisotropic scatterers, and, conversely, it falls steadily for vertically oriented particles (Marzano et al., 2010). The nonuniform beam filling is also an important source of errors for the Ψdp measurements (Gosset, 2004; Ryzhkov, 2007).
To estimate the relationship between r and Ψdp, we consider r as an independent variable, denoted as x, and Ψdp as a dependent variable, denoted as y. If the minimization of the mean square error is required, the regression function is obtained by taking the average value of y at fixed x, equivalent to estimating the expected values of y conditioned on x; i.e.,
where β is a set of unknown variables – for example, for the mixture model. Since the Gaussian mixture can be used to model any shapes of probability density with a rapid speed, the (x, y) points are then assumed to follow a joint PDF of Gaussian mixture, as defined in Eq. (4). Moreover, the properties of the multivariate Gaussian distribution in each cluster determine the Gaussianity of the marginal distribution of either variable and the conditional distribution of one variable given the other (Bishop, 2006). Therefore, the conditional PDF of y given x is expressed as
where wi, and are obtained by the EM algorithm. In Eq. (14), f(x) is the marginal PDF of x with the parameters identical to the mixture, and fi(x) is the weighted marginal PDF of each cluster; i.e., . By substituting Eq. (11) into Eq. (10) and noting the linearity of the mathematical expectation, the expected value of y conditioned on x is then obtained as
and the conditional variance is given as (see Appendix B)
Equations (15) and (18) play an important role in the joint PDF-based regression analysis, called the regression and skedastic functions (Spanos, 1999). In Eq. (15), it can be seen that the regression function in GMM consists of multiple linear kernels, which is similar to LR. However, the weighting function is not determined by the local structure but the marginal PDF of global data x. The Gaussian mixture method is flexible to capture the data information, while it still retains a finite set of parameters. Moreover, Eq. (18) readily estimates the point-wise variances σ2(y|x) that characterize the random errors in the measurements. In contrast, Eq. (3) for the LR presents the relationship between the errors σ(Ψdp) and σ(Kdp) under the ideal conditions, which does not consider the random errors in Ψdp. It indicates that the GMM has a better error characterization based on the measurements when compared to the LR.
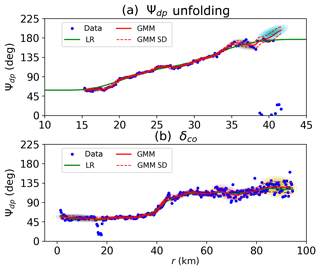
Figure 4Examples of Ψdp density estimation: (a) a Ψdp unfolding case and (b) a δco case. The blue points are the Ψdp data, the green curve represents the Ψdp profile obtained by the linear regression model (LR), and the red curve indicates the Ψdp profile produced by the Gaussian mixture method (GMM). The dashed lines are the standard deviations, while the colored ellipses show the components of the Gaussian mixture. The x axis is the radar range in kilometers.
Figure 4 compares the Ψdp profiles given by Eqs. (15) and (18) with that obtained by LR. Figure 4a gives the same example as Fig. 3a, but the EM algorithm is configured differently. In the Ψdp density estimation, the mixture with full covariance yields density ellipses of random shapes. Furthermore, the algorithm repeats the fitting procedures three times to avoid the local maxima of the log-likelihood. Meanwhile, the choice of the cluster number relies on the Bayesian information criterion calculated for each m, starting at 10 clusters. It can be seen that the mixture composed by density ellipses characterizes the data points well, since the root-mean-square error is small relative to the expected values. Between 15 and 35 km, the narrow ellipses result in Ψdp with a rising trend consistent with LR. On the other hand, the mixture has very small variances, giving a high confidence for the fitted parameters. From 35 km, the ellipses become wider, and the associated variances increase due to the low signal-to-noise ratio at the edge of radar echoes. What is notable, however, is that the Ψdp profile dramatically increases to a large value, whereas LR remains a relatively steady trend. It indicates the importance of the Ψdp unfolding for the Ψdp density estimation.
Figure 4b presents another example of the density estimation. It is clear that the Ψdp profiles produced by GMM and LR both rise considerably along the range, and the trends for the two methods are very similar with a strong correlation of 0.998. The profile starts at about 50∘ and remains relatively stable before rising dramatically between 35 and 55 km. By 65 km, Ψdp has more than doubled, and then there is a steady increase for Ψdp reaching about 130∘ at the end of the profile, which is around 70∘ up on the ranges of 0 and 35 km, and 10∘ more than recorded at the ranges of 55 and 65 km. If we examine Ψdp measured at X-band frequency, we can see that some points fall out of the dashed lines corresponding to 1 standard error (i.e., 95 % interval). Most notably, the Ψdp profile shows a sudden slump between 18 and 20 km, while the ZDR corresponds to a local peak (not shown). It may indicate the occurrence of δco. In conclusion, the expected value and the variance of Ψdp can be obtained from the joint PDF, but the mixture needs to be tuned in terms of Ψdp unfolding and δco elimination in order to obtain the PDF of Φdp.
4.3 Ψdp unfolding and δco elimination
According to the continuity and consistency of the phase data, we can discern that some issues exist in the density estimation, such as ambiguous Ψdp and δco. Since Ψdp is a range accumulative measurement of the propagation phase, depending on the initial Ψdp(0), the measurements may exceed the dynamic range of 0–180∘ when the wave propagates through a rain medium. This situation is even more significant at X-band frequency than at S-band due to the inverse relation of the wavelength and the rate of phase shift. Nevertheless, it can be noted that Ψdp gives a nonnegative trend along the range for rain, and therefore the ambiguous Ψdp may be corrected accordingly (Wang and Chandrasekar, 2009).
In LR, Ψdp is first averaged over a small window for weather data, and a linear fit is then performed to obtain the increment for the range gate next to the window. In the following stage, a reference is predicted by summing up the average and the increment and compared to the observed value at the same gate. If the difference between the predicted and observed values is larger than 90∘, the observed Ψdp is then increased by 180∘. Finally, the correction process is iteratively operated until the last gate.
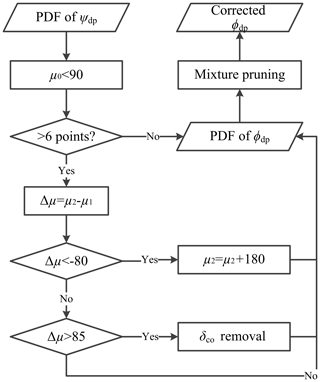
Figure 5Flowchart of the Ψdp unfolding and the δco elimination. The μ0 is the mean of the first density ellipse. The μ1 and μ2 are the means of the two consecutive density ellipses along the range. The μ1 is the mean of the former one, and the μ2 is the mean of the latter one.
On the other hand, the Ψdp unfolding is more straightforward in GMM. Figure 5 shows the flowchart of the Ψdp unfolding and the δco elimination. After obtaining the PDF of Ψdp, the initial step of the Ψdp unfolding selects the density ellipses with at least six data points. Next, the second step calculates the difference of the means μi between the two consecutive density ellipses along the range. At this point, the PDF of Ψdp is ready to be corrected for ambiguous Ψdp. In the final step, the mean of the latter density ellipse is added up 180∘, if the former mean is larger than the latter one by 80∘.
As illustrated in Fig. 4a, the profile Ψdp reaches 180∘ at about 38 km and then becomes ambiguous between 38 and 42 km. In LR, the Ψdp values at these locations are interpolated according to the trend of the previous few gates, and the maximum value is 180∘. In contrast, the corrected density ellipses in GMM show an upward trend between 38 and 42 km, while the Ψdp profile reaches a maximum value of about 195∘, indicating the effectiveness of the Ψdp unfolding in the region of heavy rain. In addition, when we apply the algorithm to a larger dataset, the rate of false alarm reaches a very small value at 0.66 %.
In addition to the ambiguous Ψdp, the estimation of the joint PDF may also be affected by nonzero δco, which is defined as the phase difference between the horizontal and vertical polarizations upon the backscattering of the particles in a radar resolution volume. This effect occurs more frequently at X-band frequency than S-band due to Mie scattering (Trömel et al., 2013). The δco is shown as a sudden phase change over a small number of gates in a monotonically increasing trend for rain. According to this manifestation, the magnitude and gate number of the Ψdp perturbation can be used to eliminate δco (Matrosov et al., 2002; Otto and Russchenberg, 2011).
The linear regression model often adopts an iterative filter technique, which generates a new Φdp profile from either the raw data or the filtered one based on a threshold (Hubbert and Bringi, 1995). If the filtering alters the data by 4∘, the new profile selects the filtered data; otherwise the raw data remain. The new profile is then used as input in the next iteration until the convergence condition is satisfied.
As shown in Fig. 5, the δco elimination is embedded into the process of the Ψdp unfolding. For two consecutive density ellipses, the latter density ellipse is removed if its mean is larger than the former one by 85∘. Prior to this step, the mean of the first density ellipse in the mixture should be below 90∘ to reduce the δco effect at the first few gates. Since δco occurs over a small number of range gates, a mixture pruning is also employed to remove the density ellipses with weights less than 0.0501, equivalent to 2 % of the data.
It is clear from Fig. 4b that δco has occurred at multiple locations in the data. The Ψdp profile starts at a high value and drops somewhat over the first two gates. Notably, there is a narrow gap between 18 and 20 km, while the corresponding ZDR presents a local peak. It signifies that nonzero δco occurs in this region. In GMM, these data are characterized by a density ellipse with a slightly decreasing trend, and the resulting expected values are consistent with the filtered data in LR. Between 70 and 90 km, a few isolated points beyond the density ellipses are associated with δco. Both of the methods can produce Φdp following the main trend of the data, which suggests that the process is effective for the δco elimination.
4.4 Kdp density estimation
As discussed in Sect. 2.1, Kdp is the first derivative of Φdp with respect to the range r. According to the mean value and dominated convergence theorems, the derivative of the expected value of Φdp conditioned on r is equal to the expected value of the derivative of Φdp with respect to r, i.e., Kdp (see Appendix C). Following the notation in Sect. 4.2, we denote Kdp as y′. Therefore, the expected value of Kdp is obtained by taking the derivative of Eq. (15), yielding
The variance of y′ conditioned on x can be approximated by the first-order Taylor series expansion (see Appendix D); i.e.,
where σ2(y|x) is given in Eq. (18). By taking the derivative of Eq. (19), is expressed as
From Eq. (C8) in Appendix C, it is clear that
where gi(x) is the summation term. Subsequently, the second derivative of is given as
Equations (19) and (20) are the regression and skedastic functions for the Kdp estimation. In Eq. (19), it is clear that the expected value of Kdp can be divided into two components, including Eqs. (C7) and (C11). On the one hand, Eq. (C7) is related to the changing rate ai weighted by the marginal distribution of each cluster in the mixture, equivalent to a linearly weighted combination of small portions of data. If a data point is dominated by a specific cluster, i.e., the weight of a cluster is significantly larger than the others, Kdp is determined by the coefficients of the cross-correlation and auto-correlation of r, and independent of the means and auto-correlation of Φdp, yielding a constant value within the dominated cluster. On the other hand, Eq. (C11) shows that the weighting function also contributes to the Kdp estimates by considering the Gaussian derivative of the Φdp estimates in two or three adjacent clusters along the range. The sign of Kdp is then determined by the marginal means and variances of the clusters, weighted by the difference of their contributions to Φdp.
In Eq. (20), it can be seen that σ2(Kdp) is proportional to σ2(Φdp), which is similar to Eq. (3). When the LR is applied to the MZZU radar, we often assume that σ(Φdp) is equal to 2.61∘ with 32 pulses, 1 m s−1 for Doppler spectrum and 0.98 for ρhv under the ideal conditions. However, in the GMM, σ2(Φdp) varies along the range due to the random errors of the Φdp estimates, indicating the GMM can provide a better model for the error characteristics in the Φdp measurements. In addition, the statistical errors with respect to signal processing may be included in Eq. (20) as an additive term, independent of Φdp. Moreover, σ2(Kdp) in GMM is closely related to the first derivative of Kdp in Eq. (20). As the changing rate of Kdp increases, the random errors associated with the Kdp estimates rise dramatically.
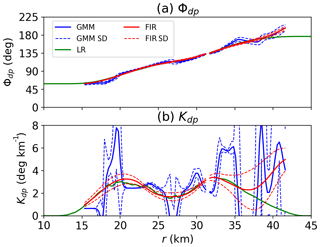
Figure 6Examples of Kdp estimation: (a) Φdp and (b) Kdp. The blue curves are the Φdp and Kdp estimates obtained by the Gaussian mixture method (GMM), the green curves represent the estimates derived from the linear regression model (LR), and the red curves indicate the reconstructed Φdp and smoothed Kdp profiles (FIR). The dashed lines are the standard deviations.
Figure 6b illustrates Kdp and its variance estimated from Φdp in Fig. 6a, which is the same case as given in Figs. 3a and 4a. It is apparent that the Kdp estimates present a large fluctuation, while the associated variances are significant. In GMM, Kdp starts from about 0.5 ∘ km−1 and then fluctuates between 17 and 20 km and between 24 and 42 km. In the profile, there are six local peaks with the maximum at about 8.5 ∘ km−1. Meanwhile, the Kdp variances vary as the Kdp estimates change. Between 15 and 17 km and between 20 and 24 km, the Kdp estimates remain constant, leading to small Kdp variances in these regions. When short excursions are present, such as that between 18 and 20 km, Kdp variances increase significantly due to the contribution of the first derivative of Kdp in Eq. (20). Furthermore, the large Φdp variances between 35 and 42 km also result in an increase in the Kdp variances. In contrast, LR gives less fluctuation in Kdp estimates with two peaks at about 20 and 34 km. The comparison of Kdp obtained by the two methods may suggest that a smoothing procedure is required to reduce the significant variance in GMM.
4.5 Kdp smoothing
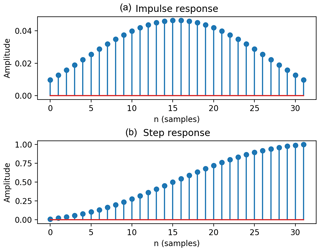
As discussed previously, the Kdp variance is small for high Kdp but relatively large for low Kdp. Therefore, an adaptive estimation is adopted in LR. For radar reflectivity (ZH) less than 20 dBZ, the gate number n in Eq. (2) is set as 15, while n is 8 for dBZ and 2 for ZH≥35 dBZ. On the other hand, GMM also applies an adaptive technique based on the finite impulse filter (FIR) to the expected values of Kdp in order to reduce the associated variances. Figure 7 shows the time responses of the FIR with the cutoff frequency of 0.053 and the Gaussian window of 28, which yield the best performance for the MZZU radar. The impulse response (Fig. 7a) is peaked at the center and gradually decreases towards the two ends. Furthermore, the step response (Fig. 7b) gives the accumulation of the impulse response, indicating that the magnitudes around the center change faster than those at the two ends. If a longer window is required, the order of the FIR is increased accordingly. In this study, we gradually increase the order number to calculate the difference between the Kdp profiles obtained by the FIR filters with two adjacent order numbers. The optimal order of the FIR filter is then set when the relative square error of the two Kdp values is below 0.001. For profiles with sufficiently large data points, the order number is between 29 and 33 for the MZZU radar.
To obtain the reduced variance, we consider the filter as a number of weighting functions, denoted as hi(x), and subsequently the smoothed data become
where y is a smoothed data point, xi is the original data within the smoothing window, and n is the window length. By taking the variance on both sides of Eq. (26), we have
Therefore, the variance of the smoothed data is the weighted sum of the variances of the original data within the smoothing window. Since the FIR coefficients are much less than unity, σ2(y) is smaller than σ2(x) at the same gate. Furthermore, the Kdp estimates with the reduced variances can be used to reconstruct Φdp to obtain smaller Φdp variances. For a fixed gate spacing Δr, the reconstructed Φdp for the jth range gate is
The red curves in Fig. 6a and b illustrate the reconstructed Φdp and the smoothed Kdp using FIR, respectively. The smoothed Kdp in Fig. 6b is more consistent with the LR results compared to the original Kdp produced by the GMM. In the first few kilometers, the smoothed Kdp gradually rises and then peaks at about 21 km. With no fluctuations, the smoothed Kdp falls gradually, followed by a growth before reaching a plateau at 33 km. After a slight decrease between 33 and 36 km, Kdp rises dramatically, which is very different from LR. Meanwhile, the variances are small at the beginning but get larger as Kdp is climbing. Between 20 and 33 km, the Kdp estimates do not change very much, leading to small variances in this region. But after 33 km, the variances begin to increase and retain large values until the end of the profile. Overall, the smoothed Kdp is stable, producing a profile considerably consistent with LR, and the variances are significantly reduced compared to the original data. In addition, the reconstructed Φdp (Fig. 6a) constantly increases with few local fluctuations, while the associated variances are smaller than the Φdp variances in GMM.
In this section, a case study is first presented to qualitatively analyze the storm structure and evolution based on Kdp. The radar–gauge dataset is then used to provide a quantitative evaluation for the Kdp estimation in terms of the root-mean-square error (RMSE), normalized bias (NB), and Pearson correlation coefficient (ρRG), which are defined as
where N is the sample size, Ri is the individual radar hourly rain amount, Gi is the gauge data, and and are the sample means for radar and gauge, respectively. The radar hourly rain amount is calculated based on the CASA radar rainfall algorithm. It is given as (Wang and Chandrasekar, 2010; Chen and Chandrasekar, 2015)
where R is the instantaneous rain rate in millimeters per hour (mm h−1). It is noted that the radar collects instantaneous measurements every 4–5 min, whereas RGs obtain the precipitation accumulations over 60 min. Therefore, it is necessary to average 12–15 consecutive radar scans to derive the hourly rain amounts.
5.1 Case study
On 24 March 2016, a severe storm developed in central Missouri and moved eastward across Columbia, MO, causing strong winds and heavy precipitation at the surface. When the storm became mature, the S-band radars at Kansas City and St. Louis observed the storm structure at high levels, since each radar was about 150 km away from the storm. Notably, the Kansas City radar showed positive and negative Doppler velocities in a small area (not shown), indicating the occurrence of a downburst. On the other hand, the MZZU radar illustrated a bow echo of ZH close to the radar center (Fig. 8b). In addition to ZH, the GMM-based Kdp (Fig. 8d, e and f) was also obtained to investigate the storm structure near the surface.
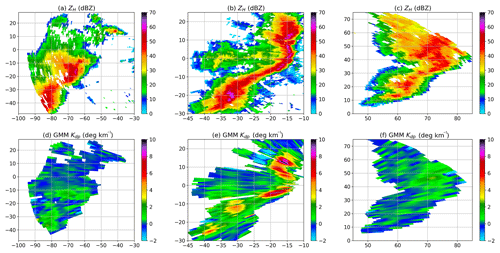
Figure 8A case study for GMM: (a) raw ZH at the development stage (03:04 UTC), (b) raw ZH at the mature stage (03:39 UTC), and (c) raw ZH at the dissipation stage (04:41 UTC). (d), (e), and (f) are the same as (a), (b), and (c), respectively, but for Kdp. The data were collected at a elevation of 0.85∘ by the MZZU radar between 03:04 and 04:41 UTC on 24 March 2016.
Figure 8 illustrates that the convective storm evolves from a strong and large echo to a bow shape echo and then dissipates at far range. At 03:04 UTC (Fig. 8a), a cell with strong ZH moves into the radar area, while Kdp is moderate with a maximum of about 3 ∘ km−1 (Fig. 8d). As the cell is transforming to a bow shape, the radar echo becomes intensive and forms a rain band with embedded convective cores (Fig. 8b). It is clear to see that Kdp reaches over 10 ∘ km−1 in these core regions (Fig. 8e), indicating very heavy precipitation at the surface. With the fast movement of the storm, the downburst is weaker, and the storm starts to dissipate (Fig. 8c). At 04:41 UTC, it can be seen that Kdp is gradually reduced at the far range, while its maximum is much lower than that at the mature stage.
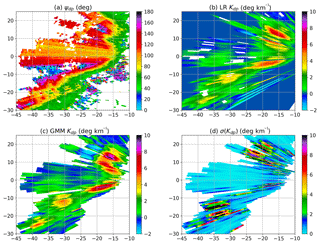
Figure 9Kdp estimation for the mature stage: (a) raw Ψdp, (b) LR-based Kdp, (c) GMM-based Kdp, and (d) GMM-based σ(Kdp). The data were collected at 03:39 UTC on 24 March 2016.
In this storm, the bow echo is shown as a number of convective cores embedded in a rain band, while the downbursts occurred at the leading edge near the echo center. The bow echo can be considered as a mesoscale convection with a horizontal dimension of more than 60 km. To gain further insight, Fig. 9 shows raw Φdp and Kdp for the bow echo. In Fig. 9a, raw Φdp presents large gradients along the leading edge, rising from about 50∘ to over 140∘. Due to the sharp increase, Φdp exceeds the maximum dynamic range, leading to ambiguity in the areas of X of −20 to −18 km and Y of 12 to 18 km as well as X of −40 to −23 km and Y of −8 to −5 km. In addition, the echoes behind the convective cores occasionally vanish as a result of signal attenuation. Nevertheless, LR (Fig. 9b) produces continuous Kdp by Φdp unfolding and linear interpolation according to the trends of the profiles, but some missing data still exist within the storm, due to the low signal-to-noise ratio. In contrast, GMM (Fig. 9c) corrects these data with the expected values derived from the joint PDF and simultaneously obtains the statistical errors in the production of Kdp. It is evident that the GMM method can efficiently handle the missing data via the mixture model, which is another advantage over the LR model. Furthermore, the statistical errors are not very large in these areas, since the missing data are filled by the distribution of the entire data profile. Additionally, the GMM Kdp estimates are generally a few degrees per kilometer (∘ km−1) higher than the LR ones, particularly for the regions of high ZH.
By taking a closer look at GMM Kdp, we can see that the bow echo is generally characterized by Kdp of above 2.5 ∘ km−1, while five pockets of high Kdp are identified. In the bow head, the first pocket presents very high Kdp associated with a rapid growth of Φdp. Behind this pocket, there is a region of negative Kdp, whereas LR generally yields positive values. It may be due to a reduction of the cross-correlation coefficient caused by the low signal-to-noise ratio, since the signals have been significantly attenuated after propagating through the pocket. In the middle of the second and third pockets in the bow center, LR and GMM both show lower Kdp compared to the two pockets, while Kdp is substantially consistent with the gradient of Φdp in the area. By considering the high ZH in Fig. 8, these moderate Kdp values may indicate less anisotropic scatterers, such as small hail in the process of wet growth. Similarly, a hail signature with maximum ZH of above 66 dBZ and small Kdp of 1–2 ∘ km−1 can also be identified in the middle of the fourth and fifth pockets in the bow tail. Along with the expected values of GMM Kdp, Fig. 9.d depicts the statistical errors σ(Kdp) in the calculation of the expected values. The five pockets of high Kdp are generally associated with small σ(Kdp) of a few tenths of a degree per kilometer. However, the estimates behind the top four pockets yield very large σ(Kdp) values with a maximum above 10 ∘ km−1, and the expected values of Kdp are sometimes below 0 ∘ km−1, such as areas of X of −25 to −20 km and Y of 11 to 20 km. In contrast, a region of high σ(Kdp) appears in front of the bottom pocket, superimposed on the high ZH area associated with hail. In conclusion, the GMM Kdp estimates of high confidence give good agreement with the gradients of Φdp in the leading edge of the bow echo, while large σ(Kdp) values are expected at the region of high variation of the Kdp estimates.
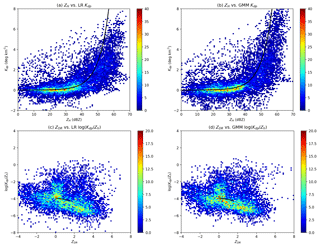
Figure 10Comparison with the self-consistency relations: (a) ZH vs. LR Kdp, (b) ZH vs. GMM Kdp, (c) ZDR vs. the ratio of LR Kdp and Zh, and (d) ZDR vs. the ratio of GMM Kdp and Zh, where ZH=10log (Zh). The color scale is the number of points, and the black curves are the theoretical self-consistency relations.
To give a further evaluation of the GMM Kdp, Fig. 10 compares the scatterplots of ZH, ZDR, and Kdp to the self-consistency (SC) relations. Referring to Park et al. (2005b), Otto and Russchenberg (2011), and Matrosov (2010), the X-band SC relations are given as
where ZH=10log Zh and Zh is in mm6 m−3. Figures 10a and b illustrate that the points concentrate at the region with ZH between 10 and 40 dBZ, where the Kdp shows a low and steady increase. Both the LR Kdp and GMM Kdp agree well with the SC relation in Eqs. (34) and (35). It is notable that the Kdp rises dramatically from a few tenths to 8 ∘ km−1 for ZH larger than 40 dBZ. As depicted in Fig. 10a, the LR Kdp increases greatly when ZH reaches 50 dBZ, showing a difference from the SC relation. In contrast, the GMM Kdp in Fig. 10b gives some improvements over the LR Kdp in Fig. 10a when compared to the SC relation. Furthermore, the points of ZDR–Kdp∕Zh in Fig. 10c and d may be grouped into two clusters with high populations. The cluster with lower Kdp∕Zh agrees with the SC relation in Eq. (36). On the other hand, the clusters centered at ZDR around 0 dB are likely caused by hails, since they are less anisotropic than raindrops with the same size. In addition, the LR Kdp and GMM Kdp produce a similar distribution of ZDR and Kdp∕Zh, though the distribution for the GMM Kdp tends to be narrower.
Moreover, the computational time is crucial for the real-time application of the Kdp retrieval algorithms. For processing the data in Fig. 9 in Window 10 on a PC or Linux 7 on a supercomputer, the GMM takes about 7.058/4.068 s to process the Kdp with/without the data masking, whereas the LR reduces the time to about 2.037 s. It indicates that the LR has the advantages of simplicity and efficiency. Nevertheless, the GMM can obtain more information from the radar data, which is useful for the model studies.
5.2 Statistical analysis
In order to quantitatively evaluate the accuracy of GMM Kdp, hourly accumulated rain amounts are derived from the X-band rainfall rate algorithm (Chen and Chandrasekar, 2015) and compared to the rain gauge data collected at Bradford, Sanborn, Auxvasse, and Williamsburg between 1 April 2016 and 2 June 2018. The scatterplots presented in Fig. 11 illustrate the comparison between GMM-based radar and gauge rain amounts, and the accompanying table (Table 2) gives the RMSE, NB, and ρRG results obtained by GMM and LR.
Table 2Statistics for the comparison between the radar and gauge. RMSE: root-mean-square error; NB: normalized bias; ρRG: Pearson correlation coefficient; LR: linear regression model; GMM: Gaussian mixture method.
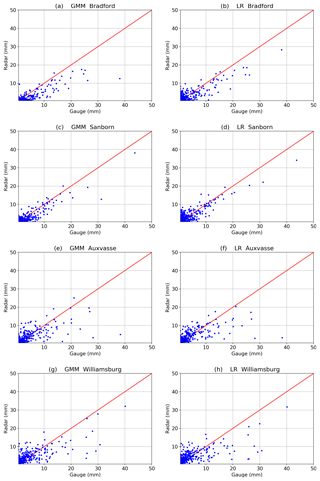
Figure 11Comparison between hourly radar and gauge data derived from GMM Kdp and LR Kdp. (a) GMM Bradford, (b) LR Bradford, (c) GMM Sanborn, (d) LR Sanborn, (e) GMM Auxvasse, (f) LR Auxvasse, (g) GMM Williamsburg, and (h) LR Williamsburg. The data were collected between 1 April 2016 and 2 June 2018.
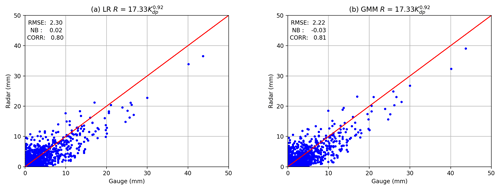
Figure 12Same as Fig. 11 but for the optimal R–Kdp relation for the four sites. (a) LR R(Kdp) and (b) GMM R(Kdp).
Consistent with the data in Table 1, the rainfall at the four sites is predominately made up of light rain with hourly rain amounts no more than 2.5 mm h−1. Nevertheless, according to Fig. 11, moderate rain with amounts between 2.6 and 8 mm h−1 provides a considerable contribution to the total rain events, followed by a small portion of heavy rain with amounts more than 8 mm h−1. When we study the scatterplots and statistics for each of the four sites, it is apparent that Bradford (Fig. 11a and b) and Sanborn (Fig. 11c and d) are more concentrated on the red line than Auxvasse (Fig. 11e and f) and Williamsburg (Fig. 11g and h), since Bradford and Sanborn are closer to the radar. Accordingly, RMSEs for Bradford and Sanborn (Table 2) are relatively small, about 13 %–35 % lower than Auxvasse and Williamsburg. Furthermore, it can be seen that Bradford and Sanborn show negative bias associated with negative NBs, indicating an underestimation of rain amounts by GMM Kdp. In contrast, a slight overestimation may be concluded for Auxvasse and Williamsburg by considering the point trends and the positive NBs. Additionally, Sanborn claims the highest ρRG out of the four sites, yielding the best consistency between the radar and gauge.
When compared to LR statistics as given in Table 2, it is clear that GMM improves the RMSEs, NBs and ρRG for Auxvasse and Williamsburg. Notably, the GMM-based NB for Auxvasse reaches a very small value of 0.04, one-fifth of LR-based NB. For Bradford, RMSE is reduced by GMM, but the absolute value of NB is slightly increased, while ρRG remains the same. On the other hand, for Sanborn, the GMM-based RMSE has been increased and the GMM-based NB and ρhv have been decreased comparing to the LR ones. It may be due to the local complex terrain near the radar. However, the difference of RMSE, NB, and ρhv between GMM and LR is a few hundredths of a millimeter, which is not significant relative to their absolute values. Overall, the rainfall estimates of GMM Kdp give a better performance than that of LR in terms of RMSE, NB, and ρRG at the far ranges.
To improve the accuracy of the radar rainfall estimation, we have optimized the R–Kdp relation in terms of the RMSE using the radar–gauge dataset. It leads to the relation as
Figure 12 shows the scatterplots of the radar–gauge data and the statistics of RMSE, NB, and ρRG obtained by Eq. (37) for all the four sites. It is clear that Eq. (37) has improved the negative trend in Eq. (33). As illustrated in Fig. 12a and b, the points give a better concentration on the one-to-one reference line with noticeable changes for higher R(Kdp). In Fig. 12a, the LR R(Kdp) achieves fairly good RMSE, NB, and ρRG values at 2.30, 0.02, and 0.80, respectively. On the other hand, the GMM R(Kdp) presents a similar distribution to the LR R(Kdp), but the points in Fig. 12b are shifted toward the vertical axis. Moreover, the GMM R(Kdp) gives better RMSE and ρRG at 2.22 and 0.81, respectively, and slightly worse NB at −0.03.
It can be found that the rain rates based on the GMM Kdp have a moderate consistency with the rain gauge data. To further improve the results, some advanced rain rate algorithms can be considered, such as the rain–ice separation technique in the IFloodS campaign (Chen et al., 2017b) and the radar–gauge comparison method in the MC3E campaign (Giangrande et al., 2014). Nevertheless, the GMM has the advantage over the existing methods, since it can yield the variance of Kdp. Furthermore, the variance of R can also be obtained by the Kdp mean and the Kdp variance via the R–Kdp relation, leading to the variability in the error characteristics of R. Thus, the variances can be used to study the streamflow trends in the hydrological model.
In this study, we proposed a probabilistic method based on the Gaussian mixture model to estimate the specific differential phase Kdp, which is the range derivative of the differential phase shift Φdp. The Gaussian mixture method (GMM) not only obtained the expected values of Kdp by differentiating the conditional expectation of Φdp, but also yielded the variance σ2(Kdp) regarding the errors in the calculation of the first derivative of Φdp.
As an initial step of GMM, the data masking was performed to eliminate the residual clutter in the measurements of the total differential phase (Ψdp). The data of r and Ψdp were first fitted into a simplified Gaussian mixture to generate a number of clusters, which were validated against the two sets of the σ(Ψdp) and σ(Ψdp)∕σ(r) thresholds given by radar reflectivity ZH. The clusters were then combined to form the rain cell segments, and the segments were classified by comparing the weight accumulations of weather and clutter clusters. Next, the clusters within each segment were reevaluated by the thresholds according to the segment types. Finally, the azimuthally isolated points were masked out.
Secondly, the joint probability density function (PDF) was obtained by fitting the data of r and Ψdp into a mixture model with full covariance, where the cluster number m, weight w, mean μ, and covariance Σ were optimized via the expectation–maximization (EM) algorithm. Subsequently, the PDF of Ψdp conditioned on r was also a mixture with parameters related to the joint PDF. Finally, the Ψdp mean was estimated by the conditional expectation, and the statistical errors σ2(Ψdp) were given by the conditional variance, which was not always constant but varied with w and the marginal PDF of r.
Thirdly, the ambiguous Ψdp and backscattering differential phase shift δco were corrected by examining the two adjacent density ellipses in the mixture. On the one hand, if the former density ellipse had a mean larger than the latter one by 80∘, the latter mean was added to 180∘ for Ψdp unfolding. On the other hand, if the former mean was smaller than the latter one by 85∘, the latter density ellipse was removed as δco. Moreover, for δco elimination, the first density ellipse mean was assumed to be below 90∘, while the density ellipses with small weights were also removed.
Fourthly, the joint PDF of r and Φdp was used in the calculations of Kdp and σ2(Kdp). Since Kdp was the range derivative of Φdp, the expected values of Kdp were then obtained via the derivative of the expected value of Φdp. Moreover, by taking the first-order Taylor series expansion, σ2(Kdp) was the product of the square of the first derivative of Kdp and σ2(Φdp), yielding nonconstant values of σ2(Kdp).
In the final step, the expected values of Kdp were smoothed to reduce the associated σ2(Kdp). An FIR filter was implemented and iteratively applied to the data to search for an optimal window length. Subsequently, the reduced σ2(Kdp) was obtained by the sum of the original σ2(Kdp) weighted by the FIR coefficient squares within the window. Additionally, new Φdp were reconstructed from the smoothed Kdp, while σ2(Φdp) was also reduced.
The experimental results with a severe storm observed by the X-band polarimetric radar in the University of Missouri (MZZU) revealed the advantages of GMM. By studying the structure and evolution of a bow echo in the storm, it was concluded that the GMM Kdp was consistent with the gradients of raw Φdp along the leading edge of the bow echo, while large σ2(Kdp) values occurred with high variation of Kdp. The GMM method produced results similar to the LR method, with the ability to handle the missing data. Moreover, the hourly rain amounts based on Kdp were compared to the rain gauge data, showing fairly good agreement between radar and gauge measurements. The rain amounts obtained by GMM Kdp gave improvements over the linear regression model, particularly for the far ranges.
The potential applications of GMM Kdp and σ2(Kdp) include quantitative precipitation estimation (Cifelli et al., 2011; Chen et al., 2017a) and attenuation correction (Park et al., 2005a). For quantitative precipitation estimation, the relationship between Kdp and rain rate R is almost linear, since Kdp is about the fourth-order moment of the raindrop size distribution, and R is the 3.67th-order moment. As illustrated in Figs. 11 and 12, the R(Kdp) algorithm is consistent with the in situ measurements. To further investigate the R errors, it is necessary to consider the Kdp errors in the calculation of the first derivative of Φdp. The standard deviation σ(Kdp) is then related to σ(R) by a factor of R∕Kdp (Bringi and Chandrasekar, 2001). In a similar manner, Kdp is linearly proportional to the specific attenuation AH and specific differential attenuation ADP (Bringi and Hendry, 1990). Therefore, the errors of radar reflectivity ZH and differential reflectivity ZDR may also be proportional to σ(Kdp) after the attenuation correction and eventually contribute to the R errors via R(ZH) and R(ZH,ZDR). Moreover, the error estimates can be used to study the propagation of uncertainty in the weather model and provide streamflow trends in the hydrological model. In the future study, the algorithm will also be extended to other frequencies, such as the C band (Vulpiani et al., 2012; May et al., 1999) and S band (Bringi and Chandrasekar, 2001). The thresholds in the data masking, the Ψdp unfolding, and the δco elimination will be adjusted according to the radar specifications. Nevertheless, the steps for the calculations of the PDFs of Ψdp and Kdp remain.
The MZZU radar data can be made available upon request to the authors. The rain gauge data are available upon request to the University of Missouri Extension via Missouri Historical Agricultural Weather Database.
Let the total differential phase Ψdp be y, and let the range gate r be x. The Ψdp profile over small range segments can be approximated by a first-order polynomial; i.e.,
where β0 and β1 are the coefficients in the linear approximation, and ϵ is an error function. It can be assumed that ϵ is independent and individually distributed with zero mean and variance of .
In the linear regression, it is easy to find that
where and are the means of x and y in the segment, respectively. Since
and
we have
where N is the number of the gates in the segment.
It is noted that the range gate r is equally spaced with an interval of Δr, Ψdp is the two-way propagation phase shift, and Kdp is the one-way specific differential phase. The Kdp is then estimated by
At the S band, the backscattering differential phase shift δco is often negligible, and thus Ψdp and Φdp are interchangeable, leading to Eq. (2).
By taking the variance on both sides of Eq. (A5) and noting ϵ is the only variable, we have
Similar to Eq. (A6), we have
We consider the range r as an independent variable, denoted as x, and Φdp as a dependent variable, denoted as y. The joint distribution of follows a Gaussian mixture as
where wi, μi, and Σi are the weight, mean, and covariance for each component, respectively. The probability of y conditioned on x is also a Gaussian mixture with parameters , , and , leading to the conditional expectation as
and the second-order moment as
Therefore, the conditional variance is expressed as
First, we need to show that the derivative of the expected value of random variable y as a function of random variable x is equal to the expected value of the derivative of the expected value of y. By the definition, the derivative of y is expressed as
where exists by the mean value theorem. By assuming , we can use the dominated convergence theorem to obtain
According to the conclusion in Eq. (C5), the expected value of y′ is expressed as
Since and , the first term is equal to
Meanwhile, the second term is given as
Based on the properties of the Gaussian function, the derivatives of fi(x) and f(x) are expressed as
By substituting Eqs. (C9) and (C10) into Eq. (C8), the second term is transformed as
By substituting Eqs. (C7) and (C11) into Eq. (C6), we obtain
The first-order Taylor expansion is defined as
where θ=E(y) is the mean of random variable y, and ϵ is the sum of the higher-order Taylor series. By considering the conclusion in Eq. (C5), it can be noted that the expected values of the coefficients associated with the derivatives in Eq. (D1) are zeros if the series is expanded at the mean value of y. By taking mathematical expectations on both sides of Eq. (D1), it is transformed as
From Eqs. (D1) and (D3), the variance of g(y) is approximated as
Let g(y) be y′, and then we have
From Eq. (B9), we can see that
By taking the derivative of Eq. (C6), the second derivative of the expected value of y conditioned on x becomes
since and . From Eq. (C8), the first derivative of the weighting function in the conditional probability is
Let gi(x) be the summation term. The second derivative is then expressed as
According to the properties of the Gaussian mixture, the first derivative of the marginal distribution of x is
Similarly, the first derivative of g(x) if given as
NIF designed the experiment and provided the radar data, GW developed the Gaussian mixture model and prepared the manuscript, GW and NIF performed the validation, and NF and PSM reviewed the paper.
The authors declare that they have no conflict of interest.
The authors would like to express our sincere thanks to the anonymous reviewers for their valuable comments and suggestions. This work was supported by Missouri Experimental Project to Stimulate Competitive Research (EPSCoR) of the National Science Foundation, under award number IIA-1355406. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
This research has been supported by the National Science Foundation (award number IIA-1355406).
This paper was edited by Gianfranco Vulpiani and reviewed by three anonymous referees.
Anagnostou, E. N., Krajewski, W. F., and Smith, J.: Uncertainty Quantification of Mean-Areal Radar-Rainfall Estimates, J. Atmos. Ocean. Tech., 16, 206–215, 1999. a
Aydin, K., Bringi, V., and Liu, L.: Rain-rate estimation in the presence of hail using S-band specific differential phase and other radar parameters, J. Appl. Meteorol., 34, 404–410, 1995. a
Balakrishnan, N. and Zrnić, D. S.: Estimation of rain and hail rates in mixed-phase precipitation, J. Atmos. Sci., 47, 565–583, 1990. a
Berne, A. and Krajewski, W. F.: Radar for hydrology: Unfulfilled promise or unrecognized potential?, Adv. Water Res., 51, 357–366, 2013. a
Bishop, C. M.: Pattern recognition and machine learning, Springer, New York, 2006. a
Bringi, V. and Chandrasekar, V.: Polarimetric Doppler weather radar: Principles and applications, Cambridge University Press, Cambridge, 2001. a, b, c, d
Bringi, V. and Hendry, A.: Technology of polarization diversity radars for meteorology, in: Radar in Meteorology, American Meteorological Society, Boston, MA, 153–190, 1990. a
Bringi, V. N., Huang, G.-J., Chandrasekar, V., and Gorgucci, E.: A Methodology for Estimating the Parameters of a Gamma Raindrop Size Distribution Model from Polarimetric Radar Data: Application to a Squall-Line Event from the TRMM/Brazil Campaign, J. Atmos. Ocean. Tech., 19, 633–645, 2002. a
Chandrasekar, V., Lim, S., and Gorgucci, E.: Simulation of X-band rainfall observations from S-band radar data, J. Atmos. Ocean. Tech., 23, 1195–1205, 2006. a
Chandrasekar, V., Wang, Y., and Chen, H.: The CASA quantitative precipitation estimation system: a five year validation study, Nat. Hazards Earth Syst. Sci., 12, 2811–2820, https://doi.org/10.5194/nhess-12-2811-2012, 2012. a
Chandrasekar, V., Chen, H., and Philips, B.: Principles of High-Resolution Radar Network for Hazard Mitigation and Disaster Management in an Urban Environment, J. Meteorol. Soc. Jpn. Ser. II, 96A, 119–139, https://doi.org/10.2151/jmsj.2018-015 2018. a
Chen, H. and Chandrasekar, V.: The quantitative precipitation estimation system for Dallas–Fort Worth (DFW) urban remote sensing network, J. Hydrol., 531, 259–271, 2015. a, b
Chen, H., Chandrasekar, V., and Bechini, R.: An improved dual-polarization radar rainfall algorithm (DROPS2.0): Application in NASA IFloodS field campaign, J. Hydrometeorol., 18, 917–937, 2017a. a
Chen, H., Chandrasekar, V., and Bechini, R.: An Improved Dual-Polarization Radar Rainfall Algorithm (DROPS2.0): Application in NASA IFloodS Field Campaign, J. Hydrometeorol., 18, 917–937, 2017b. a, b
Chen, H., Lim, S., Chandrasekar, V., and Jang, B.-J.: Urban Hydrological Applications of Dual-Polarization X-Band Radar: Case Study in Korea, J. Hydrol. Eng., 22, E5016001, https://doi.org/10.1061/(ASCE)HE.1943-5584.0001421, 2017c. a
Cifelli, R., Chandrasekar, V., Lim, S., Kennedy, P. C., Wang, Y., and Rutledge, S. A.: A new dual-polarization radar rainfall algorithm: Application in Colorado precipitation events, J. Atmos. Ocean. Tech., 28, 352–364, 2011. a, b
Cifelli, R., Chandrasekar, V., Chen, H., and Johnson, L. E.: High resolution radar quantitative precipitation estimation in the San Francisco Bay area: Rainfall monitoring for the urban environment, J. Meteorol. Soc. Jpn. Ser. II, 96, 141–155, 2018. a
Dempster, A. P., Laird, N. M., and Rubin, D. B.: Maximum likelihood from incomplete data via the EM algorithm, J. Roy. Stat. Soc. B, 39, 1–38, 1977. a
Giangrande, S. E., McGraw, R., and Lei, L.: An application of linear programming to polarimetric radar differential phase processing, J. Atmos. Ocean. Tech., 30, 1716–1729, 2013. a
Giangrande, S. E., Collis, S., Theisen, A. K., and Tokay, A.: Precipitation Estimation from the ARM Distributed Radar Network during the MC3E Campaign, J. Appl. Meteorol. Climatol., 53, 2130–2147, 2014. a
Gorgucci, E., Scarchilli, G., and Chandrasekar, V.: Specific Differential Phase Estimation in the Presence of Nonuniform Rainfall Medium along the Path, J. Atmos. Ocean. Tech., 16, 1690–1697, 1999. a
Gosset, M.: Effect of Nonuniform Beam Filling on the Propagation of Radar Signals at X-Band Frequencies, Part II: Examination of Differential Phase Shift, J. Atmos. Ocean. Tech., 21, 358–367, 2004. a
Hastie, T., Tibshirani, R., and Friedman, J.: The elements of statistical learning, Springer Series in Statistics, 2 edn., Springer, New York, 2009. a
Helmus, J. and Collis, S.: The Python ARM Radar Toolkit (Py-ART), a library for working with weather radar data in the Python programming language, J. Open Res. Softw., 4, e25, https://doi.org/10.5334/jors.119, 2016. a
Hubbart, J., Kellner, E., Hooper, L., Lupo, A., Market, P., Guinan, P., Stephan, K., Fox, N., and Svoma, B.: Localized climate and surface energy flux alterations across an urban gradient in the central US, Energies, 7, 1770–1791, 2014. a
Hubbart, J. A. and Zell, C.: Considering streamflow trend analyses uncertainty in urbanizing watersheds: a baseflow case study in the central United States, Earth Interact., 17, 1–28, 2013. a
Hubbert, J. and Bringi, V. N.: An Iterative Filtering Technique for the Analysis of Copolar Differential Phase and Dual-Frequency Radar Measurements, J. Atmos. Ocean. Tech., 12, 643–648, 1995. a, b, c
Hubbert, J., Chandrasekar, V., Bringi, V. N., and Meischner, P.: Processing and Interpretation of Coherent Dual-Polarized Radar Measurements, J. Atmos. Ocean. Tech., 10, 155–164, 1993. a, b
Hubbert, J. C., Dixon, M., Ellis, S. M., and Meymaris, G.: Weather Radar Ground Clutter, Part I: Identification, Modeling, and Simulation, J. Atmos. Ocean. Tech., 26, 1165–1180, 2009. a
Kalogiros, J., Anagnostou, M. N., Anagnostou, E. N., Montopoli, M., Picciotti, E., and Marzano, F. S.: Evaluation of a new polarimetric algorithm for rain-path attenuation correction of X-band radar observations against disdrometer, IEEE T. Geosci. Remote, 52, 1369–1380, 2014. a
Li, Z., Zhang, Y., and Giangrande, S. E.: Rainfall-Rate Estimation Using Gaussian Mixture Parameter Estimator: Training and Validation, J. Atmos. Ocean. Tech., 29, 731–744, 2012. a
Lim, S., Chandrasekar, V., and Bringi, V. N.: Hydrometeor classification system using dual-polarization radar measurements: Model improvements and in situ verification, IEEE T. Geosci. Remote, 43, 792–801, 2005. a
Lim, S., Cifelli, R., Chandrasekar, V., and Matrosov, S.: Precipitation classification and quantification using X-band dual-polarization weather radar: Application in the Hydrometeorology Testbed, J. Atmos. Ocean. Tech., 30, 2108–2120, 2013. a
Liu, L., Bringi, V., Caylor, I., and Chandrasekar, V.: Intercomparison of multiparameter radar signatures from Florida storms, in: Preprints, 26th Int. Conf. on Radar Meteorology, Norman, OK, Amer. Meteor. Soc, 733–735, 1993. a
Marzano, F. S., Botta, G., and Montopoli, M.: Iterative Bayesian Retrieval of Hydrometeor Content From X-Band Polarimetric Weather Radar, IEEE T. Geosci. Remote, 48, 3059–3074, 2010. a
Matrosov, S. Y.: Evaluating Polarimetric X-Band Radar Rainfall Estimators during HMT, J. Atmos. Ocean. Tech., 27, 122–134, 2010. a
Matrosov, S. Y., Clark, K. A., Martner, B. E., and Tokay, A.: X-band polarimetric radar measurements of rainfall, J. Appl. Meteorol., 41, 941–952, 2002. a
Matrosov, S. Y., Cifelli, R., Kennedy, P. C., Nesbitt, S. W., Rutledge, S. A., Bringi, V., and Martner, B. E.: A comparative study of rainfall retrievals based on specific differential phase shifts at X-and S-band radar frequencies, J. Atmos. Ocean. Tech., 23, 952–963, 2006. a
May, P. T. and Strauch, R. G.: Reducing the Effect of Ground Clutter on Wind Profiler Velocity Measurements, J. Atmos. Ocean. Tech., 15, 579–586, 1998. a
May, P. T., Keenan, T. D., Zrnić, D. S., Carey, L. D., and Rutledge, S. A.: Polarimetric Radar Measurements of Tropical Rain at a 5 cm Wavelength, J. Appl. Meteorol., 38, 750–765, 1999. a, b
McLachlan, G. and Peel, D.: Finite mixture models, vol. 299, JohnWiley & Sons, New York, 2000. a
Otto, T. and Russchenberg, H. W.: Estimation of specific differential phase and differential backscatter phase from polarimetric weather radar measurements of rain, IEEE T. Geosci. Remote Sens. Lett., 8, 988–992, 2011. a, b, c
Oue, M., Galletti, M., Verlinde, J., Ryzhkov, A., and Lu, Y.: Use of X-band differential reflectivity measurements to study shallow Arctic mixed-phase clouds, J. Appl. Meteorol. Climatol., 55, 403–424, 2016. a
Park, H. S., Ryzhkov, A. V., Zrnić, D. S., and Kim, K.-E.: The hydrometeor classification algorithm for the polarimetric WSR-88D: Description and application to an MCS, Weather Forecast., 24, 730–748, 2009. a
Park, S., Bringi, V., Chandrasekar, V., Maki, M., and Iwanami, K.: Correction of radar reflectivity and differential reflectivity for rain attenuation at X band, Part I: Theoretical and empirical basis, J. Atmos. Ocean. Tech., 22, 1621–1632, 2005a. a
Park, S., Maki, M., Iwanami, K., Bringi, V., and Chandrasekar, V.: Correction of radar reflectivity and differential reflectivity for rain attenuation at X band, Part II: Evaluation and application, J. Atmos. Ocean. Tech., 22, 1633–1655, 2005b. a
Petersen, K. B. and Pedersen, M. S.: The matrix cookbook (version: 15 November 2012), 2012. a
Reinoso-Rondinel, R., Unal, C., and Russchenberg, H.: Adaptive and high-resolution estimation of specific differential phase for polarimetric X-band weather radars, J. Atmos. Ocean. Tech., 35, 555–573, 2018. a
Ryzhkov, A. and Zrnić, D.: Assessment of rainfall measurement that uses specific differential phase, J. Appl. Meteorol., 35, 2080–2090, 1996. a
Ryzhkov, A. V.: The Impact of Beam Broadening on the Quality of Radar Polarimetric Data, J. Atmos. Ocean. Tech., 24, 729–744, 2007. a
Ryzhkov, A. V. and Zrnić, D. S.: Comparison of Dual-Polarization Radar Estimators of Rain, J. Atmos. Ocean. Tech., 12, 249–256, 1995. a
Ryzhkov, A. V., Schuur, T. J., Burgess, D. W., Heinselman, P. L., Giangrande, S. E., and Zrnic, D. S.: The Joint Polarization Experiment: Polarimetric Rainfall Measurements and Hydrometeor Classification, B. Am. Meteor. Soc., 86, 809–824, 2005. a
Sachidananda, M. and Zrnić, D. S.: Differential propagation phase shift and rainfall rate estimation, Radio Sci., 21, 235–247, 1986. a, b
Schneebeli, M., Grazioli, J., and Berne, A.: Improved estimation of the specific differential phase shift using a compilation of Kalman filter ensembles, IEEE T. Geosci. Remote, 52, 5137–5149, 2014. a
Seliga, T. A. and Bringi, V. N.: Differential reflectivity and differential phase shift: Applications in radar meteorology, Radio Sci., 13, 271–275, 1978. a
Simpson, M. J. and Fox, N. I.: X-band dual-polarized radar quantitative precipitation estimate analyses in the Midwestern United States, Atmos. Meas. Tech. Discuss., https://doi.org/10.5194/amt-2017-439, 2017. a, b
Spanos, A.: Probability theory and statistical inference: econometric modeling with observational data, Cambridge University Press, Cambridge, 1999. a
Sung, H.: Gaussian mixture regression and classification, Thesis, Rice University, 2004. a, b
Trömel, S., Kumjian, M. R., Ryzhkov, A. V., Simmer, C., and Diederich, M.: Backscatter differential phase–Estimation and variability, J. Appl. Meteorol. Climatol., 52, 2529–2548, 2013. a
Veneziano, D. and Villani, P.: Identification of rain cells from radar and stochastic modelling of space-time rainfall, Meccanica, 31, 27–42, 1996. a
Vulpiani, G., Montopoli, M., Passeri, L. D., Gioia, A. G., Giordano, P., and Marzano, F. S.: On the Use of Dual-Polarized C-Band Radar for Operational Rainfall Retrieval in Mountainous Areas, J. Appl. Meteorol. Climatol., 51, 405–425, 2012. a, b
Wang, Y. and Chandrasekar, V.: Algorithm for estimation of the specific differential phase, J. Atmos. Ocean. Tech., 26, 2565–2578, 2009. a, b
Wang, Y. and Chandrasekar, V.: Quantitative precipitation estimation in the CASA X-band dual-polarization radar network, J. Atmos. Ocean. Tech., 27, 1665–1676, 2010. a
Wen, G., Protat, A., May, P. T., Wang, X., and Moran, W.: A Cluster-Based Method for Hydrometeor Classification Using Polarimetric Variables, Part I: Interpretation and Analysis, J. Atmos. Ocean. Tech., 32, 1320–1340, 2015. a, b
Wen, G., Oue, M., Protat, A., Verlinde, J., and Xiao, H.: Ice particle type identification for shallow Arctic mixed-phase clouds using X-band polarimetric radar, Atmos. Res., 182, 114–131, 2016a. a
Wen, G., Protat, A., May, P. T., Moran, W., and Dixon, M.: A Cluster-Based Method for Hydrometeor Classification Using Polarimetric Variables, Part II: Classification, J. Atmos. Ocean. Tech., 33, 45–60, 2016b. a
Wen, G., Protat, A., and Xiao, H.: An Objective Prototype-Based Method for Dual-Polarization Radar Clutter Identification, Atmosphere, 8, 72, https://doi.org/10.3390/atmos8040072, 2017. a, b
Williams, C. R., Bringi, V., Carey, L. D., Chandrasekar, V., Gatlin, P. N., Haddad, Z. S., Meneghini, R., Joseph Munchak, S., Nesbitt, S. W., and Petersen, W. A.: Describing the shape of raindrop size distributions using uncorrelated raindrop mass spectrum parameters, J. Appl. Meteorol. Climatol., 53, 1282–1296, 2014. a
Zrnić, D. S. and Ryzhkov, A.: Advantages of Rain Measurements Using Specific Differential Phase, J. Atmos. Ocean. Tech., 13, 454–464, 1996. a
- Abstract
- Introduction
- Background
- Data
- Kdp retrieval
- Evaluation
- Summary and discussions
- Data availability
- Appendix A: Regression-based estimation of Kdp
- Appendix B: Variance of Φdp
- Appendix C: Conditional expectation of Kdp
- Appendix D: Variance of Kdp
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Background
- Data
- Kdp retrieval
- Evaluation
- Summary and discussions
- Data availability
- Appendix A: Regression-based estimation of Kdp
- Appendix B: Variance of Φdp
- Appendix C: Conditional expectation of Kdp
- Appendix D: Variance of Kdp
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References