the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The role of aerosol layer height in quantifying aerosol absorption from ultraviolet satellite observations
Pepijn Veefkind
Swadhin Nanda
Peter van Velthoven
Pieternel Levelt
The purpose of this study is to demonstrate the role of aerosol layer height (ALH) in quantifying the single scattering albedo (SSA) from ultraviolet satellite observations for biomass burning aerosols. In the first experiment, we retrieve SSA by minimizing the near-ultraviolet (near-UV) absorbing aerosol index (UVAI) difference between observed values and those simulated by a radiative transfer model. With the recently released S-5P TROPOMI ALH product constraining forward simulations, a significant gap in the retrieved SSA (0.25) is found between radiative transfer simulations with spectral flat aerosols and those with strong spectrally dependent aerosols, implying that inappropriate assumptions regarding aerosol absorption spectral dependence may cause severe misinterpretations of the aerosol absorption. In the second part of this paper, we propose an alternative method to retrieve SSA based on a long-term record of co-located satellite and ground-based measurements using the support vector regression (SVR) approach. This empirical method is free from the uncertainties due to the imperfection of a priori assumptions on aerosol microphysics seen in the first experiment. We present the potential capabilities of SVR using several fire events that have occurred in recent years. For all cases, the difference between SVR-retrieved SSA and AERONET are generally within ±0.05, and over half of the samples are within ±0.03. The results are encouraging, although in the current phase the model tends to overestimate the SSA for relatively absorbing cases and fails to predict SSA for some extreme situations. The spatial contrast in SSA retrieved by radiative transfer simulations is significantly higher than that retrieved by SVR, and the latter better agrees with SSA from MERRA-2 reanalysis. In the future, more sophisticated feature selection procedures and kernel functions should be taken into consideration to improve the SVR model accuracy. Moreover, the high-resolution TROPOMI UVAI and co-located ALH products will guide us to more reliable training data sets and more powerful algorithms to quantify aerosol absorption from UVAI records.
The concept of the near-ultraviolet (near-UV) absorbing aerosol index (UVAI) initially came along with the ozone product of the Total Ozone Mapping Spectrometer (TOMS) on board Nimbus 7. It detects elevated UV-absorbing aerosol layers by measuring the spectral contrast difference between a satellite observed radiance in a real atmosphere and a model simulated radiance in a Rayleigh atmosphere (Herman et al., 1997):
where the superscripts “obs” and “Ray” denote the radiance from observations and that from simulations, respectively; Iλ and Iλ0 are the radiance at wavelength λ and λ0, respectively; λ is the wavelength where the radiance difference between a Rayleigh and a measured scene is calculated; and λ0 is the longer wavelength where a spectrally constant scene reflectivity is assumed for the calculation of . A positive UVAI value indicates the presence of absorbing aerosols, whereas negative or near-zero values imply non-absorbing aerosols or clouds (Herman et al., 1997). The over 4 decades of UVAI observations (1978 to present) have been widely used for aerosol research. It would be beneficial to derive aerosol absorption properties from the long-term global UVAI records, e.g., the single scattering albedo (SSA), which is the ratio of aerosol scattering to aerosol extinction. Aerosols are considered to be the largest error source in radiative forcing assessments (IPCC, 2014), and SSA is one of the key parameters to reduce this uncertainty (Haywood and Shine, 1995).
The magnitude of UVAI depends on many factors (Herman et al., 1997; Torres et al., 1998; Hsu and Herman, 1999; de Graaf and Stammes, 2005). Although non-aerosol factors exist, such as spectral dependence of the surface, ocean color, sun glint and cloud contamination, the most dominant factors are aerosol concentration, aerosol vertical distribution and aerosol optical properties (Wang et al., 2012; Buchard et al., 2017). To derive SSA from UVAI, information on other two parameters (aerosol concentration and aerosol vertical distribution) are necessary. The aerosol concentration is usually provided in terms of the aerosol optical depth (AOD). There are many AOD products with wide spatial–temporal coverage. By contrast, there is much less information on the aerosol vertical distribution. The most well-known aerosol vertical distribution product is provided by the Cloud-Aerosol Lidar with Orthogonal Polarization (CALIOP), but the number of measurements is limited due to its narrow tracks (Winker et al., 2009). Passive sensors make efforts to retrieve the aerosol layer height (ALH) from columnar measurements. For example, Chimot et al. (2017) present the feasibility of ALH retrieval using the OMI oxygen band at 447 nm, Tilstra et al. (2018) developed an algorithm to derive absorbing aerosol layer height from GOME-2 FRESCO cloud layer height products and Xu et al. (2017, 2019) attempted to retrieve ALH from EPIC oxygen absorption bands for dust and carbonaceous layers over both land and ocean surfaces.
Recently a new ALH product has been run operationally, based on the measurements in the near-infrared (NIR) oxygen A-band of the TROPOspheric Monitoring Instrument (TROPOMI) on board the Copernicus Sentinel-5 Precursor (S-5P; Sanders et al., 2015). TROPOMI has a wide swath of 2600 km, providing daily global coverage with a spatial resolution of 7×3.5 km2 in nadir. The instrument is equipped with both the UV–visible (270–500 nm) and the near-infrared (NIR; 675–775 nm) channels, which can simultaneously provide UVAI and the co-located ALH product (Veefkind et al., 2015).
The purpose of this paper is to demonstrate the role of the ALH in quantifying aerosol absorption from UVAI using the newly released TROPOMI Level 2 ALH product. In the current phase, we only focus on biomass burning aerosols. Two experiments are conducted. First, following previous studies (Colarco et al., 2002; Hu et al., 2007; Jeong and Hsu, 2008; Sun et al., 2018), we create lookup tables (LUTs) of simulated UVAI for various aerosol optical properties by radiative transfer models (RTMs). SSA is then derived by minimizing the difference between pre-calculated UVAI and satellite observed values. The major uncertainties in the retrieved SSA are caused by assumptions regarding the wavelength-dependent refractive index and the availability of reliable aerosol vertical distribution information (Sun et al., 2018). Now, with the operational TROPOMI ALH constraining forward simulations, it is expected to partly reduce the SSA retrieval uncertainty while also quantifying the influence of assumed aerosol properties on the retrieved SSA.
Although the availability of ALH in radiative transfer calculations can improve the SSA retrieval, assumptions regarding aerosol microphysics remain inevitable. Therefore, in the second experiment, we propose an empirical method to predict aerosol absorption that is based on the long-term records of co-located UVAI, ALH, AOD and absorbing aerosol optical depth (AAOD) using machine learning (ML) techniques. ML algorithms learn the underlying behavior of a system from a given training data set. They are particularly useful to address ill-defined inversion problems in the field of geosciences and remote sensing, where theoretical understanding is incomplete but there is a significant number of observations (Lary et al., 2015). We employ ML techniques in order to avoid explicit assumptions regarding aerosol microphysics such as those made in the first experiment. Currently, ALH observations are not abundant; therefore, we will use the ALH provided in the OMAERUV product for the training procedure. Nevertheless, the recent TROPOMI ALH retrievals and other future ALH products mean that such empirical methods have great potential. Various ML algorithms have been developed to deal with classification or regression problems. In this paper, we choose support vector regression (SVR), a regression variant form of the support vector machines (SVMs; Drucker et al., 1997). Compared with other algorithms (e.g., the artificial neural network), SVR is less sensitive to the training data set size and can successfully work with a limited quantity of data (Mountrakis et al., 2011; Shin et al., 2005). We will present the capability of retrieving SSA from UVAI using this empirical method with the use of multiple case studies.
This paper is organized as follows: the first experiment is outlined in Sect. 2, including a description of the radiative transfer simulation settings and the analysis of the uncertainty trigger by the assumptions regarding aerosol absorption spectral dependence; Sect. 3 starts with introduction of SVR, followed by training data set preparation, SVR model hyper-parameter tuning, error analysis and case applications. Finally, the major conclusions and implications for future research are summarized in Sect. 4.
In this section, we present the first experiment that retrieves SSA using radiative transfer calculations as done in previous studies (Colarco et al., 2002; Hu et al., 2007; Jeong and Hsu, 2008; Sun et al., 2018). Forward radiative transfer simulations are realized by the DISAMAR (Determining Instrument Specifications and Analyzing Methods for Atmospheric Retrieval) radiative transfer model developed by the Royal Netherlands Meteorological Institute (KNMI; de Haan, 2011). Figure 1 illustrates the model inputs and the procedure. For each pixel, aerosol optical properties are first computed using Mie theory for various predefined aerosol models. DISAMAR then calculates UVAI using the corresponding satellite information: AOD, ALH, the solar zenith angle (θ0), the viewing zenith angle (θv), the solar azimuth angle (φ0), the viewing azimuth angle (φv), surface albedo (As) and the surface pressure (Ps) of the target pixel. The output of the forward simulations is a LUT of UVAI as a function of the input SSA (determined by the predefined aerosol models), which is fit by a second-order polynomial function. Finally, by specifying the corresponding satellite-observed UVAI, the SSA of the target pixel is estimated from the UVAI–SSA relationship. The retrieved SSA is reported at 500 nm in order to compare it with the results of the SVR method. Section 2.1 will introduce the input parameters for the radiative transfer simulations, followed by retrieval results in Sect. 2.2.
2.1 Radiative transfer simulation setup
2.1.1 Aerosol models
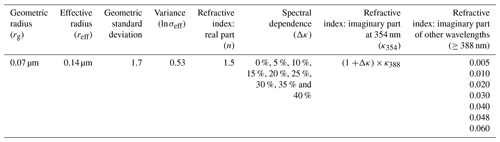
The aerosol models used for the Mie calculations are a combination of the aerosol models from the ESA Aerosol_cci project (Holzer-Popp et al., 2013) and the OMAERUV algorithm (Torres et al., 2007, 2013). We assume a fine-mode smoke aerosol type and further divide it into seven subtypes, as listed Table 1. We use the particle size distribution of the fine-mode strongly absorbing aerosol from the ESA Aerosol_cci project. The geometric radius (rg) is 0.07 µm (effective radius reff of 0.14 µm), and the geometric standard deviation (σg) is 1.7 (logarithmic variance ln σg of 0.53). The real part of the refractive index (n) uses the same value as in the OMAERUV algorithm, which is set to be 1.5 for all subtypes and is spectrally flat. We adopt the imaginary part of the refractive index at 388 nm (κ388) of the OMAERUV smoke subtypes (except for BIO-1 whose κ388 is 0) in our study and add a subtype with a κ388 of 0.06.
Many studies have shown evidence that absorption by biomass burning aerosols in the near-UV band has a strong spectral dependence (Kirchstetter et al., 2004; Bergstrom et al., 2007; Russell et al., 2010). Accordingly, a constant 20 % Δκ has been applied to all smoke subtypes in the recent OMAERUV algorithm (Jethva and Torres, 2011), where Δκ is defined as the relative difference between κ354 and κ388 (i.e., ). In this experiment, we will investigate how the retrieved SSA responds to the assumed spectral dependence by considering nine different Δκ values from 0 % (i.e., “gray” aerosols) to 40 % (very strong spectral dependence). This corresponds to an absorbing Ångström exponent (αabs) from 1 to 3.4 and from 1.3 to 4.7, depending on the aerosol subtype. Note that the Δκ is only applied between κ354 and κ388. As we only investigate the influence due to aerosol absorption spectral dependence in the near-UV range in this study, aerosol absorption at wavelengths larger than 388 nm is set equal to that at 388 nm.
To summarize, the first experiment consists of nine cases represented by different Δκ. Within each case, there are seven predefined aerosol subtypes with varying κ388. Thus, 63 forward simulations are performed for each individual pixel.
2.1.2 Inputs from satellite
Figure 1 presents the input parameters for the radiative transfer simulations of UVAI. Satellite measurement geometries (θ0, θv, φ0 and φv) and the surface pressure (Ps) from the TROPOMI UVAI reprocessed product (https://scihub.copernicus.eu, last access: 8 June 2018) are used as input for the forward simulations. The TROPOMI UVAI is calculated for two different wavelength pairs. One uses the conventional 340 and 380 nm wavelengths to continue the heritage of UVAI records from multiple sensors, and the other uses 354 and 388 nm in order to allow for comparison with OMI measurements (Stein Zweers, 2016). In this study we employ the 354 and 388 nm pair.
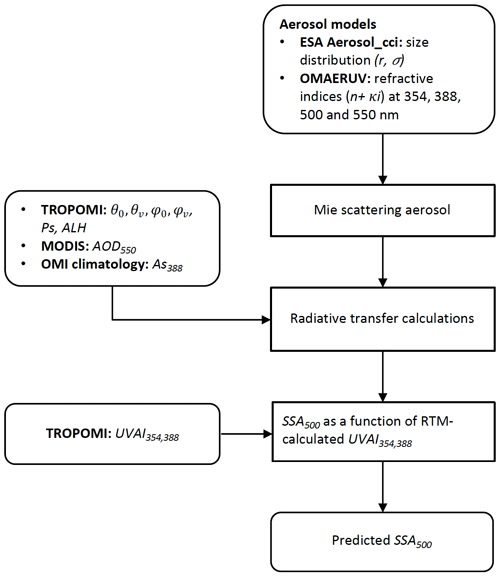
Figure 1Procedure of the radiative transfer simulation of UVAI. The aerosol models are from the ESA Aerosol_cci project (Holzer-Popp et al., 2013) and the OMAERUV algorithm (Torres et al., 2007, 2013). The satellite inputs are the TROPOMI measurement geometry and ALH, the MODIS AOD and the OMI surface climatology. The aerosol profile is parameterized as a one-layered box-shaped profile, with the central layer height set to the TROPOMI ALH and an assumed constant pressure thickness of 50 hPa.
TROPOMI ALH is retrieved at the oxygen A-band (759–770 nm), where the strong absorption of oxygen causes the highly structured spectrum (https://scihub.copernicus.eu, last access: 22 June 2018). This feature is particularly suitable for elevated, optically dense aerosol layers (Sanders et al., 2015; de Graaf et a., 2019). The ALH is reported in both altitude and pressure. For the forward radiative transfer calculations, the input aerosol profile is parameterized according to the settings in the ALH retrieval algorithm: a one-layered box-shaped profile, with a central layer height derived from TROPOMI and an assumed constant pressure thickness of 50 hPa (de Graaf et al., 2019). At the same band, there is the TROPOMI FRESCO cloud support product providing cloud fraction (CF) for mitigating cloud effects, as will be explained in the following (https://scihub.copernicus.eu last access: 19 September 2018) (Apituley et al., 2017; Wang et al., 2008).
The TROPOMI AOD product has not been operational; thus, we use AOD from the Level 2 MYD04 product (Collection 6) of Aqua MODIS (https://doi.org/10.5067/MODIS/MYD04_L2.006). Aqua has an overpass time similar to S-5P (13:30 LT – local time). The AOD at 550 nm used in the RTM-based method is a combination of the Deep_Blue_Aerosol_Optical_Depth_550_Land and the Effective_Optical_Depth_Op55um_Ocean (Levy et al., 2013).
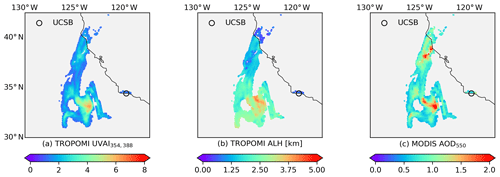
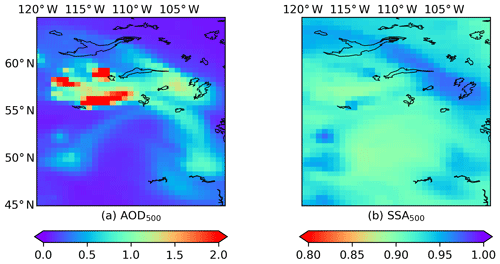
Figure 2Satellite data from the Californian fire event on 12 December 2017: (a) TROPOMI UVAI calculated by reflectance at 354 and 388 nm; (b) TROPOMI ALH (unit: km); (c) MODIS AOD at 550 nm.
The surface albedo that is used to retrieve TROPOMI UVAI is currently not available in the product. Instead, we use the Aura/OMI Level 3 Lambertian equivalent reflectance (LER) monthly climatology calculated from measurements between 2005 and 2009 (Kleipool et al., 2008) (Kleipool, 2010) (https://doi.org/10.5067/Aura/OMI/DATA3006). TROPOMI on S-5P and OMI on Aura have similar overpass times (13:30 LT) and measurement geometries (Levelt and Noordhoek, 2002; Veefkind et al., 2015).
Due to the different spatial resolutions, TROPOMI ALH, OMI LER climatology and MODIS AOD are resampled onto the TROPOMI UVAI grid. Before implementing radiative transfer calculations, preprocessing excludes pixels with a large solar zenith angle (θ0 > 70∘), weak aerosol absorption (UVAI354,388 < 1), insignificant aerosol amount (AOD550 < 0.5) or cloud contamination (CF > 0.3).
2.2 SSA retrieved by radiative transfer simulations
In the first experiment, we focus on one of the largest fire events that occurred in southern California in 2017, i.e., the Thomas Fire (http://www.fire.ca.gov/current_incidents/incidentdetails/Index/1922, last access: 25 November 2019). Figure A1 in Appendix A shows the RGB plume captured by MODIS on 12 December 2017. A brown smoke plume produced by the Thomas Fire was blown away from the continent and transported northwards. The major part of the plume was over the ocean and under cloud-free conditions, which is favorable for spaceborne aerosol observations. There is a total of 5217 pixels in this case. Figure 2 presents the UVAI, ALH and AOD data after preprocessing. The highest UVAI appeared at the southern part of the plume, where both the aerosol loading and aerosol layering were relatively high (AOD > 2 and ALH is over 2.5 km).
Figure 3a displays the mean SSA of all plume pixels retrieved by the RTM-based method as a function of Δκ. The retrieved aerosol absorption decreases with Δκ. This finding is in good agreement with Jethva and Torres (2011). “Gray” aerosols require stronger absorption to reach the same level of UVAI compared with “colored” aerosols. This also explains the high SSA standard deviation (filled area) in the cases with little or no spectral dependence on aerosol absorption. The large variability in retrieved SSA (from 0.69±0.13 to 0.94±0.03) demonstrates that inappropriate assumptions regarding the spectral dependence of near-UV aerosol absorption may significantly bias interpretations of smoke aerosol absorption and should be carefully handled in forward radiative transfer calculations.
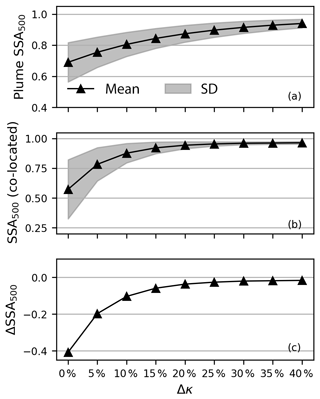
Figure 3SSA retrieved by radiative transfer simulations as a function of Δκ (): (a) SSA mean and standard deviation (filled region) of plume pixels; (b) SSA mean and standard deviation (filled region) of the 15 AERONET-co-located pixels; (c) absolute difference between the mean SSA of the 15 co-located pixels and the AERONET retrieval.
The retrieved aerosol absorption is compared with the nearby version 3 Level 1.5 AERONET inversion product (https://aeronet.gsfc.nasa.gov last access: 4 June 2019). Only one site is within 50 km of the TROPOMI plume pixels (Holben et al., 1998) (UCSB, located at 119.845∘ W, 34.415∘ N) with only one record for this case. The SSA at 500 nm at 18:54:47 UTC is 0.98 (sky radiance error 15.8 %), which is nearly 3 h ahead of the TROPOMI overpass. There are 15 TROPOMI pixels co-located with UCSB at a distance of within 50 km and a time difference of within 3 h. Hereafter we refer to them as AERONET-co-located pixels. As illustrated in Fig. 3b, the mean SSA of the co-located pixels also increases with Δκ and eventually levels off at around 0.96. The extremely low SSA and high variation (0.57±0.25) retrieved for “gray” aerosols prove that the assumption of spectral independence is not recommended for smoke aerosols.
Table 2Retrieved SSA using the radiative transfer simulations for the Californian fire on 12 December 2017.

The differences between the mean SSA of the co-located pixels and the AERONET measurement are shown in Fig. 3c. The retrieved SSA starts falling inside the uncertainty range of AERONET (±0.03) (Holben et al., 2006) when Δκ is 25 %, where the plume SSA is 0.90±0.05 and the AERONET-co-located SSA is 0.96±0.02 (Table 2). Table 2 also presents the SSA from the AOD retrieval from the OMAERUV version 3 product (https://doi.org/10.5067/Aura/OMI/DATA2004). OMI pixels are co-located with the AERONET site in the same fashion as TROPOMI. The SSA of the OMAERUV–AERONET co-located pixels is 0.06 lower than that of AERONET, which indicates that a 20 % spectral dependence of the aerosol absorption in OMAERUV algorithm may be not sufficient for this case. Although our retrieved SSA seems closer to the AERONET retrieved SSA than that provided by OMAERUV, one should keep in mind that there is only one record for this event, and that the meteorological conditions, combustion phases and even the aerosol compositions may change during the 3 h time difference.
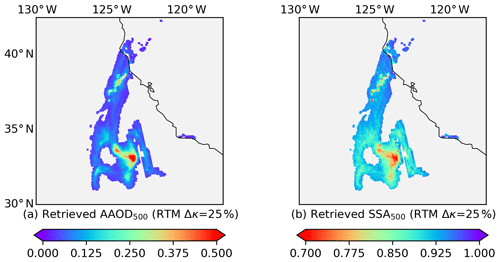
Figure 4 presents the spatial distribution of retrieved AAOD and SSA when Δκ is 25 %, which shows a strong heterogeneity in the horizontal direction. The plume center is most absorbing where the SSA is even less than 0.70. The SSA gradually increases when the plume is transported northwards. SSA is expected to be low near source flaming regions (Eck et al., 1998, 2003, 2013), whereas SSA may become higher when aerosols age during transport (Reid et al., 2005; Lewis et al., 2009). The strong spatial variability in SSA is mainly controlled by the heterogeneity of the UVAI (Fig. 3a) via the one-to-one numerical relationship. This relationship may differ from one pixel to another, as the algorithm focuses on one-pixel retrieval each time. Depending on the combustion phase and meteorological conditions, heterogeneity of the aerosol properties is expected for plume of this size. Nevertheless, whether such a large SSA difference of 0.38 (maximum SSA – minimum SSA, Table 2) is reasonable requires further investigation (discussed in Sect. 3.6.3).
In this section, we propose an empirical method to derive SSA as an alternative to the radiative transfer simulations presented in the first experiment. The motivation is that assumptions regarding aerosol microphysics in forward simulations are inevitable, although our knowledge to them is inadequate (particularly the aerosol absorption spectral dependence). An inappropriate assumption may lead to significant bias in retrieved SSA (Fig. 3). Conversely, SVR (and other ML algorithms) is applicable to solve ill-posed inversion problems by learning the underlying behavior of a system from a given data set without a priori knowledge of aerosol microphysics. In this paper, we construct a SVR model with UVAI, AOD and ALH as input features and AAOD as the output, and then derive the SSA using the following relationship:
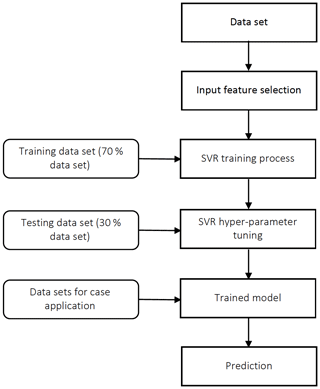
The procedure for SVR prediction is presented in Fig. 5. We start with a brief introduction of the SVR algorithm, followed by input feature selection (Sect. 3.2), training and testing data set preparation (Sect. 3.3), SVR model hyper-parameter tuning (Sect. 3.4), error analysis (Sect. 3.5) and case applications (Sect. 3.6).
3.1 Support vector regression
SVR (Drucker et al., 1997) is the regression variant of SVM, a supervised nonparametric statistical algorithm initially devised by Cortes and Vapnik (1995). The SVM algorithm is suitable for solving problems with small training data sets with a high-dimensional feature space and can provide excellent generalization performance (Durbha et al., 2007; Yao et al., 2008), which has been applied extensively to solve remote sensing problems (Lary et al., 2009; Mountrakis et al., 2011; Di Noia and Hasekamp, 2018). The basic ideal of SVM in classification problems is finding an optimal hyperplane in a high-dimensional feature space that maximizes the margin between the two classes to minimize misclassifications (Durbha et al., 2007). The same principle is applied to regression problems, where SVR attempts to find an optimal hyperplane that maximizes the margin of tolerance in order to minimize the prediction error. The error within the margin does not contribute to the total loss function, while samples on the margin are called support vectors.
For the detailed mathematical formulation of the SVR algorithm one can refer to Smola and Scholkopf (2004). Briefly, given the training data with n observations , the statistical model is assumed to be as follows:
where x is a multivariate input and y is a scalar output with length n; δ is the independent zero mean random noise. The input x is first mapped onto a feature space with dimension of m by a nonlinear transformation, and then a linear model f(x) is constructed based on it:
where the gj(x) is the nonlinear transformation, ωj is the model parameter vector and b is the bias. SVR tries to find the optical model from a set of approximate functions f(x). An approximate function is assessed by the loss function. In SVR, the loss function is defined as ε-insensitive loss:
Then the total empirical risk is as follows:
SVR performs linear regression in a high-dimension feature space using ε-insensitive loss, and reduces the model complexity by minimizing the norm ∥ω∥2. By introducing nonnegative slack variables (ξi and ) to measure the deviations of errors outside ε, SVR problems can be formulated as follows:
where C is a positive regularization constant determining the trade-off between model complexity and the degree to which deviations larger than ε are penalized. The optimization problem can be transferred into the dual problem by introducing Lagrange multipliers (αi and ) and the solution the becomes
where K(xi,x) is the kernel function that is positive semi-definite in order to satisfy Mercer's theorem. The kernel function enables the SVR to solve nonlinear problems.
According to the description above, we know that SVR generalization performance and estimation accuracy depend on the regularization constant C, the width of the tolerance margin ε and the kernel function K(xi,x). We will discuss how to determine the three hyper-parameters in Sect. 3.3.
3.2 Feature selection based on OMI and AERONET observations
Although SVR is able to deal with high-dimensional input features, feature selection is still important for generalization performance, computational efficiency and interpretational issues (Weston et al., 2001). Many sophisticated approaches have been devised for feature selection (Guyon and Elisseeff, 2003). In this study we choose features based on our empirical knowledge of UVAI and the Spearman rank correlation coefficients (ρ).
3.2.1 Collocating OMI and AERONET observations
The feature selection is based on the co-located OMAERUV version 3 product (https://doi.org/10.5067/Aura/OMI/DATA2004 last access: 17 October 2018) and AERONET version 3 Level 1.5 inversion product (https://aeronet.gsfc.nasa.gov, last access: 4 June 2019). OMAERUV is currently the only satellite product containing long-term UVAI, AOD, SSA and corresponding ALH data (Torres et al., 2007, 2013). Its AOD was validated by the multiyear AERONET record (Ahn et al., 2014), and its SSA was evaluated by AERONET almucantar retrievals (Jethva et al., 2014). The ALH is the best-guess value, either from CALIOP climatology or assumed ALH in the retrieval (if the CALIOP climatology is not available) (Torres et al., 2013). As a result, one should keep in mind that the ALH from OMAERUV may suffer from the uncertainties of CALIOP climatology and a priori assumptions, as well as collocation error between OMI pixels and the CALIOP footprint. It is also noted that there are two official OMI aerosol Level 2 products, although the OMI measurements in this paper only refer to the OMAERUV product.
We collect the measurements of OMAERUV and AERONET from 1 January 2005 to 31 December 2017. OMI pixels with θ0 larger than 70∘ or a cloud fraction larger than 0.1 are excluded. OMI observations are then considered to be co-located with an AERONET site if their spatial distance is within 50 km and their temporal difference is within 3 h. To ensure consistency between the different measurement techniques (ground-based and spaceborne), we also exclude samples if the SSA difference between OMAERUV and AERONET is larger than 0.03, or the AOD difference between OMAERUV and AERONET is larger than 5 %. The AERONET SSA and AAOD are linearly interpolated to 500 nm, as OMAERUV reports them at this wavelength. In total, 5679 samples are obtained. Figure B1 in the Appendix shows the global distribution of the co-located OMAERUV–AERONET samples. Note that these samples are not restricted to biomass burning areas, but may also contain other aerosol types.
3.2.2 Feature selection
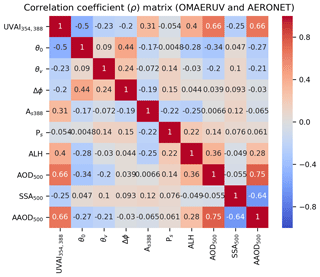
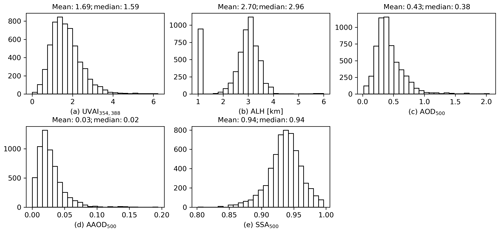
The OMAERUV–AERONET joint data set consists of the following parameters: UVAI calculated using the 354 and 388 nm wavelength pair, satellite geometries, surface albedo, surface pressure and ALH from OMAERUV, and SSA, AOD and AAOD from AERONET. Note that the UVAI used here is the “residue” field in the original OMAERUV product, where the simulated radiance ( in Eq. 1) is calculated by a simple Lambertian approximation that is consistent with TROPOMI UVAI (Torres et al., 2018). Figure 6 presents the Spearman rank correlation coefficients matrix (ρ) of those parameters. It is clear that except for AAOD, SSA is barely associated with other parameters. The correlation between UVAI and SSA is rather low (). Conversely, AAOD is highly associated with UVAI (ρ=0.66) as well as AOD (ρ=0.66) as it carries information on both aerosol absorption and aerosol loading. Therefore, it is preferred to predict AAOD from given UVAI and derive SSA via Eq. (2) afterwards rather than to directly predicting SSA from UVAI. Furthermore, as previously mentioned, AOD and ALH are the major factors influencing UVAI, which is also reflected by the relatively stronger correlation (ρ=0.4). Consequently, we construct a SVR model with UVAI, ALH and AOD as the input features, and AAOD as the output. The UVAI is also dependent on θ0; however in this study, we only focus on the aerosol-related features.
3.3 Preparing training and testing data sets
The SVR model is trained and tested based on the OMAERUV–AERONET joint data set that contains 8616 samples, as described in the last section (consisting of UVAI, ALH from OMAERUV, and AOD, AAOD from AERONET). We further partition it into a training data set and a testing data set, respectively. The testing data set is used to evaluate the generalization performance of a SVR model trained by the training data set in order to avoid high bias (underfitting) or high variance (overfitting) problems. The empirical ratio between the training data set and the testing data set is 70 % versus 30 %; thus, there are 3975 samples in the training data set and 1704 samples in the testing data set.
3.4 SVR hyper-parameters tuning
As described in Sect. 3.1, the generalization performance and model accuracy of the SVR depends on the following hyper-parameters: (1) the width of insensitive zone ε – the cost function does not consider errors in the training data as long as their deviation to the truth is smaller than ε; (2) the regularization constant C that determines the trade-off between model complexity and the degree to which deviations larger than ε are penalized; and (3) the choice of the kernel and its parameters. We adopt the methodology from Cherkassky and Ma (2004), where the SVR parameter C and ε can be directly determined from the statistics of the training data set:
where and σy are the mean and standard deviation of the output parameter in the training data set, respectively; σ is the input noise level (we set it to 0.001); and n is the number of training samples. The values determined for C and ε are shown in Table 3. We employ the widely used radial basis function (RBF) kernel function to solve the nonlinearity in the SVR model. Compared with other kernel functions, RBF is relatively less complex and more efficient. The RBF kernel is defined as
where p is the kernel width parameter that reflects the influencing area of support vectors. This parameter is determined by hyper-tuning on the testing data set (Durbha et al., 2007) (explained below).
Table 3Values for the regularization constant C, decided by Eq.(9); the width of the insensitive zone ε, decided by Eq.(10); and the BRF kernel parameter p2, decided by hyper-parameter tuning.

The RMSE of the training process may overestimate the accuracy of a SVR model, because the training and predicting processes are based on the same data set. Instead, an independent testing data set is used to represent the accuracy of the SVR model. The difference of model accuracy between training and testing process reflects the generalization performance of the SVR model. An ideal SVR model should output a low-level RMSE and the discrepancy between the training and testing process should also be small. If the RMSE of the testing process is much larger than that of the training process, the SVR may suffer from overfitting problems. Figure 7 shows the hyper-parameter tuning process. Figure 7a–c is the RMSE of the training process as a function of C and ε, Fig. 7d–f is the RMSE relative difference between the testing process and the training process and the columns indicate different values of p. The cross markers indicate values of C and ε determined by Eqs. (9) and (10). It is clear that when p2=1.67, the RMSE of training process is relatively small, as is the model accuracy difference between the training process and the testing process. The final values of C, ε and p that will be applied in the case studies are listed in Table 3. The corresponding RMSE of AAOD predicted by the training process and the testing process are at a level of 0.01 (Fig. 8a).
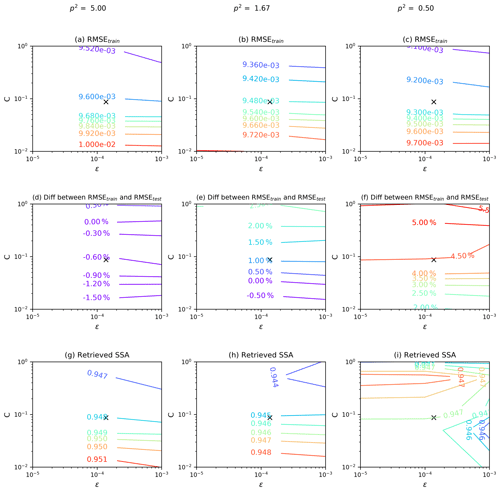
Figure 7The performance of the SVR model as a function of hyper-parameters (C, ε and p). The cross markers represent the values of C and ε according to Cherkassky and Ma (2004). A p2 value equal to 1.67 is sufficient to obtain a relatively high accuracy and also prevents overfitting of the training data set.
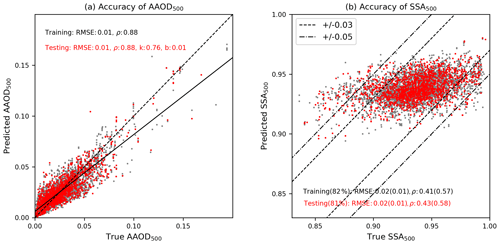
Figure 8The accuracy of the trained SVR model: (a) the predicted AAOD at 500 nm against the true AAOD at 500 nm. The dashed line is the 1:1 line, and the solid line is the linear fitting for the testing data set; (b) the predicted SSA at 500 nm against true SSA at 500 nm. Gray and red indicate samples in training and testing data sets, respectively. The values in parentheses are the statistics for samples that fall within an AERONET uncertainty of 0.03.
3.5 Error analysis
The error sources of SSA retrieval using a SVR model depends on the model accuracy as well as the quality of input data. The model accuracy can be represented by the RMSE of the testing process (0.01). As shown in Fig. 8a, the SVR model has difficult predicting AAOD values larger than 0.05, and most significant biases appear at this range. The uncertainty in AAOD is passed to the SSA by Eq. (2). Figure 8b shows the retrieved SSA in the training and testing processes. It is noted that the predicted SSA is generally positively biased, particularly in relatively stronger absorption cases (SSA <0.90). This bias is possibly due to the bias in the feature domain, where the UVAI is relatively strongly correlated with other factors (i.e., AOD and ALH) that may contain redundant information which adversely impacts model performance (Weston et al., 2001; Durbha et al., 2007). A more sophisticated feature selection scheme is suggested to reduce the redundancy, e.g., Minimum Redundancy Maximum Relevance (mRMR, Peng et al., 2005). Moreover, the RBF kernel function may not capable enough to solve the nonlinearity among the training data sets. The accuracy of SSA predicted by the testing data set is ±0.02, with 82 % of samples falling into the uncertainty range (±0.03) of the true SSA (AERONET) and their accuracy is even higher (±0.01).
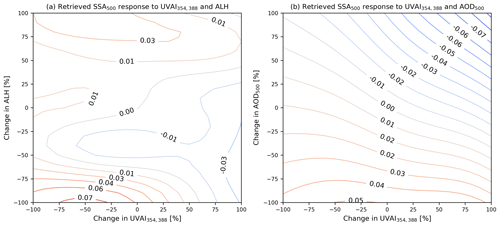
Figure 9The sensitivity of the SVR-retrieved SSA: (a) the response of predicted SSA at 500 nm as a function of changes in UVAI and ALH; (b) the response of predicted SSA at 500 nm as a function of changes in UVAI and AOD.
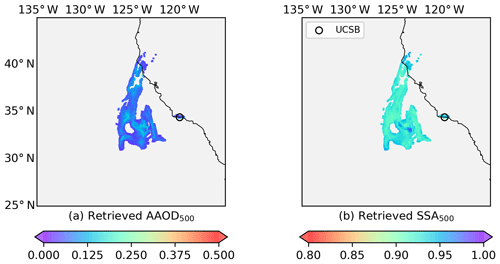
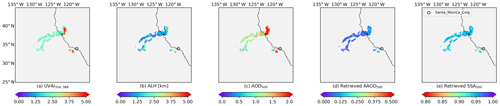
Figure 10SVR retrievals for the Californian fire event on 12 December 2017: (a) retrieved AAOD at 500 nm; (b) retrieved SSA at 500 nm.
The error of the retrieved SSA due to the input features may come from the observational or retrieval uncertainties in each parameter. In our case, the typical UVAI bias requirement is at a magnitude of 1 (Lambert et al., 2019). It is reported that TROPOMI UVAI suffers from the long-term downward wavelength-dependent trend in irradiance (Rozemeijer and Kleipool, 2018). The detected degradation in UVAI354,388 has been around 0.2 since August 2018 (Lambert et al., 2019). The typical accuracy of TROPOMI ALH is 50 hPa, although in some situations the bias may exceed this value (e.g., low aerosol loading over bright surface) (Sanders et al., 2016). Depending on the retrieval algorithm, the uncertainty of MODIS AOD is %AODAERONET (Dark Target algorithm) (Levy et al., 2010) or AODMODIS (Deep Blue algorithm) (Sayer et al., 2014). The SSA sensitivity to input features is presented in Fig. 9. We use the mean value of each parameter in the OMAERUV–AERONET data set as reference values (Fig. B2, UVAI =1.59, ALH =2.96 km, AOD =0.39), and the corresponding SSA value is 0.94. The positive bias of UVAI always leads to an underestimation of SSA, unless the aerosol layer is located at a relatively high altitude or aerosol loading is low. Conversely, the insufficient UVAI causes the overestimation of SSA, except for cases where the ALH is low or the AOD is high. The sensitivity of SSA to UVAI is weaker when the aerosol layer is close to the surface or at a very high altitude. The sensitivity of SSA to UVAI always increases with AOD.
3.6 Case applications
Once the hyper-parameters are determined (Sect. 3.4), the trained SVR model is ready to predict aerosol absorption. The first application is the Californian fire event in December 2017 (Sect. 3.6.2), which is the same as that in the first experiment. To demonstrate the generalization capability of the SVR model, we also apply it to other fire events as long as there are co-located TROPOMI and MODIS measurements and AERONET-retrieved SSA available for comparison (Sect. 3.6.2).
For all applications, the input parameters in the SVR model are TROPOMI UVAI (calculated using the 354 and 388 nm wavelength pair), TROPOMI ALH and MODIS AOD, respectively. The MODIS AOD at 550 nm is converted to 500 nm using the Ångström exponent (α) provided by the co-located AERONET site. Note that the data include pixels with a CF larger than 0.1 in order to ensure that there are satellite measurements co-located with the AERONET sites (although the CF is no larger than 0.3).
3.6.1 Californian fire event on 12 December 2017
Figure 10 presents the retrieved AAOD and corresponding SSA. It is noted that UVAI and AOD are higher in the center of the plume, whereas ALH is relatively lower (Fig. 2). The SSA should be smaller to compensate for the low altitude of the aerosol layer according to Fig. 9. However, the SVR-retrieved SSA is even higher than its surroundings. This is because the UVAI and AOD retrievals are outside of the distribution of the corresponding parameters in this region, as shown in Fig. B2. The 13-year OMAERUV–AERONET joint data cannot cover some extreme situations. The reason for this may be that the joint data set is relatively small as a result of data availability and collocation criteria, or that the quality of the joint data suffers from observational or retrieval uncertainties. As a result, the SVR model fails to handle the input values outside of the range of the training data set.
Table 4SVR-retrieved SSA. If no standard deviation is given, it indicates that only one record was available.
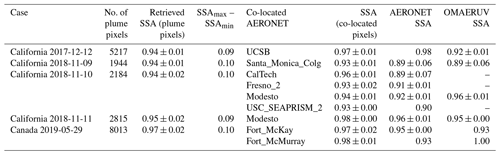
The SSA of the all plume pixels is 0.94±0.01 (including the failed pixel predictions) and that for the AERONET-co-located pixels (pixels within 50 km of UCSB) is 0.97±0.01 (Table 4). These values may be overestimated, whereas the standard deviation may be underestimated due to the SVR prediction failures of some samples. The SSA difference relative to the AERONET retrieval is only 0.01, which is within the uncertainty range of AERONET (±0.03).
3.6.2 Other case applications
To present the generalization performance of SVR, we apply it to other fire events as long as there is co-located information from TROPOMI, MODIS and AERONET. The same preprocessing is applied as in the previous case in order to exclude pixels with UVAI values smaller than 1, AOD values smaller than 0.5 or CF values larger than 0.3.
Figures 11–13 present the Californian fire events during the period from 9 to 11 November 2018. The plumes were over ocean but were partly contaminated by the underlying clouds (Figs. A2, A3 and A4 present the Aqua MODIS RGB images). Figure 14 shows the Canadian fire event on 29 May 2019. This case was over land (Fig. A5 present the Aqua MODIS RGB image), which means that the brighter surface may cause a higher bias in the input AOD and ALH than cases over dark surfaces (Remer, 2005; de Graaf et al., 2019).
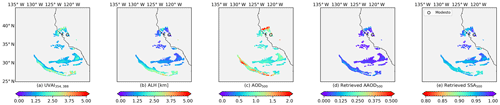
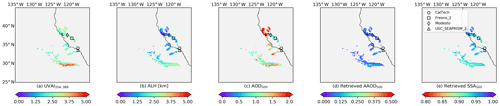
Figure 13SVR retrievals for the Californian fire event on 11 November 2018: (a) TROPOMI UVAI calculated by reflectance at 354 and 388 nm; (b) TROPOMI ALH; (c) MODIS AOD at 550 nm; (d) retrieved AAOD at 500 nm; (e) retrieved SSA at 500 nm.
The retrieved SSA for the abovementioned events is listed in Table 4. Similar to the Californian case on 12 December 2017, The SVR fails to retrieve reasonable SSA for pixels if input features fall outside their corresponding histogram in the OMAERUV–AERONET data (Fig. 2b), which may cause overestimations in plume mean SSA. The plume SSA of two Californian fire events are similar, with values of around 0.94–0.95. The retrieved SSA for the Canadian fire is relatively higher (0.97).
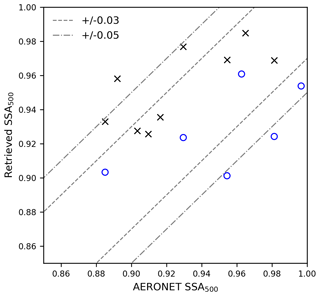
We further plot the SSA retrieved by SVR against co-located AERONET records (black crosses in Fig. 15). Including the first case (Californian fire on 12 December 2017), there are nine co-located records obtained. The difference between SVR-retrieved SSA and AERONET are almost within ±0.05, among which over half (five out of nine) fall within the AERONET SSA uncertainty range (±0.03). We also provide SSA from OMAERUV for these cases (Table 4 and blue circles in Fig. 15). Compared with OMAERUV, the SSA retrieved by SVR shows a better consistency with AERONET, although one should keep in mind that the accuracy of SVR-retrieved SSA is ±0.02 and the model tends to overestimate the SSA for relatively absorbing cases.
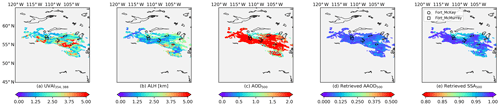
Figure 14SVR retrievals for the Canadian fire event on 29 May 2019: (a) TROPOMI UVAI calculated by reflectance at 354 and 388 nm; (b) TROPOMI ALH; (c) MODIS AOD at 550 nm; (d) retrieved AAOD at 500 nm; (e) retrieved SSA at 500 nm.
3.6.3 Spatial variability of retrieved SSA
Compared with Fig. 4b, the spatial variability of SSA retrieved by SVR is less strong (Figs. 10–14): the difference between maximum and minimum SSA ranges from 0.09 to 0.10 (Table 4). In the first experiment, SSA is determined by UVAI for each pixel individually. In the SVR model, the spatial variability of the intermediate output AAOD depends on the three input features. Furthermore, SVR predicts SSA for each pixel based on the common relationship between UVAI, AOD and ALH in the training data set.
Heterogeneity in aerosol properties is expected for plume of this size; however, the extent of this heterogeneity requires further investigation. Here we assess the SSA spatial variability of an independent data set. We employ the SSA calculated by AOD and scattering AOD from the MERRA-2 aerosol reanalysis hourly single-level product (https://disc.gsfc.nasa.gov/datacollection/M2T1NXAER_5.12.4.htm last access: 16 July 2019). The AOD and aerosol properties of MERRA-2 have proved to be in good agreement with independent measurements (Buchard et al., 2017; Randles et al., 2017). The MERRA-2 AOD and SSA for these cases are shown in Appendix C. The plume can be detected using high AOD values against their surrounding. Although the plume presented by the satellite observations significantly differs from that of model simulations, the SSA spatial difference within the plume is at an approximate magnitude of 0.1. From this aspect, the spatial variability of SSA retrieved by the SVR model is in better agreement with MERRA-2.
The long-term record of global UVAI data is a treasure with respect to deriving aerosol optical properties such as SSA, which is important for aerosol radiative forcing assessments. To quantify aerosol absorption from UVAI, information on AOD and ALH is necessary. Various AOD products are available, whereas ALH products are much less accessible. Recently, the TROPOMI oxygen A-band ALH product has been run operationally; using this product, we demonstrate the role of ALH in quantifying SSA from satellite retrieved UVAI for biomass burning aerosols.
In the first experiment, we derive the SSA using a forward radiative transfer simulation of UVAI for a fire event in California on 12 December 2017. Using the TROPOMI ALH, we are able to quantify the influence of assumed spectral dependence of near-UV aerosol absorption (represented by the relative difference between κ354 and κ388) on the retrieved SSA. A significant gap in plume mean SSA (0.25) between “gray” and strong spectral dependent aerosols (Δκ=0 % and 40 %, respectively) implies that inappropriate assumptions regarding spectral dependence may significantly bias the retrieved aerosol absorption. The SSA difference between AERONET and co-located pixels becomes smaller than the uncertainty of AERONET (±0.03) when Δκ=25 %. The corresponding plume SSA is 0.90±0.05, and the AERONET-co-located pixels' SSA is 0.96±0.02.
In the second part of this paper, we propose a statistical method based on the long-term records of UVAI, AOD, ALH and AAOD using a SVR algorithm, in order to avoid making the assumption of the aerosol absorption spectral dependence in the near-UV band. The SVR model is trained using 5679 co-located global observations from OMAERUV and AERONET during the period from 2005 to 2017. The SVR-retrieved SSA for the Californian fire event on 12 December 2017 is 0.97±0.01, which is 0.01 lower than that of AERONET. The SVR algorithm is also applied to other cases. Considering all of the case applications, the results are encouraging: the SSA discrepancy between retrievals and AERONET for almost all co-located samples is within ±0.05, and over half of them fall within the AERONET uncertainty range (±0.03). One should keep in mind that the SVR model tends to overestimate the SSA for relatively absorbing cases (e.g., SSA <0.90), and sometimes fails to predict reasonable SSA when the input values fall outside the range of the corresponding parameters in the training data set.
In terms of spatial variability, the SSA retrieved by radiative transfer simulations significantly differs from that retrieved by SVR. Spatial heterogeneity in SSA is expected, but the extent of this heterogeneity requires further investigation. We employ the SSA provided by the MERRA-2 aerosol reanalysis as a reference, and the spatial difference of this data within smoke plume is at a magnitude of approximately 0.1. The spatial pattern of SSA retrieved by SVR shows better agreement with this finding.
In this study, we present the potential to retrieve SSA based on long-term data records of UVAI, ALH, AOD and AAOD using a statistical method. The motivation is to avoid a priori assumptions on aerosol microphysics such as those made in the radiative transfer simulations. In the current phase, we choose the SVR algorithm as the training data set is relatively small. The input features are selected by the Spearman rank correlation coefficients and a priori knowledge on the relationship between UVAI and aerosol-related features. The model hyper-parameters are analytically determined. The accuracy of SVR-predicted SSA is ±0.02, with a higher tendency to overestimate the SSA for relatively absorbing cases. The OMAERUV–AERONET data set cannot cover some extreme situations, and, as a result, the SVR fails to predict reasonable SSA when the input values fall outside the range of the corresponding parameters in the training data set. In the future, more sophisticated feature selection techniques and kernel functions should be considered to improve the accuracy the algorithm. Other non-aerosol features affecting UVAI should also be taken into consideration. Moreover, the high-resolution TROPOMI Level 2 UVAI and ALH products are expected to significantly increase the size and improve the quality of the training data set, which will reduce the computational failures of the SVR model and even guide use to more powerful algorithms (e.g., ANN) to retrieve SSA.
All data used in this study can be freely accessed. The OMI/Aura Near UV Aerosol Optical Depth and Single Scattering Albedo 1-orbit L2 Swath 13×24 km V003 (OMAERUV version 3) is provided by the Goddard Earth Sciences Data and Information Services Center (GES DISC) and can be accessed via https://doi.org/10.5067/Aura/OMI/DATA2004 (Torres, 2016). The OMI/Aura Surface Reflectance Climatology L3 Global Gridded V3 (OMLER) is also provided by GES DISC and can be accessed via https://doi.org/10.5067/Aura/OMI/DATA3006 (Kleipool, 2010). The TROPOMI ROPOMI/S5P Aerosol Index 1-Orbit L2 Swath 7×3.5 km (L2_AER_AI), TROPOMI/S5P Aerosol Layer Height 1-Orbit L2 Swath yx3.5 km (L2_AER_LH) and TROPOMI/S5P FRESCO Cloud 1-Orbit L2 Swath 7×3.5 km (L2_FRESCO) are provided by Copernicus Sentinel data processed by the European Space Agency (ESA) and the Koninklijk Nederlands Meteorologisch Instituut (KNMI) and can be accessed via https://s5phub.copernicus.eu/dhus/#/home (last access: 19 September 2018). The MODIS/Aqua Aerosol 5-Min L2 Swath 10 km (MYD04_L2) is provided by the MODIS Atmosphere Science Team/Aerosol Retrieval Group, MODIS Adaptive Processing System (MODAPS) and can be accessed via https://doi.org/10.5067/MODIS/MYD04_L2.006 (Levy et al., 2015). The AERONET version 3 inversion product is provided by the NASA Goddard Space Flight Center and can be accessed via https://aeronet.gsfc.nasa.gov (NASA Goddard Space Flight Center, 2019). The radiative transfer model DISAMAR is proprietary; thus, it is not shared with the public. All of the results from this study are available with the permission of authors, and can be obtained upon request from jiyunting.sun@knmi.nl.

Figure A1Smoke plume captured by Aqua MODIS for the Californian fire event on 12 December 2017 (source: https://gibs.earthdata.nasa.gov, last access: 27 September 2018). The red regions indicate fires and thermal anomalies.

Figure A2Smoke plume captured by Aqua MODIS for the Californian fire event on 9 November 2018 (source: https://gibs.earthdata.nasa.gov, last access: 7 August 2019). The red regions indicate fires and thermal anomalies.

Figure A3Smoke plume captured by Aqua MODIS for the Californian fire event on 10 November 2018 (source: https://gibs.earthdata.nasa.gov, last access: 7 August 2019). The red regions indicate fires and thermal anomalies.

Figure A4Smoke plume captured by Aqua MODIS for the Californian fire event on 11 November 2018 (source: https://gibs.earthdata.nasa.gov, last access: 7 August 2019). The red regions indicate fires and thermal anomalies.

Figure A5Smoke plume captured by Aqua MODIS for the Canadian fire event on 29 May 2019 (source: https://gibs.earthdata.nasa.gov, last access: 7 August 2019). The red regions indicate fires and thermal anomalies.
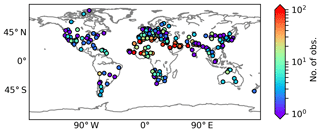
Figure B1Global distribution of the OMAERUV–AERONET joint data set. The color indicates the number of observations. Note that all aerosol types are included.
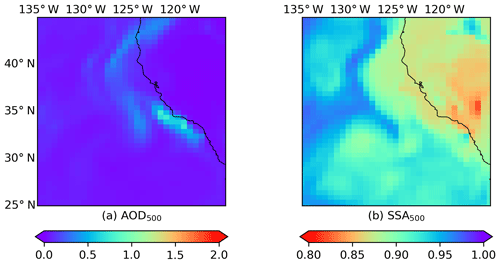
Figure C1MERRA-2 M2T1NXAER averaged between 12:00 and 15:00 LT for the Californian fire event on 12 December 2017: (a) AOD at 500 nm; (b) SSA at 500 nm.
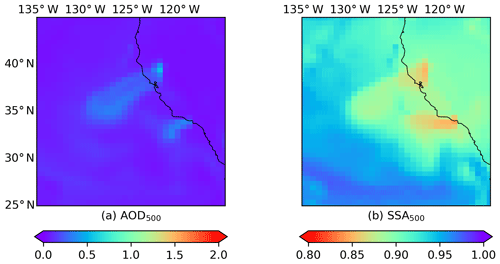
Figure C2MERRA-2 M2T1NXAER averaged between 12:00 and 15:00 LT for the Californian fire event on 9 November 2018: (a) AOD at 500 nm; (b) SSA at 500 nm.
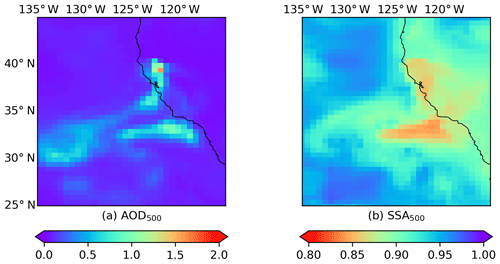
Figure C3MERRA-2 M2T1NXAER averaged between 12:00 and 15:00 LT for the Californian fire event on 10 November 2018: (a) AOD at 500 nm; (b) SSA at 500 nm.
JS, PPV and PvV conceived the study. JS was the main contributor with respect to preparing the paper, and received guidance from PV, PvV and PL. SN created and provided the TROPOMI Level 2 ALH data (at this time the product has not yet been released).
The authors declare that they have no conflict of interest.
This article is part of the special issue TROPOMI on Sentinel-5 Precursor: first year in operation (AMT/ACPT inter-journal SI)”. It is not associated with a conference.
This work was performed in the framework of the KNMI Multi-Annual Strategic Research (MSO). The authors thank NASA's GES-DISC and LAADS DAAC for free online access to the OMI and MODIS data. The authors thank the NASA Goddard Space Flight Center AERONET project for providing the data from the AERONET. The authors thank Swadhin Nanda for providing the TROPOMI aerosol layer height product.
This paper was edited by Ben Veihelmann and reviewed by Omar Torres and one anonymous referee.
Ahn, C., Torres, O., and Jethva, H.: Assessment of OMI near-UV aerosol optical depth over land, J. Geophys. Res.-Atmospheres, 119, 2457–2473, 2014.
Apituley, A., Pedergnana, M., Sneep, M., Veefkind, J. P., Loyola, D. and Wang, P.: Level 2 Product User Manual KNMI level 2 support products, KNMI, the Netherlands, 118 pp., 2017.
Bergstrom, R. W., Pilewskie, P., Russell, P. B., Redemann, J., Bond, T. C., Quinn, P. K., and Sierau, B.: Spectral absorption properties of atmospheric aerosols, Atmos. Chem. Phys., 7, 5937–5943, https://doi.org/10.5194/acp-7-5937-2007, 2007.
Buchard, V., Randles, C. A., da Silva, A. M., Darmenov, A., Colarco, P. R., Govindaraju, R., Ferrare, R., Hair, J., Beyersdorf, A. J., Ziemba, L. D., and Yu, H.: The MERRA-2 aerosol reanalysis, 1980 onward. Part II: Evaluation and case studies, J. Climate, 30, 6851–6872, https://doi.org/10.1175/JCLI-D-16-0613.1, 2017.
Cherkassky, V. and Ma, Y.: Practical selection of SVM parameters and noise estimation for SVM regression, Neural Networks, 17, 113–126, https://doi.org/10.1016/S0893-6080(03)00169-2, 2004.
Chimot, J., Veefkind, J. P., Vlemmix, T., de Haan, J. F., Amiridis, V., Proestakis, E., Marinou, E., and Levelt, P. F.: An exploratory study on the aerosol height retrieval from OMI measurements of the 477 nm O2 – O2 spectral band using a neural network approach, Atmos. Meas. Tech., 10, 783–809, https://doi.org/10.5194/amt-10-783-2017, 2017.
Colarco, P. R., Toon, O. B., Torres, O., and Rasch, P. J.: Determining the UV imaginary index of refraction of Saharan dust particles from Total Ozone Mapping Spectrometer data using a three-dimensional model of dust transport, J. Geophys. Res., 107, 1–19, 2002.
Cortes, C. and Vapnik, V.: Support-Vector Networks, IEEE Expert, 7, 63–72, https://doi.org/10.1109/64.163674, 1995.
de Graaf, M. and Stammes, P.: SCIAMACHY Absorbing Aerosol Index – calibration issues and global results from 2002–2004, Atmos. Chem. Phys., 5, 2385–2394, https://doi.org/10.5194/acp-5-2385-2005, 2005.
e Haan, J. F.: DISAMAR Algorithm description and background information, KNMI, the Netherlands, 122 pp., 2011.
de Graaf, M., de Haan, J. F., and Sanders, A. F. J.: TROPOMI ATBD of the Aerosol Layer Height product., S5P-KNMI-L2-0006-RP, 1.1.0, 81 pp., 2019.
Di Noia, A. and Hasekamp, O. P.: Neural Networks and Support Vector Machines and Their Application to Aerosol and Cloud Remote Sensing: A Review, Springer, Cham, 279–329, 2018.
Drucker, H., Burges, C. J., Kaufman, L., Smola, A. J., and Vapnik, V.: Support vector regression Machines, Adv. Neural Inf. Process. Syst., 155–161, https://doi.org/10.1145/2768566.2768568, 1997.
Durbha, S. S., King, R. L., and Younan, N. H.: Support vector machines regression for retrieval of leaf area index from multiangle imaging spectroradiometer, Remote Sens. Environ., 107, 348–36, https://doi.org/10.1016/j.rse.2006.09.031, 2007.
Eck, T. F., Holben, B. N., Slutsker, I., and Setzer, A.: Measurements of irradiance attenuation and estimation of aerosol single scattering albedo for biomass burning aerosols in Amazonia, J. Geophys. Res.-Atmos., 103, 31865–31878, 1998.
Eck, T. F., Holben, B. N., Ward, D. E., Mukelabai, M. M., Dubovik, O., Smirnov, A., Schafer, J. S., Hsu, N. C., Piketh, S. J., Queface, A., Roux, J. Le, Swap, R. J., and Slutsker, I.: Variability of biomass burning aerosol optical characteristics in southern Africa during the SAFARI 2000 dry season campaign and a comparison of single scattering albedo estimates from radiometric measurements, J. Geophys. Res., 108, 8477, https://doi.org/10.1029/2002JD002321, 2003.
Eck, T. F., Holben, B. N., Reid, J. S., Mukelabai, M. M., Piketh, S. J., Torres, O., Jethva, H. T., Hyer, E. J., Ward, D. E., Dubovik, O., Sinyuk, A., Schafer, J. S., Giles, D. M., Sorokin, M., Smirnov, A., and Slutsker, I.: A seasonal trend of single scattering albedo in southern African biomass-burning particles : Implications for satellite products and estimates of emissions for the world's largest biomass-burning source, J. Geophys. Res., 118, 6414–6432, https://doi.org/10.1002/jgrd.50500, 2013.
Guyon, I. and Elisseeff, A.: An Introduction to Variable and Feature Selection, J. Mach. Learn. Res., 3, 1157–1182, https://doi.org/10.1016/j.aca.2011.07.027, 2003.
Haywood, J. M. and Shine, K. P.: The effect of anthropogenic sulfate and soot aerosol on the clear sky planetary radiation budget, Geophys. Res. Lett., 22, 603–606, https://doi.org/10.1029/95GL00075, 1995.
Herman, J. R., Bhartia, P. K., Torres, O., Hsu, C., Seftor, C., and Celarier, E.: Global distribution of UV-absorbing aerosols from Nimbus 7/TOMS data, J. Geophys. Res., 102, 16911, https://doi.org/10.1029/96JD03680, 1997.
Holben, B. N., Eck, T. F., Slutsker, I., Tanré, D., Buis, J. P., Setzer, A., Vermote, E., Reagan, J. A., Kaufman, Y. J., Nakajima, T., Lavenu, F., Jankowiak, I., and Smirnov, A.: AERONET – A federated instrument network and data archive for aerosol characterization, Remote Sens. Environ., 66, 1–16, https://doi.org/10.1016/S0034-4257(98)00031-5, 1998.
Holben, B. N., Eck, T. F., Slutsker, I., Smirnov, A., Sinyuk, A., Schafer, J., and Dubovik, O.: AERONET's version 2.0 quality assurance criteria, Proc. SPIE 6408, Remote Sensing of the Atmosphere and Clouds, 64080Q, https://doi.org/10.1117/12.706524, 2006.
Holzer-Popp, T., de Leeuw, G., Griesfeller, J., Martynenko, D., Klüser, L., Bevan, S., Davies, W., Ducos, F., Deuzé, J. L., Graigner, R. G., Heckel, A., von Hoyningen-Hüne, W., Kolmonen, P., Litvinov, P., North, P., Poulsen, C. A., Ramon, D., Siddans, R., Sogacheva, L., Tanre, D., Thomas, G. E., Vountas, M., Descloitres, J., Griesfeller, J., Kinne, S., Schulz, M., and Pinnock, S.: Aerosol retrieval experiments in the ESA Aerosol_cci project, Atmos. Meas. Tech., 6, 1919–1957, https://doi.org/10.5194/amt-6-1919-2013, 2013.
Hsu, N. C. and Herman, J. R.: Comparisons of the TOMS aerosol index with Sun-photometer aerosol optical thickness: Results and applications, J. Geophys. Res., 104, 6269–6279, https://doi.org/10.1029/1998JD200086, 1999.
Hu, R. M., Martin, R. V., and Fairlie, T. D.: Global retrieval of columnar aerosol single scattering albedo from space-based observations, J. Geophys. Res.-Atmos., 112, https://doi.org/10.1029/2005JD006832, 2007.
IPCC: Climate Change 2014 Synthesis Report, Geneva, available at: http://www.ipcc.ch/pdf/assessment-report/ar5/syr/SYR_AR5_FINAL_full.pdf (last access: 9 July 2017), 2014.
Jeong, M. J. and Hsu, N. C.: Retrievals of aerosol single-scattering albedo and effective aerosol layer height for biomass-burning smoke: Synergy derived from “A-Train” sensors, Geophys. Res. Lett., 35, 1–6, https://doi.org/10.1029/2008GL036279, 2008.
Jethva, H. and Torres, O.: Satellite-based evidence of wavelength-dependent aerosol absorption in biomass burning smoke inferred from Ozone Monitoring Instrument, Atmos. Chem. Phys., 11, 10541–10551, https://doi.org/10.5194/acp-11-10541-2011, 2011.
Jethva, H., Torres, O., and Ahn, C.: Global assessment of OMI aerosol single-scattering albedo using ground-based AERONET inversion, J. Geophys. Res., 119, 9020–9040, https://doi.org/10.1002/2014JD021672, 2014.
Kirchstetter, T. W., Novakov, T. and Hobbs, P. V.: Evidence that the spectral dependence of light absorption by aerosols is affected by organic carbon, J. Geophys. Res.-Atmos., 109, 1–12, https://doi.org/10.1029/2004JD004999, 2004.
Kleipool, Q.: OMI/Aura Surface Reflectance Climatology L3 Global Gridded 0.5 degree x 0.5 degree V3, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC), https://doi.org/10.5067/Aura/OMI/DATA3006, 2010.
Kleipool, Q. L., Dobber, M. R., de Haan, J. F., and Levelt, P. F.: Earth surface reflectance climatology from 3 years of OMI data, J. Geophys. Res.-Atmos., 113, 1–22, https://doi.org/10.1029/2008JD010290, 2008.
Lambert, J.-C., Keppens, A., Hubert, D., Langerock, B., Eichmann, K.-U., Kleipool, Q., Sneep, M., Verhoelst, T., Wagner, T., Weber, M., Ahn, C., Argyrouli, A., Balis, D., Chan, K. L., Compernolle, S., De Smedt, I., Eskes, H., Fjæraa, A. M., Garane, K., Gleason, J. F., Goutail, F., Granville, J., Hedelt, P., Heue, K.-P., Jaross, G., Koukouli, M. L., Landgraf, J., Lutz, R., Niemejer, S., Pazmiño, A., Pinardi, G., Pommereau, J.-P., Richter, A., Rozemeijer, N., Sha, M. K., Stein Zweers, D., Theys, N., Tilstra, G., Torres, O., Valks, P., Vigouroux, C., and Wang, P.: Quarterly Validation Report of the Copernicus Sentinel-5 Precursor Operational Data Products – #03: July 2018–May 2019, S5P MPC Routine Operations Consolidated Validation Report series, Issue #03, Version 03.0.1, 125 pp., June, 2019.
Lary, D. J., Alavi, A. H., Gandomi, A. H., and Walker, A. L.: Machine learning in geosciences and remote sensing, Geosci. Front., 7, 3–10, 2015.
Lary, D. J., Remer, L. A., MacNeill, D., Roscoe, B., and Paradise, S.: Machine Learning and Bias Correction of MODIS Aerosol Optical Depth, IEEE Geosci. Remote S., 6, 694–698, https://doi.org/10.1109/LGRS.2009.2023605, 2009.
Levelt, P. F. and Noordhoek, R.: OMI algorithm theoretical basis document, I, ATBD, OMI-OI, 1–50, 2002.
Levy, R. C., Remer, L. A., Kleidman, R. G., Mattoo, S., Ichoku, C., Kahn, R., and Eck, T. F.: Global evaluation of the Collection 5 MODIS dark-target aerosol products over land, Atmos. Chem. Phys., 10, 10399–10420, https://doi.org/10.5194/acp-10-10399-2010, 2010.
Levy, R. C., Mattoo, S., Munchak, L. A., Remer, L. A., Sayer, A. M., Patadia, F., and Hsu, N. C.: The Collection 6 MODIS aerosol products over land and ocean, Atmos. Meas. Tech., 6, 2989–3034, https://doi.org/10.5194/amt-6-2989-2013, 2013.
Levy, R., Hsu, C., et al.: MODIS Atmosphere L2 Aerosol Product. NASA MODIS Adaptive Processing System, Goddard Space Flight Center, USA, https://doi.org/10.5067/MODIS/MOD04_L2.006, 2015.
Lewis, K. A., Arnott, W. P., Moosmüller, H., Chakrabarty, R. K., Carrico, C. M., Kreidenweis, S. M., Day, D. E., Malm, W. C., Laskin, A., Jimenez, J. L., Ulbrich, I. M., Huffman, J. A., Onasch, T. B., Trimborn, A., Liu, L., and Mishchenko, M. I.: Reduction in biomass burning aerosol light absorption upon humidification: Roles of inorganically-induced hygroscopicity, particle collapse, and photoacoustic heat and mass transfer, Atmos. Chem. Phys., 9, 8949–8966, https://doi.org/10.5194/acp-9-8949-2009, 2009.
Mountrakis, G., Im, J., and Ogole, C.: Support vector machines in remote sensing: A review, ISPRS J. Photogramm. Remote Sens., 66, 247–259, https://doi.org/10.1016/j.isprsjprs.2010.11.001, 2011.
NASA Goddard Space Flight Center: AERONET version 3 inversion product, available at: https://aeronet.gsfc.nasa.gov, last access: 4 June 2019.
Peng, H., Long, F., and Ding, C.: Feature Selection Based on Mutual Information (mRMR), IEEE T. Pattern Anal., 27, 1226–1238, https://doi.org/10.1007/978-3-319-03200-9_4, 2005.
Randles, C. A., da Silva, A. M., Buchard, V., Colarco, P. R., Darmenov, A., Govindaraju, R., Smirnov, A., Holben, B., Ferrare, R., Hair, J., Shinozuka, Y., and Flynn, C. J.: The MERRA-2 aerosol reanalysis, 1980 onward. Part I: System description and data assimilation evaluation, J. Climate, 30, 6823–6850, https://doi.org/10.1175/JCLI-D-16-0609.1, 2017.
Reid, J. S., Eck, T. F., Christopher, S. A., Koppmann, R., Dubovik, O., Eleuterio, D. P., Holben, B. N., Reid, E. A., and Zhang, J.: A review of biomass burning emissions part III: intensive optical properties of biomass burning particles, Atmos. Chem. Phys., 5, 827–849, https://doi.org/10.5194/acp-5-827-2005, 2005.
Remer, L. A.: The MODIS Aerosol Algorithm, Products, and Validation, J. Atmos. Sci., 62, 947–973, 2005.
Rozemeijer, N. C. and Kleipool, Q.: S5P Mission Performance Centre Level 1b Readme, S5P-MPC-KNMI-PRF-L1B, 1.0.0, 16 pp., 2018.
Russell, P. B., Bergstrom, R. W., Shinozuka, Y., Clarke, A. D., DeCarlo, P. F., Jimenez, J. L., Livingston, J. M., Redemann, J., Dubovik, O., and Strawa, A.: Absorption Angstrom Exponent in AERONET and related data as an indicator of aerosol composition, Atmos. Chem. Phys., 10, 1155–1169, https://doi.org/10.5194/acp-10-1155-2010, 2010.
Sanders, A. F. J., de Haan, J. F., Sneep, M., Apituley, A., Stammes, P., Vieitez, M. O., Tilstra, L. G., Tuinder, O. N. E., Koning, C. E., and Veefkind, J. P.: Evaluation of the operational Aerosol Layer Height retrieval algorithm for Sentinel-5 Precursor: application to O2 A band observations from GOME-2A, Atmos. Meas. Tech., 8, 4947–4977, https://doi.org/10.5194/amt-8-4947-2015, 2015.
Sayer, A. M., Hsu, N. C., Bettenhausen, C., and Jeong, M.: Validation and uncertainty estimates for MODIS Collection 6 “Deep Blue” aerosol data, 118, 7864–7873, https://doi.org/10.1002/jgrd.50600, 2014.
Shin, K. S., Lee, T. S., and Kim, H. J.: An application of support vector machines in bankruptcy prediction model, Expert Syst. Appl., 28, 127–135, https://doi.org/10.1016/j.eswa.2004.08.009, 2005.
Smola, A. J. and Scholkopf, B.: A tutorial on support vector regression, Stat. Comput., 14, 199–222, https://doi.org/10.1023/B:STCO.0000035301.49549.88, 2004.
Stein Zweers, D. C.: TROPOMI ATBD of the UV aerosol index, S5P-KNMI-L2-0008-RP, 1.1, 30 pp., 2016.
Sun, J., Veefkind, J. P., van Velthoven, P., and Levelt, P. F.: Quantifying the single-scattering albedo for the January 2017 Chile wildfires from simulations of the OMI absorbing aerosol index, Atmos. Meas. Tech., 11, 5261–5277, https://doi.org/10.5194/amt-11-5261-2018, 2018.
Tilstra, L. G., Wang, P., and Stammes, P.: ALGORITHM THEORETICAL GOME-2 Absorbing Aerosol Height, SAF/AC/KNMI/ATBD/005, 1.4, 32 pp., 2018.
Torres, O. O.: OMI/Aura Near UV Aerosol Optical Depth and Single Scattering Albedo 1-orbit L2 Swath 13x24 km V003, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC), https://doi.org/10.5067/Aura/OMI/DATA2004, 2006.
Torres, O., Bhartia, P. K., Herman, J. R., Ahmad, Z., and Gleason, J.: Derivation of aerosol properties from satellite measurements of backscattered ultraviolet radiation: Theoretical basis, J. Geophys. Res.-Atmos., 103, 17099–17110, https://doi.org/10.1029/98JD00900, 1998.
Torres, O., Tanskanen, A., Veihelmann, B., Ahn, C., Braak, R., Bhartia, P. K., Veefkind, P., and Levelt, P.: Aerosols and surface UV products from Ozone Monitoring Instrument observations: An overview, J. Geophys. Res., 112, D24S47, https://doi.org/10.1029/2007JD008809, 2007.
Torres, O., Ahn, C., and Chen, Z.: Improvements to the OMI near-UV aerosol algorithm using A-train CALIOP and AIRS observations, Atmos. Meas. Tech., 6, 3257–3270, https://doi.org/10.5194/amt-6-3257-2013, 2013.
Torres, O., Bhartia, P. K., Jethva, H., and Ahn, C.: Impact of the ozone monitoring instrument row anomaly on the long-term record of aerosol products, Atmos. Meas. Tech., 11, 2701–2715, https://doi.org/10.5194/amt-11-2701-2018, 2018.
Veefkind, J. P., Aben, I., Mcmullan, K., Förster, H., Vries, J. De, Otter, G., Claas, J., Eskes, H. J., Haan, J. F. De, Kleipool, Q., Weele, M. Van, Hasekamp, O., Hoogeveen, R., Landgraf, J., Snel, R., Tol, P., Ingmann, P., Voors, R., Kruizinga, B., Vink, R., Visser, H., and Levelt, P. F.: Remote Sensing of Environment TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications, Remote Sens. Environ., 120, 70–83, https://doi.org/10.1016/j.rse.2011.09.027, 2015.
Wang, P., Stammes, P., van der A, R., Pinardi, G., and van Roozendael, M.: FRESCO+: an improved O2 A-band cloud retrieval algorithm for tropospheric trace gas retrievals, Atmos. Chem. Phys., 8, 6565–6576, https://doi.org/10.5194/acp-8-6565-2008, 2008.
Wang, P., Tuinder, O. N. E., Tilstra, L. G., de Graaf, M., and Stammes, P.: Interpretation of FRESCO cloud retrievals in case of absorbing aerosol events, Atmos. Chem. Phys., 12, 9057–9077, https://doi.org/10.5194/acp-12-9057-2012, 2012.
Weston, J., Mukherjee, S., Chapelle, O., Pontil, M., Poggio, T., and Vapnik, V.: Feature selection for SVMs, in: Advances in neural information processing systems, 3–8 December 2001, Vancouver, British Columbia, Canada, Neural Information Processing Systems 2001 (NIPS*2001), 668–674, 2001.
Winker, D. M., Vaughan, M. A., Omar, A., Hu, Y., Powell, K. A., Liu, Z., Hunt, W. H., and Young, S. A.: Overview of the CALIPSO mission and CALIOP data processing algorithms, J. Atmos. Ocean. Tech., 26, 2310–2323, https://doi.org/10.1175/2009JTECHA1281.1, 2009.
Xu, X., Wang, J., Wang, Y., Zeng, J., Torres, O., Yang, Y., Marshak, A., Reid, J., and Miller, S.: Passive remote sensing of altitude and optical depth of dust plumes using the oxygen A and B bands: First results from EPIC/DSCOVR at Lagrange-1 point, Geophys. Res. Lett., 44, 7544–7554, https://doi.org/10.1002/2017GL073939, 2017.
Xu, X., Wang, J., Wang, Y., Zeng, J., Torres, O., Reid, J. S., Miller, S. D., Martins, J. V., and Remer, L. A.: Detecting layer height of smoke aerosols over vegetated land and water surfaces via oxygen absorption bands: hourly results from EPIC/DSCOVR in deep space, Atmos. Meas. Tech., 12, 3269–3288, https://doi.org/10.5194/amt-12-3269-2019, 2019.
Yao, X., Tham, L. G., and Dai, F. C.: Landslide susceptibility mapping based on Support Vector Machine: A case study on natural slopes of Hong Kong, China, Geomorphology, 101, 572–582, https://doi.org/10.1016/j.geomorph.2008.02.011, 2008.
- Abstract
- Introduction
- Experiment 1: SSA retrieval using radiative transfer simulations
- Experiment 2: SSA retrieval using support vector regression
- Conclusions
- Data availability
- Appendix A: Case information
- Appendix B: OMI–AERONET joint data set (based on global data from 1 January 2005 to 31 December 2017).
- Appendix C: MERRA-2 aerosol reanalysis.
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Review statement
- References
- Abstract
- Introduction
- Experiment 1: SSA retrieval using radiative transfer simulations
- Experiment 2: SSA retrieval using support vector regression
- Conclusions
- Data availability
- Appendix A: Case information
- Appendix B: OMI–AERONET joint data set (based on global data from 1 January 2005 to 31 December 2017).
- Appendix C: MERRA-2 aerosol reanalysis.
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Review statement
- References