the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A novel post-processing algorithm for Halo Doppler lidars
Ville Vakkari
Antti J. Manninen
Ewan J. O'Connor
Jan H. Schween
Pieter G. van Zyl
Eleni Marinou
Commercially available Doppler lidars have now been proven to be efficient tools for studying winds and turbulence in the planetary boundary layer. However, in many cases low signal-to-noise ratio is still a limiting factor for utilising measurements by these devices. Here, we present a novel post-processing algorithm for Halo Stream Line Doppler lidars, which enables an improvement in sensitivity of a factor of 5 or more. This algorithm is based on improving the accuracy of the instrumental noise floor and it enables longer integration times or averaging of high temporal resolution data to be used to obtain signals down to −32 dB. While this algorithm does not affect the measured radial velocity, it improves the accuracy of radial velocity uncertainty estimates and consequently the accuracy of retrieved turbulent properties. Field measurements using three different Halo Doppler lidars deployed in Finland, Greece and South Africa demonstrate how the new post-processing algorithm increases data availability for turbulent retrievals in the planetary boundary layer, improves detection of high-altitude cirrus clouds and enables the observation of elevated aerosol layers.
Turbulent mixing in the planetary boundary layer (PBL) is one of the most important processes for air quality, weather and climate (e.g. Garratt, 1994; Baklanov et al., 2011; Ryan, 2016). Mixing layer height (MLH), i.e. the height of the layer that is connected with the surface on timescales of less than 1 h, is a central parameter describing PBL turbulence (e.g. Seibert et al., 2000). Continuous measurement of MLH with good temporal resolution is not trivial, though. For instance, aerosol backscatter profiles have been commonly used to estimate MLH (Seibert et al., 2000; Pal et al., 2013). The benefit is that aerosol backscatter profiles can be obtained routinely with high temporal resolution (e.g. Emeis et al., 2008), but as this method is not a direct measure of turbulent mixing, it is prone to erroneous interpretation, especially during morning and evening transition periods of the convective PBL (Schween et al., 2014).
Development of fibre-optic Doppler lidar systems during the last 5 to 10 years has enabled direct, long-term observation of MLH with temporal resolutions of typically a few minutes or better (e.g. Tucker et al., 2009; O'Connor et al., 2010; Pearson et al., 2010; Schween et al., 2014; Vakkari et al., 2015; Smalikho and Banakhm 2017; Bonin et al., 2017, 2018). Long-range Doppler lidar systems typically have a blind range with a minimum usable distance of 50–100 m; hence scanning Doppler lidar is the only realistic option for covering the full range of MLH from close to ground level up to a few kilometres with good temporal resolution (Vakkari et al., 2015).
In addition to MLH, fibre-optic Doppler lidar systems have also enabled long-term monitoring of horizontal wind profiles within the PBL (Hirsikko et al., 2014; Päschke et al., 2015; Newsom et al., 2017; Marke et al., 2018). Together with vertical profiles of higher moments of the velocity distribution (Lothon et al., 2009), e.g vertical wind speed variance and skewness, as well as turbulent kinetic energy dissipation rate, Doppler lidar measurements enable the diagnosis of the sources of turbulence within the PBL (Hogan et al., 2009; Harvey et al., 2013; Tuononen et al., 2017; Manninen et al., 2018).
Velocity measurements using fibre-optic Doppler lidar systems operating at 1.5 µm wavelength depend on light scattering from aerosol particles and cloud droplets as these are small enough to behave as tracers of atmospheric motion. In very clean atmospheric environments, the lack of scattering particles becomes a limiting factor for utilising these systems (e.g. Manninen et al., 2016). Development of new, more powerful yet eye-safe Doppler lidar systems has helped to overcome this limitation to a large degree (e.g. Bonin et al., 2018); yet decreasing the instrumental noise level through post-processing of the data allows the utilisation of weaker signals and can lead to major improvements in data coverage (Manninen et al., 2016). The post-processing algorithm by Manninen et al. (2016) has the added benefit of improving the accuracy of the signal-to-noise ratio (SNR), which leads to more accurate uncertainty estimates of the measured radial velocity (Rye and Hardesty, 1993; Pearson et al., 2009). This is especially important for the retrieval of turbulent properties under weak signal conditions, as uncertainty in instrumental noise level propagates into turbulent properties and wind retrievals (O'Connor et al., 2010; Vakkari et al., 2015; Newsom et al., 2017). Naturally, post-processing methods can be applied to historical data sets as well.
Here we present an improved post-processing algorithm for Halo Photonics Stream Line Doppler lidars, which are currently widely used for PBL research (O'Connor et al., 2010; Pearson et al., 2010; Harvey et al., 2013; Hirsikko et al., 2014; Schween et al., 2014; Päschke et al., 2015; Vakkari et al., 2015; Banakh and Smalikho, 2016; Tuononen et al., 2017; Bonin et al., 2018). Building on the work by Manninen et al. (2016), we show that, by changing the way instrumental noise level is determined during periodic background checks, the sensitivity can be improved by as much as a factor of 5; by averaging high time resolution data, signals with an SNR as low as −32 dB can be utilised. Case studies from different environments in Finland, Greece and South Africa are presented to demonstrate how the new post-processing algorithm increases data availability for turbulent retrievals in the PBL, improves detection of high-altitude cirrus clouds and enables observation of elevated aerosol layers 2 to 4 km above ground level.
Next, in Sect. 2 we introduce the Halo Photonics Stream Line, Stream Line Pro and Stream Line XR lidars used in this study. Section 3 describes the improved SNR post-processing algorithm, and in Sect. 4 the three case studies are presented, followed by concluding remarks.
In this study we utilise data from three different versions of Halo Photonics scanning Doppler lidars (Pearson et al., 2009): lidar 46 is a Stream Line system, lidar 53 is a Stream Line Pro system and lidar 146 is a Stream Line XR system. All Halo Photonics Stream Line versions are 1.5 µm pulsed Doppler lidars with a heterodyne detector that can switch between co- and cross-polar channels (Pearson et al., 2009). The Stream Line and the more powerful Stream Line XR lidars are capable of full hemispheric scanning, and the scanning patterns are user-configurable. The Stream Line Pro version is designed for harsher environmental conditions with no exterior moving parts, which limits the scanning to within a cone of 20∘ from the vertical. In this study, however, we only utilise vertically pointing measurements in co-polar mode, and thus there is no practical difference between the limited and fully scanning versions.
The minimum range for all instruments is 90 m, and standard operating specifications for the different versions are given in Table 1. The telescope focus of the Stream Line and Stream Line Pro lidars is user-configurable between 300 m and infinity, whereas the Stream Line XR focus cannot be changed. Integration time per ray is user-adjustable and can be optimised between high sensitivity (long integration time) and high temporal resolution (short integration time) depending on the environmental conditions and research questions. In the measurements utilised in this study, 7 s integration time is used for lidars 46 and 53, while lidar 146 is operated with 10 s integration time.
In measurement mode the Halo Doppler lidars provide three parameters along the beam direction: radial Doppler velocity (vr), SNR and attenuated backscatter (β), which is calculated from SNR taking into account the telescope focus. As part of post-processing, we calculate the measurement uncertainty in vr (σvr) from SNR according to O'Connor et al. (2010). As discussed earlier, in calculating turbulent parameters from Doppler lidar observations, accurate σvr is needed to differentiate turbulence from instrumental noise (e.g. O'Connor et al., 2010; Vakkari et al., 2015; Newsom et al., 2017).
We present case studies of Halo Doppler lidar measurements at three different locations with three different instruments. Lidar 53 was deployed at Finokalia, Crete, Greece (35.34∘ N, 25.67∘ E), on 8 July 2014. Lidar 46 was deployed at Welgegund, South Africa (26.57∘ S, 26.94∘ E), on 6 September 2016 and lidar 146 was deployed at Helsinki, Finland (60.20∘ N, 24.96∘ E), on 1 and 6 May 2018.
Additionally, we utilise collocated Raman lidar measurements at Finokalia. These measurements were carried out using the OCEANET PollyXT multiwavelength Raman and polarization lidar system of the Leibniz Institute for Tropospheric Research (TROPOS). A detailed description of the instrument and its measurements is provided in Engelmann et al. (2016) and Baars et al. (2016), respectively. In brief, PollyXT operates using a Nd:YAG laser that emits light pulses at 1064 nm with a repetition frequency of 20 Hz. The radiation frequency is doubled and tripled, resulting in the simultaneous emission of 355, 532 and 1064 nm in the atmosphere. The receiver features 12 channels that enable measurements of elastically (three channels) and Raman scattered light (387 and 607 channels for aerosols, 407 for water vapour) as well as depolarisation state of the incoming light (355 and 532 nm) and near-range measurements (two elastic and two aerosol Raman channels). In this study, the measurements at 1064 nm are used. The lidar measurements at Finokalia were collected during the 2014 CHARacterization of Aerosol mixtures of Dust and Marine origin experiment (CHARADMExp) on the northern coast of Crete, Greece.
3.1 Signal-to-noise ratio in Halo Doppler lidars
Halo Doppler lidars measure the noise level during periodic background checks, typically once an hour, in which the scanner is set to point to an internal (limited scan) or external target mounted on the instrument itself (hemispheric scan) so that no atmospheric signal is recorded. The raw signal from the amplifier during the background check (Pbkg) is saved as a profile in ASCII files (“Background_ddmmyy-HHMMSS.txt”) with the range resolution configured for the normal measurement mode. For most Stream Line and Stream Line Pro firmware versions, Pbkg is written on one line with a fixed precision of six decimals but a varying field width for each range gate. In Stream Line XR firmware, the Pbkg value at each range gate is written on its own line.
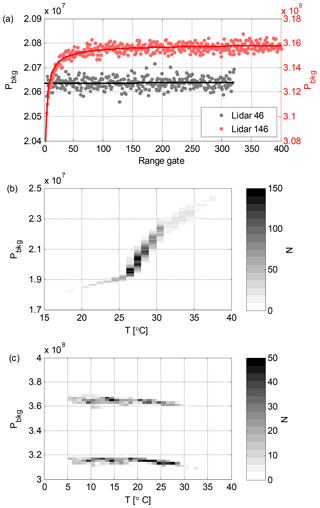
Figure 1(a) Pbkg measured by lidar 46 on 6 September 2016 at 23:00 UTC and Pbkg measured by lidar 146 on 1 May 2018 at 10:00 UTC. Pfit is also indicated for both systems. (b) 2-D histogram of mean Pbkg vs. T for lidar 46. (c) 2-D histogram of mean Pbkg vs. T for lidar 146.
In most Stream Line and Stream Line Pro instruments, the profile Pbkg(z) is flat (constant with range) or presents a small linear increase with increasing distance z from the lidar (Fig. 1a); Pbkg(z) following a second-order polynomial can also occur (Manninen et al., 2016). For Stream Line XR instruments, Pbkg(z) can vary between a linear and an inverse exponential shape (Fig. 1a), for which the inverse exponential Pbkg(z) can be represented as
where b1, b2 and b3 are scalars and can be determined from a least-squares fit.
In Stream Line and Stream Line Pro lidars, the magnitude of Pbkg increases non-linearly with instrument internal temperature (T) (Fig. 1b). For Stream Line XR lidars, which use a different amplifier, the mean Pbkg does not depend on T; however, the amplifier alternates randomly between a high mode ( for lidar 146) and a low mode ( for lidar 146) as seen in Fig. 1c. Furthermore, it appears that the inverse exponential Pbkg shape only occurs in the low mode, but not all low-mode Pbkg profiles follow Eq. (1).
The Halo Doppler lidar firmware accounts for changes in Pbkg level by calculating SNR as
where P0(z) is the raw signal from the amplifier during each measurement, Pbkg(z) has been obtained during the previous background check and scalar scaling factors A0 and Abkg are determined online for each P0 andPbkg profile. Here, we denote the unprocessed SNR output by the instrument as SNR0. Note that A0 and Abkg are not saved by the firmware, which means that the high and low mode in Stream Line XR lidars cannot be identified in the SNR0 time series.
Equation (2) is straightforward to determine online as there are no assumptions about the shape of Pbkg, and it gives a reasonably good first estimate of SNR. However, Eq. (2) is vulnerable to inaccuracy in determining A0 and Abkg as well as to any deviation from the actual noise level during measurement of Pbkg. An offset in A0 inflicts a constant offset in SNR0 in a single profile, while an offset in Abkg does the same for all profiles between two background checks (cf. Manninen et al., 2016). The magnitude of typical offsets in A0 and Abkg varies from instrument to instrument; in some cases they can have a major effect on data coverage (Manninen et al., 2016).
In all Halo Doppler lidars Pbkg contains a small but varying offset from the actual noise level at each range gate because of the finite duration of the background check. These offsets appear as a small constant offset in SNR0 at each range gate between two background checks. To minimise the effect of offset in Pbkg, the integration time of background check measurement was originally designed to be 6 times as long as the integration time in measurement mode. The duration of the background check is user-configurable; however, for long integration times of up to 6 min considered in this paper such long background checks are not a viable option. In the next section we present an improved algorithm to correct SNR0 for inaccuracies in A0, Abkg and Pbkg.
3.2 Improved SNR post-processing algorithm
Whether Pbkg(z) is linear or follows some other functional form is readily determined by fitting expected functions to it (cf. Manninen et al., 2016). For Stream Line and Stream Line Pro lidars we consider a second-order polynomial to represent Pbkg(z) better than a linear fit if it has at least 10 % lower root-mean-squared (rms) error than the linear fit to Pbkg(z). For Stream Line XR we consider Eq. (1) to represent Pbkg(z) better if it has at least 5 % lower rms error than the linear fit to Pbkg(z). Furthermore, knowing the typical noise level of a certain instrument, a rms threshold can be applied to discard bad fits and to flag periods of increased uncertainty.
Denoting the selected fit to Pbkg(z) as Pfit(z), the residual is
Averaging Pbkg,res(z) over a large number of Pbkg(z) profiles reveals a persistent structure in the residual (Fig. 2a). This part of Pbkg,res(z) originates in the amplifier response to the transmitted pulse, denoted here as Pamp(z), and it is the main reason for using the gate-by-gate defined Pbkg(z) profile in SNR calculation by the manufacturer. However, Pamp(z) stays reasonably constant over time and can be obtained from a long enough data set of Pbkg(z). Here, we used a discrete wavelet transform with a Symmlet order 8 wavelet as a low-pass filter to de-noise the averaged Pbkg,res(z). As shown in Fig. 2a, Pamp(z) is instrument-specific and needs to be determined individually for each device.
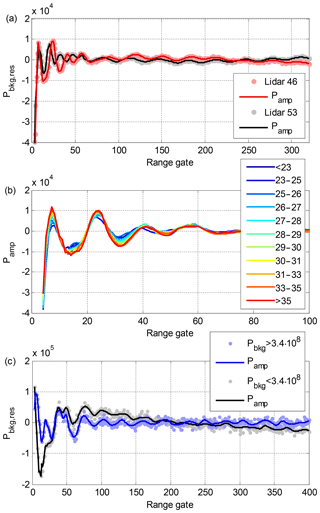
Figure 2(a) Lidar 46 Pbkg,res averaged from 20 August 2016 to 14 June 2017 (7193 background checks). Lidar 53 Pbkg,res averaged from 1 January 2014 to 30 November 2015 (16 802 background checks). Pamp is plotted for both systems. (b) First 100 range gates of lidar 46 Pamp calculated for different ranges of T. (c) Lidar 146 Pbkg,res averaged from 12 January to 31 May 2018. Pbkg,res is averaged separately for high Pbkg mode (1375 background checks) and for low Pbkg mode (1623 background checks). Pamp is plotted for both modes.
In Stream Line and Stream Line Pro lidars, T has a small effect on Pamp(z) as seen in Fig. 2b. However, this can be addressed based on a suitably long T data set and Pbkg,res(z) by determining Pamp(z) as a function of the internal temperature. In practice, at least 300 Pbkg(z) profiles are required to obtain a reliable estimate of Pamp(z). Consequently, for an 11-month measurement campaign at Welgegund, we could determine Pamp as a function of T at 1 ∘C resolution from 25 to 31 ∘C (Fig. 2b). For T<23 ∘C or T>35 ∘C we could only determine aggregate Pamp profiles, but then these temperature ranges comprise only 9 % of the measurements in this data set. For optimal data quality, additional temperature stabilisation could be applied to ensure that Pamp is always in the well-characterised temperature range.
In Stream Line XR lidars, Pamp does not depend on T; however, Pamp has to be determined separately for the high and low mode of Pbkg (see Fig. 1c). For lidar 146, we define Pbkg high mode as mean and Pbkg low mode as mean , respectively. As seen in Fig. 2c, Pamp for these two modes differs substantially.
We consider the sum of Pfit(z) and Pamp(z) as the best estimate for the actual instrumental noise level during a background check:
Using Eq. (2), we can move from a Pbkg-based SNR (i.e. SNR0) to a Pnoise-based, corrected SNR (denoted here as SNR1) simply as
Next, we utilise the Manninen et al. (2016) algorithm to identify any possible bias in the A0 to Abkg ratio. In short, Manninen et al. (2016) cloud and aerosol screening is applied first to time series of SNR1. Note that typically cloud and aerosol signal is easier to discern in SNR1 than in SNR0, and thus cloud screening is applied after Eq. (5). Then, first- and second-order polynomial fits are calculated for each cloud-screened profile of SNR1(z), and a rms threshold is used to select the appropriate fit, similar to determining Pfit(z). Denoting the selected fit to cloud- and aerosol-free measurements as SNRfit(z) we obtain
which is our final corrected SNR.
Note that to correct only for the bias in the A0 to Abkg ratio, a scalar denominator in Eq. (6) would be sufficient. However, using the fitted profile SNRfit(z) as the denominator accounts for possible changes in the slope of Pnoise since the last background check.
3.2.1 Implications for Stream Line XR lidars
The calculation of SNR2 with Eq. (6) relies on the fitting to cloud- and aerosol-free measurements. For Stream Line and Stream Line Pro lidars, which do not exhibit the inverse exponential Pbkg shape, SNRfit(z) will capture the shape of the actual noise level in nearly all cases. However, for Stream Line XR lidars the randomly occurring inverse exponential Pbkg(z) shape (Fig. 1a) is almost always masked by aerosol and/or cloud signal during measurement. Thus, it is not possible to correct for changes in shape of Pnoise(z) with SNRfit(z) during post-processing. However, the magnitude of uncertainty in Pnoise(z) can be estimated from the average depth of the inverse exponential dip in Pbkg(z) during background checks (see Fig. 3a).
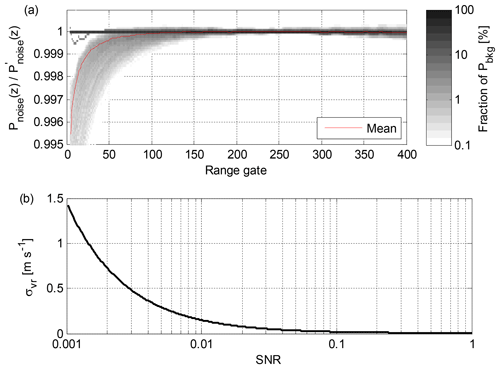
Figure 3(a) 2-D histogram of the ratio of Pnoise(z) (best estimate) to (linear fit only) for lidar 146 background checks. The mean of the ratio is also indicated. (b) σvr as a function of SNR for lidar 146.
Now as A0 is not saved, it is not possible to tell whether the amplifier was operating in high or low mode during measurement. Consequently, the difference in Pamp for the amplifier high and low modes also adds to the uncertainty in SNR for Stream Line XR systems, but, compared to the effect of the inverse exponential shape of Pbkg(z), the effect of Pamp is approximately 10 times smaller. However, any possible bias in the A0 to Abkg ratio can be corrected, and this is readily done by applying a linear fit to SNR1(z) at range gates 100–400 (for which SNR is not affected by inverse exponential Pbkg) and using this as SNRfit(z) in Eq. (6).
In practice, there are two options for SNR post-processing for Stream Line XR lidars. The first option is to accept the fitted Eq. (1) for Pfit(z) when it describes Pbkg(z) better. With this approach SNR2 may overestimate the actual SNR if the shape of Pnoise changes from Eq. (1) to being linear after the background check. Correspondingly, a change from a linear Pnoise to the inverse exponential shape during measurement results in SNR2 underestimating the actual SNR.
The second option for Stream Line XR SNR post-processing is to calculate a linear fit to Pbkg(z) based on range gates 100–400 and to always use this for Pfit(z). In this case, we only use high-mode Pamp(z) in calculating the noise level (Eq. 4) and denote it as . Consequently SNR′2 is the lower limit of the actual SNR, which can be useful if an SNR threshold is used to determine the usable signal for further analysis. For lidar 146 background checks from 12 January to 31 May 2018, the underestimation was on average 0.5 % of SNR+1 at the first usable range gate and decreased rapidly with increasing range (Fig. 3a). In the worst case, the underestimation at the first usable range gate was 3 % of SNR+1.
Uncertainty in SNR leads to uncertainty in σvr, as σvr is mostly a function of SNR (Pearson et al., 2009). However, σvr decreases rapidly with increasing SNR (Fig. 3b). Therefore, even the worst-case underestimation in SNR only has a limited effect on σvr if SNR is even moderately high (>0.03, −15.2 dB). On the other hand, for observations >2000 m away from the lidar, where signals are typically low, the uncertainty in SNR is also low (Fig. 3a). In the end, uncertainty in SNR and its effects in β and σvr need to be evaluated individually for each profile in Stream Line XR lidars.
4.1 Welgegund 6 September 2016
On 6 September 2016 lidar 46 was operating at Welgegund, South Africa, and a time series of SNR in vertically pointing measurement mode for this day is presented in Fig. 4. In this case, SNR0 is very close to 0 when there are no clouds or aerosol present (Fig. 4a), indicating that the online calculation of A0 and Abkg is quite successful. However, the presence of small but varying offsets in Pbkg(z) is apparent in Fig. 4a as horizontal stripes in SNR0 time series between the background checks conducted on the hour.
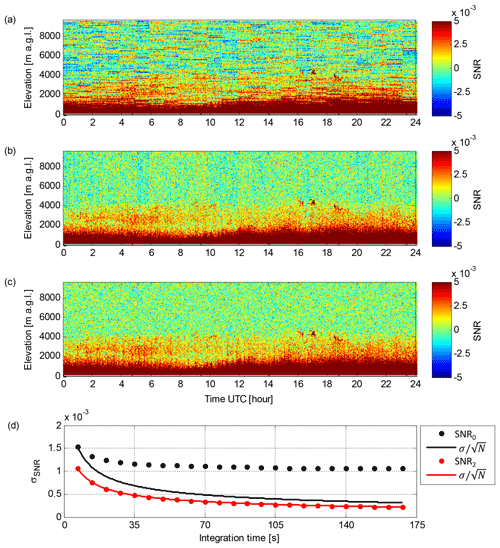
Figure 4Data from lidar 46 at Welgegund on 6 September 2016. (a) Time series of the SNR0 profile in vertically pointing mode. (b) Time series of the SNR1 profile in vertically pointing mode. (c) Time series of the SNR2 profile in vertically pointing mode. (d) σSNR as a function of integration time per profile for SNR0 and SNR2 for range gates at 4800–9000 m a.g.l. Also , where σ is σSNR at an integration time of 7 s (original integration time per profile) and N is the number of averaged profiles, is included in (d).
In the SNR1 time series (Fig. 4b) the horizontal stripes have been removed by applying the smooth Pnoise-based background using Eq. (5). At the same time, the elevated aerosol layer at 2000–4000 m above ground level (a.g.l.) becomes easily discernible. Small biases in the A0 to Abkg ratio become visible as vertical stripes, for instance between 05:00 and 06:00 UTC in Fig. 4b, which are then corrected for in the time series of SNR2 (Fig. 4c).
Comparing the standard deviation of SNR (σSNR) for cloud- and aerosol-free range gates shows a clear improvement in the noise level with the new post-processing algorithm (Fig. 4d). The main advantage of the new post-processing algorithm is that it enables averaging SNR; for SNR0 any offsets in Pbkg(z) become the limiting factor. This is clearly seen in Fig. 4d, which shows σSNR for SNR2 decreases with increasing integration time per profile following the rule closely as expected, but increasing integration time has little effect on σSNR for SNR0.
Figure 5 demonstrates how the lower noise floor with the new post-processing algorithm allows vertical wind speed variance () up to 2000 m a.g.l. (i.e. up to the top of the mixed layer) to be determined on this day. Furthermore, by averaging the originally 7 s data to 168 s integration time per profile and applying the new post-processing algorithm, the SNR threshold at the 3σ level (see Fig. 4d) can be decreased from 0.0032 (−25 dB) for SNR0 to 0.00065 (−32 dB) for SNR2. Consequently, β can be retrieved for the elevated aerosol layer at 2000–4000 m a.g.l. (Fig. 5c, d). Note that the offsets in Pbkg(z) result in horizontal stripes in the 168 s integration time β calculated from SNR0 in Fig. 5c.
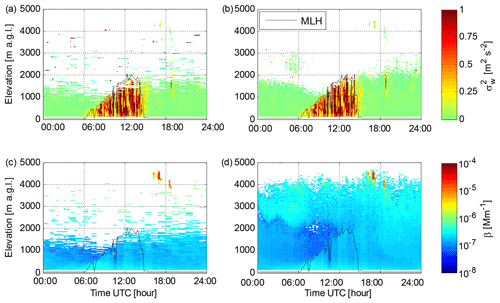
Figure 5Data from lidar 46 at Welgegund on 6 September 2016. (a) Time series of the profile, for which a threshold of 0.0031 (2σ) has been applied to SNR0. (b) Time series of the profile, for which a threshold of 0.0021 (2σ) has been applied to SNR2. In (a) and (b) the instrumental noise contribution to has been subtracted. (c) Time series of β obtained with 168s integration time from SNR0; β has been filtered with a threshold of 0.0032 (3σ) applied to SNR0. (d) Time series of β obtained with 168 s integration time from SNR2; β has been filtered with a threshold of 0.00065 (3σ) applied to SNR2. Mixing layer height (MLH) determined from panels (b) and (d) is also indicated.
A lower noise floor also enables wind retrievals with a lower SNR threshold, which increases the data availability. The effect on data availability depends on atmospheric conditions, though. In this case for instance (Welgegund, 6 September 2016), a 75∘ elevation angle velocity azimuth display (VAD) scan was utilised for horizontal wind retrieval every 15 min. With the new post-processing algorithm, the SNR threshold for wind retrieval could be decreased from 0.0045 to 0.0032. This decrease in the SNR threshold enabled the wind retrieval for 2–13 range gates more from each VAD scan; on average, winds could be determined from 7.5 additional range gates per VAD scan. That is, vertical coverage of wind retrievals increased on average by 200 m with the new post-processing.
Wind retrievals at lower SNR will have higher uncertainty due to higher instrumental noise in radial velocity measurement; yet enhanced SNR will enable more accurate determination of the instrumental uncertainty in wind retrievals. However, as a major fraction of the uncertainty in retrieved winds arises in atmospheric turbulence (Newsom et al., 2017), the more accurate SNR will only have a limited effect on the overall uncertainty in the wind retrieval. Therefore, the uncertainty in each wind retrieval should be evaluated, e.g. with the methodology of Newsom et al. (2017), before the wind retrievals are disseminated.
4.2 Helsinki 1 and 6 May 2018
Measurements using lidar 146 at Helsinki, Finland, on 6 May 2018 (Fig. 6) present all the issues with a Stream Line XR lidar at its worst. In Fig. 6a, SNR0 is negative, e.g. from 01:00 to 05:00, 06:00 to 10:00 and 12:00 to 13:00 UTC because of an erroneous Abkg coefficient. On the other hand, the individual profiles with unrealistically high SNR0 around 11:00, 14:00 to 15:00 and 20:00 to 21:00 UTC indicate errors in the A0 coefficient. Additionally, horizontal stripes in SNR0 time series similar to lidar 46 (Fig. 4a) indicate offsets in Pbkg(z). The reason for poor determination of A0 and Abkg for lidar 146 seems to be that Pbkg(z) is frequently non-linear, unlike for lidar 46, for example.
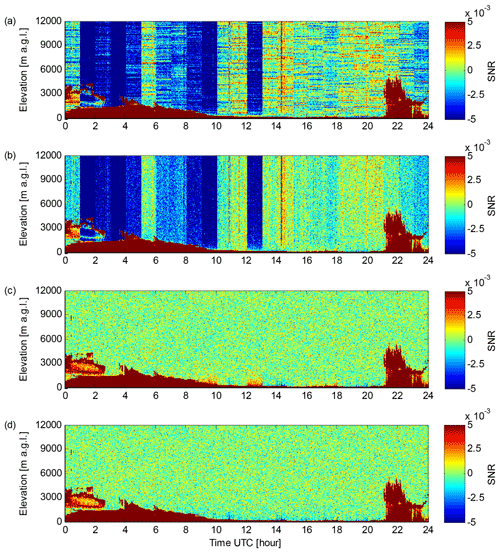
Figure 6Data from lidar 146 at Helsinki on 6 May 2018. (a) Time series of the SNR0 profile in vertically pointing mode. (b) Time series of the SNR1 profile in vertically pointing mode. (c) Time series of the SNR2 profile in vertically pointing mode. (d) Time series of the SNR′2 (always based on a linear fit to Pbkg(z)) profile in vertically pointing mode.
The new post-processing algorithm corrects the errors in A0 and Abkg as well as the stripes due to offsets in Pbkg(z) as seen in Fig. 6c. However, Fig. 6c shows that Pbkg(z) changing between the inverse exponential and linear shape causes over- and underestimation of SNR2 in the lowest 1500 m a.g.l. For instance, positive SNR2 in the lowest 1000 m at 12:00 to 13:00 UTC and negative SNR2 in the lowest 1000 m at 14:00 to 15:00 UTC are due to noise level shape changes between background check and measurement modes. During these periods, the lidar signal is fully attenuated by a cloud within the lowest 200 m, and consequently SNR2 in the 200–1000 m range should be zero. In Fig. 6d, SNR′2 is only calculated using a linear fit to Pbkg(z) as discussed in Sect. 3.2.1. This removes the overestimate of SNR at 12:00–13:00 UTC, but cannot correct the underestimates.
Measurements with lidar 146 on 1 May 2018 at Helsinki present much less noisy SNR0 than on 6 May 2018, as seen in Fig. 7a. On this day there are cirrus clouds present at 8000–12 000 m a.g.l., but the stripes due to offsets in Pbkg(z) make it difficult to distinguish the clouds from noise in SNR0. Applying the new post-processing algorithm and increasing integration time from 10 to 60 s for this day enables the SNR threshold at the 3σ level to be lowered from 0.0035 (−24.5 dB) for SNR0 to 0.0012 (−29 dB) for SNR2. This results in a significant increase in data coverage for the cirrus clouds, as shown in Fig. 7c and d.
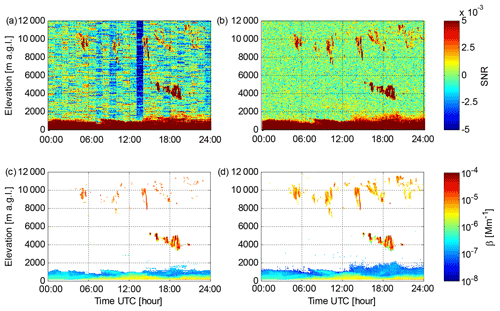
Figure 7Data from lidar 146 at Helsinki on 1 May 2018. (a) Time series of the SNR0 profile in vertically pointing mode. (b) Time series of the SNR2 profile in vertically pointing mode. (c) Time series of β obtained with 60 s integration time from SNR0; β has been filtered with a threshold of 0.0035 (3σ) applied to SNR0. (d) Time series of β obtained with 60 s integration time from SNR2; β has been filtered with a threshold of 0.0012 (3σ) applied to SNR2.
4.3 Finokalia 8 July 2014
Time series of SNR in vertically pointing mode with lidar 53 on 8 July 2014 at Finokalia, Greece, are presented in Fig. 8. On this day, SNR0 is close to 0 for 4000–9600 m a.g.l. elevation (Fig. 8a), indicating that the online calculation of A0 and Abkg is quite successful. Only at 00:00–01:00 and 20:00–21:00 UTC is SNR0 negative, indicating a small offset in Abkg. However, horizontal stripes in the SNR0 time series between the background checks are apparent in Fig. 8a, indicating the presence of small but varying offsets in Pbkg(z).
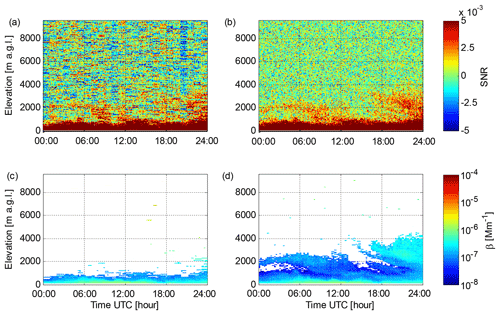
Figure 8Data from lidar 53 at Finokalia on 8 July 2014. (a) Time series of the SNR0 profile in vertically pointing mode. (b) Time series of the SNR2 profile in vertically pointing mode. (c) Time series of β obtained with 350 s integration time from SNR0; β has been filtered with a threshold of 0.0044 (3σ) applied to SNR0. (d) Time series of β obtained with 350 s integration time from SNR2; β has been filtered with a threshold of 0.00059 (3σ) applied to SNR2.
After SNR post-processing (Fig. 8b), elevated aerosol layers at 1000–4000 m a.g.l. are clearly visible on this day. These aerosol layers were also observed with a co-located multiwavelength Raman lidar, Polly XT (Baars et al., 2016; Engelman et al., 2016). A comparison of lidar 53 and the Raman lidar measurements at 1064 nm wavelength is presented in Fig. 9. Considering the wavelength difference, the agreement between the two systems is reasonably good. Further averaging of SNR2, in this case up to 350 s integration time, allows the determination of β for the elevated aerosol layers. With this long integration time we can reach a 3σ SNR threshold of 0.00059 (−32 dB) for SNR2. For SNR0, offsets in Pbkg(z) are the limiting factor in determining the SNR threshold, and at the 3σ level only 0.0044 (−24 dB) can be achieved.
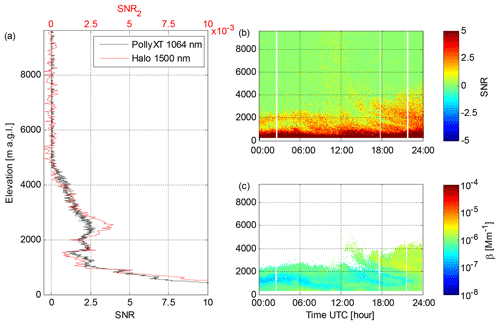
Figure 9(a) Vertical profiles of SNR from PollyXT at 1064 nm wavelength and SNR2 from lidar 53 at Finokalia on 8 July 2014. Both profiles are obtained at 21:00 UTC; the integration time of the lidar 53 profile is 350 s, and the integration time of the PollyXT profile is 360 s. (b) Time series of PollyXT SNR at 1064 nm wavelength with 360 s integration time at Finokalia on 8 July 2014. (c) Time series of PollyXT attenuated backscatter at 1064 nm wavelength with 360 s integration time at Finokalia on 8 July 2014.
In this paper we have presented an improved SNR post-processing algorithm for Halo Doppler lidars. For Stream Line and Stream Line Pro lidars, this method enables accurate SNR and β retrievals from the first usable gate onwards. For Stream Line XR lidars, we identified a previously unknown source of uncertainty in the near-range (<1500 m) SNR due to variations in the noise floor of these systems. We present a method to estimate the magnitude of this source of uncertainty, although it cannot be completely eliminated.
We have shown that defining the noise floor on a point-by-point basis during periodic background checks results in a small, variable offset in SNR at each range gate. This offset is due to finite duration of the background check and becomes the limiting factor in retrieving weaker signals with Halo Doppler lidars, or with any system based on such a point-by-point-defined noise floor. The improved SNR post-processing algorithm removes this source of error by introducing a more accurate, continuous noise floor. Independent of the noise floor, online scaling of raw signal from the amplifier by the firmware fails occasionally. This source of error in SNR was targeted by Manninen et al. (2016), and their algorithm is adapted here as part of the improved SNR post-processing algorithm (Eq. 6). Correcting for these two sources of error in SNR enables data to be retrieved at much lower SNR than before. By increasing integration time per profile to a few minutes, SNR down to (−32 dB) can be utilised.
Our analysis shows that even if the technical specifications of two Doppler lidar systems are identical, their instrumental noise characteristics can be quite different (Fig. 2). Therefore, the lidar operator should inspect each system individually to ensure the highest data quality. Note that this algorithm or similar processing is needed to define the instrumental noise level even if raw spectra are utilised instead of the processed data. The algorithm presented here can be applied in semi-operational use as long as at least 300 background checks (acquired in 2 weeks of measurements with typical configuration) are available for characterising the amplifier response to the transmitted pulse. A MATLAB implementation of this algorithm is available through GitHub (Manninen, 2019).
We have demonstrated that the improved SNR post-processing can help to retrieve turbulent properties up to the top of the mixed layer under low aerosol load. With enhanced SNR, the instrumental noise contribution to radial velocity variance can be estimated with better accuracy, which will improve the quality of turbulent parameter retrievals. The reduced noise floor enables horizontal wind retrievals with a lower SNR threshold and increases data availability, depending on atmospheric conditions. Furthermore, we have demonstrated that a combination of reduced noise floor and increased integration time allows detection of elevated aerosol layers with Stream Line and Stream Line Pro lidars. Even for the more powerful Stream Line XR lidars, the new SNR post-processing can increase data availability, e.g. in the case of high-altitude cirrus clouds. In conclusion, the improved SNR post-processing introduced in this paper enhances the capabilities of Halo Doppler lidars in studying atmospheric turbulence in weak signal conditions and opens up new possibilities for studying elevated aerosol layers, such as volcanic ash, Aeolian dust or biomass burning smoke.
Doppler lidar data are available upon request to the corresponding author. Raman lidar data are available upon request to polly@tropos.de.
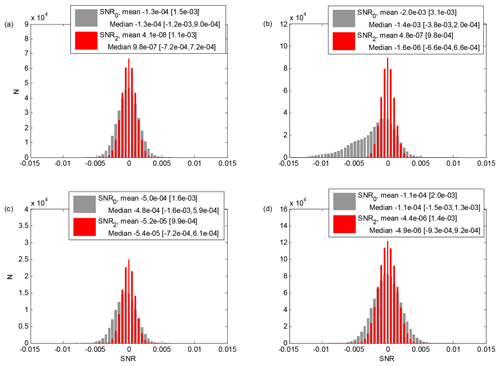
Figure A1Histograms of SNR0 and SNR2 in a cloud- and aerosol-free regime for the four case studies considered in Sect. 4. For each case, mean [standard deviation] and median [25th, 75th percentile] of SNR0 and SNR2 are included. (a) Welgegund on 6 September 2016, 00:00–24:00 UTC, 4800–9000 m a.g.l. (b) Kumpula on 1 May 2018, 02:00–24:00 UTC, 6000–12 000 m a.g.l. (c) Kumpula on 6 May 2018, 00:00–12:00 UTC, 4000–7000 m a.g.l. (d) Finokalia on 8 July 2014, 00:00–24:00 UTC, 5000–96 000 m a.g.l.
The authors declare that they have no conflict of interest.
We gratefully acknowledge financial support by TOPROF (COST Action ES1303)
and North-West University for measurements at Welgegund. CHARADMExp was an
experimental campaign of the National Observatory of Athens (NOA) and was supported by the ESA-ESTEC project “Characterization of Aerosol
mixtures of Dust And Marine origin”, contract no. IPL-PSO/FF/lf/14.489. We
acknowledge Ronny Engelmann and Holger Baars from TROPOS for providing Raman
lidar data and financial support through the High-Definition Clouds and
Precipitation for advancing Climate Prediction research program (HD(CP)2;
FKZ: 01LK1209C and 01LK1212C), funded by the Federal Ministry of Education and
Research in Germany (BMBF), ACTRIS under grant agreement no. 262254 of the
European Union Seventh Framework Programme (FP7/2007-2013) and ACTRIS-2 under
grant agreement no. 654109 of the European Union's Horizon 2020 research
and innovation programme.
Edited by: Ulla
Wandinger
Reviewed by: two anonymous referees
Baars, H., Kanitz, T., Engelmann, R., Althausen, D., Heese, B., Komppula, M., Preißler, J., Tesche, M., Ansmann, A., Wandinger, U., Lim, J.-H., Ahn, J. Y., Stachlewska, I. S., Amiridis, V., Marinou, E., Seifert, P., Hofer, J., Skupin, A., Schneider, F., Bohlmann, S., Foth, A., Bley, S., Pfüller, A., Giannakaki, E., Lihavainen, H., Viisanen, Y., Hooda, R. K., Pereira, S. N., Bortoli, D., Wagner, F., Mattis, I., Janicka, L., Markowicz, K. M., Achtert, P., Artaxo, P., Pauliquevis, T., Souza, R. A. F., Sharma, V. P., van Zyl, P. G., Beukes, J. P., Sun, J., Rohwer, E. G., Deng, R., Mamouri, R.-E., and Zamorano, F.: An overview of the first decade of PollyNET: an emerging network of automated Raman-polarization lidars for continuous aerosol profiling, Atmos. Chem. Phys., 16, 5111–5137, https://doi.org/10.5194/acp-16-5111-2016, 2016.
Baklanov, A. A., Grisogono, B., Bornstein, R., Mahrt, L., Zilitinkevich, S. S., Taylor, P., Larsen, S. E., Rotach, M. W., and Fernando, H. J. S.: The Nature, Theory, and Modeling of Atmospheric Planetary Boundary Layers, B. Am. Meteorol. Soc., 92, 123–128, https://doi.org/10.1175/2010BAMS2797.1, 2011.
Banakh, V. A. and Smalikho, I. N.: Lidar observations of atmospheric internal waves in the boundary layer of the atmosphere on the coast of Lake Baikal, Atmos. Meas. Tech., 9, 5239–5248, https://doi.org/10.5194/amt-9-5239-2016, 2016.
Bonin, T. A., Choukulkar, A., Brewer, W. A., Sandberg, S. P., Weickmann, A. M., Pichugina, Y. L., Banta, R. M., Oncley, S. P., and Wolfe, D. E.: Evaluation of turbulence measurement techniques from a single Doppler lidar, Atmos. Meas. Tech., 10, 3021–3039, https://doi.org/10.5194/amt-10-3021-2017, 2017.
Bonin, T. A., Carroll, B. J., Hardesty, R. M., Brewer, W. A., Hajny, K., Salmon, O. E., and Shepson, P. B.: Doppler Lidar Observations of the Mixing Height in Indianapolis Using an Automated Composite Fuzzy Logic Approach, J. Atmos. Ocean. Tech., 35, 473–490, https://doi.org/10.1175/JTECH-D-17-0159.1, 2018.
Emeis, S., Schäfer, K., and Münkel, C.: Surface-based remote sensing of the mixing-layer height – a review, Meteorol. Z., 17, 621–630, 2008.
Engelmann, R., Kanitz, T., Baars, H., Heese, B., Althausen, D., Skupin, A., Wandinger, U., Komppula, M., Stachlewska, I. S., Amiridis, V., Marinou, E., Mattis, I., Linné, H., and Ansmann, A.: The automated multiwavelength Raman polarization and water-vapor lidar PollyXT: the neXT generation, Atmos. Meas. Tech., 9, 1767–1784, https://doi.org/10.5194/amt-9-1767-2016, 2016.
Garratt, J.: Review: the atmospheric boundary layer, Earth-Sci. Rev., 37, 89–134, https://doi.org/10.1016/0012-8252(94)90026-4, 1994.
Harvey, N. J., Hogan, R. J., and Dacre, H. F.: A method to diagnose boundary-layer type using Doppler lidar, Q. J. Roy. Meteor. Soc., 139, 1681–1693, https://doi.org/10.1002/qj.2068, 2013.
Hirsikko, A., O'Connor, E. J., Komppula, M., Korhonen, K., Pfüller, A., Giannakaki, E., Wood, C. R., Bauer-Pfundstein, M., Poikonen, A., Karppinen, T., Lonka, H., Kurri, M., Heinonen, J., Moisseev, D., Asmi, E., Aaltonen, V., Nordbo, A., Rodriguez, E., Lihavainen, H., Laaksonen, A., Lehtinen, K. E. J., Laurila, T., Petäjä, T., Kulmala, M., and Viisanen, Y.: Observing wind, aerosol particles, cloud and precipitation: Finland's new ground-based remote-sensing network, Atmos. Meas. Tech., 7, 1351–1375, https://doi.org/10.5194/amt-7-1351-2014, 2014.
Hogan, R. J., Grant, A. L., Illingworth, A. J., Pearson, G. N., and O'Connor, E. J.: Vertical velocity variance and skewness in clear and cloud-topped boundary layers as revealed by Doppler lidar, Q. J. Roy. Meteor. Soc. A, 135, 635–643, 2009.
Lothon, M., Lenschow, D. H., and Mayor, S. D.: Doppler lidar measurements of vertical velocity spectra in the convective planetary boundary layer, Bound.-Lay. Meteorol., 132, 205–226, 2009.
Manninen, A: HALO lidar toolbox, GitHub, available at: https://github.com/manninenaj/HALO_lidar_toolbox (last access: 16 January 2019), 2019.
Manninen, A. J., O'Connor, E. J., Vakkari, V., and Petäjä, T.: A generalised background correction algorithm for a Halo Doppler lidar and its application to data from Finland, Atmos. Meas. Tech., 9, 817–827, https://doi.org/10.5194/amt-9-817-2016, 2016.
Manninen, A. J., Marke, T., Tuononen, M., and O'Connor, E. J.: Atmospheric Boundary Layer Classification with Doppler Lidar, J. Geophys. Res.-Atmos., 123, 8172–8189, https://doi.org/10.1029/2017JD028169, 2018.
Marke, T., Crewell, S., Schemann, V., Schween, J. H., and Tuononen, M.: Long-Term Observations and High-Resolution Modeling of Midlatitude Nocturnal Boundary Layer Processes Connected to Low-Level Jets, J. Appl. Meteorol. Clim., 57, 1155–1170, https://doi.org/10.1175/JAMC-D-17-0341.1, 2018.
Newsom, R. K., Brewer, W. A., Wilczak, J. M., Wolfe, D. E., Oncley, S. P., and Lundquist, J. K.: Validating precision estimates in horizontal wind measurements from a Doppler lidar, Atmos. Meas. Tech., 10, 1229–1240, https://doi.org/10.5194/amt-10-1229-2017, 2017.
O'Connor, E. J., Illingworth, A. J., Brooks, I. M., Westbrook, C. D., Hogan, R. J., Davies, F., and Brooks, B. J.: A Method for Estimating the Turbulent Kinetic Energy Dissipation Rate from a Vertically Pointing Doppler Lidar, and Independent Evaluation from Balloon-Borne In Situ Measurements, J. Atmos. Ocean. Tech., 27, 1652–1664, https://doi.org/10.1175/2010JTECHA1455.1, 2010.
Pal, S., Haeffelin, M., and Batchvarova, E.: Exploring a geophysical process-based attribution technique for the determination of the atmospheric boundary layer depth using aerosol lidar and near-surface meteorological measurements, J. Geophys. Res.-Atmos., 118, 9277–9295, 2013.
Päschke, E., Leinweber, R., and Lehmann, V.: An assessment of the performance of a 1.5 µm Doppler lidar for operational vertical wind profiling based on a 1-year trial, Atmos. Meas. Tech., 8, 2251–2266, https://doi.org/10.5194/amt-8-2251-2015, 2015.
Pearson, G., Davies, F., and Collier, C.: An Analysis of the Performance of the UFAM Pulsed Doppler Lidar for Observing the Boundary Layer, J. Atmos. Ocean. Tech., 26, 240–250, https://doi.org/10.1175/2008JTECHA1128.1, 2009.
Pearson, G., Davies, F., and Collier, C.: Remote sensing of the tropical rain forest boundary layer using pulsed Doppler lidar, Atmos. Chem. Phys., 10, 5891–5901, https://doi.org/10.5194/acp-10-5891-2010, 2010.
Ryan, W. F.: The air quality forecast rote: Recent changes and future challenges, J. Air Waste Manage., 66, 576–596, https://doi.org/10.1080/10962247.2016.1151469, 2016.
Rye, B. J. and Hardesty, R. M.: Discrete spectral peak estimation in incoherent backscatter heterodyne lidar. I. Spectral accumulation and the Cramer-Rao lower bound, IEEE T. Geosci. Remote, 31, 16–27, 1993.
Schween, J. H., Hirsikko, A., Löhnert, U., and Crewell, S.: Mixing-layer height retrieval with ceilometer and Doppler lidar: from case studies to long-term assessment, Atmos. Meas. Tech., 7, 3685–3704, https://doi.org/10.5194/amt-7-3685-2014, 2014.
Seibert, P., Beyrich, F., Gryning, S.-E., Joffre, S., Rasmussen, A., and Tercier, P.: Review and intercomparison of operational methods for the determination of the mixing height, Atmos. Environ., 34, 1001–1027, https://doi.org/10.1016/S1352-2310(99)00349-0, 2000.
Smalikho, I. N. and Banakh, V. A.: Measurements of wind turbulence parameters by a conically scanning coherent Doppler lidar in the atmospheric boundary layer, Atmos. Meas. Tech., 10, 4191–4208, https://doi.org/10.5194/amt-10-4191-2017, 2017.
Tucker, S. C., Senff, C. J., Weickmann, A. M., Brewer, W. A., Banta, R. M., Sandberg, S. P., Law, D. C., and Hardesty, R. M.: Doppler Lidar Estimation of Mixing Height Using Turbulence, Shear, and Aerosol Profiles, J. Atmos. Ocean. Tech., 26, 673–688, https://doi.org/10.1175/2008JTECHA1157.1, 2009.
Tuononen, M., O'Connor, E. J., Sinclair, V. A., and Vakkari, V.: Low-Level Jets over Utö, Finland, Based on Doppler Lidar Observations, J. Appl. Meteorol. Clim., 56, 2577–2594, https://doi.org/10.1175/JAMC-D-16-0411.1, 2017.
Vakkari, V., O'Connor, E. J., Nisantzi, A., Mamouri, R. E., and Hadjimitsis, D. G.: Low-level mixing height detection in coastal locations with a scanning Doppler lidar, Atmos. Meas. Tech., 8, 1875–1885, https://doi.org/10.5194/amt-8-1875-2015, 2015.