2.1 Experimental site T0e

The T0e site has been operating continuously since February 2011 in central Amazonia, up-wind from Manaus (02^∘53^′27${}^{\prime \prime }$ S, 59^∘58^′12${}^{\prime \prime }$ W; see Fig. 1), with a set of collocated atmospheric monitoring instruments that includes a MFRSR, a Cimel Sun photometer, and a Raman lidar (Barbosa et al., 2014). The main site goal is to provide long-term characterization of diurnal and seasonal cycles of clouds and convection and the interactions and feedback mechanisms between water vapour, clouds, radiation, and aerosol particles. It was incorporated as part of the GoAmazon2014/5 experiment (Martin et al., 2016) network sites, an international experiment designed to investigate the interactions between the natural Amazonia atmosphere conditions and the air pollution plume from Manaus.

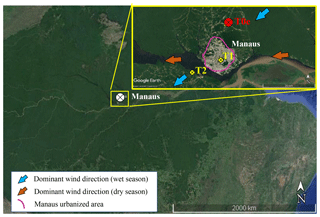
Figure 1The T0e site location in central Amazonia from an enlarged image showing the site location upwind of Manaus. During the wet season (December to May) the dominant wind direction is from the northeast (blue arrow) and during the dry season (June to November) from the east (brown arrow). The GoAmazon2014/5 experiment sites' relative position to Manaus: T2 is downwind, T1 is in the city, and T0e is upwind of the city (source: Google Earth).

Download

The GoAmazon2014/5 sites were classified from time point zero (T0) upwind of the plume, T1 in the midst of the plume, T2 just downwind of Manaus, to T3 furthest downwind of Manaus (70 km). Manaus' pollution plume composition includes nitrogen and sulfur oxides, and high concentrations of submicron aerosol particles and soot (Kuhn et al., 2010), which is consistent with the nature of the local major anthropogenic sources of air pollution: vehicle fleets, power plants, and industrial activities. The study of de Sá et al. (2018) found that the submicron particle composition is dominated by organic material across the sites upwind and downwind of Manaus, independently of the levels of pollution. However, their study pointed out that, among the sites, the absolute mass concentrations of pollutants vary significantly. Average concentrations downwind of Manaus are 100 % to 200 % higher than those upwind. In general, during the wet season, the atmosphere at the T0e site is a clean reference, since its location upwind of Manaus prevents the site of being strongly affected by the city pollution plume. Meanwhile, during the dry season the atmospheric column at T0e, as a large portion of the atmosphere across central Amazonia eventually is influenced by smoke from biomass burning emissions that occur throughout the Amazon basin.

2.2 Instruments

A multi-filter rotating shadow-band radiometer is designed to monitor global horizontal, diffuse horizontal and direct normal solar irradiances in narrow and broadband channels (Harrison et al., 1994). It has been used worldwide to derive columnar aerosol optical properties (Harrison and Michalsky, 1994; Alexandrov et al., 2002; Rosário et al., 2008; Michalsky et al., 2010; Mazzola et al., 2010; Michalsky and LeBaron, 2013), water vapour (Michalsky et al., 1995; Schneider et al., 2010), and cloud optical properties (Min and Harrison, 1996; Kassianov et al., 2011). Direct normal spectral irradiance (I_DN, λ) at the surface, needed to perform AOD retrievals, is obtained via the difference between global-horizontal and diffuse-horizontal irradiances divided by the cosine of the solar zenith angle (Harrison et al., 1994). Once MFRSR angular and spectral responses are properly characterized and the automated shadow-band system adequately adjusted, accuracy in I_DN, λ is expected to be comparable to Sun photometers (Harrison et al., 1994). However, once in field, MFRSR filters transmission may suffer degradation with time (Michalsky et al., 2001; Michalsky and LeBaron, 2013), which makes regular ERC critically necessary to keep the accuracy of AOD retrievals. The MFRSR of the present study has been operating with sporadic interruptions at T0e providing irradiances measurements at a time interval of 1 min in five narrow-band channels (415, 500, 610, 670, and 870 nm) with half-bandwidth of 10 nm and able to permit AOD retrieval. Given the high cloud cover in central Amazonia, the MFRSR high-frequency measurements are crucial to improve the frequency of AOD retrieval under cloudy sky and, therefore, minimize the AERONET AOD product known bias toward clear-sky condition (Levy et al., 2010).

2.3 Langley plot calibration and uncertainties

The Langley plot calibration method is based on Lambert–Beer law (Shaw, 1983), which describes the attenuation of a monochromatic beam propagating through a medium.

where, considering the full atmospheric column as the medium, I_DN, λ is the direct solar spectral irradiance at wavelength λ measured at the surface by the MFRSR, I_o,λ is the solar spectral irradiance that would be measured in the absence of the atmosphere at Earth–Sun mean distance d₀, f(d₀) is a correction factor related to Earth–Sun distance variation (Iqbal, 1983), and m and τ_λ represent the atmosphere relative optical air mass and total optical depth, respectively. Linearizing Eq. (1) by applying the natural logarithms to the both sides of the equation leads to a linear relation between m and ln (I_DN, λ), on which τ_λ and ln (I_o,λ) represent, respectively, the angular and linear coefficients.

Knowing ln (I_DN, λ) over a range of m, during which the atmosphere remained clean and stable, the least-squares regression method can be applied to provide a linear fit formulation between both variables, where the angular coefficient is the mean atmosphere optical depth, and the linear coefficient represents the case of m equal to zero, a hypothetical absence of atmosphere, from which an estimation of the solar extraterrestrial spectral irradiance (I_o, λ) can be made. In the present study, the atmosphere relative optical air mass (m) was calculated as a function of solar zenith angle (SZA) based on Kasten and Young's (1989) formulation and ln (I_DN, λ) taken from MFRSR direct normal irradiance measurements for 2012 and 2015. As we assumed that both the response variable, ln (I_DN, λ), and the predictor variable, m, are subject to errors, it was applied the least-square regression treatment that consider errors in both adjusted variables (Irvin and Quickenden, 1983). The errors in ln (I_DN, λ) were obtained through error propagation theory considering the estimate of uncertainty of MFRSR direct normal irradiance in Harrison et al. (1994) (${\mathit{\sigma }}_{I_{\mathrm{DN},\mathit{\lambda }}}=\mathrm{2}$ %). Regarding error in the air mass (σ_m), we used the method of Tomasi and Petkov (2014), which compared atmospheric air mass results from Kasten and Young (1989) formulation against rigorous calculation and found differences lower than 0.8 %. Therefore, we assumed 0.8 % as an estimate of uncertainty in the air mass calculated following Kasten and Young (1989). Following the suggestion of previous studies (Mazzola et al., 2010; Alexandrov et al., 2004), to apply least-square regression we adopted an air mass range from 2.0 to 5.0. For air mass larger than 5.0, high solar energy incident angles, calibration may be affected by the uncertainty of the MFRSR cosine angle correction and the shadow-band correction; meanwhile low air masses, near 1.0, increase the probability of turbulent atmospheric conditions and, therefore, reduction of the optical depth stability (Chen et al., 2013).

The quality of the linear fit derived using least-square regression is highly dependent on optical depth temporal stability, which is more likely to be observed under aerosol background conditions and stable atmosphere. To obtain a set of linear fits that are able to provide high-quality Langley plot calibration samples, for both 2012 and 2015, only morning cases were selected, to avoid the afternoon vigorous convection, and only linear fits with correlation coefficients (R²) higher than 0.990 were used. This is the minimal value usually obtained for calibration performed on high mountaintops (Schmid and Wehrli, 1995). Also, considering the Schafer et al. (2008) study on AOD climatology across the Amazon basin, only AOD values typical of background conditions were selected. For both years studied, 2012 and 2015, the MFRSR final extraterrestrial spectral response calibration ($<I_{\mathrm{o},\mathit{\lambda }}>$) was estimated from the mean of the correspondent set of extraterrestrial response calibrations (I_o, λ) obtained from individual Langley plot calibrations. The uncertainties of the derived final calibrations were estimated as the standard error of the mean (${\mathit{\sigma }}_{I_{\mathrm{o},\mathit{\lambda }}}$). Subsequently, the final calibration results were applied to retrieve (AOD_λ) over the T0e site using the MFRSR. It is worth mentioning that the selection of 2012 and 2015 to answer the question of whether it is possible to obtain accurate extraterrestrial calibration constants derived from the Langley plot method in central Amazonia was based on the evaluation that two independent years, temporally distant, would be adequate to provide findings to support our answer to the question. The temporal distance between the 2 years was meant to detect a potential scenario of filter degradations.

2.4 Aerosol optical depth (AOD_λ) inversion and uncertainty estimate

From Eq. (2), the atmospheric total optical depth τ_λ can be separated as follows:

where τ_m, λ and τ_g, λ represent, respectively, molecular scattering and gas absorption optical depths. All MFRSR channels are affected by molecular scattering, while gas absorption is highly selective, and therefore affects specific channels. The most relevant influence of gas absorption on MFRSR channels is produced by ozone (O₃) in the 610 and 670 nm channels and by nitrogen dioxide (NO₂) in the 415 nm channel. Therefore, a combination of Eqs. (3) and (2) leads to the AOD_λ retrieval equation

where τ_m, λ was calculated using the Kasten and Young (1989) formulation as a function of the climatological surface atmospheric pressure. Given its unique vertical distribution, ozone relative optical air mass ($m_{{\mathrm{O}}_{\mathrm{3}}}$) was estimated separately based on Staehelin et al. (1995). Ozone (O₃) and nitrogen dioxide (NO₂) absorption optical depths over the T0e site were obtained considering their spectral cross section absorption and average column content (O₃ $=\mathrm{267.6}\pm \mathrm{5.8}$ Dobson units, NO₂ $=\mathrm{0.076}\pm \mathrm{0.012}$ Dobson units) over the years between 2011 and 2015, taken from the Ozone Monitoring Instrument (OMI; Levelt et al., 2006) SCanning Imaging Absorption spectroMeter for Atmospheric CHartographY (SCIAMACHY, Bovensmann et al., 1999) products, respectively.

In general, the accuracy of the AOD_λ inversion is dominated by the uncertainty in the extraterrestrial response calibration ($<I_{\mathrm{o},\mathit{\lambda }}>$) and ln (I_DN, λ) measurements (Michalsky et al., 2001; Alexandrov et al., 2007; Mazzola et al., 2010). Typically, uncertainties in both terms are at least 1 order of magnitude greater than the contributions of the other terms (Mazzola et al., 2010). Considering only the uncertainties in extraterrestrial response calibration (${\mathit{\sigma }}_{<I_{\mathrm{o},\mathit{\lambda }}>}$) and in I_DN, λ measurement (${\mathit{\sigma }}_{I_{\mathrm{DN},\mathit{\lambda }}}$), an estimate of uncertainty (${\mathit{\sigma }}_{{\mathrm{AOD}}_{\mathit{\lambda }}}$) of the retrieved AOD_λ can be evaluated as

where ${\mathit{\sigma }}_{<I_{\mathrm{o},\mathit{\lambda }}>}$, as described, is based on the standard error of the mean of multiple extraterrestrial responses obtained from a set of individual Langley plot calibrations. Evaluation of the uncertainty in ln (I_DN, λ) is a challenge given its dependency on multiple factors, i.e. shadow-band adjustment, accuracy of the angular response and MFRSR positioning regarding misalignment and tilt (Harrison et al., 1994; Alexandrov et al., 2007). Harrison et al. (1994) estimated MFRSR ln (I_DN, λ) typical uncertainty to vary between 2 % and 3 %. Alexandrov et al. (2007) achieved lower estimation, roughly 1.5 % for all channels. Assuming Harrison et al. (1994) maximum uncertainty (3 %), the final uncertainty in MFRSR AOD_λ, for all channels, was evaluated for the worst-case scenario, i.e. for unit relative air mass (m=1).

Additionally, considering AOD_λ in two spectral channels (λ₁, λ₂) as reference, the spectral dependence of AOD_λ was evaluated using the Ångström exponent (${\mathit{\alpha }}_{{\mathit{\lambda }}_{\mathrm{1}},{\mathit{\lambda }}_{\mathrm{2}}}$), calculated using the following equation:

Due to its dependency on aerosol particle size distribution (Eck et al., 1999), ${\mathit{\alpha }}_{{\mathit{\lambda }}_{\mathrm{1}},{\mathit{\lambda }}_{\mathrm{2}}}$ can be used as a qualitative indicator to evaluate the predominance of submicrometric (fine particles) or micrometric aerosol particles (coarse mode) in the atmosphere. High values of ${\mathit{\alpha }}_{{\mathit{\lambda }}_{\mathrm{1}},{\mathit{\lambda }}_{\mathrm{2}}}$, greater than 2.0, indicate dominance of fine aerosol particles, while values lower than 1.0 are typically related to coarse aerosol particle dominance (Eck et al., 1999). In central Amazonia, for regions upwind of Manaus urban area, such as the T0e site, air masses rich in fine aerosol particles are typically associated with smoke transport from biomass burning regions. Air masses dominated by coarse particle fraction are in general associated with local and regional biogenic and soil particles (Artaxo et al., 1998). Eventually, under favourable atmospheric circulation, air mass containing coarse dust particles transported from the Sahara desert may also affect the T0e site atmospheric column (Koren et al., 2006; Ben-Ami et al., 2010; Moran-Zuloaga et al., 2018).

Retrievals of AOD_λ and ${\mathit{\alpha }}_{{\mathit{\lambda }}_{\mathrm{1}},{\mathit{\lambda }}_{\mathrm{2}}}$ from MFRSR measurements were validated against AERONET direct Sun products Level 2.0, retrieved by a Cimel Sun photometer also installed at the T0e site. AERONET provides AOD at seven wavelengths 340, 380, 440, 500, 670, 870, and 1020 nm, three being coincident with MFRSR wavelengths (500, 670, and 870 nm). In order to evaluate the MFRSR AOD_λ in the remaining channels, 415 and 610 nm, the Ångström exponent from AERONET was used to perform interpolation to derive AOD_λ in those channels for the network. Specifically, for comparison purposes, MFRSR AOD_λ at 1 min rate was averaged within a 5 min interval centred on AERONET Sun photometer retrieval; large standard deviations from the mean, i.e. higher than 0.08 (considering 4× AERONET field Sun photometer AOD_λ uncertainty, which is 0.02), were interpreted as potential cloud contamination in MFRSR, and therefore excluded from the analysis. Afterwards, MFRSR results were used to describe and analyse the seasonal variability of columnar aerosol particle optical properties over the T0e site.

The statistical metrics used to compare MFRSR AOD (AOD_MFR) with AERONET Sun photometer AOD (AOD_Aer), assuming the latter as the reference, are the root mean square error (RMSE), a measure of average deviation from the reference, and bias, a measure of overall bias error or systematic error.

3.1 MFRSR Langley plot calibration and uncertainty

An example of the diurnal cycle of the spectral solar direct normal irradiance measured (20 June 2012) by the MFRSR prone to a successful Langley plot is presented in Fig. 2. In the morning, before vigorous convection initiates, the direct normal irradiance in all channels is characterized by a continuous increase. The suitability of a successful Langley plot is evidenced in the quality of the linear fit achieved, as can be confirmed in Table 1 for the 500 nm channel. Tables 1 and 2 present for the 500 nm channels for 2012 and 2015, respectively, the obtained extraterrestrial response calibrations ($<I_{\mathrm{o},\mathit{\lambda }}>$) for each individual Langley plot that met the criteria defined, i.e. (R²≥0.990) and background AOD_550 nm(≤0.15). The tables with the results for the remaining channels (415, 610, 670, and 870 nm) are presented in the Supplement.

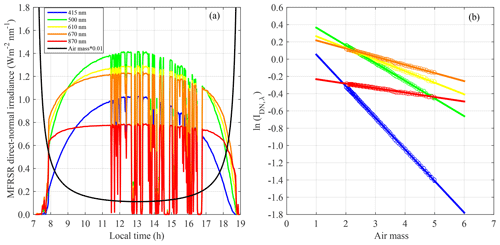
Figure 2(a) Diurnal cycle of air mass and direct normal spectral solar irradiance measured by the MFRSR operating at the T0e site in central Amazonia. (b) Example of the Langley plot calibration applied to MFRSR spectral irradiance measurements taken during the clear sky period (08:00 to 11:00 local time) of the diurnal cycle shown in (a) (day of measurements: 20 June 2012).

Download

Table 1Individual extraterrestrial calibration results (I_{o, 500 nm}) applying the Langley plot technique to measurements of solar direct normal irradiance at 500 nm from a MFRSR operating at the T0e site in central Amazonia for 2012. The individual uncertainty (${\mathit{\sigma }}_{I_{\mathrm{o},\mathrm{500}\mathrm{nm}}}$) used to obtain the relative error (${\mathit{\sigma }}_{I_{\mathrm{o},\mathrm{500}\mathrm{nm}}}$(%)) was estimated from the intercept and its respective uncertainty (σ_intercept) derived from the least-square regression method.

Download Print Version | Download XLSX

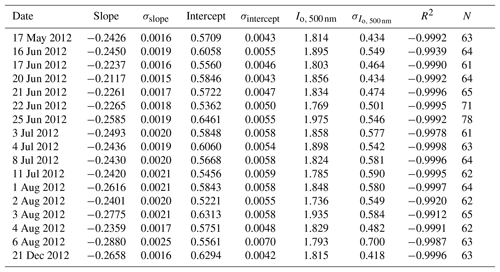
Depending on the year and wavelength, the number of individual Langley calibration constants obtained varied from 14 to 22, which are figures able to provide consistent statistics for calibration constants according to previous studies (Schmid and Wehrli, 1995; Michalsky et al., 2001; Augustine et al., 2003). Another important aspect to corroborate the quality of the individual Langley plots performed is that more than 60 points per individual Langley plot were obtained, when 20 is suggested as a minimum to obtain good results (Augustine et al., 2003). It is also worth mentioning that the slopes derived from the Langley plot and presented in Tables 1 and 2 represent the daily average of total atmospheric optical depth (including molecular, gaseous absorption, and aerosol optical depths). Mean molecular and ozone absorption optical depth in central Amazonia in the visible spectrum are ≈0.14 and ≈0.01, respectively. Therefore, assuming these typical values, the subtraction of ozone and molecular optical depth from the total atmospheric optical depth (slopes) would result in daily mean AOD values in the range of 0.05–0.15, which is typically observed in the Amazonian background atmosphere (Schafer et al., 2008).

Table 2Individual extraterrestrial calibration results (I_{o, 500 nm}) applying the Langley plot technique to measurements of solar direct normal irradiance at 500 nm from a MFRSR operating at the T0e site in central Amazonia for 2015. The individual uncertainty (${\mathit{\sigma }}_{I_{\mathrm{o},\mathrm{500}\mathrm{nm}}}$) used to obtain the relative error (${\mathit{\sigma }}_{I_{\mathrm{o},\mathrm{500}\mathrm{nm}}}$(%)) was estimated from the intercept and its respective uncertainty (σ_intercept) derived from the least-square regression method.

Download Print Version | Download XLSX

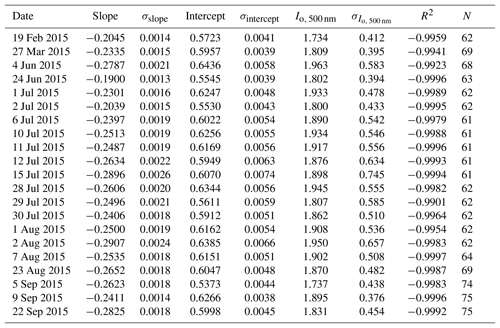
The final extraterrestrial response estimations, $<I_{\mathrm{o},\mathit{\lambda }}>$, for both years and all channels, based on average of all individual Langley plot calibrations, are presented in Table 3 along with the standard error from the mean as the uncertainty (${\mathit{\sigma }}_{<I_{\mathrm{o},\mathit{\lambda }}>}$) and sample number (N) for 2012 and 2015. The relative uncertainty among the channels varied from 0.7 % (870 nm) to 1.0 % (415 nm) in 2012, and from 0.4  % (870 nm) to 1.0 % (415 nm) in 2015, which is surprisingly satisfactory for conditions diverse from those that are recommended (clean mountaintops). Additionally, alternative final extraterrestrial response estimations were calculated based on the median of the set of individual Langley plot calibrations. In general, the differences between median and mean based final extraterrestrial response estimations were less than 1 %, which would result in AOD differences lower than 0.01, i.e. half of the typical uncertainty of AOD derived from AERONET field Sun photometer measurements. In our case, extraterrestrial response estimations based on mean were consistent with estimations based on median; therefore, we used mean based values as a reference for estimating MFRSR AOD. Optional techniques may be applied to derive extraterrestrial response calibrations; Michalsky et al. (2001) used Forgan's (1988) ratio Langley technique, based on ratioing values of individual Langley plot calibrations of the 500 nm channel to those of the 860 nm channel, to select best individual Langley plot calibration, in order to improve the final extraterrestrial response estimations. In the current study, the lower stability of the 870 nm channel prevents applying the method of Michalsky et al. (2001). Regarding the relative difference (−0.4 %) between mean calibration constants derived for the 2 years, the difference for the 415 nm channel is not statistically significant, suggesting that between 2012 and 2015 the correspondent transmission filter did not suffer relevant degradation. Meanwhile, a drift of 4.8 % was observed for the 870 nm channel, an indication of the lower stability of its transmission filter. The remaining channel (500, 613, 670 nm) calibrations are constant, the opposite of the 870 nm channel, which presented a positive trend between the 2012 and 2015 calibrations. However, given the values of the uncertainty (${\mathit{\sigma }}_{<I_{\mathrm{o},\mathit{\lambda }}>}$) in their calibration constants, we are not able to attest statistically that the 500, 613, and 670 nm channels have suffered degradation.

Concerning the seasonal dependence seen in extraterrestrial response calibration from other MFRSRs (Michalsky et al., 2001), we were not able to provide an evaluation since most of the individual Langley plots performed consisted of days in the dry season (see Tables 1 and 2). Outside of the dry season, mainly during the central Amazonian wet season, the high frequency of clouds precludes the favourable atmospheric conditions required to perform the Langley plot method. Nonetheless, a lack of seasonal dependence is very likely since the temperature of central Amazonia is rather stable throughout the year.

Table 3MFRSR final extraterrestrial calibration estimates for the years 2012 and 2015 based on the mean ($<I_{\mathrm{o},\mathit{\lambda }}{>}_{\mathrm{mean}}$) results and median ($<I_{\mathrm{o},\mathit{\lambda }}{>}_{\mathrm{median}}$) of individual Langley plot calibration from Tables 1, 2 and tables in the Supplement. The uncertainty estimation (${\mathit{\sigma }}_{<I_{\mathrm{o},\mathit{\lambda }}>}$) is based on the correspondent standard error of the average.

Download Print Version | Download XLSX

Considering the estimation uncertainties in the obtained extraterrestrial calibration constant (0.4 %–1.0 %), and the Harrison et al. (1994) maximum uncertainty (3 %) for MFRSR I_DN, λ measurements, accordingly to the error propagation analysis (Eq. 6), the worst estimation (i.e. for unit air mass) for our absolute uncertainty in AOD_λ is ≈0.03, which is comparable with uncertainty of AOD_λ retrieved from AERONET field Sun photometer measurements (≈0.02, Eck et al., 1999). However, if a lower uncertainty in I_DN, λ is assumed, for instance 1.5 % (as suggested by Alexandrov et al., 2007), it would reduce MFRSR AOD_λ uncertainty from ≈0.03 to ≈0.02.

In general, perfect linear Langley plots are associated with stable AOD; however, it is possible that not all nearly linear Langley plots are able to provide correct calibration. Air mass assumption, mainly regarding aerosol particle air mass (Schmid and Wehrli, 1995), instrument-induced artefacts, and the shadow-band system alignment (Chen et al., 2013), may contribute to error in calibration. These influences are all challenging to estimate. Therefore, taking the mean (or median) of a set of individual Langley plot calibrations as the estimate for the final calibration constant, along with the comparison of the AOD results with AERONET Sun photometer retrievals, should provide a good reference to evaluate the quality of the calibration constant obtained. The results obtained for RMSEs derived from the comparison between MFRSR retrievals and AERONET Sun photometer AOD are lower than the estimated uncertainty for MFRSR AOD_λ retrievals (i.e. ≈0.02–≈0.03, depending on the I_DN, λ uncertainty assumed, 1.5 % or 3 %) and just above the maximum uncertainty for the AERONET field instrument (≈0.02), demonstrating that, in spite of eventual error associated with assumption made during the Langley plot application, the final derived constants are able to provide reliable AOD retrievals.

3.2 Aerosol optical depth (AOD_λ) inversion and uncertainty estimate

Once the MFRSR channel's final extraterrestrial response calibration was determined, direct normal irradiance measurements taken along 2012 and 2015 were applied to retrieve AOD_λ and to calculate the Ångström exponent. Figure 3 illustrates, for a specific day (22 November 2012), results of cloud screening and a comparison between the diurnal variability of AOD_λ from the MFRSR and the AERONET Sun photometer. The cloud screening criteria captured the majority of contaminated measurements, but a few suspicious remaining points are likely related to subvisible and optically thin cirrus. Using lidar measurements performed at the T0e site, Gouveia et al. (2017) showed that the frequency of subvisible cirrus (optical depth <0.03) in central Amazonia can be as high as 42 %, while for thin cirrus ($\mathrm{0.03}<\text{optical depth}<\mathrm{0.3}$) it can be as high as 38 %. Therefore, both MFRSR and Cimel operational AOD retrievals are exposed to the influence of this subvisible and thin cirrus. A more conservative cloud screening algorithm would remove a significant amount of cloud-free cases, as seems to be the case for AERONET Sun photometer retrievals. The inter-comparison showed the consistency of MFRSR retrievals regarding AOD_λ diurnal variability. It is worth emphasizing the higher frequency of MFRSR retrieval during the afternoon when compared with the AERONET product. This is a critical aspect regarding the representativity of AOD_λ diurnal variation in regions marked by a strong diurnal cycle of convection and cloud cover such as central Amazonia. The MFRSR 1 min frequency is expected to improve the statistic of AOD under cloudy conditions, since the current AERONET Sun photometer statistics are recognized to be biased toward cloudless sky conditions (Levy et al., 2010).

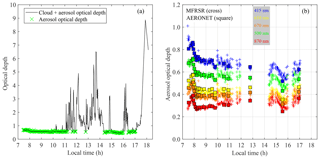
Figure 3(a) Example of the cloud screening procedure applied to the MFRSR aerosol optical depth retrievals (22 November 2012). (b) Cloud screened diurnal cycle of multichannel aerosol optical depth from MFRSR compared with AOD retrievals from the AERONET Level 2.0 product.

Download

A comparison focusing on seasonal variability was also performed. Figure 4 presents the 2012 seasonal variability of AOD_500 nm and α_{415∕670 nm} over the T0e site, as seen by the MFRSR (based on a 1 min time resolution) and the AERONET Sun photometer. When all MFRSR instantaneous retrievals are analysed against the AERONET Sun photometer AOD there is an apparent overestimation of AOD and underestimation of the Ångström exponent (AE). However, when analysing only coincident retrievals in time from both the MFRSR and the AERONET Sun photometer, the AOD and most of AE results are consistent. Therefore, the apparent higher AOD retrievals and low AE seen in MFRSR results are related to the period during which the AERONET AOD product does not provide retrieval. MFRSR retrievals were able to consistently represent the major seasonal features. From March to June, central Amazonia presents its lowest AOD 500 nm levels, ranging from ≈0.05 to ≈0.20. In a completely opposite scenario, during the biomass burning season (August to November), AOD_500 nm hardly goes down below 0.20 and values above 0.50 are quite frequent. During the transition periods, from background conditions to biomass burning (June to July) and from biomass burning to background conditions (December to February), AOD_500 nm oscillated between typical background and biomass burning season values. Considering that the enhancement of AOD_λ during the biomass burning season across central Amazonia is dominated by increases in small particles (Eck et al., 1999; Rosario, 2011), α_{415∕670 nm} variability (Fig. 4) is consistent with the AOD_500 nm discussion; i.e. as the aerosol loading increases from July to the biomass burning months (August–November), α_{415∕670 nm} also shows an enhancement. Ångström exponents ranging from 0.4 to 0.8, which are dominant under background conditions, became rare throughout the biomass burning season and intermittent during the transition periods, a feature consistently described by the MFRSR and the AERONET Sun photometer. Similar results, for both AOD_500 nmm and α_{415∕670 nm}, were observed regarding 2015 (not shown here).

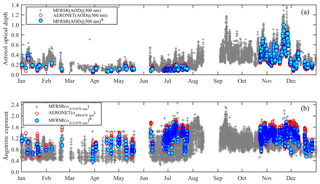
Figure 4Seasonal variability of (a) aerosol optical depth and (b) the Ångström exponent (AE) in the visible spectrum region in central Amazonia for 2012. MFRSR (AOD@500 nm) represents MFRSR instantaneous AOD retrieval at 1 min rate; MFRSR (AOD@500 nm)^& represents only MFRSR AOD retrieved that have been collocated in time with AERONET Sun photometer AOD retrieval (AERONET (AOD@500 nm)). MFRSR (α_{415∕670 nm}) represents MFRSR instantaneous AE at 1 min rate; MFRSR (α_{415, 670 nm})^& represents only MFRSR AE retrieved that have been collocated in time with AERONET Sun photometer AE retrieval (AERONET (α_{440, 670 nm})).

Download

Figures 5 and 6 show scatter plots and statistic metrics (bias, RMSE, and correlation coefficient) comparing MFRSR and AERONET Sun photometer retrievals for 2012 and 2015, respectively. In general, there is a good agreement between both AOD_λ retrievals. However, non-negligible trends are seen, especially for 2012, and in particular for the lower and higher AOD edges. For low AOD_λ values, a systematic underestimation by MFRSR is observed for all channels, while for high AOD_λ, the longer wavelength channels (610 and 670 nm) tend to underestimate AOD. The trends in 2015 are less evident, mainly for the low aerosol loading when compared with 2012. Nevertheless, overall the statistical metrics used to evaluate MFRSR retrievals performance against the AERONET Sun photometer suggest that, when it is not possible to perform calibration on high mountaintops, the extraterrestrial response calibration performed in central Amazonia has the reliability required to support consistent retrievals of AOD. The obtained RMSEs are lower than the estimated uncertainty for MFRSR AOD_λ retrievals (i.e. ≈0.02–≈0.03, depending on the I_DN, λ uncertainty assumed) and slightly above the maximum uncertainty for the AERONET field instrument (≈0.02).

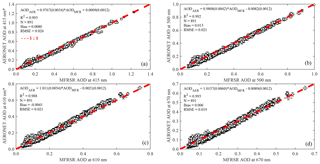
Figure 5Spectral AOD retrieval from the on-site calibrated MFRSR as a function of AOD from the AERONET direct Sun product level 2.0 for 2012. The asterisk (^*) indicates that the AOD at that wavelength was estimated using the Ångström exponent and the dashed red line represents the 1 : 1 line.

Download

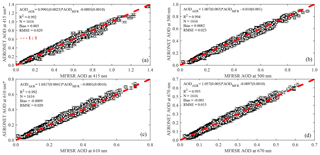
Figure 6Spectral AOD retrieval from the on-site calibrated MFRSR as a function of AOD from the AERONET direct Sun product level 2.0 for 2015. The asterisk (^*) indicates that the AOD at that wavelength was estimated using the Ångström exponent and the red dashed line represents the 1 : 1 line.

Download

Figure 7 compares Ångström exponents derived using AOD retrieved from the AERONET Sun photometer and MFRSR measurements, although comparisons are not as good as those observed for AOD, MFRSR results provide a consistent range of the Ångström exponent in respect to the AERONET results.

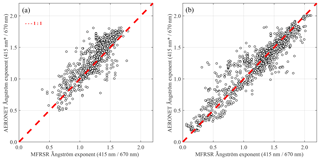
Figure 7The Ångström exponent (AE) for the visible spectrum derived using AOD at 415 and 670 nm from the on-site calibrated MFRSR as a function of AE derived from AOD at 415 nm^* and 670 nm corresponding to the AERONET direct Sun product level 2.0 for (a) 2012 and (b) 2015. The asterisk (^*) indicates that AERONET AOD at 415 nm was estimated using AE since this channel is not present in network Sun photometers. The red dashed line represents 1 : 1 line.

Download