the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Unsupervised classification of vertical profiles of dual polarization radar variables
Dmitri Moisseev
Vertical profiles of polarimetric radar variables can be used to identify fingerprints of snow growth processes. In order to systematically study such manifestations of precipitation processes, we have developed an unsupervised classification method. The method is based on k-means clustering of vertical profiles of polarimetric radar variables, namely reflectivity, differential reflectivity and specific differential phase. For rain events, the classification is applied to radar profiles truncated at the melting layer top. For the snowfall cases, the surface air temperature is used as an additional input parameter. The proposed unsupervised classification was applied to 3.5 years of data collected by the Finnish Meteorological Institute Ikaalinen radar. The vertical profiles of radar variables were computed above the University of Helsinki Hyytiälä station, located 64 km east of the radar. Using these data, we show that the profiles of radar variables can be grouped into 10 and 16 classes for rainfall and snowfall events, respectively. These classes seem to capture most important snow growth and ice cloud processes. Using this classification, the main features of the precipitation formation processes, as observed in Finland, are presented.
- Article
(2946 KB) -
Supplement
(11432 KB) - BibTeX
- EndNote
Globally, the majority of precipitation during both winter and summer originates from ice clouds (Field and Heymsfield, 2015). At higher latitudes winter precipitation occurs in the form of snow, which can have a dramatic impact on human life (Juga et al., 2012). There are a number of challenges in remote sensing of winter precipitation or ice clouds, i.e., quantitative estimation of ice water content or precipitation rate (von Lerber et al., 2017), identification of dangerous weather conditions, etc. To address these challenges, advances in identifying and documenting the processes that take place in ice clouds are needed.
There are several pathways by which ice particles grow, such as vapor deposition, aggregation and riming. Occurrence of these processes depends on environmental conditions. Interpretation of radar observations is based on our understanding of the link between microphysical and scattering properties of hydrometeors. By identifying particle types in observations, we may conclude what processes took place. Currently, dual-polarization radar observations are used in fuzzy logic classification to identify the dominant hydrometeor type present in a radar volume (e.g., Chandrasekar et al., 2013; Thompson et al., 2014). Such methods work very well for classification of hydrometeors of summer precipitations and some features of winter precipitation types. The main challenge is the lack of distinction in dual-polarization radar variables between some ice particle habits. For example, large low-density aggregates and graupel may have similar radar characteristics. Furthermore, these methods perform classification on radar volume by volume basis, without taking into account surrounding observations. Recently, a modification for the hydrometeor classifiers was proposed to make the algorithms aware of the surroundings by incorporating measurements from neighboring radar volumes (Bechini and Chandrasekar, 2015; Grazioli et al., 2015b). This step has greatly improved classification robustness, but it aims to identify particle types instead of fingerprints of microphysical processes.
In the past 10 years, a number of studies reported signatures of ice growth processes in dual-polarization radar observations. Kennedy and Rutledge (2011) have reported bands of increased values of specific differential phase, Kdp, and differential reflectivity, ZDR, in Colorado snowstorms. These bands took place at altitudes where ambient air temperature was around −15 ∘C and their occurrence was attributed to growth of dendritic crystals. Andrić et al. (2013) have implemented a simple steady-state single-column snow growth model to explain the main features of the bands. It was also observed that the occurrence of Kdp bands can be linked to heavier surface precipitation (Kennedy and Rutledge, 2011; Bechini et al., 2013). Moisseev et al. (2015) have advocated that the Kdp bands occur only in precipitation systems with high enough cloud-top heights, where a large number of ice crystals can be generated by either heterogeneous or homogeneous ice nucleation. Using a larger dataset, Griffin et al. (2018) have shown that the Kdp bands can be linked to formation of ice by homogeneous ice nucleation at cloud tops. Furthermore, it was shown that the Kdp bands can be linked to onset of aggregation (Moisseev et al., 2015), which tends to occur more frequently in environments with higher water vapor content (Schneebeli et al., 2013). In addition to the above-listed studies, different aspects of these bands were presented by Trömel et al. (2014), Oue et al. (2018), and Kumjian and Lombardo (2017). Besides Kdp bands in the dendritic growth zone, several studies (e.g., Grazioli et al., 2015a; Sinclair et al., 2016; Kumjian et al., 2016; Giangrande et al., 2016) have reported Kdp observations in the temperature region where Hallett–Mossop (H–M; Hallett and Mossop, 1974) rime-splintering secondary ice production takes place (Field et al., 2016). Sinclair et al. (2016) have shown that such observations can be used to test representation of the secondary ice production in numerical weather prediction models. Other dual-polarization observations that show notable features are high-ZDR regions surrounding the cores of snow-generating cells (Kumjian et al., 2014) and at the top of ice clouds which can be linked to the presence of planar crystals and further to the presence of supercooled liquid water, providing very favorable conditions for their growth at these temperatures (Williams et al., 2015; Oue et al., 2016).
As presented above, the fingerprints of snow growth processes can occur in the form of bands in stratiform clouds, either embedded in the precipitation or on top of a cloud, or in the form of convective generating cells. To identify and document such features, a classification method that uses vertical profiles of dual-polarization radar observations can be used. In this study, we have developed such an unsupervised classification method based on k-means clustering of vertical profiles of polarimetric radar variables, namely reflectivity, differential reflectivity and specific differential phase. The proposed classification is applied to 3.5 years of data collected with the Finnish Meteorological Institute Ikaalinen radar.
The paper is structured as follows. Section 2 describes polarimetric radar and temperature data and their preprocessing. The unsupervised classification method is presented in Sect. 3. Section 4 is dedicated to the analysis and interpretation of the classification results and Sect. 5 presents the conclusions.
In this study, we use vertical profiles of polarimetric radar observables of precipitation over the Hyytiälä forestry station in Juupajoki, Finland, collected using Ikaalinen weather radar, hereafter IKA. The radar is located 64 km west from the station. The measurements were performed between January 2014 and May 2017, partly during the Biogenic Aerosols – Effects on Clouds and Climate (BAECC; Petäjä et al., 2016) field campaign which took place at the measurement site in 2014.
The classification training material includes all precipitation events from this period, where, after preprocessing (see Sect. 2.2), there were no major data quality problems identified. Since synoptic conditions may be similar even in cases where there are gaps in observed precipitation, we define any two precipitation events to be separate from each other if a continuous gap in reflectivity between them exceeds 12 h. See Sect. 4 for more discussion. During the observation period, we identified 74 snow and 123 rain events that meet these conditions. Generally, the full temporal extent of an event includes radar profiles in which precipitation has not reached the ground. A list of the precipitation events is given in the Supplement.
In order to link features identified in vertical profiles of radar variables to precipitation processes, information on the ambient temperature is needed. For this purpose we use vertical profiles of temperature from the National Center for Environmental Prediction (NCEP) Global Data Assimilation System (GDAS) output for Hyytiälä interpolated to match the temporal and vertical resolution of the vertical profiles of radar variables used in this study. The original temporal resolution of the NCEP GDAS data over Hyytiälä is 3 h, and the vertical resolution is 25 hPa between the 1000 and 900 hPa levels and 50 hPa elsewhere.
2.1 Vertical profiles of dual-polarization radar observables
The radar profiles are extracted from IKA C-band radar range height indicator (RHI) measurements. IKA performs RHI scans directly towards Hyytiälä station every 15 min. The values of the radar profiles above Hyytiälä are estimated as horizontal medians over a range of 1 km from the station. The medians are taken over constant altitudes using linear spatial interpolation between the rays. The target bin size of the height interpolation is 50 m.
In this investigation, vertical profiles of equivalent reflectivity factor, Ze, differential reflectivity, ZDR, and specific differential phase, Kdp, are considered in the classification. The Kdp values were computed using the Maesaka et al. (2012) method as implemented in the Python ARM Radar Toolkit (Py-ART; Helmus and Collis, 2016). The method assumes that propagation differential phase, ϕDP, increases monotonically with increasing range from the radar. In this study, we mainly focus on precipitation processes typically occurring in stratiform precipitation, where negative Kdp is not important. The Maesaka et al. (2012) algorithm should be avoided when studying precipitation events with lightning activity, where negative Kdp may occur due to electrification (Caylor and Chandrasekar, 1996). Negative Kdp has also been reported during events of conical graupel which have been linked to observations of generating cells (Oue et al., 2015). The total fraction of profiles analyzed in this study where conical graupel appear or which represent strong convective cells with a possibility for lightning activity is expected to be marginal, as discussed further in Sect. 4.
2.2 Radar data preprocessing
Prior to training or using the polarimetric radar vertical profile data for the classification, noise and clutter filtering is applied to the binned profiles, which is followed by normalization and smoothing. Additionally, there are different preprocessing procedures for rain and snow events that allow ambient temperature to be taken into account in the classification. This section describes the mentioned preprocessing steps in more detail.
2.2.1 Profile truncation
This paper focuses on identifying, characterizing and investigating the frequencies of different types of vertical structures of dual-polarization radar variables specifically from the perspective of detecting, documenting and studying ice processes. Therefore, before the classification, vertical profiles of radar variables are truncated at the top of the melting layer (ML), if one is present. Cases where melting layer signatures were not identified and surface air temperature was 1 ∘C or lower are placed in the snowfall category and investigated separately.
Following Wolfensberger et al. (2015), who have used gradient detection on a combination of normalized ZH and ρhv for ML detection, we combine ρhv and standardized Ze and ZDR into a melting layer indicator:
The same standardization of Ze and ZDR is used here as in classification, as described in Sect. 3.1. In this study, instead of gradient detection, we use peak detection on smoothed IML to find the ML. Peaks are defined as any sample whose direct neighbors have a smaller amplitude and are found in three steps.
-
Peak detection is performed with thresholds for absolute peak amplitude and prominence (, as described below), with chosen values of 2 and 0.3, respectively. The SciPy (version 1.3; Virtanen et al., 2020) implementation of the peak detection algorithm1 is used here.
-
Median ML height, , is computed as the weighted median of the peak altitudes, hi, using the product of peak absolute amplitude and as weights. Peaks above a chosen height threshold of hthresh=4200 m are ignored in this step.
-
Step 1 is run again, this time only considering data within with a chosen ΔhML value of 1500 m. If multiple peaks exceed the threshold values within a profile, the one with the highest amplitude is used.
The ML top height hML,top is estimated as the altitude corresponding to the upper contour of the peak. Peak prominence, H, is a measure of how much a peak stands out from the surrounding baseline value and is defined as the difference between the peak value and its baseline. The baseline is the lowest contour line of the peak encircling it but containing no higher peak (Virtanen et al., 2020).
It should be noted that in steps 2 and 3, the analysis height is limited to reflect the climatology of temperature profiles on the measurement site. In step 2, we assume the ML to be always below hthresh, and in step 3 we expect melting layer height not to change more than ΔhML during an event. Such use of domain knowledge allows more robust ML detection in situations where IML has high values elsewhere. This may occur in the dendritic growth layer (DGL), for example, where the crystals can be pristine enough to cause a significant increase in ZDR and a decrease in ρ.
Sensitivity of the retrieved hML,top is tested for small changes in peak detection parameters discarding inconsistent values. A moving window median threshold filter is applied on time series of hML,top in order to discard rapid high-amplitude fluctuations caused by noise in ZDR, for example. A rolling triangle mean with a window size of five profiles, corresponding to 1 h, is used for smoothing. Finally, linear interpolation and constant extrapolation is applied to hML,top on a per-precipitation-event basis to make the estimate continuous. This robust, albeit fairly complex, procedure produces a smooth estimate for melting layer top height. The results from the ML detection were analyzed manually and the events with errors were discarded. In 90 % of events in the original dataset, the ML was detected without errors.
The analysis of rain profiles is limited to a layer from Δhmargin=300 m to 10 km above hML,top. The purpose of the margin Δhmargin is to prevent properties of the melting layer from leaking to the clustering features. The truncation described in this section has no effect on the height bin size.
2.2.2 Absence of melting layer
Cutting the rain profiles at the top of the melting layer effectively provides information about the ambient temperature at the profile base. As temperature is a key factor driving the ice processes, such information should also be included in the classification process when there is no ML present. In order to introduce corresponding information on ambient temperature at the profile base, we use surface temperature as an extra classification parameter for events with snowfall on the surface. While it would be possible to use whole temperature profiles from soundings or numerical models as classification parameters, we feel that this may not be feasible for many potential key use cases of the classification method. With the wide availability of surface temperature observations in high temporal resolution and in real time, presumably this choice makes the classification method more accessible, especially for operational applications.
The analysis of snow profiles is limited to a layer between 0.2 and 10 km above ground level.
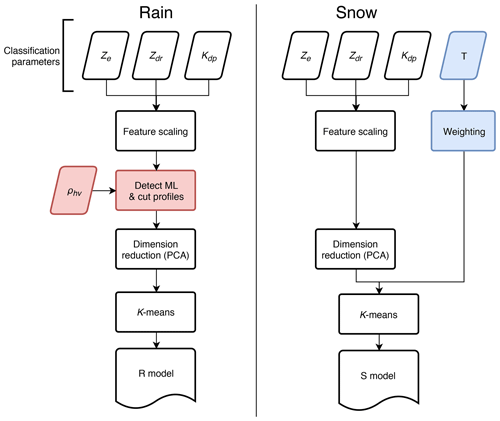
The unsupervised classification method used in this study is based on clustering of dual-polarization radar observations, namely vertical profiles of Kdp, ZDR and Ze. Feature extraction is performed by applying principal component analysis (PCA) on standardized profiles. Clustering is applied to the principal components of the profiles using the k-means method (Lloyd, 1982). A flowchart of the whole process is shown in Fig. 1.
While the core method is identical for processing of all radar profiles, information on temperature is included in a slightly different way based on if it is raining or snowing on the surface. These differences are explained in Sect. 2.2.1 and 2.2.2 and highlighted in Fig. 1: for rain events, the profiles are cut at the top of the melting layer, and for events without a ML surface temperature is included as an extra classification variable. Using this approach, information on profile base ambient temperature is included in the classification process, and the analysis is limited to ice processes.
3.1 Feature extraction
The vertical resolution of the interpolated data is 50 m with bins from 200 m to 10 km altitude for snow events and from 300 m to 10 km above the melting layer top for rain events. Thus, with the three radar variables, each profile is described by a vector of 588 and 582 dimensions for snow and rain events, respectively. In this study, we apply PCA to standardized profiles of the polarimetric radar variables to extract features for the clustering phase.
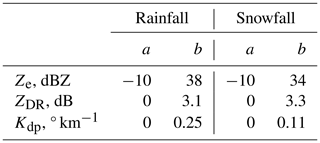
A standardization of the preprocessed polarimetric radar data is performed to allow adequate weights for each variable in clustering. This was done separately for the snow and rain datasets in order to account for seasonal differences in the average values. We used standardization similar to that of Wolfensberger et al. (2015), normalizing typical ranges of values , with the additional condition that the standardized variables should have approximately equal variances. The values a,b used in this study are listed in Table 1. The values of the standardized variables are not capped, but values greater than 1 are allowed when the unscaled values exceed b. Without the standardization, the dominance of each variable in classification would be determined by their variance.
The number of components explaining a significant portion of the total variance for the two training datasets was determined considering the scree test (Cattell, 1966), the Kaiser method, and the component and cumulative explained variance criteria. However, these criteria alone would allow such a low number of components that the inverse transformation from principal component space to the original would result in unrealistic profiles. Thus, the number of components was increased such that, visually, the inverse transformed profiles presented the significant features in the original profiles, up to the point where adding more components seemed to start explaining trivial features such as noise. For both rain and snow profile classification, the first 30 components are used as features. The high number of significant components suggests that reducing the dimensionality of radar observations is not trivial. An advantage of using PCA over simply sampling the profiles is that the former interconnects data from different heights and radar variables such that the components effectively represent features in the profile shapes, while sampling would rather be driven by absolute values at the individual sampling heights.
With snow profile classification, a proxy of the surface temperature, P(Ts)=aTs, where a is a scaling parameter, is used as an additional feature. Thus, essentially, within a cluster is decreased with increasing a. In this study, the value of a was determined in an iterative process during the clustering phase, described in Sect. 3.2, such that, over the clusters, ∘C. Thus, assuming Ts is normally distributed within a given cluster, approximately 95 % of the values of Ts would be typically within a range of 3 ∘C from the cluster mean. A value of a=0.75 was used in this study.
3.2 Clustering
In the present study, the widely used k-means method was chosen for clustering. The algorithm is known for its speed and easy implementation and interpretation. Limitations of the method include the assumption of isotropic data space, sensitivity to outliers (Raykov et al., 2016) and the possibility to converge into a local minimum which may result in counterintuitive results. In our analysis, the anisotropy of the data space is partly mitigated by the PCA transformation. After the transformation, there is still anisotropy, but the transitions in density of the data points in PCA space are smooth (not shown), such that the k-means method seems to produce clusters of meaningful sizes and shapes. The problem of local minima is addressed using the k-means++ method (Arthur and Vassilvitskii, 2007) to distribute the initial cluster seeds in a way that optimizes their spread. The k-means++ is repeated 40 times and the best result in terms of the sum of squared distances of samples from their closest cluster center is used for seeding.
3.3 Selecting the number of classes
An important consideration in using k-means clustering is the choice of number of clusters, k. A good model should explain the data well while being simple. Several methods exist for estimating the optimal number of classes. Nevertheless, often domain- and problem-specific criteria have to be applied for the best results.
The optimal number of clusters depends on variability in the data and correlations between different variables. The more variability and degrees of freedom, the more clusters are generally needed to describe different features in a dataset. Since one important use case for the method is ice process detection, particular attention is paid in separation of fingerprints of different processes between classes. An optimal set of classes would maximize this separation without introducing too many classes to make their interpretation complicated.
As the problem of the number of classes is complex, it is difficult to find an unambiguous quantitative measure for evaluating the correct number of classes. Attempts to create a scoring function for optimizing the separation of ice processes alone did not yield satisfactory results, but were rather used to support the manual selection process.
Silhouette analysis (Rousseeuw, 1987), which is a method for measuring how far each sample is from other clusters (separation) compared to its own cluster (cohesion), was also considered for selecting k. The metric, silhouette coefficient s, takes values between −1 and 1. The higher the value, the better the profile represents the cluster it is assigned to. A profile with s=0 would be a borderline case between clusters, and negative values indicate that the profiles might have been assigned to wrong clusters. Silhouette score can generally be used for choosing k. Unfortunately, when applied to the radar profile clustering results, decreases almost monotonically with increasing k in the ranges of k analyzed and thus did not prove very useful for this purpose. Rather, in this study, we calculate s for each profile classification result individually as a measure of how well the profile represents the class it is assigned to.
The process of selecting the number of rain and snow profile clusters, kR and kS, respectively, was as follows. First, the k-means clustering was repeated 12 times for each k in [5,21] with 40 k-means++ initializations. This is where the above-described silhouette analysis was performed for each set of clusters and the stability of the initialization process was analyzed for each k. Between the 12 repetitions, the clustering converges to identical results for each kR<12 and kS<10. With higher values of k, there are multiple solutions to the clustering problem with only minor differences between them. Moreover, the properties of the cluster centroids are not highly sensitive to k. Clustering performed with k=k0 and would typically result in sets of clusters sharing k0−1 to k0 very similar centroids.
This stability of the clustering results makes it convenient to select k manually. In the second stage, we analyzed each separate clustering solution for differences between the clusters from the point of view of snow processes and surface precipitation. Specifically, an important criterion was to separate the typical Kdp signatures of dendritic growth (e.g., Kennedy and Rutledge, 2011) and the H–M process (Field et al., 2016) into different classes. On the other hand, the use of an unsupervised classification method should also allow us to discover previously undocumented features in the radar profiles if they are present in the data in significant numbers.
The goal in this step is to find as many significant unique fingerprints with as low k as possible by manual evaluation. Significant differences between clusters in this context include variations in profile shapes and altitudes of characteristics such as peaks, clear differences in echo-top heights or differences of cluster centroid Ts of more than 3 ∘C. The most common trivial difference between a pair of clusters was a difference in the intensity of polarimetric radar variables while the shapes of the cluster centroid profiles were almost identical. Altitude differences between fingerprints of overhanging precipitation were also considered trivial.
During this process, allowing some profile classes with only trivial characteristics was inevitable in order to include others with significant unique fingerprints. For this reason, some classes likely reflect natural variability of the same microphysical process rather than unique processes and need to be combined. However, the optimal way of combining the classes may depend on the application. Thus, we present the classes uncombined in this paper.
In snow profile clustering, Ts as an extra classification parameter adds a significant additional degree of freedom. Thus, a larger number of snow profile classes are needed to meet the criteria described above. In clustering, there is a distinguishable separation between clusters representing Ts close to 0 ∘C and around −10 ∘C. The vast majority of profiles belong to the warmer group.
Taking all the mentioned considerations into account, we chose to use 10 and 16 classes for rain and snow profiles, respectively. In 12 of the snow profile class centroids, ∘C. In this paper, the rain and snow profile classification models are termed the R model and S model, respectively.
In this section we have described our approach for optimizing the number of classes with the main criteria of separating the main profile characteristics and the fingerprints of ice processes into individual classes. It should be noted, however, that there is a large spectrum of research problems and operational applications where an unsupervised profile classification method such as the one described in this paper could be potentially useful. The optimal number of classes may depend on the application.
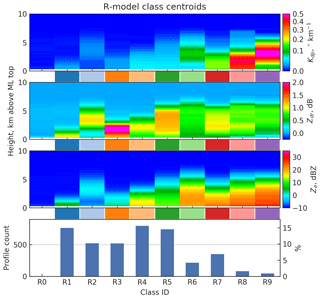
Figure 2Class centroid profiles of the R model. Profile counts per class are shown at the bottom omitting the count for low-reflectivity class R0. Between the panes, each class has been assigned a color code.
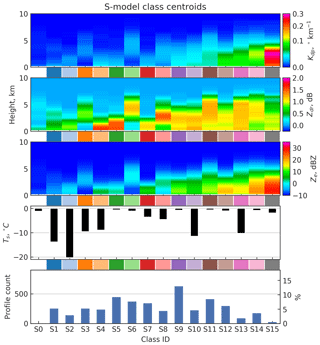
Class centroids of rain and snow profile classes are shown in Figs. 2 and 3, respectively. The centroid profiles of dual-polarization radar variables are inverse transformed from corresponding centroids in PCA space. Classes are numbered in the ascending order by the value of the first principal component in the class centroids. By definition, the first component has the largest variance and therefore has the biggest influence on the clustering and classification results. The value of this component is strongly correlated with intensities of Kdp and Ze.
A number of class centroids in both classification models display distinct features in dual-polarization radar variables often linked to snow processes, such as peaks and gradients in Kdp and ZDR. Such features and their connection to other characteristics in the vertical structure of the profiles and finally to the precipitation processes are discussed in this section.
As a general pattern in Figs. 2 and 3 we see that the highest values of ZDR are associated with low echo tops while the highest Kdp values occur in deeper clouds. This is in line with the previously reported findings (Kennedy and Rutledge, 2011; Bechini et al., 2013; Moisseev et al., 2015; Schrom et al., 2015; Griffin et al., 2018) that echo tops in the DGL are associated with high ZDR and low Kdp in the layer, whereas high Kdp in the DGL with low ZDR is associated with echo tops in ∘C where homogeneous freezing occurs. Using the NCEP GDAS model output, we analyzed the echo top temperatures, Ttop, of each vertical profile radar observation. The results, grouped by profile class, are visualized in Fig. 4. It should be noted that in the summer cold echo tops may be caused by strong updrafts in convection, whereas during the winter, echo tops colder than approximately −37 ∘C are a more unambiguous indication of homogenous freezing. Inspecting the class centroids in Figs. 2 and 3, and comparing them to echo top heights in Fig. 4, it is evident that Kdp layers, especially elevated ones, are strongly associated with high echo tops.
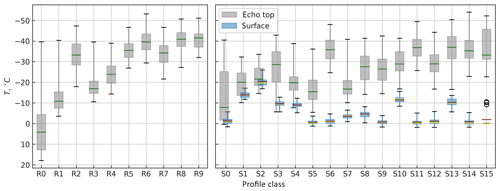
Figure 4Cloud-top temperature distributions by class (gray) with the green line marking the medians. For S classes, surface temperature distribution is also shown (blue) with red lines marking the class centroid and yellow lines marking the median. Boxes extend between the first and the third quantiles, and whiskers cover 95 % of the data.
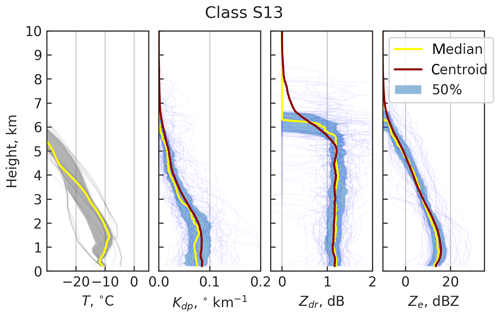
Figure 5The class S13 centroid is visualized in the three rightmost panes. Individual class member profiles are marked with thin lines. The pane on the left shows corresponding NCEP GDAS temperature profiles. The areas between the first and the third quantiles are shaded, radar data is in blue and GDAS is in gray.
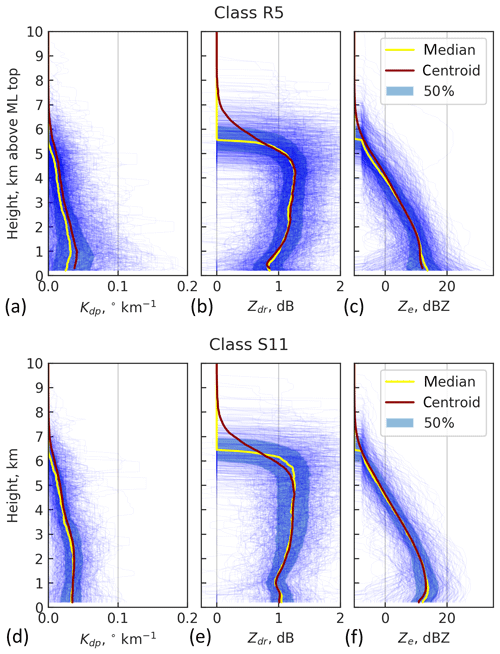
Figure 6Comparing classes R5 (a, b, c) and S11 (d, e, f) shows evident similarities. Individual class member profiles are marked with thin blue lines and the areas between the first and the third quantiles are shaded with blue.
The clustering results expose a prominent seasonal difference in Kdp intensity: consistently lower values are present in snow events. There are four rain profile classes in contrast to only two snow profile classes with peak cluster centroid Kdp exceeding 0.1 ∘ km−1. They represent total fractions of 13 % and 4 % of rain and snow profiles, respectively. Corresponding to this difference, in Figs. 2 and 3, as well as in Figs. 7 and 8 introduced later, Kdp is visualized in different ranges in relation to rain and snow profiles. The seasonal differences in ZDR and Ze intensities are less prominent. High Kdp in the summer may be linked to higher water content during the season. Additionally, the seasonal variability of vertical motion could impact the ZDR and Kdp enhancements.
Convection in the summer, especially in the presence of hail, is linked to extreme values of radar variables and high echo tops (Voormansik et al., 2017), which may also have a small contribution to the seasonal differences (Mäkelä et al., 2014). However, convective rainstorms are of short duration and thus typically present in just a couple of profiles per convective cell. Therefore, their impact on the class properties is expected to be limited. Manual analysis revealed that classes R6 and R9 have the highest and R5 the lowest fractions of profiles measured in convective cells. Further details of this analysis are presented in Sect. 4.2.
Class frequencies are presented in the bottom panels of Figs. 2 and 3. Classes S0 and R0 represent very low values of Ze throughout the column, i.e., profiles with very weak or no echoes. Therefore their frequencies depend merely on the subjective selection of observation period boundaries and are thus omitted in the figures. Boundaries of the precipitation events are partly based on these two 0 classes. Events are considered independent and separate if between them there are profiles classified as S0 or R0 continuously for at least 12 h.
With respect to Kdp intensity, classes in the R model can be divided into four categories: R0 through R3 with negligible Kdp, low-Kdp classes R4 and R5 with ∘ km−1, high-Kdp classes R6 and R7 with ∘ km−1, and classes R8 and R9 representing extreme values . The subscript “c” denotes a class centroid value as opposed to values in individual profiles. The peak Kdp,c of both R6 and R9 is at 3 km, corresponding to class mean GDAS temperatures of −16 and −18 ∘C, respectively. Essentially, these two classes represent clear Kdp features in the DGL.
Classes R7 and R8 feature considerable Kdp in 2–3 km thick layers right above the ML, with centroid values slightly below 0.2 ∘ km−1 and around 0.4 ∘ km−1, respectively. Essentially, both classes represent Kdp signatures in both the DGL and temperatures favored by the H–M process. Sinclair et al. (2016) found that the typical Kdp values for the H–M process are capped at 0.2…0.3 ∘ km−1 for the C band due to onset of aggregation. Based on this, it can be argued that R7 is a more likely indicator of H–M than R8.
Classes R3 and R4 were found to often coexist in precipitation events. Both are characterized by low Kdp and a layer of ZDR in the DGL. In Fig. 4, we see that the echo tops are lower for the R3 profiles, typically in the DGL. Therefore, we would expect growth of pristine crystals in low number concentrations and consequently with no significant aggregation. This would explain why peak ZDR values from 3 to 5 dB are common in relation with R3. Profiles classified as R4, on the other hand, have slightly higher echo tops ( ∘C), which are expected to result in higher number concentrations, leading to aggregation. The R4 profiles are characterized by much lower ZDR values.
In the S model (Fig. 3), classes S0 through S3 represent profiles with low values of all three radar variables, each with dBZ, dB and ∘ km−1. These four low-reflectivity classes represent different surface temperatures, which is likely a major driver for the separation of these classes in the clustering process. Classes S4 and S5 represent low echo top profiles with high ZDR, with class centroid surface temperatures of −9.0 and −0.6 ∘C, respectively. Further analysis of NCEP GDAS temperature profiles reveals that, across the board, there is an inversion layer present where radar profiles are classified as S4, typically with temperatures below −10 ∘C within the lowest kilometer. This corresponds well with the bump in ZDR,c close to the surface, suggesting possible growth of pristine dendrites within a strong inversion layer. In contrast, there is no inversion in connection with profiles belonging to S5, and the enhancement in ZDR occurs already at 2 to 3 km above the surface, where the median NCEP GDAS temperature for S5 profiles is roughly between −18 and −10 ∘C. S5 is the second most common class in S-model classification results.
Classes S6 and S8 represent situations where precipitation is detached from the surface. These types of profiles are typically present in association with approaching frontal systems before the onset of surface precipitation. The most frequent class of the S model is S9 covering 13 % of the profiles. It represents moderate values of polarimetric radar variables and cloud-top height. The most extreme values of reflectivity and Kdp values in the S model are represented by classes S14 and S15. For both classes, Kdp,c peaks above 3 km, suggesting dendritic growth in the member profiles. Values of ZDR,c are significantly lower compared to other high echo top classes with weaker Kdp,c. Class S15 can be seen as a more extreme variant of S14 with much stronger Kdp,c and Ze,c. In addition, S15 represents lower values of ZDR near the DGL, having slightly elevated values in the bottom 3 km instead. These differences are likely due to even higher ice number concentrations in S15 profiles, which lead to more intense aggregation.
Comparing class centroid Ts and class frequencies in Fig. 3 it can be seen that most snowfall occurs at Ts≈0 ∘C. Further analysis of GDAS temperature profiles for the snow events revealed that typically cold surface temperatures ( ∘C) are heavily contributed to by strong inversion layers. The centroid and members of S13 are visualized in Fig. 5, along with the member GDAS temperature profiles. The profile class is characterized by a thick layer of considerable Kdp from 2 to 3 km to the surface, and ∘C. As seen in the left panel of Fig. 5, S13 represents conditions where T typically falls below −10 ∘C close to the surface. This finding suggests that a second DGL may occur in a strong inversion layer.
Using the double-moment Morrison microphysics scheme (Morrison et al., 2005), Sinclair et al. (2016) showed that Kdp at the −8 to −3 ∘C temperature range can be used for identifying the H–M process. Such fingerprints are present in particular in profiles classified as R7 or S12. However, manual analysis of the profile data revealed that both of these classes represent a mixture of fingerprints indicating H–M, dendritic growth or the co-presence of both processes. In several events, there were continuous time frames of profiles classified as either R7 or S12 during which the altitude of the Kdp signal was changing from profile to profile between the DGL and 0 ∘C level and was occasionally bimodal. One example of such a time frame is shown in Fig. 7 and discussed further in Sect. 4.1.1. Some bimodality is also present in the centroid Kdp,c of both classes, suggesting that the elevated Kdp,c values in the H–M region cannot be explained solely by sedimenting planar crystals generated aloft but are contributed by the H–M process.
While there are no classes with clear-cut Kdp,c peaks at altitudes corresponding to temperatures preferred by the H–M process in either rain or snow profile classification, there are, in contrast, several classes with strong elevated Kdp,c layers. The proposal of Sinclair et al. (2016) that Kdp fingerprints of the H–M process are not very pronounced may explain the tendency of the classification method not to produce more pure H–M classes. Nevertheless, R7 and S12 can be used as indicators for conditions where H–M may occur.
Despite the differences in the classification methods for rain and snow profiles, there are prominent similarities between the two models and profile classes therein. Archetypal classes such as high echo tops in the presence of elevated Kdp layers (R6, R9, S14, S15) or high ZDR in shallow precipitation (R3, S4, S5) exist in both classification models. Frequent classes R5 and S11, visualized side by side in Fig. 6, can be considered direct counterparts of each other. The vertical structure of polarimetric radar variables above the ML in R5 match strikingly well with S11. The two classes are characterized by weak Kdp and typical values of ZDR slightly above 1 dB aloft, decreasing towards the altitude corresponding to 0 ∘C. Presumably, this indicates the presence of aggregation.
4.1 Case studies
In Figs. 2 and 3, each class is assigned a color code (between the panels). This color coding is used in Figs. 7 and 8 to mark classification results in a rain and a snow case, respectively. Note that the same set of colors is used for denoting rain and snow profile classification, but they should not be confused with each other.
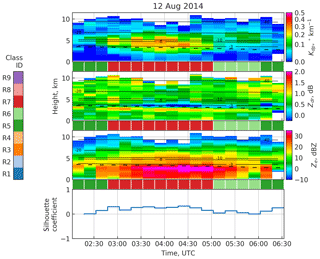
Figure 7Classification analysis of a rain case with silhouette scores. The automatically detected melting layer is marked with a dashed line, the solid lines show the NCEP GDAS temperature contours and the colors between the panes denote classification results.
4.1.1 12 August 2014
In Fig. 7, rain profile classification has been applied to a precipitation event from 12 August 2014. During this event, echo tops repeatedly exceed 10 km. Only the parts of the profiles above the melting layer top are analyzed here, since everything below that level is invisible to the classifier. The first two and the last two profiles shown in the figure are characterized by low Ze and low Kdp, while ZDR has values around 1 dB. These profiles are classified as R5 (dark green). Between 02:30 and 03:00 UTC, a significant increase in Kdp occurs, followed by an increase in reflectivity and decrease in ZDR. The temperature (altitude) of the downward increase in Kdp varies from the −20 ∘C level to closer to the ML. In this phase, there is also a small increase in ZDR in the DGL whenever the increase in Kdp also occurs in the DGL. This phase in the event is sustained until around 05:00 UTC and is classified as R7 (dark red). It is followed by approximately an hour of a weaker elevated Kdp layer at around 4 to 6 km altitude with profiles classified as class R6 (light green). The silhouette coefficient is positive throughout the event indicating good confidence of the classification results. The silhouette of the profiles classified as R6 is not very high, though, which is likely due to lower values of Ze compared to the class centroid.
Similar analysis of more rain events in the dataset reveals that, similar to the 12 August event, R7 typically coincides with an increase in Kdp in the DGL, H–M layer or both, often with varying altitude. Without in situ observations or analysis of Doppler spectra, it is not trivial to tell whether this variability is due to co-presence of dendritic growth and H–M or simply fall streaks. Class R6, on the other hand, is more specific to a Kdp fingerprint in the DGL. The more infrequent profiles with clear Kdp bands above the DGL are typically also classified as R6 or R9.
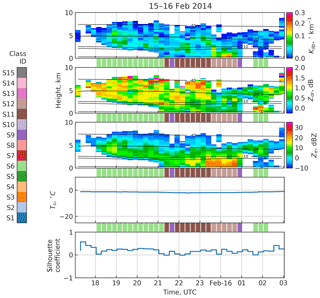
4.1.2 15–16 February 2014
Classification results for 15–16 February 2014 are shown in Fig. 8. The event has a clear structure of an approaching frontal system. Between 17:00 and 18:00 UTC Ze is very low, corresponding to class S0, which is marked with white color between the panels. Between 18:00 and 21:00 UTC, the event starts with overhanging precipitation, classified as S6 (light green). This is followed by light precipitation with echo tops at roughly 7 to 8 km and relatively high ZDR near the echo top, decreasing downwards. This corresponds well with class S11 (dark brown). After 23:30 UTC, The echo top height is decreased to roughly 6 km, ZDR is decreased and Kdp signals appear close to ground level. The increase in Kdp occurs within the −8 to −3 ∘C temperature range, suggesting the presence of the H–M process. Indeed, Kneifel et al. (2015) report needles, needle aggregates and rimed particles on the surface at the measurement site during this period and favorable conditions for rime splintering. Further, using the Weather Research and Forecast (WRF) model, Sinclair et al. (2016) showed that secondary ice processes are needed to explain the observed number concentrations during this time period. The corresponding profiles are classified as S12 (light brown). Within this case study, two profiles, marked with dark purple, are classified as S9, likely due to the momentary absence of any strong Kdp or ZDR signals.
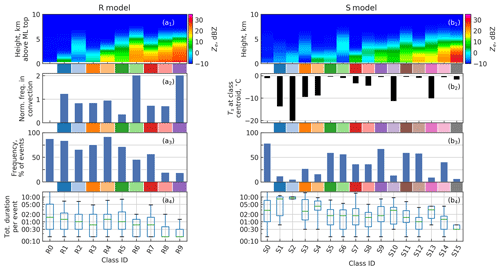
Figure 9Statistics on frequency of each profile class. Classes are identified by class centroid Ze (a1, b1) and class centroid Ts for snow profile classes (b2), with color codes between the panels and class IDs at the bottom. Panel (a2) has the ratios of the number of profiles in convective cases per class to the expected value in uniform distribution. In (a4, b4), the class frequencies are given as percentage of events (a3, b3) and total durations (a4, b4) within events.
4.2 Statistics
Frequency statistics of the profile classes are presented in Fig. 9. We analyzed a subset of rain events as either convective or stratiform using a number of sources of publicly available satellite and numerical model data. Out of 70 events analyzed, 15 were convective and 55 stratiform. Panel (a2) in Fig. 9 shows the ratios of the number of profiles in convective cases per class to the expected value in uniform distribution. On average, twice as many profiles are classified as R6 and R9 in convective situations compared to their average frequencies. Both classes are characterized by high echo tops and elevated Kdp bands. On the other hand, classes R7 and R8, also representing high Kdp values, but closer to the melting layer than R6 and R9, appear in lower-than-average frequency in convective situations. Class R5 is most pronouncedly characteristic for stratiform events, with frequency in convective events roughly one-third of the average value.
Panels (a3) and (b3) of Fig. 9 show the fractions of independent precipitation events in which each class occurs. With rain events, this frequency correlates inversely with Kdp,c. Rain profiles classified as R8 and R9, which represent the strongest Kdp signatures, occur in 20 % and 19 % of the events, respectively, with at least one of the two occurring in 25 % of the events. Classes R6 and R7, representing more modest Kdp features, occur in 45 % and 57 % of cases, respectively, and the rest of the classes between 67 % and 92 % of the cases.
With snow events, the likelihood of a given class occurring within an event correlates not only with peak Kdp,c but also with surface temperature. Any class representing low Kdp values and surface temperature close to 0 ∘C occurs in more than half of the snow events.
The per precipitation event class persistence is visualized in the bottom panels of Fig. 9. Profile classes representing the highest values of Ze at the surface, namely R6–R9, S12, S14 and S15, are short-lived, whereas snow profile classes characterized by cold surface temperatures are the most persistent. Profiles classified as R0 or S0 omitted, the median durations of rain and snow events in the dataset are 5.5 and 11.5 h, respectively. This difference explains why S classes are on average more persistent than R classes.
A novel method of dual-polarization radar profile classification for investigating vertical structure of snow processes in the profiles was presented in this paper. The method is based on clustering of PCA components of vertical profiles of Kdp, ZDR and Ze and surface temperature. It was applied to vertical profile data extracted from C-band RHI scans over Hyytiälä measurement station in southern Finland. We applied separate versions of the method based on if surface precipitation type was rain (R model) or snow (S model). In the R model, profiles are truncated at the melting layer top, and in the S model surface temperature is used as an additional classification feature. The content of the vertical profile classes was manually interpreted.
In the present investigation, some class centroids resembled textbook examples of previously documented snow process fingerprints, while others may represent a mixture of different conditions. If temperature profiles from either soundings or numerical models are available, the interpretation can be done in the absence of surface crystal type reports. Notably, this is prerequisite in cases of rainfall when direct observations of crystal types cannot be performed at the surface.
The year-round variability in the vertical structure of Kdp, ZDR and Ze can be described using a total of 26 profile classes: 10 and 16 in the presence and absence of the ML, respectively. One of the main goals of this study was to associate profile classes with snow processes for their automated identification. It should be noted, though, that the profile classification is not based on expressly selected characteristics of radar fingerprints of the processes, but rather the general, complete structure of the profiles. Nevertheless, some profile classes seem to be strong indicators of specific processes or their combinations within the vertical profiles. From both classification models we can identify a total of seven archetypes with the following characteristics.
-
Profiles have a strong Kdp peak in the DGL, while the peak in ZDR is not pronounced. This archetype appears in deep precipitation systems with homogeneous freezing at the cloud top. It is associated with intensified dendritic growth leading to aggregation and high precipitation rate. (Classes R6, R9, S14, S15)
-
There is a Kdp signature between the DGL and the 0 ∘C level, possibly due to simultaneous occurrence of dendritic growth and secondary ice production. Homogeneous freezing occurs at the cloud top. (R7, R8, S12)
-
Profiles are characterized by high echo tops, negligible Kdp, and ZDR>1 dB, which decreases closer to the melting level due to aggregation. Typically, Ze<20 dBZ. (R5, S11)
-
The cloud top is between the −30 and −20 ∘C levels, and there is only a weak ZDR band present at the −15 ∘C level. Ze is moderate at roughly 20–30 dBZ, and Kdp is weak. (R4, S9)
-
ZDR is typically higher than 1.5 dB at the cloud to at around −15 ∘C and is associated with the growth of pristine planar crystals in low number concentrations. No Kdp is present, and low values of Ze indicate the absence of aggregation. (R3, S5)
-
The radar echo is detached from the surface either due to snow particles not having reached the surface yet or because they are sublimating due to a dry layer. (R2, S3, S6, S8)
-
Ze is weak throughout the profile. (R0, S0–S2)
In addition to these archetypes found in both summer and winter storms, there are S classes representing situations where strong inversions interfere with snow processes. Notably, we found indications of dendritic growth in strong inversion layers, manifested as class S13. As the colder arctic air mass seldom occurs in southern Finland, ∘C can usually be attributed to a strong lower-level inversion. Such inversions may have an important effect on the frequency of occurrence of some ice processes. Further, this implies that temperature information near the surface is necessary in order to determine whether a low altitude Kdp signature in the winter is an implication of the H–M process or dendritic growth.
Our approach to the classification problem is pronouncedly data-driven. This way, if the training material represents the climatology of ice processes and their radar signatures, as was the aim in this study, the resulting classes will reflect the statistical properties of this climatology. Hand picking the training material, on the other hand, would introduce human bias into the class boundaries.
However, there are possible drawbacks in the data-driven approach. The typical radar fingerprints of the H–M process were found to be much more scarce than those of dendritic growth, and often less pronounced. This negatively affects how the typical fingerprints of the H–M process are represented in the classes. This could be enhanced by introducing a larger fraction of H–M profiles in the training data.
Another disadvantage in the data-driven approach is that covering a meaningful collection of unique fingerprints requires a large number of clusters, some of which do not represent unique microphysical processes. This problem may be mitigated to some extent by further optimizing the scaling of the radar variables such that the clustering would be less driven by differences in the intensities of the signatures in contrast to their shapes. Another way to address this issue is to simply combine classes that seem to represent the same processes, in like manner of the archetypes presented above. Reducing the number of classes by simply choosing a smaller k in the k-means clustering would reduce the amount of manual work involved in defining the class boundaries at the cost of decreased detail and accuracy in separating the processes. With a smaller k, the clustering would be driven by more general features of the profiles such as the overall shape and intensity of the polarimetric radar variables, whereas especially the typical characteristics of the H–M process fingerprints involve a higher level of detail.
The classification method presented in this study should be considered a starting point in studying vertical profiles of radar variables using unsupervised classification. As such, there is a vast range of potentially useful opportunities for further development of the method. The method is built on reasoned use of well-known, proven algorithms such as PCA and k-means. We showed that this combination of machine learning algorithms allows both identification of known fingerprints and a more explorative approach in studying the characteristics of a regional climatology of precipitation processes. Limitations of the k-means method include the spherical shape and similar area occupied by the clusters, which involve a risk of suboptimal separation of the microphysical processes to different classes. In this study, we addressed these limitations by allowing a rather large number of initial classes and combining similar ones by identifying the archetypes based on known fingerprints of the processes. Another possible approach would be to explore the numerous alternative clustering methods for a more optimal separation of the precipitation processes. A comprehensive comparison of such methods, however, is outside the scope of this study.
In the present classification method, ambient temperature is known only at the profile base. Compared to the use of full temperature profiles, this simplifies the method and, perhaps even more importantly, the requirements for the input data. However, future studies should investigate if the use of full temperature profiles allows more accurate separation of precipitation processes into different classes.
The unsupervised nature of the classification method is expected to allow extension of its application to the detection of ice processes not covered in this study. Recently, Li et al. (2018) showed that certain combinations of Ze, ZDR and Kdp signatures can potentially be used for detecting heavy riming. Furthermore, the process is frequently observed in Finland, highlighting the potential of using an unsupervised method for its identification.
It should be noted that wind shear effects induce differential advection of hydrometeors at different altitudes, affecting the gradients in the vertical profiles of radar variables (Lauri et al., 2012). Therefore caution should be used in interpreting microphysical processes corresponding to class centroid profiles. The wind shear effects are difficult to correct for using vertical profile or RHI radar observations due to the limitations in horizontal sampling. Such adjustments become more viable if classification is performed on profiles extracted from volume scans, which will be investigated in future work.
The ability to describe a climatology of vertical structure of dual-polarization radar variables and, further, precipitation processes using a finite number of classes has evident potential in improving quantitative precipitation estimation. We anticipate that automated detection of ice processes may allow the development of adaptive relation for snowfall rate S=S(Ze), in which the parameters could be chosen based on the profile classification result. Adaptive S(Ze) relations, in turn, have potential in improving the vertical profile of reflectivity correction methods. Future work will be devoted to investigating the use of unsupervised profile classification in such applications.
The FMI radar and surface temperature data are available from the Finnish Meteorological Institute (2019) open data portal: https://en.ilmatieteenlaitos.fi/open-data-sets-available (last access: 1 October 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/amt-13-1227-2020-supplement.
The study was designed by both authors. JT implemented and ran the classification and made the figures. JT wrote the manuscript, with contributions from DM. Both authors discussed the results and commented on the manuscript.
The authors declare that they have no conflict of interest.
We would like to thank the personnel of Hyytiälä station and Matti Leskinen for their support in field observation.
This research has been supported by the Academy of Finland's Center of Excellence (CoE) (grant no. 307331). The research of Jussi Tiira has been supported by the Doctoral Programme in Atmospheric Sciences (ATM-DP, University of Helsinki).
Open access funding provided by Helsinki University Library.
This paper was edited by S. Joseph Munchak and reviewed by two anonymous referees.
Andrić, J., Kumjian, M. R., Zrnić, D. S., Straka, J. M., and Melnikov, V. M.: Polarimetric Signatures above the Melting Layer in Winter Storms: An Observational and Modeling Study, J. Appl. Meteorol. Clim., 52, 682–700, https://doi.org/10.1175/JAMC-D-12-028.1, 2013. a
Arthur, D. and Vassilvitskii, S.: k-means++: The advantages of careful seeding, 1027–1035, Society for Industrial and Applied Mathematics, 2007. a
Bechini, R. and Chandrasekar, V.: A Semisupervised Robust Hydrometeor Classification Method for Dual-Polarization Radar Applications, J. Atmos. Ocean. Tech., 32, 22–47, https://doi.org/10.1175/JTECH-D-14-00097.1, 2015. a
Bechini, R., Baldini, L., and Chandrasekar, V.: Polarimetric Radar Observations in the Ice Region of Precipitating Clouds at C-Band and X-Band Radar Frequencies, J. Appl. Meteorol. Clim., 52, 1147–1169, https://doi.org/10.1175/JAMC-D-12-055.1, 2013. a, b
Cattell, R. B.: The Scree Test For The Number Of Factors, Multivar. Behav. Res., 1, 245–276, 1966. a
Caylor, I. and Chandrasekar, V.: Time-varying ice crystal orientation in thunderstorms observed with multiparameter radar, IEEE T. Geosci. Remote Sens., 34, 847–858, https://doi.org/10.1109/36.508402, 1996. a
Chandrasekar, V., Keränen, R., Lim, S., and Moisseev, D.: Recent advances in classification of observations from dual polarization weather radars, Atmos. Res., 119, 97–111, https://doi.org/10.1016/j.atmosres.2011.08.014, 2013. a
Field, P. R. and Heymsfield, A. J.: Importance of snow to global precipitation: IMPORTANCE OF SNOW TO PRECIPITATION, Geophys. Res. Lett., 42, 9512–9520, https://doi.org/10.1002/2015GL065497, 2015. a
Field, P. R., Lawson, R. P., Brown, P. R. A., Lloyd, G., Westbrook, C., Moisseev, D., Miltenberger, A., Nenes, A., Blyth, A., Choularton, T., Connolly, P., Buehl, J., Crosier, J., Cui, Z., Dearden, C., DeMott, P., Flossmann, A., Heymsfield, A., Huang, Y., Kalesse, H., Kanji, Z. A., Korolev, A., Kirchgaessner, A., Lasher-Trapp, S., Leisner, T., McFarquhar, G., Phillips, V., Stith, J., and Sullivan, S.: Chapter 7. Secondary Ice Production – Current State of the Science and Recommendations for the Future, Meteorol. Monogr., 58, 7.1–7.20, https://doi.org/10.1175/AMSMONOGRAPHS-D-16-0014.1, 2016. a, b
Finnish Meteorological Institute: The Finnish Meteorological Institute's open data, available at: https://en.ilmatieteenlaitos.fi/open-data, last access: 1 October 2019. a
Giangrande, S. E., Toto, T., Bansemer, A., Kumjian, M. R., Mishra, S., and Ryzhkov, A. V.: Insights into riming and aggregation processes as revealed by aircraft, radar, and disdrometer observations for a 27 April 2011 widespread precipitation event: Insights into Riming and Aggregation, J. Geophys. Res.-Atmos., 121, 5846–5863, https://doi.org/10.1002/2015JD024537, 2016. a
Grazioli, J., Lloyd, G., Panziera, L., Hoyle, C. R., Connolly, P. J., Henneberger, J., and Berne, A.: Polarimetric radar and in situ observations of riming and snowfall microphysics during CLACE 2014, Atmos. Chem. Phys., 15, 13787–13802, https://doi.org/10.5194/acp-15-13787-2015, 2015a. a
Grazioli, J., Tuia, D., and Berne, A.: Hydrometeor classification from polarimetric radar measurements: a clustering approach, Atmos. Meas. Tech., 8, 149–170, https://doi.org/10.5194/amt-8-149-2015, 2015b. a
Griffin, E. M., Schuur, T. J., and Ryzhkov, A. V.: A Polarimetric Analysis of Ice Microphysical Processes in Snow, Using Quasi-Vertical Profiles, J. Appl. Meteorol. Clim., 57, 31–50, https://doi.org/10.1175/JAMC-D-17-0033.1, 2018. a, b
Hallett, J. and Mossop, S. C.: Production of secondary ice particles during the riming process, Nature, 249, 26–28, https://doi.org/10.1038/249026a0, 1974. a
Helmus, J. J. and Collis, S. M.: The Python ARM Radar Toolkit (Py-ART), a Library for Working with Weather Radar Data in the Python Programming Language, Journal of Open Research Software, 4, e25, https://doi.org/10.5334/jors.119, 2016. a
Juga, I., Hippi, M., Moisseev, D., and Saltikoff, E.: Analysis of weather factors responsible for the traffic “Black Day” in Helsinki, Finland, on 17 March 2005, Met. Apps, 19, 1–9, https://doi.org/10.1002/met.238, 2012. a
Kennedy, P. C. and Rutledge, S. A.: S-Band Dual-Polarization Radar Observations of Winter Storms, J. Appl. Meteorol. Clim., 50, 844–858, https://doi.org/10.1175/2010JAMC2558.1, 2011. a, b, c, d
Kneifel, S., von Lerber, A., Tiira, J., Moisseev, D., Kollias, P., and Leinonen, J.: Observed relations between snowfall microphysics and triple-frequency radar measurements: Triple Frequency Signatures of Snowfall, J. Geophys. Res.-Atmos., 120, 6034–6055, https://doi.org/10.1002/2015JD023156, 2015. a
Kumjian, M. R. and Lombardo, K. A.: Insights into the Evolving Microphysical and Kinematic Structure of Northeastern U.S. Winter Storms from Dual-Polarization Doppler Radar, Mon. Weather Rev., 145, 1033–1061, https://doi.org/10.1175/MWR-D-15-0451.1, 2017. a
Kumjian, M. R., Rutledge, S. A., Rasmussen, R. M., Kennedy, P. C., and Dixon, M.: High-Resolution Polarimetric Radar Observations of Snow-Generating Cells, J. Appl. Meteorol. Clim., 53, 1636–1658, https://doi.org/10.1175/JAMC-D-13-0312.1, 2014. a
Kumjian, M. R., Mishra, S., Giangrande, S. E., Toto, T., Ryzhkov, A. V., and Bansemer, A.: Polarimetric radar and aircraft observations of saggy bright bands during MC3E: SAGGY BRIGHT BANDS, J. Geophys. Res.-Atmos., 121, 3584–3607, https://doi.org/10.1002/2015JD024446, 2016. a
Lauri, T., Koistinen, J., and Moisseev, D.: Advection-Based Adjustment of Radar Measurements, Mon. Weather Rev., 140, 1014–1022, https://doi.org/10.1175/MWR-D-11-00045.1, 2012. a
Li, H., Moisseev, D., and von Lerber, A.: How Does Riming Affect Dual-Polarization Radar Observations and Snowflake Shape?, J. Geophys. Res.-Atmos., 123, 6070–6081, https://doi.org/10.1029/2017JD028186, 2018. a
Lloyd, S.: Least squares quantization in PCM, IEEE T. Informa. Theory, 28, 129–137, https://doi.org/10.1109/TIT.1982.1056489, 1982. a
Maesaka, T., Iwanami, K., and Maki, M.: Non-negative K DP estimation by monotone increasing Φ DP assumption below melting layer, in: Extended Abstracts, Seventh European Conf. on Radar in Meteorology and Hydrology, 3 June 2012, Toulouse, France, 2012. a, b
Moisseev, D. N., Lautaportti, S., Tyynela, J., and Lim, S.: Dual-polarization radar signatures in snowstorms: Role of snowflake aggregation, J. Geophys. Res.-Atmos., 120, 12644–12655, https://doi.org/10.1002/2015jd023884, 2015. a, b, c
Morrison, H., Curry, J. A., and Khvorostyanov, V. I.: A New Double-Moment Microphysics Parameterization for Application in Cloud and Climate Models. Part I: Description, J. Atmos. Sci., 62, 1665–1677, https://doi.org/10.1175/JAS3446.1, 2005. a
Mäkelä, A., Enno, S.-E., and Haapalainen, J.: Nordic Lightning Information System: Thunderstorm climate of Northern Europe for the period 2002–2011, Atmos. Res., 139, 46–61, https://doi.org/10.1016/j.atmosres.2014.01.008, 2014. a
Oue, M., Kumjian, M. R., Lu, Y., Jiang, Z., Clothiaux, E. E., Verlinde, J., and Aydin, K.: X-Band Polarimetric and Ka-Band Doppler Spectral Radar Observations of a Graupel-Producing Arctic Mixed-Phase Cloud, J. Appl. Meteorol. Clim., 54, 1335–1351, https://doi.org/10.1175/JAMC-D-14-0315.1, 2015. a
Oue, M., Galletti, M., Verlinde, J., Ryzhkov, A., and Lu, Y.: Use of X-Band Differential Reflectivity Measurements to Study Shallow Arctic Mixed-Phase Clouds, J. Appl. Meteorol. Clim., 55, 403–424, https://doi.org/10.1175/JAMC-D-15-0168.1, 2016. a
Oue, M., Kollias, P., Ryzhkov, A., and Luke, E. P.: Toward Exploring the Synergy Between Cloud Radar Polarimetry and Doppler Spectral Analysis in Deep Cold Precipitating Systems in the Arctic, J. Geophys. Res.-Atmos., 123, 2797–2815, https://doi.org/10.1002/2017JD027717, 2018. a
Petäjä, T., O’Connor, E. J., Moisseev, D., Sinclair, V. A., Manninen, A. J., Väänänen, R., von Lerber, A., Thornton, J. A., Nicoll, K., Petersen, W., Chandrasekar, V., Smith, J. N., Winkler, P. M., Krüger, O., Hakola, H., Timonen, H., Brus, D., Laurila, T., Asmi, E., Riekkola, M.-L., Mona, L., Massoli, P., Engelmann, R., Komppula, M., Wang, J., Kuang, C., Bäck, J., Virtanen, A., Levula, J., Ritsche, M., and Hickmon, N.: BAECC A field campaign to elucidate the impact of Biogenic Aerosols on Clouds and Climate, B. Am. Meteorol. Soc., 97, 1909–1928, https://doi.org/10.1175/BAMS-D-14-00199.1, 2016. a
Raykov, Y. P., Boukouvalas, A., Baig, F., and Little, M. A.: What to Do When K-Means Clustering Fails: A Simple yet Principled Alternative Algorithm, PLOS ONE, 11, e0162259, https://doi.org/10.1371/journal.pone.0162259, 2016. a
Rousseeuw, P. J.: Silhouettes: A graphical aid to the interpretation and validation of cluster analysis, J. Comput. Appl. Math., 20, 53–65, https://doi.org/10.1016/0377-0427(87)90125-7, 1987. a
Schneebeli, M., Dawes, N., Lehning, M., and Berne, A.: High-Resolution Vertical Profiles of X-Band Polarimetric Radar Observables during Snowfall in the Swiss Alps, J. Appl. Meteorol. Clim., 52, 378–394, https://doi.org/10.1175/JAMC-D-12-015.1, 2013. a
Schrom, R. S., Kumjian, M. R., and Lu, Y.: Polarimetric Radar Signatures of Dendritic Growth Zones within Colorado Winter Storms, J. Appl. Meteorol. Clim., 54, 2365–2388, https://doi.org/10.1175/JAMC-D-15-0004.1, 2015. a
Sinclair, V. A., Moisseev, D., and von Lerber, A.: How dual-polarization radar observations can be used to verify model representation of secondary ice, J. Geophys. Res.-Atmos., 121, 10954–10970, https://doi.org/10.1002/2016JD025381, 2016. a, b, c, d, e, f
Thompson, E. J., Rutledge, S. A., Dolan, B., Chandrasekar, V., and Cheong, B. L.: A Dual-Polarization Radar Hydrometeor Classification Algorithm for Winter Precipitation, J. Atmos. Ocean. Tech., 31, 1457–1481, https://doi.org/10.1175/JTECH-D-13-00119.1, 2014. a
Trömel, S., Ryzhkov, A. V., Zhang, P., and Simmer, C.: Investigations of Backscatter Differential Phase in the Melting Layer, J. Appl. Meteorol. Clim., 53, 2344–2359, https://doi.org/10.1175/JAMC-D-14-0050.1, 2014. a
Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S. J., Brett, M., Wilson, J., Millman, K. J., Mayorov, N., Nelson, A. R. J., Jones, E., Kern, R., Larson, E., Carey, C. J., Polat, İ, Feng, Y., Moore, E. W., VanderPlas, J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen, I., Quintero, E. A., Harris, C. R., Archibald, A. R., Ribeiro, A. H., Pedregosa, F., van Mulbregt, P., and SciPy 1.0 Contributors: SciPy 1.0: fundamental algorithms for scientific computing in Python, Nat. Methods, 17, 261–272, https://doi.org/10.1038/s41592-019-0686-2, 2020. a, b
von Lerber, A., Moisseev, D., Bliven, L. F., Petersen, W., Harri, A.-M., and Chandrasekar, V.: Microphysical Properties of Snow and Their Link to Ze–S Relations during BAECC 2014, J. Appl. Meteorol. Clim., 56, 1561–1582, https://doi.org/10.1175/JAMC-D-16-0379.1, 2017. a
Voormansik, T., Rossi, P. J., Moisseev, D., Tanilsoo, T., and Post, P.: Thunderstorm hail and lightning detection parameters based on dual-polarization Doppler weather radar data, Met. Apps, 24, 521–530, https://doi.org/10.1002/met.1652, 2017. a
Williams, E. R., Smalley, D. J., Donovan, M. F., Hallowell, R. G., Hood, K. T., Bennett, B. J., Evaristo, R., Stepanek, A., Bals-Elsholz, T., Cobb, J., Ritzman, J., Korolev, A., and Wolde, M.: Measurements of Differential Reflectivity in Snowstorms and Warm Season Stratiform Systems, J. Appl. Meteorol. Clim., 54, 573–595, https://doi.org/10.1175/JAMC-D-14-0020.1, 2015. a
Wolfensberger, D., Scipion, D., and Berne, A.: Detection and characterization of the melting layer based on polarimetric radar scans, Q. J. Roy. Meteor. Soc., 142, 108–124, https://doi.org/10.1002/qj.2672, 2015. a, b
Function scipy.signal.find_peaks.