the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Analysis of functional groups in atmospheric aerosols by infrared spectroscopy: method development for probabilistic modeling of organic carbon and organic matter concentrations
Charlotte Bürki
Matteo Reggente
Ann M. Dillner
Jenny L. Hand
Stephanie L. Shaw
Satoshi Takahama
The Fourier transform infrared (FTIR) spectra of fine particulate matter (PM2.5) contain many important absorption bands relevant for characterizing organic matter (OM) and obtaining organic matter to organic carbon (OM∕OC) ratios. However, extracting this information quantitatively – accounting for overlapping absorption bands and relating absorption to molar abundance – and furthermore relating abundances of functional groups to that of carbon atoms poses several challenges. In this work, we define a set of parameters that model these relationships and apply a probabilistic framework to identify values consistent with collocated field measurements of thermal–optical reflectance organic carbon (TOR OC). Parameter values are characterized for various sample types identified by cluster analysis of sample FTIR spectra, which are available for 17 sites in the Interagency Monitoring of Protected Visual Environments (IMPROVE) monitoring network (7 sites in 2011 and 10 additional sites in 2013). The cluster analysis appears to separate samples according to predominant influence by dust, residential wood burning, wildfire, urban sources, and biogenic aerosols.
Functional groups calibrations of aliphatic CH, alcohol COH, carboxylic acid COOH, carboxylate COO, and amine NH2 combined together reproduce TOR OC concentrations with reasonable agreement (r=0.96 for 2474 samples) and provide OM∕OC values generally consistent with our current best estimate of ambient OC. The mean OM∕OC ratios corresponding to sample types determined from cluster analysis range between 1.4 and 2.0, though ratios for individual samples exhibit a larger range. Trends in OM∕OC for sites aggregated by region or year are compared with another regression approach for estimating OM∕OC ratios from a mass closure equation of the major chemical species contributing to PM fine mass. Differences in OM∕OC estimates are observed according to estimation method and are explained through the sample types determined from spectral profiles of the PM.
- Article
(1314 KB) -
Supplement
(1048 KB) - BibTeX
- EndNote
Organic mass to organic carbon (OM∕OC) was originally characterized using gas chromatograph–mass spectrometry (GC-MS) data (White and Roberts, 1977; Turpin and Lim, 2001) by estimating molecular weight per carbon for individual molecules. However, the analyzed compounds only comprised a small fraction of the overall OM mass, and their representativeness for actual aerosol mixtures has been a subject of perennial inquiry. An alternative approach to estimate OM from mass balance of chemical species obtained by sequential extraction has been demonstrated (El-Zanan et al., 2005, 2009; Polidori et al., 2008), but the labor-intensive operation limits the number of samples that can be analyzed. To obtain an effective OM∕OC over a large number of samples for a given site or season, regressing concentrations of a suite of particulate matter (PM) components to the gravimetric mass (via the “reconstructed fine mass” equation) in monitoring network measurements has been proposed (Frank, 2006; Malm and Hand, 2007; Simon et al., 2011). However, the results can be difficult to interpret on account of combined measurement errors and intercorrelations among PM component concentrations.
In this work, we advance our ability to estimate OM∕OC from Fourier Transform infrared (FTIR) spectra of PM (Allen et al., 1994; Russell, 2003; Takahama and Ruggeri, 2017). In this approach, OM and OC is estimated from organic molecular structures in the PM detected by absorption of mid-infrared radiation. The model for OC estimation from functional groups (FGs), referred to as “FG-OC”, and relevant background are presented in Sect. 1.1. A new framework for constraining estimates through a combination of laboratory and ambient measurements and chemical simulations is described in Sect. 1.2.
1.1 OM∕OC by FG estimation
Another bottom-up approach for deriving estimates of OM∕OC is to use chemical measurements of atomic composition of the organic fraction using mass fragments from high-resolution aerosol mass spectrometry (Aiken et al., 2008) and FGs from FTIR. Here we focus on FTIR based on its demonstrated capability to characterize PM2.5 on polytetrafluoroethylene (PTFE) filters collected in US monitoring networks. The original concept of calibrating by FGs was outlined by Anderson and Seyfried (1948) and Allen et al. (1994) and further developed by Russell (2003) and Ruthenburg et al. (2014).
The areal FG-OC mass density mC on each sampled filter i is constructed from the areal molar densities n of several FGs, denoted by the index g:
where MC=12.01 is the atomic mass of carbon, α is the mass recovery fraction, and λC is a coefficient that can be interpreted as the mean “fractional carbon” associated with each FG within the set of measured FGs, 𝒢*. Mass and molar densities typically take on units of µg m−3 and µmol m−3, respectively. The molar densities of each FG are related to spectral absorbances x by a separate linear model (Ruthenburg et al., 2014):
The approximation made by Eq. (2) is that the absorbance due to a substance is proportional to its abundance (Beer–Lambert–Bouguer law) (Griffiths and Haseth, 2007); the coefficients of β embody the extent of overlap among target analyte and interferents, and relation between absorbance and molar densities. The coefficients are determined by calibration of laboratory-standard spectra to known molar densities of FGs; however, regularization must be used to solve for β because the number of variables (spectral absorbances) are typically greater than number of calibration samples, absorbances are multicollinear, and the inverse solution is sensitive to small perturbations to the data. Partial least squares (PLS) regression (Wold et al., 1983; Martens and Næs, 1991) projects the spectra matrix and areal density of target analyte onto a set of common latent variables, and regularization is imposed by truncating the number of these variables. Therefore, β is a function of the regularization parameter – the number of latent variables k retained – for each FG. Further details for PLS are provided in Appendix B, and a summary of symbols related to the FG-OC model is provided in Table A1.
From the same molar densities of FGs used to estimate mC, molar densities of non-carbon atoms in set 𝒜* can be added to provide an estimate of OM:
where λag are integers relating FG abundances to composition of atoms a and – unlike λC,g – are well defined. OM∕OC is estimated by normalization to estimated carbon:
There are two specific challenges associated with OC estimation from FGs, which also affect OM and OM∕OC estimates. The first is to select the appropriate model (β) when a nonunique set of regularization parameters generate similar predictions for laboratory standards used for validation but vary widely in their predictions in ambient samples (Reggente et al., 2019). The second is to determine a relationship between FG abundance to number of carbon atoms (through λC and α) since many carbon atoms can be polyfunctional, functionalized with FGs that are not measured, or not functionalized to be detectable by FTIR. The fractional carbon parameter λC takes on values of unity or less to prevent multiplicitous enumeration of the same carbon atom from knowledge of FG abundance. For instance, for methylene carbon leads to the correct estimate of one carbon atom for every two aliphatic CH (aCH) groups measured. Similarly, corresponds to methyl carbon, to methine carbon, and so on. Conventionally, λC was obtained by assuming the most numerous configurations of carbon present in assumed archetypal molecules (e.g., linear hydrocarbon or ring-structured compounds). Values assumed in previous works range between 0.39 and 0.88 (Allen et al., 1994; Russell, 2003; Reff et al., 2007; Chhabra et al., 2011; Ruthenburg et al., 2014; Table S1 in the Supplement); similar uncertainties exist for other FGs. Takahama and Ruggeri (2017) proposed an extension to this approach whereby organic molecules and molecular mixtures are conceptualized as a collection of functionalized carbon atoms. Based on the FGs for which calibrations are built, λC can be estimated from the number of measured bonds on each carbon atom or by regression over a collection of carbon atoms. Likewise, the detectable fraction of carbon atoms, α, in molecules and molecular mixtures can be calculated exactly within this scheme. This approach was illustrated for molecules found in the aerosol phase from a simulation of α-pinene photooxidation (in the presence of NOx) coupled with gas–particle partitioning (Ruggeri et al., 2016).
Parameter selection based on surrogate samples (either laboratory samples or virtual molecules in simulation) and independent estimation of ambient OC and OM is the ultimate objective for operational use of FTIR. However, there are inherent differences in chemical composition (i.e., molecular structure, mixture complexity) between such surrogate samples or mixtures with real, ambient PM. Past studies to evaluate a limited number of parameter selection approaches, however, have led to various degrees of agreement between FG-OC and thermal–optical reflectance organic carbon (TOR OC), and it was unclear how this bias was manifested in OM∕OC estimates reported by FTIR. Therefore, at the current stage of development, we define our objective to devise a framework to characterize the multitude of plausible parameters that are consistent with available field measurements. Because we do not have reference values for each FG in ambient samples, we turn to available observational data with lower chemical resolution (TOR OC) as reference, together with a probabilistic framework (Sect. 1.2) for providing plausible estimates for model parameters. Despite known artifacts (Watson et al., 2005; Chow et al., 2005; Cheng et al., 2011; Chan et al., 2019), TOR OC serves as a useful target for FG-OC calibration at this stage to constrain its parameter uncertainties. The implications of these artifacts are also taken into consideration in the model evaluation stage. This strategy furthermore allows estimation of OM∕OC from FTIR that are consistent with TOR OC, which is widely used as a reference for OC.
1.2 Probabilistic framework
The inverse problem of parameter estimation in calibration is ill-posed, meaning that small differences in the input – either data or model parameters – may lead to instabilities in the solution (i.e., parameter estimates) (Kabanikhin, 2008; Calvetti and Somersalo, 2018). Bayes' theorem (Bayes, 1763; Robert and Casella, 2010; Gelman et al., 2013) provides a theoretical foundation for introducing regularization (i.e., auxiliary knowledge) in natural units of the parameters to stabilize the solution and for characterizing plausibility of candidate parameters. Letting p broadly denote any probability density or mass function, the theorem can be written as
where , y is the observed data (TOR OC), is the parameter vector of dimension D (which includes unfixed FG-OC and PLS parameters), p(θ) is the prior distribution of parameters, p(y|θ) is the likelihood, and p(θ|y) is the posterior distribution. The model for FG-OC (mC, Eq. 1) and explanatory variables (ambient sample spectra, denoted by x in Eq. 2) corresponding to each TOR OC observation are assumed given and are excluded in this notation (Gelman et al., 2013). In this multivariate context, a single integral denotes an integral or sum over all parameters. Notation related to probabilistic modeling is summarized in Table A2; data and models used for each of these terms are further described in later sections.
As apparent from Eq. (4), model parameters are treated as random variables and therefore intrinsically associated with probability distributions. p(θ) serves as the mechanism for regularization, and its influence on final estimates p(y|θ) becomes diminishingly small with increasing number of observations y. p(y|θ) reflects plausibility of parameters evaluated from model–measurement agreement; the epistemic uncertainty characterized by this distribution (O'Hagan, 2004) is reduced in accordance with informativeness of y. As a point of contrast, conventional modeling approaches typically rely on expected values of p(θ) to fix model parameters for forward estimation of y from x. Possibly using their distributions for error propagation. The inverse problem is formulated as an optimization problem to obtain a point estimate of θ that maximizes p(y|θ), without incorporating knowledge of p(θ). Confidence intervals or prediction intervals obtained through this classical approach reflect the aleatoric uncertainty attributed to measurement errors and limitations of statistical sampling (Dowd, 2018).
Bayesian inference has been used previously in atmospheric modeling (e.g., Pinder et al., 2006; San Martini et al., 2006; Thompson et al., 2011; Henderson et al., 2012; Wang et al., 2013; Tukiainen et al., 2016) for estimating under-constrained parameters using field observations in several different contexts. We adopt this approach to provide probabilistic estimates to unknown parameters; starting from prior distributions derived from laboratory measurements and available molecular structures, and updating them based on their plausibility for modeling OC as reported by TOR. In particular, the mass recovery fraction of OC is explicitly included as an unknown parameter for estimation to allow better understanding of potentially measured and unmeasured contributions of carbon to FG-OC, separate from remaining biases with respect to the TOR measurements. We describe the measurements used in Sect. 2 and adaptation of this modeling framework in Sect. 3. Results are presented in Sect. 4, and concluding remarks are provided in Sect. 5.
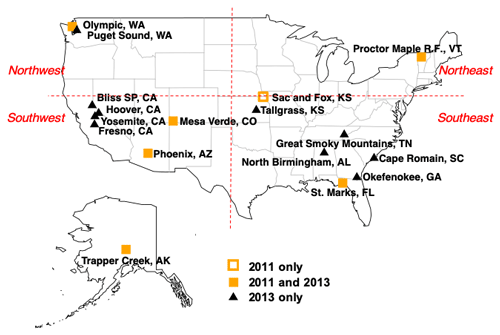
Figure 1Map of IMPROVE network monitoring sites used in this work. For analysis in Sect. 4.4, the contiguous US is divided into four quadrants (vertical and horizontal dashed red lines centered at 40∘ N and −100∘ W); Alaska is considered a separate region.
We apply this method to the Interagency Monitoring of Protected Visual Environments (IMPROVE) (http://vista.cira.colostate.edu/Improve/, last access: 25 March 2020) 2011 and 2013 data set (2474 samples) used by Reggente et al. (2016) and Takahama et al. (2019), except that the Baengnyeong Island, South Korea, site is excluded to focus on the US sites (Fig. 1). The Sac and Fox, KS, site was discontinued mid-2011 and so is not included in the analysis for the 2013 data set. Contiguous US sites are further demarcated into Northeast, Southeast, Southwest, and Northwest regions by the position 40∘ N and W following the convention of Hand et al. (2019). The data set consists of reported values and uncertainties for gravimetry, TOR, X-ray fluorescence (XRF), and ion chromatography (IC), which are used for Bayesian calibration and regression analysis of the reconstructed fine mass (RCFM) equation (Sect. 3.3). The reported data were obtained from the Federal Land Manager Environmental Database (FED) (http://views.cira.colostate.edu/fed/; last access: 16 August 2019).
For FG calibrations, we use 250 laboratory-standard samples consisting of nine type of organic compounds and organic blanks (ammonium sulfate standards with no organics) previously prepared by Ruthenburg et al. (2014). The calibration models of Kamruzzaman et al. (2018) and Boris et al. (2019) are additionally adapted for quantification of the amine and carboxylate content, respectively. PTFE of ambient and laboratory samples were analyzed nondestructively by FTIR in transmission mode (Maria et al., 2003) after placing them in a custom mini-chamber purged with air passed through a molecular sieve to remove water vapor and carbon dioxide (Ruthenburg et al., 2014; Debus et al., 2019). Spectra were truncated to the region above 1500 cm−1 and baseline-corrected (Kuzmiakova et al., 2016) to reduce scattering contributions from the PTFE filter (McClenny et al., 1985) and particles (Takahama et al., 2019). Further details on the sample collection, analysis, and spectra processing steps are described by previous works (Ruthenburg et al., 2014; Reggente et al., 2016; Debus et al., 2019; Takahama et al., 2019). This body of work leads to a collective set of measured functional groups 𝒢* consisting of aliphatic CH (aCH), alcohol COH (aCOH), carboxylic COOH (COOH), nonacid carbonyl (naCO) (which includes ketone and ester), carboxylate COO (oxOCO), and amine NH2 (NH2). Uncertainties in PLS calibration and molecular structure parameters only associated with aCH, aCOH, and COOH are considered, since the other species did not contribute an appreciable amount to the FG-OC over a range of parameters considered. Because of the inclusion of COOH (for which ) and additional fixed contributions from several FGs, the mass recovery parameter α in Eq. (1) can be uniquely distinguished from λC,aCH and λC,aCOH, leading to a model that is identifiable (Walter and Pronzato, 1997).
3.1 Cluster analysis of spectra
Effective model parameters for a group of samples can be estimated at the level of each site or season directly. However, estimating parameters for a group of chemically similar samples instead is favorable in that parameter values associated with molecular structure are more likely to be representative for each sample in a less diverse population. Normalized FTIR spectra are used as indicators of chemical composition and grouped by hierarchical cluster analysis according to similarity (Hastie et al., 2009; Russell et al., 2009) (further details are provided in Sect. S3 in the Supplement). Model parameters are then applied to each member sample and aggregate statistics for OM and OM∕OC are obtained for each site and season from their constituent samples.
3.2 Bayesian calibration
The following statistical model,
assumes that systematic variations in TOR OC y in each sample i are modeled by FG-OC mC and that non-systematic contributions of measurement errors ε are normally distributed with standard deviation σ (San Martini et al., 2006; Skoog et al., 2017). The likelihood function in this model corresponds to
where the product is taken over all samples in the set denoted by 𝒮.
Choosing a prior distribution p(θ) (Eq. 4) is not a trivial task (Bishop, 2009). Where possible, it is desirable to have an informative but weak prior that does not have disproportionate impact on the results. The prior distribution also imposes bounds on the solution in that the likelihood estimated from Eq. (6) is substantially downweighted in near-zero probability density regions specified by the prior (or not considered in regions where the density is identically zero for distributions with finite bounds).
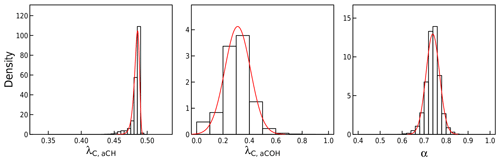
Figure 2Prior distributions for λC and α. Histograms are generated from estimates from subsets of molecules representing a combination of primary and secondary organic aerosols, and red lines are fitted parametric distributions (Weibull for λC to capture asymmetry and normal for α).
We parameterize the uncertainty σ2 in Eq. (6) as
with denoting the irreducible error and κ2 denoting a coefficient for the heteroscedastic (concentration-dependent) error. These terms have familiar interpretations as 2σ0 is a typical measure of the minimum detection limit (MDL), and κ corresponds to the relative standard deviation (σ∕y) in the limit of high concentrations (y≫σ0). σ2 for each sample is calculated from combined uncertainties of the thermal fractions of TOR OC, and initial estimates for these two parameters are obtained via regression to y. As reported to the IMPROVE database, TOR OC uncertainties are assumed to be independent across samples, and correlation of errors across thermal fractions for each sample are omitted. σ0 is kept fixed to the fitted value of 0.04 µg m−3, as 2σ0 is higher than that reported for the TOR OC MDL (0.05 µg m−3) (Dillner and Takahama, 2015), and serves as a conservative estimate. The fitted κ is approximately 7 %, which is lower than collocated precision or overall errors (κ∼15 %) that have been reported elsewhere (Dillner and Takahama, 2015; Brown et al., 2017). Therefore, we include κ2 as an additional unknown parameter to be estimated and assume an inverse gamma distribution around the fitted value for the prior. Uncertainties in n and molecular structure parameters due to model variance of Eqs. (2) and (C2) are not included in this estimate. The analytical precision (typically within 5 %) is greater than that of TOR (Debus et al., 2019), but collocated precision can be similar in magnitude (Dillner and Takahama, 2015). Incorporating these considerations into Eq. (6) poses additional challenges (Rock et al., 1977) and is not considered for this study. Because of the heteroscedastic error model (Eq. 7), samples with lower concentrations can have comparable or greater impact on the likelihood; the abundance of lower-concentration samples (according to approximately lognormal concentrations in atmospheric samples; Ott, 1994) means a few high-concentration points have less influence on parameter estimation (Sect. S2).
To estimate probabilities associated with the number of PLS latent variables, we use mean-square error of cross validation (MSECV) typically used for model selection and convert it into probabilities using Boltzmann weighting (Appendix C1). The proposed approach leads to a prior favoring solutions with lower MSECV estimated for the calibration set (laboratory standards) and downweighting substantially high-bias (high MSECV) solutions that are not sufficiently complex to capture the spectral variations for quantification of the FG (Fig. S1 in the Supplement).
The priors for structural parameters λC,g and α are estimated from virtual mixtures of primary organic aerosol compounds from automobile exhaust and wood burning measured by GC-MS (Rogge et al., 1993, 1998) and secondary organic aerosol compounds in the Master Chemical Mechanism v3.3.1 database (Jenkin et al., 1997; Saunders et al., 2003). In both data sets, compounds likely to be in the aerosol phase were selected based on volatility (equilibrium vapor concentration C0≤103.5 µg m−3) (e.g., Robinson et al., 2007). Further details of the method are provided in Appendix C2, and results of the analysis are given in Sect. 4.1.
Having defined the likelihood function and prior distributions, we obtain the posterior probability p(θ|y) from measurements of y in two ways. Our primary technique is Markov chain Monte Carlo (MCMC), which evaluates the unnormalized posterior p(y|θ)p(θ) for numerically sampled values of θ. We also confirm our results using Laplace's method, which is a Gaussian approximation of the maximum of the unnormalized posterior. This method can only be used for continuous variables, so it is applied for each combination of kg. More details on these techniques are provided in Appendix D.
3.3 Reconstructed fine mass regression
For comparison, we estimate OM∕OC as interpreted by coefficients of the RCFM equation (a statement of mass closure) used by the IMPROVE network (Malm et al., 1994; Malm and Hand, 2007; Chow et al., 2015). Given the atmospheric concentration (µg m−3) c of a substance, regression is used to obtain coefficients a:
FM is the dry fine mass concentration, measured by gravimetric analysis and corrected for particle-bound water using available relative humidity measurements of the analysis laboratory and hygroscopic growth factors for constituent species as described by Hand et al. (2019). AS and AN are ammonium sulfate and nitrate, respectively, estimated from the sulfate and nitrate under the assumption of full neutralization. SS is sea salt, estimated as 1.8 times the chloride concentration. Dust, also referred to as “soil,” is calculated from assumed oxide forms of silicon, calcium, iron, and titanium. OC and EC are as quantified by the TOR method (Sect. 2). To reduce collinearity among variables, EC and SS are not included in the regression but subtracted from FM a priori (Simon et al., 2011; Hand et al., 2019). The coefficients and their confidence intervals are obtained by multiple linear regression (MLR) solved by ordinary least squares (OLS) (Weisberg, 2013) and error-in-variables regression (EIV) (Fuller, 1987) as described by Hand et al. (2019) and Simon et al. (2011), respectively. To avoid confusion with other approaches described in this study, the two methods for solving Eq. (8) will be collectively referred to as RCFM regression and labeled as RCFM-OLS and RCFM-EIV. Furthermore, the results of aOC will be referred to as the OM∕OC ratio estimate according to this approach. OLS does not consider heteroscedasticity or relative magnitude of measurement errors of any variable, which can lead to biased coefficient estimates and confidence intervals that do not reflect the actual uncertainty (Fuller, 1987; Simon et al., 2011; Weisberg, 2013). The latter issue is addressed in this work by providing confidence intervals obtained by bootstrapping (Davison and Hinkley, 1997). EIV regression alleviates this problem by considering measurement errors of both explanatory and response variables explicitly (neglecting error covariances in this implementation); however, the estimates are subject to the accuracy of estimated measurement errors. The implementation provided by Simon et al. (2011) is used for estimation of coefficients and their uncertainties. Analytical uncertainties reported for each measurement are used for their estimates, but unaccounted systematic biases can affect the coefficient aOC (Hand et al., 2019).
For this paper, we limit our focus on topics related to the estimation of parameters that generate FG-OC congruent with TOR OC concentrations and comparisons of new OM∕OC ratios obtained by FTIR with RCFM regression estimates. Obtaining FG composition for each filter sample enables analysis of site-specific OM∕OC ratios and source-class characteristics in much greater detail, and is reserved for a separate, dedicated paper on the subject. The following subsections cover characterization of prior distributions estimated for the unknown molecular structure parameters λC and α (Sect. 4.1), description of spectral clusters formed (Sect. 4.2), posterior parameter estimates (Sect. 4.3), and comparison with RCFM regression (Sect. 4.4).
4.1 Prior distributions
Prior distributions of structural parameters obtained by the method described in Sect. 3.2 are summarized in Fig. 2. The values between 0.46 and 0.48 for λC,aCH are consistent methylene (CH2) group structures, though another reason this narrow distribution can occur is that single aliphatic CH bonds are often found together with one other measured FG on the same carbon atom (Takahama and Ruggeri, 2017). In such cases, a value of λC,aCH close to 0.5 prevents double counting of carbon by the two bonds (Sect. 1.1). The broad values for λC,aCOH reflect the diverse carbon types in which alcohol groups are found. The α value centered around 0.74 reflects the undetected carbon fraction, typically missed due to branched molecular structure or functionalization by unmeasured FGs.
Several examples for molecules with incomplete carbon recovery (α<1) are shown in Fig. 3. More generally, the types of carbon atoms undetected vary widely in their structure (Fig. S3). These molecules contain un-functionalized carbon atoms (only bonded to other carbon atoms) and carbon atoms functionalized by, for example, aldehyde, peroxide, aromatic, phenolic, and organonitrate groups, which have absorption bands in the mid-infrared but are not included in our set of calibrations. These FGs have not been prioritized for calibration following the hypothesis that molecules with these functionalities are not found in great abundance in IMPROVE samples. Aldehydes are susceptible to hydration in aqueous solutions, leading to formation of alcohols (Schwarzenbach et al., 2002; Takahama et al., 2013b). Peroxides have been shown to be labile under various (light and dark) conditions (Epstein et al., 2014; Krapf et al., 2016). Phenolic OH and aromatic groups exhibit sharp absorption peaks near 3500 and 3100 cm−1, respectively (Bahadur et al., 2010), which are not observed in ambient sample spectra; in previous studies, Russell et al. (2011) suggested the aromatic and unsaturated FGs contributed to less than 5 % of OM mass. Organonitrates also hydrolyze in the presence of water to form alcohols and nitric acid (Liu et al., 2012; Zare et al., 2019), and organosulfate FGs are not included in this analysis but their contribution to the overall OM mass concentration is often bound to be less than a few percent (Hawkins et al., 2010; Russell et al., 2011; Takahama et al., 2013a; Budisulistiorini et al., 2015; Hettiyadura et al., 2017). Additionally, oxygen has been found to be the heteroatom contributing most to the variability OM∕OC ratios in ambient samples (Pang et al., 2006).
The procedure of parameter updating with ambient OC estimates can help place these values in the proper context. Previous estimates of FG-OM generally reported agreement of 70 %–100 % for submicrometer OM compared against AMS (Russell et al., 2009; Gilardoni et al., 2009; Corrigan et al., 2013), and FG-OC was estimated to be 60 %–70 % of TOR OC in PM2.5 in the IMPROVE network samples (2011 data set) (Ruthenburg et al., 2014; Reggente et al., 2019). While these differences have been partially attributed to incomplete mass recovery of carbon by FTIR, now the estimated mass recovery fraction based on molecular structure information is included explicitly into the calibration model.
In reporting OM∕OC using Eq. (3), we can expect a systematic underestimation of OM∕OC on account of unmeasured FGs. An alternative estimate can be obtained by considering the OM∕OC of only the measured, functionalized carbon (i.e., using αmC for normalization in Eq. 3). This latter approach can on average lead to a more representative value of the overall OM∕OC (Fig. S4) in oxygenated aerosol. For this work, we use Eq. (3), which likely provides a lower bound on OM∕OC and a means to gauge improvement in OM∕OC estimates with the inclusion of additional FG calibrations.
4.2 Cluster descriptions
While the primary objective of cluster analysis for this study is to create chemically similar groups for parameter estimation, we include a brief remark on interpreted source classes or composition associated with each spectra type. For this analysis, we use spectral characteristics visualized in Fig. 4, concentrations of tracer species or magnitude of tracer variables (Fig. S7; consisting of RCFM components and additional trace elements analyzed by XRF), and location and time of occurrence as indicators of source classes (Fig. S8).
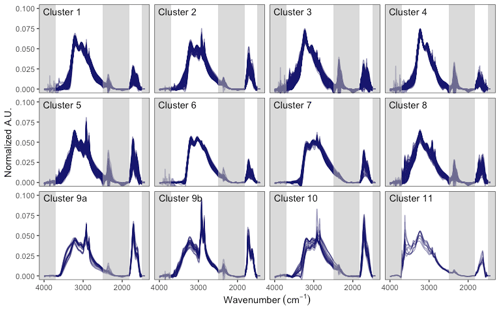
Clusters 1 and 4 are high-sulfate, low-organic samples found predominantly in rural areas, suggesting the likely association of the organic fraction with biogenic secondary organic aerosol (SOA). Samples in cluster 1 are found predominantly in the Southeast and Northeast with a notable absence in the Southwest. Nearly half of samples in clusters 2 and 5 are found in urban areas – particularly in Phoenix, AZ – and the remaining found in rural areas are likely influenced by nearby urban sources. Clusters 3, 8, and 11 occur predominantly in the Southwest and are associated with mineral dust, as evidenced by sharp Si-O-H peaks above 3500 (Reggente et al., 2019) and supported by observations of elevated contributions of elements: Al, Ca, Fe, Si, and Ti. Clusters 6 and 7 occur predominantly in the Southeast and largely consist of samples originally identified by Ruthenburg et al. (2014) as being “anomalous” in their agreement of FG-OC with respect to TOR OC. Reggente et al. (2019) later proposed that these samples contained large ammonium sulfate and ammonium nitrate particles (consistent with IC concentrations) that exhibited an optical artifact known as the Christiansen peak effect, which leads to an increase in transmittance in the vicinity of the wavelength where (i) the refractive index of the substance approaches that of air and (ii) the particle size and wavelength of radiation also become similar (∼3300 cm−1). Thus, these samples share a particular absorbance profile, and quantification based on assumption of Beer–Lambert–Bouguer law can be challenged in some wavenumber regions – especially near the absorption band of alcohol aCOH – for these samples. Samples in clusters 9 and 10 are associated with burning. For purposes of interpretation, cluster 9 is split according to child nodes of the hierarchical clustering tree into wildfire (cluster 9a) and residential wood burning (cluster 9b) groups, which are labeled according to their occurrence during a known fire period (Rim) and during winter months where residential burning takes place (Phoenix, AZ; Ramadan et al., 2011; Pope et al., 2017) (more in Sect. 4.3).
Previous work in cluster analysis with aerosol FTIR spectra resolved differences among urban (fossil fuel combustion), terrestrial vegetation (burning and non-burning), and marine aerosols (e.g., Russell et al., 2009; Liu et al., 2009; Takahama et al., 2011; Corrigan et al., 2013). These studies focused on spectra collected during short, intensive field campaigns (typically considering samples from a single location and single season each) with higher time resolution (typically 4 h) and used an inlet with nominal size cut of one micrometer. Spectra types from monitoring networks are not expected to have a direct correspondence to their work, due to the use of a 2.5 µm size cut (more influence of dust and larger inorganic particles) and time resolution (24 h) of measurements (more mixing of source classes and degrees of aging). In particular, the naCO fraction in IMPROVE network samples has been estimated to be negligible using several methods (Reggente et al., 2019), while naCO varies substantially across spectra types in the submicrometer samples collected during intensive field campaigns and has been used as an indicator of biogenic and biomass burning aerosol (Russell et al., 2011). Nevertheless, some similar spectra categories are found through differences apparent in absorption profiles.
That such a large number of samples from a wide range of sites and seasons are considered together in this work suggests that selecting a limited number of clusters for statistical estimation is likely to provide only a crude separation in chemical and spectral variations that differentiate source classes or mixture proportions of source classes. In addition, first differentiation in spectra (i.e., initial branches of the hierarchical tree) is determined by ammonium NH, alcohol aCOH, and carboxylic COH, as their broad absorption bands comprise a substantial portion of the absorbance in the spectrum. These factors can lead to clusters which contain both rural and urban samples that differ primarily by aliphatic CH absorption (which affects the overall OM∕OC but not its oxygenated fractionation), and surprising associations across regions (e.g., Fresno, CA, samples associated with samples in the Southeast in the same cluster). However, for the purposes of parameter estimation this level of disaggregation is found to be computationally tractable and sufficient in that estimates for smaller subsets of spectra do not substantially change the OM∕OC estimated with this limited number of clusters.
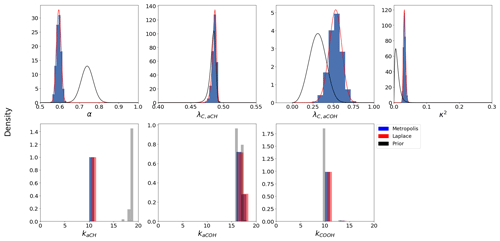
Figure 5Example posterior distribution of cluster 2 from MCMC. Dark lines correspond to prior distributions, blue histograms correspond to sampled posterior distributions, and red lines correspond to Laplace estimation. “Density” refers to the probability or mass density and the variables are described in Sects. 1.1 and 3.2. Nonparametric densities are approximated by kernel density estimation (Hastie et al., 2009), shown in the top row of this figure.
4.3 Estimated parameters
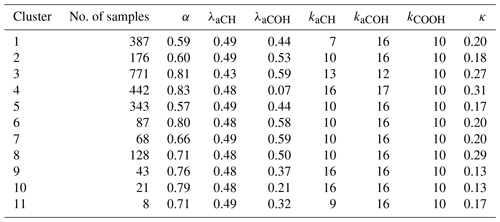
Estimates of parameter distributions obtained by MCMC are generally confirmed by the Laplace method (Fig. 5 shown as an example for a single cluster and Fig. S9 for all clusters). Therefore, the following results will focus on results of MCMC analysis. The posterior distributions for most parameters show a departure from the mode of their prior distributions, suggesting that the results are not dominated by influence of the priors. The mode of each posterior parameter distribution for every cluster is shown in Table 1. The number of latent variables kaCH and kaCOH vary by cluster, suggesting that a different model is appropriate for different spectra types (and presumably different types of PM). The mass recovery fraction α ranges between 0.57 and 0.83, consistent with the range estimated for primary and secondary OM species (Sect. 3.2). Given our expectations for low abundance of unmeasured FGs (Sect. 4.1), low α may indicate a surprising amount of branched molecules with un-functionalized carbon atoms – though we cannot rule out the need to examine additional FGs or that some systematic discrepancies (e.g., in absorption coefficients) between molecules in laboratory and ambient samples are also incorporated into parameter estimates. λaCH is consistently near 0.48, with the exception of cluster 3, but this is possibly due to the strong prior. λaCOH varies much more substantially across clusters and this is likely due to the different configurations of the carbon atom functionalized by aCOH. The coefficient κ for heteroscedastic measurement error varies between 0.13 and 0.31, which is greater than the reported TOR OC analytical error of 0.07. The variations in κ across clusters may partially reflect differences in thermal fractions or sensitivity to different types of compounds, but it more likely reflects the range of discrepancies between modeled and measured OC across samples that arises from a given set of parameter values. Nonetheless, the estimates of remaining parameters are robust with respect to this assumption, as assessed with simulations in which κ is kept fixed at the prior estimate of 0.07.
The comparison of fitted FG-OC with reference TOR OC (Fig. 6) with 95 % intervals of the posterior predictive distribution (Robert, 2007; Vehtari and Ojanen, 2012; Gelman et al., 2013; Sect. S4) shows reasonable agreement with regards to correlation and bias. There is an underprediction for several high-concentration samples due to the larger number of samples with lower concentrations that collectively influence the likelihood (Sect. S2). Posterior predictive distributions are symmetric, and FG-OC estimated from their modes is almost identical to that obtained from single-point estimates of parameters obtained as the mode of their respective distributions (Fig. S11). TOR OC measurements are out-of-range of 95 % prediction intervals of the posterior distribution in approximately 5 % of samples. No abnormalities are detected in spectra upon investigation, which may indicate that these samples are not well served by the current calibration model (e.g., the selection of calibration standards). That the cluster containing anomalous samples (clusters 6 and 7) can reproduce TOR OC – in contrast to previous works of Ruthenburg et al. (2014) and Reggente et al. (2019) – is surprising but that the alcohol aCOH is estimated to be zero could be due to the effect of anomalous dispersion (Sect. 4.2), and some compensation may be incorporated into the value of α for these samples.
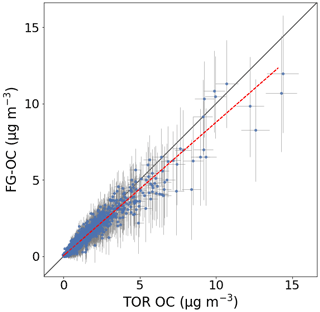
Figure 6Comparison of reference TOR OC measurements and FG-OC estimated by Bayesian calibration. FG-OC corresponds to the mode of the posterior predictive distribution (Sect. S4). The lines span the 95 % uncertainty intervals in TOR measurements horizontally and 95 % prediction intervals of the posterior distribution vertically. Diagonal line corresponds to 1:1 relation, and the dotted red line corresponds to the best-fit line (Pearson's r=0.96; slope =0.87; intercept =0.04 µg m−3).
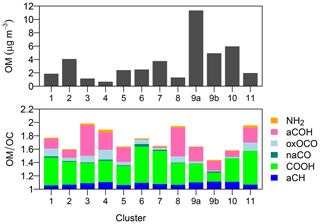
Figure 7 shows the mean OM and OM∕OC for each spectra type. Trends in OM estimates across these types are consistent with trends in TOR OC, with burning samples (clusters 9 and 10) exhibiting the highest OM and biogenic and dust-related samples (clusters 1, 3, 4, 8, and 11) having the lowest OM, on average. Samples with urban influences (clusters 2 and 5) have, on average, lower OM∕OC than those more associated with oxidized, biogenic (clusters 1 and 4). The high aCOH contribution to OM∕OC in the dust samples (clusters 3, 8, and 11) may be indicative of condensed secondary OM (Murphy et al., 2006; Hawkins et al., 2010; Takahama et al., 2010) but may also partially be due to misappropriated hydroxyl groups or hydrates of water associated with inorganic substances (Hudson et al., 2008; Frossard and Russell, 2012). Wildfire burning samples (cluster 9a) consistently display higher OM∕OC than residential wood burning samples (cluster 9b). Because these two sample types occur during warm and cold months, respectively, the contribution of photochemical aging relative to emission characteristics cannot be easily determined from this type of analysis.
Some variability in OM∕OC across samples is present within several clusters. For instance, cluster 9 of the 11 original clusters exhibited a bimodal distribution in OM∕OC from distinguishable contributions from urban wood burning and rural wildfire samples (Fig. S10), and has already been disaggregated for discussion (Sect. 4.2). Within clusters 1, 2, and 5, contrast in OM∕OC ratios between samples from urban and rural sites can be observed, with values lower by ∼0.2 in the former. Further inspection of child nodes does not clearly separate urban and rural samples as with cluster 9, and this is largely because urban and rural samples in the same cluster differ primarily by the aliphatic aCH content, while the oxygenated groups are present in similar proportions. Due to its sharp peaks, aCH absorbances comprise a small portion of the overall variation in spectra considered in the clustering technique and do not exhibit substantial influence in cluster determination. The OM∕OC distribution samples in clusters containing dust-influenced samples are broad (regardless of site type) due to the high variability in estimated alcohol aCOH content.
4.4 Spatial and temporal characteristics
A large number of samples are required to evaluate meaningful difference in coefficients due to the number of RCFM components, range of variations in their concentrations, and their combined measurement errors. Therefore, multiple sites or multiple years of data for a given site are often used for analysis (Simon et al., 2011; Hand et al., 2019). For this work, we report coefficients for the combined years of 2011 and 2013 and sites aggregated by region (restricted to those for which FTIR spectra are available, Sect. 2) to examine spatial and seasonal differences, or six sites for which FTIR spectra are available in both years to examine temporal trends between the 2 years.
Estimates across regions and seasons for the 2 years combined are shown in Fig. 8. Given the limited number of sites analyzed in this work, the region labels are used only to summarize results across multiple sites and may not be indicative of results for the entire region. For instance, the highest OM∕OC estimated by RCFM-OLS for all (∼160) IMPROVE sites between 2011 and 2015 were found in the Southeast and Northeast regions (Hand et al., 2019), whereas their annual average values are, on average, below that of the Northwest region, according to the sites and years considered in this study.
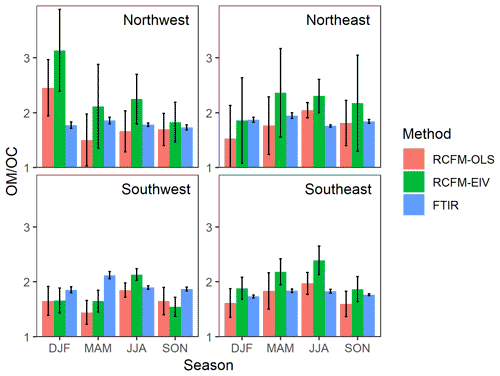
Figure 8Estimates of OM∕OC with 95 % confidence interval made by different techniques for the same sites for which FTIR measurements are available (Sect. 2). OLS (ordinary least squares) and EIV (error-in-variables) provide solutions to RCFM regression, and FTIR estimates are constructed from contributing functional groups. The x axes denote seasons: DJF (December, January, February) is winter, MAM (March, April, May) is spring, JJA (June, July, August) is summer, and SON (September, October, November) is fall.
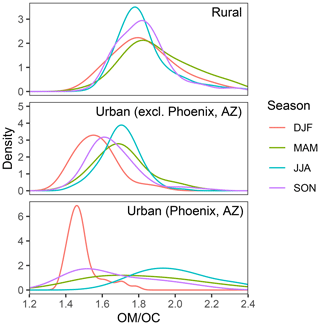
Figure 9Probability densities of OM∕OC estimated by FTIR for sites included in Fig. 8, separated by site type. Densities for urban sites are separated into Phoenix, AZ, which is shown in its own panel, and the remaining five sites.
Estimated trends in OM∕OC between the two RCFM regressions are consistent in that they generally predict higher OM∕OC during spring and summer, except in the Northwest sites where the highest OM∕OC is observed in the winter. This type of agreement is not unexpected as the two methods use the same mass balance approach and concentration measurements. However, OM∕OC estimates from RCFM-OLS (ranging between 1.4 and 2.5) generally underestimate that from RCFM-EIV (1.5–3.1) by ∼0.3 on average. This pattern of underestimation was also reported previously (Simon et al., 2011) – this difference may be partly due to the disproportionate impact of high-OC (and low OM∕OC) samples on squared residuals and subsequent regression coefficient estimates by RCFM-OLS, which are downweighted by uncertainties in RCFM-EIV that increase together with concentration. The large confidence intervals for the Northwest and Northeast sites reflect the fact that only one or two sites are included in these regions, and displays the limit of resolution by the RCFM regression approach for limited sample sizes. Smaller confidence intervals shown for FTIR estimates reflect the fact that regional estimates are calculated as the mean of OM∕OC values obtained for each sample. Magnitude of uncertainties in FTIR OM∕OC due to posterior parameter uncertainties (Hoff, 2009) for any individual sample is typically below 6 % but can be higher for samples in two clusters (Sect. S4).
FTIR estimates of OM∕OC for these regions (1.7–2.2) are on average more similar to RCFM-OLS than RCFM-EIV but show less variability across regions and seasons. In general, we expect that FTIR estimates reported here may be conservative (low) if important FGs are missing in our calibration models (Sect. 4.1). While mean OM∕OC ratios and FG composition can be estimated for each location or period explicitly, its magnitude can be roughly anticipated by (i) the frequency of cluster types (Fig. S13) and (ii) variability of OM∕OC within each cluster (i.e., urban samples having lower OM∕OC in each cluster; Sect. 4.3).
Disaggregating FTIR estimates by site type reveals that seasonal differences are greater in urban areas (∼0.2 between winter and summer) and less pronounced in rural areas (Fig. 9); regional averages are more indicative of trends in the latter because there are fewer urban sites and hence a smaller number of samples. OM∕OC distributions indicate that rural samples over all seasons and urban samples during the summer have a mode close to 1.8, which is the OM∕OC multiplier currently assumed for the IMPROVE network. Phoenix, AZ, is an urban site that exhibits particularly extreme differences in OM∕OC, with low values due to wood burning and possibly less aged urban emissions in the winter (clusters 9b and 5, respectively), and high values from the influence of dust particles in the spring and summer (clusters 5 and 8) (Fig. S13). The broad OM∕OC distribution during these warmer months is due to the variability in alcohol aCOH contribution estimated for the dust-influenced samples. More generally, the higher OM∕OC ratios estimated for the Southwest sites – particularly HOOV (Hoover, CA), BLIS (Bliss, CA), and MEVE (Mesa Verde, CO) – during the spring season are due to the prevalence of dust-impacted samples. Because organic mass loadings of these dust-impacted samples are relatively low (Sect. 4.2), the mean OM∕OC values during spring are similar to that of summer months if ratios are alternatively calculated taking OC-weighting into account. The higher OM∕OC estimated during the spring (1.93) in comparison to summer (1.76) in the single Northeast site (Proctor Maple, VT) is not confirmed by the other two methods as their seasonal differences are not statistically significant, but inspection of spectra types indicates that the biogenic-type samples (cluster 4) were prevalent during the spring, while more urban-influenced samples (cluster 5) with lower OM∕OC values were found during the summer in comparison.
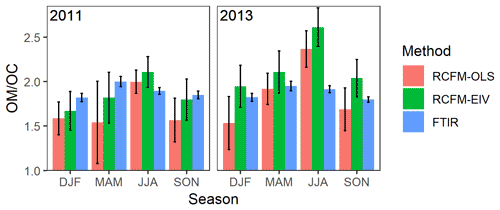
Figure 10Estimates of OM∕OC with 95 % confidence intervals for the same six sites for which FTIR measurements are available (one urban and six rural sites). The same notation as Fig. 8 is used here.
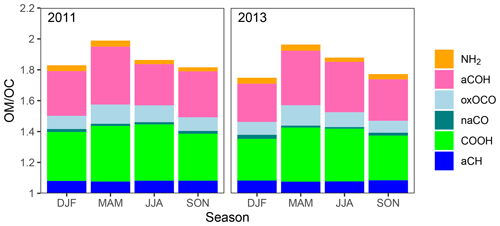
Figure 11Mean OM∕OC ratios partitioned by FG contributions for the FTIR estimates shown in Fig. 10.
Considering only the six sites – Phoenix, AZ; Olympic, WA; Proctor Maple, VT; St. Marks, FL; Mesa Verde, CO; and Trapper Creek, AL – for which FTIR measurements are available between 2011 and 2013, we compare differences in mean OM∕OC ratios (Fig. 10). Hand et al. (2019) previously reported increasing trends in mean OM∕OC ratios between 2011 and 2013 over the entire network; particularly with an increase of ∼0.2 during summer months. RCFM-OLS and RCFM-EIV for these sites also show increasing OM∕OC (by 0.35 and 0.5, respectively) for the summer months for the subset of sites analyzed in this work, and a difference of 0.4 is also significant for RCFM-OLS for the spring months. However, FTIR estimates show no such trend, and the FG composition is also remarkably consistent between the 2 years at these sites (Fig. 11). The sample type composition determined by the FTIR spectra between the 2 years are also similar (Fig. S14), which explains this similar estimate of OM∕OC. Inspection of other regression coefficients of Eq. (8) indicate other changes such as a decrease in adust between the 2 years, which may suggest changing atmospheric composition or changes in analytical bias (Hand et al., 2019) that affect estimates of aOC. This comparison may support the need for further evaluation along two directions. One is in interpreting aOC from RCFM regression as a surrogate for the OM∕OC ratio (Hand et al., 2019). The other is in understanding the changing contributions of FGs not included in our set of calibrations (that also are excluded from or have negligible influence on the spectral cluster analysis) over this period. For instance, recent studies of trends in the Southeast US suggest that aromatic-, organosulfate-, organonitrate-, and peroxide-containing compounds in OM have declined in response to reduced anthropogenic emissions of volatile organic compounds, SO2, and NOx (the latter two affecting OM through their influence over aqueous-phase reactions and oxidant levels) over the last decades (Pye et al., 2015; Blanchard et al., 2016; Marais et al., 2017; Carlton et al., 2018; Pye et al., 2019). While most of these trends would contradict the direction of discrepancy in OM∕OC trends estimated by RCFM and FTIR, the magnitude of changes in emissions and the response of OM likely differ across sites and years considered in this study.
We presented a new framework to enable estimation of OM and OM∕OC from FG calibrations of FTIR spectra that are also consistent with the current best estimate of ambient OC, which is taken from TOR measurements. In contrast to RCFM regression approaches that estimate OM∕OC from mass balance of all other major components contributing to particulate fine mass, estimation of this metric by FTIR uses spectra of particles collected on PTFE filters together with laboratory standards of organic molecules. In contrast to standard multivariable optimization approaches for parameter estimation, the proposed probabilistic approach incorporates prior knowledge of model parameters based on performance against laboratory standards and sensible structural parameter values derived from atmospherically relevant molecules compiled from measurements or computer models. While this information was exclusively used for parameter determination in previous works, the Bayesian framework used here weighs plausibility of parameter values against ambient observations. The clustering approach used for selecting subgroups with similar spectral profiles also leads to estimation of model parameters that better reflect samples in each subgroup and provides a way for associating model parameters and OM∕OC estimates to various chemical classes of PM.
Model parameters that reproduce TOR OC measurements could be found for more than 94 % of samples; this approach also identifies samples for which calibration models are potentially unsuitable. Spectra types associated with dust, wildfire, residential wood burning, urban, and biogenic-influenced samples were found in the IMPROVE 2011 and 2013 samples. Mean OM∕OC ratios for various locations or periods are consistent with occurrences of these spectra types. In contrast to RCFM regression methods, no consistent increase in OM∕OC was found between 2011 and 2013, and the spectra type composition was also consistent between the 2 years. This work enables many directions for future studies. OM∕OC ratios and FG composition can be further related to sources and specific sites or seasons for the samples introduced in this calibration study. Furthermore, the framework is described generally such that it can be applied to samples in monitoring networks or chamber experiments, and systematically evaluate improvements in calibrations with new standards or FGs. Parameters that can be applied to new samples for prediction can potentially be determined by assessing spectral similarity of new samples to the sample types established through cluster analysis. For increasingly refined spectral types, hierarchical Bayesian modeling (Gelman and Hill, 2007) can be used to model relationships among subgroups (e.g., spectral clusters) and overcome limitations in dealing with smaller sample sizes, albeit with added complexity. Additional constraints – such as residual FM (Boris et al., 2019) or additional measurements of FGs by nuclear magnetic resonance (NMR) or spectrophotometry (Decesari et al., 2007; Ranney and Ziemann, 2016; Duarte and Duarte, 2017) – can be introduced to the maximum likelihood expression to explore solutions which are consistent with other available measurements.
The origin of the regularization term in Eq. (2) specifically for PLS regression is explained in this section. The nonlinear iterative least squares (NIPALS) algorithm (Wold et al., 1983) is used to project a matrix of mean-centered laboratory-standard spectra with absorption xij, defined for each wavenumber j (indexed from 1 to J) and sample i, onto a basis set of spectral profiles (loadings) whose elements are pℓj, with ℓ representing the index of the reduced dimension (also referred to as a latent variable or component). The PLS scores tiℓ embody both the contribution of component ℓ to the spectra and its contribution to the FG abundance (determined by gravimetric analysis for known aerosol composition) after additional scaling by coefficient qℓg.
. For a selected value of kg, the components beyond kg+1 comprise the residual terms ex,ij and eig. Using the provided training samples, q, and p are found such that the new variables t maximize the covariance with n during the calibration process. Each new spectrum (of laboratory and ambient samples) are then projected onto this basis set and its scores used to estimate the FG abundance.
C1 Number of latent variables k
For each FG, we estimate a prior for the number of latent variables (denoted as k rather than kg in this section for readability) by Boltzmann weighting (Adamson, 1979) of their mean squared error of cross validation (MSECV) from laboratory calibrations. The MSECV is written in terms of the chi-square statistic χ2:
where s2 is the expected magnitude of error, which we use as a scaling variable fixed to the condition that (reduced chi-square is unity) for the minimum MSECV solution. The form of Eq. (C1) is also consistent with the notion of likelihood ratios used in model selection and Akaike weighting (Burnham and Anderson, 2003). The upper limit on k is selected to balance inclusiveness of plausible solutions against computational considerations; for each component k is chosen to include several solutions within one standard error of the MSECV and exclude physically unrealistic ones (with high proportion of negative predictions in concentration). The choice of upper limit for k can change the overall probability, but the relative probability among solutions remains approximately similar for a range of upper limits considered.
C2 Carbon fractions λC and mass recovery fraction α
This work extends the approach of Takahama and Ruggeri (2017) to study functionalization at the level of each carbon atom for a larger set of atmospherically relevant molecules with known structure. We consider the set of molecules in primary aerosols ℳprimary from GC-MS measurements by Rogge and coworkers (Rogge et al., 1993, 1998) that was previously analyzed for FG composition by Ruggeri and Takahama (2016) and the set of gas-phase photooxidation products ℳsecondary from MCM v3.3.1. Considering species with equilibrium vapor concentrations C0≤103.5 µg m3, there are 193 molecules in ℳprimary and 1221 molecules in ℳsecondary (Fig. S2).
A subset of molecules ℳ(s) are constructed by varying the fraction ζ of primary vs. secondary aerosol molecules between 0 and 1 by 0.05 increments and randomly sampling from the required number from each population to satisfy the balance:
where denotes the cardinality (number of elements) of the set. To accommodate the limited number of primary compounds available for random selection, the total number of molecules considered for any subset was 50–150 so that each contained a random subset of ℳprimary even for ζ(s)=1. We therefore estimate λC by nonnegative least squares regression of measurable carbon abundance on FG abundances repeated over various subsets s:
where nC,ik is the number of carbon atoms for molecule i in carbon type k, which is summed over detectable carbon types 𝒞*. nig is the number of FGs g in molecule i for the measured set 𝒢*. The carbon associated with carboxylic COOH is subtracted from before regression since , and only aliphatic CH and alcohol aCOH are included in the fitting procedure. The detectable carbon fraction is estimated from the same mixtures by normalizing the abundance of detectable carbon over the total carbon (denoted by set 𝒞):
where p(λC,g) and p(α) are derived from the distribution of values estimated over realizations of subsets s.
Equation (4) is typically posed as a mathematical problem to obtain the posterior distribution, written in this Appendix as for simplicity, from its unnormalized estimate :
is referred to as the loss function and Z is the normalizing constant (integral of or e−L(θ)). In our model (Eq. 1), we have both discrete and continuous parameters which we discriminate with superscripts (d) and (c), respectively. To explicitly expound on this notation, , , and . With denoting the set of all parameters except θi (i.e., the complement of θi with respect to θ), the marginal posterior distribution for θi is given by
with . As with integral notation in Eq. (4), the single integral or summation symbol applies over all parameters in the indexed set, i.e., and . A summary of notation for posterior sampling is provided in Table A2. We use Markov chain Monte Carlo (MCMC) as our primary tool to sample π(θ). To diagnose convergence and accuracy of the MCMC calculations, we additionally use a simple approximation (Laplace method) to confirm our parameter distributions. We first summarize the Laplace method, as it is a close extension of maximum likelihood estimation (MLE) typically used in conventional parameter estimation before describing MCMC sampling.
D1 Laplace method
The Laplace approximation (Tierney and Kadane, 1986; Murphy et al., 2012) solves Eqs. (D1) and (D2) by making a local Gaussian approximation to the posterior distribution of the continuous variables about their maximum a posteriori (MAP) estimate (i.e., maximum of the function ). This method improves on the classical MLE approach through the weighting of a prior (for a flat prior, the MAP estimate is equivalent to the MLE estimate) and estimating probabilities from the surface curvature of Eq. (D1) in the vicinity of the MAP. The approximation only applies in the domain of continuous parameters, so the calculation is performed for every selected realization of discrete parameter combinations. The probability estimate is formulated from the normalization constant of a multivariate normal distribution, with D(c)×D(c) Hessian of L about θ(c)*:
Laplace's method is typically associated with a second-order Taylor series expansion about θ(c)*, which further provides the following approximation: for each realization of θ(d). Covariance among the continuous variables can further be obtained from the inverse of the Hessian matrix. The marginal posterior for each realization of the variable θi is obtained by a Gaussian approximation for each integral in Eq. (D2) and calculating the Hessian about the MAP defined as :
While analytically elegant and deterministic, the Laplace approximation is best suited for applications that primarily involve real (continuous) variables with a single mode in its probability density or in the limit of large N as the density converges to a normal one (Bernstein–von Mises theorem). However, its Gaussian estimates can become unreliable toward domain boundaries that might be imposed due to physical constraints, or in the limit of large number of variables when the high-dimensional space tends to become non-Gaussian.
We screen solutions by finding the MAP for each combination of discrete parameter values using L-BFGS-B (limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm with box constraints) and removing those which are 1020 below than the absolute maximum. θ(c)* for each realization of θ(d) is found using L-BFGS-B, a box-constrained, limited-memory extension of the quasi-Newton method BFGS. BFGS uses an approximation of the Hessian matrix to steer its search. The Hessian matrix is not recomputed at each iteration but updated using the secant equation to account for the curvature estimated during the most recent step (Nocedal and Wright, 2006). While L-BFGS-B simultaneously provides estimation of the Hessian matrix with the MAP, as it is based on an approximation for the purposes of speeding up the optimization, we recompute these matrices and their determinants from numerical differentiation at the corresponding MAPs.
D2 MCMC
MCMC (Bishop, 2009; Aster et al., 2013) approximates the posterior probability π(θ) from an algorithmically generated Markov sequence . This sequence or chain is constructed through a series of trial and acceptance moves. The Metropolis–Hastings algorithm (Metropolis et al., 1953; Hastings, 1970) describes conditions under which the generated sequence fulfills the conditions of detailed balance necessary for convergence toward a stationary (statistically invariant) distribution. For any θ[t], a candidate value θ* is generated from a proposal distribution . θ* is designated as the next value in the sequence θ[t+1] with acceptance probability , defined to preserve detailed balance for a move from θ[t] to θ*:
The ratio has been used in place of so that explicit evaluation of the normalization constant Z (Eq. D1) is not required. For a symmetric proposal distribution, and further simplification to Eq. (D5) can be obtained (Metropolis algorithm). Assignment of θ[t+1] is implemented by comparison of against the realization u of a random variable uniformly distributed over [0,1]:
The initial value θ[0] of the Metropolis–Hastings algorithm is set at the maximum a posterior (MAP) estimated for the Laplace method. Proposal distributions for the discrete parameters kg are truncated normal distributions which bounds the range of possible values. For continuous variables, the covariance matrix Σ of the target distribution is estimated using the first iterations of sampling, after which efficient proposal distributions are defined (Gelman et al., 2013):
Two MCMC chains were run for each model, and convergence was monitored using chain trace plots and Gelman–Rubin diagnostics (Gelman and Rubin, 1992). The posterior probability distribution p(θ), marginal distributions p(θi), population statistics of θ (including covariances), and posterior predictive distributions (Sect. 3.2) are then calculated from the numerically sampled sequence.
The distribution-free approach of this technique makes it applicable to discontinuous, non-differentiable functions, solutions at constraint boundaries, and smaller data sets where the limiting distribution need not be normal. Sampling across models for model selection can also be handled by a special case of Metropolis–Hastings – transdimensional or reversible jump MCMC – in which the number of parameters for each model can vary (Green, 1995; Gallagher et al., 2009). While candidate PLS solutions generated with a different kg (Eq. B1) can also be interpreted as different models, for this study kg is treated as a discrete tuning parameter for the PLS model corresponding to a fixed calibration set. The typical downside of MCMC is the high computational cost, as a large number of samples is needed for convergence and to ensure that the parameters sampled non-independently can provide adequate characterization of the target density. Where possible, use of MCMC together with simpler methods to confirm results is recommended (Brooks et al., 2011).
Code for posterior sampling by MCMC and Laplace approximation is available at https://gitlab.com/aprl/fgoc-bayes (last access: 25 March 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/amt-13-1517-2020-supplement.
ST, AMD, and SLS conceived of the project. CB wrote the code, performed simulations, and analyzed results. MR prepared calibration models and guidance on their use. ST and CB wrote the manuscript. AMD and JLH provided regular input on the analysis and further editing of the manuscript. ST provided overall supervision of the project.
The authors declare that they have no conflict of interest.
The authors would like to thank Anthony Davison for helpful suggestions regarding Bayesian statistics.
This research has been supported by the Electric Power Research Institute (contract no. 10003745).
This paper was edited by Hartmut Herrmann and reviewed by three anonymous referees.
Adamson, A. W.: A Textbook of Physical Chemistry, Academic Press, 2nd edn., 1979. a
Aiken, A. C., Decarlo, P. F., Kroll, J. H., Worsnop, D. R., Huffman, J. A., Docherty, K. S., Ulbrich, I. M., Mohr, C., Kimmel, J. R., Sueper, D., Sun, Y., Zhang, Q., Trimborn, A., Northway, M., Ziemann, P. J., Canagaratna, M. R., Onasch, T. B., Alfarra, M. R., Prevot, A. S. H., Dommen, J., Duplissy, J., Metzger, A., Baltensperger, U., and Jimenez, J. L.: O/C and OM∕OC ratios of primary, secondary, and ambient organic aerosols with high-resolution time-of-flight aerosol mass spectrometry, Environ. Sci. Technol., 42, 4478–4485, https://doi.org/10.1021/es703009q, 2008. a
Allen, D. T., Palen, E. J., Haimov, M. I., Hering, S. V., and Young, J. R.: Fourier-transform Infrared-spectroscopy of Aerosol Collected In A Low-pressure Impactor (LPI/FTIR) – Method Development and Field Calibration, Aerosol Sci. Tech., 21, 325–342, https://doi.org/10.1080/02786829408959719, 1994. a, b, c
Anderson, J. A. and Seyfried, W. D.: Determination of Oxygenated and Olefin Compound Types by Infrared Spectroscopy, Anal. Chem., 20, 998–1006, https://doi.org/10.1021/ac60023a002, 1948. a
Aster, R. C., Borchers, B., and Thurber, C. H.: Parameter estimation and inverse problems, Academic Press, Waltham, MA, https://doi.org/10.1016/C2009-0-61134-X, 2013. a
Bahadur, R., Uplinger, T., Russell, L. M., Sive, B. C., Cliff, S. S., Millet, D. B., Goldstein, A., and Bates, T. S.: Phenol Groups in Northeastern US Submicrometer Aerosol Particles Produced from Seawater Sources, Environ. Sci. Technol., 44, 2542–2548, https://doi.org/10.1021/es9032277, 2010. a
Bayes, T.: An essay towards solving a problem in the doctrine of chances, Philos. T. R. Soc. Lond., 53, 370–418, https://doi.org/10.1098/rstl.1763.0053, 1763. a
Bishop, C. M.: Pattern recognition and machine learning, Springer, New York, NY, 2009. a, b
Blanchard, C. L., Hidy, G. M., Shaw, S., Baumann, K., and Edgerton, E. S.: Effects of emission reductions on organic aerosol in the southeastern United States, Atmos. Chem. Phys., 16, 215–238, https://doi.org/10.5194/acp-16-215-2016, 2016. a
Boris, A. J., Takahama, S., Weakley, A. T., Debus, B. M., Fredrickson, C. D., Esparza-Sanchez, M., Burki, C., Reggente, M., Shaw, S. L., Edgerton, E. S., and Dillner, A. M.: Quantifying organic matter and functional groups in particulate matter filter samples from the southeastern United States – Part 1: Methods, Atmos. Meas. Tech., 12, 5391–5415, https://doi.org/10.5194/amt-12-5391-2019, 2019. a, b
Brooks, S., Gelman, A., Jones, G., and Meng, X.: Handbook of Markov Chain Monte Carlo, Chapman & Hall/CRC Handbooks of Modern Statistical Methods, CRC Press, 2011. a
Brown, R. J. C., Beccaceci, S., Butterfield, D. M., Quincey, P. G., Harris, P. M., Maggos, T., Panteliadis, P., John, A., Jedynska, A., Kuhlbusch, T. A. J., Putaud, J.-P., and Karanasiou, A.: Standardisation of a European measurement method for organic carbon and elemental carbon in ambient air: results of the field trial campaign and the determination of a measurement uncertainty and working range, Environmental Science: Processes & Impacts, 19, 1249–1259, https://doi.org/10.1039/C7EM00261K, 2017. a
Budisulistiorini, S. H., Li, X., Bairai, S. T., Renfro, J., Liu, Y., Liu, Y. J., McKinney, K. A., Martin, S. T., McNeill, V. F., Pye, H. O. T., Nenes, A., Neff, M. E., Stone, E. A., Mueller, S., Knote, C., Shaw, S. L., Zhang, Z., Gold, A., and Surratt, J. D.: Examining the effects of anthropogenic emissions on isoprene-derived secondary organic aerosol formation during the 2013 Southern Oxidant and Aerosol Study (SOAS) at the Look Rock, Tennessee ground site, Atmos. Chem. Phys., 15, 8871–8888, https://doi.org/10.5194/acp-15-8871-2015, 2015. a
Burnham, K. and Anderson, D.: Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, Springer, New York, 2003. a
Calvetti, D. and Somersalo, E.: Inverse problems: From regularization to Bayesian inference, Wiley Interdisciplinary Reviews: Computational Statistics, 10, e1427, https://doi.org/10.1002/wics.1427, 2018. a
Carlton, A. G., de Gouw, J., Jimenez, J. L., Ambrose, J. L., Attwood, A. R., Brown, S., Baker, K. R., Brock, C., Cohen, R. C., Edgerton, S., Farkas, C. M., Farmer, D., Goldstein, A. H., Gratz, L., Guenther, A., Hunt, S., Jaeglé, L., Jaffe, D. A., Mak, J., McClure, C., Nenes, A., Nguyen, T. K., Pierce, J. R., de Sa, S., Selin, N. E., Shah, V., Shaw, S., Shepson, P. B., Song, S., Stutz, J., Surratt, J. D., Turpin, B. J., Warneke, C., Washenfelder, R. A., Wennberg, P. O., and Zhou, X.: Synthesis of the Southeast Atmosphere Studies: Investigating Fundamental Atmospheric Chemistry Questions, B. Am. Meteorol. Soc., 99, 547–567, https://doi.org/10.1175/BAMS-D-16-0048.1, 2018. a
Chan, T. W., Huang, L., Banwait, K., Zhang, W., Ernst, D., Wang, X., Watson, J. G., Chow, J. C., Green, M., Czimczik, C. I., Santos, G. M., Sharma, S., and Jones, K.: Inter-comparison of elemental and organic carbon mass measurements from three North American national long-term monitoring networks at a co-located site, Atmos. Meas. Tech., 12, 4543–4560, https://doi.org/10.5194/amt-12-4543-2019, 2019. a
Cheng, Y., Duan, F.-K., He, K.-B., Zheng, M., Du, Z.-Y., Ma, Y.-L., and Tan, J.-H.: Intercomparison of Thermal–Optical Methods for the Determination of Organic and Elemental Carbon: Influences of Aerosol Composition and Implications, Environ. Sci. Technol., 45, 10117–10123, https://doi.org/10.1021/es202649g, 2011. a
Chhabra, P. S., Ng, N. L., Canagaratna, M. R., Corrigan, A. L., Russell, L. M., Worsnop, D. R., Flagan, R. C., and Seinfeld, J. H.: Elemental composition and oxidation of chamber organic aerosol, Atmos. Chem. Phys., 11, 8827–8845, https://doi.org/10.5194/acp-11-8827-2011, 2011. a
Chow, J. C., Watson, J. G., Chen, L.-W. A., Paredes-Miranda, G., Chang, M.-C. O., Trimble, D., Fung, K. K., Zhang, H., and Zhen Yu, J.: Refining temperature measures in thermal/optical carbon analysis, Atmos. Chem. Phys., 5, 2961–2972, https://doi.org/10.5194/acp-5-2961-2005, 2005. a
Chow, J. C., Lowenthal, D. H., Chen, L.-W. A., Wang, X., and Watson, J. G.: Mass reconstruction methods for PM2.5: a review, Air Quality, Atmosphere & Health, 8, 243–263, https://doi.org/10.1007/s11869-015-0338-3, 2015. a
Corrigan, A. L., Russell, L. M., Takahama, S., Äijälä, M., Ehn, M., Junninen, H., Rinne, J., Petäjä, T., Kulmala, M., Vogel, A. L., Hoffmann, T., Ebben, C. J., Geiger, F. M., Chhabra, P., Seinfeld, J. H., Worsnop, D. R., Song, W., Auld, J., and Williams, J.: Biogenic and biomass burning organic aerosol in a boreal forest at Hyytiälä, Finland, during HUMPPA-COPEC 2010, Atmos. Chem. Phys., 13, 12233–12256, https://doi.org/10.5194/acp-13-12233-2013, 2013. a, b
Davison, A. C. and Hinkley, D. V.: Bootstrap Methods and their Application, Cambridge Series in Statistical and Probabilistic Mathematics, Cambridge University Press, Cambridge, https://doi.org/10.1017/CBO9780511802843, 1997. a
Debus, B., Takahama, S., Weakley, A. T., Seibert, K., and Dillner, A. M.: Long-Term Strategy for Assessing Carbonaceous Particulate Matter Concentrations from Multiple Fourier Transform Infrared (FT-IR) Instruments: Influence of Spectral Dissimilarities on Multivariate Calibration Performance, Appl. Spectrosc., 73, 271–283, https://doi.org/10.1177/0003702818804574, 2019. a, b, c
Decesari, S., Mircea, M., Cavalli, F., Fuzzi, S., Moretti, F., Tagliavini, E., and Facchini, M. C.: Source attribution of water-soluble organic aerosol by nuclear magnetic resonance spectroscopy, Environ. Sci. Technol., 41, 2479–2484, https://doi.org/10.1021/es061711l, 2007. a
Dillner, A. M. and Takahama, S.: Predicting ambient aerosol thermal-optical reflectance (TOR) measurements from infrared spectra: organic carbon, Atmos. Meas. Tech., 8, 1097–1109, https://doi.org/10.5194/amt-8-1097-2015, 2015. a, b, c
Dowd, P.: Quantifying the Impacts of Uncertainty, Springer International Publishing, Cham, 349–373, https://doi.org/10.1007/978-3-319-78999-6_18, 2018. a
Duarte, R. M. and Duarte, A. C.: NMR Studies of Organic Aerosols, vol. 92 of Annual Reports on NMR Spectroscopy, Academic Press, 83–135, https://doi.org/10.1016/bs.arnmr.2017.04.003, 2017. a
El-Zanan, H. S., Lowenthal, D. H., Zielinska, B., Chow, J. C., and Kumar, N.: Determination of the organic aerosol mass to organic carbon ratio in IMPROVE samples, Chemosphere, 60, 485–496, https://doi.org/10.1016/j.chemosphere.2005.01.005, 2005. a
El-Zanan, H. S., Zielinska, B., Mazzoleni, L. R., and Hansen, D. A.: Analytical Determination of the Aerosol Organic Mass-to-Organic Carbon Ratio, J. Air Waste Manage., 59, 58–69, https://doi.org/10.3155/1047-3289.59.1.58, 2009. a
Epstein, S. A., Blair, S. L., and Nizkorodov, S. A.: Direct Photolysis of a-Pinene Ozonolysis Secondary Organic Aerosol: Effect on Particle Mass and Peroxide Content, Environ. Sci. Technol., 48, 11251–11258, https://doi.org/10.1021/es502350u, 2014. a
Frank, N. H.: Retained Nitrate, Hydrated Sulfates, and Carbonaceous Mass in Federal Reference Method Fine Particulate Matter for Six Eastern U.S. Cities, J. Air Waste Manage., 56, 500–511, https://doi.org/10.1080/10473289.2006.10464517, 2006. a
Frossard, A. A. and Russell, L. M.: Removal of Sea Salt Hydrate Water from Seawater-Derived Samples by Dehydration, Environ. Sci. Technol., 46, 13326–13333, https://doi.org/10.1021/es3032083, 2012. a
Fuller, W. A.: Measurement Error Models, John Wiley & Sons, New York, NY, 1987. a, b
Gallagher, K., Charvin, K., Nielsen, S., Sambridge, M., and Stephenson, J.: Markov chain Monte Carlo (MCMC) sampling methods to determine optimal models, model resolution and model choice for Earth Science problems, Mar. Petrol. Geol., 26, 525–535, https://doi.org/10.1016/j.marpetgeo.2009.01.003, 2009. a
Gelman, A. and Hill, J.: Data Analysis Using Regression and Multileve//Hierarchical Models, Cambridge Univ. Press, Cambridge, 2007. a
Gelman, A. and Rubin, D. B.: Inference from iterative simulation using multiple sequences, Stat. Sci., 7, 457–472, https://doi.org/10.1214/ss/1177011136, 1992. a
Gelman, A., Carlin, J., Stern, H., Dunson, D., Vehtari, A., and Rubin, D.: Bayesian Data Analysis, Chapman & Hall/CRC Texts in Statistical Science, Chapman & Hall/CRC, New York, NY, 3rd edn., 2013. a, b, c, d
Gilardoni, S., Liu, S., Takahama, S., Russell, L. M., Allan, J. D., Steinbrecher, R., Jimenez, J. L., De Carlo, P. F., Dunlea, E. J., and Baumgardner, D.: Characterization of organic ambient aerosol during MIRAGE 2006 on three platforms, Atmos. Chem. Phys., 9, 5417–5432, https://doi.org/10.5194/acp-9-5417-2009, 2009. a
Green, P. J.: Reversible jump Markov chain Monte Carlo computation and Bayesian model determination, Biometrika, 82, 711–732, https://doi.org/10.1093/biomet/82.4.711, 1995. a
Griffiths, P. and Haseth, J. A. D.: Fourier Transform Infrared Spectrometry, John Wiley & Sons, In, 2nd edn., 2007. a
Hand, J., Prenni, A., Schichtel, B., Malm, W., and Chow, J.: Trends in remote PM2.5 residual mass across the United States: Implications for aerosol mass reconstruction in the IMPROVE network, Atmos. Environ., 203, 141–152, https://doi.org/10.1016/j.atmosenv.2019.01.049, 2019. a, b, c, d, e, f, g, h, i, j
Hastie, T., Tibshirani, R., and Friedman, J.: The elements of statistical learning: data mining, inference, and prediction, Springer Verlag, New York, NY, 2009. a, b
Hastings, W. K.: Monte Carlo sampling methods using Markov chains and their applications, Biometrika, 57, 97–109, https://doi.org/10.1093/biomet/57.1.97, 1970. a
Hawkins, L. N., Russell, L. M., Covert, D. S., Quinn, P. K., and Bates, T. S.: Carboxylic acids, sulfates, and organosulfates in processed continental organic aerosol over the southeast Pacific Ocean during VOCALS-REx 2008, J. Geophys. Res.-Atmos., 115, D13201, https://doi.org/10.1029/2009JD013276, 2010. a, b
Henderson, B. H., Pinder, R. W., Crooks, J., Cohen, R. C., Carlton, A. G., Pye, H. O. T., and Vizuete, W.: Combining Bayesian methods and aircraft observations to constrain the reaction rate, Atmos. Chem. Phys., 12, 653–667, https://doi.org/10.5194/acp-12-653-2012, 2012. a
Hettiyadura, A. P. S., Jayarathne, T., Baumann, K., Goldstein, A. H., de Gouw, J. A., Koss, A., Keutsch, F. N., Skog, K., and Stone, E. A.: Qualitative and quantitative analysis of atmospheric organosulfates in Centreville, Alabama, Atmos. Chem. Phys., 17, 1343–1359, https://doi.org/10.5194/acp-17-1343-2017, 2017. a
Hoff, P. D.: A First Course in Bayesian Statistical Methods, Springer, New York, NY, https://doi.org/10.1007/978-0-387-92407-6, 2009. a
Hudson, P. K., Gibson, E. R., Young, M. A., Kleiber, P. D., and Grassian, V. H.: Coupled infrared extinction and size distribution measurements for several clay components of mineral dust aerosol, J. Geophys. Res.-Atmos., 113, D01201, https://doi.org/10.1029/2007JD008791, 2008. a
Jenkin, M. E., Saunders, S. M., and Pilling, M. J.: The tropospheric degradation of volatile organic compounds: a protocol for mechanism development, Atmos. Environ., 31, 81–104, https://doi.org/10.1016/S1352-2310(96)00105-7, 1997. a
Kabanikhin, S. I.: Definitions and examples of inverse and ill-posed problems, J. Inverse Ill-Pose. P., 16, 317–357, https://doi.org/10.1515/JIIP.2008.019, 2008. a
Kamruzzaman, M., Takahama, S., and Dillner, A. M.: Quantification of amine functional groups and their influence on OM∕OC in the IMPROVE network, Atmos. Environ., 172, 124–132, https://doi.org/10.1016/j.atmosenv.2017.10.053, 2018. a
Krapf, M., El Haddad, I., Bruns, E., Molteni, U., Daellenbach, K., Prévôt, A. H., Baltensperger, U., and Dommen, J.: Labile Peroxides in Secondary Organic Aerosol, Chem, 1, 603–616, https://doi.org/10.1016/j.chempr.2016.09.007, 2016. a
Kuzmiakova, A., Dillner, A. M., and Takahama, S.: An automated baseline correction protocol for infrared spectra of atmospheric aerosols collected on polytetrafluoroethylene (Teflon) filters, Atmos. Meas. Tech., 9, 2615–2631, https://doi.org/10.5194/amt-9-2615-2016, 2016. a
Liu, S., Takahama, S., Russell, L. M., Gilardoni, S., and Baumgardner, D.: Oxygenated organic functional groups and their sources in single and submicron organic particles in MILAGRO 2006 campaign, Atmos. Chem. Phys., 9, 6849–6863, https://doi.org/10.5194/acp-9-6849-2009, 2009. a
Liu, S., Shilling, J. E., Song, C., Hiranuma, N., Zaveri, R. A., and Russell, L. M.: Hydrolysis of Organonitrate Functional Groups in Aerosol Particles, Aerosol Sci. Tech., 46, 1359–1369, https://doi.org/10.1080/02786826.2012.716175, 2012. a
Malm, W. C. and Hand, J. L.: An examination of the physical and optical properties of aerosols collected in the IMPROVE program, Atmos. Environ., 41, 3407–3427, https://doi.org/10.1016/j.atmosenv.2006.12.012, 2007. a, b
Malm, W. C., Sisler, J. F., Huffman, D., Eldred, R. A., and Cahill, T. A.: Spatial and seasonal trends in particle concentration and optical extinction in the United States, J. Geophys. Res.-Atmos., 99, 1347–1370, https://doi.org/10.1029/93JD02916, 1994. a
Marais, E. A., Jacob, D. J., Turner, J. R., and Mickley, L. J.: Evidence of 1991–2013 decrease of biogenic secondary organic aerosol in response to SO2 emission controls, Environ. Res. Lett., 12, 054018, https://doi.org/10.1088/1748-9326/aa69c8, 2017. a
Maria, S. F., Russell, L. M., Turpin, B. J., Porcja, R. J., Campos, T. L., Weber, R. J., and Huebert, B. J.: Source signatures of carbon monoxide and organic functional groups in Asian Pacific Regional Aerosol Characterization Experiment (ACE-Asia) submicron aerosol types, J. Geophys. Res.-Atmos., 108, 8637, https://doi.org/10.1029/2003JD003703, 2003. a
Martens, H. and Næs, T.: Multivariate Calibration, John Wiley & Sons, New York, 1991. a
McClenny, W. A., Childers, J. W., Röhl, R., and Palmer, R. A.: FTIR transmission spectrometry for the nondestructive determination of ammonium and sulfate in ambient aerosols collected on teflon filters, Atmos. Environ., 19, 1891–1898, https://doi.org/10.1016/0004-6981(85)90014-9, 1985. a
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., and Teller, E.: Equation of State Calculations by Fast Computing Machines, J. Chem. Phys., 21, 1087–1092, https://doi.org/10.1063/1.1699114, 1953. a
Murphy, B. N., Donahue, N. M., Fountoukis, C., Dall'Osto, M., O'Dowd, C., Kiendler-Scharr, A., and Pandis, S. N.: Functionalization and fragmentation during ambient organic aerosol aging: application of the 2-D volatility basis set to field studies, Atmos. Chem. Phys., 12, 10797–10816, https://doi.org/10.5194/acp-12-10797-2012, 2012. a
Murphy, D. M., Cziczo, D. J., Froyd, K. D., Hudson, P. K., Matthew, B. M., Middlebrook, A. M., Peltier, R. E., Sullivan, A., Thomson, D. S., and Weber, R. J.: Single-particle mass spectrometry of tropospheric aerosol particles, J. Geophys. Res.-Atmos., 111, D23S32, https://doi.org/10.1029/2006JD007340, 2006. a
Nocedal, J. and Wright, S. J.: Numerical Optimization, Springer, New York, NY, https://doi.org/10.1007/978-0-387-40065-5, 2006. a
O'Hagan, T.: Dicing with the unknown, Significance, 1, 132–133, https://doi.org/10.1111/j.1740-9713.2004.00050.x, 2004. a
Ott, W.: Environmental Statistics and Data Analysis, Taylor & Francis, 1994. a
Pang, Y., Turpin, B. J., and Gundel, L. A.: On the Importance of Organic Oxygen for Understanding Organic Aerosol Particles, Aerosol Sci. Tech., 40, 128–133, https://doi.org/10.1080/02786820500423790, 2006. a
Pinder, R. W., Adams, P. J., Pandis, S. N., and Gilliland, A. B.: Temporally resolved ammonia emission inventories: Current estimates, evaluation tools, and measurement needs, J. Geophys. Res.-Atmos., 111, D16310, https://doi.org/10.1029/2005JD006603, 2006. a
Polidori, A., Turpin, B. J., Davidson, C. I., Rodenburg, L. A., and Maimone, F.: Organic PM2.5: Fractionation by polarity, FTIR spectroscopy, and OM∕OC ratio for the Pittsburgh aerosol, Aerosol Sci. Tech., 42, 233–246, https://doi.org/10.1080/02786820801958767, 2008. a
Pope, R., Stanley, K. M., Domsky, I., Yip, F., Nohre, L., and Mirabelli, M. C.: The relationship of high PM2.5 days and subsequent asthma-related hospital encounters during the fireplace season in Phoenix, AZ, 2008–2012, Air Quality, Atmosphere & Health, 10, 161–169, https://doi.org/10.1007/s11869-016-0431-2, 2017. a
Pye, H. O. T., Luecken, D. J., Xu, L., Boyd, C. M., Ng, N. L., Baker, K. R., Ayres, B. R., Bash, J. O., Baumann, K., Carter, W. P. L., Edgerton, E., Fry, J. L., Hutzell, W. T., Schwede, D. B., and Shepson, P. B.: Modeling the Current and Future Roles of Particulate Organic Nitrates in the Southeastern United States, Environ. Sci. Technol., 49, 14195–14203, https://doi.org/10.1021/acs.est.5b03738, 2015. a
Pye, H. O. T., D’Ambro, E. L., Lee, B. H., Schobesberger, S., Takeuchi, M., Zhao, Y., Lopez-Hilfiker, F., Liu, J., Shilling, J. E., Xing, J., Mathur, R., Middlebrook, A. M., Liao, J., Welti, A., Graus, M., Warneke, C., Gouw, J. A. d., Holloway, J. S., Ryerson, T. B., Pollack, I. B., and Thornton, J. A.: Anthropogenic enhancements to production of highly oxygenated molecules from autoxidation, P. Natl. Acad. Sci. USA, 116, 6641–6646, https://doi.org/10.1073/pnas.1810774116, 2019. a
Ramadan, Z., Song, X.-H., and Hopke, P. K.: Identification of Sources of Phoenix Aerosol by Positive Matrix Factorization, J. Air Waste Manage., 50, 1308–1320, https://doi.org/10.1080/10473289.2000.10464173, 2011. a
Ranney, A. P. and Ziemann, P. J.: Microscale spectrophotometric methods for quantification of functional groups in oxidized organic aerosol, Aerosol Sci. Tech., 50, 881–892, https://doi.org/10.1080/02786826.2016.1201197, 2016. a
Reff, A., Turpin, B. J., Offenberg, J. H., Weisel, C. P., Zhang, J., Morandi, M., Stock, T., Colome, S., and Winer, A.: A functional group characterization of organic PM2.5 exposure: Results from the RIOPA study RID C-3787-2009, Atmos. Environ., 41, 4585–4598, https://doi.org/10.1016/j.atmosenv.2007.03.054, 2007. a
Reggente, M., Dillner, A. M., and Takahama, S.: Predicting ambient aerosol thermal–optical reflectance (TOR) measurements from infrared spectra: extending the predictions to different years and different sites, Atmos. Meas. Tech., 9, 441–454, https://doi.org/10.5194/amt-9-441-2016, 2016. a, b
Reggente, M., Dillner, A. M., and Takahama, S.: Analysis of functional groups in atmospheric aerosols by infrared spectroscopy: systematic intercomparison of calibration methods for US measurement network samples, Atmos. Meas. Tech., 12, 2287–2312, https://doi.org/10.5194/amt-12-2287-2019, 2019. a, b, c, d, e, f
Robert, C. P.: The Bayesian Choice: From Decision-Theoretic Foundations to Computational Implementation, Springer Texts in Statistics, Springer, New York, NY, 2nd edn., 2007. a
Robert, C. P. and Casella, G.: Introducing Monte Carlo Methods with R, Springer Verlag, New York, https://doi.org/10.1007/978-1-4419-1576-4, 2010. a
Robinson, A. L., Donahue, N. M., Shrivastava, M. K., Weitkamp, E. A., Sage, A. M., Grieshop, A. P., Lane, T. E., Pierce, J. R., and Pandis, S. N.: Rethinking organic aerosols: Semivolatile emissions and photochemical aging, Science, 315, 1259–1262, https://doi.org/10.1126/science.1133061, 2007. a
Rock, D., Werts, C., Linn, R., and Joreskog, K.: A Maximum Likelihood Solution To The Errors In Variables And Errors In Equations Model, Multivar. Behav. Res., 12, 187–197, https://doi.org/10.1207/s15327906mbr1202_6, 1977. a
Rogge, W. F., Hildemann, L. M., Mazurek, M. A., Cass, G. R., and Simoneit, B. R. T.: Sources of Fine Organic Aerosol. 2. Noncatalyst and Catalyst-equipped Automobiles and Heavy-duty Diesel Trucks, Environ. Sci. Technol., 27, 636–651, https://doi.org/10.1021/es00041a007, 1993. a, b
Rogge, W. F., Hildemann, L. M., Mazurek, M. A., Cass, G. R., and Simoneit, B. R. T.: Sources of fine organic aerosol. 9. Pine, oak and synthetic log combustion in residential fireplaces, Environ. Sci. Technol., 32, 13–22, https://doi.org/10.1021/es960930b, 1998. a, b
Ruggeri, G. and Takahama, S.: Technical Note: Development of chemoinformatic tools to enumerate functional groups in molecules for organic aerosol characterization, Atmos. Chem. Phys., 16, 4401–4422, https://doi.org/10.5194/acp-16-4401-2016, 2016. a
Ruggeri, G., Bernhard, F. A., Henderson, B. H., and Takahama, S.: Model–measurement comparison of functional group abundance in α-pinene and 1,3,5-trimethylbenzene secondary organic aerosol formation, Atmos. Chem. Phys., 16, 8729–8747, https://doi.org/10.5194/acp-16-8729-2016, 2016. a
Russell, L. M.: Aerosol organic-mass-to-organic-carbon ratio measurements, Environ. Sci. Technol., 37, 2982–2987, https://doi.org/10.1021/es026123w, 2003. a, b, c
Russell, L. M., Bahadur, R., Hawkins, L. N., Allan, J., Baumgardner, D., Quinn, P. K., and Bates, T. S.: Organic aerosol characterization by complementary measurements of chemical bonds and molecular fragments, Atmos. Environ., 43, 6100–6105, https://doi.org/10.1016/j.atmosenv.2009.09.036, 2009. a, b, c
Russell, L. M., Bahadur, R., and Ziemann, P. J.: Identifying organic aerosol sources by comparing functional group composition in chamber and atmospheric particles, P. Natl. Acad. Sci. USA, 108, 3516–3521, https://doi.org/10.1073/pnas.1006461108, 2011. a, b, c
Ruthenburg, T. C., Perlin, P. C., Liu, V., McDade, C. E., and Dillner, A. M.: Determination of organic matter and organic matter to organic carbon ratios by infrared spectroscopy with application to selected sites in the IMPROVE network, Atmos. Environ., 86, 47–57, https://doi.org/10.1016/j.atmosenv.2013.12.034, 2014. a, b, c, d, e, f, g, h, i
San Martini, F. M., Dunlea, E. J., Volkamer, R., Onasch, T. B., Jayne, J. T., Canagaratna, M. R., Worsnop, D. R., Kolb, C. E., Shorter, J. H., Herndon, S. C., Zahniser, M. S., Salcedo, D., Dzepina, K., Jimenez, J. L., Ortega, J. M., Johnson, K. S., McRae, G. J., Molina, L. T., and Molina, M. J.: Implementation of a Markov Chain Monte Carlo method to inorganic aerosol modeling of observations from the MCMA-2003 campaign – Part II: Model application to the CENICA, Pedregal and Santa Ana sites, Atmos. Chem. Phys., 6, 4889–4904, https://doi.org/10.5194/acp-6-4889-2006, 2006. a, b
Saunders, S. M., Jenkin, M. E., Derwent, R. G., and Pilling, M. J.: Protocol for the development of the Master Chemical Mechanism, MCM v3 (Part A): tropospheric degradation of non-aromatic volatile organic compounds, Atmos. Chem. Phys., 3, 161–180, https://doi.org/10.5194/acp-3-161-2003, 2003. a
Schwarzenbach, R. P., Gschwend, P. M., and Imboden, D. M.: Environmental Organic Chemistry, John Wiley & Sons, 2nd edn., 2002. a
Simon, H., Bhave, P. V., Swall, J. L., Frank, N. H., and Malm, W. C.: Determining the spatial and seasonal variability in OM∕OC ratios across the US using multiple regression, Atmos. Chem. Phys., 11, 2933–2949, https://doi.org/10.5194/acp-11-2933-2011, 2011. a, b, c, d, e, f, g
Skoog, D., Holler, F., and Crouch, S.: Principles of Instrumental Analysis, Brooks/Cole Pub Co., Belmont, CA, 7th edn., 2017. a
Takahama, S. and Ruggeri, G.: Technical note: Relating functional group measurements to carbon types for improved model–measurement comparisons of organic aerosol composition, Atmos. Chem. Phys., 17, 4433–4450, https://doi.org/10.5194/acp-17-4433-2017, 2017. a, b, c, d
Takahama, S., Liu, S., and Russell, L. M.: Coatings and clusters of carboxylic acids in carbon-containing atmospheric particles from spectromicroscopy and their implications for cloud-nucleating and optical properties, J. Geophys. Res.-Atmos., 115, D01202, https://doi.org/10.1029/2009JD012622, 2010. a
Takahama, S., Schwartz, R. E., Russell, L. M., Macdonald, A. M., Sharma, S., and Leaitch, W. R.: Organic functional groups in aerosol particles from burning and non-burning forest emissions at a high-elevation mountain site, Atmos. Chem. Phys., 11, 6367–6386, https://doi.org/10.5194/acp-11-6367-2011, 2011. a
Takahama, S., Johnson, A., Morales, J. G., Russell, L. M., Duran, R., Rodriguez, G., Zheng, J., Zhang, R., Toom-Sauntry, D., and Leaitch, W. R.: Submicron organic aerosol in Tijuana, Mexico, from local and Southern California sources during the CalMex campaign, Atmos. Environ., 70, 500–512, https://doi.org/10.1016/j.atmosenv.2012.07.057, 2013a. a
Takahama, S., Johnson, A., and Russell, L. M.: Quantification of Carboxylic and Carbonyl Functional Groups in Organic Aerosol Infrared Absorbance Spectra, Aerosol Sci. Tech., 47, 310–325, https://doi.org/10.1080/02786826.2012.752065, 2013b. a
Takahama, S., Dillner, A. M., Weakley, A. T., Reggente, M., Bürki, C., Lbadaoui-Darvas, M., Debus, B., Kuzmiakova, A., and Wexler, A. S.: Atmospheric particulate matter characterization by Fourier transform infrared spectroscopy: a review of statistical calibration strategies for carbonaceous aerosol quantification in US measurement networks, Atmos. Meas. Tech., 12, 525–567, https://doi.org/10.5194/amt-12-525-2019, 2019. a, b, c
Thompson, R. L., Gerbig, C., and Rödenbeck, C.: A Bayesian inversion estimate of N2O emissions for western and central Europe and the assessment of aggregation errors, Atmos. Chem. Phys., 11, 3443–3458, https://doi.org/10.5194/acp-11-3443-2011, 2011. a
Tierney, L. and Kadane, J. B.: Accurate Approximations for Posterior Moments and Marginal Densities, J. Am. Stat. Assoc., 81, 82–86, https://doi.org/10.1080/01621459.1986.10478240, 1986. a
Tukiainen, S., Railo, J., Laine, M., Hakkarainen, J., Kivi, R., Heikkinen, P., Chen, H., and Tamminen, J.: Retrieval of atmospheric CH4 profiles from Fourier transform infrared data using dimension reduction and MCMC, J. Geophys. Res.-Atmos., 121, 1312–1327, https://doi.org/10.1002/2015JD024657, 2016. a
Turpin, B. J. and Lim, H. J.: Species contributions to PM2.5 mass concentrations: Revisiting common assumptions for estimating organic mass, Aerosol Sci. Tech., 35, 602–610, https://doi.org/10.1080/02786820152051454, 2001. a
Vehtari, A. and Ojanen, J.: A survey of Bayesian predictive methods for model assessment, selection and comparison, Statist. Surv., 6, 142–228, https://doi.org/10.1214/12-SS102, 2012. a
Walter, E. and Pronzato, L.: Identification of Parametric Models from Experimental Data, Springer-Verlag, Berlin, 1997. a
Wang, Y., Jiang, X., Yu, B., and Jiang, M.: A Hierarchical Bayesian Approach for Aerosol Retrieval Using MISR Data, J. Am. Stat. Assoc., 108, 483–493, https://doi.org/10.1080/01621459.2013.796834, 2013. a
Watson, J. G., Chow, J. C., and Chen, L.-W. A.: Summary of Organic and Elemental Carbon/Black Carbon Analysis Methods and Intercomparisons, Aerosol Air Qual. Res., 5, 65–102, https://doi.org/10.4209/aaqr.2005.06.0006, 2005. a
Weisberg, S.: Applied Linear Regression, Wiley Series in Probability and Statistics, Wiley, 2013. a, b
White, W. and Roberts, P.: On the nature and origins of visibility-reducing aerosols in the los angeles air basin, Atmos. Environ., 11, 803–812, https://doi.org/10.1016/0004-6981(77)90042-7, 1977. a
Wold, S., Martens, H., and Wold, H.: The Multivariate Calibration-problem In Chemistry Solved By the PLS Method, Lect. Notes Math., 973, 286–293, 1983. a, b
Zare, A., Fahey, K. M., Sarwar, G., Cohen, R. C., and Pye, H. O. T.: Vapor-Pressure Pathways Initiate but Hydrolysis Products Dominate the Aerosol Estimated from Organic Nitrates, ACS Earth Space Chem., 3, 1426–1437, https://doi.org/10.1021/acsearthspacechem.9b00067, 2019. a
- Abstract
- Introduction
- Experimental data
- Statistical analysis
- Results
- Conclusions
- Appendix A: Notation
- Appendix B: Partial least squares calibration
- Appendix C: Estimation of priors
- Appendix D: Sampling the posterior distribution
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Experimental data
- Statistical analysis
- Results
- Conclusions
- Appendix A: Notation
- Appendix B: Partial least squares calibration
- Appendix C: Estimation of priors
- Appendix D: Sampling the posterior distribution
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement