the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Long-term reliability of the Figaro TGS 2600 solid-state methane sensor under low-Arctic conditions at Toolik Lake, Alaska
Werner Eugster
James Laundre
Jon Eugster
George W. Kling
The TGS 2600 was the first low-cost solid-state sensor that shows a response to ambient levels of CH4 (e.g., range ≈1.8–2.7 µmol mol−1). Here we present an empirical function to correct the TGS 2600 signal for temperature and (absolute) humidity effects and address the long-term reliability of two identical sensors deployed from 2012 to 2018. We assess the performance of the sensors at 30 min resolution and aggregated to weekly medians. Over the entire period the agreement between TGS-derived and reference CH4 mole fractions measured by a high-precision Los Gatos Research instrument was R2=0.42, with better results during summer (R2=0.65 in summer 2012). Using absolute instead of relative humidity for the correction of the TGS 2600 sensor signals reduced the typical deviation from the reference to less than ±0.1 µmol mol−1 over the full range of temperatures from −41 to 27 ∘C. At weekly resolution the two sensors showed a downward drift of signal voltages indicating that after 10–13 years a TGS 2600 may have reached its end of life. While the true trend in CH4 mole fractions measured by the high-quality reference instrument was 10.1 (2012–2018), part of the downward trend in sensor signal (ca. 40 %–60 %) may be due to the increase in CH4 mole fraction because the sensor voltage decreases with increasing CH4 mole fraction. Weekly median diel cycles tend to agree surprisingly well between the TGS 2600 and reference measurements during the snow-free season, but in winter the agreement is lower. We suggest developing separate functions for deducing CH4 mole fractions from TGS 2600 measurements under cold and warm conditions. We conclude that the TGS 2600 sensor can provide data of research-grade quality if it is adequately calibrated and placed in a suitable environment where cross-sensitivities to gases other than CH4 are of no concern.
Low-cost trace gas sensors open new deployment opportunities for environmental observations. Still, their long-term performance in real-world applications is largely unknown, and thus, scientific research with such low-cost sensors is challenged with a high risk of failure and questionable data quality. Hence low-cost sensors are only considered as a complementary source of information on air quality (e.g., Lewis et al., 2018; Castell et al., 2017). Here we report on a 7-year (2012–2018) deployment of two low-cost Figaro TGS 2600 methane (CH4) sensors during summer and winter conditions in the relatively harsh low-Arctic climate of northern Alaska to explore the long-term stability and reliability of CH4 mole fraction estimates. The sensors were previously deployed over Toolik Lake during the ice-free season in 2011 (Eugster and Kling, 2012), where similar values between TGS-derived and reference CH4 mole fractions were only found if measurements were integrated over at least 6 h or if they were aggregated to mean diel cycles over the season. Other studies have deployed the same sensor type in complex rural and urban environments along the Colorado Front Range (Collier-Oxandale et al., 2018), in an oil and gas production region (Greeley, Colorado; Casey et al., 2019), and in urban south Los Angeles (Shamasunder et al., 2018). An application on an unmanned aerial vehicle, however, did not successfully detect CH4 hotspots (Falabella et al., 2018). These are all pioneering studies but are mostly restricted to a few days to months of measurements. Thus, our study is the first long-term comparison of high-precision measurements to those from CH4 sensitive, low-cost sensors under challenging climatic conditions.
Typically, new sensors are first calibrated under controlled conditions in a laboratory environment. Extensive calibration tests with a similar low-cost sensor (Figaro TGS2611-E00) from the same manufacturer as our TGS 2600 have been carried out by van den Bossche et al. (2017). Despite the care taken in their calibration effort, the residual CH4 mole fraction after calibration was still on the order of ±1.7 µmol mol−1, which is acceptable for chamber flux measurements, for example, over water (as done by, e.g., Duc et al., 2019) but not sufficient to measure ambient atmospheric mole fractions, which are of the same order of magnitude as the calibration uncertainty. The issue of important differences between laboratory assessments of low-cost sensors and their real-world performance is well known and typically relates to different data correction and calibration approaches in real-world rather than laboratory applications (Lewis et al., 2018). Hence we decided to use outdoor measurements obtained over a wide range of temperatures and relative humidity – the major cross-sensitivities experienced by such sensors – and derive a calibration function via parameter extraction using this dataset. Our goals were thus to (1) establish a statistical calibration function from field measured conditions that can also be used in different contexts to linearize the TGS 2600 sensor signal (which then can still be fine-tuned with a two-point calibration in a specific application); (2) assess the reliability of the TGS 2600 low-cost sensor under winter and summer conditions in the Arctic over 7 years of continuous deployment; and (3) explore potential improvements for sensor data processing, which includes (3a) wind effects that are neglected in laboratory environments and (3b) artificial neural networks (ANNs) to find out whether results can be improved over standard statistical regression methods for calibration of the sensor.
2.1 Study site
Field measurements were carried out at the Toolik wet sedge site (TWE; 68∘37′27.62′′ N, 149∘36′08.10′′ W; 728.14 m elevation, WGS 84 datum) where seasonal eddy covariance flux measurements were carried out during the summer seasons of 2010–2015 and partially during winters starting in 2014 until 15 June 2016, with the continuation as a meteorological station until present. The site is a wetland that is a local source of CH4 with a flux rate that is roughly 1 order of magnitude stronger than adjacent Toolik Lake, where the Eugster and Kling (2012) study was performed. The site is a wet graminoid tundra dominated by sedge species, namely cotton grass (Eriophorum angustifolium) and Carex aquatilis (Walker and Everett, 1991).
2.2 Instrumentation and measurements
Two Figaro TGS 2600 sensors (Figaro, 2005a, b) that were already deployed over Toolik Lake (TOL) during the ice-free season in 2011 (Eugster and Kling, 2012) were installed at the TWE site in late June 2012 (Fig. 1). Sensor 1 is the primary sensor used in this study, whereas sensor 2 was only used as a replicate to simplify assessing potential problems with sensor 1. Because no such problems occurred, we will focus only on the results obtained with sensor 1 except in Sect. 3.2, where we used both sensors to assess their performance at weekly time resolution. The TGS 2600 is a high-sensitivity solid-state sensor for the detection of air contaminants (Figaro, 2005a). It is sensitive to methane at low mole fractions but also to hydrogen, carbon monoxide, isobutane, and ethanol. It is the only low-cost solid-state sensor that we are aware of for which the manufacturer indicates a sensitivity to methane even under ambient (≈2 µmol mol−1) methane mole fractions, whereas most other sensors are only sensitive at mole fractions that exceed ambient levels by at least 1 or 2 orders of magnitude. This high sensitivity to low-methane mole fractions comes at the expense that no specific molecular filter prevents the other components from reaching the sensor surface. Thus, our considerations made here assume that deployment is made in an area like the Arctic, where levels of carbon monoxide, isobutane, ethanol, and hydrogen are rather constant and do not vary as strongly as methane so that the sensor signal can be interpreted as a first approximation of a methane mole fraction signal. For additional details on the TGS 2600 sensor the reader is referred to Eugster and Kling (2012).
The TWE site receives line power from the Toolik Field Station (TFS) power generator. During the snow- and ice-free summer season (typically late June to mid-August) measurements are almost interruption-free, but during the cold season (typically September to late May) longer power interruptions limit the winter data coverage. Nevertheless, this is the first study that provides low-cost sensor methane mole fraction measurements over a temperature range from Arctic winter temperatures of −41 ∘C to a relatively balmy 27 ∘C during short periods of the Arctic summer. Reference CH4 dry mole fractions were measured by a Fast Methane Analyzer (FMA, Los Gatos Research, Inc., San Jose, CA, USA; years 2012–2016), which was replaced by a Fast Greenhouse Gas Analyzer (FGGA, Los Gatos Research, Inc., San Jose, CA, USA; since 2016) for combined CH4, CO2, and H2O dry mole fraction measurements. Until 18 June 2016 the CH4 mole fractions were calculated as 1 min averages from the raw eddy covariance flux data files. We report all gas mole fractions in micromoles per mole or nanomoles per mole. The FMA and FGGA sampling rate was set to 20 Hz, and the flow rate of sample air was ca. 20 L min−1. After the termination of eddy covariance flux measurements, the FGGA measurements were continued with the instrument's internal pump (flow rate ca. 0.65 L min−1) with 1 Hz raw data sampling. In addition to digital recording, the CH4 signal was converted to an analog voltage that was recorded on a CR23X data logger (Campbell Scientific Inc., CSI, Logan, UT, USA). The same data logger also recorded air temperature, relative humidity (HMP45AC, CSI), wind speed, and wind direction (034B Windset, MetOne, Grants Pass, OR, USA) as well as ancillary meteorological and soil variables not used in this study. The factory-calibrated HMP45AC sensor head was exchanged for a newly calibrated one ca. every 3 years to minimize long-term drift effects in temperature and relative humidity measurements (James Laundre, personal communication, 2020). Sensors were measured every 5 s, and 1 min averages were stored on the logger. These data were then screened for outliers and instrumental errors and failures, and 30 min averages were calculated for the present analysis.
Both FMA and the later FGGA analyzers were used for eddy covariance applications, and thus the instruments were not calibrated as frequently as is done in applications for the Global Atmosphere Watch network (WMO, 2001). Both sensors were more accurate than the available calibration CH4 gases at TFS. In 2015 it was possible for the first time to use an NOAA (National Oceanographic and Atmospheric Administration, Boulder, CO, USA) reference gas cylinder (no. CB09837) to fine-tune the FGGA. This was typically done in the early summer season, when field personnel arrived at TFS (late May).
Because the TGS 2600 sensors only show a weak response to CH4 but are highly sensitive to temperature and humidity, a LinPicco A05 Basic sensor (IST Innovative Sensor Technology, Wattwil, Switzerland) was added next to the TGS 2600 (see Fig. 1). The A05 is a capacitive humidity module that also has a Pt1000 platinum 1 kΩ thermistor on board to measure ambient temperature. The relative humidity output by the A05 is a linearized voltage in the range of 0–5 V, and the Pt1000 thermistor was measured in three-wire half-bridge mode using an excitation voltage of 4.897 V.
2.3 Calculations
Before analyses the data were processed in the following way: (1) outliers were removed (2) relative humidities greater than 105 % (accuracy of capacitive humidity sensors) were deleted, and (3) reference CH4 mole fractions obtained from the FGGA (since 2016) were filtered based on hard boundaries of housekeeping variables available for quality control. For the latter we used the following hard boundaries for filtering: (a) sample cell pressure had to be in the range of 130–143 Torr and (b) the instrument-specific ringdown time of the laser for CH4 measurements had to be in the range of 13–17 ms. The accepted reference CH4 mole fractions were thus all measured in the narrow range of cell pressures between 139.7 and 140.3 Torr and laser ringdown times between 14.02 and 14.94 ms, which indicates best performance of the analyzer. Before 2016 (FMA instrument) these housekeeping variables were not recorded.
The basic principle of operation of the TGS 2600 sensor was described in detail by Eugster and Kling (2012). The methane sensing mechanisms of different active materials used in solid-state sensors were described by Aghagoli and Ardyanian (2018). The TGS 2600 uses an SnO2 microcrystal surface (Figaro, 2005b). Whereas the manufacturer defines the sensor signal as Rs∕R0, the ratio of the electrical resistance Rs of the heated sensor material surface normalized over its resistance R0 in the air under absence of CH4, Hu et al. (2016) define the sensor signal as the ratio between Rs and Rg, the resistance of the surface in the pure gas of interest (here CH4). In all cases, considerations of technical sensor information are made for high mole fractions of CH4 (e.g., 200 µmol mol−1) for an SnO2 surface according to Hu et al. (2016), not for ambient mole fractions in the typical range of 1.7–4 µmol mol−1 (or less). Hence, some adaptations are always necessary because present-day sensors are not yet designed for such low mole fractions. In order to simplify calculations compared to what we presented in Eugster and Kling (2012) – which closely followed the technical information provided by the manufacturer (Figaro, 2005a, b) – we define the sensor signal as but with R0 arbitrarily set to the resistance observed when the sensor delivers V0=0.8 V output at Vc=5.0 V supply voltage. The highest voltages measured at TWE were 0.7501 and 0.7683 V from sensors 1 and 2, respectively (which theoretically corresponds to the lowest CH4 mole fractions). With these assumptions the sensor signal Sc can easily be approximated as a function of the inverse of the measured TGS signal voltage Vs,
The full derivation is
Here RL is the load resistor over which Vs is measured (see Figaro, 2005a, or Eugster and Kling, 2012, for more details) but which can be eliminated in this algebraic simplification.
To compute absolute humidity, we used the Magnus equation to estimate saturation vapor pressure esat (in hPa) at ambient temperature Ta (in ∘C),
with coefficients a=7.5 and b=235.0 for Ta≥0 ∘C and a=9.5 and b=265.5 for Ta<0 ∘C.
Actual vapor pressure e (hPa) was then determined as
with relative humidity RH in percent and converted to absolute humidity ρv (kg m−3) with
with p being atmospheric pressure (hPa) and Rv the gas constant for water vapor (461.53 ).
2.4 Statistical analyses
Statistical analyses were performed with R version 3.5.2 (R Core Team, 2018). Trend analyses were performed for both trend in CH4 mole fraction and drift of TGS 2600 measurements using the Mann–Kendall trend test implemented in the rkt package that is based on Marchetto et al. (2013). The annual linear trend (or drift) was calculated using the robust Theil–Sen estimator (Akritas et al., 1995) using weekly median values, and the significance of the trend (or drift) was assessed using Kendall's τ parameter. All trend and drift estimates were significant at p<0.05. The highest two-sided p value of the presented results was p=0.000054, and thus no detailed information on p values is given when statistical significance of trends or drift is mentioned in the following.
For assessing the quality of the proposed calculation of CH4 mole fractions from TGS 2600 sensors we inspected weekly aggregated data using four key indicators:
Bias. This is the mean of the difference of each 30 min averaged pair of CH4 mole fractions in micromoles per mole, CH4,TGS – CH4,ref.
Stability. This is the bias expressed as a percent deviation from the reference CH4 mole fraction, .
Variability. This is the mean relative deviation of the 95 % confidence interval (CI) observed with the TGS 2600 sensor from the corresponding 95 % CI of the CH4 reference measurements (in percent), .
Correlation of median diel cycles. Pearson's product-moment correlation coefficient between hourly aggregated median diel cycles of CH4 measured by the TGS 2600 and reference instruments.
In addition to conventional linear model fits (least square method) we used an ANN approach. This was performed in Python 3.7.1 using MLPRegressor from sklearn.neural_network version 0.20.2 (Pedregosa et al., 2011). We used a network with four hidden layers of sizes 500, 100, 50, and 5, respectively, and an adaptive learning rate. Learning was done with the data obtained during the calibration period 2014–2016, whereas the remaining years 2012–2013 and 2017–2018 were used for validation.
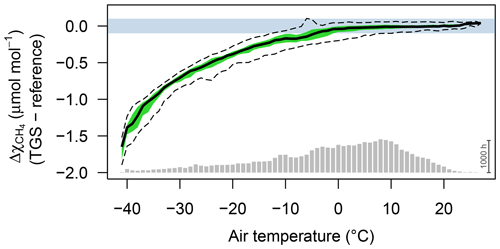
Figure 2Difference between TGS 2600 and reference CH4 measurements (30 min averages) as a function of air temperature when using the Eugster and Kling (2012) conversion. Agreement was good when ambient temperature was above freezing. The horizontal color bar shows the ±0.1 µmol mol−1 range around a perfect agreement. The green band shows the interquartile range of bin-averaged differences (TGS 2600 sensor 1), and dashed lines show the extent of the 95 % confidence intervals. Gray bars at the bottom show the number of 30 min averages in each bin. The scale bar (1000 h) on the right specifies their size.
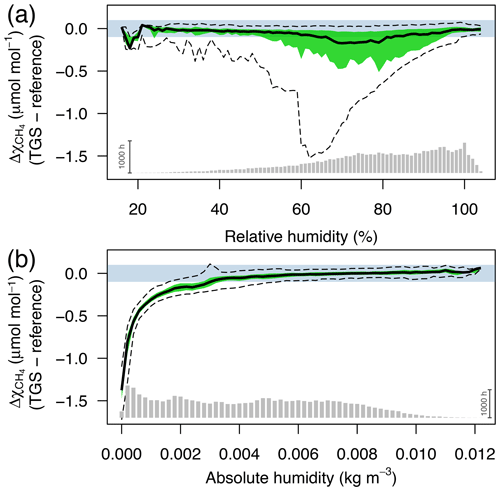
Figure 3Difference between TGS 2600 and reference CH4 measurements (30 min averages) as a function of (a) relative humidity (in %) and (b) absolute humidity (in kg m−3). The horizontal color bar shows the ±0.1 µmol mol−1 range around a perfect agreement. The green band shows the interquartile range of bin-averaged differences (TGS 2600 sensor 1), and dashed lines show the extent of the 95 % confidence intervals. Gray bars at the bottom show the number of 30 min averages in each bin. The scale bar (1000 h) on the right specifies their size.
CH4 mole fractions estimated from TGS 2600 measurements during the cold seasons differed strongly from the reference measurements when the Eugster and Kling (2012) approach was used (not shown); that approach translated the information from the technical specifications of the TGS 2600 sensor (Figaro, 2005a, b) to outdoor applications. The agreement with the CH4 reference measurements was within ±0.1 µmol mol−1 with temperatures above freezing (Fig. 2) but not so during cold conditions (Ta<0 ∘C). The differences between TGS estimates and CH4 reference measurements were largest with the Eugster and Kling (2012) approach when relative humidity was between 50 % and 90 % (Fig. 3a). When converting relative humidity to absolute humidity, the results became satisfactory for absolute humidity values greater than 0.004 kg m−3 (Fig. 3b). Using absolute humidity in place of relative humidity for the correction of the TGS 2600 was already attempted by Collier-Oxandale et al. (2018); this contrasts with the manufacturer's suggestion (Figaro, 2005a). Because absolute humidity above 0.004 kg m−3 is only possible at temperatures above 0 ∘C it appears quite obvious that temperature and humidity corrections of solid-state sensors most likely do not relate to relative humidity but to either actual vapor pressure (in hPa) or absolute humidity (in kg m−3). In all tested models absolute humidity performed marginally better than vapor pressure or mixing ratio (measured by R2; not shown); hence we suggest the following model and parameterization to estimate CH4 mole fractions in micromoles per mole from TGS 2600 signal voltage measurements:
with Sc being the dimensionless sensor signal (see Eq. 1), Ta the ambient air temperature in ∘C, and ρv the absolute humidity in kilograms per cubic meter. The parameter estimates were derived from the entire 2012–2018 dataset for TGS sensor 1 (Table 1, “entire period”). For other sensors the result from Eq. (2) can be considered as a linearized signal that can be fine-tuned with a sensor-specific two-point calibration as suggested in Sect. 3.4 of Eugster and Kling (2012).
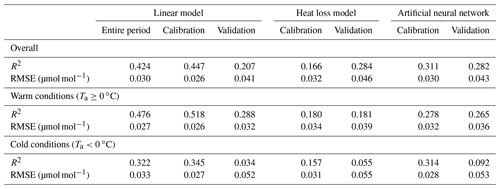
Table 1Goodness of fit of TGS 2600 (sensor 1)-derived CH4 mole fractions (30 min averages) obtained from a linear model using air temperature and absolute humidity (Eq. 2), a heat loss model (Eq. 3), and an artificial neural network (ANN). For the goodness of fit the coefficient of determination (R2) and the root mean square error (RMSE) of the residuals are reported for the overall model and separately for warm and cold conditions. The parametrization of the linear model given in Eq. (2) used the entire 2012–2018 period. For a more rigorous model test, all three approaches were calibrated with the data measured in years 2014–2016, and the remaining data (2012–2013 and 2017–2018) were used for validation.
The linear model in Eq. (2) was derived from a suite of candidate models including interactions among predictors and quadratic terms of each variable, and then stepwise elimination using the stepAIC function in the MASS package of R was employed to find the model with the lowest AIC (Akaike's information criterion). Unless explicitly mentioned, we analyzed CH4 mole fractions computed with Eq. (2) using the parameters obtained from all data measured by TGS 2600 sensor 1. Only in the direct comparison with the ANN (Sect. 3.1) did we determine an additional parameter set using the same calibration period as the ANN used (Sect. 2.4), making a direct comparison of performance in validation possible.
If ambient temperature influences the signal of the TGS 2600 in such a way as expected from the technical documentation (Figaro, 2005a, b), then wind speed could be a third factor influencing the conversion from TGS 2600 sensor voltages to CH4 mole fractions. To investigate this additional factor, we produced a heat loss model, assuming that the sensor correction is related to the cooling of the heated surface of the solid-state sensor, which has a nominal surface temperature Ts of 400 ∘C (Falabella et al., 2018). This is the typical operation temperature of SnO2–Ni2O3 sensors (Hu et al., 2016). Our candidate model for heat loss (HL in W) was
with being mean horizontal wind speed (m s−1), Ts and Ta the sensor surface and ambient air temperature (K), respectively, ρd the density of dry air (kg m−3), ρv the absolute humidity (kg m−3), and Cd and Cv the heat capacity of dry air and water vapor, respectively (). The scaling coefficient ξ is a best-fit model parameter (units: s m). The assumption made here was that the wind speed governs the eddy diffusivity of heat transported along the temperature gradient between the sensor surface and ambient air, and the moisture correction is only associated with the fact that water vapor has a higher heat capacity (1859 ) than dry air (1005.5 ), and hence the heat capacity of moist air increases accordingly with ρv.
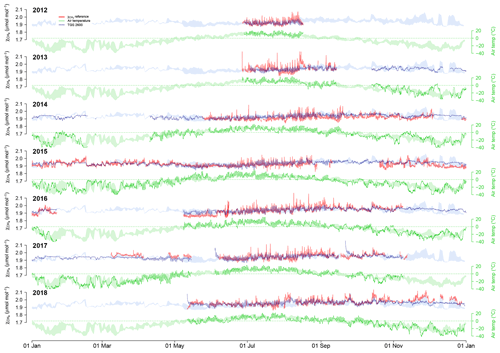
Figure 4Overview over annual courses of 30 min averaged air temperature (green) and CH4 mole fractions (blue and red). Pale color bands show the daily interquartile range (50 % of values between the first and third quartiles) of measurements from all years. Solid lines show actual measurements. Red lines are the reference CH4 measurements, and blue lines show the CH4 mole fraction derived from TGS 2600 measurements (sensor 1). Actual measurements show 30 min mean values.
3.1 Performance of the TGS 2600 sensor at 30 min resolution
Using Eq. (2) yields satisfying agreement with 30 min averaged data under both typical low-Arctic summer and winter conditions (Fig. 4) with an overall R2 of 0.424 (Table 1). When testing the linear model approach (Eq. 2) more rigorously by splitting the available data into a calibration period (years 2014–2016) and a validation period (years 2012–2013 and 2017–2018), some limitations can be seen, in particular under cold conditions, where none of the approaches performed very well in the validation period. The ANN had a more balanced performance between the calibration and validation periods, although it performed slightly less well under warm conditions (Ta≥0 ∘C).
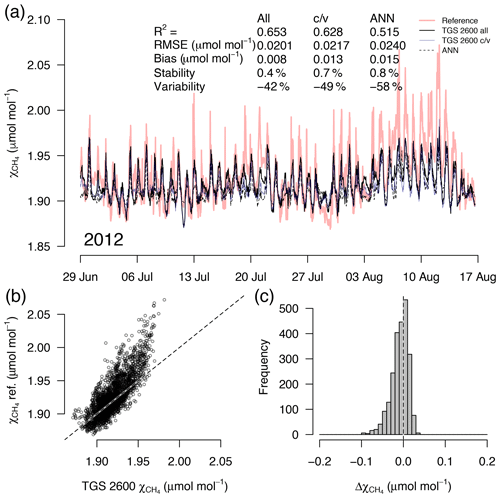
Figure 5(a) Time series of TGS 1-derived CH4 during a 7-week snow- and ice-free period in the first year of the long-term deployment (2012), (b) correlation with reference mole fraction, and (c) residuals (TGS 2600 all minus the reference) of 30 min averaged measurements. Thin solid lines in (a) show the result when all data are used with Eq. (2), reference mole fraction is shown with a red bold line, c/v shows an alternative fit from splitting the available data into a calibration and a validation part, and the dashed line shows the performance of an artificial neural network (ANN) fit. This example belongs to the validation period of the TGS 2600 c/v and ANN fits.
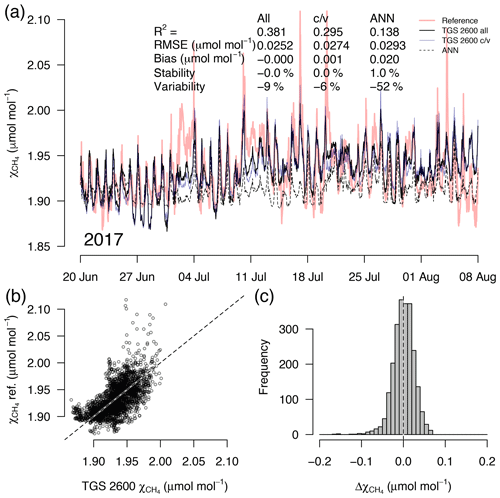
Figure 6As in Fig. 5 but with measurements from a 7-week snow- and ice-free period in 2017 at a sensor age of 7 years. This example belongs to the validation period of the TGS 2600 c/v and ANN fits.
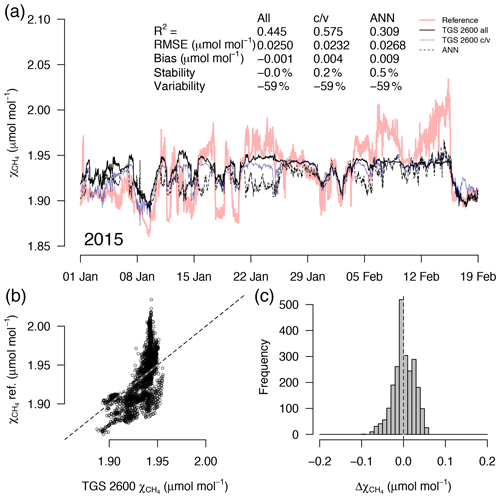
Figure 7As in Fig. 5 but with measurements from a 7-week period in midwinter with temperatures plunging down to −40 ∘C. High CH4 mole fractions coincide with the coldest temperatures (see Fig. 4). This example belongs to the validation period of the TGS 2600 c/v and ANN fits.
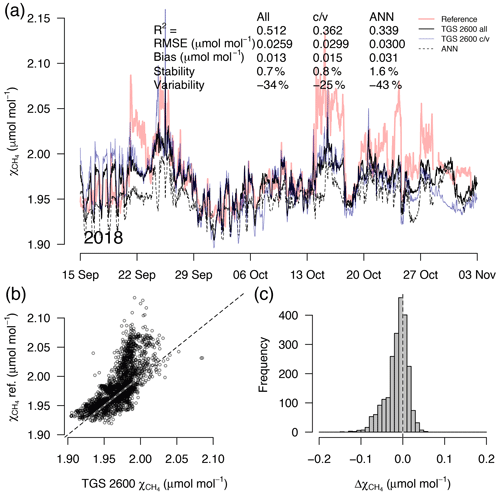
Figure 8As in Fig. 5 but with measurements from a 7-week period during the transition from fall to early winter. This example belongs to the validation period of the TGS 2600 c/v and ANN fits.
A detailed inspection of four representative 7-week time periods at full 30 min resolution is shown in Figs. 5–8. Typical summer conditions at the beginning of this study (Fig. 5) and towards the end of the analyzed period (Fig. 6) indicate that the short-term agreement (R2=0.653; Fig. 5) was better when the TGS sensor was still relatively new than when it was 7 years old (R2=0.381; Fig. 6), but the variability decreased (improved) from −42 % to −9 % with no relevant difference in bias and stability (0.01 µmol mol−1 and 0.4 % vs. 0.00 µmol mol−1 and 0.0 %, respectively). In winter the timing of most events is correctly captured (Fig. 7) with an R2 of 0.445, but the dynamics are not satisfactorily captured by the TGS sensor, indicated by a 59 % underestimation of the 95 % CI during this midwinter period. The transition from warm to cold season (Fig. 8) shows a mixture of days when the regular diel cycle, which is typical for the warm season, is still adequately captured, but the dynamics of periods with an air temperature below 0 ∘C (see Fig. 4), when CH4 mole fractions tend to be highest as in winter (Fig. 7), are not adequately captured. Still, with an R2 of 0.512 (Fig. 8) more than 50 % of the variance observed in the 30 min averaged CH4 reference measurements is captured by the low-cost TGS 2600 sensor.
Because of the absence of local sources of carbon monoxide and other air pollutants to which the TGS 2600 sensor is also sensitive (besides CH4), we investigated a special case when smoke and haze from wildfires south of the Books Range polluted the air in the TFS area on 26 June 2015 and compared the performance of both TGS sensors during that day with conditions 3 d before that event and on the same date in the following 3 years. The net effect of increased air pollutants was an apparent small decrease in the CH4 mole fractions calculated via Eq. (2) by approximately −0.03 µmol mol−1. At the same time the variability of the residuals increased from typically ±0.014 to ±0.027 µmol mol−1 (24 h averages). Thus, the influence of the wildfire smoke was of the same order of magnitude as the difference between TGS-derived CH4 mole fractions and the reference instrument on most other days of the year (see Figs. 5–8).
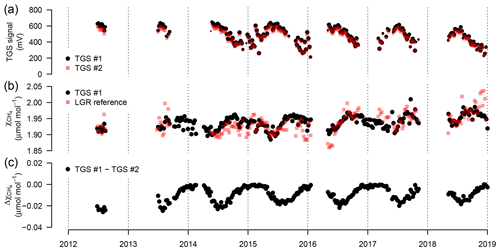
Figure 9(a) Weekly median sensor signals from both TGS 2600 sensors, (b) CH4 derived with Eq. (2) for TGS sensor 1 and measured by the Los Gatos Research reference instrument, and (c) absolute difference between the two TGS 2600 sensors. The signals from both sensors were converted to CH4 using Eq. (2) parameterized with data from TGS sensor 1. Symbol size is proportional to relative data coverage.
3.2 Performance of weekly aggregated data
The TGS 2600 is not expected to provide short-term accuracy comparable to high-quality instrumentation (see also Lewis et al., 2018). However, Eugster and Kling (2012) argued that such measurements may still provide additional insights as compared to the passive samplers described by Godbout et al. (2006a, b) by integrating over longer time frames. Thus, here we inspected the performance of weekly aggregated estimates derived from the TGS 2600 in order to inspect drift of the two sensors and their performance over the 7-year deployment period. Note that in Eq. (2) we did not include a drift correction. Figure 9 shows weekly medians of sensor signals, the agreement with the reference signal, and the difference between the CH4 mole fractions obtained from both TGS 2600 sensors mounted at the same position (Fig. 1). The two TGS 2600 sensors (1 and 2) showed a trend in their signals of −18.8 and −15.5 mV yr−1, respectively (Fig. 9a). Thus, with typical signals on the order of 200–700 mV (Fig. 9a) the lowest (winter) readings may no longer be measurable after 10–13 years of continuous operation, indicating the end of life of a TGS 2600.
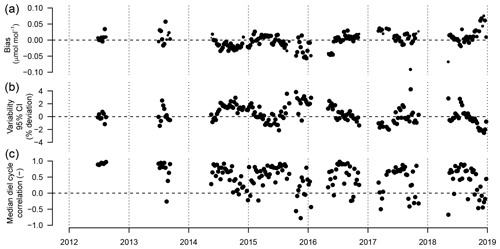
Figure 10(a) Weekly median bias, (b) median variability, and (c) correlation between weekly median diel cycles of TGS 2600 sensor 1 and the reference. Symbol size is proportional to relative data coverage.
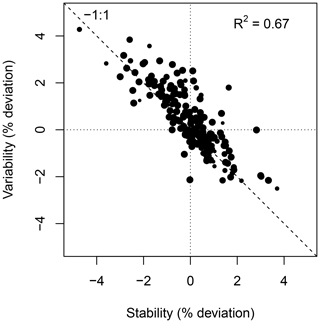
Figure 10 shows the weekly median bias, variability, and the correlation between the weekly aggregated median diel cycle of CH4 at hourly resolution between the TGS 1 measurements and the reference. Despite the trend of the sensor signal shown in Fig. 9a and b, both the bias and variability primarily show a seasonal pattern with a slightly negative bias (around −0.02 µmol mol−1) during peak growing season and a corresponding positive deviation in midwinter when temperatures can be well below −30 ∘C (Fig. 10a). The variability (Fig. 10b) shows the inverse pattern of the bias. If bias is expressed as the relative bias (i.e., stability), the stability vs. variability plot (Fig. 11) shows points lying uniformly around the line of a relationship (R2=0.67). This indicates that both variability and stability can be improved at the same time because there is no tradeoff visible in Fig. 11.
3.3 Linear trend and drift estimates
All linear trend estimates were statistically significant (see Sect. 2.4). However, our measurements started with warm-season measurements only (2012–2014) that were successively expanded to include cold-season measurements. Thus, all interpretation of the trends and drifts presented here should be considered with caution given the long gaps in data due to the technical challenges of operating such equipment under adverse winter conditions. The CH4 mole fraction trend observed with the high-quality reference measurements was 10.1 . This is 2.5 times the trend observed from 2005 to 2011 by NOAA (28.6±0.9 nmol mol−1 or 4.09 ; Table 2.1 in Hartmann et al., 2014) but of the same order of magnitude reported by Nisbet et al. (2014) for 2013 (last year covered by that study) for latitudes north of the Tropic of Cancer. Thus, this trend may be real, and hence all trends seen in low-cost sensor signals are not necessarily solely an artifact of such sensors. However, it remains a challenge to deduce the true trend in CH4 mole fractions over longer time periods using such a low-cost sensor because of drifting signals. Thus, we inspected the drift of the TGS 2600-derived mole fraction with respect to the (true) CH4 trend observed with the high-quality reference instrument. These drifts appear to be smaller than the true trend but are still considerable: the bias of TGS-derived CH4 mole fractions drifted by 4–6 (40 %–60 % of actual trend), and variability drifted by −0.24 % yr−1. They provide encouraging results suggesting that with occasional (infrequent) calibration with a high-quality standard, e.g., using a traveling standard operating during a few good days with adequate coverage of the near-surface diel cycle of CH4, TGS 2600 measurements might be suitable for the monitoring of CH4 mole fractions in other areas as well. As shown in Fig. 10c the correlation of median diel cycles between TGS estimates and CH4 reference measurements is one of the weak points in the current performance of the TGS 2600 sensors. Furthermore, we observed a significant negative trend of the correlation coefficient of −0.051 yr−1 (Fig. 10c). However, the key finding is that the typical diel cycle during the warm season (air temperature >0 ∘C) disappears during winter conditions (Figs. 4, 7), and thus separate transfer functions for warm and cold temperatures might be a solution for future studies (Table 1). Our Eq. (2) is thus intentionally derived from the entire dataset to provide a starting point for more elaborate fine-tuning in projects where this is desired.
3.4 Potential of using artificial neural networks
Casey et al. (2019) found that artificial neural networks (ANNs) outperformed linear models in mitigating curvature and linear trends in trace gas measurements when used with the same set of input variables during a 3-month comparison period. To inspect the potential of ANNs at our Arctic long-term dataset, we added the ANN results to Figs. 5–8. In summer (Figs. 5, 6) we did not find a substantial difference between an ANN and the linear approach of Eq. (2) in terms of root mean square error (RMSE) or R2 between predicted and measured CH4 mole fractions (Table 1). In winter, with temperatures below freezing, the ANN performed clearly better in the validation than the linear approach, but both approaches remained unsatisfactory (R2<0.1) despite the fact that both approaches were similar in the calibration period (R2≈0.3, Table 1).
During the warm period we found cases where the ANN was much better in capturing a specific daily feature, as for example on 11 July 2012 (Fig. 5a), when the daily minimum was nicely captured by the ANN, but the linear model was much too low. Contrastingly, in 2017 (Fig. 6a) periods could be found when the daily dynamics were correctly captured by the ANN but at too low of mixing ratios (e.g., 10–18 July 2017; Fig. 6a). It should be noted that at this latitude the sun does not set between 24 May and 20 July; thus nocturnal conditions are clearly different from conditions at lower latitudes such as the ones investigated by Casey et al. (2019). Similarly, the transition from warm to cold season (Fig. 8) was challenging with both the linear model and ANN approach. We have only used two variables, Ta and humidity, that according to manufacturer specifications (Figaro, 2005a, b) influence the TGS 2600 sensor signal. In reality, the same two variables also influence the CH4 production in water-logged ecosystems and thus contribute to the true CH4 signal in addition to the cross-sensitivity, which we try to correct with Eq. (2).
An ANN that can separate the effect of ambient variations of CH4 mole fractions from the artifact of cross-sensitivity of the TGS 2600 to Ta and humidity may however outperform a linear model approach in future studies if more potentially important driving variables are included than only those specified by the manufacturer (Figaro, 2005a, b).
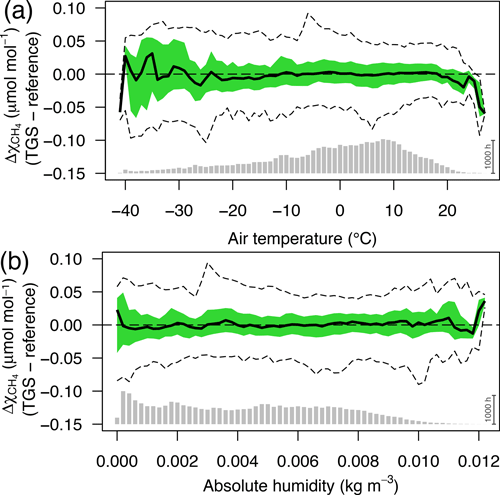
Figure 12Residuals of 30 min averaged TGS 2600 vs. reference CH4 measurements as a function of (a) air temperature and (b) absolute humidity. Colored areas show the interquartile range (50 % CI), bold lines show the median, and dashed lines show the bin-averaged 95 % confidence interval. Bin size was 1 ∘C and 0.0002 kg m−3, respectively. Gray bars at the bottom show the number of 30 min averages in each bin; the scale bar (1000 h) on the right specifies their size.
3.5 Suggestions for future work
The interquartile ranges and 95 % confidence intervals of each air temperature (Fig. 12a) or absolute humidity bin (Fig. 12b) are very similar over a wide range of temperatures and humidity levels but tend to become more variable in bins with few data (i.e., lowest and highest temperatures and highest absolute humidities in Fig. 12). Deviations are generally constrained within ±0.1 µmol mol−1 or better but with higher variability at both temperature ends, where data coverage is poor (gray bars at bottom of Fig. 12a) as temperatures below −30 ∘C were not frequently covered due to technical problems with the measurement station and summer temperatures above 20 ∘C are still rather rare at this low-Arctic latitude (Hobbie and Kling, 2014). A slightly different picture emerges for low absolute humidity: 56 % of measurements are at lower humidities than the saturation humidity at 0 ∘C (0.0049 kg m−3); thus the rather homogenous variances at low humidity (Fig. 12b) indicate that humidity is not of concern at low temperatures, and future attempts for improvements should rather focus on humidity above 0.01 kg m−3 and temperatures above 20 ∘C that are not normally found in the Arctic.
Based on physical considerations one might expect that specific humidity or water vapor mixing ratio instead of absolute humidity could lead to further improvements because absolute humidity still depends on temperature. However, our tests have not indicated a relevant gain of information or accuracy of prediction, but future work should also try to find a better physical correction model than the purely empirical one used here based on manufacturer information.
Another approach was taken by van den Bossche et al. (2017), who performed an in-depth laboratory calibration of the very similar but less sensitive Figaro TGS 2611-E00 sensor (the manufacturer only specifies a response above 300 µmol mol−1 CH4; Figaro, 2013) at different temperatures and levels of relative humidity over a CH4 calibration range starting at ≈2 µmol mol−1 ambient mole fraction up to 10 µmol mol−1 CH4. Despite the effort, the residual mole fractions remained large (range of ca. −1.5 µmol mol−1 to +1.1 µmol mol−1) – too large for the application we present here. Our efforts to calibrate our TGS 2600 sensors in a laboratory climate chamber in a similar way were not satisfactory (Eugster, unpublished), hence our approach presented here to determine the sensor behavior from long-term outdoor measurements under real-world conditions. Contrastingly, Kneer et al. (2014) are convinced that “to be of use for advanced applications metal-oxide gas sensors need to be carefully prepared and characterized in laboratory environments prior to deployment”. While this is theoretically correct, it remains difficult to carry out laboratory treatments from −41 to 27 ∘C as would be required for our Arctic site. The data we present indicate that it is most likely absolute humidity (or specific humidity or mixing ratio), not relative humidity, that should be used for such calibrations, which in principle should provide the best quality results if the relevant factors are known and can be included in the calibration setup. Ideally, manufacturers should carry out both laboratory tests and field trials and provide the necessary correction functions together with sensors. However, due to the expense and time it takes to carry out long tests, be it in the laboratory or in the field, the present development goes in the direction of collocation studies (Piedrahita et al., 2014) en route to certification of sensors (Nick Martin, NPL, UK, personal communication, 2020), similar to what we have done in the Arctic.
The TGS 2600 sensor's best performance is in applications where passive samplers would be another option (see also Eugster and Kling, 2012). Contrastingly, using the TGS 2600 for short-term measurements (resolution of seconds to minutes) has not yet led to satisfactory results (Kirsch, 2012; Falabella et al., 2018). In our dataset we found that adding wind speed to the empirical linear model slightly improved the model fit during the warm season, but because no reliable continuous winter wind speed measurements were possible at the TWE site we did not include wind speed in our Eq. (2). However, this may be a key component for understanding the variability of TGS 2600 measurements when flying an unmanned aerial vehicle (UAV) where turbulent conditions may change within seconds to minutes. To address this additional factor, we used the heat loss model given in Eq. (3). However, although this approach is more mechanistic than Eq. (2), it was much less able to predict CH4 mole fraction from TGS 2600 measurements than the empirical linear model and ANN approaches (Table 1). But in order to make further progress on improving the transfer function from TGS 2600 signals to defensible CH4 mole fractions it will be essential to increase our understanding of the physical processes that influence such measurements. This is not an easy task since there is substantial proprietary knowledge that the manufacturer has not revealed. Newer, promising developments are underway that work with a mixed-potential sensor using tin-doped indium oxide and platinum electrodes in combination with yttria-stabilized zirconia electrolytes that show a logarithmic signal range of 0–10 mV for the 1–3 µmol mol−1 CH4 range of interest for ambient air studies (Sekhar et al., 2016). The basic principle that the active metal oxide is charged with O2 (or O2−), which then oxidizes CH4, seems to be similar to the SnO2-based TGS 2600; thus there is a good chance that our findings for the TGS 2600 are also useful for assessing the performance of newer solid-state sensors with different active materials.
We present the first long-term deployment of two identical, low-cost TGS 2600 sensors that show a sensitivity to ambient levels of CH4 (here: range of 1.824–2.682 µmol mol−1 as measured by a high-quality Los Gatos Research reference instrument). We suggest a new transfer function to correct the TGS 2600 signal for cross-sensitivity to ambient temperature and humidity that also yields satisfactory results under cold climate (Arctic) conditions with temperatures down to −40 ∘C. This was only possible by using absolute humidity and not relative humidity for the correction. With this correction determined over the entire 2012–2018 data period, the 30 min average CH4 mole fraction could be derived from TGS 2600 measurements within ±0.1 µmol mol−1. The two completely different regimes of diel CH4 mole fraction variations during the cold season (typically with a snow cover and frozen surface waters) and the warm season (when plants are active in the low Arctic) suggest that further improvements can be obtained by more specifically developing separate transfer functions for cold and warm conditions.
We consider the quality of TGS 2600-derived CH4 estimates adequate if aggregated over reasonable periods (e.g., days or one week), but caution should be taken with application where short-term response is of key relevance (e.g., within seconds to minutes as required for mobile measurements with UAVs). The deterioration of the sensor signal over time indicates that a TGS 2600 that is operated under ambient conditions as in our deployment at a low-Arctic site in northern Alaska (Toolik wet sedge site) has an estimated lifetime of ca. 10–13 years. Thus, there is potential beyond preliminary studies if the TGS 2600 sensor is adequately calibrated and placed in a suitable environment where cross-sensitivities to gases other than CH4 are of no concern.
The data used in this study can be downloaded from the Environmental Data Initiative (EDI) portal via https://doi.org/10.6073/pasta/dddeb05b2806e2f5788fadd6fc590ef1 (Eugster et al., 2020). The statistical fits shown in Figs. 5–8 are made available via the ETH Zurich Research Collection: https://doi.org/10.3929/ethz-b-000369689 (Eugster and Eugster, 2020).
WE, JL, and GWK designed the study, set up the instrumentation, and serviced the site. WE carried out the main analyses. JE helped with the main analyses as well as set up and carried out the ANN calculations. WE wrote the manuscript, and all coauthors worked, commented, and revised various versions.
The authors declare that they have no conflict of interest.
The authors are independent from the producers of the instruments and sensors referenced in this article, and thus the authors do not have a commercial interest in promoting any of the mentioned products.
We thank Jeb Timm, Colin Edgar, and other members of the Toolik Field Station science support staff for field help under difficult conditions. We also thank support staff from CPS for help with power supplies in addition to the technicians and students supported by several NSF grants and several students supported by the NSF-REU program for help in the field over the years.
We acknowledge support received from Arctic LTER grants (grant nos. NSF-DEB-1637459, 1026843, 1754835, and NSF-PLR 1504006) and supplemental funding from the NSF-NEON and OPP-AON programs. Gaius R. Shaver (MBL) is acknowledged for initiating the study and supporting our activities in all aspects. ETH is acknowledge for supporting the purchase of the Fast Greenhouse Gas Analyzer that replaced the older Fast Methane Analyzer in 2016 (grant no. 0-43683-11).
We thank the two anonymous reviewers for their careful and helpful assessments.
This paper was edited by Huilin Chen and reviewed by two anonymous referees.
Aghagoli, Z. and Ardyanian, M.: Synthesis and study of the structure, magnetic, optical and methane gas sensing properties of cobalt doped zinc oxide microstructures, J. Mater. Sci., 29, 7130–7141, https://doi.org/10.1007/s10854-018-8701-4, 2018. a
Akritas, M. G., Murphy, S. A., and Lavalley, M. P.: The Theil-Sen estimator with doubly censored data and applications to astronomy, J. Am. Stat. Assoc., 90, 170–177, https://doi.org/10.1080/01621459.1995.10476499, 1995. a
Casey, J. G., Collier-Oxandale, A., and Hannigan, M.: Performance of artificial neural networks and linear models to quantify 4 trace gas species in an oil and gas production region with low-cost sensors, Sensor. Actuat. B-Chem., 283, 504–514, https://doi.org/10.1016/j.snb.2018.12.049, 2019. a, b, c
Castell, N., Dauge, F. R., Schneider, P., Vogt, M., Lerner, U., Fishbain, B., Broday, D., and Bartonova, A.: Can commercial low-cost sensor platforms contribute to air quality monitoring and exposure estimates?, Environ. Int., 99, 293–302, https://doi.org/10.1016/j.envint.2016.12.007, 2017. a
Collier-Oxandale, A., Casey, J. G., Piedrahita, R., Ortega, J., Halliday, H., Johnston, J., and Hannigan, M. P.: Assessing a low-cost methane sensor quantification system for use in complex rural and urban environments, Atmos. Meas. Tech., 11, 3569–3594, https://doi.org/10.5194/amt-11-3569-2018, 2018. a, b
Eugster, W. and Eugster, J.: Statistical fits shown in Figs. 5–8, ETH Zürich, https://doi.org/10.3929/ethz-b-000369689, 2020. a
Eugster, W. and Kling, G. W.: Performance of a low-cost methane sensor for ambient concentration measurements in preliminary studies, Atmos. Meas. Tech., 5, 1925–1934, https://doi.org/10.5194/amt-5-1925-2012, 2012. a, b, c, d, e, f, g, h, i, j, k, l, m
Eugster, W., Kling, G., and Laundre, J.: Climate data from Arctic LTER Toolik Inlet Wet Sedge site, Toolik Field Station, Alaska 2012 to 2018, ver 1, Environmental Data Initiative, https://doi.org/10.6073/pasta/dddeb05b2806e2f5788fadd6fc590ef1, 2020. a
Falabella, A. D., Wallin, D. O., and Lund, J. A.: Application of a customizable sensor platform to detection of atmospheric gases by UAS, in: 2018 International Conference on Unmanned Aircraft Systems (ICUAS), IEEE, https://doi.org/10.1109/icuas.2018.8453480, 2018. a, b, c
Figaro: TGS 2600 – for the detection of air contaminants, Online product data sheet, Rev. 01/05, available at: http://www.figarosensor.com/product/docs/TGS2600B00% 20% 280913% 29.pdf (last access: 29 September 2019), 2005a. a, b, c, d, e, f, g, h, i
Figaro: Technical information on usage of TGS sensors for toxic and explosive gas leak detectors, Online product information sheet, Rev. 03/05, available at: https://www.electronicaembajadores.com/datos/pdf2/ss/ssga/tgs.pdf (last access: 29 September 2019), 2005b. a, b, c, d, e, f, g
Figaro: TGS 2611 – for the detection of methane, Online product data sheet, Rev. 10/13, available at: http://www.figarosensor.com/products/docs/TGS% 202611C00% 281013% 29.pdf (last access: 29 September 2019), 2013. a
Godbout, S., Phillips, V. R., and Sneath, R. W.: Passive flux samplers to measure nitrous oxide and methane emissions from agricultural sources, Part 1: Adsorbent selection, Biosyst. Eng., 94, 587–596, https://doi.org/10.1016/j.biosystemseng.2006.04.014, 2006a. a
Godbout, S., Phillips, V. R., and Sneath, R. W.: Passive flux samplers to measure nitrous oxide and methane emissions from agricultural sources, Part 2: Desorption improvements, Biosyst. Eng., 95, 1–6, https://doi.org/10.1016/j.biosystemseng.2006.05.007, 2006b. a
Hartmann, D. L., Tank, A. M. K., Rusticucci, M., Alexander, L., Broennimann, S., Charabi, Y. A.-R., Dentener, F., Dlugokencky, E., Easterling, D., Kaplan, A., Soden, B., Thorne, P., Wild, M., and Zhai, P.: Observations: Atmosphere and Surface, chap. 2, IPCC AR5, Cambridge University Press, Cambridge, UK and New York, NY, USA, 2014. a
Hobbie, J. E. and Kling, G. W. (Eds.): Alaska's Changing Arctic: Ecological Consequences for Tundra, Streams, and Lakes, Long-Term Ecological Research (LTER) Network Series, Oxford University Press, New York, USA, 331 pp., 2014. a
Hu, J., Gao, F., Zhao, Z., Sang, S., Li, P., Zhang, W., Zhou, X., and Chen, Y.: Synthesis and characterization of Cobalt-doped ZnO microstructures for methane gas sensing, Appl. Surf. Sci., 363, 181–188, https://doi.org/10.1016/j.apsusc.2015.12.024, 2016. a, b, c
Kirsch, O.: Entwicklung, Bau und Einsatz einer autonomen Drohne zur Messung von Gaskonzentrationen in der Luft, Maturarbeit mit beteiligung am wettbewerb schweizer jugend forscht, Kantonsschule Chur, Chur, Switzerland, 17 pp., 2012. a
Kneer, J., Eberhardt, A., Walden, P., Pérez, A. O., Wöllenstein, J., and Palzer, S.: Apparatus to characterize gas sensor response under real-world conditions in the lab, Rev. Sci. Instr., 85, 055006, https://doi.org/10.1063/1.4878717, 2014. a
Lewis, A. C., von Schneidemesser, E., and Peltier, R.: Low-cost sensors for the measurement of atmospheric composition: overview of topic and future applications, Tech. Rep. WMO-No. 1215, WMO, Geneva, Switzerland, available at: http://www.wmo.int/pages/prog/arep/gaw/documents/Low_cost_sensors_post_review_final.pdf (last access: 24 February 2019), 2018. a, b, c
Marchetto, A., Rogora, M., and Arisci, S.: Trend analysis of atmospheric deposition data: A comparison of statistical approaches, Atmos. Environ., 64, 95–102, https://doi.org/10.1016/j.atmosenv.2012.08.020, 2013. a
Nisbet, E. G., Dlugokencky, E. J., and Bousquet, P.: Methane on the rise – again, Science, 343, 493–495, https://doi.org/10.1126/science.1247828, 2014. a
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., Vanderplas, J., Passos, A., Cournapeau, D., Brucher, M., Perrot, M., and Duchesnay, É.: Scikit-learn: machine learning in Python, J. Mach. Learning Res., 12, 2825–2830, 2011. a
Piedrahita, R., Xiang, Y., Masson, N., Ortega, J., Collier, A., Jiang, Y., Li, K., Dick, R. P., Lv, Q., Hannigan, M., and Shang, L.: The next generation of low-cost personal air quality sensors for quantitative exposure monitoring, Atmos. Meas. Tech., 7, 3325–3336, https://doi.org/10.5194/amt-7-3325-2014, 2014. a
R Core Team: R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, available at: https://www.R-project.org/ (last access: 14 May 2020), 2018. a
Sekhar, P. K., Kysar, J., Brosha, E. L., and Kreller, C. R.: Development and testing of an electrochemical methane sensor, Sensor. Actuat. B-Chem., 228, 162–167, https://doi.org/10.1016/j.snb.2015.12.100, 2016. a
Shamasunder, B., Collier-Oxandale, A., Blickley, J., Sadd, J., Chan, M., Navarro, S., Hannigan, M., and Wong, N.: Community-Based Health and Exposure Study around Urban Oil Developments in South Los Angeles, Int. J. Env. Res. Pub. He., 15, 138, https://doi.org/10.3390/ijerph15010138, 2018. a
Thanh Duc, N., Silverstein, S., Wik, M., Crill, P., Bastviken, D., and Varner, R. K.: Greenhouse gas flux studies: An automated online system for gas emission measurements in aquatic environments, Hydrol. Earth Syst. Sci. Discuss., https://doi.org/10.5194/hess-2019-83, in review, 2019. a
van den Bossche, M., Rose, N. T., and De Wekker, S. F. J.: Potential of a low-cost gas sensor for atmospheric methane monitoring, Sensor. Actuat. B-Chem., 238, 501–509, https://doi.org/10.1016/j.snb.2016.07.092, 2017. a, b
Walker, D. A. and Everett, K. R.: Loess Ecosystems of Northern Alaska: Regional Gradient and Toposequence at Prudhoe Bay, Ecol. Monogr., 61, 437–464, 1991. a
WMO: Global Atmosphere Watch Measurements Guide, Tech. Rep. TD No. 1073, World Meteorological Organisation, available at: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.360.4587&rep=rep1&type=pdf (last access: 14 May 2020), 87 pp., 2001. a