the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Photophoretic spectroscopy in atmospheric chemistry – high-sensitivity measurements of light absorption by a single particle
Nir Bluvshtein
Ulrich K. Krieger
Thomas Peter
Light-absorbing organic atmospheric particles, termed brown carbon, undergo chemical and photochemical aging processes during their lifetime in the atmosphere. The role these particles play in the global radiative balance and in the climate system is still uncertain. To better quantify their radiative forcing due to aerosol–radiation interactions, we need to improve process-level understanding of aging processes, which lead to either “browning” or “bleaching” of organic aerosols. Currently available laboratory techniques aim to simulate atmospheric aerosol aging and measure the evolving light absorption, but they suffer from low sensitivity and precision. This study describes the use of electrodynamic balance photophoretic spectroscopy (EDB-PPS) for high-sensitivity and high-precision measurements of light absorption by a single particle. We demonstrate the retrieval of the time-evolving imaginary part of the refractive index for a single levitated particle in the range of 10−4 to 10−5 with uncertainties of less than 25 % and 60 %, respectively. The experimental system is housed within an environmental chamber, in which aging processes can be simulated in realistic atmospheric conditions and lifetimes of days to weeks. This high level of sensitivity enables future studies to explore the major processes responsible for formation and degradation of brown carbon aerosols.
Most radiative transfer schemes in climate models treat organic aerosol, a major subset of atmospheric aerosols that comprise 20 %–90 % of the total particulate mass (Kanakidou et al., 2005; Zhang et al., 2007), as non-absorbing in the UV–vis wavelength range, attributing them with a negative (cooling) radiative effect. However, light-absorbing organic aerosol, termed brown carbon (BrC), with wavelength-dependent light absorption () in the UV–vis wavelength range (Chen and Bond, 2010; Hoffer et al., 2004; Kaskaoutis et al., 2007; Kirchstetter et al., 2004; Lack et al., 2012b; Moosmuller et al., 2011; Sun et al., 2007), may be the dominant light absorber downwind of urban and industrialized areas and in biomass burning plumes (Feng et al., 2013). Recently, it has been shown that including BrC absorption properties in radiative transfer models leads to a stronger wavelength dependency of light absorption by aerosols and to significant changes in the overall effective radiative forcing from aerosol–radiation interactions (ERFari) (Feng et al., 2013; Lack and Cappa, 2010). Atmospheric aging processes of organic aerosol can lead, through complex mechanisms, to formation of light-absorbing compounds (“browning”) or to their degradation (“bleaching”). The accurate characterization of these processes is one of the main open questions in atmospheric chemistry research and has been the focus of many recent studies (see Laskin et al., 2015, for a review). Although significant advances have been made, the contribution of BrC to anthropogenic radiative forcing still poses significant uncertainty. The estimated ERFari attributed to BrC is 0.1 to 0.25 W m−2, offsetting 10 % to 25 % of the global mean aerosol cooling effect ( W m−2) (Bond et al., 2013; Brown et al., 2018; Feng et al., 2013; Myhre et al., 2013). On a regional scale surrounding megacities and industrial areas, this value may be up to an order of magnitude higher (Feng et al., 2013), which nearly doubles the local warming effect caused by the increase in the CO2 concentration. For this reason, it is imperative to (i) better understand the formation and degradation of BrC aerosols resulting from chemical and photochemical aging processes (Dasari et al., 2019; Drozd and McNeill, 2014; Hems and Abbatt, 2018; Lambe et al., 2013; Lee et al., 2013, 2014; Marrero-Ortiz et al., 2019; Powelson et al., 2014; Romonosky et al., 2015; Saleh et al., 2014; Schnitzler and Abbatt, 2018; Zhao et al., 2015; Zheng et al., 2013), (ii) quantify the BrC wavelength-dependent light absorption, and (iii) identify the main molecular species responsible for this absorption.
Laboratory studies simulating BrC formation and degradation mechanisms generally take one of two approaches to quantify wavelength-dependent light absorption in the UV–vis wavelength range, which is described using the imaginary part (κ) of the complex refractive index (CRI; ). The first approach uses bulk liquid phase or gas–liquid multiphase experiments to simulate atmospheric chemical processes. This is then followed by UV–vis spectroscopy absorption measurements (Nguyen et al., 2012; Nozière et al., 2010; Nozière and Córdova, 2008; Updyke et al., 2012). The advantages are high sample volume available for analysis and the extremely high sensitivity of UV–vis absorption spectroscopy. The disadvantage is that supersaturated conditions often encountered in atmospheric aerosol particles are impossible to generate in a bulk volume. This is an important disadvantage of the bulk approach as chemical activity, viscosity, and diffusivity under supersaturated conditions may alter the chemical aging significantly.
The second approach uses an environmental chamber, reactor, or flow tube to reproduce atmospheric processes. In this context, particles are generated by aerosolization into the experimental volume or by gas-phase chemistry leading to reduced volatility of precursor compounds with subsequent gas-to-particle conversion. These aerosols are then subjected to chemical or physical aging processes using radiation, relative humidity, and reactive gaseous components. The aged material may then be collected on filter substrates, extracted with a liquid solvent, and analyzed by UV–vis spectroscopy. Alternatively, aerosols may be measured with a suite of particle-ensemble, flow-through optical methods, such as cavity-enhanced and photoacoustic spectroscopy, for both direct and indirect measurements of light absorption (Flores et al., 2014a, b; He et al., 2018; Nakayama et al., 2013). To maintain particle size and concentration high enough for analysis using these techniques and to simulate atmospheric exposure of up to several days, precursor concentrations often far exceed those of the ambient atmosphere. This difference in environment between the reactor and the real atmosphere may affect the final distribution of products after multi-generation chemical aging, which may lead to misleading interpretations of the experimental results. An advantage of the optical instruments compared with the filter extraction techniques is the independence from solubility, extraction efficiency, and solvent matrix effects. Additionally, particles are measured in situ and with higher time resolution. Disadvantages are the relatively low sensitivity to absorption and, for some instruments, the frequent need for calibration (Lack et al., 2012a). As a result, κ for BrC aerosols is often reported with values near the limit of quantification of the retrieval technique or actually conflicts with results from analyses of similar chemical systems (Liu et al., 2013, 2012; Nakayama et al., 2013; Ofner et al., 2011) and with uncertainties that can exceed 100 % (Bluvshtein et al., 2016; Flores et al., 2014a, b; He et al., 2018; Lack et al., 2012b; Lavi et al., 2013; Nakayama et al., 2010, 2013; Trainic et al., 2011; Washenfelder et al., 2013).
To make significant progress, reduce uncertainties, and resolve contradictions, this study aims to extend the approach of electrodynamic balance photophoretic spectroscopy (EDB-PPS) for high-sensitivity and high-precision measurements of UV–vis light absorption by a single particle, in an environmental chamber, exposed to realistic atmospheric aging processes.
Photophoresis describes the optical forces acting on an illuminated particle. Direct photophoresis (or “radiation pressure” force, Frp), always in the direction of light propagation (away from the light source), and indirect photophoresis (Fph), a less recognized force, central to this work, that strongly depends on the absorption of light. Unlike radiation pressure, indirect photophoresis is a result of an uneven temperature distribution on the surface of the particle resulting from absorption. It acts through momentum transfer with the surrounding gas molecules, and thereby it is temperature and pressure dependent. To resolve the direction (away from or towards the light source) and the magnitude of the indirect photophoresis force, one needs to determine the internal electric field distribution (Bohren, 1983; Mackowski, 1989). Pope et al. (1979) and Arnold et al. (1980) conceived the idea of PPS on a single levitated particle and described the spectrally dependent ratio of the measured photophoretic force to the gravitational force on the particle. Building upon their seminal work with the following developments in the mathematical description of indirect photophoresis (Beresnev et al., 1992; Mackowski, 1989; Rohatschek, 1995), computational advances in Mie theory, and internal field calculation (Mackowski and Mishchenko, 2011), we extend the use of PPS. Here we describe how PPS can be used for high-sensitivity retrieval of the imaginary part of the refractive index of organic aerosol proxy particles levitated in an environmental chamber EDB and subject to aging processes. The EDB is a well-established tool in atmospheric science, used for the study of thermodynamic and chemical properties of single levitated particles (Krieger et al., 2000; Steimer et al., 2015; Tang and Munkelwitz, 1994; Zardini et al., 2008). Its high sensitivity to changes in the net vertical force acting on the particle makes it ideal for measurements of photophoresis, i.e., the miniscule optical forces acting on the levitated particle as a result of its interaction with light. With this approach we gain from combining the advantage of light absorption sensitivity nearing that of bulk UV–vis measurements with the advantage of studying chemical processes in the particle phase (accessible supersaturated conditions) in an environmental chamber able to simulate a wide range of atmospheric conditions. This could contribute to the study of light absorption evolution during atmospheric aging of BrC aerosols.
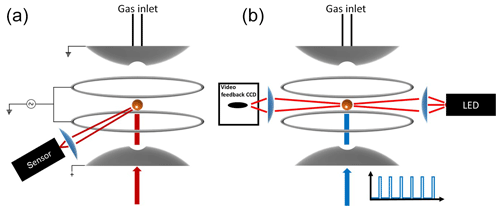
Figure 1Schematic diagram of the experimental setup. (a) Measurement of high-resolution elastic light scattering at 90∘ by illuminating the particle with a 765–781 nm TDL. (b) Continuous illumination of the particle with a red light-emitting diode (LED) used for the active feedback adjustment of the DC voltage and alternating illumination with the 473 nm laser used to impose vertical optical forces on the particle.
2.1 Electrodynamic balance
Over 100 years ago Robert Millikan and Harvey Fletcher, in their famous oil drop experiment, showed that tuning the electric potential between two capacitor plates, required to levitate a charged particle, can be used as a balance with a sensitivity of about 10−13 g. Today, the electrodynamic balance (EDB) is an established tool used to derive thermodynamic and physical information of a single, levitated particle. The EDB used in this study (Fig. 1) is based on the double-ring design characterized by Davis et al. (1990) and described in previous publications (Colberg et al., 2004; Steimer et al., 2015). Only a brief description follows. The EDB is hosted within a 180 cm3 environmental chamber, which allows temperature and pressure regulation with precision of ±0.02 K and ±2 hPa. Mass flow controllers are used to regulate gas flow rate and composition to 5 cm3 min−1 of dry N2. A single-droplet generator (Hewlett-Packard 51633A ink jet cartridge) is used to inject an electrically charged diluted aqueous solution of the sample material to the center of the trap. After complete loss of water, the resulting particle (typically 7–13 µm in radius) is balanced by a DC voltage that is regulated with a 25 Hz automated video feedback loop. The DC voltage (U) that is applied between the EDB endcap electrodes, to hold the particle in the center of the trap, is proportional to the net vertical force acting on the particle. A sensitivity on the applied DC voltage as low as 0.01 % is equivalent to changes in mass in the range of 10−13 to 10−12 g depending on the particle's size and density. This is commonly used to measure small changes in particle mass due to loss or uptake of gaseous components by the particle (Steimer et al., 2015; Tang and Munkelwitz, 1994; Zardini et al., 2008). In this study, we alternately illuminate a suspended particle with a 473 nm, 33 mW mm−2 (±15 %) diode laser (Laser Quantum, gem 473) at 25 % duty 40 s cycles (Fig. 1b). Variations in the DC voltage from “laser off” to “laser on” (Fig. 2, ΔU∕U0) in each cycle were used to measure changes in the net vertical force induced by illumination of the particle:
Here, Fph and Frp are the indirect photophoretic and radiation pressure forces. The subscripts “on” and “off” relate to the light source. Gravity (Fg) and Stokes drag (Fs) caused by the gas flow are constant at the timescale of the measurement, and are given by
where a and ρp are radius and mass density of the levitated particle, g is the standard acceleration due to gravity, η is the gas dynamic viscosity, qv is volumetric flow rate, S is a characteristic flow cross section, and Cc is the Cunningham slip correction factor (Kim et al., 2005). This formulation enables the direct measurement of the sum of the optical forces (Fph+Frp), which are related to the particle size and CRI. After determining the particle size and the real part of the refractive index n (Sect. 2.2.), the sum Fph+Frp is iteratively calculated by varying κ to minimize the difference between the measured and calculated ΔU∕U0.
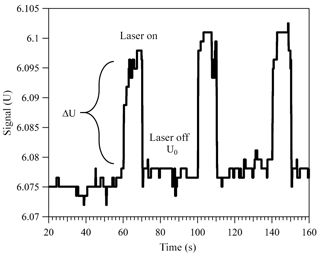
Figure 2Change in the applied DC voltage in response to alternately illuminating a trapped light-absorbing particle. Here, a particle with 12.72 µm radius and was levitated in 400 mbar of dry nitrogen. For more details on how the particle size and imaginary part of the CRI were determined, refer to Sects. 2.2 and 3.
The following section describes how the particle size and real refractive index are determined from high-resolution light-scattering measurements, and Sect. 2.3 describes how Fph+Frp is finally calculated and used to retrieve the imaginary part of the CRI.
2.2 Determination of size and real refractive index
Mie resonance spectroscopy is used to simultaneously retrieve the particle's radius (a) and real part (n) of the CRI defined as
and
Here, n(λ) is the wavelength-dependent real refractive index, nD is the refractive index at the sodium D line, m1 is a dispersion coefficient, and x is the size parameter. Polynomial regression parameters between the refractive index and size parameter of transverse electric (TE) and transverse magnetic (TM) mode resonances were calculated (Lam et al., 1992; Preston and Reid, 2013, 2015) and a look-up table of these parameters was generated for all possible TE and TM resonances with order numbers of 3 to 8 and mode numbers of 26 to 180. We obtained high-resolution spectra by illuminating the levitated particle with a tunable diode laser at both parallel and perpendicular linear polarizations (tunable diode laser – TDL, New Focus, model Velocity 6312) in the range λ=765–781 nm and recording the elastic light scattering at a π∕2 angle (Steimer et al., 2015) (Figs. 1a, 4). Then, a, nD, and m1 are retrieved by minimizing the sum of absolute values of the differences between measured and calculated wavelengths of the Mie resonances over the three-dimensional parameter space.
2.3 Photophoretic spectroscopy
Direct photophoresis or radiation pressure is readily calculated from
where I is the radiant flux density (W m−2) and c is the speed of light. Qext and Qbs are Mie extinction and backscattering efficiencies (unitless). We use the Mie MATLAB functions developed by Mätzler (2002) to calculate the efficiencies.
Indirect photophoresis (Fph) is directed away from the light source for a highly absorbing particle (positive photophoresis) but towards the light source for low absorptivity (negative photophoresis). This is a result of the structure of the internal electric field within a spherical particle interacting with radiation. Multiple refractions and internal reflections lead to size-dependent, nano-focusing of the incident beam within the particle volume. For particles larger than the wavelength of the incident light, the energy is “focused” closer to the non-illuminated side of the particle. In highly absorbing particles, however, most of the energy is absorbed by the illuminated hemisphere of the particle, heating it more than the “dark” hemisphere. Therefore, a key parameter determining the direction and amplitude of Fph is the temperature asymmetry parameter (J), resulting from the uneven internal electric field and, consequently, uneven temperature distribution (Yalamov et al., 1976). To calculate J, one can use an integration of the source function over the particle volume:
Here B(t,μ) is the dimensionless electric field distribution inside the particle, and t (fraction of a) and μ=cosθ are the spherical coordinates. Simply put, J indirectly describes the temperature gradient between the illuminated and the dark side of the particle surface.
Unlike radiation pressure, Fph acts through the presence of gas molecules around the illuminated particle. Impaction and reflection of the surrounding gas molecules, and consequent momentum transfer with the particle's surface, are temperature dependent and thus lead to a net force directed from the warmer to the colder particle hemisphere. Indirect photophoresis is also strongly pressure (p) dependent. It reaches its maximum value at pressures where the Knudsen number () is around unity, i.e., where the gas mean free path (L) is comparable to the radius of the particle (a). In the free molecular regime, i.e., Kn ≫1, Fph is proportional to p, whereas in the continuum regime, i.e., Kn≪1, Fph is inversely proportional to p. Rohatschek (1995) provided a pressure-dependent model of Fph interpolating previous formulations at the two pressure regime limits. His approach provides a convenient estimate of Fph between the free molecular and continuum limits:
with
where αT is the thermal accommodation coefficient, kp is the particle thermal conductivity, and T is the gas temperature away from the particle surface. Further, D relates to gas phase parameters as follows:
where Cs is the thermal slip coefficient and is the mean thermal velocity of the gas molecules
in which R is the gas constant and M is the gas molar mass.
Our experimental setup (particle radius of 7–13 µm and pressure range of 400–800 hPa) is limited to Kn=0.0075–0.03. We are therefore constrained to a transition flow regime referred to as the slip-flow regime (typically 10−2 < Kn < 10−1), where Fph deviates significantly from Rohatschek's interpolation. Mackowski (1989) presented an analytical solution of the spherical geometry heat conduction equation in three dimensions for calculating Fph in the slip-flow regime by adding a tangential velocity slip boundary condition (also referred to as thermal stress slip flow) to the continuum regime solution of Yalamov et al. (1976):
The momentum exchange coefficient is taken as (Reed, 1977), while the thermal slip (Cs) (Ivchenko et al., 1993) and temperature jump (Ct) (Loyalka, 1968) coefficients
are functions of the thermal accommodation coefficient αT. Here we used a value of to accommodate a range of values published for a variety of materials (Ganta et al., 2011; Li et al., 2001; Shaw and Lamb, 1999; Trott et al., 2007). It was shown that with increased absorption (i.e., steep interface temperature jump) or decreasing particle size, Eq. (14) deviates from experimental measurements (Mackowski, 1989; Soong et al., 2010). A solution to this problem was presented by Soong et al. (2010), who adopted a modified slip boundary condition from Lockerby et al. (2004). The authors developed the following correction to Mackowski's solution:
From Eq. (16) it is clear that at Kn≪1 the correction factor approaches unity. For the purpose of this study, i.e., low absorptivity particles and Kn=0.0075–0.03, the correction is small, but we nevertheless apply it in our evaluation and term the corrected photophoretic force hereafter Fph.
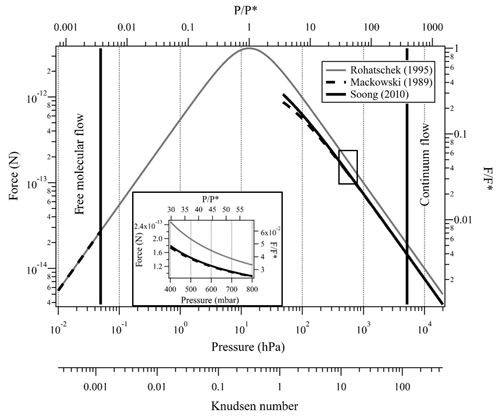
Figure 3Indirect photophoretic force calculated with the Rohatschek (1995) approximation at the full pressure range (gray line), Mackowski (1989) analytical solution (dashed line), and Soong et al. (2010) correction (solid line) for a slightly absorbing particle with radius of 10 µm, T=20 ∘C, , λ=473 nm, I=35 mW mm−2 and full thermal accommodation. The black rectangle and the insert plot show the pressure range that is possible with our experimental system.
As mentioned above, J is the key parameter linking the particle's CRI to Fph. Mackowski (1989) also presented an expression for J by analytical integration of Eq. (7):
where the coefficients CN, RN, SN, cN, and dN are
Here, and are the Mie coefficients for the internal field, computed using the MATLAB Mie routines by Mätzler (2002), and ΨN is the Ricatti–Bessel function of the order of N. For clarity, the prime denotes the differentiation with respect to the argument in brackets and the superscript * denotes the complex conjugate. Figure 3 shows Fph calculated with the above three models over a wide pressure range extending from the free molecular to the continuum flow regimes. From Eq. (13) and Fig. 3, one can show that Mackowski's formulation equals Rohatschek's solution at the continuum limit (i.e., Kn≪1) only for particles that are good heat conductors compared with the surrounding gas (i.e., ).
For applications involving slightly absorbing () micron-sized, organic particles, the indirect photophoretic force is generally 1–2 orders of magnitude larger than radiation pressure but about 2–3 orders of magnitude lower than gravity. High sensitivity and stability of the EDB is therefore imperative for high-sensitivity retrieval of κ from EDB-PPS measurement.
To test the methodology a slightly absorbing organic particle with known CRI and thermal properties is required. For this purpose, we selected PEG400 (polyethylene glycol with mean molecular weight of ≈400 g mol−1) as a proxy. PEG400 has the advantage of being an organic, non-volatile liquid, miscible with water (needed for injection of a droplet into the EDB). Additionally, PEG400 has well-characterized optical and thermodynamic properties (Francesconi et al., 2007; Han et al., 2008; Marcos et al., 2018; Reyes et al., 2000), which we assume to be unchanged by addition of 0.23 wt % (0.19 % mole) of carminic acid (CA, Sigma-Aldrich). The imaginary part of the refractive index for this PEG400-CA solution was determined with a simple Beer–Lambert setup composed of the 473 nm laser introduced in Sect. 2.1, a 1 mm cuvette, and a power meter and using the following relations (Sun et al., 2007):
where A is the optical attenuation or absorption of a bulk sample with an optical path length L and attenuation coefficient α at wavelength λ. Combining Eqs. (23) and (24) leads to
High viscosity of the PEG400 (105–130 mPa s at 293 K; Merck) leads to slight heterogeneity of the liquid in the cuvette. For this reason, we repeated these spectroscopic measurements with the laser beam (< 1 mm in diameter) crossing the cuvette at different positions on its surface. This led to the 3.6 % uncertainty in the value of κ stated above.
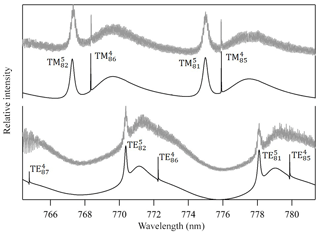
Figure 4Measured Mie scattering spectra at π∕2 angle of a levitated particle. The positions of the TE and TM resonance modes (e.g., TM; identified by their order (l) and mode (n) numbers) were used to retrieve the particle's real refractive index (nD=1.4665, m1=2745) and size (a=9.2906 µm). We note that the lower-order modes in the fitted TE spectrum are too narrow to be observed in the measured spectrum with the current resolution. Residual noise in the measured spectrum originates mostly from laser power oscillations due to frequency scanning operation and from horizontal oscillation of the particle due to the applied AC field.
A droplet with 3 % wt of the PEG400-CA solution in water was injected into the EDB under dry N2 flow as described in Sect. 2.1. Following size stabilization and water evaporation, high-resolution Mie resonance spectra were measured to determine the particle real part of the CRI (nD=1.4665, m1=2745) and size (a=9.2906 µm). Figure 4 shows the measured TE and TM mode spectra and the fitted resonance peaks along with their identification by order (l) and mode (n) numbers. Figure 5 shows the response of the EDB to changes in the net vertical force due to illumination of the levitated particle (ΔU∕U0) at different pressure values within the range of our experimental setup. Also shown in Fig. 5 is the response calculated using the three models described in Sect. 2.3. It is clear that both the Mackowski and the Soong formulations, which are barely distinguishable within the resolution of Fig. 5, fit the measured data very well, whereas the Rohatschek interpolation, which assumes and does not account for slip-flow conditions, overestimates the response. The error bars on the measured data represent the standard deviation over five illumination cycles and the gray shaded area represents the uncertainty propagated through the Soong model calculation. The major contributor to the latter is a 15 % uncertainty on the radiant flux, which is measured in our experiment with a power meter (nova-display, Ophir Optronics LTD) and a beam profiler (CMOS-1.001-Nano, CINOGY Technologies GmbH).
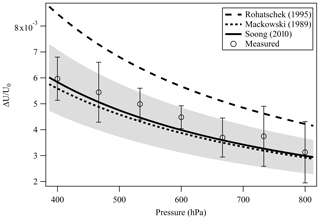
Figure 5Measured and simulated EDB response (ΔU∕U0) to the illumination of a slightly absorbing particle due to the photophoretic effect. The two analytical solutions Mackowski (1989) (dotted line) and Soong et al. (2010) (solid line) that account for slip-flow conditions agree well with our measurements (empty circles). Error bars: standard deviation over five illumination cycles. Gray shaded area: measurement uncertainty propagated through the Soong model calculation, dominated by the 15 % uncertainty on the radiant flux measured with a power meter and a beam profiler.
It is important to note that as expected, for a pure PEG400 particle (i.e., no measurable absorption at 473 nm) at similar conditions, but a slightly less sensitive setup, no signal could be detected.
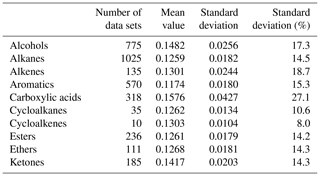
Table 1Thermal conductivity (W m−1 K−1) of organic compounds from Latini et al. (2014) and references therein.
To further demonstrate the potential of the EDB-PPS approach in determining the imaginary RI with high sensitivity and precision, an additional particle from the same PEG400-CA batch, with a radius of 12.858 µm was levitated and the response of the EDB to change in the net vertical force was recorded over about 16 h of illumination cycles. To take advantage of the inverse pressure dependence of the photophoretic effect, this experiment was conducted at 400 hPa, which is at the lower limit of our experimental setup. Figure 6 shows the measured ΔU∕U0 and the point-by-point retrieved κ, which decreases from about to about over the laser on time (i.e., 25 % of the total experiment time). Both traces demonstrate a decay feature as a result of slow photolysis of the CA (Jørgensen and Skibsted, 1991). The initial retrieved value is about 20 % lower than the value retrieved from the bulk cuvette experiment but with overlapping uncertainty range. The overall uncertainty in retrieved κ demonstrated in Fig. 6b is estimated to be up to 25 % for and up to 60 % for . The gray shaded area on the ΔU∕U0 plot (Fig. 6a) is the uncertainty in each ΔU∕U0 data point determined from the standard deviation on the value of U averaged during laser off and laser on stages of each individual illumination cycle. These experimental uncertainties, with values of (unitless) together with point-by-point variability of up to , are a result of the sum of system instabilities. These are independent of the value of ΔU∕U0 and are a significant component limiting the sensitivity to κ of this experimental approach. The experimental uncertainty contributes up to 10 % uncertainty on the value of the retrieved κ for values down to and about 30 % for . The uncertainty on the radiant flux used in the model calculation is the major limiting factor for the sensitivity of the experimental approach contributing about 15 % to the uncertainty of the retrieved κ down to .
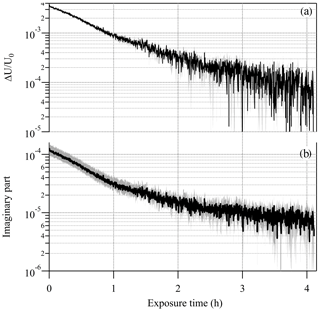
Figure 6(a) Decay of the EDB photophoretic response (ΔU∕U0) during illumination of a slightly absorbing particle (PEG400 with 0.23 % wt of carminic acid; CA). The decay is due to the slow photolysis of the CA. (b) The retrieved imaginary part of the complex refractive index. Gray shaded area in both plots represents the uncertainty in the measured and retrieved values.
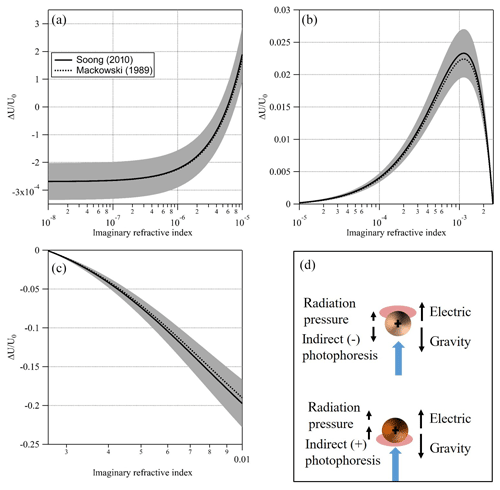
Figure 7Simulated signal (and uncertainty) for a PEG400 particle, 10 µm in radius at T=20 ∘C, P=400 mbar, nD=1.466, λ=473 nm, and I=35 mW mm−2 and full thermal accommodation with the increasing imaginary part of the CRI. (a) Transition from negligible absorptivity and negative signal (i.e., dominated by radiation pressure) to positive signal (i.e., dominated by negative indirect photophoresis). (b) Increasing absorptivity leads to an increasing positive asymmetry parameter and stronger positive signal (i.e., negative indirect photophoresis). Additional absorptivity leads to an asymmetry parameter of zero as the surfaces of the upper and lower hemispheres of the particle are effectively at equal temperature. (c) Additional increase in absorptivity leads to an increase in a negative asymmetry parameter and stronger positive indirect photophoresis. (d) An illustration of the positive and negative indirect photophoresis regimes. Black arrows represent the various forces acting on a “strongly” (lower) and “slightly” (upper) absorbing particle when illuminated with the laser beam (blue arrow).
We determine the overall sensitivity of this approach to the imaginary RI (within the limitation of our experimental setup) to be in the range of –. The accumulated uncertainty of κ from all other parameters in Eqs. (14) and (17) is below 10 % for κ down to . These include uncertainties in the particle size, real part of the CRI, density, and thermal properties. However, the major contributor to this uncertainty is the range of selected values of the thermal accommodation coefficient mentioned in Sect. 2.3. An uncertainty of 18 % on the thermal accommodation coefficient () propagates to 4 %–7 % uncertainty on the retrieved κ. This small contribution to the overall uncertainty demonstrates the usefulness of the EDB-PPS approach for the retrieval of the imaginary RI of organic particles with unknown composition following accurate Mie resonance spectroscopy (for determination of size and real RI) as long as assumptions of sphericity and homogeneity hold.
Additional potential source for uncertainty in case the particle is composed mostly of unknown or not well-characterized substances is the particle's thermal conductivity. A solution would be to consider that many organic compounds are very similar with respect to their thermal properties and use an approximated value with an appropriate uncertainty. Latini et al. (2014) published a literature survey of 4740 thermal conductivity data sets of organic compounds at atmospheric pressure and reduced temperature of about 0.6±0.14. A partial list of the data from this publication (excluding 1340 data sets of refrigerant compounds) is presented in Table 1. The list clearly shows the similarity in thermal conductivity for many organic compounds abundant in atmospheric aerosols.
This study demonstrates the usefulness of the electrodynamic balance – photophoretic spectroscopy (EDB-PPS) technique to retrieve the imaginary component of the complex refractive index of a slightly absorbing organic particle levitated in an environmental chamber. We showed agreement between measurements and model calculation and reliable retrieval of the imaginary RI at a wavelength of 473 nm, in the range of with uncertainty of about 25 % for and 60 % for . The major limiting factor for sensitivity and precision within our setup is the uncertainty in the radiant flux.
In this study, we chose to emphasize the usefulness of EDB-PPS at the lower range of κ due to availability of other, simpler to implement, particle phase techniques suitable for retrieval of higher values of κ. Nevertheless, EDB-PPS is not limited to . Figure 7 shows a simulated signal (ΔU∕U0) over 6 orders of magnitude of κ, from 10−8 to 10−2, for a PEG400-based particle with a radius of 10 µm. At the lower end of this range (left side of Fig. 7a) κ is effectively zero and the simulated signal is negative (i.e., the particle moves away from the light source) due to direct photophoresis (radiation pressure) alone. Note how, as κ increases, the signal increases to positive values (Fig. 7a and b) due to an increase in the thermal asymmetry parameter that results in negative indirect photophoresis. With additional increase in κ, more energy is absorbed on the illuminated side of the particle. This offsets the hot spot of absorbed energy on the surface of the dark side of the particle. As a result, the thermal asymmetry parameter and the magnitude of the signal are reduced. As κ continues to increase, the asymmetry parameter changes sign from positive to negative as the illuminated side of the particle becomes warmer than the dark side. This is shown in Fig. 7c as a negative signal and illustrated in Fig. 7d as the particle shifts from the regime described in the upper part of Fig. 7d to the one described by the lower part. Based on this simulation and on our system's sensitivity limitations, we determined the lower limit for retrieval of κ at 10−5 and do not determine an upper limit. We do however, note areas with high uncertainty, namely, around , where the change in signal flattens and around the point where the regime changes from negative to positive indirect photophoresis. The latter depends heavily on the particle size. An important caveat is the non-injective behavior observed in Fig. 7b were two values of κ could solve for the same signal. To address the issue one would need to have prior knowledge on the order of magnitude of the particle's absorption (for example, below or above ). Alternatively, in aging experiments, as κ evolves, the direction of the change of the signal would clarify the direction of the change of κ.
The range of environmental conditions allowed by the chamber are pressure of 400–800 hPa, RH of 0 %–90 %, and temperature of 200–300 K. This means that we can measure and understand heterogeneous chemistry and photochemical aging processes of a single particle in the full range of boundary layer conditions with atmospherically relevant gas concentration and residence time. The combination of high sensitivity and quantification level with the wide application range of the environmental chamber enables us to improve process level understanding of formation and degradation of BrC aerosols resulting from chemical and photochemical aging processes that is beyond the reach of previously available aerosol flow-through techniques.
This study laid the needed foundations for future development of a new methodology aimed to simultaneously measure the evolution of light absorption and the molecular composition of atmospheric aerosol proxies by coupling photophoretic spectroscopy to electrodynamic balance–soft ionization mass spectroscopy (EDB-MS) (Birdsall et al., 2018). This will lead to a step change in our understanding of how such particles evolve in the atmosphere by directly linking optical properties to chemical composition.
The data presented in this publication is available in the ETHZ Research Collection https://doi.org/10.3929/ethz-b-000419840 (Bluvshtein et al., 2020).
NB contributed by conceptualization, investigation, formal analysis, software development, methodology, and writing and preparation of the original draft. UKK also contributed to the conceptualization and methodology, supervision, and review and editing of the manuscript. TP contributed with review and editing of the manuscript.
The authors declare that they have no conflict of interest.
Nir Bluvshtein is grateful for support from the ETH Zurich Postdoctoral Fellowship program. The authors would like to thank Thomas C. Preston and collaborators for fruitful discussions on Mie resonance mode assignment and for making their scripts available for the community.
This research has been supported by the Swiss National Science Foundation (grant no. CRSK-2_190477).
This paper was edited by Mingjin Tang and reviewed by two anonymous referees.
Arnold, S., Amani, Y., and Orenstein, A.: Photophoretic spectrometer, Rev. Sci. Instrum., 51, 1202–1204, https://doi.org/10.1063/1.1136395, 1980.
Beresnev, S., Chernyak, V., and Fomyagin, G.: Photophoresis of a spherical particle in a rarefied gas, Phys. Fluid. A, 5, 2043–2052, https://doi.org/10.1063/1.858540, 1992.
Birdsall, A. W., Krieger, U. K., and Keutsch, F. N.: Electrodynamic balance–mass spectrometry of single particles as a new platform for atmospheric chemistry research, Atmos. Meas. Tech., 11, 33–47, https://doi.org/10.5194/amt-11-33-2018, 2018.
Bluvshtein, N., Flores, J. M., Segev, L., and Rudich, Y.: A new approach for retrieving the UV–vis optical properties of ambient aerosols, Atmos. Meas. Tech., 9, 3477–3490, https://doi.org/10.5194/amt-9-3477-2016, 2016.
Bluvshtein, N., Krieger, U., and Peter, T.: Photophoretic spectroscopy in atmospheric chemistry – high-sensitivity measurements of light absorption by a single particle, ETH Zurich, https://doi.org/10.3929/ethz-b-000419840, 2020.
Bohren, C. F.: Absorption and scattering of light by small particles, John Wiley & sons, INC, USA, 1983.
Bond, T. C., Doherty, S. J., Fahey, D. W., Forster, P. M., Berntsen, T., DeAngelo, B. J., Flanner, M. G., Ghan, S., Karcher, B., Koch, D., Kinne, S., Kondo, Y., Quinn, P. K., Sarofim, M. C., Schultz, M. G., Schulz, M., Venkataraman, C., Zhang, H., Zhang, S., Bellouin, N., Guttikunda, S. K., Hopke, P. K., Jacobson, M. Z., Kaiser, J. W., Klimont, Z., Lohmann, U., Schwarz, J. P., Shindell, D., Storelvmo, T., Warren, S. G., Zender, C. S., Kärcher, B., Koch, D., Kinne, S., Kondo, Y., Quinn, P. K., Sarofim, M. C., Schultz, M. G., Schulz, M., Venkataraman, C., Zhang, H., Zhang, S., Bellouin, N., Guttikunda, S. K., Hopke, P. K., Jacobson, M. Z., Kaiser, J. W., Klimont, Z., Lohmann, U., Schwarz, J. P., Shindell, D., Storelvmo, T., Warren, S. G., and Zender, C. S.: Bounding the role of black carbon in the climate system: A scientific assessment, J. Geophys. Res.-Atmos., 118, 5380–5552, https://doi.org/10.1002/jgrd.50171, 2013.
Brown, H., Liu, X., Feng, Y., Jiang, Y., Wu, M., Lu, Z., Wu, C., Murphy, S., and Pokhrel, R.: Radiative effect and climate impacts of brown carbon with the Community Atmosphere Model (CAM5), Atmos. Chem. Phys., 18, 17745–17768, https://doi.org/10.5194/acp-18-17745-2018, 2018.
Chen, Y. and Bond, T. C.: Light absorption by organic carbon from wood combustion, Atmos. Chem. Phys., 10, 1773–1787, https://doi.org/10.5194/acp-10-1773-2010, 2010.
Colberg, C. A., Krieger, U. K., and Peter, T.: Morphological Investigations of Single Levitated Aerosol Particles during Deliquescence/Efflorescence Experiments, J. Phys. Chem. A, 108, 2700–2709, https://doi.org/10.1021/jp037628r, 2004.
Dasari, S., Andersson, A., Bikkina, S., Holmstrand, H., Budhavant, K., Satheesh, S., Asmi, E., Kesti, J., Backman, J., Salam, A., Bisht, D. S., Tiwari, S., Hameed, Z., and Gustafsson, Ö.: Photochemical degradation affects the light absorption of water-soluble brown carbon in the South Asian outflow, Sci. Adv., 5, eaau8066, https://doi.org/10.1126/sciadv.aau8066, 2019.
Davis, E. J., Buehler, M. F., and Ward, T. L.: The double-ring electrodynamic balance for microparticle characterization, Rev. Sci. Instrum., 61, 1281–1288, https://doi.org/10.1063/1.1141227, 1990.
Drozd, G. T. and McNeill, V. F.: Organic matrix effects on the formation of light-absorbing compounds from α-dicarbonyls in aqueous salt solution, Environ. Sci.-Proc. Imp., 16, 741–747, https://doi.org/10.1039/C3EM00579H, 2014.
Feng, Y., Ramanathan, V., and Kotamarthi, V. R.: Brown carbon: a significant atmospheric absorber of solar radiation?, Atmos. Chem. Phys., 13, 8607–8621, https://doi.org/10.5194/acp-13-8607-2013, 2013.
Flores, J. M., Washenfelder, R. A., Adler, G., Lee, H. J., Segev, L., Laskin, J., Laskin, A., Nizkorodov, S. A., Brown, S. S., and Rudich, Y.: Complex refractive indices in the near-ultraviolet spectral region of biogenic secondary organic aerosol aged with ammonia, Phys. Chem. Chem. Phys., 16, 10629–10642, https://doi.org/10.1039/c4cp01009d, 2014a.
Flores, J. M., Zhao, D. F., Segev, L., Schlag, P., Kiendler-Scharr, A., Fuchs, H., Watne, Å. K., Bluvshtein, N., Mentel, Th. F., Hallquist, M., and Rudich, Y.: Evolution of the complex refractive index in the UV spectral region in ageing secondary organic aerosol, Atmos. Chem. Phys., 14, 5793–5806, https://doi.org/10.5194/acp-14-5793-2014, 2014b.
Francesconi, R., Bigi, A., Rubini, K., and Comelli, F.: Molar Heat Capacities, Densities, Viscosities, and Refractive Indices of Poly(ethylene glycols) + 2-Methyltetrahydrofuran at (293.15, 303.15, and 313.15) K, J. Chem. Eng. Data, 52, 2020–2025, https://doi.org/10.1021/je7003066, 2007.
Ganta, D., Dale, E. B., Rezac, J. P., and Rosenberger, A. T.: Optical method for measuring thermal accommodation coefficients using a whispering-gallery microresonator, J. Chem. Phys., 135, 084313, https://doi.org/10.1063/1.3631342, 2011.
Han, F., Zhang, J., Chen, G., and Wei, X.: Density, Viscosity, and Excess Properties for Aqueous Poly(ethylene glycol) Solutions from (298.15 to 323.15) K, J. Chem. Eng. Data, 53, 2598–2601, https://doi.org/10.1021/je800464t, 2008.
He, Q. F., Bluvshtein, N., Segev, L., Meidan, D., Flores, J. M., Brown, S. S., Brune, W., and Rudich, Y.: Evolution of the Complex Refractive Index of Secondary Organic Aerosols during Atmospheric Aging, Environ. Sci. Technol., 52, 3456–3465, https://doi.org/10.1021/acs.est.7b05742, 2018.
Hems, R. F. and Abbatt, J. P. D.: Aqueous Phase Photo-oxidation of Brown Carbon Nitrophenols: Reaction Kinetics, Mechanism, and Evolution of Light Absorption, ACS Earth Sp. Chem., 2, 225–234, https://doi.org/10.1021/acsearthspacechem.7b00123, 2018.
Hoffer, A., Kiss, G., Blazso, M., and Gelencser, A.: Chemical characterization of humic-like substances (HULIS) formed from a lignin-type precursor in model cloud water, Geophys. Res. Lett., 31, 3563–3570, https://doi.org/10.1029/2003gl018962, 2004.
Ivchenko, I. N., Loyalka, S. K., and Tompson, R. V.: A boundary model for the thermal creep problem, Fluid Dynam., 28, 876–878, https://doi.org/10.1007/BF01049795, 1993.
Jørgensen, K. and Skibsted, L. H.: Light sensitivity of cochineal. Quantum yields for photodegradation of carminic acid and conjugate bases in aqueous solution, Food Chem., 40, 25–34, https://doi.org/10.1016/0308-8146(91)90016-H, 1991.
Kanakidou, M., Seinfeld, J. H., Pandis, S. N., Barnes, I., Dentener, F. J., Facchini, M. C., Van Dingenen, R., Ervens, B., Nenes, A., Nielsen, C. J., Swietlicki, E., Putaud, J. P., Balkanski, Y., Fuzzi, S., Horth, J., Moortgat, G. K., Winterhalter, R., Myhre, C. E. L., Tsigaridis, K., Vignati, E., Stephanou, E. G., and Wilson, J.: Organic aerosol and global climate modelling: a review, Atmos. Chem. Phys., 5, 1053–1123, https://doi.org/10.5194/acp-5-1053-2005, 2005.
Kaskaoutis, D. G., Kambezidis, H. D., Hatzianastassiou, N., Kosmopoulos, P. G., and Badarinath, K. V. S.: Aerosol climatology: dependence of the Angstrom exponent on wavelength over four AERONET sites, Atmos. Chem. Phys. Discuss., 7, 7347–7397, https://doi.org/10.5194/acpd-7-7347-2007, 2007.
Kim, J. H., Mulholland, G. W., Kukuck, S. R., and Pui, D. Y. H.: Slip correction measurements of certified PSL nanoparticles using a nanometer differential mobility analyzer (Nano-DMA) for knudsen number from 0.5 to 83, J. Res. Natl. Inst. Stand., 110, 31–54, https://doi.org/10.6028/jres.110.005, 2005.
Kirchstetter, T. W., Novakov, T., and Hobbs, P. V: Evidence that the spectral dependence of light absorption by aerosols is affected by organic carbon, J. Geophys. Res., 109, D21208, https://doi.org/10.1029/2004jd004999, 2004.
Krieger, U. K., Colberg, C. A., Weers, U., Koop, T., and Peter, T.: Supercooling of single H2SO4∕H2O aerosols to 158 K: No evidence for the occurrence of the octrahydrate, Geophys. Res. Lett., 27, 2097–2100, https://doi.org/10.1029/2000GL011613, 2000.
Lack, D. A. and Cappa, C. D.: Impact of brown and clear carbon on light absorption enhancement, single scatter albedo and absorption wavelength dependence of black carbon, Atmos. Chem. Phys., 10, 4207–4220, https://doi.org/10.5194/acp-10-4207-2010, 2010.
Lack, D. A., Richardson, M. S., Law, D., Langridge, J. M., Cappa, C. D., McLaughlin, R. J., and Murphy, D. M.: Aircraft Instrument for Comprehensive Characterization of Aerosol Optical Properties, Part 2: Black and Brown Carbon Absorption and Absorption Enhancement Measured with Photo Acoustic Spectroscopy, Aerosol Sci. Technol., 46, 555–568, https://doi.org/10.1080/02786826.2011.645955, 2012a.
Lack, D. A., Langridge, J. M., Bahreini, R., Cappa, C. D., Middlebrook, A. M., and Schwarz, J. P.: Brown carbon and internal mixing in biomass burning particles, P. Natl. Acad. Sci. USA, 109, 14802–14807, https://doi.org/10.1073/pnas.1206575109, 2012b.
Lam, C. C., Leung, P. T., and Young, K.: Explicit asymptotic formulas for the positions, widths, and strengths of resonances in Mie scattering, J. Opt. Soc. Am. B, 9, 1585, https://doi.org/10.1364/josab.9.001585, 1992.
Lambe, A. T., Cappa, C. D., Massoli, P., Onasch, T. B., Forestieri, S. D., Martin, A. T., Cummings, M. J., Croasdale, D. R., Brune, W. H., Worsnop, D. R., and Davidovits, P.: Relationship between oxidation level and optical properties of secondary organic aerosol, Environ. Sci. Technol., 47, 6349–6357, https://doi.org/10.1021/es401043j, 2013.
Laskin, A., Laskin, J., and Nizkorodov, S. A.: Chemistry of Atmospheric Brown Carbon, Chem. Rev., 115, 4335–4382, https://doi.org/10.1021/cr5006167, 2015.
Latini, G., Di Nicola, G., and Pierantozzi, M.: A critical survey of thermal conductivity literature data for organic compounds at atmospheric pressure and an equation for aromatic compounds, in: Energy Procedia, 45, 616–625, Elsevier Ltd., 2014.
Lavi, A., Bluvshtein, N., Segre, E., Segev, L., Flores, M., and Rudich, Y.: Thermochemical, Cloud Condensation Nucleation Ability, and Optical Properties of Alkyl Aminium Sulfate Aerosols, J. Phys. Chem. C, 117, 22412–22421, https://doi.org/10.1021/jp403180s, 2013.
Lee, A. K. Y., Zhao, R., Li, R., Liggio, J., Li, S.-M., and Abbatt, J. P. D.: Formation of Light Absorbing Organo-Nitrogen Species from Evaporation of Droplets Containing Glyoxal and Ammonium Sulfate, Environ. Sci. Technol., 47, 12819–12826, https://doi.org/10.1021/es402687w, 2013.
Lee, H. J., Aiona, P. K., Laskin, A., Laskin, J., and Nizkorodov, S. A.: Effect of Solar Radiation on the Optical Properties and Molecular Composition of Laboratory Proxies of Atmospheric Brown Carbon, Environ. Sci. Technol., 48, 10217–10226, https://doi.org/10.1021/es502515r, 2014.
Li, Y. Q., Davidovits, P., Shi, Q., Jayne, T., Kolb, C. E. and Worsnop, D. R.: Mass and thermal accommodation coefficients of H2O(g) on liquid water as a function of temperature, J. Phys. Chem. A, 105, 10632–10634, https://doi.org/10.1021/jp012758q, 2001.
Liu, P., Zhang, Y., and Martin, S. T.: Complex Refractive Indices of Thin Films of Secondary Organic Materials by Spectroscopic Ellipsometry from 220 to 1200 nm, Environ. Sci. Technol., 47, 13594–13601, https://doi.org/10.1021/es403411e, 2013.
Liu, S., Shilling, J. E., Song, C., Hiranuma, N., Zaveri, R. A., and Russell, L. M.: Hydrolysis of Organonitrate Functional Groups in Aerosol Particles, Aerosol Sci. Technol., 46, 1359–1369, https://doi.org/10.1080/02786826.2012.716175, 2012.
Lockerby, D. A., Reese, J. M., Emerson, D. R., and Barber, R. W.: Velocity boundary condition at solid walls in rarefied gas calculations, Phys. Rev. E, 70, 017303, https://doi.org/10.1103/PhysRevE.70.017303, 2004.
Loyalka, S. K.: Momentum and temperature-slip coefficients with arbitrary accommodation at the surface, J. Chem. Phys., 48, 5432–5436, https://doi.org/10.1063/1.1668235, 1968.
Mackowski, D. W.: Photophoresis of aerosol particles in the free molecular and slip-flow regimes, Int. J. Heat Mass Tran., 32, 843–854, https://doi.org/10.1016/0017-9310(89)90233-0, 1989.
Mackowski, D. W. and Mishchenko, M. I.: A multiple sphere T-matrix Fortran code for use on parallel computer clusters, J. Quant. Spectrosc. Ra., 112, 843–854, https://doi.org/10.1016/j.jqsrt.2011.02.019, 2011.
Marcos, M. A., Cabaleiro, D., Guimarey, M. J. G., Comuñas, M. J. P., Fedele, L., Fernández, J., and Lugo, L.: PEG 400-based phase change materials nano-enhanced with functionalized graphene nanoplatelets, Nanomaterials, 8, https://doi.org/10.3390/nano8010016, 2018.
Marrero-Ortiz, W., Hu, M., Du, Z., Ji, Y., Wang, Y., Guo, S., Lin, Y., Gomez-Hermandez, M., Peng, J., Li, Y., Secrest, J., Zamora, M. L., Wang, Y., An, T., and Zhang, R.: Formation and Optical Properties of Brown Carbon from Small α-Dicarbonyls and Amines, Environ. Sci. Technol., 53, 117–126, https://doi.org/10.1021/acs.est.8b03995, 2019.
Matzler, C.: Matlab codes foe mie scattering and absorption, Version 2, Research Report No. 2002-11, Institute of Applied Physics, University of Bern, Switzerland, 13, 125–128, 2002.
Moosmüller, H., Chakrabarty, R. K., Ehlers, K. M., and Arnott, W. P.: Absorption Ångström coefficient, brown carbon, and aerosols: basic concepts, bulk matter, and spherical particles, Atmos. Chem. Phys., 11, 1217–1225, https://doi.org/10.5194/acp-11-1217-2011, 2011.
Myhre, G., Samset, B. H., Schulz, M., Balkanski, Y., Bauer, S., Berntsen, T. K., Bian, H., Bellouin, N., Chin, M., Diehl, T., Easter, R. C., Feichter, J., Ghan, S. J., Hauglustaine, D., Iversen, T., Kinne, S., Kirkevåg, A., Lamarque, J.-F., Lin, G., Liu, X., Lund, M. T., Luo, G., Ma, X., van Noije, T., Penner, J. E., Rasch, P. J., Ruiz, A., Seland, Ø., Skeie, R. B., Stier, P., Takemura, T., Tsigaridis, K., Wang, P., Wang, Z., Xu, L., Yu, H., Yu, F., Yoon, J.-H., Zhang, K., Zhang, H., and Zhou, C.: Radiative forcing of the direct aerosol effect from AeroCom Phase II simulations, Atmos. Chem. Phys., 13, 1853–1877, https://doi.org/10.5194/acp-13-1853-2013, 2013.
Nakayama, T., Matsumi, Y., Sato, K., Imamura, T., Yamazaki, A., and Uchiyama, A.: Laboratory studies on optical properties of secondary organic aerosols generated during the photooxidation of toluene and the ozonolysis of α-pinene, J. Geophys. Res., 115, D24204, https://doi.org/10.1029/2010jd014387, 2010.
Nakayama, T., Sato, K., Matsumi, Y., Imamura, T., Yamazaki, A., and Uchiyama, A.: Wavelength and NOx dependent complex refractive index of SOAs generated from the photooxidation of toluene, Atmos. Chem. Phys., 13, 531–545, https://doi.org/10.5194/acp-13-531-2013, 2013.
Nguyen, T. B., Lee, P. B., Updyke, K. M., Bones, D. L., Laskin, J., Laskin, A., and Nizkorodov, S. A.: Formation of nitrogen- and sulfur-containing light-absorbing compounds accelerated by evaporation of water from secondary organic aerosols, J. Geophys. Res.-Atmos., 117, D01207, https://doi.org/10.1029/2011jd016944, 2012.
Nozière, B. and Córdova, A.: A Kinetic and Mechanistic Study of the Amino Acid Catalyzed Aldol Condensation of Acetaldehyde in Aqueous and Salt Solutions, J. Phys. Chem. A, 112, 2827–2837, https://doi.org/10.1021/jp7096845, 2008.
Nozière, B., Dziedzic, P., and Córdova, A.: Inorganic ammonium salts and carbonate salts are efficient catalysts for aldol condensation in atmospheric aerosols, Phys. Chem. Chem. Phys., 12, 3864–3872, https://doi.org/10.1039/B924443C, 2010.
Ofner, J., Krüger, H.-U., Grothe, H., Schmitt-Kopplin, P., Whitmore, K., and Zetzsch, C.: Physico-chemical characterization of SOA derived from catechol and guaiacol – a model substance for the aromatic fraction of atmospheric HULIS, Atmos. Chem. Phys., 11, 1–15, https://doi.org/10.5194/acp-11-1-2011, 2011.
Pope, M., Arnold, S., and Rozenshtein, L.: Photophoretic spectroscopy, Chem. Phys. Lett., 62, 589–591, https://doi.org/10.1016/0009-2614(79)80770-8, 1979.
Powelson, M. H., Espelien, B. M., Hawkins, L. N., Galloway, M. M., and De Haan, D. O.: Brown Carbon Formation by Aqueous-Phase Carbonyl Compound Reactions with Amines and Ammonium Sulfate, Environ. Sci. Technol., 48, 985–993, https://doi.org/10.1021/es4038325, 2014.
Preston, T. C. and Reid, J. P.: Accurate and efficient determination of the radius, refractive index, and dispersion of weakly absorbing spherical particle using whispering gallery modes, J. Opt. Soc. Am. B, 30, 2113, https://doi.org/10.1364/josab.30.002113, 2013.
Preston, T. C. and Reid, J. P.: Determining the size and refractive index of microspheres using the mode assignments from Mie resonances, J. Opt. Soc. Am. A, 32, 2210, https://doi.org/10.1364/josaa.32.002210, 2015.
Reed, L. D.: Low Knudsen number photophoresis, J. Aerosol Sci., 8, 123–131, https://doi.org/10.1016/0021-8502(77)90073-8, 1977.
Reyes, C. A., Medina, M., Crespo-Hernandez, C., Cedeno, M. Z., Arce, R., Rosario, O., Steffenson, D. M., Ivanov, I. N., Sigman, M. E., and Dabestani, R.: Photochemistry of pyrene on unactivated and activated silica surfaces, Environ. Sci. Technol., 34, 415–421, https://doi.org/10.1021/es9905391, 2000.
Rohatschek, H.: Semi-empirical model of photophoretic forces for the entire range of pressures, J. Aerosol Sci., 26, 717–734, https://doi.org/10.1016/0021-8502(95)00011-Z, 1995.
Romonosky, D. E., Laskin, A., Laskin, J., and Nizkorodov, S. A.: High-Resolution Mass Spectrometry and Molecular Characterization of Aqueous Photochemistry Products of Common Types of Secondary Organic Aerosols, J. Phys. Chem. A, 119, 2594–2606, https://doi.org/10.1021/jp509476r, 2015.
Saleh, R., Robinson, E. S., Tkacik, D. S., Ahern, A. T., Liu, S., Aiken, A. C., Sullivan, R. C., Presto, A. A., Dubey, M. K., Yokelson, R. J., Donahue, N. M., and Robinson, A. L.: Brownness of organics in aerosols from biomass burning linked to their black carbon content, Nat. Geosci., 7, 647–650, https://doi.org/10.1038/NGEO2220, 2014.
Schnitzler, E. G. and Abbatt, J. P. D.: Heterogeneous OH oxidation of secondary brown carbon aerosol, Atmos. Chem. Phys., 18, 14539–14553, https://doi.org/10.5194/acp-18-14539-2018, 2018.
Shaw, R. A. and Lamb, D.: Experimental determination of the thermal accommodation and condensation coefficients of water, J. Chem. Phys., 111, 10659–10663, https://doi.org/10.1063/1.480419, 1999.
Soong C.-Y., Li, W.-K., Liu, C.-H., and Tzeng, P.-Y.: Effect of thermal stress slip on microparticle photophoresis in gaseous media, Opt. Lett., 35, 625–627, https://doi.org/10.1364/ol.35.000625, 2010.
Steimer, S. S., Krieger, U. K., Te, Y.-F., Lienhard, D. M., Huisman, A. J., Luo, B. P., Ammann, M., and Peter, T.: Electrodynamic balance measurements of thermodynamic, kinetic, and optical aerosol properties inaccessible to bulk methods, Atmos. Meas. Tech., 8, 2397–2408, https://doi.org/10.5194/amt-8-2397-2015, 2015.
Sun, H. L., Biedermann, L., and Bond, T. C.: Color of brown carbon: A model for ultraviolet and visible light absorption by organic carbon aerosol, Geophys. Res. Lett., 34, L17813, https://doi.org/10.1029/2007gl029797, 2007.
Tang, I. N. and Munkelwitz, H. R.: Water activities, densities, and refractive indices of aqueous sulfates and sodium nitrate droplets of atmospheric importance, J. Geophys. Res.-Atmos., 99, 18801–18808, https://doi.org/10.1029/94jd01345, 1994.
Trainic, M., Abo Riziq, A., Lavi, A., Flores, J. M., and Rudich, Y.: The optical, physical and chemical properties of the products of glyoxal uptake on ammonium sulfate seed aerosols, Atmos. Chem. Phys., 11, 9697–9707, https://doi.org/10.5194/acp-11-9697-2011, 2011.
Trott, W. M., Rader, D. J., Castañeda, J. N., Torczynski, J. R., and Gallis, M. A.: Experimental measurements of thermal accommodation coefficients for microscale gas-phase heat transfer, in: Collection of Technical Papers – 39th AIAA Thermophysics Conference, 25–28 June 2007, Miami, Florida, 1, 233–244, 2007.
Updyke, K. M., Nguyen, T. B., and Nizkorodov, S. A.: Formation of brown carbon via reactions of ammonia with secondary organic aerosols from biogenic and anthropogenic precursors, Atmos. Environ., 63, 22–31, https://doi.org/10.1016/j.atmosenv.2012.09.012, 2012.
Washenfelder, R. A., Flores, J. M., Brock, C. A., Brown, S. S., and Rudich, Y.: Broadband measurements of aerosol extinction in the ultraviolet spectral region, Atmos. Meas. Tech., 6, 861–877, https://doi.org/10.5194/amt-6-861-2013, 2013.
Yalamov, Y. I., Kutukov, V. B., and Shchukin, E. R.: Theory of the photophoretic motion of the large-size volatile aerosol particle, J. Colloid Interf. Sci., 57, 564–571, https://doi.org/10.1016/0021-9797(76)90234-4, 1976.
Zardini, A. A., Sjogren, S., Marcolli, C., Krieger, U. K., Gysel, M., Weingartner, E., Baltensperger, U., and Peter, T.: A combined particle trap/HTDMA hygroscopicity study of mixed inorganic/organic aerosol particles, Atmos. Chem. Phys., 8, 5589–5601, https://doi.org/10.5194/acp-8-5589-2008, 2008.
Zhang, Q., Jimenez, J. L., Canagaratna, M. R., Allan, J. D., Coe, H., Ulbrich, I., Alfarra, M. R., Takami, A., Middlebrook, A. M., Sun, Y. L., Dzepina, K., Dunlea, E., Docherty, K., DeCarlo, P. F., Salcedo, D., Onasch, T., Jayne, J. T., Miyoshi, T., Shimono, A., Hatakeyama, S., Takegawa, N., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Williams, P., Bower, K., Bahreini, R., Cottrell, L., Griffin, R. J., Rautiainen, J., Sun, J. Y., Zhang, Y. M., and Worsnop, D. R.: Ubiquity and dominance of oxygenated species in organic aerosols in anthropogenically-influenced Northern Hemisphere midlatitudes, Geophys. Res. Lett., 34, L1380, https://doi.org/10.1029/2007gl029979, 2007.
Zhao, R., Lee, A. K. Y., Huang, L., Li, X., Yang, F., and Abbatt, J. P. D.: Photochemical processing of aqueous atmospheric brown carbon, Atmos. Chem. Phys., 15, 6087–6100, https://doi.org/10.5194/acp-15-6087-2015, 2015.
Zheng, G., He, K., Duan, F., Cheng, Y., and Ma, Y.: Measurement of humic-like substances in aerosols: A review, Environ. Pollut., 181, 301–314, https://doi.org/10.1016/j.envpol.2013.05.055, 2013.





